Anthropic Principle and the Hubble-Lemaître Constant
Abstract
:1. Introduction
2. Local Hubble Expansion
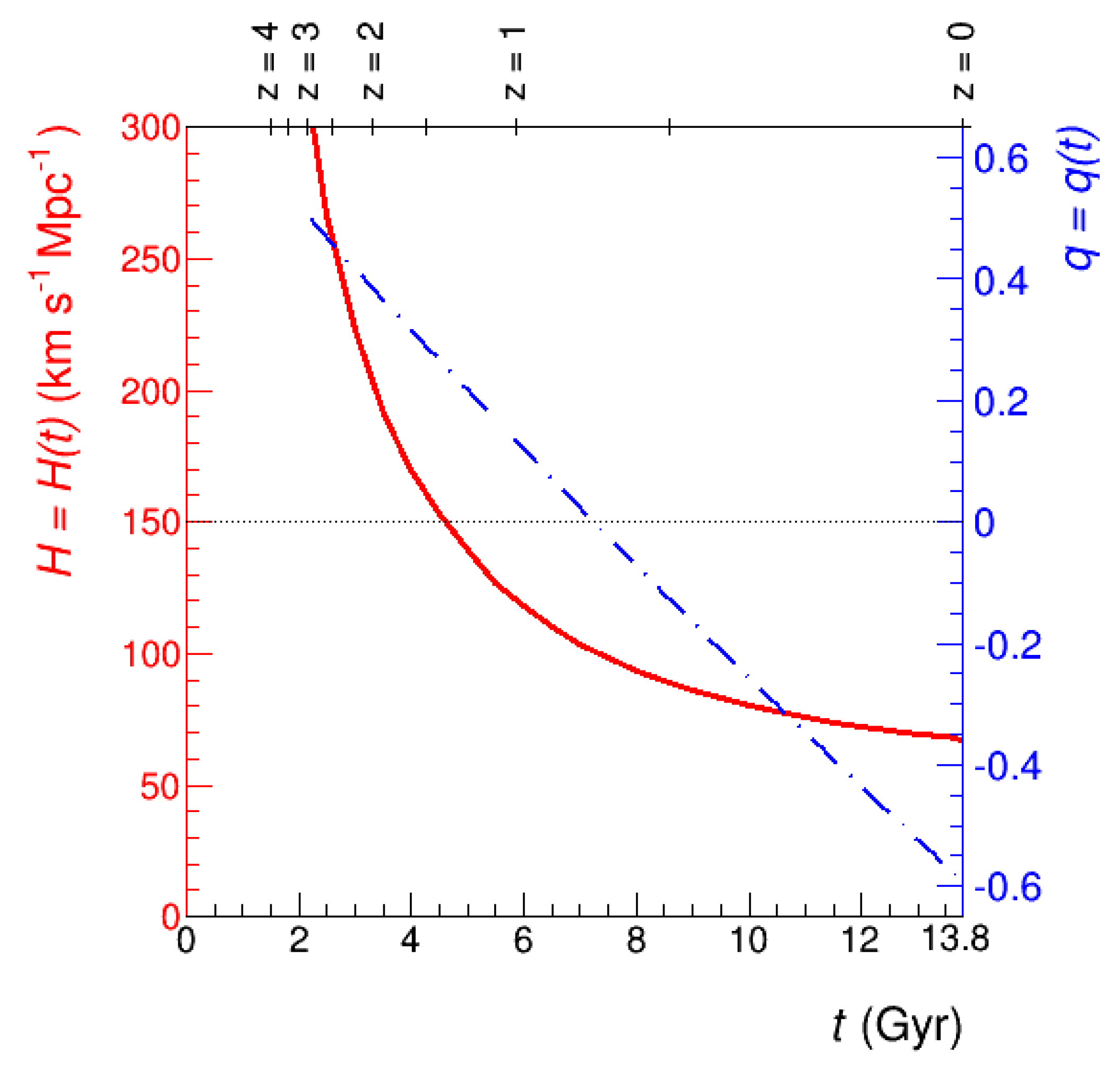
3. Hubble Parameter
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Note
| 1 | We can always choose physical units so that , , , etc., instead of the standard SI units. |
References
- Křížek, M.; Křížek, F.; Somer, L. Antigravity—Its Origin and Manifestations; Lambert Academic Publishing: Saarbrücken, Germany, 2015. [Google Scholar]
- Křížek, M.; Somer, L. Anthropic principle and the local Hubble expansion. In Proceedings of the Cosmology on Small Scales 2016, Prague, Czech RepublicK, 21–24 September 2016; pp. 65–94. [Google Scholar]
- Novotný, V. Cosmological coincidences in the expanding universe. In Proceedings of the International Conference Cosmology on Small Scales 2020, Prague, Czech Republic, 23–26 September 2020; pp. 111–120. [Google Scholar]
- Křížek, M.; Křížek, P. Why has nature invented three stop codons of DNA and only one start codon? J. Theor. Biol. 2012, 304, 183–187. [Google Scholar] [CrossRef] [PubMed]
- Watson, J.D.; Crick, F.H.C. Genetic implications of the structure of deoxyribonucleic acid. Nature 1953, 171, 964–969. [Google Scholar] [CrossRef] [PubMed]
- Barrow, J.D.; Tipler, F.J. The Anthropic Cosmological Principle; Oxford Univeristy Press: Oxford, UK, 1986. [Google Scholar]
- Carr, B.J.; Rees, M.J. The anthropic principle and the structure of the physical world. Nature 1979, 278, 605–612. [Google Scholar] [CrossRef]
- Carter, B. The significance of numerical coincidences in nature, Part I, Line by line transcript of the stenciled preprint issued in 1967. arXiv 1967, arXiv:0710.3543. [Google Scholar]
- Carter, B. Large number coincidences and the Anthropic Principle in cosmology. In Proceedings of the IAU Symposium 63, Confrontation of Cosmological Theories with Observational Data, Heidelberg, Germany, 26–30 June 1995; pp. 291–298. [Google Scholar]
- Karachentsev, I.D.; Karachentseva, V.E.; Huchtmeier, W.K.; Makarov, D.I. A catalog of neighboring galaxies. Astrophys. J. 2004, 127, 2031–2068. [Google Scholar] [CrossRef]
- Fahr, H.J.; Heyl, M. Structure formation after the era of cosmic matter recombination. Adv. Theor. Comput. Phys. 2021, 4, 253–258. [Google Scholar]
- Martínez-Lombilla, C.; Trujillo, I.; Knapen, J.H. Discovery of disc truncations above the galaxies’ mid-plane in Milky Way-like galaxies. Mon. Not. R. Astron. Soc. 2019, 483, 664–691. [Google Scholar] [CrossRef] [Green Version]
- Buitrago, F.; Conselice, C.J.; Epinat, B.; Bedregal, A.G.; Trujillo, I.; Grützbauch, R. Shaping massive galaxies: Their morphology and kinematics at z = 1–3. In Proceedings of the Highlights of Spanish Astrophysics VI, Proceedings of the IX Scientific Meeting of the Spanish Astronomical Society, Madrid, Spain, 13–17 September 2010; pp. 154–160. [Google Scholar]
- Rudnick, G.; Labbé, I.; Schreiber, N.M.F.; Wuyts, S.; Franx, M.; Finlator, K.; Kriek, M.; Moorwood, A.; Rix, H.-W.; Röttgering, H.; et al. Measuring the average evolution of luminous galaxies at z < 3: The rest-frame optical luminosity density, spectral energy distribution, and stellar mass density. Astrophys. J. 2006, 650, 624–643. [Google Scholar]
- Trujillo, I.; Conselice, C.J.; Bundy, K.; Cooper, M.C.; Eisenhardt, P.; Ellis, R.S. Strong size evolution of the most massive galaxies since z ∼ 2. Mon. Not. R. Astron. Soc. 2007, 382, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Carrera, M.; Giulini, D. Influence of global cosmological expansion on local dynamics and kinematics. Rev. Mod. Phys. 2010, 82, 169–208. [Google Scholar] [CrossRef]
- Cooperstock, F.I.; Faraoni, V.; Vollick, D.N. The influence of the cosmological expansion on local systems. Astrophys. J. 1998, 503, 61–66. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E. Measurements of Omega and Lambda from 42 high-redshift supernovae. Astrophys. J. 1997, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astrophys. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Křížek, M. Dark energy and the anthropic principle. New Astron. 2012, 17, 1–7. [Google Scholar] [CrossRef]
- Kump, L.R.; Kastings, J.F.; Crane, R.G. The Earth System; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Tegmark, M. Life 3.0: Being Human in the Age of Artificial Intelligence; Alfred A. Knopf: New York, NY, USA, 2017. [Google Scholar]
- Zhang, W.J.; Li, Z.B.; Lei, Y. Experimental measurements of growth patterns on fossil corals: Secular variation in ancient Earth-Sun distance. Chin. Sci. Bull. 2010, 55, 4010–4017. [Google Scholar] [CrossRef]
- Dickey, J.O.; Bender, P.L.; Faller, J.E.; Newhall, X.X.; Ricklefs, R.L.; Ries, J.G.; Shelus, P.J.; Veillet, C.; Whipple, A.L.; Yoder, C.F.; et al. Lunar laser ranging: A continuing legacy of the Apollo program. Science 1994, 265, 482–490. [Google Scholar] [CrossRef] [Green Version]
- Křížek, M. Does a gravitational aberration contribute to the accelerated expansion of the Universe? Commun. Comput. Phys. 2009, 5, 1030–1044. [Google Scholar]
- Dumin, Y.V. A new application of the Lunar laser retroreflectors: Searching for the “local” Hubble expansion. Adv. Space Res. 2003, 31, 2461–2466. [Google Scholar] [CrossRef] [Green Version]
- Dumin, Y.V. The faint young Sun paradox in the context of modern cosmology. Astron. Tsirkulyar 2015, 1623, 1–5. [Google Scholar]
- Dumin, Y.V. Local Hubble expansion: Current state of the problem. In Proceedings of the International Conference Cosmology on Small Scales 2016, Local Hubble Expansion and Selected Controversies in Cosmology, Prague, Czech Republic, 21–24 September 2016; pp. 23–40. [Google Scholar]
- Maeder, A.M.; Gueorguiev, V.G. On the relation of the lunar recession and the length-of-the-day. Astrophys. Space Sci. 2021, 366, 101. [Google Scholar] [CrossRef]
- Maeder, A.; Bouvier, P. Scale invariance, metrical connection and the motions of astronomical bodies. Astron. Astrophys. 1979, 73, 82–89. [Google Scholar]
- Manning, R.; Simon, W.L. Mars Rover Curiosity; Smithsonian Books: Washington, DC, USA, 2014. [Google Scholar]
- Bristow, T.F.; Haeberle, R.M.; Blake, D.F.; Des Marais, D.J.; Eigenbrode, J.L.; Fairén, A.G.; Grotzinger, J.P.; Stack, K.M.; Mischna, M.A.; Rampe, E.B.; et al. Low Hesperian PCO2 constraints from in situ mineralogical analysis of Gale Crater, Mars. Proc. Nat. Acad. Sci. USA 2017, 114, 2166–2170. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donn, W.L.; Donn, B.D.; Valentine, W.G. On the early history of the earth. Bull. Geol. Soc. Am. 1965, 76, 287–306. [Google Scholar] [CrossRef]
- Lang, K.K. Cambridge Encyclopedia of the Sun; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Lainey, V.; Casajus, L.G.; Fuller, J.; Zannoni, M.; Tortora, P.; Cooper, N.; Murray, C.; Modenini, D.; Park, R.S.; Zhang, Q. Resonance locking in giant planets indicated by the rapid orbital expansion of Titan. Nat. Astron. 2020, 4, 1053–1058. [Google Scholar] [CrossRef]
- Křížek, M.; Gueorguiev, V.G.; Maeder, A. An alternative explanation of the orbital expansion of Titan. Gravit. Cosmol. 2022, 28, 122–132. [Google Scholar]
- Neveu, M.; Rhoden, A.R. Evolution of Saturn’s mid-sized moons. Nat. Astron. 2019, 3, 543–552. [Google Scholar] [CrossRef]
- Maeder, A. An alternative to the ΛCDM model: The case of scale invariance. Astrophys. J. 2017, 834, 194–209. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Gabi, S.; Goldhaber, G.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pain, R.; et al. Measurements of the cosmological parameters Ω and Λ from the first seven supernovae at z ≥ 0.35. Astrophys. J. 1997, 483, 565–581. [Google Scholar] [CrossRef] [Green Version]
- Vavryčuk, V. Universe opacity and Type Ia supernova dimming. Mon. Not. R. Astron. Soc. 2019, 489, L63–L68. [Google Scholar] [CrossRef]
- Vavryčuk, V.; Kroupa, P. The failure of testing for cosmic opacity via the distance-duality relation. Mon. Not. R. Astron. Soc. 2020, 497, 378–388. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.-G.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Gold, B.; Challis, P.J.; Filippenko, A.V.; Jha, S.; Li, W.; et al. New Hubble space telescope discoveries of Type Ia supernova at z ≥ 1: Narrowing constraints on the early behavior of dark energy. Astrophys. J. 2007, 659, 98–121. [Google Scholar] [CrossRef] [Green Version]
- McVittie, C.G. The mass-particle in expanding universe. Mon. Not. R. Astron. Soc. 1933, 93, 325–339. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A.; Straus, E.G. The influence of the expansion of space on the gravitation fields surrounding individual stars. Rev. Mod. Phys. 1945, 17, 120–124, Correction in Rev. Mod. Phys. 1946, 18, 148–149. [Google Scholar] [CrossRef]
- Fahr, H.J.; Siewert, M. Imprints from the global cosmological expansion to the local space-time dynamics. Naturwissenschaften 2008, 95, 413–425. [Google Scholar] [CrossRef]
- Křížek, M.; Somer, L. Manifestations of dark energy in the Solar system. Gravit. Cosmol. 2015, 21, 58–71. [Google Scholar] [CrossRef]
- Křížek, M.; Somer, L. Excessive extrapolations in cosmology. Gravit. Cosmol. 2016, 22, 270–280. [Google Scholar] [CrossRef]
- Peacock, J.A. Cosmological Physics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Mashhoon, B.; Mobed, N.; Singh, D. Tidal dynamics in cosmological spacetimes. Class. Quant. Grav. 2007, 24, 5031–5046. [Google Scholar] [CrossRef] [Green Version]
- Krasinski, G.A.; Brumberg, V.A. Secular increase of astronomical unit from analysis of the major planet motions, and its interpretation. Celest. Mech. Dyn. Astr. 2004, 90, 267–288. [Google Scholar] [CrossRef]
- Poincaré, H. Sur la dynamique de l’électron. C. R. Acad. Sci. Paris 1905, 140, 1504–1508. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger observation of a binary neutron star merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Carlip, S. Aberration and the speed of gravity. Phys. Lett. A 2000, 267, 81–87. [Google Scholar] [CrossRef] [Green Version]
- Křížek, M.; Somer, L. Why masses of binary black hole mergers are overestimated? Galaxies 2022, 10, 52. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. Cosmological constraints from the Hubble diagram of quasars at high redshifts. Nat. Astron. 2019, 3, 272–277. [Google Scholar] [CrossRef] [Green Version]
- Obreschkow, D. (Ed.) Galactic angular momentum. In Proceedings of the XXXth IAU General Assembly, Focus Meeting, Vienna, Austria, 20–31 August 2018. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Křížek, M.; Somer, L. Anthropic Principle and the Hubble-Lemaître Constant. Galaxies 2022, 10, 71. https://doi.org/10.3390/galaxies10030071
Křížek M, Somer L. Anthropic Principle and the Hubble-Lemaître Constant. Galaxies. 2022; 10(3):71. https://doi.org/10.3390/galaxies10030071
Chicago/Turabian StyleKřížek, Michal, and Lawrence Somer. 2022. "Anthropic Principle and the Hubble-Lemaître Constant" Galaxies 10, no. 3: 71. https://doi.org/10.3390/galaxies10030071
APA StyleKřížek, M., & Somer, L. (2022). Anthropic Principle and the Hubble-Lemaître Constant. Galaxies, 10(3), 71. https://doi.org/10.3390/galaxies10030071




