The Basics of Primordial Black Hole Formation and Abundance Estimation
Abstract
1. Introduction
2. PBH Formation Process: Three-Zone Model
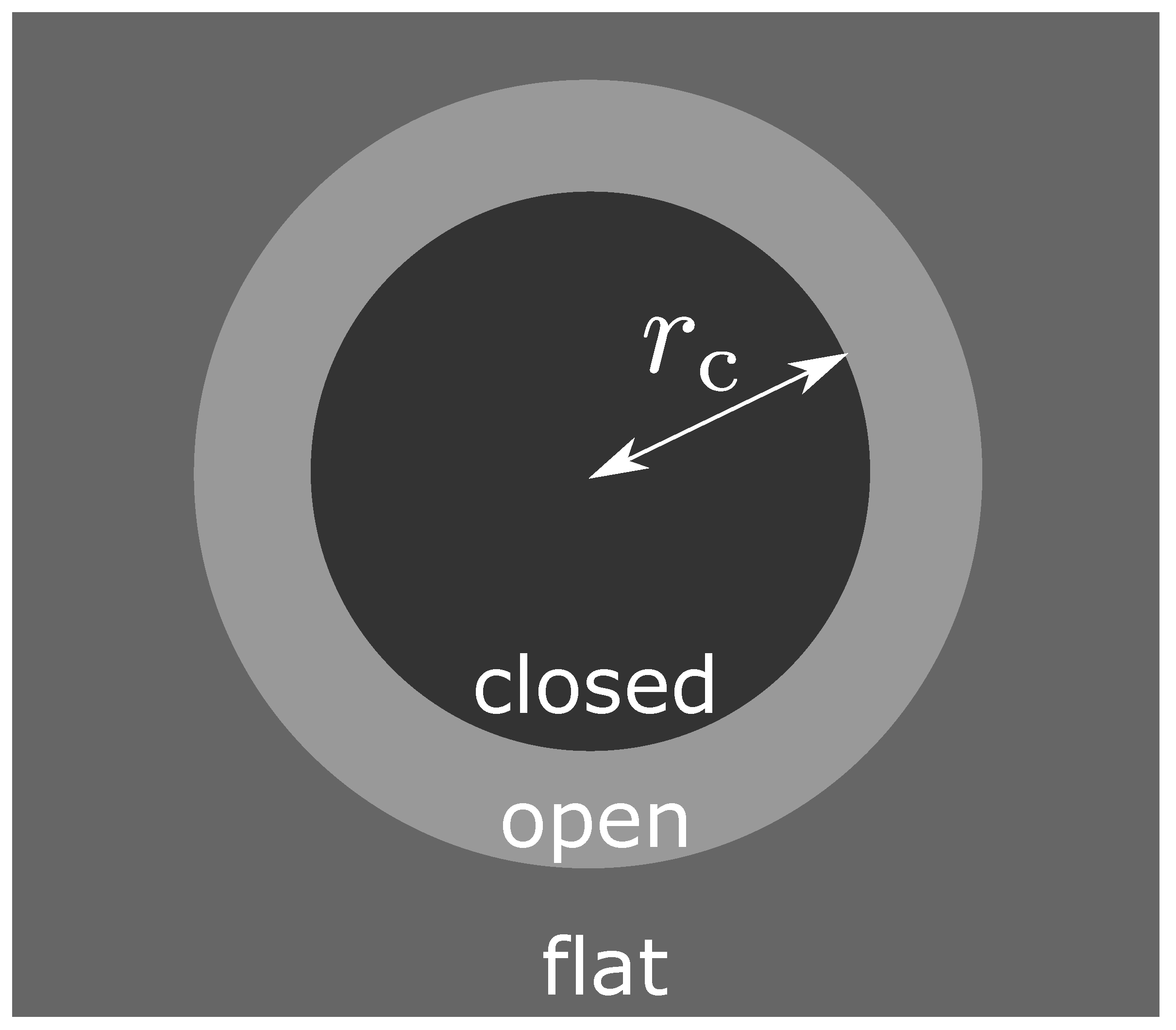
2.1. FLRW Models
2.2. Background Flat FLRW
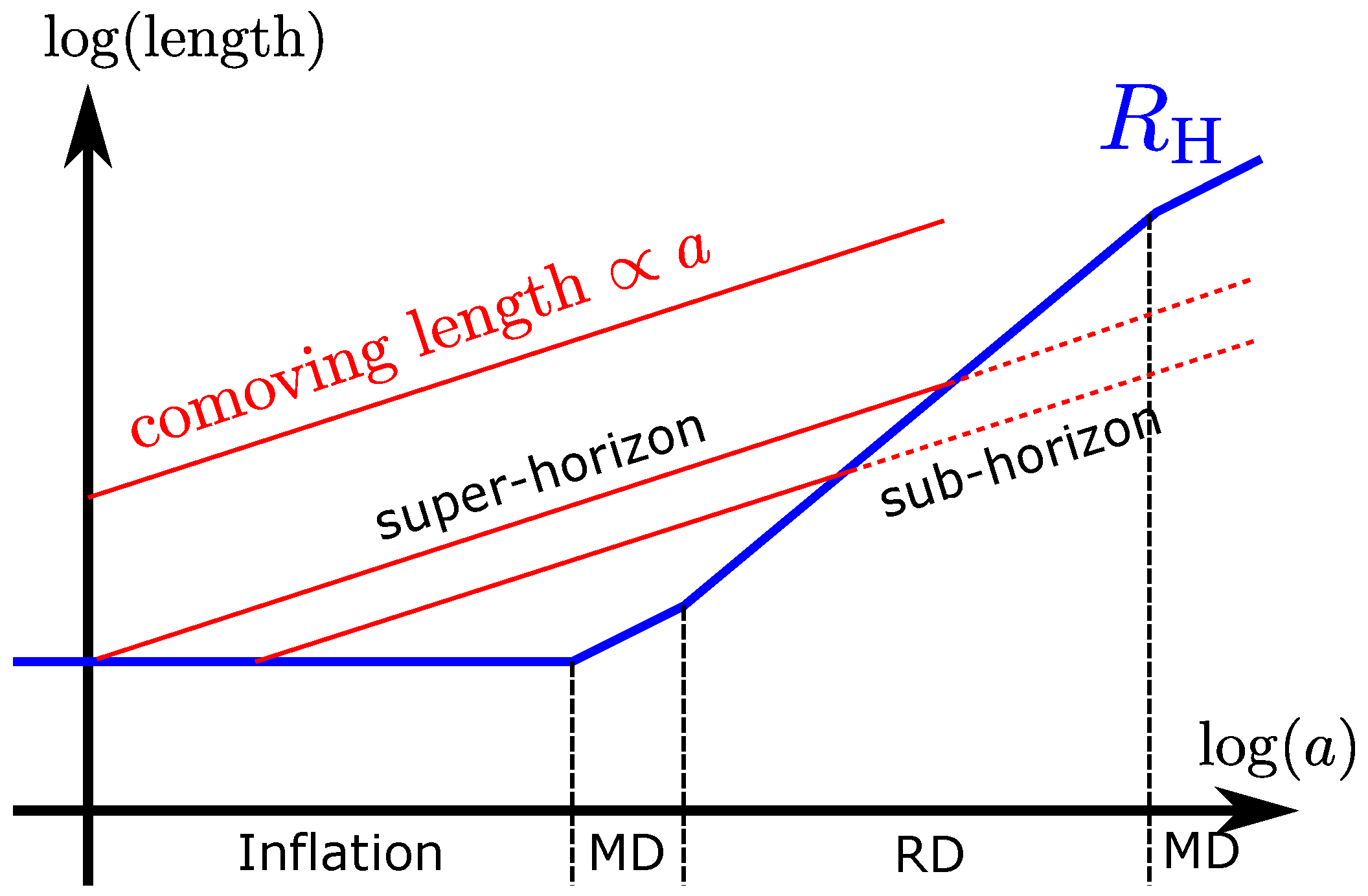
2.3. Super-Horizon Inhomogeneity
2.4. Three-Zone Model
2.5. Jeans Criterion
2.6. Refinement of the Threshold
3. Cosmological Long-Wavelength Solutions
3.1. Cosmological 3 + 1 Decomposition
3.2. Gradient Expansion
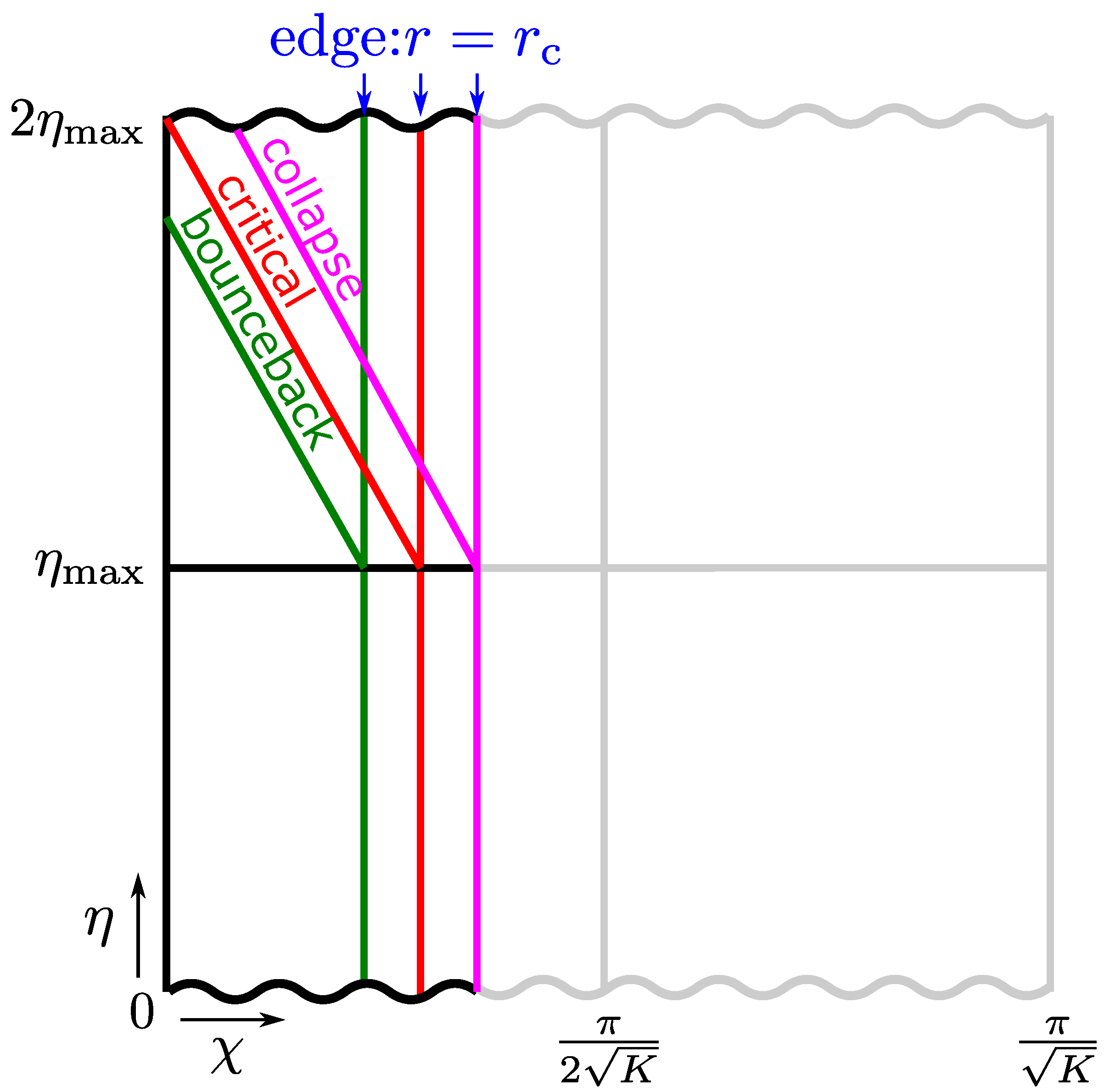
4. PBH Formation Criterion
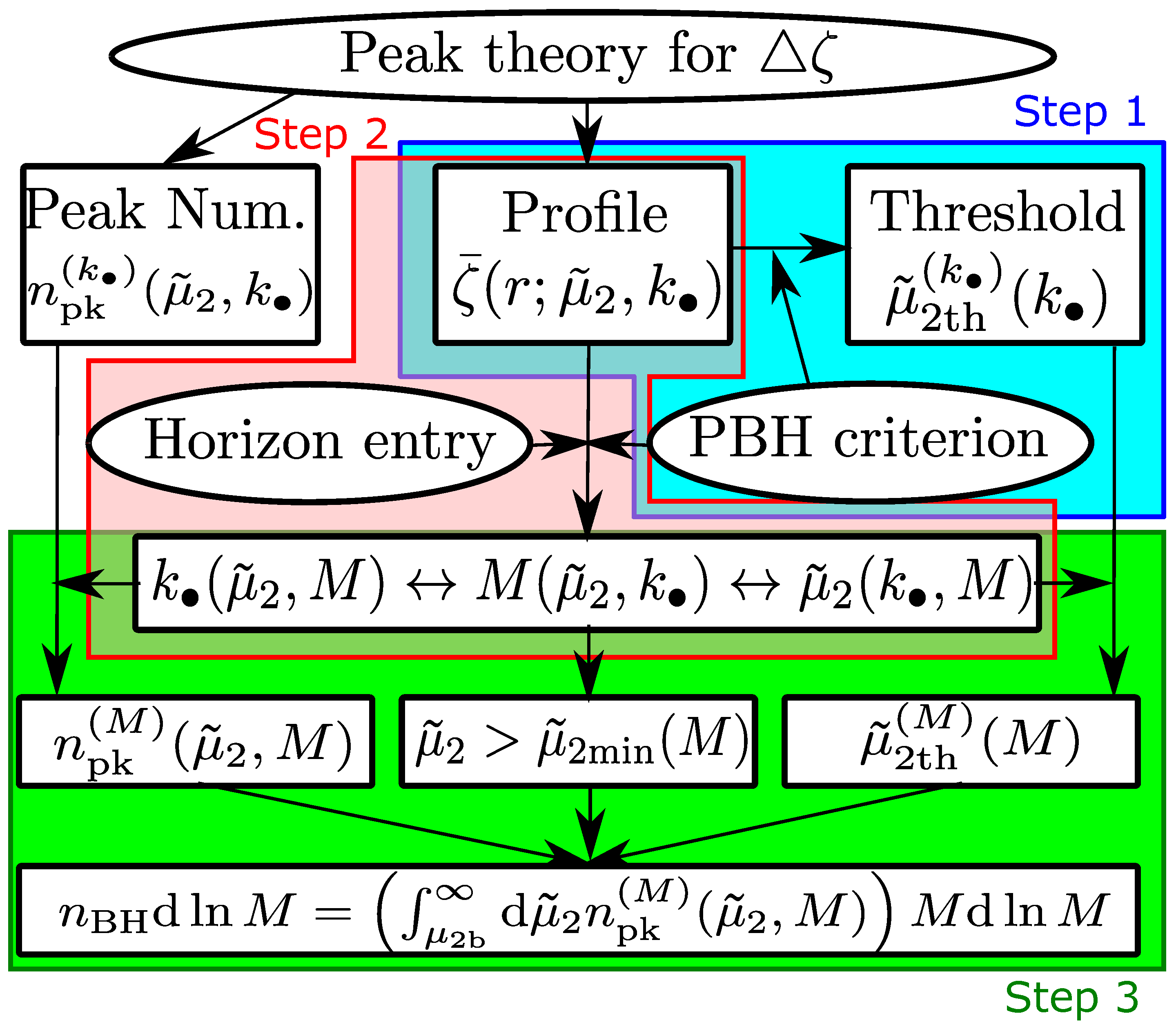
5. Estimation of PBH Abundance in Peak Theory
5.1. Step 1: Rewriting the Criterion
5.2. Step 2: Derivation of the PBH Mass Expression
5.3. Step 3: Derivation of the Mass Function
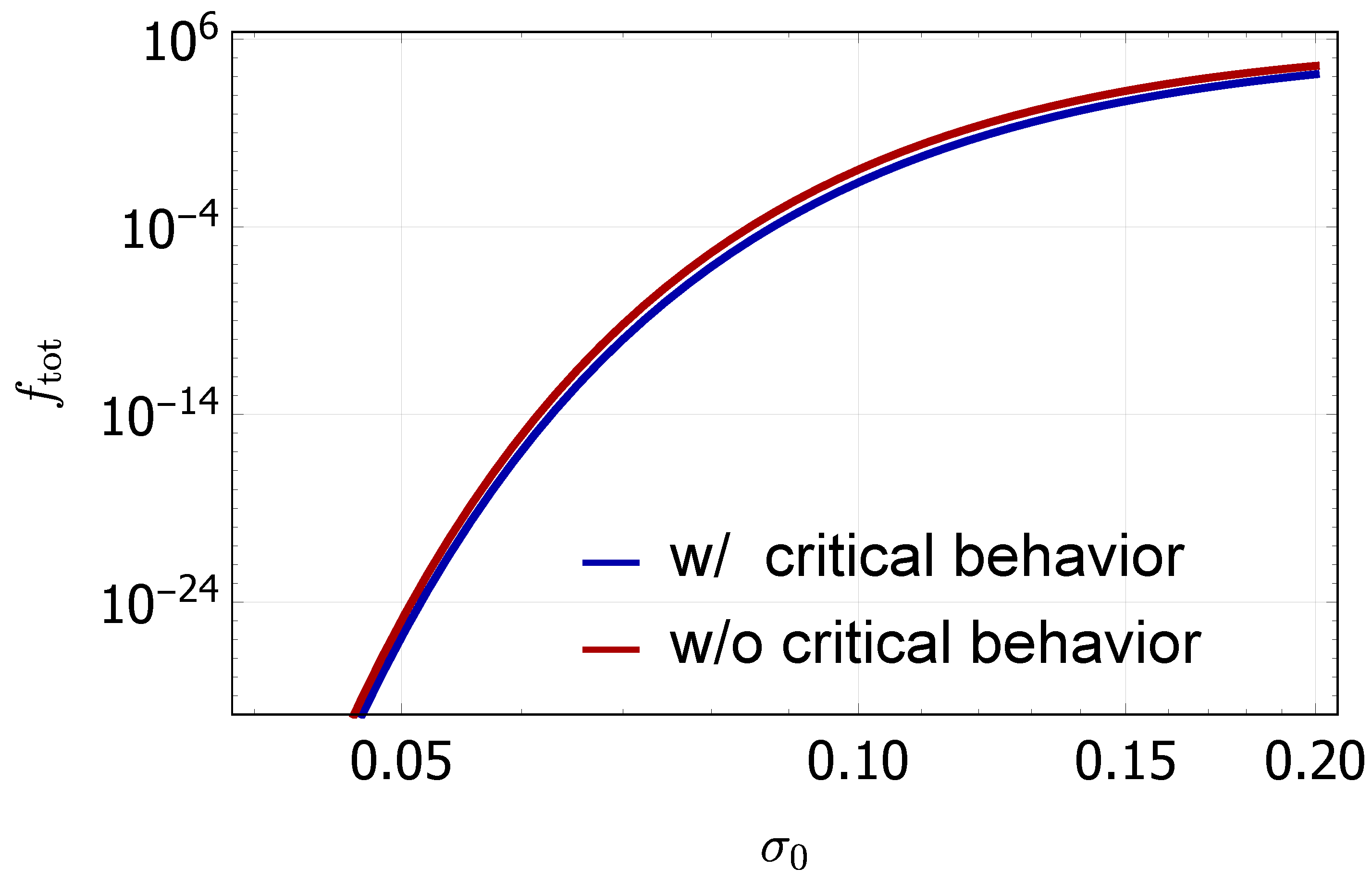
5.4. Critical Behavior
5.5. The Monochromatic Curvature Power Spectrum
6. Summary and Further Related Topics
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Horizon and Mass
Appendix B. Peak Number Density in Peak Theory
Appendix C. Typical Profile in Peak Theory
Appendix D. Equations for Peaks of Δζ
| 1 | The under-dense region is necessary for the dust case to be an exact solution. |
| 2 | We choose the sign convention so that the spatial metric will be given by . |
| 3 | In Refs. [28,34], the second term in the integrand of Equation (77) has been erroneously dropped, and the authors got the wrong relation . The original definition of given in Equation (74) would have been provided based on this wrong calculation neglecting the difference between the CMC and comoving slice conditions. |
| 4 |
References
- Zel’dovich, Y.B.; Novikov, I.D. The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model. Soviet Ast. 1967, 10, 602. [Google Scholar]
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. R. Astron. Soc. 1971, 152, 75–78. [Google Scholar] [CrossRef]
- Carr, B.J.; Hawking, S. Black holes in the early Universe. Mon. Not. R. Astron. Soc. 1974, 168, 399–415. [Google Scholar] [CrossRef]
- Carr, B.J.; Kohri, K.; Sendouda, Y.; Yokoyama, J. New cosmological constraints on primordial black holes. Phys. Rev. D 2010, 81, 104019. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on Primordial Black Holes. arXiv 2020, arXiv:2002.12778. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F. Primordial Black Holes as Dark Matter: Recent Developments. arXiv 2020, arXiv:2006.02838. [Google Scholar] [CrossRef]
- Bird, S.; Cholis, I.; Muñoz, J.B.; Ali-Haïmoud, Y.; Kamionkowski, M.; Kovetz, E.D.; Raccanelli, A.; Riess, A.G. Did LIGO detect dark matter? Phys. Rev. Lett. 2016, 116, 201301. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914. Phys. Rev. Lett. 2016, 117, 061101. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. Seven Hints for Primordial Black Hole Dark Matter. arXiv 2017, arXiv:1711.10458. [Google Scholar]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial black holes-perspectives in gravitational wave astronomy. Class. Quantum Gravity 2018, 35, 063001. [Google Scholar] [CrossRef]
- Niikura, H.; Takada, M.; Yokoyama, S.; Sumi, T.; Masaki, S. Constraints on Earth-mass primordial black holes from OGLE 5-year microlensing events. Phys. Rev. D 2019, 99, 083503. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Chatterjee, S.; Chen, S.; Cordes, J.M.; et al. The NANOGrav 12.5 yr Data Set: Search for an Isotropic Stochastic Gravitational-wave Background. Astrophys. J. Lett. 2020, 905, L34. [Google Scholar] [CrossRef]
- Vaskonen, V.; Veermäe, H. Did NANOGrav see a signal from primordial black hole formation? Phys. Rev. Lett. 2021, 126, 051303. [Google Scholar] [CrossRef] [PubMed]
- De Luca, V.; Franciolini, G.; Riotto, A. NANOGrav Data Hints at Primordial Black Holes as Dark Matter. Phys. Rev. Lett. 2021, 126, 041303. [Google Scholar] [CrossRef] [PubMed]
- Kohri, K.; Terada, T. Solar-Mass Primordial Black Holes Explain NANOGrav Hint of Gravitational Waves. Phys. Lett. B 2021, 813, 136040. [Google Scholar] [CrossRef]
- Sugiyama, S.; Takhistov, V.; Vitagliano, E.; Kusenko, A.; Sasaki, M.; Takada, M. Testing Stochastic Gravitational Wave Signals from Primordial Black Holes with Optical Telescopes. Phys. Lett. B 2021, 814, 136097. [Google Scholar] [CrossRef]
- Domènech, G.; Pi, S. NANOGrav hints on planet-mass primordial black holes. Sci. China Phys. Mech. Astron. 2022, 65, 230411. [Google Scholar] [CrossRef]
- Inomata, K.; Kawasaki, M.; Mukaida, K.; Yanagida, T. NANOGrav Results and LIGO-Virgo Primordial Black Holes in Axionlike Curvaton Models. Phys. Rev. Lett. 2021, 126, 131301. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kusenko, A.; Yanagida, T. Primordial seeds of supermassive black holes. Phys. Lett. B 2012, 711, 1–5. [Google Scholar] [CrossRef]
- Kohri, K.; Nakama, T.; Suyama, T. Testing scenarios of primordial black holes being the seeds of supermassive black holes by ultracompact minihalos and CMB μ-distortions. Phys. Rev. D 2014, 90, 083514. [Google Scholar] [CrossRef]
- Nakama, T.; Suyama, T.; Yokoyama, J. Supermassive black holes formed by direct collapse of inflationary perturbations. Phys. Rev. D 2016, 94, 103522. [Google Scholar] [CrossRef]
- Carr, B.; Silk, J. Primordial Black Holes as Generators of Cosmic Structures. Mon. Not. R. Astron. Soc. 2018, 478, 3756. [Google Scholar] [CrossRef]
- Serpico, P.D.; Poulin, V.; Inman, D.; Kohri, K. Cosmic microwave background bounds on primordial black holes including dark matter halo accretion. Phys. Rev. Res. 2020, 2, 023204. [Google Scholar] [CrossRef]
- Ünal, C.; Kovetz, E.D.; Patil, S. Multimessenger probes of inflationary fluctuations and primordial black holes. Phys. Rev. D 2021, 103, 063519. [Google Scholar] [CrossRef]
- Kohri, K.; Sekiguchi, T.; Wang, S. Cosmological 21-cm line observations to test scenarios of super-Eddington accretion on to black holes being seeds of high-redshifted supermassive black holes. Phys. Rev. D 2022, 106, 043539. [Google Scholar] [CrossRef]
- Niemeyer, J.C.; Jedamzik, K. Near-critical gravitational collapse and the initial mass function of primordial black holes. Phys. Rev. Lett. 1998, 80, 5481. [Google Scholar] [CrossRef]
- Niemeyer, J.C.; Jedamzik, K. Dynamics of primordial black hole formation. Phys. Rev. D 1999, 59, 124013. [Google Scholar] [CrossRef]
- Shibata, M.; Sasaki, M. Black hole formation in the Friedmann universe: Formulation and computation in numerical relativity. Phys. Rev. D 1999, 60, 084002. [Google Scholar] [CrossRef]
- Hawke, I.; Stewart, J. The dynamics of primordial black-hole formation. Class. Quantum Gravity 2002, 19, 3687. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C.; Rezzolla, L. Computations of primordial black hole formation. Class. Quantum Gravity 2005, 22, 1405. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.-M.; Kohri, K. Threshold of primordial black hole formation. Phys. Rev. 2013, D88, 084051, Erratum in Phys. Rev. 2014, D89, 029903. [Google Scholar] [CrossRef]
- Nakama, T.; Harada, T.; Polnarev, A.G.; Yokoyama, J. Identifying the most crucial parameters of the initial curvature profile for primordial black hole formation. JCAP 2014, 1401, 037. [Google Scholar] [CrossRef]
- Nakama, T. The double formation of primordial black holes. JCAP 2014, 1410, 040. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.-M.; Nakama, T.; Koga, Y. Cosmological long-wavelength solutions and primordial black hole formation. Phys. Rev. D 2015, 91, 084057. [Google Scholar] [CrossRef]
- Musco, I. Threshold for primordial black holes: Dependence on the shape of the cosmological perturbations. Phys. Rev. D 2019, 100, 123524. [Google Scholar] [CrossRef]
- Escrivà, A. Simulation of primordial black hole formation using pseudo-spectral methods. Phys. Dark Univ. 2020, 27, 100466. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R. Universal threshold for primordial black hole formation. Phys. Rev. D 2020, 101, 044022. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Analytical thresholds for black hole formation in general cosmological backgrounds. arXiv 2020, arXiv:2007.05564. [Google Scholar] [CrossRef]
- Escrivà, A. PBH Formation from Spherically Symmetric Hydrodynamical Perturbations: A Review. Universe 2022, 8, 66. [Google Scholar] [CrossRef]
- Musco, I.; Papanikolaou, T. Primordial black hole formation for an anisotropic perfect fluid: Initial conditions and estimation of the threshold. Phys. Rev. D 2022, 106, 083017. [Google Scholar] [CrossRef]
- Escrivà, A.; Bagui, E.; Clesse, S. Simulations of PBH formation at the QCD epoch and comparison with the GWTC-3 catalog. arXiv 2022, arXiv:2209.06196. [Google Scholar]
- Franciolini, G.; Musco, I.; Pani, P.; Urbano, A. From inflation to black hole mergers and back again: Gravitational-wave data-driven constraints on inflationary scenarios with a first-principle model of primordial black holes across the QCD epoch. arXiv 2022, arXiv:2209.05959. [Google Scholar]
- Papanikolaou, T. Toward the primordial black hole formation threshold in a time-dependent equation-of-state background. Phys. Rev. D 2022, 105, 124055. [Google Scholar] [CrossRef]
- Toussaint, D.; Treiman, S.B.; Wilczek, F.; Zee, A. Matter-antimatter accounting, thermodynamics, and black-hole radiation. Phys. Rev. D 1979, 19, 1036. [Google Scholar] [CrossRef]
- Barrow, J.D.; Copeland, E.; Kolb, E.; Liddle, A.R. Baryogenesis in extended inflation. 2. Baryogenesis via primordial black holes. Phys. Rev. D 1991, 43, 984. [Google Scholar] [CrossRef] [PubMed]
- Baumann, D.; Steinhardt, P.J.; Turok, N. Primordial Black Hole Baryogenesis. arXiv 2007, arXiv:hep-th/0703250. [Google Scholar]
- Inomata, K.; Kawasaki, M.; Mukaida, K.; Terada, T.; Yanagida, T.T. Gravitational Wave Production right after a Primordial Black Hole Evaporation. Phys. Rev. D 2020, 101, 123533. [Google Scholar] [CrossRef]
- Papanikolaou, T.; Vennin, V.; Langlois, D. Gravitational waves from a universe filled with primordial black holes. JCAP 2021, 053. [Google Scholar] [CrossRef]
- Domènech, G.; Lin, C.; Sasaki, M. Gravitational wave constraints on the primordial black hole dominated early universe. JCAP 2021, 062, Erratum in JCAP 2021, 11, E01. [Google Scholar] [CrossRef]
- Bhaumik, N.; Jain, R.K. Small scale induced gravitational waves from primordial black holes, a stringent lower mass bound, and the imprints of an early matter to radiation transition. Phys. Rev. D 2021, 104, 023531. [Google Scholar] [CrossRef]
- Hooper, D.; Krnjaic, G.; March-Russell, J.; McDermott, S.D.; Petrossian-Byrne, R. Hot Gravitons and Gravitational Waves From Kerr Black Holes in the Early Universe. arXiv 2020, arXiv:2004.00618. [Google Scholar]
- Domènech, G.; Takhistov, V.; Sasaki, M. Exploring evaporating primordial black holes with gravitational waves. Phys. Lett. B. 2021, 823, 136722. [Google Scholar] [CrossRef]
- Ananda, K.N.; Clarkson, C.; Wands, D. The Cosmological gravitational wave background from primordial density perturbations. Phys. Rev. D 2007, 75, 123518. [Google Scholar] [CrossRef]
- Baumann, D.; Steinhardt, P.J.; Takahashi, K.; Ichiki, K. Gravitational Wave Spectrum Induced by Primordial Scalar Perturbations. Phys. Rev. D 2007, 76, 084019. [Google Scholar] [CrossRef]
- Saito, R.; Yokoyama, J. Gravitational wave background as a probe of the primordial black hole abundance. Phys. Rev. Lett. 2009, 102, 161101, Erratum in Phys. Rev. Lett. 2011, 107, 069901. [Google Scholar] [CrossRef]
- Saito, R.; Yokoyama, J. Gravitational-Wave Constraints on the Abundance of Primordial Black Holes. Prog. Theor. Phys. 2010, 123, 867, Erratum in Prog. Theor. Phys. 2011, 126, 351–352. [Google Scholar] [CrossRef]
- Assadullahi, H.; Wands, D. Gravitational waves from an early matter era. Phys. Rev. D 2009, 79, 083511. [Google Scholar] [CrossRef]
- Bugaev, E.; Klimai, P. Induced gravitational wave background and primordial black holes. Phys. Rev. D. 2010, 81, 023517. [Google Scholar] [CrossRef]
- Bugaev, E.; Klimai, P. Constraints on the induced gravitational wave background from primordial black holes. Phys. Rev. D. 2011, 83, 083521. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Racco, D.; Riotto, A. A Cosmological Signature of the SM Higgs Instability: Gravitational Waves. JCAP 2018, 012. [Google Scholar] [CrossRef]
- Kohri, K.; Terada, T. Semianalytic calculation of gravitational wave spectrum nonlinearly induced from primordial curvature perturbations. Phys. Rev. D 2018, 97, 123532. [Google Scholar] [CrossRef]
- Domènech, G. Scalar Induced Gravitational Waves Review. Universe 2021, 7, 398. [Google Scholar] [CrossRef]
- Escrivà, A.; Kuhnel, F.; Tada, Y. Primordial Black Holes. arXiv 2022, arXiv:2211.05767. [Google Scholar]
- Villanueva-Domingo, P.; Mena, O.; Palomares-Ruiz, S. A brief review on primordial black holes as dark matter. Front. Astron. Space Sci. 2021, 8, 87. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Cole, P.S. Lecture notes on inflation and primordial black holes. arXiv 2021, arXiv:2112.05716. [Google Scholar]
- Yoo, C.-M.; Harada, T.; Garriga, J.; Kohri, K. Primordial black hole abundance from random Gaussian curvature perturbations and a local density threshold. PTEP 2018, 2018, 123E01. [Google Scholar] [CrossRef]
- Yoo, C.-M.; Harada, T.; Hirano, S.; Kohri, K. Abundance of Primordial Black Holes in Peak Theory for an Arbitrary Power Spectrum. arXiv 2020, arXiv:2008.02425. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Bond, J.R.; Kaiser, N.; Szalay, A.S. The statistics of peaks of Gaussian random fields. Astrophys. J. 1986, 304, 15. [Google Scholar] [CrossRef]
- Kopp, M.; Hofmann, S.; Weller, J. Separate Universes Do Not Constrain Primordial Black Hole Formation. Phys. Rev. 2011, D83, 124025. [Google Scholar] [CrossRef]
- Carr, B.J. The Primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1. [Google Scholar] [CrossRef]
- Misner, C.W.; Sharp, D.H. Relativistic equations for adiabatic, spherically symmetric gravitational collapse. Phys. Rev. 1964, 136, B571. [Google Scholar] [CrossRef]
- Polnarev, A.G.; Musco, I. Curvature profiles as initial conditions for primordial black hole formation. Class. Quantum Gravity 2007, 24, 1405. [Google Scholar] [CrossRef]
- Lyth, D.H.; Malik, K.A.; Sasaki, M. A General proof of the conservation of the curvature perturbation. JCAP 2005, 004. [Google Scholar] [CrossRef]
- Nadezhin, D.K.; Novikov, I.D.; Polnarev, A.G. The hydrodynamics of primordial black hole formation. Soviet Ast. 1978, 22, 129. [Google Scholar]
- Novikov, I.D.; Polnarev, A.G. The Hydrodynamics of Primordial Black Hole Formation—Dependence on the Equation of State. Soviet Ast. 1980, 24, 147. [Google Scholar]
- Musco, I.; Miller, J.C.; Polnarev, A.G. Primordial black hole formation in the radiative era: Investigation of the critical nature of the collapse. Class. Quantum Gravity 2009, 26, 235001. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C. Primordial black hole formation in the early universe: Critical behaviour and self-similarity. Class. Quantum Gravity 2013, 30, 145009. [Google Scholar] [CrossRef]
- Yoo, C.-M.; Gong, J.-O.; Yokoyama, S. Abundance of primordial black holes with local non-Gaussianity in peak theory. JCAP 2019, 033. [Google Scholar] [CrossRef]
- Kitajima, N.; Tada, Y.; Yokoyama, S.; Yoo, C.-M. Primordial black holes in peak theory with a non-Gaussian tail. JCAP 2021, 10, 053. [Google Scholar] [CrossRef]
- Escrivà, A.; Tada, Y.; Yokoyama, S.; Yoo, C.-M. Simulation of primordial black holes with large negative non-Gaussianity. JCAP 2022, 5, 012. [Google Scholar] [CrossRef]
- Choptuik, M.W. Universality and scaling in gravitational collapse of a massless scalar field. Phys. Rev. Lett. 1993, 70, 9. [Google Scholar] [CrossRef] [PubMed]
- Koike, T.; Hara, T.; Adachi, S. Critical behavior in gravitational collapse of radiation fluid: A Renormalization group (linear perturbation) analysis. Phys. Rev. Lett. 1995, 74, 5170. [Google Scholar] [CrossRef] [PubMed]
- Yokoyama, J. Cosmological constraints on primordial black holes produced in the near critical gravitational collapse. Phys. Rev. D 1998, 58, 107502. [Google Scholar] [CrossRef]
- Green, A.M.; Liddle, A.R. Critical collapse and the primordial black hole initial mass function. Phys. Rev. D 1999, 60, 063509. [Google Scholar] [CrossRef]
- Kuhnel, F.; Rampf, C.; Sandstad, M. Effects of Critical Collapse on Primordial Black-Hole Mass Spectra. Eur. Phys. J. C 2016, 76, 93. [Google Scholar] [CrossRef]
- Germani, C.; Musco, I. Abundance of Primordial Black Holes Depends on the Shape of the Inflationary Power Spectrum. Phys. Rev. Lett. 2019, 122, 141302. [Google Scholar] [CrossRef]
- Biagetti, M.; DeLuca, V.; Franciolini, G.; Kehagias, A.; Riotto, A. The formation probability of primordial black holes. Phys. Lett. B 2021, 820, 136602. [Google Scholar] [CrossRef]
- Yoo, C.-M.; Harada, T.; Hirano, S.; Okawa, H.; Sasaki, M. Primordial black hole formation from massless scalar isocurvature. Phys. Rev. D 2022, 105, 103538. [Google Scholar] [CrossRef]
- Germani, C.; Sheth, R.K. Nonlinear statistics of primordial black holes from Gaussian curvature perturbations. Phys. Rev. D 2020, 101, 063520. [Google Scholar] [CrossRef]
- Musco, I.; DeLuca, V.; Franciolini, G.; Riotto, A. Threshold for primordial black holes. II. A simple analytic prescription. Phys. Rev. D 2021, 103, 063538. [Google Scholar] [CrossRef]
- Suyama, T.; Yokoyama, S. A novel formulation of the PBH mass function. PTEP 2020, 2020, 023E03. [Google Scholar]
- Bullock, J.S.; Primack, J.R. NonGaussian fluctuations and primordial black holes from inflation. Phys. Rev. D 1997, 55, 7423. [Google Scholar] [CrossRef]
- Ivanov, P. Nonlinear metric perturbations and production of primordial black holes. Phys. Rev. D 1998, 57, 7145. [Google Scholar] [CrossRef]
- Hidalgo, J.C. The effect of non-Gaussian curvature perturbations on the formation of primordial black holes. arXiv 2007, arXiv:0708.3875. [Google Scholar]
- Byrnes, C.T.; Copeland, E.J.; Green, A.M. Primordial black holes as a tool for constraining non-Gaussianity. Phys. Rev. D 2012, 86, 043512. [Google Scholar] [CrossRef]
- Bugaev, E.V.; Klimai, P.A. Primordial black hole constraints for curvaton models with predicted large non-Gaussianity. Int. J. Mod. Phys. D 2013, 22, 1350034. [Google Scholar] [CrossRef]
- Young, S.; Regan, D.; Byrnes, C.T. Influence of large local and non-local bispectra on primordial black hole abundance. JCAP 2016, 2, 029. [Google Scholar] [CrossRef][Green Version]
- Nakama, T.; Silk, J.; Kamionkowski, M. Stochastic gravitational waves associated with the formation of primordial black holes. Phys. Rev. D 2017, 95, 043511. [Google Scholar] [CrossRef]
- Ando, K.; Inomata, K.; Kawasaki, M.; Mukaida, K.; Yanagida, T.T. Primordial black holes for the LIGO events in the axionlike curvaton model. Phys. Rev. D 2018, 97, 123512. [Google Scholar] [CrossRef]
- Franciolini, G.; Kehagias, A.; Matarrese, S.; Riotto, A. Primordial Black Holes from Inflation and non-Gaussianity. JCAP 2018, 1803, 016. [Google Scholar] [CrossRef]
- Cai, R.-g.; Pi, S.; Sasaki, M. Gravitational Waves Induced by non-Gaussian Scalar Perturbations. Phys. Rev. Lett. 2019, 122, 201101. [Google Scholar] [CrossRef] [PubMed]
- Atal, V.; Germani, C. The role of non-gaussianities in Primordial Black Hole formation. Phys. Dark Univ. 2019, 24, 100275. [Google Scholar] [CrossRef]
- Passaglia, S.; Hu, W.; Motohashi, H. Primordial black holes and local non-Gaussianity in canonical inflation. Phys. Rev. D 2019, 99, 043536. [Google Scholar] [CrossRef]
- Taoso, M.; Urbano, A. Non-gaussianities for primordial black hole formation. JCAP 2021, 8, 016. [Google Scholar] [CrossRef]
- Atal, V.; Garriga, J.; Marcos-Caballero, A. Primordial black hole formation with non-Gaussian curvature perturbations. JCAP 2019, 073. [Google Scholar] [CrossRef]
- Atal, V.; Cid, J.; Escrivà, A.; Garriga, J. PBH in single field inflation: The effect of shape dispersion and non-Gaussianities. JCAP 2020, 022. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Polnarev, A.G. Primordial black holes as a cosmological test of grand unification. Phys. Lett. 1980, 97B, 383. [Google Scholar] [CrossRef]
- Polnarev, A.G.; Khlopov, M.Y. Cosmology, primordial black holes, and supermassive particles. Sov. Phys. Usp. 1985, 28, 213. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.-M.; Kohri, K.; Nakao, K.-i.; Jhingan, S. Primordial black hole formation in the matter-dominated phase of the Universe. Astrophys. J. 2016, 833, 61. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.-M.; Kohri, K.; Nakao, K.-I. Spins of primordial black holes formed in the matter-dominated phase of the Universe. arXiv 2017, arXiv:1707.03595. [Google Scholar] [CrossRef]
- Kokubu, T.; Kyutoku, K.; Kohri, K.; Harada, T. Effect of Inhomogeneity on Primordial Black Hole Formation in the Matter Dominated Era. Phys. Rev. D 2018, 98, 123024. [Google Scholar] [CrossRef]
- Yoo, C.-M.; Harada, T.; Okawa, H. Threshold of Primordial Black Hole Formation in Nonspherical Collapse. arXiv 2020, arXiv:2004.01042. [Google Scholar] [CrossRef]
- Chiba, T.; Yokoyama, S. Spin Distribution of Primordial Black Holes. PTEP 2017, 2017, 083E01. [Google Scholar] [CrossRef]
- DeLuca, V.; Franciolini, G.; Pani, P.; Riotto, A. The evolution of primordial black holes and their final observable spins. JCAP 2020, 052. [Google Scholar] [CrossRef]
- Mirbabayi, M.; Gruzinov, A.; Noreña, J. Spin of Primordial Black Holes. JCAP 2020, 017. [Google Scholar] [CrossRef]
- He, M.; Suyama, T. Formation threshold of rotating primordial black holes. Phys. Rev. D 2019, 100, 063520. [Google Scholar] [CrossRef]
- Flores, M.M.; Kusenko, A. Spins of primordial black holes formed in different cosmological scenarios. Phys. Rev. D 2021, 104, 063008. [Google Scholar] [CrossRef]
- Koga, Y.; Harada, T.; Tada, Y.; Yokoyama, S.; Yoo, C.-M. Effective inspiral spin distribution of primordial black hole binaries. arXiv 2022, arXiv:2208.00696. [Google Scholar] [CrossRef]
- Jedamzik, K. Primordial black hole formation during the QCD epoch. Phys. Rev. D 1997, 55, 5871. [Google Scholar] [CrossRef]
- Schmid, C.; Schwarz, D.J.; Widerin, P. Amplification of cosmological inhomogeneities from the QCD transition. Phys. Rev. D 1999, 59, 043517. [Google Scholar] [CrossRef]
- Widerin, P.; Schmid, C. Primordial black holes from the QCD transition? arXiv 1998, arXiv:astro-ph/9808142. [Google Scholar]
- Boeckel, T.; Schettler, S.; Schaffner-Bielich, J. The Cosmological QCD Phase Transition Revisited. Prog. Part. Nucl. Phys. 2011, 66, 266. [Google Scholar] [CrossRef]
- Sobrinho, J.L.G.; Augusto, P.; Gonçalves, A.L. New thresholds for Primordial Black Hole formation during the QCD phase transition. Mon. Not. Roy. Astron. Soc. 2016, 463, 2348. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Hindmarsh, M.; Young, S.; Hawkins, M.R.S. Primordial black holes with an accurate QCD equation of state. JCAP 2018, 041. [Google Scholar] [CrossRef]
- Carr, B.; Clesse, S.; García-Bellido, J.; Kühnel, F. Cosmic conundra explained by thermal history and primordial black holes. Phys. Dark Univ. 2021, 31, 100755. [Google Scholar] [CrossRef]
- Carr, B.; Clesse, S.; García-Bellido, J. Primordial black holes from the QCD epoch: Linking dark matter, baryogenesis and anthropic selection. Mon. Not. R. Astron. Soc. 2021, 501, 1426. [Google Scholar] [CrossRef]
- Clesse, S.; Garcia-Bellido, J. GW190425, GW190521 and GW190814: Three candidate mergers of primordial black holes from the QCD epoch. arXiv 2020, arXiv:2007.06481. [Google Scholar] [CrossRef]
- Gao, F.; Oldengott, I.M. Cosmology Meets Functional QCD: First-Order Cosmic QCD Transition Induced by Large Lepton Asymmetries. Phys. Rev. Lett. 2022, 128, 131301. [Google Scholar] [CrossRef]
- Juan, J.I.; Serpico, P.D.; FrancoAbellán, G. The QCD phase transition behind a PBH origin of LIGO/Virgo events? JCAP 2022, 009. [Google Scholar] [CrossRef]
- Passaglia, S.; Sasaki, M. Primordial Black Holes from CDM Isocurvature. arXiv 2021, arXiv:2109.12824. [Google Scholar]
- Kodama, H. Conserved Energy Flux for the Spherically Symmetric System and the Back Reaction Problem in the Black Hole Evaporation. Prog. Theor. Phys. 1980, 63, 1217. [Google Scholar] [CrossRef]
- Hayward, S.A. General laws of black hole dynamics. Phys. Rev. D 1994, 49, 6467. [Google Scholar] [CrossRef] [PubMed]
- Hayward, S.A. Gravitational energy in spherical symmetry. Phys. Rev. D 1996, 53, 1938. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, C.-M. The Basics of Primordial Black Hole Formation and Abundance Estimation. Galaxies 2022, 10, 112. https://doi.org/10.3390/galaxies10060112
Yoo C-M. The Basics of Primordial Black Hole Formation and Abundance Estimation. Galaxies. 2022; 10(6):112. https://doi.org/10.3390/galaxies10060112
Chicago/Turabian StyleYoo, Chul-Moon. 2022. "The Basics of Primordial Black Hole Formation and Abundance Estimation" Galaxies 10, no. 6: 112. https://doi.org/10.3390/galaxies10060112
APA StyleYoo, C.-M. (2022). The Basics of Primordial Black Hole Formation and Abundance Estimation. Galaxies, 10(6), 112. https://doi.org/10.3390/galaxies10060112





