Observational Imprints of Enhanced Scalar Power on Small Scales in Ultra Slow Roll Inflation and Associated Non-Gaussianities
Abstract
1. Introduction
2. Inflationary Models, Power Spectra and Reverse Engineered Potentials
2.1. Arriving at the Equations Governing the Background and the Perturbations at the Linear Order
2.1.1. Equations of Motion Describing the Background and the Slow Roll Parameters
2.1.2. Scalar and Tensor Perturbations, Equations of Motion, Quantization and Power Spectra
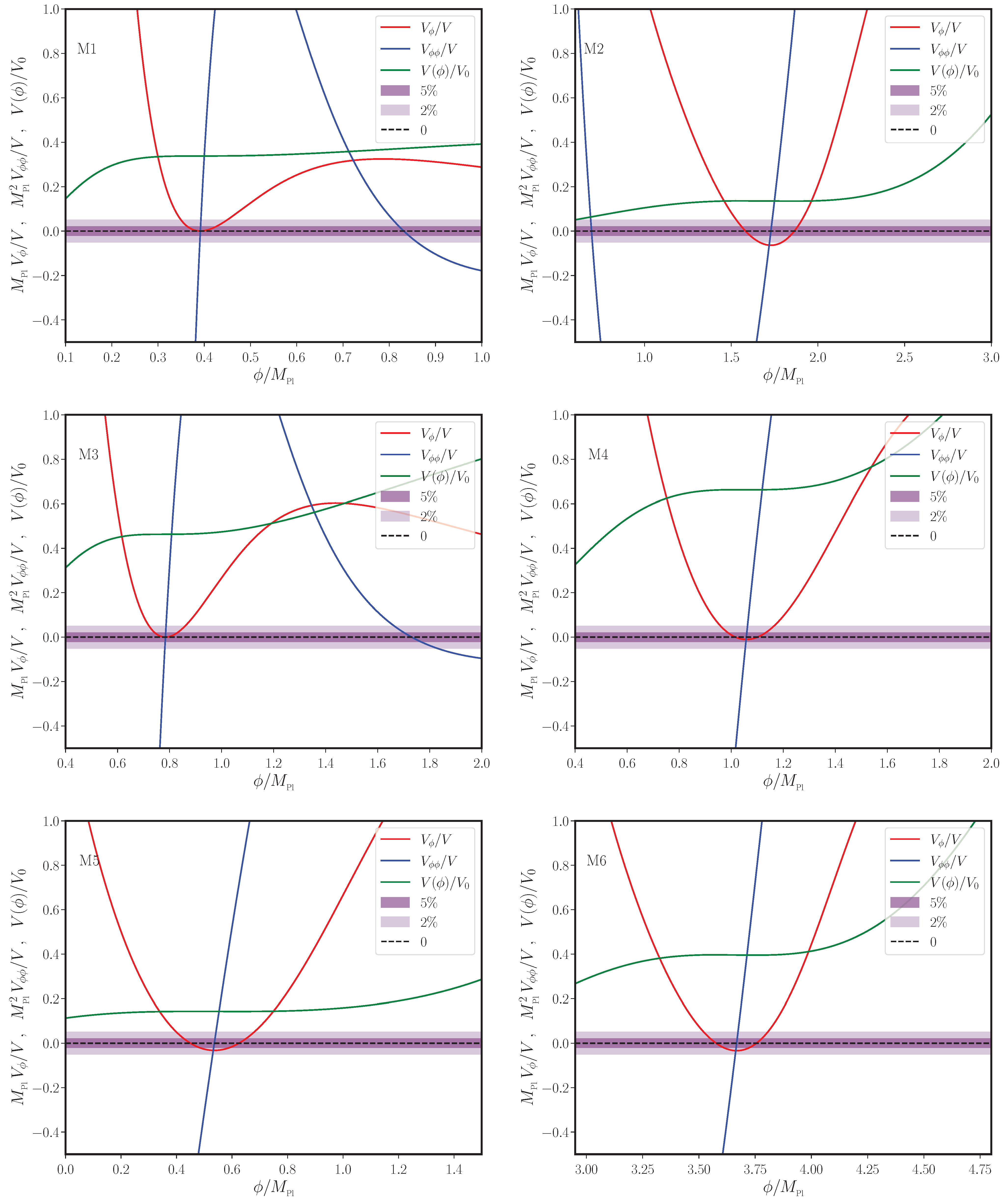
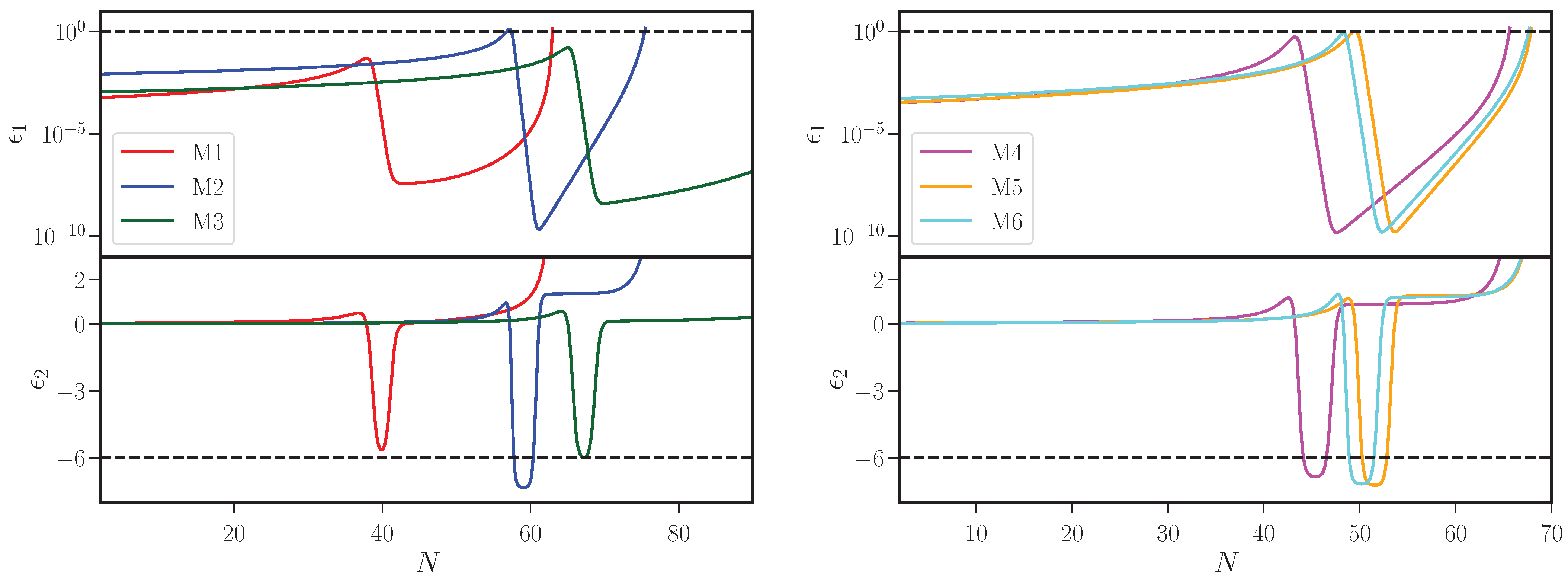
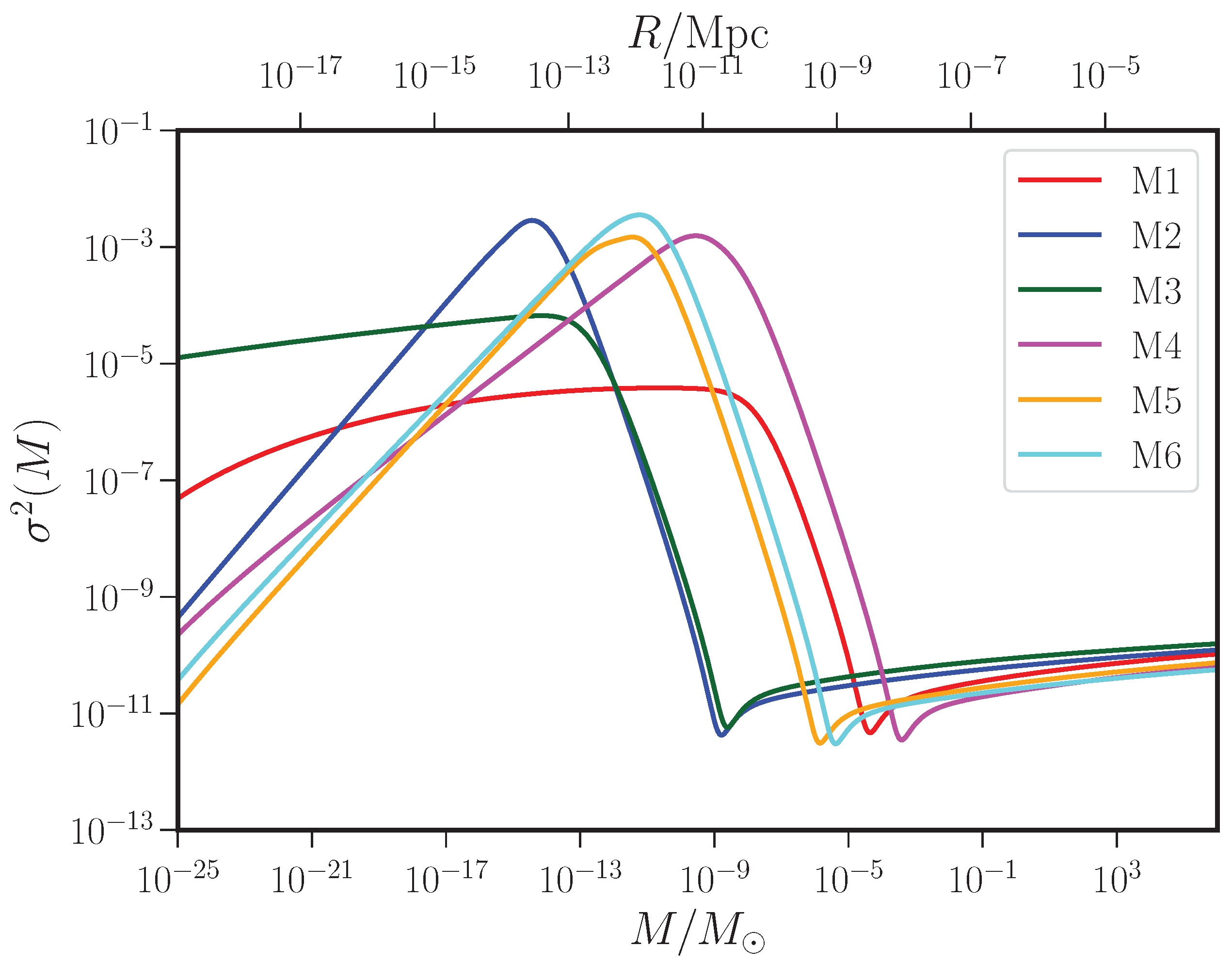
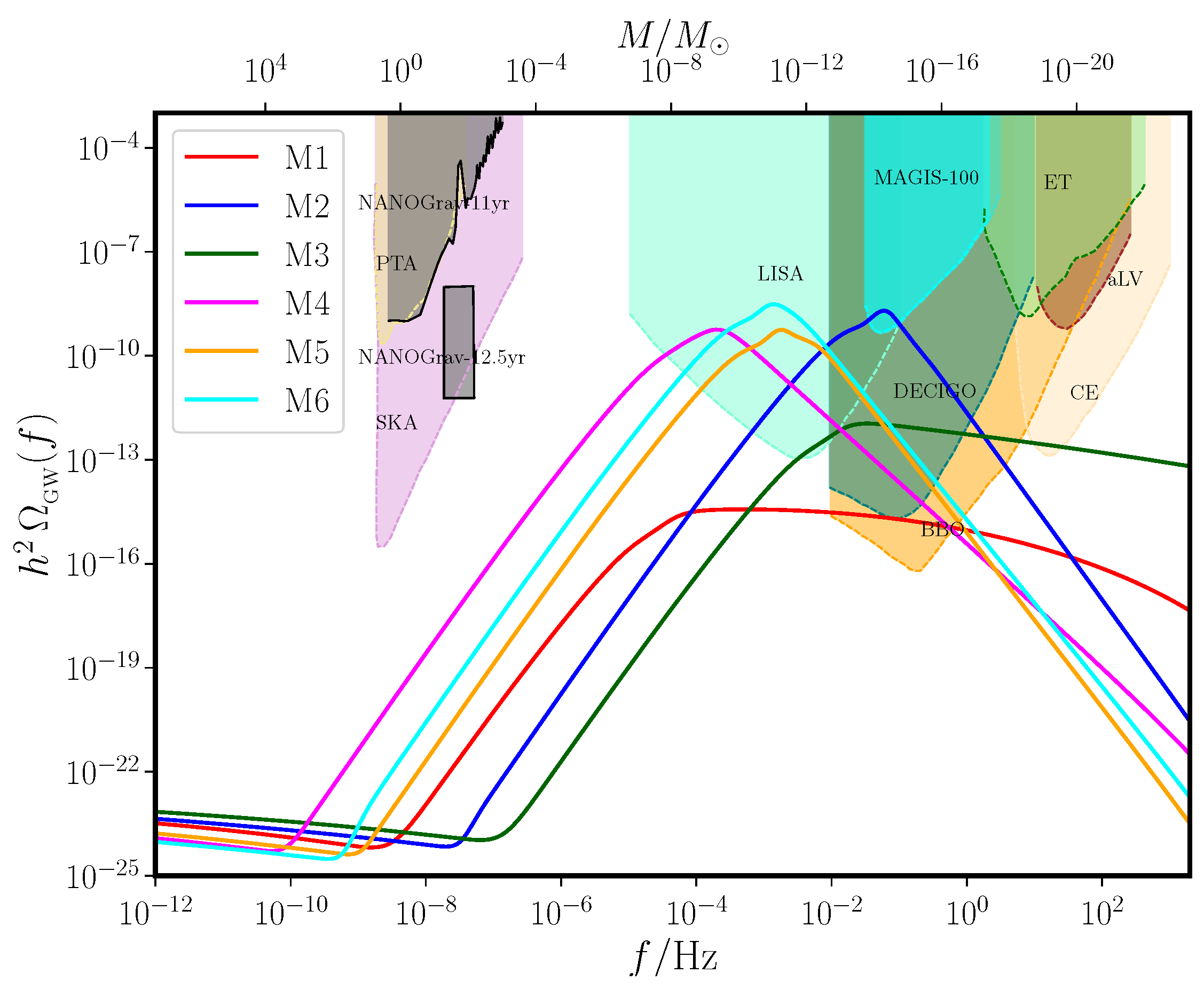
2.2. A Short List of Models Permitting Ultra Slow Roll Inflation
- Model 1: The first of the models that we shall consider, which leads to a period of ultra slow roll inflation, is described by a potential that can be written in the following fashion [39]:where , with v being a constant. We shall work with the following choices for the four parameters that describe the potential: , , and . For these values of the parameters, the (near) inflection point, say, , is located at . (For a discussion on the determination of the inflection points numerically in the inflationary models being considered, see Appendix A). If we choose the initial value of the field to be and (which determines , cf. Equation (9)), we find that inflation lasts for about 63 e-folds in the model. Also, in this case, we shall set .
- Model 2: The second potential that we shall consider can expressed in terms of the quantity that we had introduced in the first model, and is given by [46]We shall consider the following set of values for the six parameters involved: , , , , and . For these values of the parameters and the initial conditions and , inflation continues for about 75 e-folds before it is terminated. Also, the point of inflection is located at . For this model, we shall choose .
- Model 3: A potential referred to as the critical Higgs model is given by [42,43,47]:where and we shall set . We shall choose the values of the other parameters that describe the potential to be , , and . For these values, the point of inflection occurs at . The initial values of the field and the first slow roll parameter are taken to be and . In such a case, we achieve about 103 e-folds of inflation. The pivot scale is set to exit the Hubble radius at about 70 e-folds before the end of inflation to achieve the feature at the desired wave number.
- Model 4: The fourth potential that we shall consider is given by [45]and we shall work with the following values of the parameters involved: , and . For these values of the parameters, we find that a point of inflection arises at . If we set initial value of the field to be and the first slow roll parameter to be , we obtain about 66 e-folds of inflation in the model. Also, we shall choose .
- Model 5: A model constructed from supergravity which permits a period of ultra slow inflation is described by the potential [45,48]We shall work with the following values for the parameters involved: , , , , and . This model too contains a point of inflection and, for the above values for the parameters, the inflection point is located at . We find that, for the initial values and , inflation ends after about 68 e-folds. Also, in this case, we shall set .
- Model 6: The sixth and last model that we shall consider is motivated by string theory, and is described by the potential [44]where , , , , , , , , , and . To achieve the required duration of inflation, we shall set and . These initial conditions lead to about 68 e-folds of inflation. We shall set to compute the power spectra arising in the model.
2.3. Evolution of the Background in Ultra Slow Roll Inflation
2.4. Scalar and Tensor Power Spectra in Ultra Slow Roll Inflation
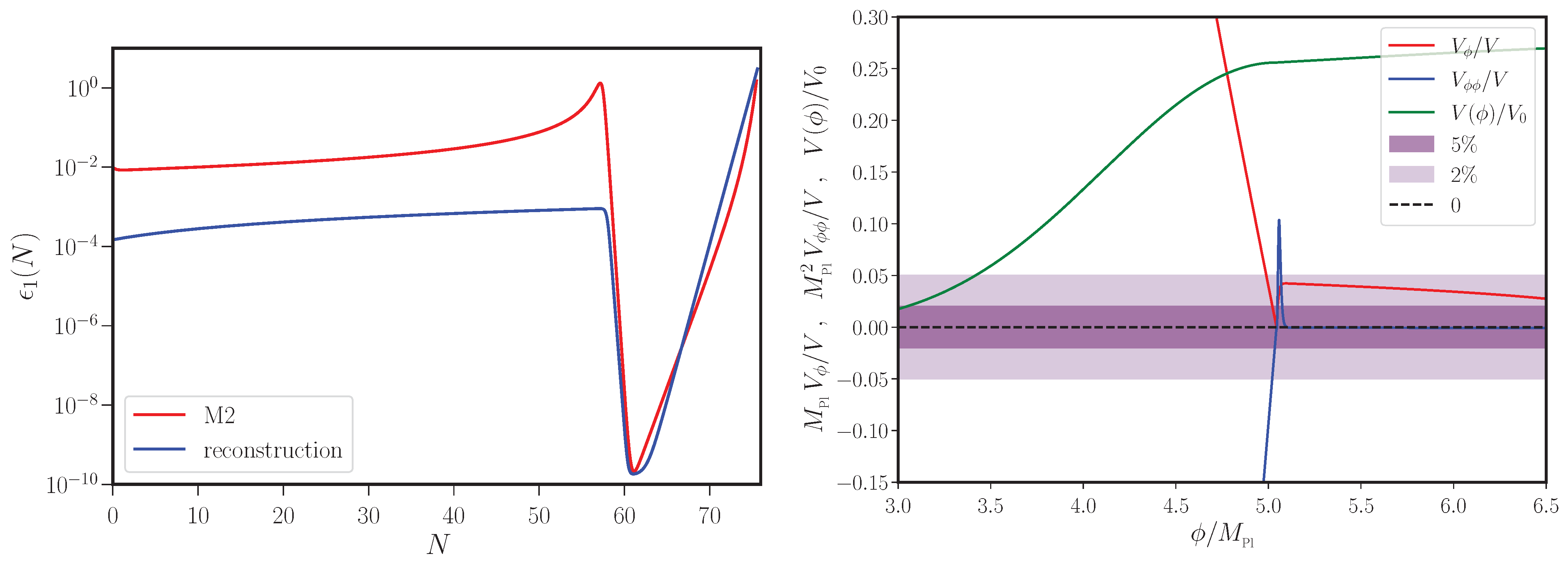
2.5. Reverse Engineering Desired Potentials
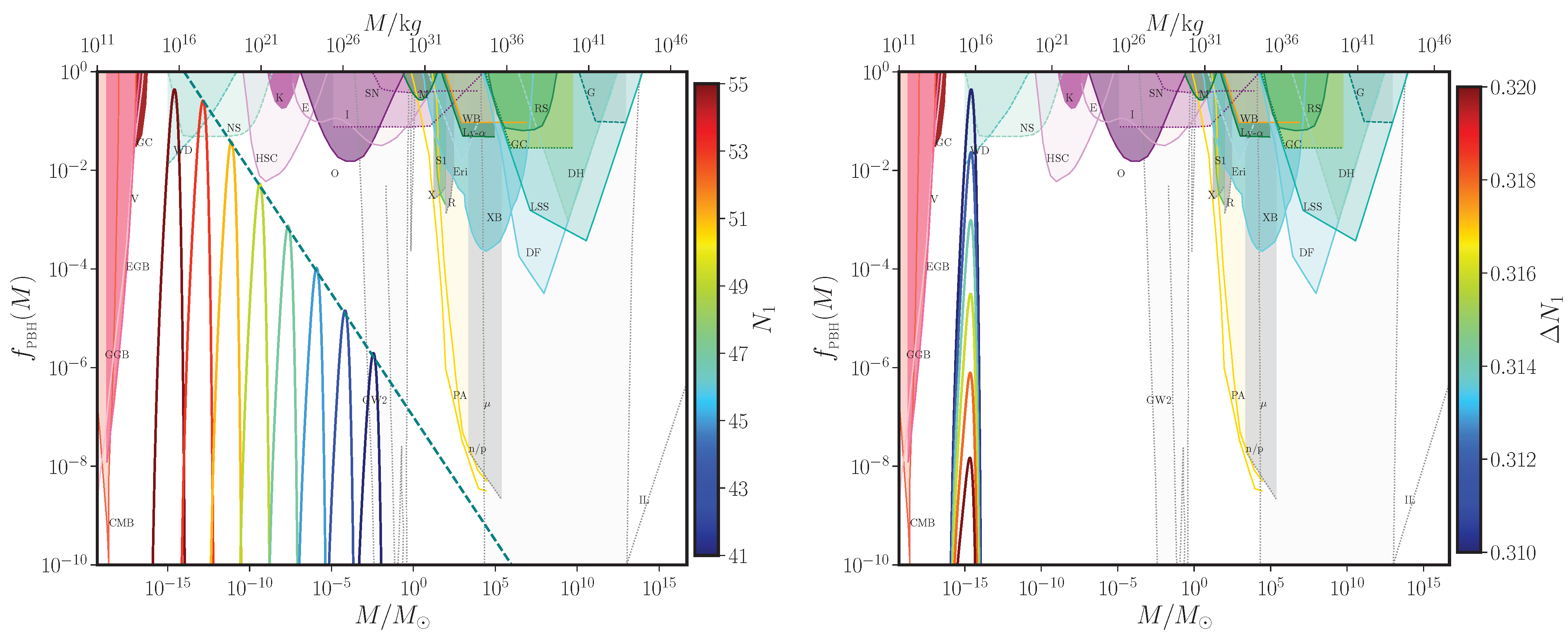
3. Formation of PBHs in the Radiation Dominated Epoch
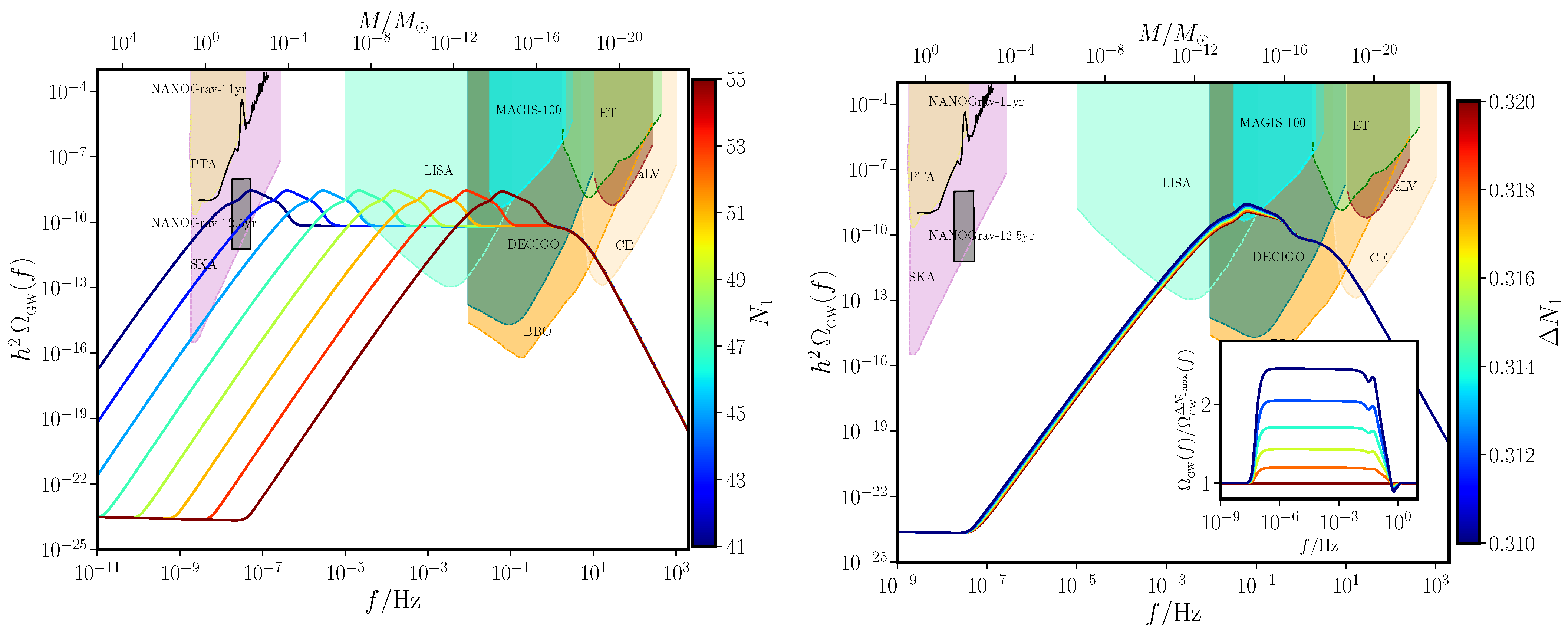
4. Generation of Secondary GWs in the Radiation Dominated Epoch
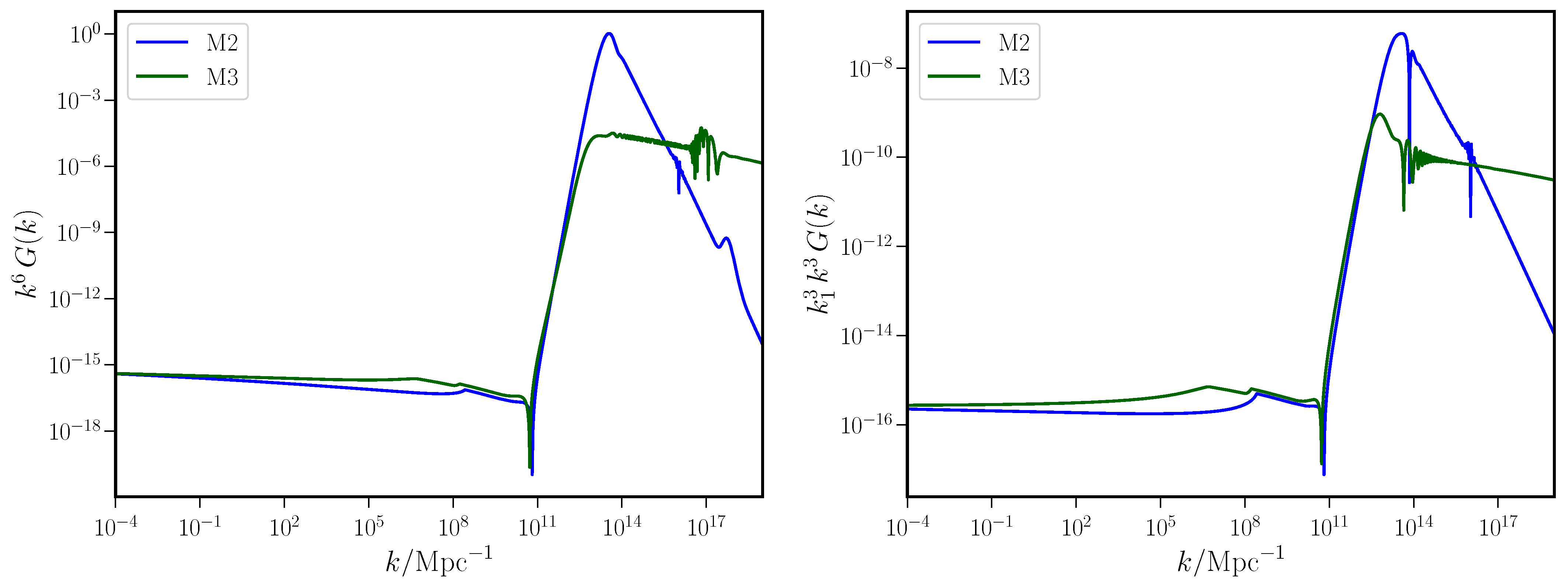
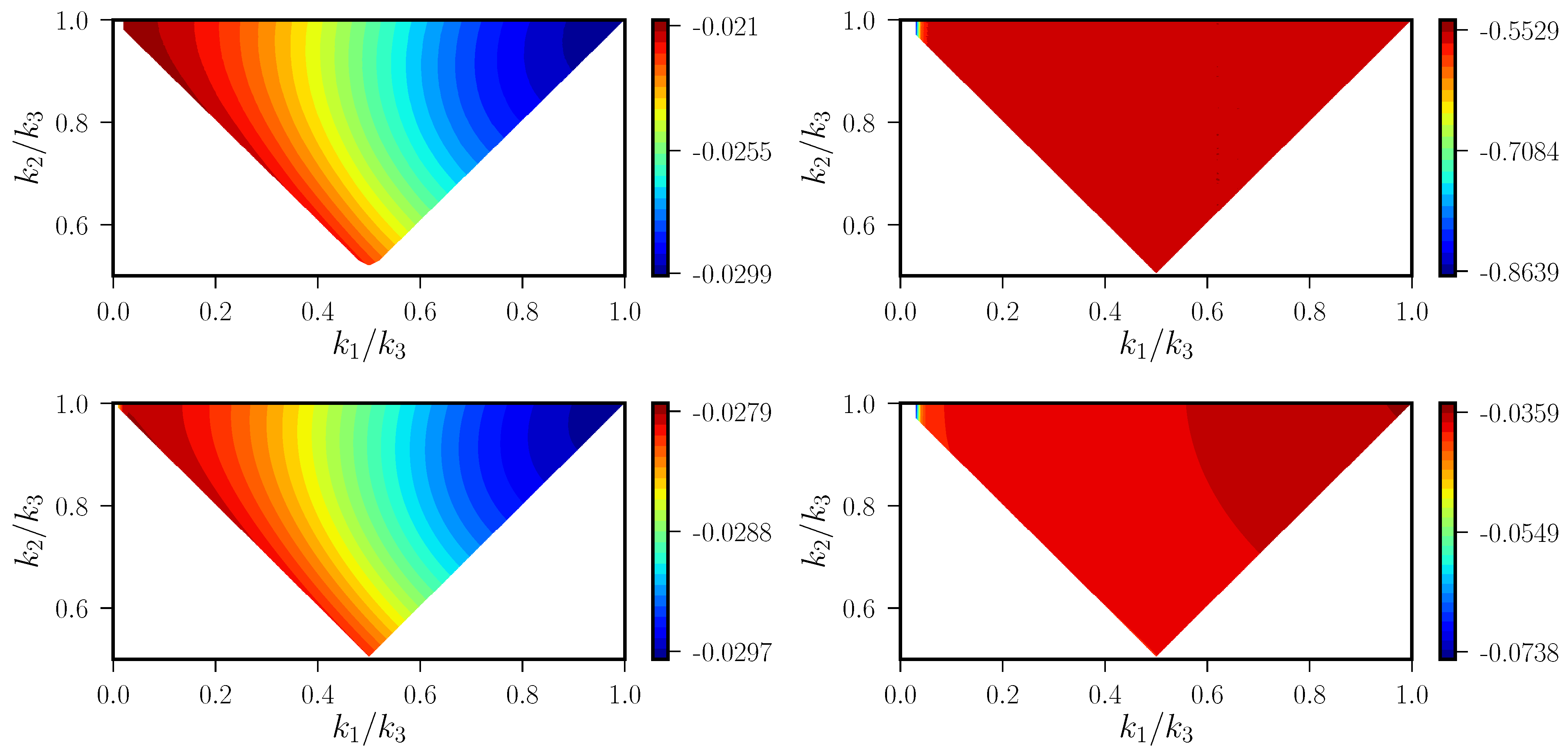
5. Non-Gaussianities on Small Scales
5.1. The Complete Third Order Action Governing the Scalar Bispectrum
5.2. Numerical Computation of the Scalar Bispectrum and the Associated Non-Gaussianity Parameter
6. Outlook
- Effects of non-Gaussianities on the formation of PBHs: In our discussion, we have restricted our attention to the effects of the increased scalar power (due to the epoch of ultra slow roll) on the number of PBHs produced. Since the amplitude of the bispectrum generated due to ultra slow roll is significantly higher than the slow roll values, the non-Gaussianities can be expected to boost the extent of PBHs formed (for earlier discussions on this point, see, for instance, Refs. [51,87,151,152]). There has been recent efforts to account for a skewness in the probability distribution describing the density contrast (cf. Equation (38)), arising due to increased strengths of the scalar bispectrum on small scales, and calculate the corresponding effects on the number of PBHs produced [90,91,92]. We should point out that alternative methods have also been proposed to account for the scalar non-Gaussianity in such calculations (see Refs. [153,154]; for a brief summary of the different methods, see Ref. [93]).
- Effects of non-Gaussianities on secondary GWs: It has been argued that large amplitudes of , as arising in ultra slow roll models, can considerably influence the strengths of secondary GWs that are generated during the radiation dominated epoch [67,95,99]. However, rather than calculate the bispectrum arising in specific inflationary models, these attempts often assume certain well motivated amplitudes and shapes of to calculate the corresponding contributions to . There have also been efforts to compute such non-Gaussian contributions to , while accounting for complete scale dependence of , arising from the bispectrum in specific models of ultra slow roll (in this regard, see Ref. [100]). These computations suggest that the non-Gaussian contributions to are highly model dependent and can, in principle, alter the shape and amplitude of around the peak of the spectra.
- Loop corrections to the primordial power spectrum: There is a gathering interest in the literature towards computing the contributions due to the loops to the scalar and tensor power spectra generated during inflation (for related early efforts, see, for example Refs. [155,156,157,158]). These contributions capture the effects of the higher order correlations on the power spectra and can lead to characteristic signatures on the predicted observables. There have been attempts to investigate such effects on observables such as and the 21-cm signals from neutral hydrogen of the Dark Ages [159,160,161]. There have also been efforts to theoretically restrict models of ultra slow roll inflation based on the amplitude of the corrections due to the loops and the associated consequences for the validity of perturbative treatment of the correlations (in this regard, see Refs. [162,163,164,165]).
Funding
Data Availability Statement
Conflicts of Interest
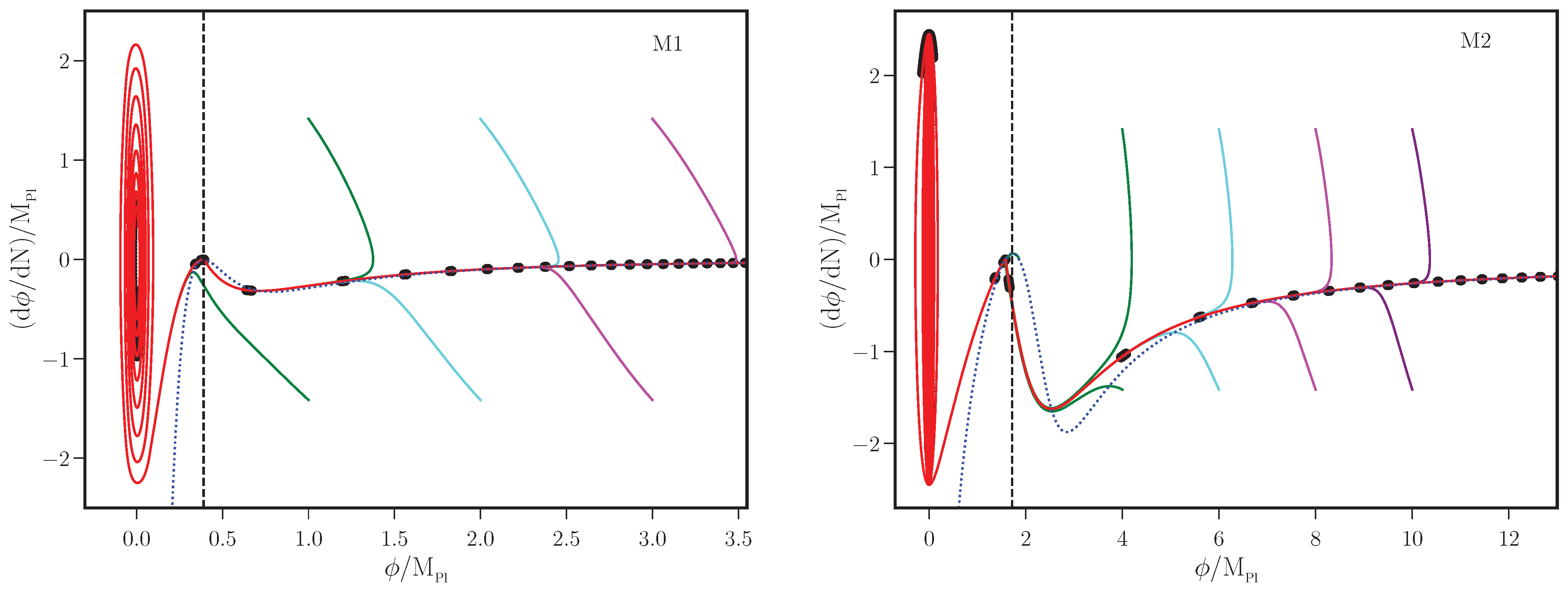
Appendix A. Determining the Locations of the Point of Inflection
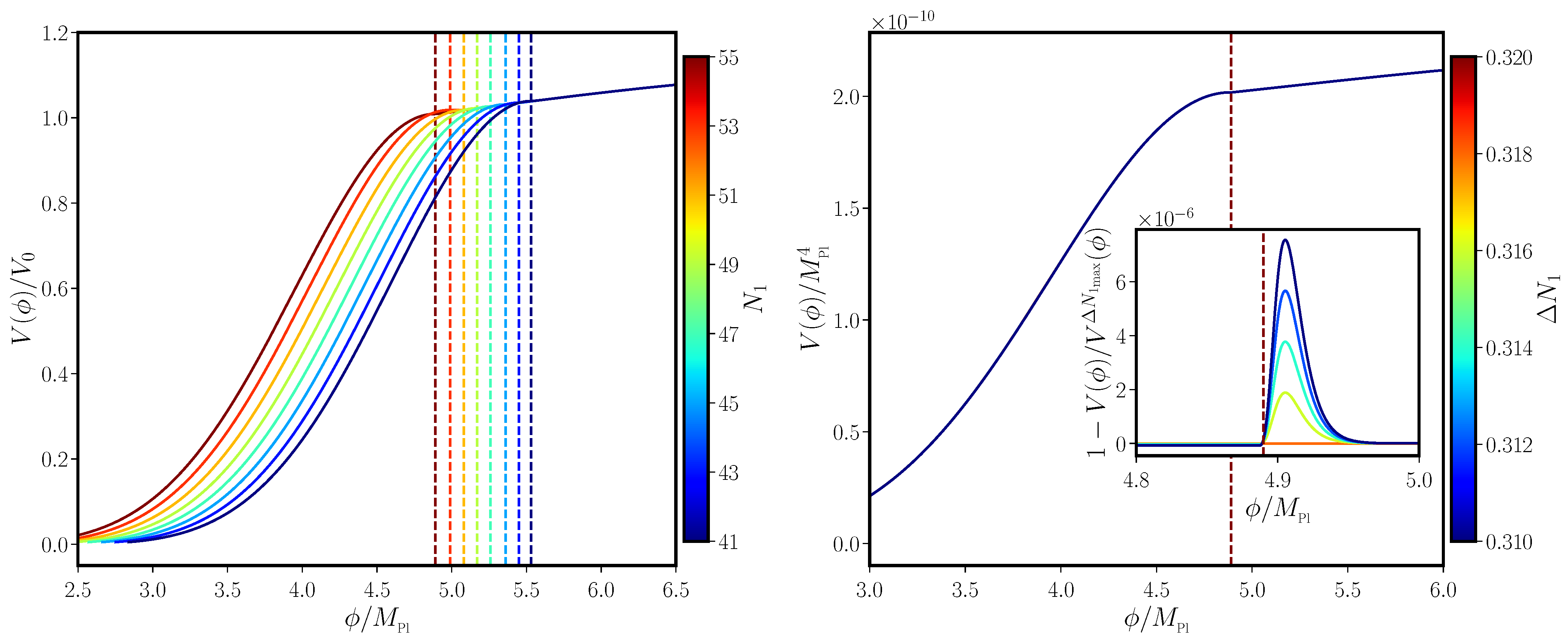
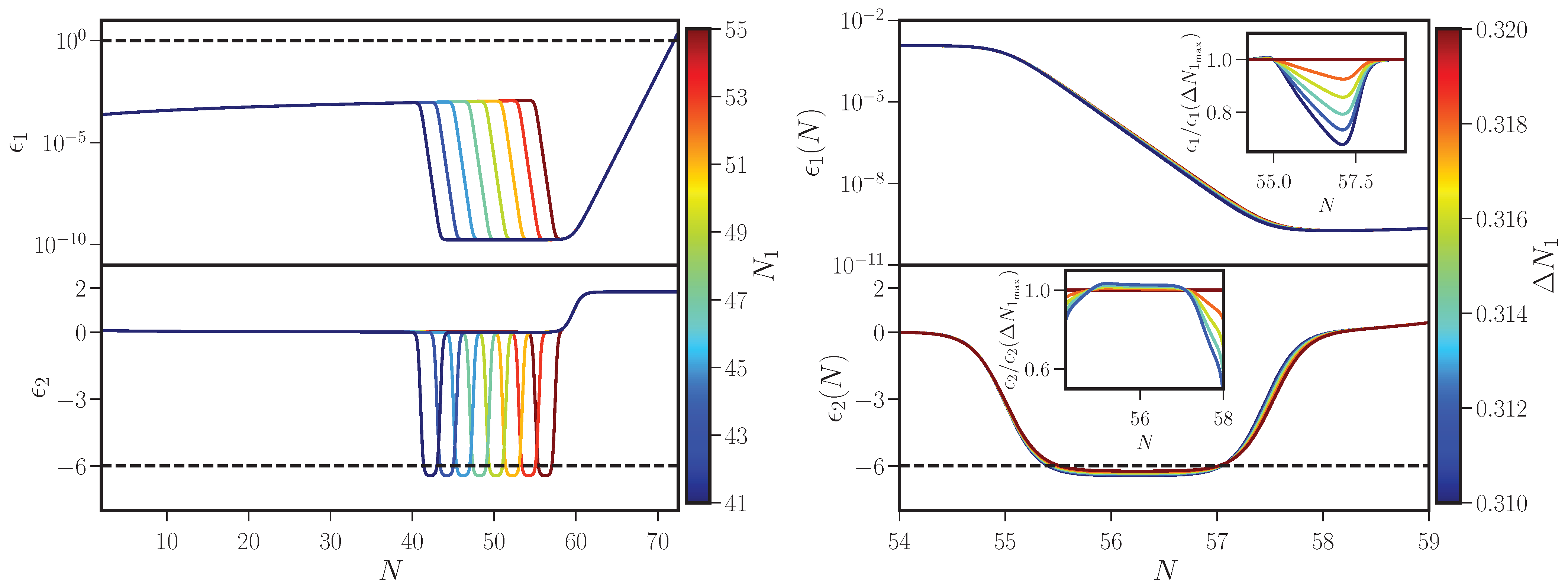
| 1 | In fact, if the duration of the ultra slow roll phase is, say, , then the range of wave numbers that are affected can be quantified as , where is the wave number that exits the Hubble radius at the onset of the ultra slow roll phase. This range corresponds to the region around the peak of the scalar power spectrum. Besides, there is another range of wave numbers that are affected by the phase of ultra slow roll. These correspond to wave numbers which leave the Hubble radius a few e-folds prior to the onset of the ultra slow roll phase (for earlier discussions in this regard, see Refs. [116,117,118]; for a more recent discussion, see Ref. [78]). Over these range of wave numbers, there arises a sharp dip and a rise in the power spectra leading to the peak. The wave number at the dip, say, , can be estimated to be and the range between the dip and the approach to the peak corresponds to (in this regard, see Ref. [119]). |
| 2 | The second order tensor perturbations should not be confused with the quantity which had denoted the spatial components of the metric in the ADM form of the line-element (1). |
| 3 | A clarification is in order at this stage of the discussion. Note that computing the scalar and tensor power spectra only require the evaluation of the corresponding Fourier mode functions and at the end of inflation (cf. Equation (20)). These can be calculated numerically without difficulty. However, as we have seen, the calculation of the scalar bispectrum also involves carrying out integrals over quantities that describe the background, the mode functions and their time derivatives (cf. Equation (65)). As we mentioned, in slow roll inflation, the super-Hubble contributions to the integrals can be shown to be negligible [77]. But, when there arise departures from slow roll, particularly at late times as in the ultra slow roll scenarios of our interest here, it becomes important to calculate the integrals until after the epoch of ultra slow roll and as close to the end of inflation as possible. In some models, computing the integrals right until the end of inflation (for a wide range of scales) becomes numerically taxing and it can also induce some numerical inaccuracies at large wave numbers. In such situations, we calculate the integrals until as close to the end of inflation as numerically feasible. We should hasten to add that, in these cases, we have checked that the late time contributions to the scalar bispectra are indeed insignificant. It is for this reason we have said that we evaluate the power and bi-spectra close to the end of inflation rather than at the end of inflation. |
| 4 | Users making use of the code in part or whole can cite this manuscript in their publications. |
References
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Part 1. Classical perturbations. Part 2. Quantum theory of perturbations. Part 3. Extensions. Phys. Rep. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Martin, J. Inflation and precision cosmology. Braz. J. Phys. 2004, 34, 1307–1321. [Google Scholar] [CrossRef]
- Martin, J. Inflationary cosmological perturbations of quantum-mechanical origin. Lect. Notes Phys. 2005, 669, 199–244. [Google Scholar] [CrossRef]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation dynamics and reheating. Rev. Mod. Phys. 2006, 78, 537–589. [Google Scholar] [CrossRef]
- Sriramkumar, L. An introduction to inflation and cosmological perturbation theory. arXiv 2009, arXiv:astro-ph.CO/0904.4584. [Google Scholar]
- Baumann, D.; Peiris, H.V. Cosmological Inflation: Theory and Observations. Adv. Sci. Lett. 2009, 2, 105–120. [Google Scholar] [CrossRef]
- Baumann, D. Inflation. In Physics of the Large and the Small, TASI 09, Proceedings of the Theoretical Advanced Study Institute in Elementary Particle Physics, Boulder, CO, USA, 1–26 June 2009; World Scientific Publishing: Singapore, 2011; pp. 523–686. [Google Scholar] [CrossRef]
- Sriramkumar, L. On the generation and evolution of perturbations during inflation and reheating. In Vignettes in Gravitation and Cosmology; Sriramkumar, L., Seshadri, T.R., Eds.; World Scientific: Singapore, 2012; pp. 207–249. [Google Scholar] [CrossRef]
- Linde, A. Inflationary Cosmology after Planck 2013. In Proceedings of the 100th Les Houches Summer School: Post-Planck Cosmology, Les Houches, France, 8 July–2 August 2013; pp. 231–316. [Google Scholar] [CrossRef]
- Martin, J. The Observational Status of Cosmic Inflation after Planck. Astrophys. Space Sci. Proc. 2016, 45, 41–134. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration] Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar] [CrossRef]
- Akrami, Y. et al. [Planck Collaboration] Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [BICEP/Keck Collaboration] Bullock Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration] Barreiro Planck 2015 results. XVII. Constraints on primordial non-Gaussianity. Astron. Astrophys. 2016, 594, A17. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration] Planck 2018 results. IX. Constraints on primordial non-Gaussianity. Astron. Astrophys. 2020, 641, A9. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia Inflationaris. Phys. Dark Univ. 2014, 5-6, 75–235. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Trotta, R.; Vennin, V. The Best Inflationary Models After Planck. J. Cosmol. Astropart. Phys. 2014, 3, 039. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration, the Virgo Collaboration] Affeldt GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, R. et al. [The LIGO Scientific Collaboration, the Virgo Collaboration]. GWTC-2.1: Deep Extended Catalog of Compact Binary Coalescences Observed by LIGO and Virgo during the First Half of the Third Observing Run. arXiv 2020, arXiv:gr-qc/2108.01045.
- Abbott, R. et al. [The LIGO Scientific Collaboration, the Virgo Collaboration, the KAGRA Collaboration]. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2020, arXiv:gr-qc/2111.03606.
- Bird, S.; Cholis, I.; Muñoz, J.B.; Ali-Haïmoud, Y.; Kamionkowski, M.; Kovetz, E.D.; Raccanelli, A.; Riess, A.G. Did LIGO detect dark matter? Phys. Rev. Lett. 2016, 116, 201301. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Pani, P.; Riotto, A. Primordial Black Holes Confront LIGO/Virgo data: Current situation. J. Cosmol. Astropart. Phys. 2020, 6, 044. [Google Scholar] [CrossRef]
- Jedamzik, K. Primordial Black Hole Dark Matter and the LIGO/Virgo observations. J. Cosmol. Astropart. Phys. 2020, 9, 022. [Google Scholar] [CrossRef]
- Jedamzik, K. Consistency of Primordial Black Hole Dark Matter with LIGO/Virgo Merger Rates. Phys. Rev. Lett. 2021, 126, 051302. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.L.; Kimura, R.; Yamaguchi, M. Reconstruction of Power Spectrum of Primordial Curvature Perturbations on small scales from Primordial Black Hole Binaries scenario of LIGO/VIRGO detection. arXiv 2022, arXiv:astro-ph.CO/2209.12911. [Google Scholar]
- Carr, B.J. The Primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Khlopov, M.Y. Primordial Black Holes. Res. Astron. Astrophys. 2010, 10, 495–528. [Google Scholar] [CrossRef]
- Carr, B.J.; Kohri, K.; Sendouda, Y.; Yokoyama, J. New cosmological constraints on primordial black holes. Phys. Rev. 2010, D81, 104019. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F.; Sandstad, M. Primordial Black Holes as Dark Matter. Phys. Rev. D 2016, 94, 083504. [Google Scholar] [CrossRef]
- Carr, B.; Silk, J. Primordial Black Holes as Generators of Cosmic Structures. Mon. Not. R. Astron. Soc. 2018, 478, 3756–3775. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial black holes—Perspectives in gravitational wave astronomy. Class. Quant. Grav. 2018, 35, 063001. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F. Primordial Black Holes as Dark Matter: Recent Developments. Ann. Rev. Nucl. Part. Sci. 2020, 70, 355–394. [Google Scholar] [CrossRef]
- Escrivà, A.; Kuhnel, F.; Tada, Y. Primordial Black Holes. arXiv 2022, arXiv:astro-ph.CO/2211.05767. [Google Scholar]
- Özsoy, O.; Tasinato, G. Inflation and Primordial Black Holes. arXiv 2023, arXiv:astro-ph.CO/2301.03600. [Google Scholar]
- Tsamis, N.C.; Woodard, R.P. Improved estimates of cosmological perturbations. Phys. Rev. D 2004, 69, 084005. [Google Scholar] [CrossRef]
- Kinney, W.H. Horizon crossing and inflation with large eta. Phys. Rev. D 2005, 72, 023515. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A.; Pal, S. Low & High scale MSSM inflation, gravitational waves and constraints from Planck. J. Cosmol. Astropart. Phys. 2013, 7, 041. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A. Primordial blackholes and gravitational waves for an inflection-point model of inflation. Phys. Lett. B 2014, 733, 270–275. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Ruiz Morales, E. Primordial black holes from single field models of inflation. Phys. Dark Univ. 2017, 18, 47–54. [Google Scholar] [CrossRef]
- Ballesteros, G.; Taoso, M. Primordial black hole dark matter from single field inflation. Phys. Rev. D 2018, 97, 023501. [Google Scholar] [CrossRef]
- Germani, C.; Prokopec, T. On primordial black holes from an inflection point. Phys. Dark Univ. 2017, 18, 6–10. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Garcia-Bellido, J.; Ruiz Morales, E. Primordial Black Hole production in Critical Higgs Inflation. Phys. Lett. B 2018, 776, 345–349. [Google Scholar] [CrossRef]
- Bezrukov, F.; Pauly, M.; Rubio, J. On the robustness of the primordial power spectrum in renormalized Higgs inflation. J. Cosmol. Astropart. Phys. 2018, 2, 040. [Google Scholar] [CrossRef]
- Cicoli, M.; Diaz, V.A.; Pedro, F.G. Primordial Black Holes from String Inflation. J. Cosmol. Astropart. Phys. 2018, 1806, 034. [Google Scholar] [CrossRef]
- Dalianis, I.; Kehagias, A.; Tringas, G. Primordial black holes from α-attractors. J. Cosmol. Astropart. Phys. 2019, 1, 037. [Google Scholar] [CrossRef]
- Bhaumik, N.; Jain, R.K. Primordial black holes dark matter from inflection point models of inflation and the effects of reheating. J. Cosmol. Astropart. Phys. 2020, 1, 37. [Google Scholar] [CrossRef]
- Drees, M.; Xu, Y. Overshooting, Critical Higgs Inflation and Second Order Gravitational Wave Signatures. Eur. Phys. J. C 2021, 81, 182. [Google Scholar] [CrossRef]
- Dalianis, I.; Kritos, K. Exploring the Spectral Shape of Gravitational Waves Induced by Primordial Scalar Perturbations and Connection with the Primordial Black Hole Scenarios. Phys. Rev. D 2021, 103, 023505. [Google Scholar] [CrossRef]
- Ragavendra, H.V.; Saha, P.; Sriramkumar, L.; Silk, J. Primordial black holes and secondary gravitational waves from ultraslow roll and punctuated inflation. Phys. Rev. D 2021, 103, 083510. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Spectrum of adiabatic perturbations in the universe when there are singularities in the inflation potential. JETP Lett. 1992, 55, 489–494. [Google Scholar]
- Atal, V.; Germani, C. The role of non-gaussianities in Primordial Black Hole formation. Phys. Dark Univ. 2019, 24, 100275. [Google Scholar] [CrossRef]
- Mishra, S.S.; Sahni, V. Primordial Black Holes from a tiny bump/dip in the Inflaton potential. J. Cosmol. Astropart. Phys. 2020, 4, 007. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Cole, P.S.; Patil, S.P. Steepest growth of the power spectrum and primordial black holes. J. Cosmol. Astropart. Phys. 2019, 6, 028. [Google Scholar] [CrossRef]
- Cheng, S.L.; Lee, W.; Ng, K.W. Superhorizon curvature perturbation in ultraslow-roll inflation. Phys. Rev. D 2019, 99, 063524. [Google Scholar] [CrossRef]
- Özsoy, O.; Parameswaran, S.; Tasinato, G.; Zavala, I. Mechanisms for Primordial Black Hole Production in String Theory. J. Cosmol. Astropart. Phys. 2018, 7, 005. [Google Scholar] [CrossRef]
- Carrilho, P.; Malik, K.A.; Mulryne, D.J. Dissecting the growth of the power spectrum for primordial black holes. Phys. Rev. D 2019, 100, 103529. [Google Scholar] [CrossRef]
- Liu, J.; Guo, Z.K.; Cai, R.G. Analytical approximation of the scalar spectrum in the ultraslow-roll inflationary models. Phys. Rev. D 2020, 101, 083535. [Google Scholar] [CrossRef]
- Tasinato, G. An analytic approach to non-slow-roll inflation. Phys. Rev. D 2021, 103, 023535. [Google Scholar] [CrossRef]
- Motohashi, H.; Mukohyama, S.; Oliosi, M. Constant Roll and Primordial Black Holes. J. Cosmol. Astropart. Phys. 2020, 3, 002. [Google Scholar] [CrossRef]
- Ng, K.W.; Wu, Y.P. Constant-rate inflation: Primordial black holes from conformal weight transitions. J. High Energy Phys. 2021, 11, 076. [Google Scholar] [CrossRef]
- Ananda, K.N.; Clarkson, C.; Wands, D. The Cosmological gravitational wave background from primordial density perturbations. Phys. Rev. 2007, D75, 123518. [Google Scholar] [CrossRef]
- Baumann, D.; Steinhardt, P.J.; Takahashi, K.; Ichiki, K. Gravitational Wave Spectrum Induced by Primordial Scalar Perturbations. Phys. Rev. 2007, D76, 084019. [Google Scholar] [CrossRef]
- Saito, R.; Yokoyama, J. Gravitational wave background as a probe of the primordial black hole abundance. Phys. Rev. Lett. 2009, 102, 161101. [Google Scholar] [CrossRef]
- Saito, R.; Yokoyama, J. Gravitational-Wave Constraints on the Abundance of Primordial Black Holes. Prog. Theor. Phys. 2010, 123, 867–886, Erratum in Prog. Theor. Phys. 2011, 126, 351–352. [Google Scholar] [CrossRef]
- Kohri, K.; Terada, T. Semianalytic calculation of gravitational wave spectrum nonlinearly induced from primordial curvature perturbations. Phys. Rev. D 2018, 97, 123532. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Racco, D.; Riotto, A. A Cosmological Signature of the SM Higgs Instability: Gravitational Waves. J. Cosmol. Astropart. Phys. 2018, 1809, 012. [Google Scholar] [CrossRef]
- Pi, S.; Sasaki, M. Gravitational Waves Induced by Scalar Perturbations with a Lognormal Peak. J. Cosmol. Astropart. Phys. 2020, 9, 037. [Google Scholar] [CrossRef]
- Domènech, G. Scalar Induced Gravitational Waves Review. Universe 2021, 7, 398. [Google Scholar] [CrossRef]
- Balaji, S.; Silk, J.; Wu, Y.P. Induced gravitational waves from the cosmic coincidence. J. Cosmol. Astropart. Phys. 2022, 6, 008. [Google Scholar] [CrossRef]
- Moore, C.; Cole, R.; Berry, C. Gravitational-wave sensitivity curves. Class. Quant. Grav. 2015, 32, 015014. [Google Scholar] [CrossRef]
- Maldacena, J.M. Non-Gaussian features of primordial fluctuations in single field inflationary models. J. High Energy Phys. 2003, 5, 013. [Google Scholar] [CrossRef]
- Seery, D.; Lidsey, J.E. Primordial non-Gaussianities in single field inflation. J. Cosmol. Astropart. Phys. 2005, 506, 003. [Google Scholar] [CrossRef]
- Chen, X.; Huang, M.x.; Kachru, S.; Shiu, G. Observational signatures and non-Gaussianities of general single field inflation. J. Cosmol. Astropart. Phys. 2007, 701, 002. [Google Scholar] [CrossRef]
- Chen, X.; Easther, R.; Lim, E.A. Generation and Characterization of Large Non-Gaussianities in Single Field Inflation. J. Cosmol. Astropart. Phys. 2008, 804, 010. [Google Scholar] [CrossRef]
- Chen, X. Primordial Non-Gaussianities from Inflation Models. Adv. Astron. 2010, 2010, 638979. [Google Scholar] [CrossRef]
- Martin, J.; Sriramkumar, L. The scalar bi-spectrum in the Starobinsky model: The equilateral case. J. Cosmol. Astropart. Phys. 2012, 1201, 008. [Google Scholar] [CrossRef]
- Hazra, D.K.; Sriramkumar, L.; Martin, J. BINGO: A code for the efficient computation of the scalar bi-spectrum. J. Cosmol. Astropart. Phys. 2013, 1305, 026. [Google Scholar] [CrossRef]
- Ragavendra, H.V.; Chowdhury, D.; Sriramkumar, L. Suppression of scalar power on large scales and associated bispectra. Phys. Rev. D 2022, 106, 043535. [Google Scholar] [CrossRef]
- Chongchitnan, S.; Efstathiou, G. Accuracy of slow-roll formulae for inflationary perturbations: Implications for primordial black hole formation. J. Cosmol. Astropart. Phys. 2007, 1, 011. [Google Scholar] [CrossRef]
- Seery, D.; Hidalgo, J. Non-Gaussian corrections to the probability distribution of the curvature perturbation from inflation. J. Cosmol. Astropart. Phys. 2006, 7, 008. [Google Scholar] [CrossRef]
- Hidalgo, J. The effect of non-Gaussian curvature perturbations on the formation of primordial black holes. arXiv 2007, arXiv:astro-ph/0708.3875. [Google Scholar]
- Motohashi, H.; Hu, W. Primordial Black Holes and Slow-Roll Violation. Phys. Rev. D 2017, 96, 063503. [Google Scholar] [CrossRef]
- Franciolini, G.; Kehagias, A.; Matarrese, S.; Riotto, A. Primordial Black Holes from Inflation and non-Gaussianity. J. Cosmol. Astropart. Phys. 2018, 3, 016. [Google Scholar] [CrossRef]
- Kehagias, A.; Musco, I.; Riotto, A. Non-Gaussian Formation of Primordial Black Holes: Effects on the Threshold. J. Cosmol. Astropart. Phys. 2019, 12, 029. [Google Scholar] [CrossRef]
- Atal, V.; Cid, J.; Escrivà, A.; Garriga, J. PBH in single field inflation: The effect of shape dispersion and non-Gaussianities. J. Cosmol. Astropart. Phys. 2020, 5, 022. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Kehagias, A.; Peloso, M.; Riotto, A.; Ünal, C. The Ineludible non-Gaussianity of the Primordial Black Hole Abundance. J. Cosmol. Astropart. Phys. 2019, 7, 048. [Google Scholar] [CrossRef]
- Passaglia, S.; Hu, W.; Motohashi, H. Primordial black holes and local non-Gaussianity in canonical inflation. Phys. Rev. D 2019, 99, 043536. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; García-Bellido, J.; Vennin, V. The exponential tail of inflationary fluctuations: Consequences for primordial black holes. J. Cosmol. Astropart. Phys. 2020, 3, 029. [Google Scholar] [CrossRef]
- Germani, C.; Sheth, R.K. Nonlinear statistics of primordial black holes from Gaussian curvature perturbations. Phys. Rev. D 2020, 101, 063520. [Google Scholar] [CrossRef]
- Taoso, M.; Urbano, A. Non-gaussianities for primordial black hole formation. J. Cosmol. Astropart. Phys. 2021, 8, 016. [Google Scholar] [CrossRef]
- Riccardi, F.; Taoso, M.; Urbano, A. Solving peak theory in the presence of local non-gaussianities. J. Cosmol. Astropart. Phys. 2021, 8, 060. [Google Scholar] [CrossRef]
- Matsubara, T.; Sasaki, M. Non-Gaussianity effects on the primordial black hole abundance for sharply-peaked primordial spectrum. J. Cosmol. Astropart. Phys. 2022, 10, 094. [Google Scholar] [CrossRef]
- Ferrante, G.; Franciolini, G.; Iovino, A., Jr.; Urbano, A. Primordial non-gaussianity up to all orders: Theoretical aspects and implications for primordial black hole model. arXiv 2022, arXiv:astro-ph.CO/2211.01728. [Google Scholar]
- Pi, S.; Sasaki, M. Logarithmic Duality of the Curvature Perturbation. arXiv 2022, arXiv:astro-ph.CO/2211.13932. [Google Scholar]
- Unal, C. Imprints of Primordial Non-Gaussianity on Gravitational Wave Spectrum. Phys. Rev. D 2019, 99, 041301. [Google Scholar] [CrossRef]
- Cai, R.G.; Pi, S.; Sasaki, M. Gravitational Waves Induced by non-Gaussian Scalar Perturbations. Phys. Rev. Lett. 2019, 122, 201101. [Google Scholar] [CrossRef] [PubMed]
- Cai, R.G.; Pi, S.; Wang, S.J.; Yang, X.Y. Pulsar Timing Array Constraints on the Induced Gravitational Waves. J. Cosmol. Astropart. Phys. 2019, 10, 059. [Google Scholar] [CrossRef]
- Ragavendra, H.V.; Sriramkumar, L.; Silk, J. Could PBHs and secondary GWs have originated from squeezed initial states? J. Cosmol. Astropart. Phys. 2021, 5, 010. [Google Scholar] [CrossRef]
- Adshead, P.; Lozanov, K.D.; Weiner, Z.J. Non-Gaussianity and the induced gravitational wave background. J. Cosmol. Astropart. Phys. 2021, 10, 080. [Google Scholar] [CrossRef]
- Ragavendra, H.V. Accounting for scalar non-Gaussianity in secondary gravitational waves. arXiv 2021, arXiv:astro-ph.CO/2108.04193. [Google Scholar] [CrossRef]
- Arnowitt, R.L.; Deser, S.; Misner, C.W. Canonical variables for general relativity. Phys. Rev. 1960, 117, 1595–1602. [Google Scholar] [CrossRef]
- Arroja, F.; Tanaka, T. A note on the role of the boundary terms for the non-Gaussianity in general k-inflation. J. Cosmol. Astropart. Phys. 2011, 1105, 005. [Google Scholar] [CrossRef]
- Sreenath, V.; Tibrewala, R.; Sriramkumar, L. Numerical evaluation of the three-point scalar-tensor cross-correlations and the tensor bi-spectrum. J. Cosmol. Astropart. Phys. 2013, 1312, 037. [Google Scholar] [CrossRef]
- Maldacena, J.M.; Pimentel, G.L. On graviton non-Gaussianities during inflation. J. High Energy Phys. 2011, 9, 045. [Google Scholar] [CrossRef]
- Bunch, T.S.; Davies, P.C.W. Quantum Field Theory in de Sitter Space: Renormalization by Point Splitting. Proc. R. Soc. Lond. A 1978, 360, 117–134. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. Primordial black holes from Gauss-Bonnet-corrected single field inflation. Phys. Rev. D 2021, 104, 083545. [Google Scholar] [CrossRef]
- Liddle, A.R.; Leach, S.M. How long before the end of inflation were observable perturbations produced? Phys. Rev. D 2003, 68, 103503. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Fehlberg, E. Low-Order Classical Runge-Kutta Formulas with Stepsize Control and Their Application to Some Heat Transfer Problems; National Aeronatics and Space Administration: Washington, DC, USA, 1969; Volume 315. [Google Scholar]
- Jain, R.K.; Chingangbam, P.; Gong, J.O.; Sriramkumar, L.; Souradeep, T. Punctuated inflation and the low CMB multipoles. J. Cosmol. Astropart. Phys. 2009, 901, 009. [Google Scholar] [CrossRef]
- Jain, R.K.; Chingangbam, P.; Sriramkumar, L.; Souradeep, T. The tensor-to-scalar ratio in punctuated inflation. Phys. Rev. D 2010, 82, 023509. [Google Scholar] [CrossRef]
- Adams, J.A.; Cresswell, B.; Easther, R. Inflationary perturbations from a potential with a step. Phys. Rev. D 2001, 64, 123514. [Google Scholar] [CrossRef]
- Mortonson, M.J.; Dvorkin, C.; Peiris, H.V.; Hu, W. CMB polarization features from inflation versus reionization. Phys. Rev. D 2009, 79, 103519. [Google Scholar] [CrossRef]
- Agocs, F.J.; Handley, W.J.; Lasenby, A.N.; Hobson, M.P. Efficient method for solving highly oscillatory ordinary differential equations with applications to physical systems. Phys. Rev. Res. 2020, 2, 013030. [Google Scholar] [CrossRef]
- Handley, W. Primordial power spectra for curved inflating universes. Phys. Rev. D 2019, 100, 123517. [Google Scholar] [CrossRef]
- Leach, S.M.; Liddle, A.R. Inflationary perturbations near horizon crossing. Phys. Rev. D 2001, 63, 043508. [Google Scholar] [CrossRef]
- Leach, S.M.; Sasaki, M.; Wands, D.; Liddle, A.R. Enhancement of superhorizon scale inflationary curvature perturbations. Phys. Rev. D 2001, 64, 023512. [Google Scholar] [CrossRef]
- Jain, R.K.; Chingangbam, P.; Sriramkumar, L. On the evolution of tachyonic perturbations at super-Hubble scales. J. Cosmol. Astropart. Phys. 2007, 710, 003. [Google Scholar] [CrossRef]
- Balaji, S.; Ragavendra, H.V.; Sethi, S.K.; Silk, J.; Sriramkumar, L. Observing Nulling of Primordial Correlations via the 21-cm Signal. Phys. Rev. Lett. 2022, 129, 261301. [Google Scholar] [CrossRef]
- Hertzberg, M.P.; Yamada, M. Primordial Black Holes from Polynomial Potentials in Single Field Inflation. Phys. Rev. D 2018, 97, 083509. [Google Scholar] [CrossRef]
- Franciolini, G.; Urbano, A. Primordial black hole dark matter from inflation: The reverse engineering approach. arXiv 2022, arXiv:astro-ph.CO/2207.10056. [Google Scholar] [CrossRef]
- Green, A.M.; Liddle, A.R.; Malik, K.A.; Sasaki, M. A New calculation of the mass fraction of primordial black holes. Phys. Rev. 2004, D70, 041502. [Google Scholar] [CrossRef]
- Germani, C.; Musco, I. Abundance of Primordial Black Holes Depends on the Shape of the Inflationary Power Spectrum. Phys. Rev. Lett. 2019, 122, 141302. [Google Scholar] [CrossRef] [PubMed]
- Escrivà, A. Simulation of primordial black hole formation using pseudo-spectral methods. Phys. Dark Univ. 2020, 27, 100466. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Universal threshold for primordial black hole formation. Phys. Rev. D 2020, 101, 044022. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Analytical thresholds for black hole formation in general cosmological backgrounds. arXiv 2020, arXiv:gr-qc/2007.05564. [Google Scholar] [CrossRef]
- Nakama, T.; Harada, T.; Polnarev, A.G.; Yokoyama, J. Identifying the most crucial parameters of the initial curvature profile for primordial black hole formation. J. Cosmol. Astropart. Phys. 2014, 1, 037. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C.; Rezzolla, L. Computations of primordial black hole formation. Class. Quant. Grav. 2005, 22, 1405–1424. [Google Scholar] [CrossRef]
- Young, S. The primordial black hole formation criterion re-examined: Parameterisation, timing, and the choice of window function. arXiv 2019, arXiv:astro-ph.CO/1905.01230. [Google Scholar] [CrossRef]
- Ade, P.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Planck Collaboration:, N. Aghanim, Y. Akrami, M. Ashdown, J. Aumont, C. Baccigalupi, M. Ballardini, A. J. Banday, R. B. Barreiro, N. Bartolo, S. Basak Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on Primordial Black Holes. arXiv 2020, arXiv:astro-ph.CO/2002.12778. [Google Scholar] [CrossRef] [PubMed]
- Green, A.M.; Kavanagh, B.J. Primordial Black Holes as a dark matter candidate. J. Phys. G 2021, 48, 043001. [Google Scholar] [CrossRef]
- Franciolini, G.; Maharana, A.; Muia, F. Hunt for light primordial black hole dark matter with ultrahigh-frequency gravitational waves. Phys. Rev. D 2022, 106, 103520. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Charisi, M.; Chatterjee, S.; Chen, S. Searching for Gravitational Waves from Cosmological Phase Transitions with the NANOGrav 12.5-Year Dataset. Phys. Rev. Lett. 2021, 127, 251302. [Google Scholar] [CrossRef]
- Mu, B.; Cheng, G.; Liu, J.; Guo, Z.K. Constraints on ultra-slow-roll inflation from the third LIGO-Virgo observing run. arXiv 2022, arXiv:astro-ph.CO/2211.05386. [Google Scholar]
- Maggiore, M. Gravitational wave experiments and early universe cosmology. Phys. Rep. 2000, 331, 283–367. [Google Scholar] [CrossRef]
- Bartolo, N.; Caprini, C.; Domcke, V.; Figueroa, D.G.; Garcia-Bellido, J.; Guzzetti, M.C.; Liguori, M.; Matarrese, S.; Peloso, M.; Petiteau, A. Science with the space-based interferometer LISA. IV: Probing inflation with gravitational waves. J. Cosmol. Astropart. Phys. 2016, 12, 026. [Google Scholar] [CrossRef]
- Bartolo, N.; De Luca, V.; Franciolini, G.; Lewis, A.; Peloso, M.; Riotto, A. Primordial Black Hole Dark Matter: LISA Serendipity. Phys. Rev. Lett. 2019, 122, 211301. [Google Scholar] [CrossRef] [PubMed]
- Bartolo, N.; De Luca, V.; Franciolini, G.; Peloso, M.; Racco, D.; Riotto, A. Testing primordial black holes as dark matter with LISA. Phys. Rev. D 2019, 99, 103521. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.J.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F. The NANOGrav 11-year Data Set: Pulsar-timing Constraints On The Stochastic Gravitational-wave Background. Astrophys. J. 2018, 859, 47. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Becsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Chatterjee, S.; Chen, S.; Corde, J.M. The NANOGrav 12.5 yr Data Set: Search for an Isotropic Stochastic Gravitational-wave Background. Astrophys. J. Lett. 2020, 905, L34. [Google Scholar] [CrossRef]
- Guzzetti, M.C.; Bartolo, N.; Liguori, M.; Matarrese, S. Gravitational waves from inflation. Riv. Nuovo Cim. 2016, 39, 399–495. [Google Scholar] [CrossRef]
- Caprini, C.; Figueroa, D.G. Cosmological Backgrounds of Gravitational Waves. Class. Quant. Grav. 2018, 35, 163001. [Google Scholar] [CrossRef]
- Hazra, D.K.; Antony, A.; Shafieloo, A. One spectrum to cure them all: Signature from early Universe solves major anomalies and tensions in cosmology. J. Cosmol. Astropart. Phys. 2022, 8, 063. [Google Scholar] [CrossRef]
- Braglia, M.; Chen, X.; Hazra, D.K.; Pinol, L. Back to the features: Assessing the discriminating power of future CMB missions on inflationary models. arXiv 2022, arXiv:astro-ph.CO/2211.05386. [Google Scholar]
- Goswami, G.; Souradeep, T. Power spectrum nulls due to non-standard inflationary evolution. Phys. Rev. D 2011, 83, 023526. [Google Scholar] [CrossRef]
- Özsoy, O.; Tasinato, G. CMB μT cross correlations as a probe of primordial black hole scenarios. Phys. Rev. D 2021, 104, 043526. [Google Scholar] [CrossRef]
- Özsoy, O.; Tasinato, G. Consistency conditions and primordial black holes in single field inflation. Phys. Rev. D 2022, 105, 023524. [Google Scholar] [CrossRef]
- Ragavendra, H.V.; Sriramkumar, L.; Martin, J. 2021; manuscript in preparation.
- Atal, V.; Garriga, J.; Marcos-Caballero, A. Primordial black hole formation with non-Gaussian curvature perturbations. J. Cosmol. Astropart. Phys. 2019, 9, 073. [Google Scholar] [CrossRef]
- Yoo, C.M.; Gong, J.O.; Yokoyama, S. Abundance of primordial black holes with local non-Gaussianity in peak theory. J. Cosmol. Astropart. Phys. 2019, 9, 033. [Google Scholar] [CrossRef]
- Cai, Y.F.; Ma, X.H.; Sasaki, M.; Wang, D.G.; Zhou, Z. Highly non-Gaussian tails and primordial black holes from single-field inflation. arXiv 2022, arXiv:astro-ph.CO/2207.11910. [Google Scholar] [CrossRef]
- Gow, A.D.; Assadullahi, H.; Jackson, J.H.P.; Koyama, K.; Vennin, V.; Wands, D. Non-perturbative non-Gaussianity and primordial black holes. arXiv 2022, arXiv:astro-ph.CO/2211.08348. [Google Scholar]
- Seery, D. One-loop corrections to the curvature perturbation from inflation. J. Cosmol. Astropart. Phys. 2008, 2, 006. [Google Scholar] [CrossRef]
- Yokoyama, S.; Suyama, T.; Tanaka, T. Efficient diagrammatic computation method for higher order correlation functions of local type primordial curvature perturbations. J. Cosmol. Astropart. Phys. 2009, 2, 012. [Google Scholar] [CrossRef]
- Cogollo, H.R.S.; Rodriguez, Y.; Valenzuela-Toledo, C.A. On the Issue of the zeta Series Convergence and Loop Corrections in the Generation of Observable Primordial Non-Gaussianity in Slow-Roll Inflation. Part I: The Bispectrum. J. Cosmol. Astropart. Phys. 2008, 8, 029. [Google Scholar] [CrossRef]
- Rodriguez, Y.; Valenzuela-Toledo, C.A. On the Issue of the zeta Series Convergence and Loop Corrections in the Generation of Observable Primordial Non-Gaussianity in Slow-Roll Inflation. Part 2. The Trispectrum. Phys. Rev. D 2010, 81, 023531. [Google Scholar] [CrossRef]
- Yamauchi, D. Signature of primordial non-Gaussianity on the 21 cm power spectrum from dark ages. Prog. Theor. Exp. Phys. 2022, 2022, 073E02. [Google Scholar] [CrossRef]
- Chen, C.; Ota, A.; Zhu, H.Y.; Zhu, Y. Missing one-loop contributions in secondary gravitational waves. arXiv 2022, arXiv:astro-ph.CO/2210.17176. [Google Scholar]
- Ota, A.; Sasaki, M.; Wang, Y. One-loop tensor power spectrum from an excited scalar field during inflation. arXiv 2022, arXiv:astro-ph.CO/2211.12766. [Google Scholar]
- Cheng, S.L.; Lee, D.S.; Ng, K.W. Power spectrum of primordial perturbations during ultra-slow-roll inflation with back reaction effects. Phys. Lett. B 2022, 827, 136956. [Google Scholar] [CrossRef]
- Kristiano, J.; Yokoyama, J. Why Must Primordial Non-Gaussianity Be Very Small? Phys. Rev. Lett. 2022, 128, 061301. [Google Scholar] [CrossRef] [PubMed]
- Kristiano, J.; Yokoyama, J. Perturbative region on non-Gaussian parameter space in single-field inflation. J. Cosmol. Astropart. Phys. 2022, 7, 007. [Google Scholar] [CrossRef]
- Kristiano, J.; Yokoyama, J. Ruling Out Primordial Black Hole Formation From Single-Field Inflation. arXiv 2022, arXiv:hep-th/2211.03395. [Google Scholar]



| Models | M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|---|
| 50 | 55 | 70 | 50 | 50 | 50 | |
| r |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ragavendra, H.V.; Sriramkumar, L. Observational Imprints of Enhanced Scalar Power on Small Scales in Ultra Slow Roll Inflation and Associated Non-Gaussianities. Galaxies 2023, 11, 34. https://doi.org/10.3390/galaxies11010034
Ragavendra HV, Sriramkumar L. Observational Imprints of Enhanced Scalar Power on Small Scales in Ultra Slow Roll Inflation and Associated Non-Gaussianities. Galaxies. 2023; 11(1):34. https://doi.org/10.3390/galaxies11010034
Chicago/Turabian StyleRagavendra, H. V., and L. Sriramkumar. 2023. "Observational Imprints of Enhanced Scalar Power on Small Scales in Ultra Slow Roll Inflation and Associated Non-Gaussianities" Galaxies 11, no. 1: 34. https://doi.org/10.3390/galaxies11010034
APA StyleRagavendra, H. V., & Sriramkumar, L. (2023). Observational Imprints of Enhanced Scalar Power on Small Scales in Ultra Slow Roll Inflation and Associated Non-Gaussianities. Galaxies, 11(1), 34. https://doi.org/10.3390/galaxies11010034





