Synthetic Light Curve Design for Pulsating Binary Stars to Compare the Efficiency in the Detection of Periodicities
Abstract
1. Introduction
2. Simulation Design
Designs of Synthetic Light Curves
- 1.
- Beating phenomenon ().
- 2.
- Period of the pulsation ().
- 3.
- Amplitude of the pulsation with respect to the depth of the primary eclipse ().
- 4.
- Number of pulsation periods ().
- 5.
- Light-time effect ().
- 6.
- Quasi-regular pulsations ().
3. Time Series Analysis Methods
3.1. The Period04 Tool
3.2. The WaveletComp Package
3.3. Period Detection Criteria
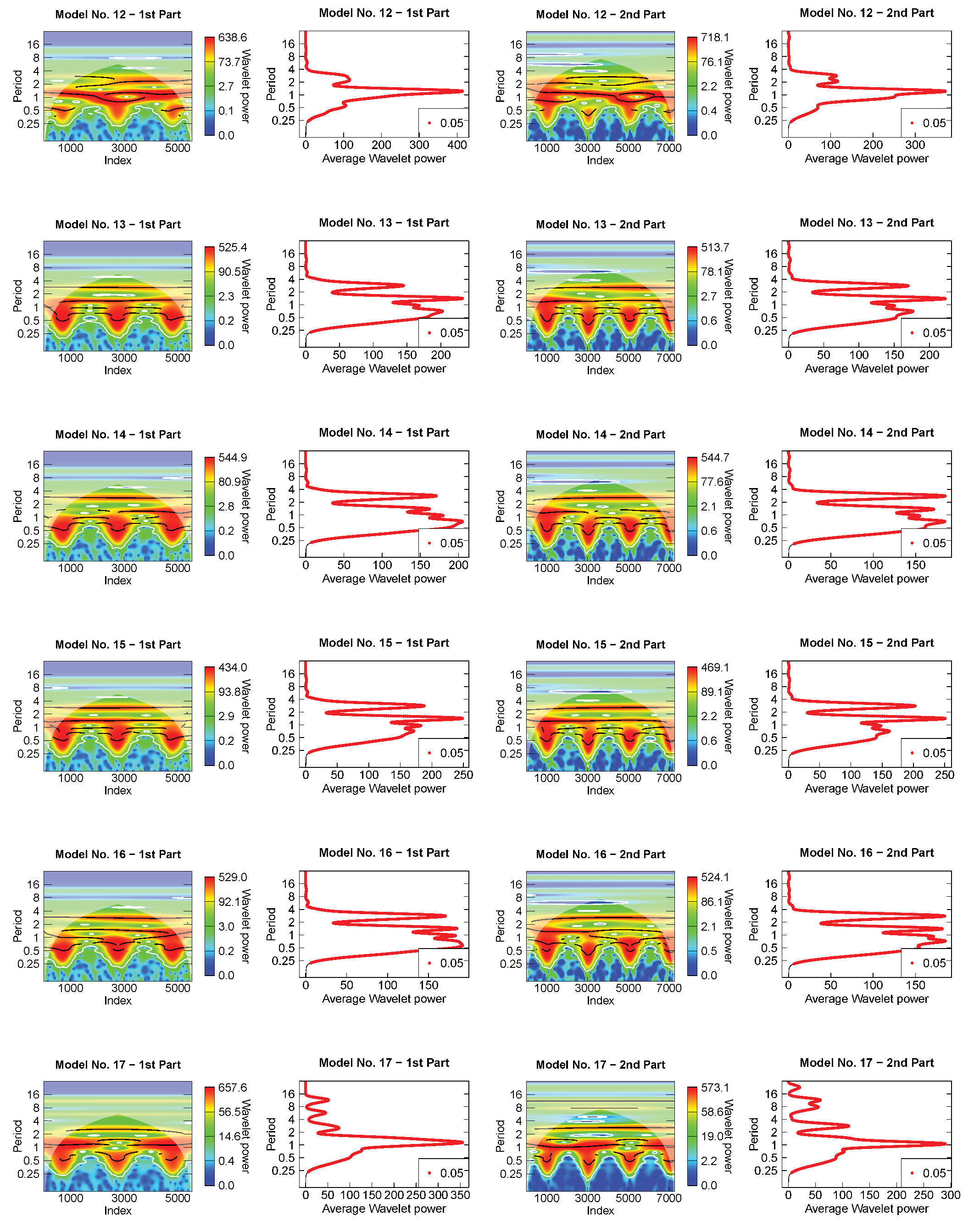
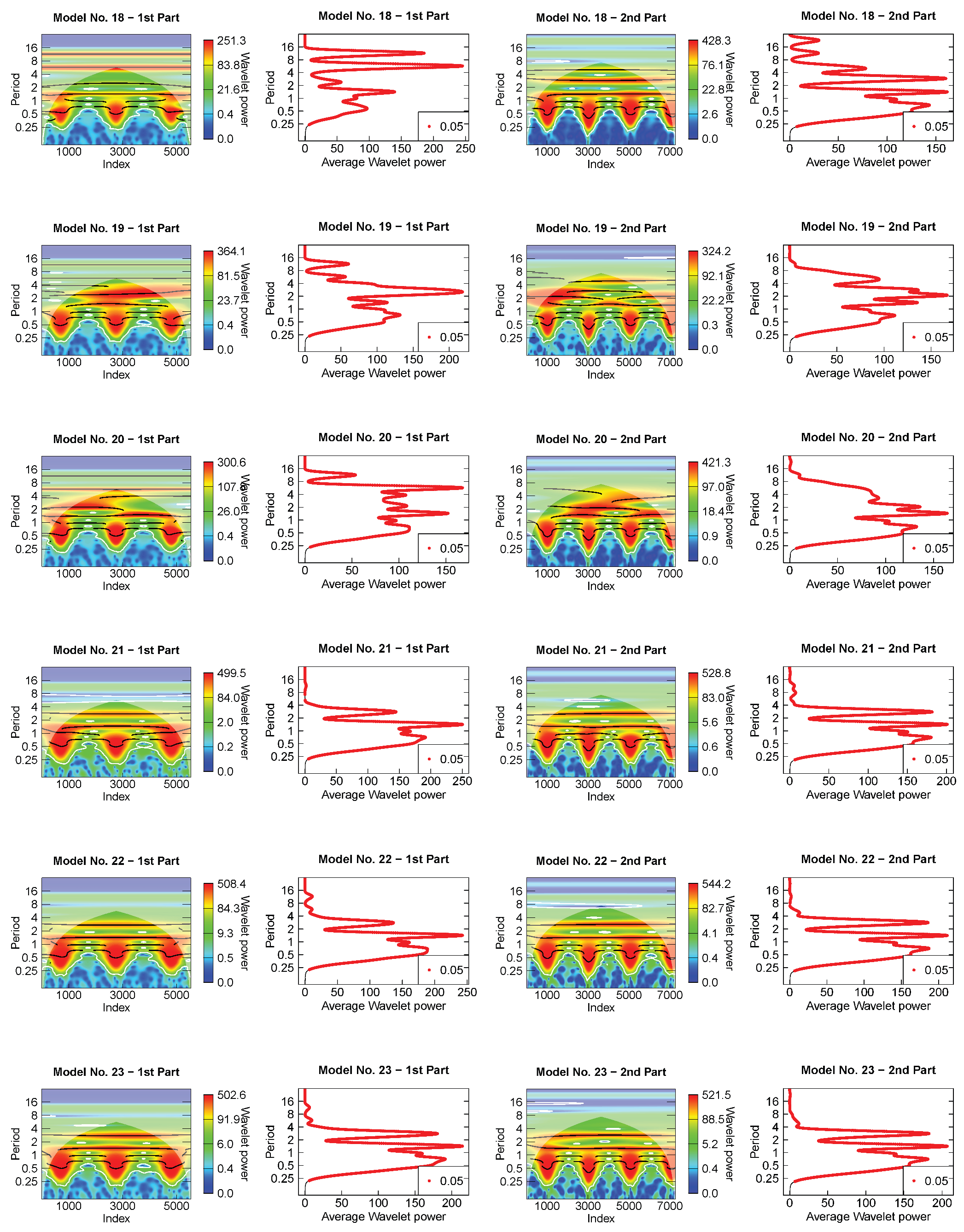
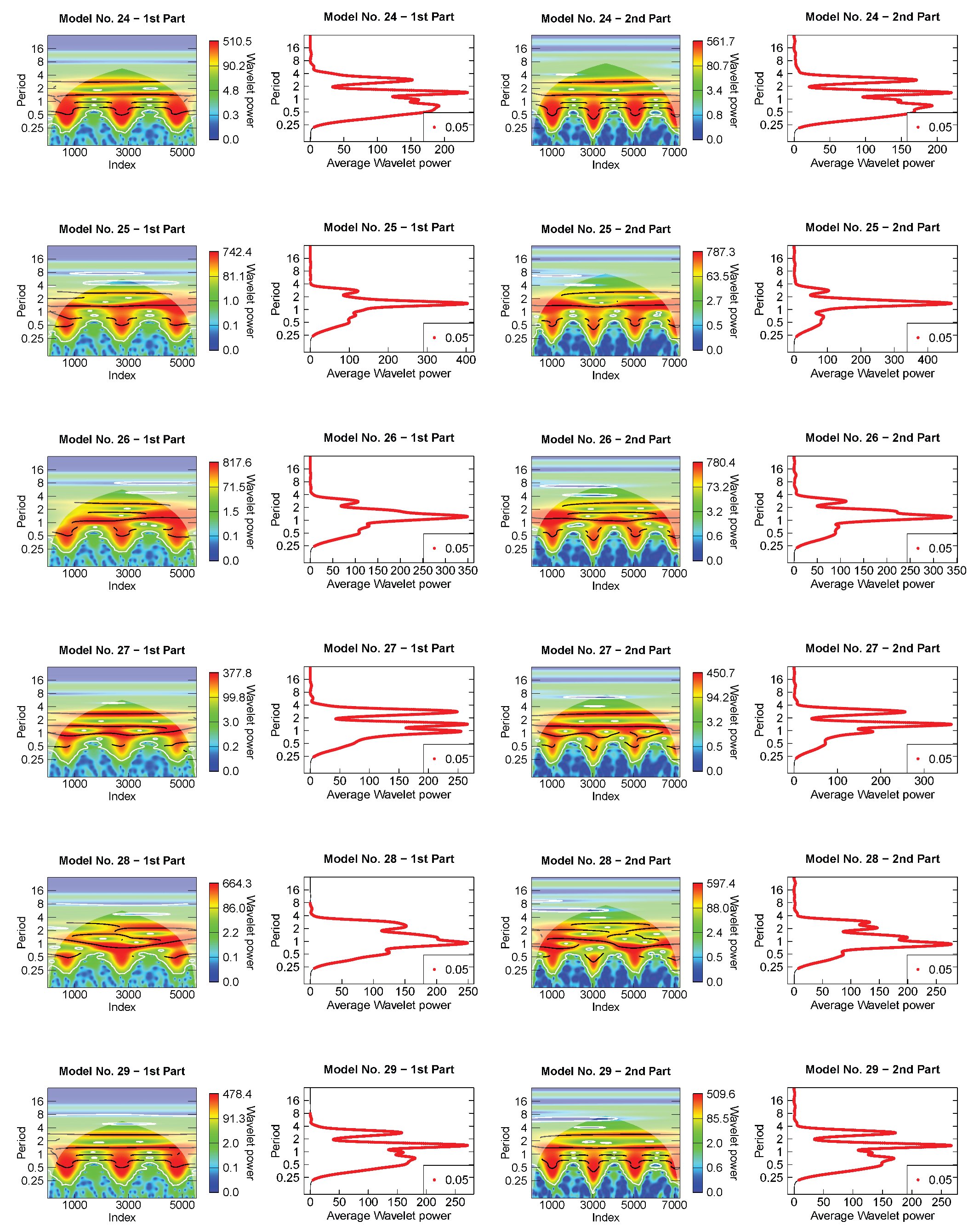
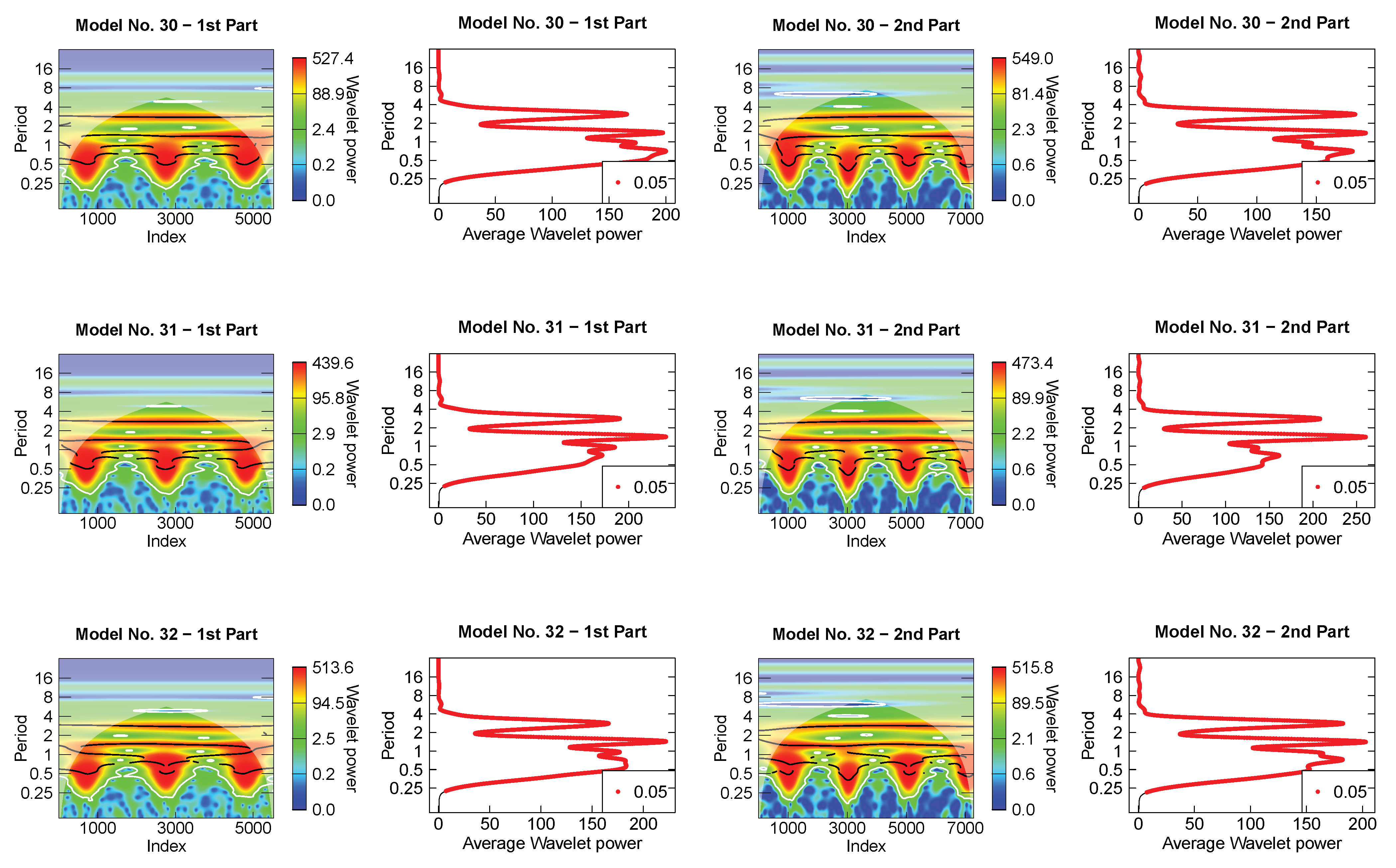
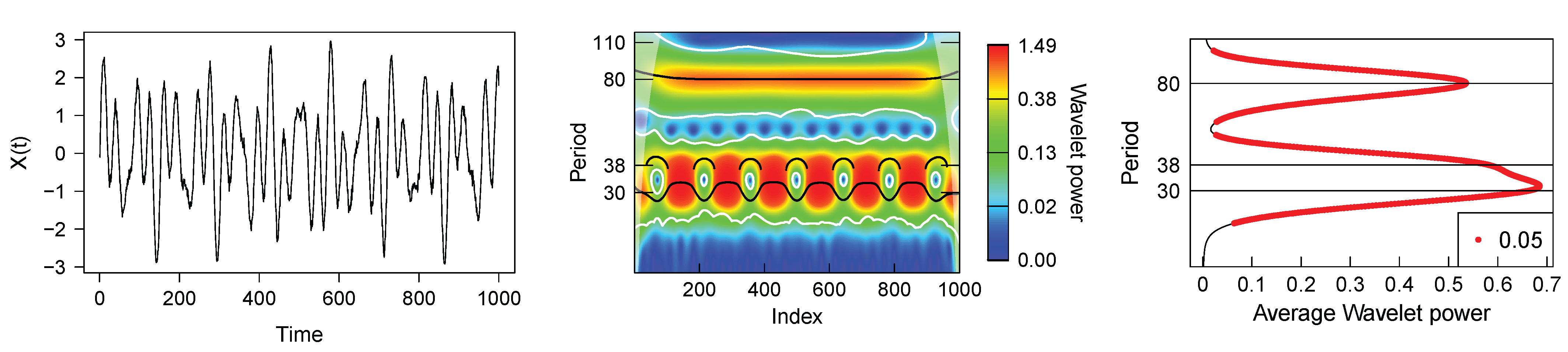
- For the wavelet analysis, each light-curve model was separated into two parts because they present a discontinuity (or a gap) in the time sequence (see Figure 3). For all periods that showed a maximum average wavelet power greater than 10, the mean value of each period across time and its standard deviation were calculated as suggested by Roesch and Schmidbauer [51]. The latter was used as a measurement uncertainty of the period. They were considered more or less significant according to the color code of the scalogram, even those outside the cone of influence, since there is a significant improvement in the reconstruction of the light curves when considering those periods as well [37]. The period’s harmonics were identified for all independent periods. For the harmonics of the orbital period, we searched for the values included in the intervals with endpoints given by FWHM (see Table A2), where is an harmonic in the Model No. 0 and FWHM, being FWHM the full width at half maximum of a normal distribution with standard deviation at any expectation value.
- In the Fourier analysis, frequencies with a signal/noise ratio ≥ 5 were selected [57]. Then, the uncertainties of the frequencies were calculated following a nonlinear least squares fitting procedure available in the software [49]. According to Bognár, Zs. et al. [58] and Lenz and Breger [49], we accepted a peak as a combination of frequencies if the amplitudes of the main frequencies were greater than that of their presumed combination term and the difference between the observed and predicted frequency was not greater than the Rayleigh resolution criterion of the data sample. Once the independent frequencies were selected, we reported the corresponding periods.
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TESS | Transiting Exoplanet Survey Satellite |
| PHOEBE | PHysics Of Eclipsing BinariEs |
Appendix A. Fourier Analysis Results
| Model | Fixed Period Values [Days] | Frequencies [Days] | Indep. Period [Days] | Comment |
|---|---|---|---|---|
| No. 0 | 2.87 | 0.6970 ± 4 | ||
| 0.3473 ± 4 | 2.878 ± 3 | |||
| 1.3941 ± 3 | ||||
| 1.0467 ± 6 | ||||
| 2.0912 ± 7 | ||||
| 1.7419 ± 5 | ||||
| 2.4386 ± 1 | ||||
| 2.7883 ± 2 | ||||
| 3.1380 ± 1 | ||||
| 3.4824 ± 3 | ||||
| No. 1 | 3e–8.96–10 | 0.1079 ± 2 | 9.262 ± 1.3 | |
| 0.9036 ± 3 | 1.106 ± 2 | |||
| 0.3473 ± 4 | 2.878 ± 3 | |||
| 0.6970 ± 4 | ||||
| 1.3941 ± 5 | ||||
| 1.0467 ± 6 | ||||
| 2.0935 ± 7 | ||||
| 1.7438 ± 7 | ||||
| 2.4409 ± 9 | ||||
| 2.7883 ± 1.1 | ||||
| 0.0774 ± 1.3 | 12.911 ± 1 | |||
| 3.1380 ± 1.6 | ||||
| No. 2 | 7–7.70–10 | 0.1079 ± 2 | 9.262 ± 1 | |
| 0.6970 ± 3 | ||||
| 0.3473 ± 3 | 2.878 ± 1 | |||
| 1.3941 ± 4 | ||||
| 1.0467 ± 5 | ||||
| 2.0935 ± 6 | ||||
| 1.7438 ± 6 | ||||
| 0.1502 ± 6 | 6.657 ± 2 | |||
| 2.4409 ± 8 | ||||
| 2.7883 ± 9 | ||||
| No. 3 | 3e–2.12–4.42–8.96 | 0.1173 ± 2 | 8.521 ± 1 | |
| 0.3497 ± 3 | 2.859 ± 1 | |||
| 0.2182 ± 3 | 4.581 ± 1 | |||
| 0.6970 ± 3 | ||||
| 0.4717 ± 3 | 2.179 ± 2 | |||
| 1.3941 ± 4 | ||||
| 1.0467 ± 5 | ||||
| 2.0935 ± 6 | ||||
| 1.7438 ± 6 | ||||
| 2.4385 ± 8 | ||||
| 2.7883 ± 9 | ||||
| 0.0821 ± 1.2 | 12.173 ± 1 | |||
| No. 4 | 7–2.03–4.86–7.70 | 0.1338 ± 2 | 7.475 ± 1 | |
| 0.6971 ± 5 | 1.435 ± 1 | |||
| 0.2793 ± 4 | ||||
| 0.4228 ± 4 | 2.367 ± 2 | |||
| 1.3942 ± 5 | ||||
| 1.0468 ± 5 | ||||
| 1.7438 ± 6 | ||||
| 2.0912 ± 6 | ||||
| 0.0962 ± 6 | 10.391 ± 6 | |||
| 0.5632 ± 1 | ||||
| 2.4385 ± 1 | ||||
| 2.7883 ± 1 | ||||
| No. 5 | 3e–8.96–10 | 0.6970 ± 3.8 | ||
| 0.3497 ± 3.6 | 2.859 ± 3 | |||
| 1.3941 ± 4.7 | ||||
| 1.0468 ± 5 | ||||
| 2.0912 ± 6.2 | ||||
| 1.7439 ± 1 | ||||
| 0.1056 ± 7 | 9.467 ± 3 | |||
| 2.4409 ± 8.6 | ||||
| 2.7883 ± 9.6 | ||||
| 0.9083 ± 1.35 | 1.100 ± 1 | |||
| 3.1380 ± 1.49 | ||||
| No. 6 | 7–7.70–10 | 0.6970 ± 3.7 | ||
| 0.3497 ± 3 | 2.859 ± 3 | |||
| 1.3941 ± 4 | ||||
| 1.0467 ± 4 | ||||
| 2.0912 ± 6 | ||||
| 1.7438 ± 6 | ||||
| 2.4409 ± 8 | ||||
| 2.7883 ± 9 | 9.468 ± 3 | |||
| 3.1380 ± 1.4 | ||||
| 0.1502 ± 3.1 | 6.657 ± 1 | |||
| No. 7 | 3e–2.12–4.42–8.96 | 0.3497 ± 3 | 2.859 ± 3 | |
| 0.6970 ± 3 | ||||
| 1.3941 ± 4 | ||||
| 1.0467 ± 5 | ||||
| 2.0912 ± 6 | ||||
| 1.7438 ± 6 | ||||
| 2.4409 ± 8 | ||||
| 2.7883 ± 9 | ||||
| 0.1150 ± 1.1 | 8.695 ± 8 | |||
| 3.1380 ± 1 | ||||
| 0.2206 ± 3 | 4.532 ± 7 | |||
| 0.4717 ± 3 | 2.119 ± 3 | |||
| No. 8 | 7–2.03–4.86–7.70 | 0.6970 ± 3 | ||
| 0.3473 ± 3 | 2.859 ± 3 | |||
| 1.3941 ± 4 | ||||
| 1.0467 ± 5 | ||||
| 2.0912 ± 6 | ||||
| 1.7438 ± 6 | ||||
| 2.4409 ± 8 | ||||
| 2.7883 ± 9 | ||||
| 0.1361 ± 1.2 | 7.345 ± 6 | |||
| 3.1380 ± 1.4 | ||||
| 0.4905 ± 3.1 | 2.038 ± 4 | |||
| 0.2112 ± 3 | 4.734 ± 3 | |||
| No. 9 | –1.27–1.6 | 0.7017 ± 4 | ||
| 0.6196 ± 8 | 1.613 ± 2 | |||
| 0.7909 ± 8 | 1.264 ± 1 | |||
| 0.3473 ± 1 | 2.878 ± 8 | |||
| 1.3941 ± 1.3 | ||||
| 1.0468 ± 1.4 | ||||
| 2.0936 ± 1.7 | ||||
| 1.7439 ± 1.7 | ||||
| 2.4386 ± 2.4 | ||||
| 2.7883 ± 2.7 | ||||
| 3.1380 ± 4.1 | ||||
| No. 10 | 1.2–1.32–1.6 | 0.8308 ± 4 | 1.203 ± 1 | |
| 0.3473 ± 7 | 2.878 ± 6 | |||
| 0.6243 ± 5 | 1.601 ± 1 | |||
| 1.3941 ± 9 | ||||
| 0.7416 ± 5 | 1.348 ± 1 | |||
| 1.0468 ± 1 | ||||
| 2.0912 ± 1 | ||||
| 1.7415 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 2.4386 ± 1 | ||||
| No. 11 | –0.94–2.78–1.27 | 0.6970 ± 4 | 1.434 ± 1 | |
| 0.3544 ± 4 | 2.821 ± 3 | |||
| 1.0515 ± 5 | 0.951 ± 1 | |||
| 0.7886 ± 5 | 1.268 ± 1 | |||
| 1.3941 ± 9 | ||||
| 2.0936 ± 1 | ||||
| 1.7415 ± 1 | ||||
| 2.4386 ± 1 | ||||
| 2.7883 ± 2 | ||||
| No. 12 | 1.2–0.84–2.06–1.32 | 0.8355 ± 7 | 1.196 ± 1 | |
| 0.3473 ± 8 | 2.878 ± 6 | |||
| 0.4858 ± 8 | 2.058 ± 3 | |||
| 1.1759 ± 8 | 0.850 ± 1 | |||
| 1.3918 ± 1 | ||||
| 1.0468 ± 1 | ||||
| 0.7011 ± 1 | ||||
| 2.0912 ± 1 | ||||
| 1.7415 ± 1 | ||||
| 2.4409 ± 2 | ||||
| 2.7883 ± 2 | ||||
| 0.7440 ± 2 | 1.344 ± 1 | |||
| 3.1380 ± 3 | ||||
| No. 13 | –1.27–1.6 | 0.6970 ± 4 | ||
| 0.3473 ± 4 | 2.878 ± 3 | |||
| 1.3941 ± 5 | ||||
| 1.0468 ± 6 | ||||
| 2.0912 ± 7 | ||||
| 1.7439 ± 7 | ||||
| 2.4386 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 3.1380 ± 1 | ||||
| 0.6219 ± 1 | 1.607 ± 4 | |||
| 3.4854 ± 2 | ||||
| 0.7909 ± 1 | 1.264 ± 2 | |||
| No. 14 | 1.2–1.32–1.6 | 0.3473 ± 4 | 2.878 ± 3 | |
| 1.3941 ± 5 | ||||
| 0.6994 ± 4 | ||||
| 1.0467 ± 5 | ||||
| 2.0912 ± 7 | ||||
| 1.7438 ± 7 | ||||
| 2.4409 ± 1 | ||||
| 0.8332 ± 1 | 1.200 ± 1 | |||
| 2.7883 ± 1 | ||||
| 3.1380 ± 1 | ||||
| 3.4853 ± 2 | ||||
| 0.6290 ± 1 | 1.589 ± 4 | |||
| 0.7557 ± 2 | 1.323 ± 3 | |||
| No. 15 | –0.94–2.78–1.27 | 0.6970 ± 4 | ||
| 0.3497 ± 4 | 2.8594 ± 3 | |||
| 1.3941 ± 6 | ||||
| 1.0468 ± 6 | ||||
| 2.0912 ± 9 | ||||
| 1.7439 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 3.1380 ± 2 | ||||
| 0.7886 ± 2 | 1.268 ± 1 | |||
| 3.4854 ± 2 | ||||
| No. 16 | 1.2–0.84–2.06–1.32 | 0.3473 ± 5 | 2.878 ± 3 | |
| 0.6970 ± 5 | ||||
| 1.3941 ± 6 | ||||
| 1.0467 ± 7 | ||||
| 2.0912 ± 8 | ||||
| 1.7438 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 0.8308 ± 2 | 1.203 ± 1 | |||
| 3.1380 ± 2 | ||||
| 3.4853 ± 2 | ||||
| 0.4881 ± 2 | 2.048 ± 5 | |||
| 1.1805 ± 2 | 0.847 ± 1 | |||
| 0.7510 ± 2 | 1.331 ± 3 | |||
| No. 17 | 3e–10 | 0.9036 ± 4 | 1.106 ± 2 | |
| 0.0985 ± 4 | 10.144 ± 4 | |||
| 0.6970 ± 6 | ||||
| 0.3497 ± 6 | 2.859 ± 1 | |||
| 1.3941 ± 7 | ||||
| 1.0468 ± 8 | ||||
| 2.0912 ± 1 | ||||
| 1.7439 ± 1 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 2 | ||||
| 3.1380 ± 2 | ||||
| No. 18 | 7–10 | 0.1502 ± 4 | 6.657 ± 1 | |
| 0.1009 ± 4 | 9.908 ± 4 | |||
| 0.6979 ± 6 | ||||
| 0.3473 ± 5 | 2.878 ± 1 | |||
| 1.3941 ± 7 | ||||
| 1.0468 ± 8 | ||||
| 2.0912 ± 9 | ||||
| 1.7439 ± 9 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 3.1380 ± 2 | ||||
| No. 19 | 3e–2.12–4.42 | 0.3497 ± 6 | 2.878 ± 3 | |
| 0.2182 ± 7 | 4.581 ± 1 | |||
| 0.4717 ± 7 | 2.119 ± 3 | |||
| 0.6970 ± 7 | ||||
| 0.1173 ± 7 | 8.521 ± 5 | |||
| 1.3941 ± 8 | ||||
| 1.0467 ± 9 | ||||
| 2.0935 ± 1 | ||||
| 1.7438 ± 1 | ||||
| 2.4385 ± 1 | ||||
| 2.7883 ± 2 | ||||
| 3.1380 ± 2 | ||||
| No. 20 | 7–2.03–4.86 | 0.1408 ± 1 | 7.101 ± 5 | |
| 0.6970 ± 1 | 1.434 ± 2 | |||
| 0.2792 ± 1 | ||||
| 0.4224 ± 9 | ||||
| 1.3941 ± 1 | ||||
| 1.0467 ± 1 | ||||
| 1.7438 ± 1 | ||||
| 2.0912 ± 2 | ||||
| 0.5609 ± 1 | ||||
| 2.4409 ± 2 | ||||
| 2.7883 ± 2 | ||||
| 0.2041 ± 1 | 4.897 ± 3 | |||
| No. 21 | 3e–10 | 0.6970 ± 5 | ||
| 0.3473 ± 4 | 2.878 ± 4 | |||
| 1.3941 ± 6 | ||||
| 1.0467 ± 6 | ||||
| 2.0912 ± 8 | ||||
| 1.7438 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 0.9059 ± 1 | 1.103 ± 1 | |||
| 3.1380 ± 2 | ||||
| 0.0985 ± 1 | 10.144 ± 1.8 | |||
| No. 22 | 7–10 | 0.6970 ± 5 | ||
| 0.3473 ± 4 | 2.878 ± 4 | |||
| 1.3941 ± 6 | ||||
| 1.0467 ± 6 | ||||
| 2.0912 ± 8 | ||||
| 1.7438 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 0.1478 ± 1 | 6.762 ± 8 | |||
| 3.1380 ± 2 | ||||
| 0.1009 ± 1 | 9.908 ± 1.7 | |||
| No. 23 | 3e–2.12–4.42 | 0.3473 ± 4 | 2.878 ± 4 | |
| 0.6970 ± 5 | ||||
| 1.3941 ± 6 | ||||
| 1.0467 ± 6 | ||||
| 2.0912 ± 8 | ||||
| 1.7438 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 3.1380 ± 2 | ||||
| 0.2182 ± 2 | 4.581 ± 5 | |||
| 0.4717 ± 3 | 2.119 ± 1 | |||
| 0.1173 ± 3 | 8.521 ± 1.8 | |||
| No. 24 | 7–2.03–4.86 | 0.6970 ± 7 | ||
| 0.3473 ± 7 | 2.878 ± 1 | |||
| 1.3941 ± 9 | ||||
| 1.0467 ± 1 | ||||
| 2.0912 ± 1 | ||||
| 1.7438 ± 1 | ||||
| 2.4409 ± 2 | ||||
| 2.7883 ± 2 | ||||
| 3.1380 ± 3 | ||||
| 0.1408 ± 3 | 7.101 ± 1.6 | |||
| 0.4881 ± 3 | 2.048 ± 2 | |||
| No. 25 | –1.6 | 0.7064 ± 2 | ||
| 0.6243 ± 4 | 1.601 ± 1 | |||
| 0.3473 ± 5 | 2.878 ± 3 | |||
| 1.3941 ± 7 | ||||
| 1.0444 ± 7 | ||||
| 2.0912 ± 9 | ||||
| 1.7438 ± 9 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| No. 26 | 1.2–1.6 | 0.8332 ± 4 | 1.200 ± 1 | |
| 0.3473 ± 6 | 2.878 ± 4 | |||
| 0.6219 ± 4 | 1.607 ± 1 | |||
| 1.3941 ± 7 | ||||
| 0.6970 ± 6 | ||||
| 1.0467 ± 8 | ||||
| 2.0912 ± 1 | ||||
| 1.7438 ± 1 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 3.1380 ± 2 | ||||
| No. 27 | –0.94–2.78 | 0.7017 ± 5 | ||
| 0.3544 ± 4 | 2.821 ± 3 | |||
| 1.0514 ± 6 | 0.951 ± 1 | |||
| 1.3941 ± 1 | ||||
| 2.0912 ± 1 | ||||
| 1.7438 ± 2 | ||||
| 2.4409 ± 2 | ||||
| 2.7883 ± 2 | ||||
| 3.1380 ± 3 | ||||
| No. 28 | 1.2–0.84–2.06 | 0.3473 ± 6 | 2.878 ± 4 | |
| 0.8355 ± 6 | 1.196 ± 1 | |||
| 1.1782 ± 6 | 0.848 ± 1 | |||
| 0.4834 ± 6 | 2.068 ± 2 | |||
| 0.6970 ± 6 | ||||
| 1.3941 ± 8 | ||||
| 1.0467 ± 8 | ||||
| 2.0912 ± 1 | ||||
| 1.7438 ± 1 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 2 | ||||
| 3.1380 ± 3 | ||||
| No. 29 | –1.6 | 0.3473 ± 4 | 2.878 ± 3 | |
| 0.6994 ± 4 | ||||
| 1.3941 ± 6 | ||||
| 1.0468 ± 6 | ||||
| 2.0912 ± 8 | ||||
| 1.7439 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 3.1380 ± 2 | ||||
| 0.6243 ± 1 | 1.601 ± 4 | |||
| No. 30 | 1.2–1.6 | 0.3473 ± 4 | 2.878 ± 3 | |
| 0.6970 ± 5 | ||||
| 1.3941 ± 6 | ||||
| 1.0467 ± 6 | ||||
| 2.0912 ± 8 | ||||
| 1.7438 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 0.8332 ± 2 | 1.200 ± 2 | |||
| 3.1380 ± 2 | ||||
| 0.6243 ± 2 | 1.601 ± 3 | |||
| No. 31 | –0.94–2.78 | 0.3497 ± 4 | 2.859 ± 3 | |
| 0.6994 ± 4 | ||||
| 1.3941 ± 6 | ||||
| 1.0468 ± 6 | ||||
| 2.0912 ± 8 | ||||
| 1.7439 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 3.1380 ± 2 | ||||
| No. 32 | 1.2–0.84–2.06 | 0.3473 ± 5 | 2.878 ± 4 | |
| 0.6947 ± 5 | ||||
| 1.3941 ± 6 | ||||
| 1.0467 ± 7 | ||||
| 2.0912 ± 9 | ||||
| 1.7438 ± 8 | ||||
| 2.4409 ± 1 | ||||
| 2.7883 ± 1 | ||||
| 3.1380 ± 2 | ||||
| 3.4853 ± 2 | ||||
| 1.1805 ± 3 | 0.847 ± 1 | |||
| 0.4834 ± 3 | 2.068 ± 1 | |||
| 0.8332 ± 3 | 1.200 ± 3 |

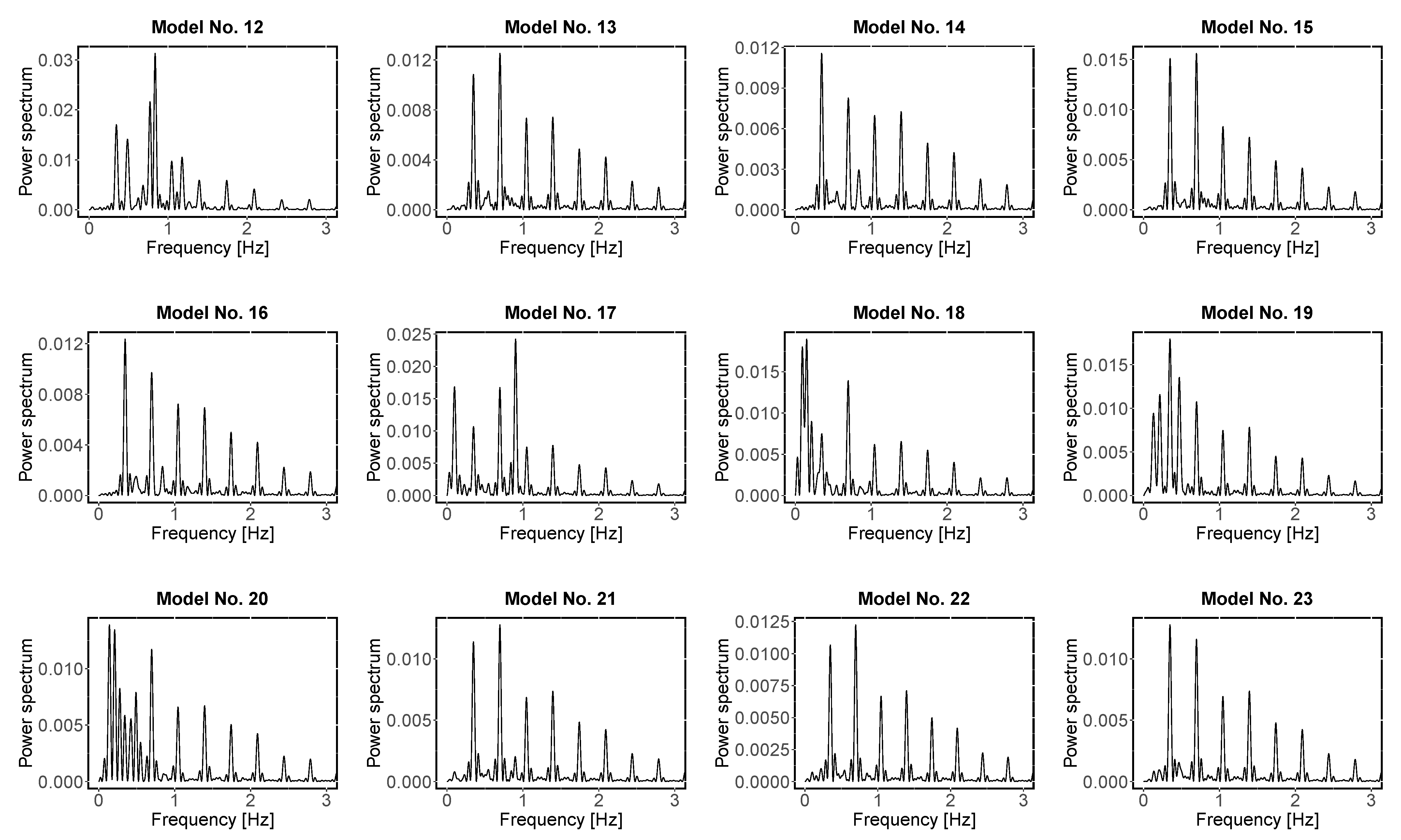
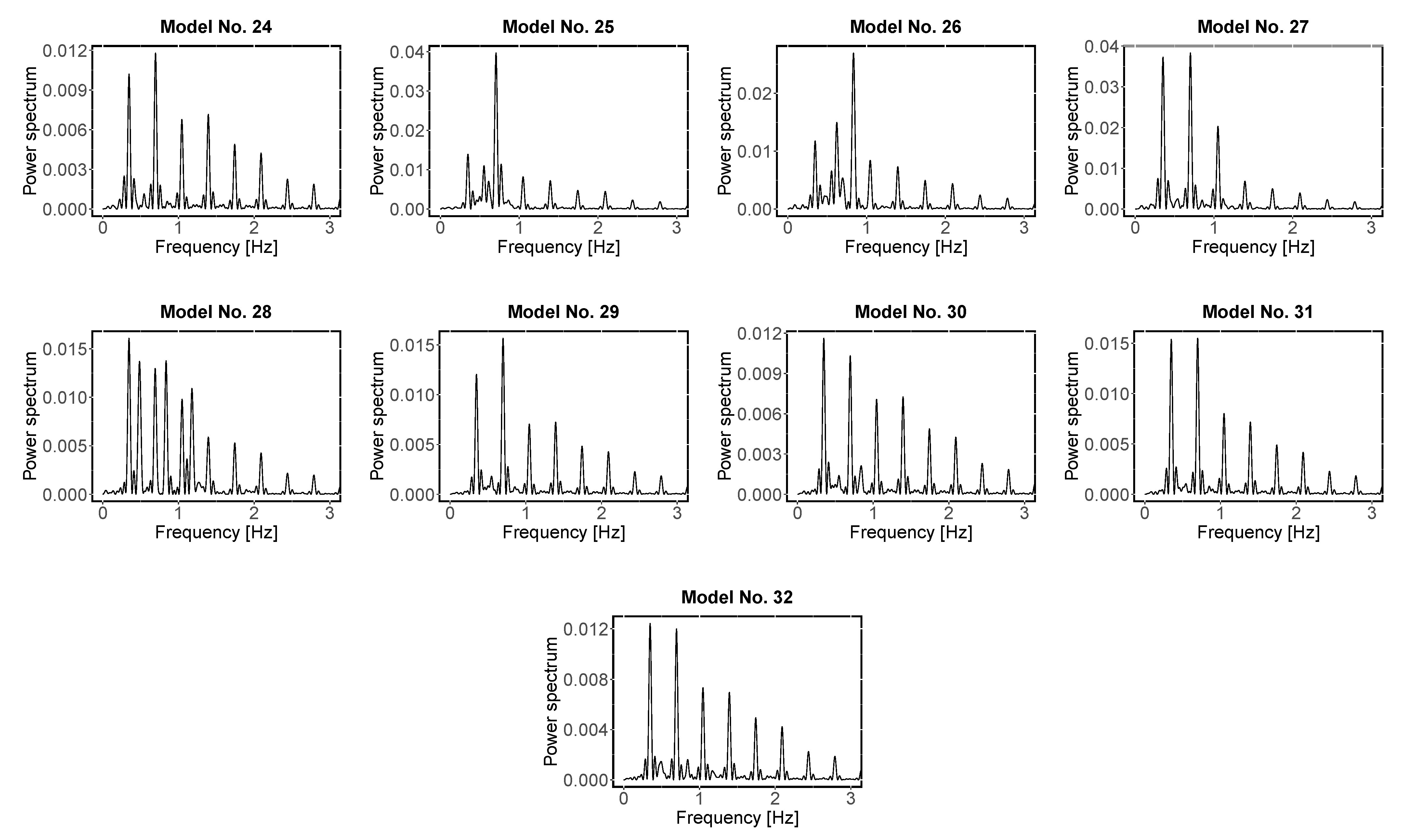
Appendix B. Wavelet Analysis Results
| Model | Fixed Period Values [Days] | Periods [Days] | Comment | |
|---|---|---|---|---|
| First Part | Second Part | |||
| No. 0 | 2.87 | 0.548 ± 2.9 | 0.539 ± 7.3 | |
| 0.728 ± 1.62 | 0.72 ± 5.4 | |||
| 0.979 ± 1.52 | 0.943 ± 2.3 | |||
| 1.43 ± 2.28 | 1.442 ± 3.8 | |||
| 2.785 ± 2.4 | 2.811 ± 7.2 | |||
| No. 1 | 3e–8.96–10 | |||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| No. 2 | 7–7.70–10 | ⋯ | ||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| No. 3 | 3e–2.12–4.42–8.96 | |||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| No. 4 | 7–2.03–4.86–7.70 | |||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| No. 5 | 3e–8.96–10 | |||
| ⋯ | ||||
| ⋯ | ||||
| No. 6 | 7–7.70–10 | |||
| No. 7 | 3e–2.12–4.42–8.96 | |||
| No. 8 | 7–2.03–4.86–7.70 | |||
| No. 9 | –1.27–1.6 | |||
| No. 10 | 1.2–1.32–1.6 | |||
| ⋯ | ||||
| No. 11 | –0.94–2.78–1.27 | |||
| ⋯ | ||||
| No. 12 | 1.2–0.84–2.06–1.32 | ⋯ | ||
| No. 13 | –1.27–1.6 | |||
| No. 14 | 1.2–1.32–1.6 | |||
| No. 15 | –0.94–2.78–1.27 | |||
| No. 16 | 1.2–0.84–2.06–1.32 | |||
| No. 17 | 3e–10 | |||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| No. 18 | 7–10 | ⋯ | ||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| No. 19 | 3e–2.12–4.42 | |||
| ⋯ | ||||
| ⋯ | ||||
| No. 20 | 7–2.03–4.86 | |||
| No. 21 | 3e–10 | |||
| ⋯ | ||||
| No. 22 | 7–10 | |||
| ⋯ | ||||
| No. 23 | 3e–2.12–4.42 | |||
| No. 24 | 7–2.03–4.86 | |||
| No. 25 | –1.6 | |||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| No. 26 | 1.2–1.6 | |||
| ⋯ | ||||
| ⋯ | ||||
| No. 27 | –0.94–2.78 | |||
| No. 28 | 1.2–0.84–2.06 | |||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| No. 29 | –1.6 | |||
| No. 30 | 1.2–1.6 | |||
| No. 31 | –0.94–2.78 | |||
| No. 32 | 1.2–0.84–2.06 | |||
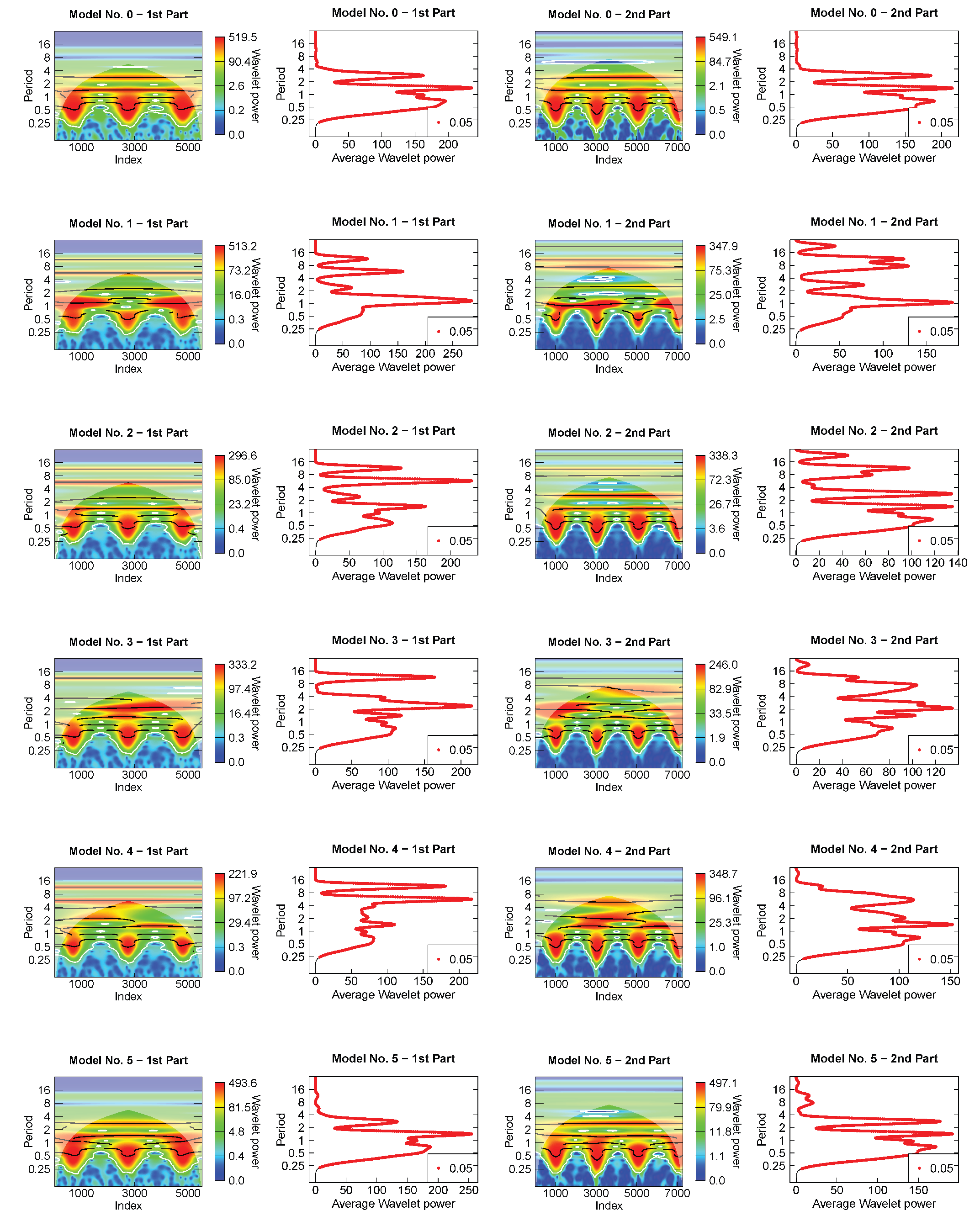
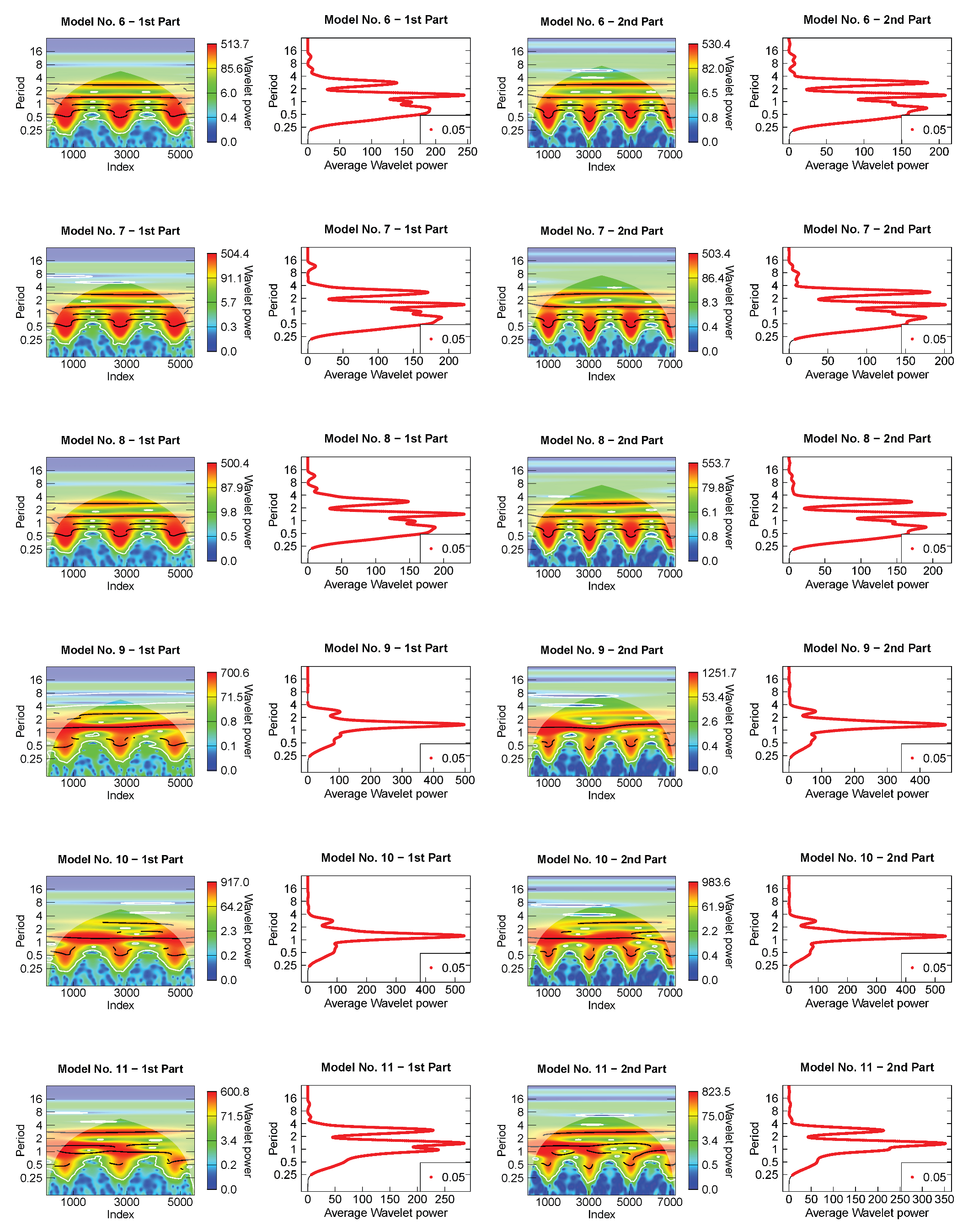
| 1 | The search for the most important factors that may be varied in a simulated system. |
References
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Le Bouquin, J.B.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444. [Google Scholar] [CrossRef]
- Mason, B.D.; Hartkopf, W.I.; Henry, T.J.; Jao, W.C.; Subasavage, J.; Riedel, A.; Winters, J. Nearby Dwarf Stars: Duplicity, Binarity, and Masses. Noao Propos. 2009, 2009B-0044, 44. [Google Scholar]
- Sana, H.; Le Bouquin, J.B.; Lacour, S.; Berger, J.P.; Duvert, G.; Gauchet, L.; Norris, B.; Olofsson, J.; Pickel, D.; Zins, G.; et al. Southern Massive Stars at High Angular Resolution: Observational Campaign and Companion Detection. Astrophys. J. Suppl. Ser. 2014, 215, 15. [Google Scholar] [CrossRef]
- Dunstall, P.R.; Dufton, P.L.; Sana, H.; Evans, C.J.; Howarth, I.D.; Simón-Díaz, S.; de Mink, S.E.; Langer, N.; Maíz Apellániz, J.; Taylor, W.D. The VLT-FLAMES Tarantula Survey. XXII. Multiplicity properties of the B-type stars. Astron. Astrophys. 2015, 580, A93. [Google Scholar] [CrossRef]
- Villaseñor, J.I.; Taylor, W.D.; Evans, C.J.; Ramírez-Agudelo, O.H.; Sana, H.; Almeida, L.A.; de Mink, S.E.; Dufton, P.L.; Langer, N. The B-type binaries characterization programme I. Orbital solutions for the 30 Doradus population. Mon. Not. R. Astron. Soc. 2021, 507, 5348–5375. [Google Scholar] [CrossRef]
- Barbá, R.H.; Gamen, R.; Arias, J.I.; Morrell, N.I. OWN Survey: A spectroscopic monitoring of Southern Galactic O and WN-type stars. In Proceedings of the The Lives and Death-Throes of Massive Stars; Eldridge, J.J., Bray, J.C., McClelland, L.A.S., Xiao, L., Eds.; Cambridge University Press: Cambridge, UK, 2017; Volume 329, pp. 89–96. [Google Scholar] [CrossRef]
- Godart, M.; Grotsch-Noels, A.; Dupret, M.A. Pulsations in hot supergiants. In Proceedings of the Precision Asteroseismology; Guzik, J.A., Chaplin, W.J., Handler, G., Pigulski, A., Eds.; Cambridge University Press: Cambridge, UK, 2014; Volume 301, pp. 313–320. [Google Scholar] [CrossRef]
- Saio, H.; Kuschnig, R.; Gautschy, A.; Cameron, C.; Walker, G.A.H.; Matthews, J.M.; Guenther, D.B.; Moffat, A.F.J.; Rucinski, S.M.; Sasselov, D.; et al. MOSTDetectsg- andp-Modes in the B Supergiant HD 163899 (B2 Ib/II). Astrophys. J. 2006, 650, 1111–1118. [Google Scholar] [CrossRef]
- Mennickent, R.E.; Kołaczkowski, Z.; Soszyński, I.; Cabezas, M.; Garrido, H.E. The SMC B-type supergiant AzV322: A g-mode pulsator with a circumstellar disc. Mon. Not. R. Astron. Soc. 2018, 473, 4055–4063. [Google Scholar] [CrossRef]
- Glatzel, W. Nonlinear strange-mode pulsations. Commun. Asteroseismol. 2009, 158, 252. [Google Scholar]
- Godart, M.; Dupret, M.A.; Noels, A.; Aerts, C.; Simón-Díaz, S.; Lefever, K.; Puls, J.; Montalban, J.; Ventura, P. Pulsations in massive stars: Effect of the atmosphere on the strange mode pulsations. In Proceedings of the Active OB Stars: Structure, Evolution, Mass Loss, and Critical Limits; Neiner, C., Wade, G., Meynet, G., Peters, G., Eds.; Cambridge University Press: Cambridge, UK, 2011; Volume 272, pp. 503–504. [Google Scholar] [CrossRef]
- Kraus, M.; Haucke, M.; Cidale, L.S.; Venero, R.O.J.; Nickeler, D.H.; Németh, P.; Niemczura, E.; Tomić, S.; Aret, A.; Kubát, J.; et al. Interplay between pulsations and mass loss in the blue supergiant 55 Cygnus = HD 198 478. Astron. Astrophys. 2015, 581, A75. [Google Scholar] [CrossRef]
- Yadav, A.P.; Glatzel, W. Stability analysis, non-linear pulsations and mass loss of models for 55 Cygni (HD 198478). Mon. Not. R. Astron. Soc. 2016, 457, 4330–4339. [Google Scholar] [CrossRef]
- Sterken, C. Some thoughts on pulsation and binarity. Astrophys. Space Sci. 2006, 304, 139–143. [Google Scholar] [CrossRef]
- Simón-Díaz, S.; Herrero, A.; Uytterhoeven, K.; Castro, N.; Aerts, C.; Puls, J. Observational Evidence for a Correlation Between Macroturbulent Broadening and Line-profile Variations in OB Supergiants. Astrophys. J. Lett. 2010, 720, L174–L178. [Google Scholar] [CrossRef]
- Aerts, C.; Puls, J.; Godart, M.; Dupret, M.A. Collective pulsational velocity broadening due to gravity modes as a physical explanation for macroturbulence in hot massive stars. Astron. Astrophys. 2009, 508, 409–419. [Google Scholar] [CrossRef]
- Shibahashi, H.; Kurtz, D.W. FM stars: A Fourier view of pulsating binary stars, a new technique for measuring radial velocities photometrically. Mon. Not. R. Astron. Soc. 2012, 422, 738–752. [Google Scholar] [CrossRef]
- Murphy, S. Pulsating stars in binary systems: A review. arXiv 2018. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-Squares Frequency Analysis of Unequally Spaced Data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. Part 1 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Hübner, M.; Huppenkothen, D.; Lasky, P.D.; Inglis, A.R. Pitfalls of Periodograms: The Nonstationarity Bias in the Analysis of Quasiperiodic Oscillations. Astrophys. J. Suppl. Ser. 2022, 259, 32. [Google Scholar] [CrossRef]
- Foster, G. Wavelets for period analysis of unevenly sampled time series. Astron. J. 1996, 112, 1709–1729. [Google Scholar] [CrossRef]
- López-Santiago, J. On the use of wavelets to reveal oscillatory patterns in stellar flare emission. Philos. Trans. R. Soc. Lond. Ser. A 2018, 376, 20170253. [Google Scholar] [CrossRef]
- Zhou, A.Y.; Hintz, E.G.; Schoonmaker, J.N.; Rodríguez, E.; Costa, V.; Lopez-Gonzalez, M.J.; Smith, H.A.; Sanders, N.; Monninger, G.; Pagel, L. A Pulsational Time-evolution Study for the δ Scuti Star AN Lyncis. arXiv 2017. [Google Scholar] [CrossRef]
- Bravo, J.P.; Roque, S.; Estrela, R.; Leã o, I.C.; Medeiros, J.R.D. Wavelets: A powerful tool for studying rotation, activity, and pulsation in Kepler and CoRoT stellar light curves. Astron. Astrophys. 2014, 568, A34. [Google Scholar] [CrossRef]
- Graham, M.J.; Drake, A.J.; Djorgovski, S.G.; Mahabal, A.A.; Donalek, C.; Duan, V.; Maker, A. A comparison of period finding algorithms. Mon. Not. R. Astron. Soc. 2013, 434, 3423–3444. [Google Scholar] [CrossRef]
- Frescura, F.A.M.; Engelbrecht, C.A.; Frank, B.S. Significance of periodogram peaks and a pulsation mode analysis of the Beta Cephei star V403 Car. Mon. Not. R. Astron. Soc. Mon. Not. R. Astron. Soc. 2008, 388, 1693–1707. [Google Scholar] [CrossRef]
- Votruba, V.; Koubský, P.; Korčáková, D.; Hroch, F. False periods in complex chaotic systems. Astron. Astrophys. 2009, 496, 217–222. [Google Scholar] [CrossRef]
- Baluev, R.V. Distinguishing between a true period and its alias, and other tasks of model discrimination. Mon. Not. R. Astron. Soc. 2012, 422, 2372–2385. [Google Scholar] [CrossRef]
- Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.M. Wavelets and Their Applications; Iste: London, UK, 2007. [Google Scholar]
- Stéphane, M. Discrete Revolution. In A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 2009; pp. 59–88. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; CBMS-NSF Regional Conference Series in Applied Mathematics, Society for Industrial and Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley and Sons (WIE): Brisbane, Australia, 2000. [Google Scholar]
- Box, G.E.P.; Hunter, J.S.; Hunter, W.G. Statistics for Experimenters, 2nd ed.; Wiley Series in Probability and Statistics; Wiley-Blackwell: Chichester, UK, 2005. [Google Scholar]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS); SPIE: Bellingham, WA, USA, 2014; Volume 9143, p. 914320. [Google Scholar] [CrossRef]
- Kallrath, J.; Milone, E.F. TheWilson–Devinney Program: Extensions and Applications. In Eclipsing Binary Stars: Modeling and Analysis; Springer New York: New York, NY, USA, 2009; pp. 305–330. [Google Scholar] [CrossRef]
- Alberici, A.A. Uso Del anáLisis Wavelet Para La Detección De Períodos En Curvas De Luz. Master’s Thesis, Facultad de Ciencias Astronómicas y Geofísicas, Buenos Aires, Argentina, 2022. [Google Scholar]
- Wecht, K. Determination of Mass Loss and Mass Transfer Rates of Algol (Beta Persei) from the Analysis of Absorption Lines in the UV Spectra Obtained by the IUE Satellite. Doctoral Dissertation, Cornell University, Bethlehem, PA, USA, 2006. [Google Scholar]
- Feigelson, E.D.; Babu, G.J.; Caceres, G.A. Autoregressive times series methods for time domain astronomy. Front. Phys. 2018, 6, 80. [Google Scholar] [CrossRef]
- Caceres, G.A.; Feigelson, E.D.; Babu, G.J.; Bahamonde, N.; Christen, A.; Bertin, K.; Meza, C.; Curé, M. Autoregressive Planet Search: Application to the Kepler Mission. Astron. J. 2019, 158, 58. [Google Scholar] [CrossRef]
- Whittle, P. Hypothesis Testing in Time Series Analysis; Almqvist & Wiksell: Stockholm, Sweden, 1951. [Google Scholar]
- Caceres, G.A.; Feigelson, E.D.; Babu, G.J.; Bahamonde, N.; Christen, A.; Bertin, K.; Meza, C.; Curé, M. Autoregressive Planet Search: Methodology. Astron. J. 2019, 158, 57. [Google Scholar] [CrossRef]
- Shi, X.; Qian, S.; Li, L. New Pulsating Stars Detected in EA-type Eclipsing-binary Systems Based on TESS Data. Astrophys. J. 2022, 259, 50. [Google Scholar] [CrossRef]
- McLaughlin, J.A.; Nakariakov, V.M.; Dominique, M.; Jelínek, P.; Takasao, S. Modelling Quasi-Periodic Pulsations in Solar and Stellar Flares. Space Sci. Rev. 2018, 214, 45. [Google Scholar] [CrossRef]
- van Leeuwen, F.; van Genderen, A.M.; Zegelaar, I. HIPPARCOS photometry of 24 variable massive stars (alpha Cygni variables). Astron. Astrophys. Suppl. Ser. 1998, 128, 117–129. [Google Scholar] [CrossRef]
- Saio, H.; Georgy, C.; Meynet, G. Strange-Mode Instability for Micro-Variations in Luminous Blue Variables. arXiv 2013. [Google Scholar] [CrossRef]
- Nieto, N.; Orozco, D.M. El uso de la transformada wavelet discreta en la reconstrucción de señales senosoidales. Sci. Tech. 2008, 14, 381–386. [Google Scholar]
- Castro, L.; Castro, S. Wavelets y Sus Aplicaciones; Universidad Nacional de Colombia: Bogota, Colombia, 1995. [Google Scholar]
- Lenz, P.; Breger, M. Period04 User Guide. Commun. Asteroseismol. 2005, 146, 53–136. [Google Scholar] [CrossRef]
- Contreras, J.M.; Molina Portillo, E.; Arteaga Cezón, P. Introducción a La Programación Estadística Con R Para Profesores. 2010. Available online: https://1library.co/document/z14pk5dz-introducci%C3%B3n-programaci%C3%B3n-estad%C3%ADstica-profesores-contreras-garc%C3%ADa-portillo-arteaga.html (accessed on 1 May 2023).
- Roesch, A.; Schmidbauer, H. WaveletComp: ComputationalWavelet Analysis. R Package Version 1.1. 2018. Available online: https://cran.r-project.org/web/packages/WaveletComp/index.html (accessed on 1 May 2023).
- Polanco-Martinez, J.M. Análisis espectral de wavelet: Una concisa revisión. Rev. Climatol. 2022, 22, 51–95. [Google Scholar]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Meyers, S.D.; Kelly, B.G.; O’Brien, J.J. An Introduction to Wavelet Analysis in Oceanography and Meteorology: With Application to the Dispersion of Yanai Waves. Mon. Weather Rev. 1993, 121, 2858–2866. [Google Scholar] [CrossRef]
- Deeming, T.J. Fourier Analysis with Unequally-Spaced Data. Astrophys. Space Sci. 1975, 36, 137–158. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Baran, A.S.; Koen, C. A Detection Threshold in the Amplitude Spectra Calculated from TESS Time-Series Data. Acta Astron. 2021, 71, 113–121. [Google Scholar] [CrossRef]
- Bognár, Z.; Lampens, P.; Frémat, Y.; Southworth, J.; Sódor, Á.; De Cat, P.; Isaacson, H.T.; Marcy, G.W.; Ciardi, D.R.; Gilliland, R.L.; et al. KIC3489: A genuine adusScuti Kepler hybrid pulsator with transit events. Astron. Astrophys. 2015, 581, A77. [Google Scholar] [CrossRef]
- Distefano, E.; Lanzafame, A.C.; Lanza, A.F.; Messina, S.; Korn, A.J.; Eriksson, K.; Cuypers, J. Determination of rotation periods in solar-like stars with irregular sampling: The Gaia case. Mon. Not. R. Astron. Soc. 2012, 421, 2774–2785. [Google Scholar] [CrossRef]

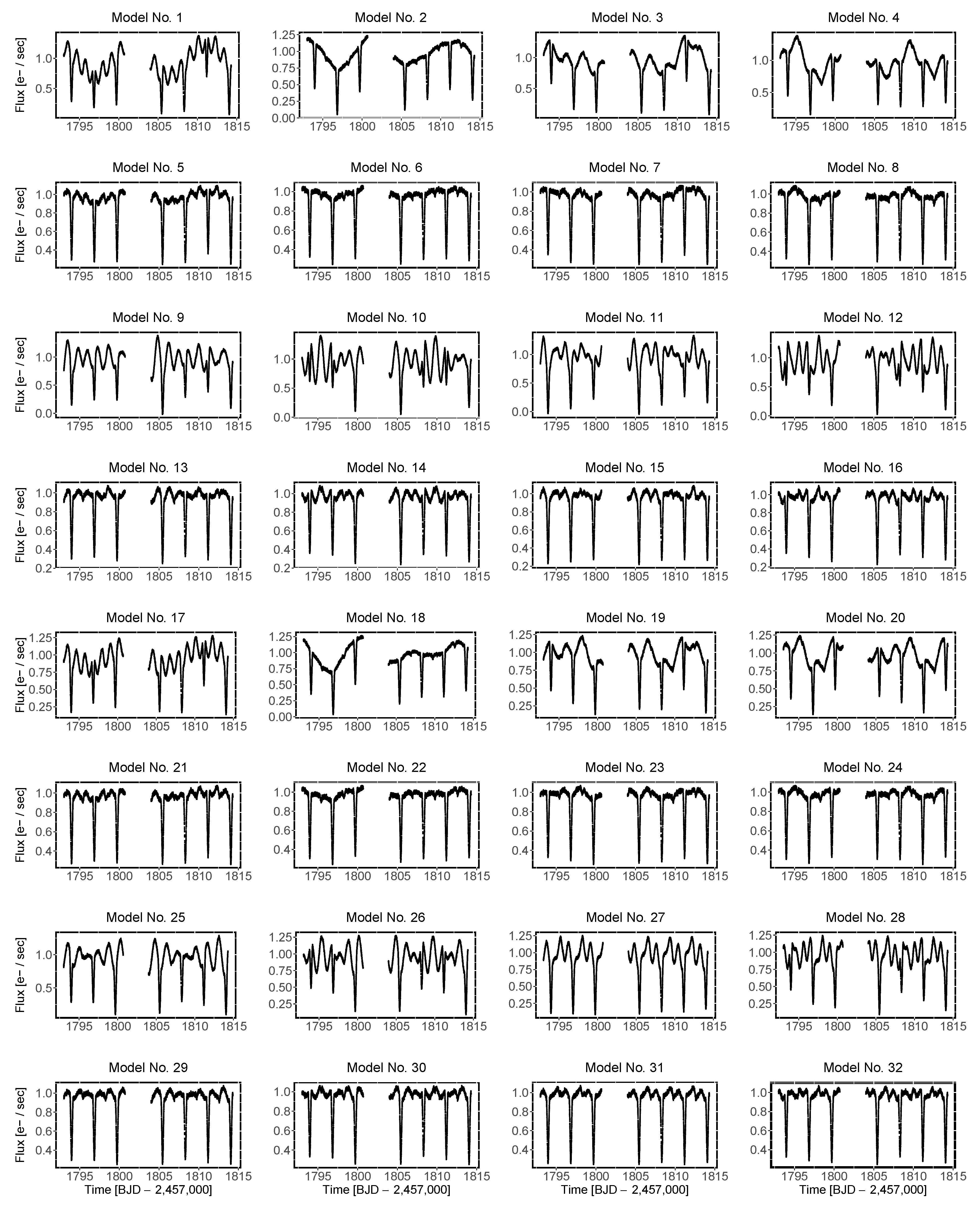

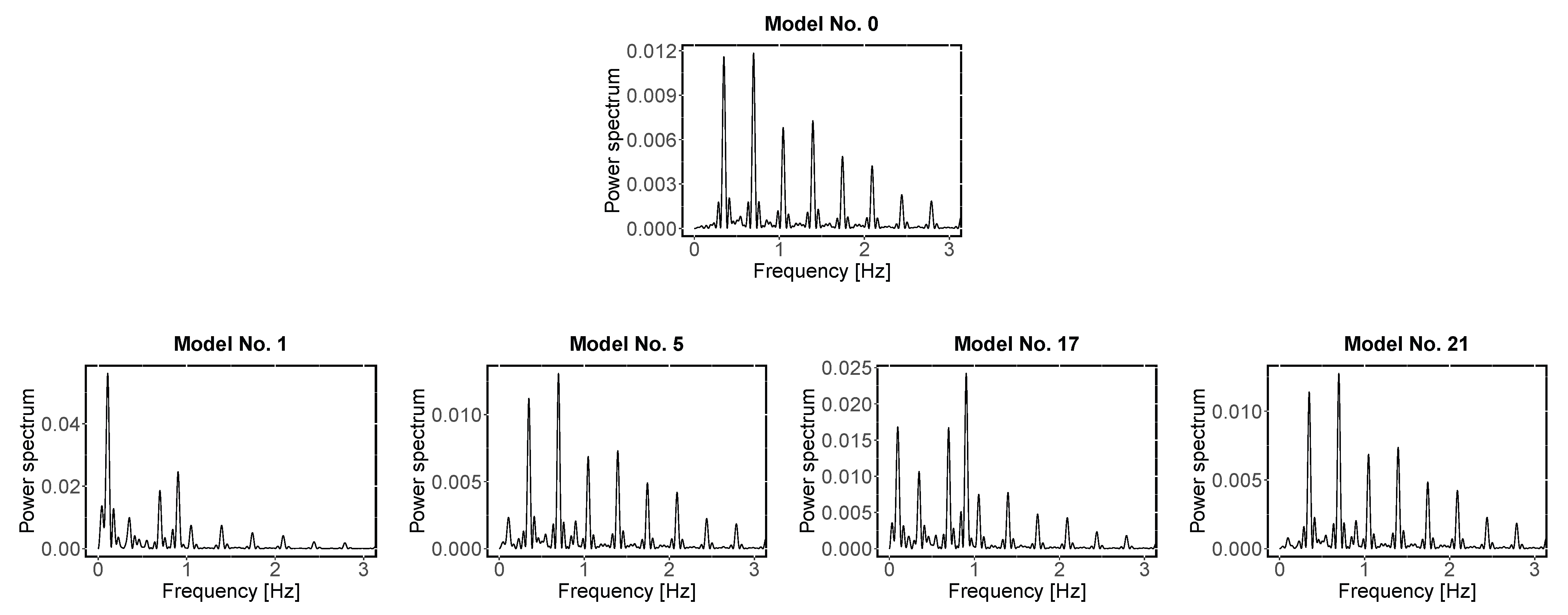

| Model | Beating Phenomena | Light Time Effect | Relation to the Orbital Period | N. of Pul. | Quasi-Regular Periods | Amplitude a [%] | Fixed Period Values c [Days] |
|---|---|---|---|---|---|---|---|
| No. 1 | Yes | No | Higher | 2 | Yes | 20 | 3e–8.96–10 |
| No. 2 | Yes | No | Higher | 2 | No | 20 | 7– 7.70–10 |
| No. 3 | Yes | Yes | Higher | 1 | Yes | 20 | 3e–2.12–4.42–8.96 |
| No. 4 | Yes | Yes | Higher | 1 | No | 20 | 7–2.03–4.86–7.70 |
| No. 5 | Yes | No | Higher | 2 | Yes | 4 | 3e–8.96–10 |
| No. 6 | Yes | No | Higher | 2 | No | 4 | 7– 7.70–10 |
| No. 7 | Yes | Yes | Higher | 1 | Yes | 4 | 3e–2.12–4.42–8.96 |
| No. 8 | Yes | Yes | Higher | 1 | No | 4 | 7–2.03–4.86–7.70 |
| No. 9 | Yes | No | Lower | 2 | Yes | 20 | –1.27–1.6 |
| No. 10 | Yes | No | Lower | 2 | No | 20 | 1.2– 1.32–1.6 |
| No. 11 | Yes | Yes | Lower | 1 | Yes | 20 | –0.94–2.78–1.27 |
| No. 12 | Yes | Yes | Lower | 1 | No | 20 | 1.2–0.84–2.06–1.32 |
| No. 13 | Yes | No | Lower | 2 | Yes | 4 | –1.27–1.6 |
| No. 14 | Yes | No | Lower | 2 | No | 4 | 1.2–1.32–1.6 |
| No. 15 | Yes | Yes | Lower | 1 | Yes | 4 | –0.94–2.78–1.27 |
| No. 16 | Yes | Yes | Lower | 1 | No | 4 | 1.2–0.84–2.06–1.32 |
| No. 17 | No | No | Higher | 2 | Yes | 20 | 3e–10 |
| No. 18 | No | No | Higher | 2 | No | 20 | 7–10 |
| No. 19 | No | Yes | Higher | 1 | Yes | 20 | 3e–2.12–4.42 |
| No. 20 | No | Yes | Higher | 1 | No | 20 | 7–2.03–4.86 |
| No. 21 | No | No | Higher | 2 | Yes | 4 | 3e–10 |
| No. 22 | No | No | Higher | 2 | No | 4 | 7–10 |
| No. 23 | No | Yes | Higher | 1 | Yes | 4 | 3e–2.12–4.42 |
| No. 24 | No | Yes | Higher | 1 | No | 4 | 7–2.03–4.86 |
| No. 25 | No | No | Lower | 2 | Yes | 20 | –1.6 |
| No. 26 | No | No | Lower | 2 | No | 20 | 1.2–1.6 |
| No. 27 | No | Yes | Lower | 1 | Yes | 20 | –0.94–2.78 |
| No. 28 | No | Yes | Lower | 1 | No | 20 | 1.2–0.84–2.06 |
| No. 29 | No | No | Lower | 2 | Yes | 4 | –1.6 |
| No. 30 | No | No | Lower | 2 | No | 4 | 1.2–1.6 |
| No. 31 | No | Yes | Lower | 1 | Yes | 4 | – 0.94–2.78 |
| No. 32 | No | Yes | Lower | 1 | No | 4 | 1.2–0.84–2.06 |
| Model | Input Period [Days] | Amplitude [%] | Detected Period (w) [Days] | Detected Period (F) [Days] |
|---|---|---|---|---|
| No. 0 | 2.87 | ⋯ | 2.790 ± 0.051 | 2.878 ± 0.003 |
| No. 1 | 10 8.96 3e 2.87 | 20 | ⋯ ⋯ 7.852 ± 0.036 2.787 ± 0.061 1.147 ± 0.105 | 12.911 ± 0.001 9.262 ± 0.013 ⋯ 2.878 ± 0.003 1.106 ± 0.002 |
| No. 5 | 4 | ⋯ 7.865 ± 0.046 2.812 ± 0.048 ⋯ | 9.467 ± 0.003 ⋯ 2.859 ± 0.003 1.100 ± 0.001 | |
| No. 17 | 10 3e 2.87 | 20 | ⋯ 7.928 ± 0.061 2.809 ± 0.067 2.506 ± 0.058 1.139 ± 0.103 | 10.144 ± 0.004 ⋯ 2.859 ± 0.001 ⋯ 1.106 ± 0.002 |
| No. 21 | 4 | ⋯ 7.924 ± 0.062 2.803 ± 0.053 ⋯ | 10.144 ± 0.018 ⋯ 2.878 ± 0.004 1.103 ± 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alberici Adam, A.; Avila Marín, G.F.; Christen, A.; Cidale, L.S. Synthetic Light Curve Design for Pulsating Binary Stars to Compare the Efficiency in the Detection of Periodicities. Galaxies 2023, 11, 69. https://doi.org/10.3390/galaxies11030069
Alberici Adam A, Avila Marín GF, Christen A, Cidale LS. Synthetic Light Curve Design for Pulsating Binary Stars to Compare the Efficiency in the Detection of Periodicities. Galaxies. 2023; 11(3):69. https://doi.org/10.3390/galaxies11030069
Chicago/Turabian StyleAlberici Adam, Aldana, Gunther F. Avila Marín, Alejandra Christen, and Lydia Sonia Cidale. 2023. "Synthetic Light Curve Design for Pulsating Binary Stars to Compare the Efficiency in the Detection of Periodicities" Galaxies 11, no. 3: 69. https://doi.org/10.3390/galaxies11030069
APA StyleAlberici Adam, A., Avila Marín, G. F., Christen, A., & Cidale, L. S. (2023). Synthetic Light Curve Design for Pulsating Binary Stars to Compare the Efficiency in the Detection of Periodicities. Galaxies, 11(3), 69. https://doi.org/10.3390/galaxies11030069






