A Review of the Mixing Length Theory of Convection in 1D Stellar Modeling
Abstract
:1. Introduction
- .
- .
- Bag of Stellar Tracks and Isochrones (BaSTI; Pietrinferni et al. [8]);
- .
- Cambridge STARS (Eggleton [9]);
- .
- Code d’Evolution Stellaire Adaptatif et Modulaire (CESAM; Morel and Lebreton [10]);
- .
- The Dartmouth Stellar Evolution Program (DSEP; Dotter et al. [11]);
- .
- The Garching Stellar Evolution Code (GARSTEC; Weiss and Schlattl [12]);
- .
- The Geneva Stellar Evolution Code (GENEC; e.g., Charbonnel et al. [13]);
- .
- .
- .
- The PAdova and TRieste Stellar Evolution Code (PARSEC; Bressan et al. [24]);
- .
- The Yale Rotating Stellar Evolution Code (YREC; Demarque et al. [25]).
2. History
3. Stellar Structure Context
3.1. Stellar Structure Equations
3.2. Thermodynamic Quantities and Convective Stability Criteria
4. Where Does the Choice of Matter in Stellar Models?
5. Limitations and Physics Not Captured by MLT
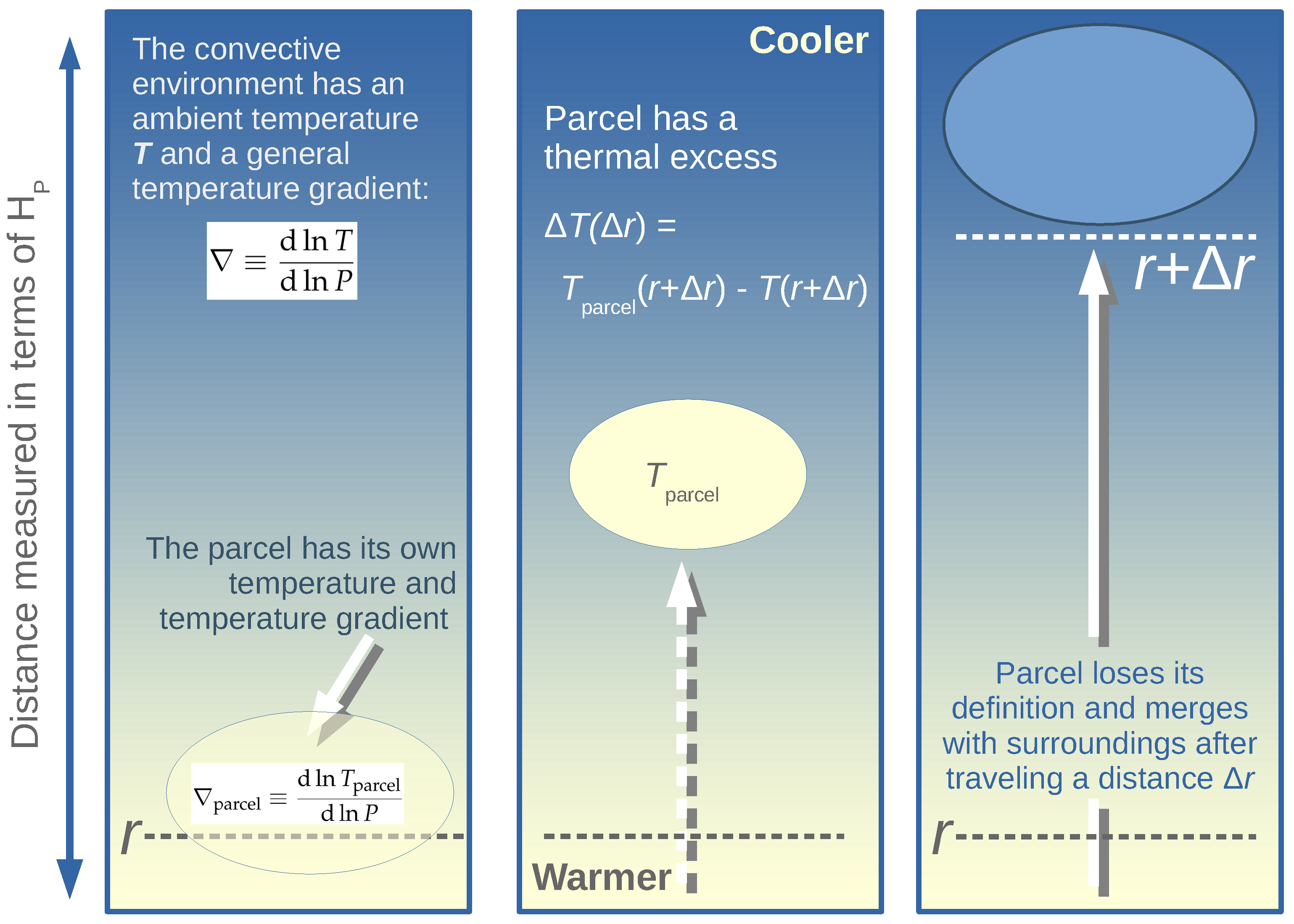
6. Mixing Length Formulation
Specific Formulations
7. Alternatives and Extensions
7.1. Alternative 1D Formulations
7.2. Extensions to 3D
8. Standard 1D MLT and Its Interplay with Other Modeling Physics
8.1. Atmospheric Boundary Conditions
8.2. Convective Boundaries
8.3. Opacities
8.4. Magnetic Fields
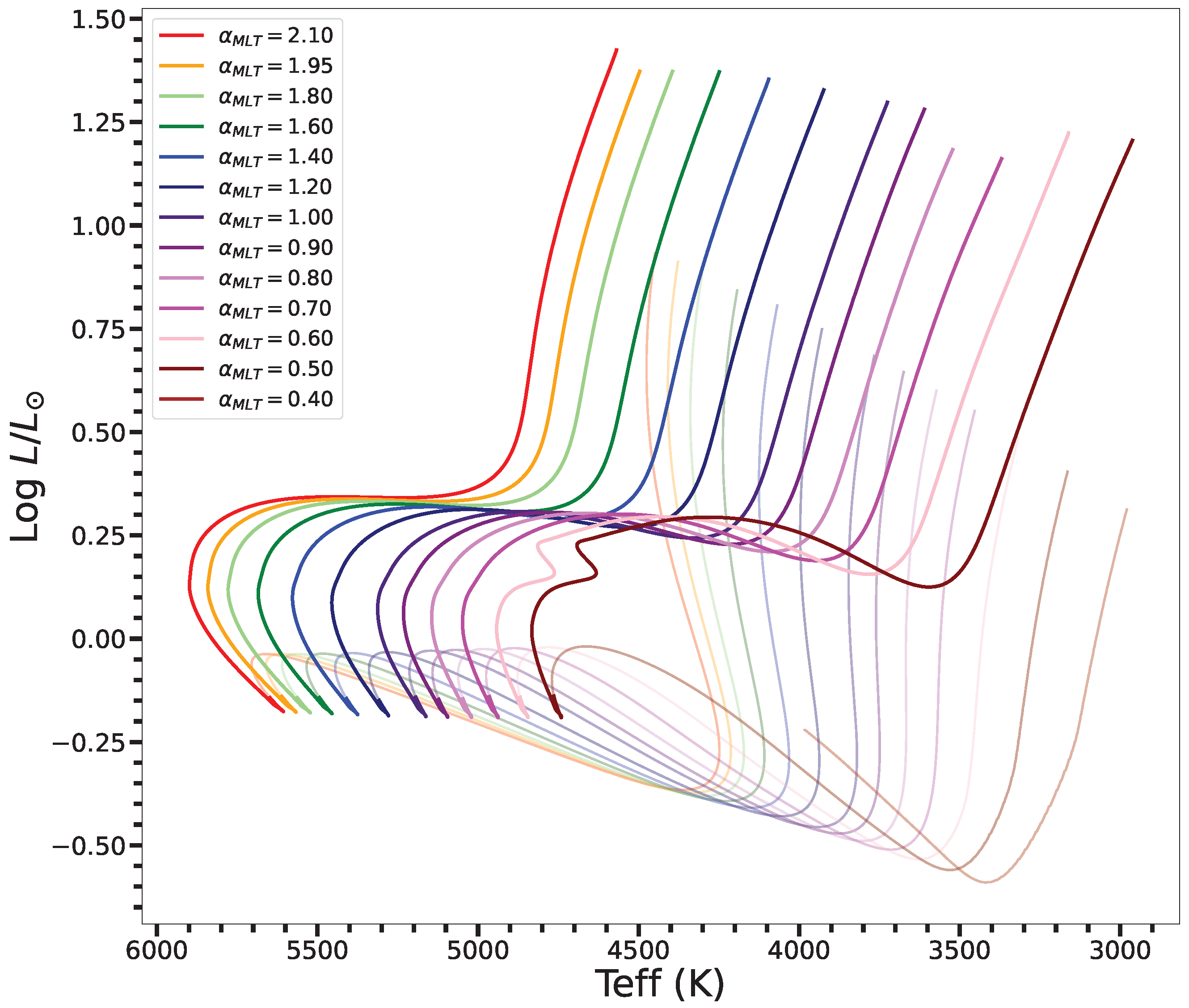
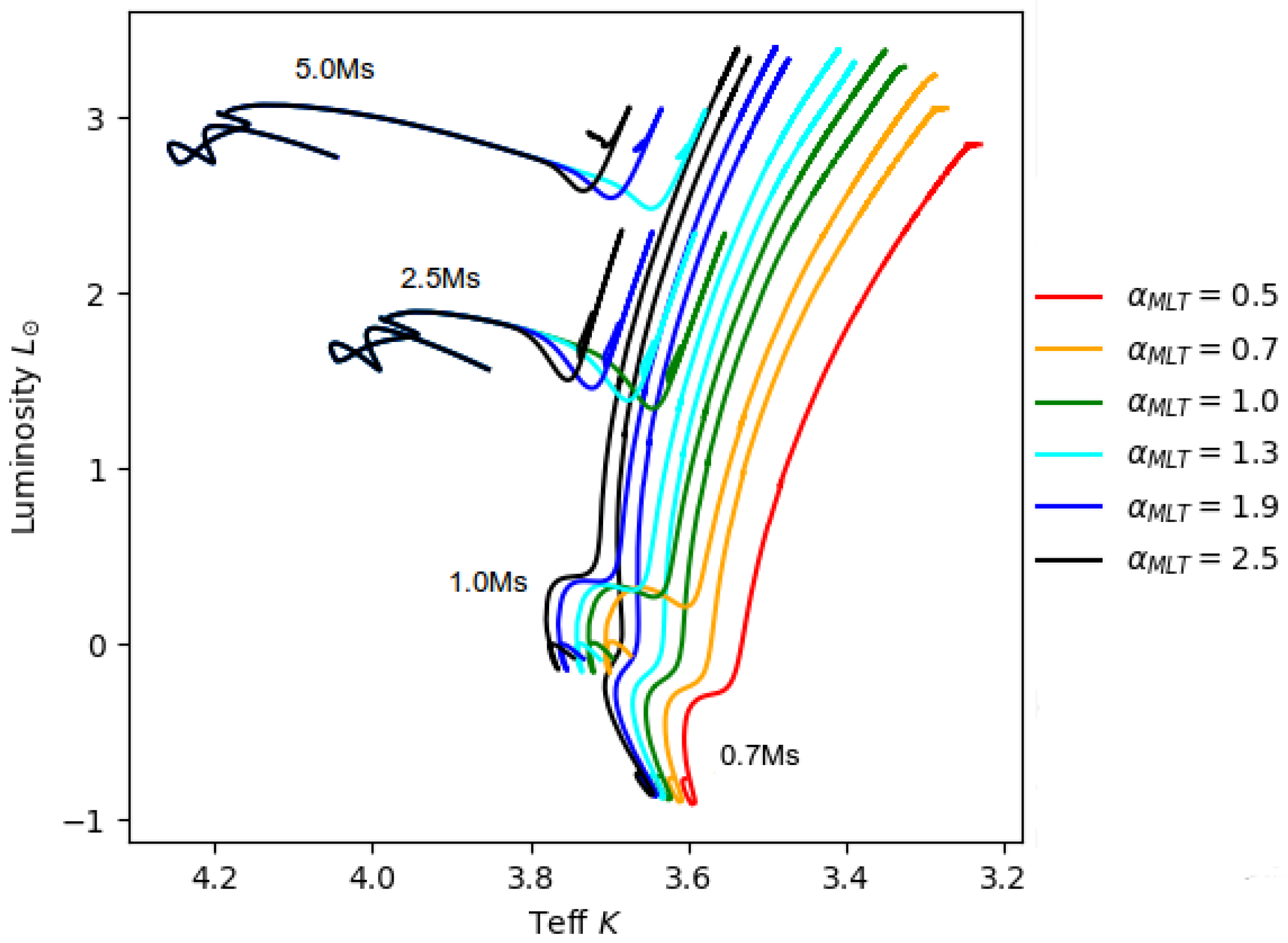
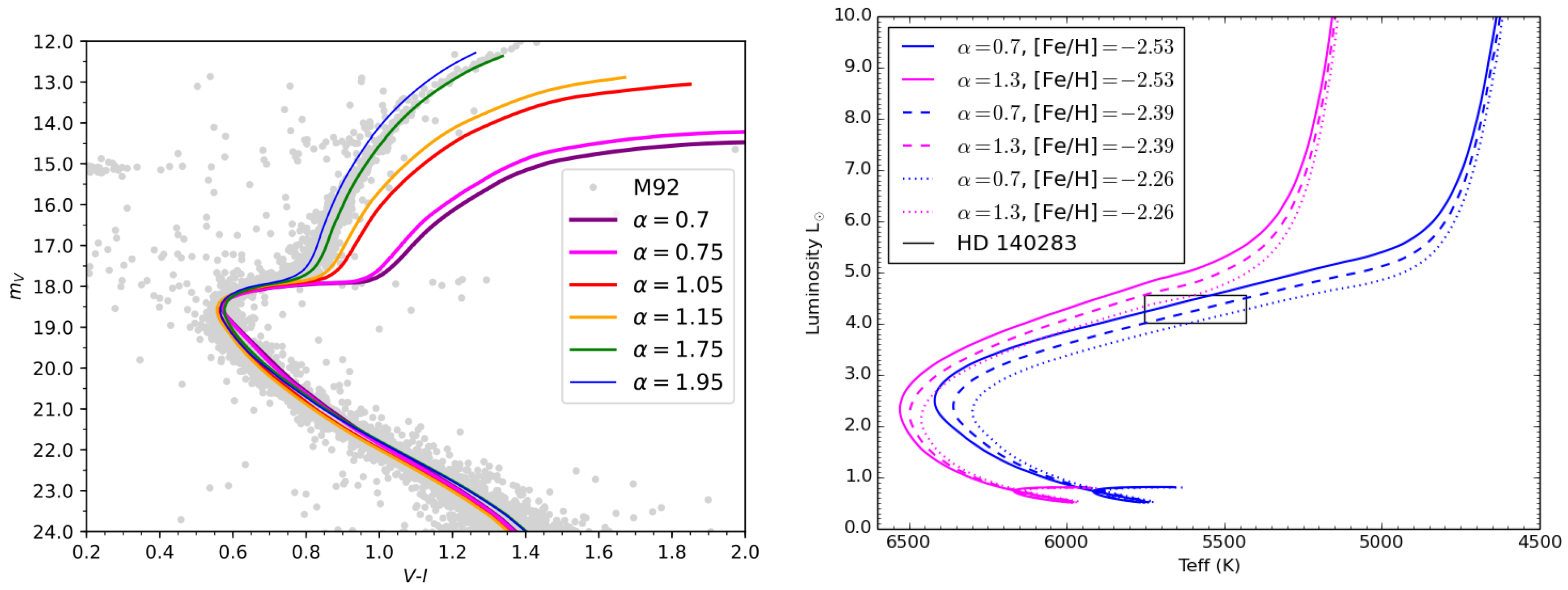
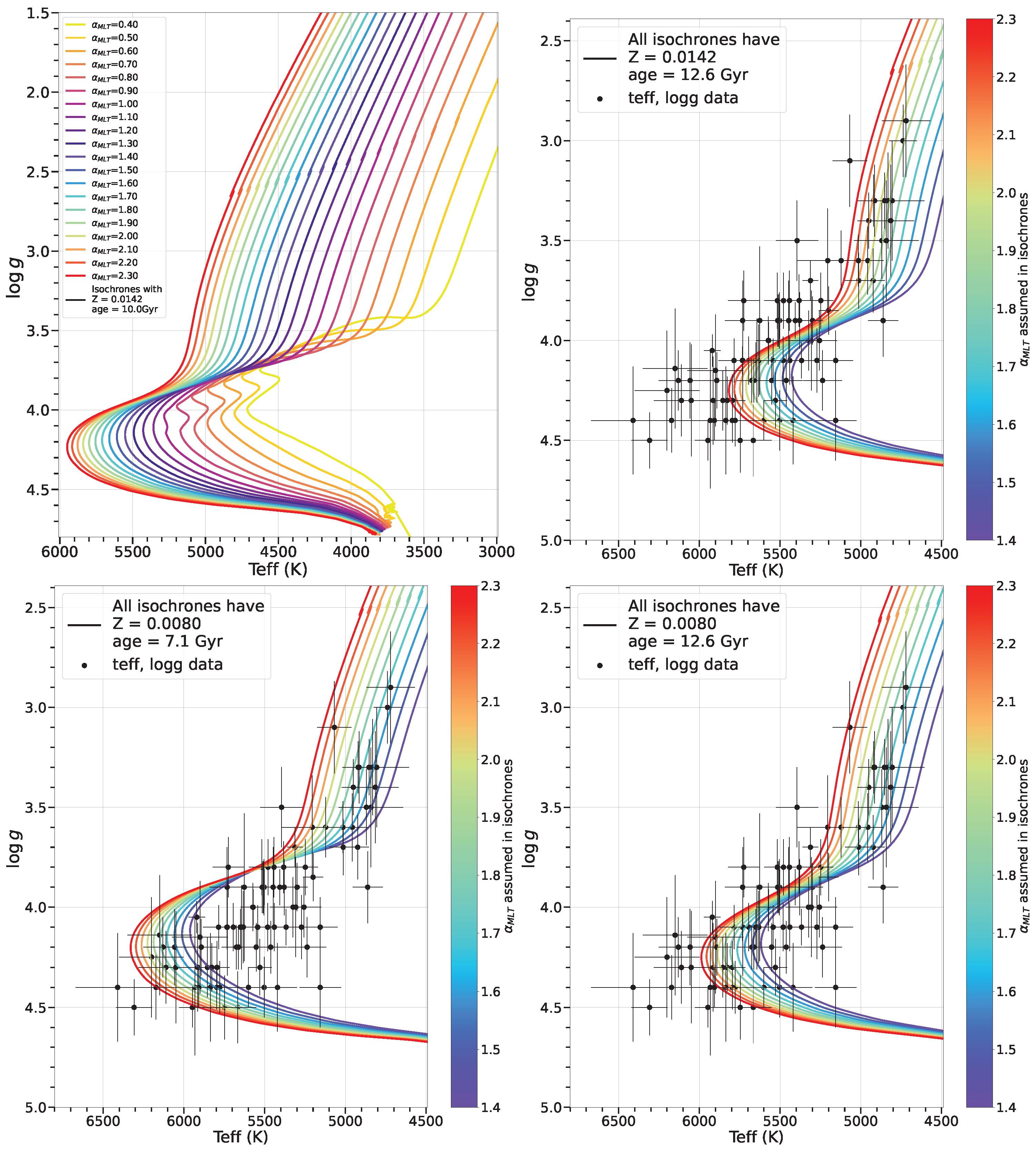
9. What Does Changing the Mixing Length Do in Stellar Models?
- (1)
- The shift towards cooler temperatures with lower ;
- (2)
- The difference in effect of a 10% change in at, e.g., , compared to ;
- (3)
- The extension of the subgiant branch in duration, and towards cooler temperatures, with decreasing ;
- (4)
- The negligible impact on luminosity.
Impact on Isochrones
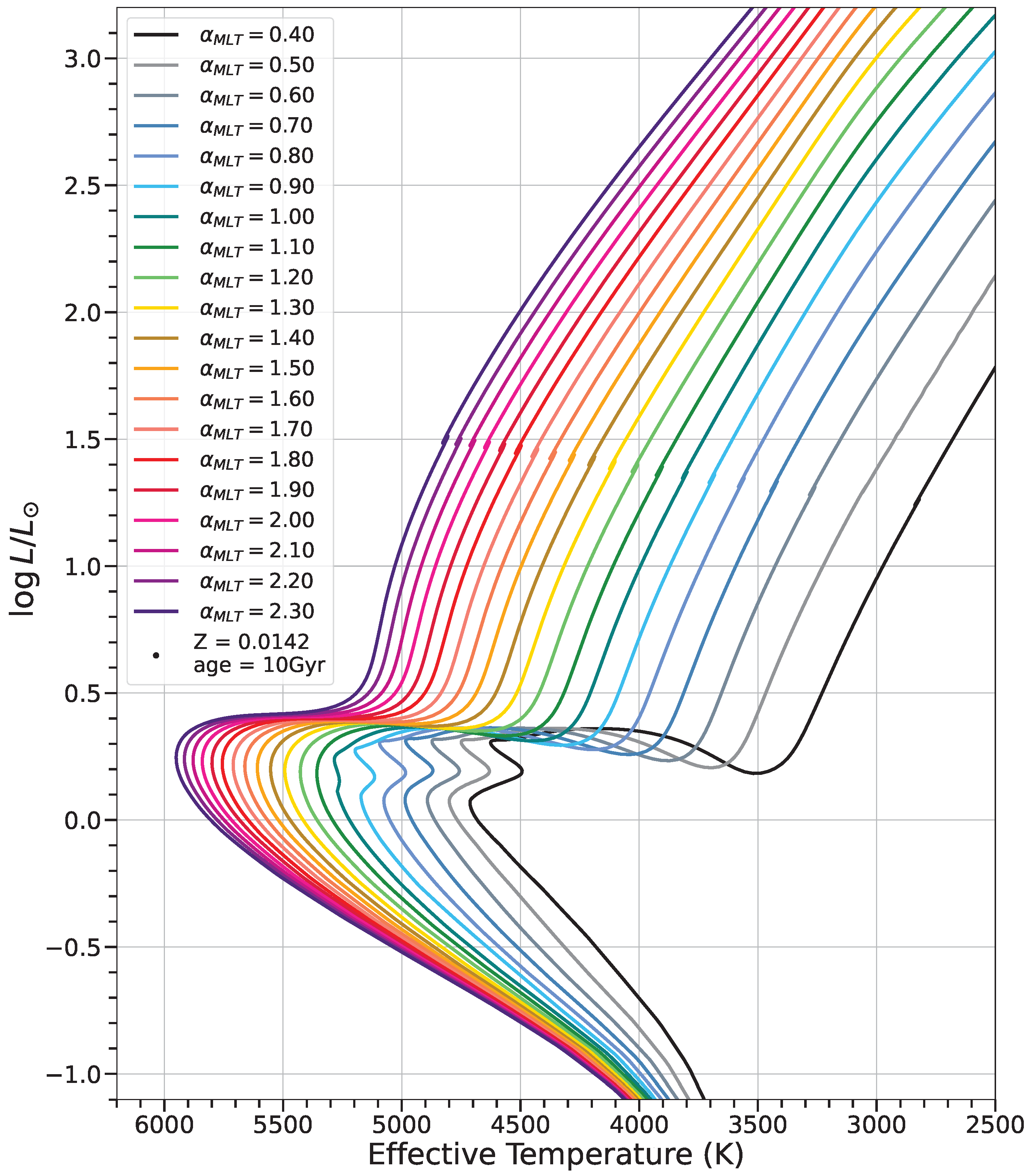
10. Solar Calibration of
11. Non-Solar Calibrations
12. Scientific Applications of Changing the Mixing Length
12.1. Implications for Age Measurements
12.2. Implications for Nucleosynthesis
12.3. Implications for Stars in the Instability Strip
12.4. Implications for Galaxies
13. Successes of Mixing Length
13.1. MLT and the Standard Solar Model
13.2. MLT and Asteroseismology
14. Observational Challenges of Mixing Length
15. The Future of MLT
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Meaning the one-dimensional distance element is taken to be the fractional radius , rather than the mass, . |
| 2 | |
| 3 | That is, where entropy is constant. |
| 4 | More precisely, it is the lack of an efficiency differential in the convective core that makes the choice of irrelevant in this regime. |
| 5 | The treatment of core convective boundaries is particularly important for determining whether massive stars will meet the criterion for death as a supernova. |
References
- Choi, J.; Dotter, A.; Conroy, C.; Ting, Y.S. On the Red Giant Branch: Ambiguity in the Surface Boundary Condition Leads to ≈100 K Uncertainty in Model Effective Temperatures. Astrophys. J. 2018, 860, 131. [Google Scholar] [CrossRef] [Green Version]
- Tayar, J.; Claytor, Z.R.; Huber, D.; van Saders, J. A Guide to Realistic Uncertainties on the Fundamental Properties of Solar-type Exoplanet Host Stars. Astrophys. J. 2022, 927, 31. [Google Scholar] [CrossRef]
- Cinquegrana, G.C.; Joyce, M.; Karakas, A.I. Bridging the Gap between Intermediate and Massive Stars. I. Validation of MESA against the State-of-the-Art Monash Stellar Evolution Program for a 2M ⊙ AGB Star. Astrophys. J. 2022, 939, 50. [Google Scholar] [CrossRef]
- Joyce, M.; Johnson, C.I.; Marchetti, T.; Rich, R.M.; Simion, I.; Bourke, J. The Ages of Galactic Bulge Stars with Realistic Uncertainties. arXiv 2022, arXiv:2205.07964. [Google Scholar] [CrossRef]
- Böhm-Vitense, E. Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Z. Astrophys. 1958, 46, 108. [Google Scholar]
- Ventura, P.; Zeppieri, A.; Mazzitelli, I.; D’Antona, F. Full spectrum of turbulence convective mixing: I. theoretical main sequences and turn-off for 0.6/∖15 M_∖odot. Astron. Astrophys. 1998, 334, 953–968. [Google Scholar]
- Ventura, P.; Di Criscienzo, M.; Carini, R.; D’Antona, F. Yields of AGB and SAGB models with chemistry of low- and high-metallicity globular clusters. Mon. Not. R. Astron. Soc. 2013, 431, 3642–3653. [Google Scholar] [CrossRef]
- Pietrinferni, A.; Cassisi, S.; Salaris, M.; Castelli, F. A large stellar evolution database for population synthesis studies. I. Scaled solar models and isochrones. Astrophys. J. 2004, 612, 168. [Google Scholar] [CrossRef]
- Eggleton, P.P. The evolution of low mass stars. Mon. Not. R. Astron. Soc. 1971, 151, 351–364. [Google Scholar] [CrossRef] [Green Version]
- Morel, P.; Lebreton, Y. CESAM: A free code for stellar evolution calculations. Astrophys. Space Sci. 2008, 316, 61–73. [Google Scholar] [CrossRef]
- Dotter, A.; Chaboyer, B.; Jevremović, D.; Kostov, V.; Baron, E.; Ferguson, J.W. The Dartmouth Stellar Evolution Database. Astrophys. J. Suppl. Ser. 2008, 178, 89–101. [Google Scholar] [CrossRef] [Green Version]
- Weiss, A.; Schlattl, H. GARSTEC—the Garching Stellar Evolution Code. Astrophys. Space Sci. 2008, 316, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Charbonnel, C.; Meynet, G.; Maeder, A.; Schaerer, D. Grids of stellar models. VI. Horizontal branch and early asymptotic giant branch for low mass stars (Z = 0.020, 0.001). Astron. Astrophys. Suppl. Ser. 1996, 115, 339. [Google Scholar]
- Jermyn, A.S.; Bauer, E.B.; Schwab, J.; Farmer, R.; Ball, W.H.; Bellinger, E.P.; Dotter, A.; Joyce, M.; Marchant, P.; Mombarg, J.S.G.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Time-Dependent Convection, Energy Conservation, Automatic Differentiation, and Infrastructure. arXiv 2022, arXiv:2208.03651. [Google Scholar] [CrossRef]
- Paxton, B.; Smolec, R.; Schwab, J.; Gautschy, A.; Bildsten, L.; Cantiello, M.; Dotter, A.; Farmer, R.; Goldberg, J.A.; Jermyn, A.S.; et al. Modules for experiments in stellar astrophysics (MESA): Pulsating variable stars, rotation, convective boundaries, and energy conservation. Astrophys. J. Suppl. Ser. 2019, 243, 10. [Google Scholar] [CrossRef]
- Paxton, B.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Blinnikov, S.; Duffell, P.; Farmer, R.; Goldberg, J.A.; Marchant, P.; Sorokina, E.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. Astrophys. J. Suppl. Ser. 2018, 234, 34. [Google Scholar] [CrossRef]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for experiments in stellar astrophysics (MESA): Binaries, pulsations, and explosions. Astrophys. J. Suppl. Ser. 2015, 220, 15. [Google Scholar] [CrossRef]
- Paxton, B.; Cantiello, M.; Arras, P.; Bildsten, L.; Brown, E.F.; Dotter, A.; Mankovich, C.; Montgomery, M.; Stello, D.; Timmes, F.; et al. Modules for experiments in stellar astrophysics (MESA): Planets, oscillations, rotation, and massive stars. Astrophys. J. Suppl. Ser. 2013, 208, 4. [Google Scholar] [CrossRef] [Green Version]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for experiments in stellar astrophysics (MESA). Astrophys. J. Suppl. Ser. 2010, 192, 3. [Google Scholar] [CrossRef]
- Lattanzio, J.C. The Evolution of Initially Inhomogeneous Stars and Low Mass AGB Stars. Ph.D. Thesis, Monash University, Clayton, Australia, 1984. [Google Scholar]
- Lattanzio, J.C. The asymptotic giant branch evolution of 1.0-3.0 solar mass stars as a function of mass and composition. Astrophys. J. 1986, 311, 708–730. [Google Scholar] [CrossRef]
- Frost, C.; Lattanzio, J. On the numerical treatment and dependence of the third dredge-up phenomenon. Astrophys. J. 1996, 473, 383. [Google Scholar] [CrossRef] [Green Version]
- Karakas, A.; Lattanzio, J.C. Stellar models and yields of asymptotic giant branch stars. Pub. Astron. Soc. Aus. 2007, 24, 103–117. [Google Scholar] [CrossRef] [Green Version]
- Bressan, A.; Marigo, P.; Girardi, L.; Salasnich, B.; Dal Cero, C.; Rubele, S.; Nanni, A. PARSEC: Stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 2012, 427, 127–145. [Google Scholar] [CrossRef] [Green Version]
- Demarque, P.; Guenther, D.; Li, L.; Mazumdar, A.; Straka, C. YREC: The Yale rotating stellar evolution code. Astrophys. Space Sci. 2008, 316, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Canuto, V.M.; Mazzitelli, I. Stellar Turbulent Convection: A New Model and Applications. Astrophys. J. 1991, 370, 295–311. [Google Scholar] [CrossRef]
- Canuto, V.; Goldman, I.; Mazzitelli, I. Stellar turbulent convection: A self-consistent model. Astrophys. J. 1996, 473, 550. [Google Scholar] [CrossRef] [Green Version]
- Gaia Collaboration; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Evans, D.W.; Eyer, L.; et al. Gaia Early Data Release 3. Summary of the contents and survey properties. Astron. Astrophys. 2021, 649, A1. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instruments Syst. 2015, 1, 014003. [Google Scholar] [CrossRef] [Green Version]
- Borucki, W.J.; Koch, D.; Basri, G.; Batalha, N.; Brown, T.; Caldwell, D.; Caldwell, J.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; et al. Kepler Planet-Detection Mission: Introduction and First Results. Science 2010, 327, 977. [Google Scholar] [CrossRef] [Green Version]
- LSST Science Collaboration; Marshall, P.; Anguita, T.; Bianco, F.B.; Bellm, E.C.; Brandt, N.; Clarkson, W.; Connolly, A.; Gawiser, E.; Ivezic, Z.; et al. Science-Driven Optimization of the LSST Observing Strategy. arXiv 2017, arXiv:1708.04058. [Google Scholar]
- Majewski, S.R.; Schiavon, R.P.; Frinchaboy, P.M.; Allende Prieto, C.; Barkhouser, R.; Bizyaev, D.; Blank, B.; Brunner, S.; Burton, A.; Carrera, R.; et al. The Apache Point Observatory Galactic Evolution Experiment (APOGEE). Astron. J. 2017, 154, 94. [Google Scholar] [CrossRef]
- Cui, X.Q.; Zhao, Y.H.; Chu, Y.Q.; Li, G.P.; Li, Q.; Zhang, L.P.; Su, H.J.; Yao, Z.Q.; Wang, Y.N.; Xing, X.Z.; et al. The Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST). Res. Astron. Astrophys. 2012, 12, 1197–1242. [Google Scholar] [CrossRef]
- Buder, S.; Sharma, S.; Kos, J.; Amarsi, A.M.; Nordlander, T.; Lind, K.; Martell, S.L.; Asplund, M.; Bland-Hawthorn, J.; Casey, A.R.; et al. The GALAH+ survey: Third data release. Mon. Not. R. Astron. Soc. 2021, 506, 150–201. [Google Scholar] [CrossRef]
- Prandtl, L. Bericht über Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 1925, 136. [Google Scholar] [CrossRef]
- Vitense, E. Die wasserstoffkonvektionszone der sonne. Mit 11 textabbildungen. Z. Astrophys. 1953, 32, 135. [Google Scholar]
- Henyey, L.; Vardya, M.; Bodenheimer, P. Studies in stellar evolution. III. The calculation of model envelopes. Astrophys. J. 1965, 142, 841. [Google Scholar] [CrossRef]
- Cox, J.; Giuli, R. Principles of Stellar Structure; Gordon and Breach: New York, NY, USA, 1968. [Google Scholar]
- Bohm, K.H.; Cassinelli, J. Convective Envelopes and Acoustic Noise Generation in White Dwarfs. Astron. Astrophys. 1971, 12, 21. [Google Scholar]
- Mihalas, D.; Auer, L.H.; Mihalas, B.R. Two-dimensional radiative transfer. I. Planar geometry. Astrophys. J. 1978, 220, 1001–1023. [Google Scholar] [CrossRef]
- Mihalas, D. Stellar Atmospheres; WH Freeman: San Francisco, CA, USA, 1978. [Google Scholar]
- Kurucz, R.L. Model atmospheres for G, F, A, B, and O stars. Astrophys. J. Suppl. Ser. 1979, 40, 1–340. [Google Scholar] [CrossRef]
- Basu, S.; Antia, H.M.; Narasimha, D. Helioseismic measurement of the extent of overshoot below the solar convection zone. Mon. Not. R. Astron. Soc. 1994, 267, 209. [Google Scholar] [CrossRef] [Green Version]
- Basu, S.; Pinsonneault, M.H.; Bahcall, J.N. How Much Do Helioseismological Inferences Depend on the Assumed Reference Model? Astrophys. J. 2000, 529, 1084–1100. [Google Scholar] [CrossRef] [Green Version]
- Demarque, P.; Guenther, D.B.; Kim, Y.C. The Run of Superadiabaticity in Stellar Convection Zones. I. The Sun. Astrophys. J. 1997, 474, 790–797. [Google Scholar] [CrossRef] [Green Version]
- Demarque, P.; Guenther, D.B.; Kim, Y.C. The Run of Superadiabaticity in Stellar Convection Zones. II. Effect of Photospheric Convection on Solar p-Mode Frequencies. Astrophys. J. 1999, 517, 510–515. [Google Scholar] [CrossRef] [Green Version]
- Schwarzschild, M. Structure and Evolution of the Stars; Princeton University Press: Princeton, NJ, USA, 1958. [Google Scholar]
- Ledoux, P. Stellar Models with Convection and with Discontinuity of the Mean Molecular Weight. Astrophys. J. 1947, 105, 305. [Google Scholar] [CrossRef]
- Gabriel, M.; Noels, A.; Montalbán, J.; Miglio, A. Proper Use of Schwarzschild Ledoux Criteria in Stellar Evolution Computations. Astron. Astrophys. 2014, 569, A63. [Google Scholar] [CrossRef] [Green Version]
- Salaris, M.; Cassisi, S. Chemical element transport in stellar evolution models. R. Soc. Open Sci. 2017, 4, 170192. [Google Scholar] [CrossRef] [Green Version]
- Anders, E.H.; Jermyn, A.S.; Lecoanet, D.; Fraser, A.E.; Cresswell, I.G.; Joyce, M.; Fuentes, J. Schwarzschild and Ledoux are equivalent on evolutionary timescales. Astrophys. J. Lett. 2022, 928, L10. [Google Scholar] [CrossRef]
- Kippenhahn, R.; Weigert, A. Stellar Structure and Evolution; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Stein, R.F.; Nordlund, A. Topology of convection beneath the solar surface. Astrophys. J. 1989, 342, L95–L98. [Google Scholar] [CrossRef]
- Salaris, M.; Cassisi, S. Evolution of Stars and Stellar Populations; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Henyey, L.G.; Forbes, J.E.; Gould, N.L. A New Method of Automatic Computation of Stellar Evolution. Astrophys. J. 1964, 139, 306. [Google Scholar] [CrossRef]
- Kurucz, R.L. Progress on model atmospheres and line data. In Proceedings of the IAU Symposium, Kyoto, Japan, 18–22 August 1997; Volume 189, pp. 217–226. [Google Scholar]
- Unno, W. Stellar Radial Pulsation Coupled with the Convection. Publ. Astron. Soc. Jpn. 1967, 19, 140. [Google Scholar]
- Gough, D.O.; Ostriker, J.P.; Stobie, R.S. On the Periods of Pulsating Stars. Astrophys. J. 1965, 142, 1649–1652. [Google Scholar] [CrossRef]
- Houdek, G.; Dupret, M.A. Interaction Between Convection and Pulsation. Living Rev. Sol. Phys. 2015, 12, 8. [Google Scholar] [CrossRef]
- Kuhfuss, R. A model for time-dependent turbulent convection. Astron. Astrophys. 1986, 160, 116–120. [Google Scholar]
- Gough, D.O. Mixing-length theory for pulsating stars. Astrophys. J. 1977, 214, 196–213. [Google Scholar] [CrossRef]
- Renzini, A. Some embarrassments in current treatments of convective overshooting. Astron. Astrophys. 1987, 188, 49–54. [Google Scholar]
- Grossman, S.A.; Narayan, R. A Theory of Nonlocal Mixing-Length Convection. II. Generalized Smoothed Particle Hydrodynamics Simulations. Astrophys. J. Suppl. Ser. 1993, 89, 361. [Google Scholar] [CrossRef]
- Eggleton, P.P. Towards consistency in simple prescriptions for stellar convection. Mon. Not. R. Astron. Soc. 1983, 204, 449–461. [Google Scholar] [CrossRef] [Green Version]
- Xiong, D.R. The evolution of massive stars using a non-local theory of convection. Astron. Astrophys. 1986, 167, 239–246. [Google Scholar]
- Xiong, D.R. Radiation-hydrodynamic equations for stellar oscillations. Astron. Astrophys. 1989, 209, 126–134. [Google Scholar]
- Xiong, D.R. Numerical simulations of nonlocal convection. Astron. Astrophys. 1989, 213, 176–182. [Google Scholar]
- Grossman, S.A. A theory of non-local mixing-length convection-III. Comparing theory and numerical experiment. Mon. Not. R. Astron. Soc. 1996, 279, 305–336. [Google Scholar] [CrossRef] [Green Version]
- Ireland, L.G.; Browning, M.K. The Radius and Entropy of a Magnetized, Rotating, Fully Convective Star: Analysis with Depth-dependent Mixing Length Theories. Astrophys. J. 2018, 856, 132. [Google Scholar] [CrossRef] [Green Version]
- Marcus, P.S.; Press, W.H.; Teukolsky, S.A. Multiscale model equations for turbulent convection and convective overshoot. Astrophys. J. 1983, 267, 795–821. [Google Scholar] [CrossRef]
- Arnett, W.D.; Meakin, C.; Viallet, M.; Campbell, S.W.; Lattanzio, J.C.; Mocák, M. Beyond Mixing-length Theory: A Step Toward 321D. Astrophys. J. 2015, 809, 30. [Google Scholar] [CrossRef] [Green Version]
- Arnett, W.D.; Hirschi, R.; Campbell, S.W.; Mocák, M.; Georgy, C.; Meakin, C.; Cristini, A.; Scott, L.J.A.; Kaiser, E.A.; Viallet, M. 3D Simulations and MLT: II. Onsager’s Ideal Turbulence. arXiv 2018, arXiv:1810.04659. [Google Scholar] [CrossRef]
- Trampedach, R.; Stein, R.F.; Christensen-Dalsgaard, J.; Nordlund, Å.; Asplund, M. Improvements to stellar structure models, based on a grid of 3D convection simulations—II. Calibrating the mixing-length formulation. Mon. Not. R. Astron. Soc. 2014, 445, 4366–4384. [Google Scholar] [CrossRef]
- Magic, Z.; Weiss, A.; Asplund, M. The Stagger-grid: A grid of 3D stellar atmosphere models. III. The relation to mixing length convection theory. Astron. Astrophys. 2015, 573, A89. [Google Scholar] [CrossRef]
- Sonoi, T.; Ludwig, H.G.; Dupret, M.A.; Montalban, J.; Belkacem, K.; Caffau, E. Calibration of the mixing length of the MLT and FST models using 3D hydrodynamical models. In PHysics of Oscillating STars, Proceedings of the PHOST (PHysics of Oscillating STars) Symposium Hosted by the Oceanographic Observatory in Banyuls-sur-mer (France) from 2–7 September 2018; This Conference Honours the Life Work of Professor Hiromoto Shibahashi; Tokyo University: Tokyo, Japan, 2018; p. 27. [Google Scholar] [CrossRef]
- Tanner, J.D.; Basu, S.; Demarque, P. The Effect of Metallicity-dependent T-τ Relations on Calibrated Stellar Models. Astrophys. J. 2014, 785, L13. [Google Scholar] [CrossRef] [Green Version]
- Salaris, M.; Cassisi, S. Stellar models with mixing length and T(τ) relations calibrated on 3D convection simulations. Astron. Astrophys. 2015, 577, A60. [Google Scholar] [CrossRef] [Green Version]
- Mosumgaard, J.R.; Ball, W.H.; Silva Aguirre, V.; Weiss, A.; Christensen-Dalsgaard, J. Stellar models with calibrated convection and temperature stratification from 3D hydrodynamics simulations. Mon. Not. R. Astron. Soc. 2018, 478, 5650–5659. [Google Scholar] [CrossRef]
- Zhou, Y.; Asplund, M.; Collet, R.; Joyce, M. Convective excitation and damping of solar-like oscillations. Mon. Not. R. Astron. Soc. 2020, 495, 4904–4923. [Google Scholar] [CrossRef]
- Spada, F.; Demarque, P. Testing the entropy calibration of the radii of cool stars: Models of α Centauri A and B. Mon. Not. R. Astron. Soc. 2019, 489, 4712–4720. [Google Scholar] [CrossRef]
- Spada, F.; Demarque, P.; Kupka, F. Stellar evolution models with entropy-calibrated mixing-length parameter: Application to red giants. Mon. Not. R. Astron. Soc. 2021, 504, 3128–3138. [Google Scholar] [CrossRef]
- Bonaca, A.; Tanner, J.D.; Basu, S.; Chaplin, W.J.; Metcalfe, T.S.; Monteiro, M.J.P.F.G.; Ballot, J.; Bedding, T.R.; Bonanno, A.; Broomhall, A.M.; et al. Calibrating Convective Properties of Solar-like Stars in the Kepler Field of View. Astrophys. J. 2012, 755, L12. [Google Scholar] [CrossRef] [Green Version]
- Creevey, O.L.; Thévenin, F.; Berio, P.; Heiter, U.; von Braun, K.; Mourard, D.; Bigot, L.; Boyajian, T.S.; Kervella, P.; Morel, P.; et al. Benchmark stars for Gaia Fundamental properties of the Population II star HD 140283 from interferometric, spectroscopic, and photometric data. Astron. Astrophys. 2015, 575, A26. [Google Scholar] [CrossRef] [Green Version]
- Tayar, J.; Somers, G.; Pinsonneault, M.H.; Stello, D.; Mints, A.; Johnson, J.A.; Zamora, O.; García-Hernández, D.A.; Maraston, C.; Serenelli, A.; et al. The Correlation between Mixing Length and Metallicity on the Giant Branch: Implications for Ages in the Gaia Era. Astrophys. J. 2017, 840, 17. [Google Scholar] [CrossRef] [Green Version]
- Joyce, M.; Chaboyer, B. Not All Stars Are the Sun: Empirical Calibration of the Mixing Length for Metal-poor Stars Using One-dimensional Stellar Evolution Models. Astrophys. J. 2018, 856, 10. [Google Scholar] [CrossRef]
- Joyce, M.; Chaboyer, B. Classically and Asteroseismically Constrained 1D Stellar Evolution Models of α Centauri A and B Using Empirical Mixing Length Calibrations. Astrophys. J. 2018, 864, 99. [Google Scholar] [CrossRef] [Green Version]
- Viani, L.S.; Basu, S.; Joel Ong J., M.; Bonaca, A.; Chaplin, W.J. Investigating the Metallicity-Mixing-length Relation. Astrophys. J. 2018, 858, 28. [Google Scholar] [CrossRef] [Green Version]
- Valle, G.; Dell’Omodarme, M.; Prada Moroni, P.G.; Degl’Innocenti, S. Mixing-length calibration from field stars. An investigation on statistical errors, systematic biases, and spurious metallicity trends. Astron. Astrophys. 2019, 623, A59. [Google Scholar] [CrossRef] [Green Version]
- Krishna Swamy, K.S. Profiles of Strong Lines in K-Dwarfs. Astrophys. J. 1966, 145, 174–195. [Google Scholar] [CrossRef]
- Ball, W.H. A Novel Analytic Atmospheric T(τ) Relation for Stellar Models. Res. Notes Am. Astron. Soc. 2021, 5, 7. [Google Scholar] [CrossRef]
- Castelli, F.; Kurucz, R.L. New Grids of ATLAS9 Model Atmospheres. arXiv 2004, arXiv:astro-ph/0405087. [Google Scholar]
- Hauschildt, P.H.; Allard, F.; Baron, E. The NextGen Model Atmosphere Grid for 3000 ≤ Teff ≤ 10,000 K. Astrophys. J. 1999, 512, 377–385. [Google Scholar] [CrossRef] [Green Version]
- Gustafsson, B. Is the Sun unique as a star—and if so, why? Phys. Scr. Vol. T 2008, 130, 014036. [Google Scholar] [CrossRef]
- Song, N.; Alexeeva, S.; Sitnova, T.; Wang, L.; Grupp, F.; Zhao, G. Impact of the convective mixing-length parameter α on stellar metallicity. Astron. Astrophys. 2020, 635, A176. [Google Scholar] [CrossRef] [Green Version]
- Mosumgaard, J.R.; Jørgensen, A.C.S.; Weiss, A.; Silva Aguirre, V.; Christensen-Dalsgaard, J. Coupling 1D stellar evolution with 3D-hydrodynamical simulations on-the-fly II: Stellar evolution and asteroseismic applications. Mon. Not. R. Astron. Soc. 2020, 491, 1160–1173. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, M.G.; Aerts, C.; Pápics, P.I.; Michielsen, M.; Gebruers, S.; Rogers, T.M.; Molenberghs, G.; Burssens, S.; Garcia, S.; Bowman, D.M. Internal mixing of rotating stars inferred from dipole gravity modes. Nat. Astron. 2021, 5, 715–722. [Google Scholar] [CrossRef]
- Karakas, A.I.; Cinquegrana, G.; Joyce, M. The most metal-rich asymptotic giant branch stars. Mon. Not. R. Astron. Soc. 2022, 509, 4430–4447. [Google Scholar] [CrossRef]
- Mirouh, G.M.; Garaud, P.; Stellmach, S.; Traxler, A.L.; Wood, T.S. A New Model for Mixing by Double-diffusive Convection (Semi-convection). I. The Conditions for Layer Formation. Astrophys. J. 2012, 750, 61. [Google Scholar] [CrossRef]
- Pietrinferni, A.; Cassisi, S.; Salaris, M.; Percival, S.; Ferguson, J.W. A Large Stellar Evolution Database for Population Synthesis Studies. V. Stellar Models and Isochrones with CNONa Abundance Anticorrelations. Astrophys. J. 2009, 697, 275–282. [Google Scholar] [CrossRef]
- Beom, M.; Na, C.; Ferguson, J.W.; Kim, Y.C. The Effects of Individual Metal Contents on Isochrones for C, N, O, Na, Mg, Al, Si, and Fe. Astrophys. J. 2016, 826, 155. [Google Scholar] [CrossRef] [Green Version]
- van Saders, J.L.; Pinsonneault, M.H. The Sensitivity of Convection Zone Depth to Stellar Abundances: An Absolute Stellar Abundance Scale from Asteroseismology. Astrophys. J. 2012, 746, 16. [Google Scholar] [CrossRef] [Green Version]
- Cinquegrana, G.C.; Joyce, M. Solar Calibration of the Convective Mixing Length for Use with the ÆSOPUS Opacities in MESA. Res. Notes AAS 2022, 6, 77. [Google Scholar] [CrossRef]
- Roudier, T.; Ballot, J.; Malherbe, J.M.; Chane-Yook, M. Texture of average solar photospheric flows and the donut-like pattern. arXiv 2023, arXiv:2301.07988. [Google Scholar] [CrossRef]
- Gosnell, N.M.; Gully-Santiago, M.A.; Leiner, E.M.; Tofflemire, B.M. Observationally Constraining the Starspot Properties of Magnetically Active M67 Sub-subgiant S1063. Astrophys. J. 2022, 925, 5. [Google Scholar] [CrossRef]
- Libby-Roberts, J.E.; Schutte, M.; Hebb, L.; Kanodia, S.; Canas, C.; Stefansson, G.; Lin, A.S.J.; Mahadevan, S.; Parts, W.; Powers, L.; et al. An In-Depth Look at TOI-3884b: A Super-Neptune Transiting a M4 Dwarf with Persistent Star Spot Crossings. arXiv 2023, arXiv:2302.04757. [Google Scholar] [CrossRef]
- Somers, G.; Pinsonneault, M.H. Older and Colder: The Impact of Starspots on Pre-main-sequence Stellar Evolution. Astrophys. J. 2015, 807, 174. [Google Scholar] [CrossRef] [Green Version]
- Chabrier, G.; Gallardo, J.; Baraffe, I. Evolution of low-mass star and brown dwarf eclipsing binaries. Astron. Astrophys. 2007, 472, L17–L20. [Google Scholar] [CrossRef] [Green Version]
- Somers, G.; Pinsonneault, M.H. A Tale of Two Anomalies: Depletion, Dispersion, and the Connection between the Stellar Lithium Spread and Inflated Radii on the Pre-main Sequence. Astrophys. J. 2014, 790, 72. [Google Scholar] [CrossRef] [Green Version]
- Feiden, G.A.; Chaboyer, B. Self-consistent Magnetic Stellar Evolution Models of the Detached, Solar-type Eclipsing Binary EF Aquarii. Astrophys. J. 2012, 761, 30. [Google Scholar] [CrossRef] [Green Version]
- Somers, G.; Cao, L.; Pinsonneault, M.H. The SPOTS Models: A Grid of Theoretical Stellar Evolution Tracks and Isochrones for Testing the Effects of Starspots on Structure and Colors. Astrophys. J. 2020, 891, 29. [Google Scholar] [CrossRef]
- Mann, A.W.; Feiden, G.A.; Gaidos, E.; Boyajian, T.; von Braun, K. How to Constrain Your M Dwarf: Measuring Effective Temperature, Bolometric Luminosity, Mass, and Radius. Astrophys. J. 2015, 804, 64. [Google Scholar] [CrossRef] [Green Version]
- Dotter, A. MESA Isochrones and Stellar Tracks (MIST) 0: Methods for the construction of stellar isochrones. Astrophys. J. Suppl. Ser. 2016, 222, 8. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef] [Green Version]
- Song, F.; Li, Y.; Wu, T.; Pietrinferni, A.; Poon, H.; Xie, Y. The Influence of the Metal Mass Fraction Z, Age, and Mixing-length Parameter on the RGB Bump Magnitude for the M4 Cluster. Astrophys. J. 2018, 869, 109. [Google Scholar] [CrossRef]
- Choi, J.; Dotter, A.; Conroy, C.; Cantiello, M.; Paxton, B.; Johnson, B.D. Mesa Isochrones and Stellar Tracks (MIST). I. Solar-scaled Models. Astrophys. J. 2016, 823, 102. [Google Scholar] [CrossRef]
- Pietrinferni, A.; Hidalgo, S.; Cassisi, S.; Salaris, M.; Savino, A.; Mucciarelli, A.; Verma, K.; Silva Aguirre, V.; Aparicio, A.; Ferguson, J.W. Updated BaSTI Stellar Evolution Models and Isochrones. II. α-enhanced Calculations. Astrophys. J. 2021, 908, 102. [Google Scholar] [CrossRef]
- Charbonnel, C.; Lebreton, Y. Standard solar model: Interplay between the equation of state, the opacity and the determination of the initial helium content. Astron. Astrophys. 1993, 280, 666–674. [Google Scholar]
- Guenther, D.B.; Demarque, P. α Centauri AB. Astrophys. J. 2000, 531, 503–520. [Google Scholar] [CrossRef]
- Nsamba, B.; Monteiro, M.J.P.F.G.; Campante, T.L.; Cunha, M.S.; Sousa, S.G. α Centauri A as a potential stellar model calibrator: Establishing the nature of its core. Mon. Not. R. Astron. Soc. 2018, 479, L55–L59. [Google Scholar] [CrossRef] [Green Version]
- Freytag, B.; Ludwig, H.G.; Steffen, M. A Calibration of the Mixing-Length for Solar-Type Stars Based on Hydrodynamical Models of Stellar Surface Convection. In Stellar Structure: Theory and Test of Connective Energy Transport; Gimenez, A., Guinan, E.F., Montesinos, B., Eds.; Number 173 in ASP Conf. Ser.; Astronomical Society of the Pacific: San Francisco, CA, USA, 1999; pp. 225–228. [Google Scholar]
- Kervella, P.; Mérand, A.; Pichon, B.; Thévenin, F.; Heiter, U.; Bigot, L.; ten Brummelaar, T.A.; McAlister, H.A.; Ridgway, S.T.; Turner, N.; et al. The radii of the nearby K5V and K7V stars 61 Cygni A & B. CHARA/FLUOR interferometry and CESAM2k modeling. Astron. Astrophys. 2008, 488, 667–674. [Google Scholar] [CrossRef]
- Tang, J.; Joyce, M. Revised Best Estimates for the Age and Mass of the Methuselah Star HD 140283 Using MESA and Interferometry and Implications for 1D Convection. Res. Notes Am. Astron. Soc. 2021, 5, 117. [Google Scholar] [CrossRef]
- Bensby, T.; Feltzing, S.; Gould, A.; Yee, J.C.; Johnson, J.A.; Asplund, M.; Meléndez, J.; Lucatello, S.; Howes, L.M.; McWilliam, A.; et al. Chemical evolution of the Galactic bulge as traced by microlensed dwarf and subgiant stars. VI. Age and abundance structure of the stellar populations in the central sub-kpc of the Milky Way. Astron. Astrophys. 2017, 605, A89. [Google Scholar] [CrossRef] [Green Version]
- Lugaro, M.; Doherty, C.L.; Karakas, A.I.; Maddison, S.T.; Liffman, K.; García-Hernández, D.A.; Siess, L.; Lattanzio, J.C. Short-lived radioactivity in the early solar system: The Super-AGB star hypothesis. Meteorit. Planet. Sci. 2012, 47, 1998–2012. [Google Scholar] [CrossRef] [Green Version]
- Karakas, A.I.; Lattanzio, J.C. The Dawes Review 2: Nucleosynthesis and Stellar Yields of Low- and Intermediate-Mass Single Stars. Publ. Astron. Soc. Aust. 2014, 31, e030. [Google Scholar] [CrossRef] [Green Version]
- Doherty, C.L.; Gil-Pons, P.; Lau, H.H.B.; Lattanzio, J.C.; Siess, L. Super and massive AGB stars-II. Nucleosynthesis and yields-Z = 0.02, 0.008 and 0.004. Mon. Not. R. Astron. Soc. 2014, 437, 195–214. [Google Scholar] [CrossRef] [Green Version]
- Ventura, P.; Dell’Agli, F.; Lugaro, M.; Romano, D.; Tailo, M.; Yagüe, A. Gas and dust from metal-rich AGB stars. Astron. Astrophys. 2020, 641, A103. [Google Scholar] [CrossRef]
- Cinquegrana, G.C.; Karakas, A.I. The most metal-rich stars in the universe: Chemical contributions of low- and intermediate-mass asymptotic giant branch stars with metallicities within 0.04 ≤ Z ≤ 0.10. Mon. Not. R. Astron. Soc. 2022, 510, 1557–1576. [Google Scholar] [CrossRef]
- Dupret, M.A.; Grigahcène, A.; Garrido, R.; Gabriel, M.; Scuflaire, R. Theoretical instability strips for δ Scuti and γ Doradus stars. Astron. Astrophys. 2004, 414, L17–L20. [Google Scholar] [CrossRef] [Green Version]
- Van Reeth, T.; Tkachenko, A.; Aerts, C.; Pápics, P.I.; Triana, S.A.; Zwintz, K.; Degroote, P.; Debosscher, J.; Bloemen, S.; Schmid, V.S.; et al. Gravity-mode Period Spacings as a Seismic Diagnostic for a Sample of γ Doradus Stars from Kepler Space Photometry and High-resolution Ground-based Spectroscopy. Astrophys. J. Suppl. Ser. 2015, 218, 27. [Google Scholar] [CrossRef] [Green Version]
- Murphy, S.J.; Hey, D.; Van Reeth, T.; Bedding, T.R. Gaia-derived luminosities of Kepler A/F stars and the pulsator fraction across the δ Scuti instability strip. Mon. Not. R. Astron. Soc. 2019, 485, 2380–2400. [Google Scholar] [CrossRef] [Green Version]
- Antoci, V.; Cunha, M.S.; Bowman, D.M.; Murphy, S.J.; Kurtz, D.W.; Bedding, T.R.; Borre, C.C.; Christophe, S.; Daszyńska-Daszkiewicz, J.; Fox-Machado, L.; et al. The first view of δ Scuti and γ Doradus stars with the TESS mission. Mon. Not. R. Astron. Soc. 2019, 490, 4040–4059. [Google Scholar] [CrossRef]
- Aerts, C.; Molenberghs, G.; De Ridder, J. Astrophysical properties of 15062 Gaia DR3 gravity-mode pulsators: Pulsation amplitudes, rotation, and spectral line broadening. arXiv 2023, arXiv:2302.07870. [Google Scholar] [CrossRef]
- Bowman, D.M.; Kurtz, D.W. Characterizing the observational properties of δ Sct stars in the era of space photometry from the Kepler mission. Mon. Not. R. Astron. Soc. 2018, 476, 3169–3184. [Google Scholar] [CrossRef] [Green Version]
- Yecko, P.A.; Kollath, Z.; Buchler, J.R. Turbulent convective cepheid models: Linear properties. Astron. Astrophys. 1998, 336, 553–564. [Google Scholar] [CrossRef]
- Stellingwerf, R.F. Convection in pulsating stars. I. Non linear hydro-dynamics. Astrophys. J. 1982, 262, 330–338. [Google Scholar] [CrossRef]
- Baker, N.H.; Gough, D.O. Convection in Pulsating Stars: Quasi-Adiabatic Cepheid Models. Astron. J. 1967, 72, 784. [Google Scholar] [CrossRef]
- Stellingwerf, R.F. Convection in pulsating stars. II. RR LYR convection and stability. Astrophys. J. 1982, 262, 339–343. [Google Scholar] [CrossRef]
- Bono, G.; Caputo, F.; Castellani, V.; Marconi, M.; Staiano, L.; Stellingwerf, R.F. The RR Lyrae Fundamental Red Edge. Astrophys. J. 1995, 442, 159. [Google Scholar] [CrossRef]
- Kolláth, Z.; Buchler, J.R.; Szabó, R.; Csubry, Z. Nonlinear beat Cepheid and RR Lyrae models. Astron. Astrophys. 2002, 385, 932–939. [Google Scholar] [CrossRef]
- Smolec, R.; Moskalik, P. Double-Mode Classical Cepheid Models, Revisited. AcA 2008, 58, 233–261. [Google Scholar] [CrossRef]
- Jurkovic, M.I.; Plachy, E.; Molnár, L.; Groenewegen, M.A.T.; Bódi, A.; Moskalik, P.; Szabó, R. Type II and anomalous Cepheids in the Kepler K2 mission. Mon. Not. R. Astron. Soc. 2023, 518, 642–661. [Google Scholar] [CrossRef]
- Maraston, C. Evolutionary synthesis of stellar populations: A modular tool. Mon. Not. R. Astron. Soc. 1998, 300, 872–892. [Google Scholar] [CrossRef] [Green Version]
- Maraston, C. Evolutionary population synthesis: Models, analysis of the ingredients and application to high-z galaxies. Mon. Not. R. Astron. Soc. 2005, 362, 799–825. [Google Scholar] [CrossRef]
- Bruzual, G.; Charlot, S. Stellar population synthesis at the resolution of 2003. Mon. Not. R. Astron. Soc. 2003, 344, 1000–1028. [Google Scholar] [CrossRef] [Green Version]
- Conroy, C.; Gunn, J.E.; White, M. The Propagation of Uncertainties in Stellar Population Synthesis Modeling. I. The Relevance of Uncertain Aspects of Stellar Evolution and the Initial Mass Function to the Derived Physical Properties of Galaxies. Astrophys. J. 2009, 699, 486–506. [Google Scholar] [CrossRef]
- Goddard, D.; Thomas, D.; Maraston, C.; Westfall, K.; Etherington, J.; Riffel, R.; Mallmann, N.D.; Zheng, Z.; Argudo-Fernández, M.; Lian, J.; et al. SDSS-IV MaNGA: Spatially resolved star formation histories in galaxies as a function of galaxy mass and type. Mon. Not. R. Astron. Soc. 2017, 466, 4731–4758. [Google Scholar] [CrossRef] [Green Version]
- Cowling, T.G. The stability of gaseous stars. Mon. Not. R. Astron. Soc. 1934, 94, 768–782. [Google Scholar] [CrossRef] [Green Version]
- Oke, J.B. A Theoretical Hertzsprung-Russell Diagram for Red Dwarf Stars. J. R. Astron. Soc. Can. 1950, 44, 135. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Pinsonneault, M. Standard solar models, with and without helium diffusion, and the solar neutrino problem. Rev. Mod. Phys. 1992, 64, 885. [Google Scholar] [CrossRef]
- Perkins, D.H. The remarkable history of the discovery of neutrino oscillations. Eur. Phys. J. H 2014, 39, 505–515. [Google Scholar] [CrossRef]
- Grevesse, N.; Noels, A. La composition chimique du Soleil. In Proceedings of the Perfectionnement de l’Association Vaudoise des Chercheurs en Physique, Grimentz, Switzerland, 16–21 March 1992; pp. 205–257. [Google Scholar]
- Grevesse, N.; Sauval, A.J. Standard Solar Composition. Space Sci. Rev. 1998, 85, 161–174. [Google Scholar] [CrossRef]
- Basu, S.; Antia, H.M. Seismic measurement of the depth of the solar convection zone. Mon. Not. R. Astron. Soc. 1997, 287, 189–198. [Google Scholar] [CrossRef]
- Appel, S.; Bagdasarian, Z.; Basilico, D.; Bellini, G.; Benziger, J.; Biondi, R.; Caccianiga, B.; Calaprice, F.; Caminata, A.; Cavalcante, P.; et al. Improved Measurement of Solar Neutrinos from the Carbon-Nitrogen-Oxygen Cycle by Borexino and Its Implications for the Standard Solar Model. Phys. Rev. Lett. 2022, 129, 252701. [Google Scholar] [CrossRef]
- Magg, E.; Bergemann, M.; Serenelli, A.; Bautista, M.; Plez, B.; Heiter, U.; Gerber, J.M.; Ludwig, H.G.; Basu, S.; Ferguson, J.W.; et al. Observational constraints on the origin of the elements. IV. Standard composition of the Sun. Astron. Astrophys. 2022, 661, A140. [Google Scholar] [CrossRef]
- Aerts, C.; Thoul, A.; Daszyńska, J.; Scuflaire, R.; Waelkens, C.; Dupret, M.A.; Niemczura, E.; Noels, A. Asteroseismology of HD 129929: Core Overshooting and Nonrigid Rotation. Science 2003, 300, 1926–1928. [Google Scholar] [CrossRef] [Green Version]
- Basu, S.; Chaplin, W.J. Asteroseismic Data Analysis. Foundations and Techniques; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Pedersen, M.G. On the Diversity of Mixing and Helium Core Masses of B-type Dwarfs from Gravity-mode Asteroseismology. Astrophys. J. 2022, 930, 94. [Google Scholar] [CrossRef]
- Deheuvels, S.; Brandão, I.; Silva Aguirre, V.; Ballot, J.; Michel, E.; Cunha, M.S.; Lebreton, Y.; Appourchaux, T. Measuring the extent of convective cores in low-mass stars using Kepler data: Toward a calibration of core overshooting. Astron. Astrophys. 2016, 589, A93. [Google Scholar] [CrossRef] [Green Version]
- Constantino, T.; Campbell, S.W.; Christensen-Dalsgaard, J.; Lattanzio, J.C.; Stello, D. The treatment of mixing in core helium burning models-I. Implications for asteroseismology. Mon. Not. R. Astron. Soc. 2015, 452, 123–145. [Google Scholar] [CrossRef] [Green Version]
- Beck, P.G.; Bedding, T.R.; Mosser, B.; Stello, D.; Garcia, R.A.; Kallinger, T.; Hekker, S.; Elsworth, Y.; Frandsen, S.; Carrier, F.; et al. Kepler Detected Gravity-Mode Period Spacings in a Red Giant Star. Science 2011, 332, 205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deheuvels, S.; García, R.A.; Chaplin, W.J.; Basu, S.; Antia, H.M.; Appourchaux, T.; Benomar, O.; Davies, G.R.; Elsworth, Y.; Gizon, L.; et al. Seismic Evidence for a Rapidly Rotating Core in a Lower-giant-branch Star Observed with Kepler. Astrophys. J. 2012, 756, 19. [Google Scholar] [CrossRef] [Green Version]
- Mosser, B.; Goupil, M.J.; Belkacem, K.; Marques, J.P.; Beck, P.G.; Bloemen, S.; De Ridder, J.; Barban, C.; Deheuvels, S.; Elsworth, Y.; et al. Spin down of the core rotation in red giants. Astron. Astrophys. 2012, 548, A10. [Google Scholar] [CrossRef] [Green Version]
- Rui, N.Z.; Fuller, J. Asteroseismic fingerprints of stellar mergers. Mon. Not. R. Astron. Soc. 2021, 508, 1618–1631. [Google Scholar] [CrossRef]
- Deheuvels, S.; Ballot, J.; Gehan, C.; Mosser, B. Seismic signature of electron degeneracy in the core of red giants: Hints for mass transfer between close red-giant companions. Astron. Astrophys. 2022, 659, A106. [Google Scholar] [CrossRef]
- Li, Y.; Bedding, T.R.; Murphy, S.J.; Stello, D.; Chen, Y.; Huber, D.; Joyce, M.; Marks, D.; Zhang, X.; Bi, S.; et al. Discovery of post-mass-transfer helium-burning red giants using asteroseismology. Nat. Astron. 2022, 6, 673–680. [Google Scholar] [CrossRef]
- Matteuzzi, M.; Montalbán, J.; Miglio, A.; Vrard, M.; Casali, G.; Stokholm, A.; Tailo, M.; Ball, W.; van Rossem, W.E.; Valentini, M. Red Horizontal Branch stars: An asteroseismic perspective. arXiv 2023, arXiv:2301.08761. [Google Scholar] [CrossRef]
- Tayar, J.; Moyano, F.D.; Soares-Furtado, M.; Escorza, A.; Joyce, M.; Martell, S.L.; García, R.A.; Breton, S.N.; Mathis, S.; Mathur, S.; et al. Spinning up the Surface: Evidence for Planetary Engulfment or Unexpected Angular Momentum Transport? Astrophys. J. 2022, 940, 23. [Google Scholar] [CrossRef]
- García, R.A.; Ceillier, T.; Salabert, D.; Mathur, S.; van Saders, J.L.; Pinsonneault, M.; Ballot, J.; Beck, P.G.; Bloemen, S.; Campante, T.L.; et al. Rotation and magnetism of Kepler pulsating solar-like stars. Towards asteroseismically calibrated age-rotation relations. Astron. Astrophys. 2014, 572, A34. [Google Scholar] [CrossRef] [Green Version]
- Stello, D.; Cantiello, M.; Fuller, J.; Huber, D.; García, R.A.; Bedding, T.R.; Bildsten, L.; Silva Aguirre, V. A prevalence of dynamo-generated magnetic fields in the cores of intermediate-mass stars. Nature 2016, 529, 364–367. [Google Scholar] [CrossRef] [Green Version]
- Fuller, J.; Cantiello, M.; Stello, D.; Garcia, R.A.; Bildsten, L. Asteroseismology can reveal strong internal magnetic fields in red giant stars. Science 2015, 350, 423–426. [Google Scholar] [CrossRef] [Green Version]
- Bugnet, L.; Prat, V.; Mathis, S.; Astoul, A.; Augustson, K.; García, R.A.; Mathur, S.; Amard, L.; Neiner, C. Magnetic signatures on mixed-mode frequencies. I. An axisymmetric fossil field inside the core of red giants. Astron. Astrophys. 2021, 650, A53. [Google Scholar] [CrossRef]
- Pinsonneault, M.H.; Elsworth, Y.P.; Tayar, J.; Serenelli, A.; Stello, D.; Zinn, J.; Mathur, S.; García, R.A.; Johnson, J.A.; Hekker, S.; et al. The Second APOKASC Catalog: The Empirical Approach. Astrophys. J. Suppl. Ser. 2018, 239, 32. [Google Scholar] [CrossRef]
- Silva Aguirre, V.; Bojsen-Hansen, M.; Slumstrup, D.; Casagrande, L.; Kawata, D.; Ciucǎ, I.; Handberg, R.; Lund, M.N.; Mosumgaard, J.R.; Huber, D.; et al. Confirming chemical clocks: Asteroseismic age dissection of the Milky Way disc(s). Mon. Not. R. Astron. Soc. 2018, 475, 5487–5500. [Google Scholar] [CrossRef] [Green Version]
- Chaplin, W.J.; Serenelli, A.M.; Miglio, A.; Morel, T.; Mackereth, J.T.; Vincenzo, F.; Kjeldsen, H.; Basu, S.; Ball, W.H.; Stokholm, A.; et al. Age dating of an early Milky Way merger via asteroseismology of the naked-eye star ν Indi. Nat. Astron. 2020, 4, 382–389. [Google Scholar] [CrossRef] [Green Version]
- Grunblatt, S.K.; Zinn, J.C.; Price-Whelan, A.M.; Angus, R.; Saunders, N.; Hon, M.; Stokholm, A.; Bellinger, E.P.; Martell, S.L.; Mosser, B.; et al. Age-dating Red Giant Stars Associated with Galactic Disk and Halo Substructures. Astrophys. J. 2021, 916, 88. [Google Scholar] [CrossRef]
- Ness, M.; Hogg, D.W.; Rix, H.W.; Martig, M.; Pinsonneault, M.H.; Ho, A.Y.Q. Spectroscopic Determination of Masses (and Implied Ages) for Red Giants. Astrophys. J. 2016, 823, 114. [Google Scholar] [CrossRef]
- Leung, H.W.; Bovy, J.; Mackereth, J.T.; Miglio, A. A variational encoder-decoder approach to precise spectroscopic age estimation for large Galactic surveys. arXiv 2023, arXiv:2302.05479. [Google Scholar] [CrossRef]
- Brasseur, C.M.; Stetson, P.B.; VandenBerg, D.A.; Casagrande, L.; Bono, G.; Dall’Ora, M. Fiducial Stellar Population Sequences for the VJKS Photometric System. Astron. J. 2010, 140, 1672–1686. [Google Scholar] [CrossRef] [Green Version]
- Cohen, R.E.; Hempel, M.; Mauro, F.; Geisler, D.; Alonso-Garcia, J.; Kinemuchi, K. Wide Field Near-infrared Photometry of 12 Galactic Globular Clusters: Observations Versus Models on the Red Giant Branch. Astron. J. 2015, 150, 176. [Google Scholar] [CrossRef] [Green Version]
- Smiljanic, R.; Franciosini, E.; Randich, S.; Magrini, L.; Bragaglia, A.; Pasquini, L.; Vallenari, A.; Tautvaišienė, G.; Biazzo, K.; Frasca, A.; et al. The Gaia-ESO Survey: Inhibited extra mixing in two giants of the open cluster Trumpler 20? Astron. Astrophys. 2016, 591, A62. [Google Scholar] [CrossRef] [Green Version]
- Ness, M.; Freeman, K.; Athanassoula, E.; Wylie-de-Boer, E.; Bland-Hawthorn, J.; Asplund, M.; Lewis, G.F.; Yong, D.; Lane, R.R.; Kiss, L.L. ARGOS-III. Stellar populations in the Galactic bulge of the Milky Way. Mon. Not. R. Astron. Soc. 2013, 430, 836–857. [Google Scholar] [CrossRef] [Green Version]
- Metcalfe, T.S.; Creevey, O.L.; Doğan, G.; Mathur, S.; Xu, H.; Bedding, T.R.; Chaplin, W.J.; Christensen-Dalsgaard, J.; Karoff, C.; Trampedach, R.; et al. Properties of 42 Solar-type Kepler Targets from the Asteroseismic Modeling Portal. Astrophys. J. Suppl. Ser. 2014, 214, 27. [Google Scholar] [CrossRef] [Green Version]
- Creevey, O.; Metcalfe, T.S.; Schultheis, M.; Salabert, D.; Bazot, M.; Thevenin, F.; Mathur, S.; Xu, H.; Garcia, R.A. Characterizing solar-type stars from full-length Kepler data sets using the Asteroseismic Modeling Portal. arXiv 2016, arXiv:1612.08990. [Google Scholar] [CrossRef] [Green Version]
- Silva Aguirre, V.; Lund, M.N.; Antia, H.M.; Ball, W.H.; Basu, S.; Christensen-Dalsgaard, J.; Lebreton, Y.; Reese, D.R.; Verma, K.; Casagrande, L.; et al. Standing on the Shoulders of Dwarfs: The Kepler Asteroseismic LEGACY Sample. II.Radii, Masses, and Ages. Astrophys. J. 2017, 835, 173. [Google Scholar] [CrossRef] [Green Version]
- Miesch, M.S. Large-Scale Dynamics of the Convection Zone and Tachocline. Living Rev. Sol. Phys. 2005, 2, 1. [Google Scholar] [CrossRef] [Green Version]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joyce, M.; Tayar, J. A Review of the Mixing Length Theory of Convection in 1D Stellar Modeling. Galaxies 2023, 11, 75. https://doi.org/10.3390/galaxies11030075
Joyce M, Tayar J. A Review of the Mixing Length Theory of Convection in 1D Stellar Modeling. Galaxies. 2023; 11(3):75. https://doi.org/10.3390/galaxies11030075
Chicago/Turabian StyleJoyce, Meridith, and Jamie Tayar. 2023. "A Review of the Mixing Length Theory of Convection in 1D Stellar Modeling" Galaxies 11, no. 3: 75. https://doi.org/10.3390/galaxies11030075
APA StyleJoyce, M., & Tayar, J. (2023). A Review of the Mixing Length Theory of Convection in 1D Stellar Modeling. Galaxies, 11(3), 75. https://doi.org/10.3390/galaxies11030075






