On the Evolution of, and Hot Gas in, Wind-Blown Bubbles around Massive Stars - Wind Bubbles Are Not Energy-Conserving
Abstract
:1. Introduction
- As pointed out by authors such as Nazé et al. [40], some observed bubbles do not appear to conform to the theoretical predictions. Instead, wind mechanical luminosities (), calculated using the Weaver et al. [10] model, can be up to two orders of magnitude lower than those expected from the stellar parameters.
- Wind bubbles should technically be found around every massive star since they all have fast winds. However, they are rarely seen around main-sequence O and B stars [41].
- The wind velocities of O, B, and W-R stars are of the order of 1000–3000 km s. The post-shock temperature in the shocked wind region would then bewhere is the mean molecular weight of the gas, the Boltzmann constant, and is the mass of a hydrogen atom. for a fully ionized gas has been used. In this calculation, the wind termination shock is assumed to be slowly moving in the laboratory frame, which is generally true.Given the expectation of such high temperatures in this large volume of shocked wind, wind-blown nebulae should be visible as regions of diffuse X-ray emission, with X-ray temperatures on the order of 1–10 keV. However, although extensive searches have been carried out using Chandra and XMM, diffuse X-ray emission has been detected in only a few cases [42,43,44,45]. Even in those cases, the observed X-ray temperatures are 10–100 times smaller than what would be expected from the Weaver et al. [10] model. For the WBBs NGC 6888 and S308 surrounding W-R stars, the inferred X-ray temperatures are a few times 10 K, which is lower than expected. In the case of NGC 6888, a higher temperature component (>2 keV) inferred from Suzaku data by Zhekov and Park [46] is not supported by Chandra and XMM-Newton data [47,48]. A high temperature component (>4.5 keV) for NGC 2359 was found by Toalá et al. [49], but the contribution of this component to the total X-ray flux was less than 10%. Diffuse X-ray emission has also been seen in the W-R nebula NGC 3199 around the W-R star WR 18 [50]. Here, again, the dominant plasma temperature is around 0.15 keV, with a hotter component contributing less than 8% of the flux. Deep X-ray observations of NGC 7635 [51] failed to reveal any signs of X-ray emission. Many other wind-blown bubbles around massive stars do not show the presence of X-ray emission at all [41,52].
2. Results from Ionization-Gasdynamic Simulations
3. Bubble Radius and Expansion
4. Energy Loss and Bubble Evolution
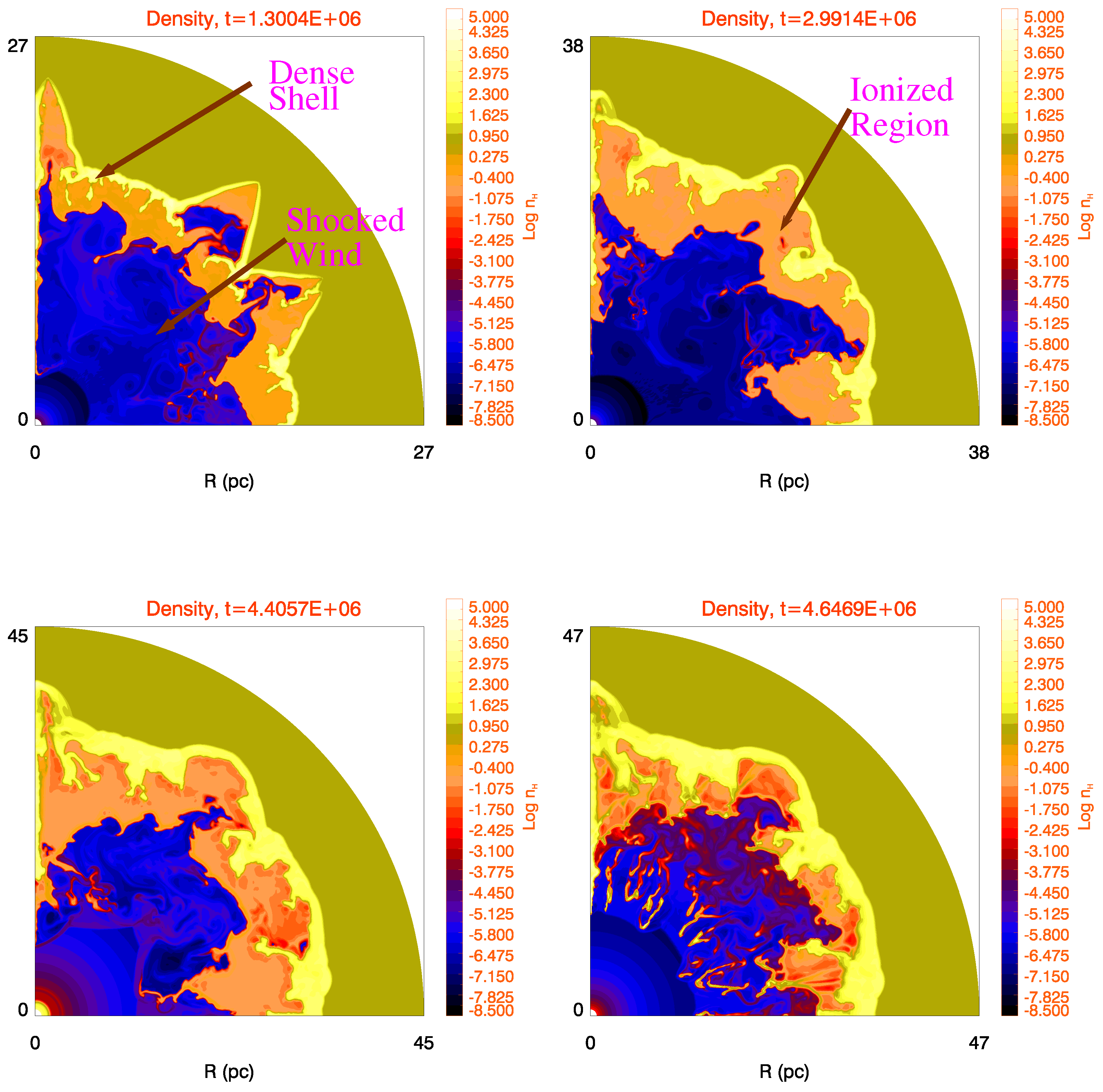
- Instabilities: The 2D simulations show the presence of several hydrodynamic and ionization front instabilities. Instabilities are an inherent feature of multi-dimensional simulations. Paper 1 identified various instabilities found in different regions.
- –
- The ionization front is found to be unstable to D-type ionization front instabilities. These are mainly prevalent in the early evolution of the bubble (see Figure 1).
- –
- Finger-like projections, due to various instabilities, combined with photo-evaporative absorption, are seen at the inner edge of the dense shell during the evolution. These are seen throughout the evolution.
- –
- The interface of the hot shocked wind region with the ionized HII region is susceptible to Rayleigh–Taylor and Kelvin–Helmholtz instabilities (Figure 1). These instabilities grow throughout the evolution. The hot shocked wind region itself does not maintain a spherical geometry. Mixing of the cooler HII region material (at ≈10 K) with the hotter bubble material can lead to cooling and an overall reduction in temperature in the hot bubble.
- –
- Hydrodynamic simulations [7] have shown that the RSG wind shell is unstable to Rayleigh–Taylor instabilities. The W-R wind expanding within the RSG wind is also unstable to the Rayleigh–Taylor (R-T) instability [7], with the R-T fingers pointing inwards. The high momentum W-R wind breaks apart the unstable RSG wind, leading to the formation of clumps and filaments that are mixed into the hot shocked wind region.
The various instabilities can lead to a high rate of cooling at the interfaces, which will be absent in spherically symmetric simulations. Mixing can occur between the dense ionized region and the shocked wind region, adding mass and cooler material to the hot shocked wind. The instabilities themselves are a function of grid resolution and the hydrodynamic methods used to carry out the simulation; the number, size, and growth may vary between 2D and 3D simulations. A comparison between 2D and 3D instabilities in circumstellar shells around massive stars, without photoionization, was carried out by [57]. Highly resolved 3D simulations are required to properly account for the effect of various instabilities. We plan to carry these out in the future. - Vorticity within the bubble: A wind termination shock separates the freely expanding wind from the shocked wind. The position and shape of the shock changes with time (Figure 1). The shape of the shock front responds to inhomogeneities in the flow, the presence of clumps and other density perturbations, and hydrodynamical instabilities. This is also seen in simulations of planetary nebulae [58], which are wind bubbles around lower-mass stars. The change in the position and shape introduces vorticity within the bubble. The vorticity deposition is carried out with the flow and results in the formation of vortices in the shocked wind region. Figure 3 shows the velocity vectors (blue) imprinted over the density contours (red) for the simulation in Figure 1. The formation of vortices in the shocked wind region is clearly visible. The vortices are long-lasting, and tend to cluster and sometimes merge together, forming larger vortices. This could be a function of the 2D nature of the simulations. In 2D, the energy cascades to longer wavelengths, unlike 3D simulations, where the energy is expected to cascade to smaller scales.The evolution of vorticity is shown mainly in the MS phase. In the RSG phase, the low velocity RSG wind does not travel far into the shocked bubble, while the high density of the wind leads to a new pressure equilibrium. In the W-R phase, the various instabilities, and the transport of the RSG and W-R material into the shocked wind, make visualization of the velocity vectors and the vortexes difficult. Dwarkadas [25] carried out a calculation of the energy in non-radial motions in the nebula, and concluded that 15–20% of the energy in the W-R phase goes into turbulent motions, thus reducing the energy that can go into heating the diffuse gas.Two-dimensional (2D) turbulence is known to have properties that differ from 3D turbulence. Specifically, 2D turbulence results in an inverse cascade in energy, as opposed to 3D turbulence, where energy cascades to the lowest scales [59,60,61,62,63,64]. 2D turbulence also results in a clustering of long-lived vortices, which is not seen in 3D. These results, while well documented, are generally based on experiments conducted with 2D incompressible flows. Our simulations are axially symmetric and involve compressible flows. Therefore, the applicability of the results is unclear. As the motion and change in shape of the wind termination shock are physically motivated, qualitatively we expect similar results in 3D to those obtained herein. Vorticity deposition at the inner shock would be expected, although the extent of the turbulence may differ. The size and structure of vortices will differ in the 3D calculations as compared to our 2D ones. Therefore, the amount of energy expended in turbulence in 3D may be different from 2D, but there is no doubt that turbulence will deplete the energy in the shocked wind region and thereby the pressure driving the bubble expansion.
- Mass loading: Koo and McKee [12] showed that the shocked wind in an adiabatic bubble with a radiative shell can transition to a partially radiative bubble only if there is additional mass injection. A partially radiative bubble is one where the cooling time of the gas in the hot shocked wind is larger than the crossing time, but smaller than the age of the bubble. In the MS phase, hydrodynamic and ionization front instabilities lead to the formation of clumps and fingers that are injected into the wind bubble. The size of the bubble, and hence its volume, is mainly set in the main-sequence phase, while most of the mass emitted by the star, which is mixed in with the shocked wind region, arises in the RSG and W-R stages. The post-MS phases occupy only about 10% of the lifetime of the star, adding a substantial amount of mass to the bubble without a significant increase in volume. The breakup of the RSG material by the W-R wind results in the formation of clumps and filaments that are mixed in with the hot shocked wind material. This increases the mass without changing the volume appreciably, thus enhancing the density. In our simulations, the average density in the hot shocked wind region is still not large enough to make the cooling time smaller than the bubble age. However, there are regions of very high density, such as clumps and filaments, where the cooling time becomes shorter than the age of the bubble, leading to local cooling of the shocked wind material.
5. Discussion
- Dynamics and Kinematics of WBBs around massive stars: If WBBs are better described by a momentum-conserving solution, then the radius of the bubble is smaller than that expected from Weaver et al. [10]. Conversely, given the bubble radius R and the shell velocity v in the Weaver et al. [10] solution, the time of expansion (the age of the bubble), assuming a constant velocity, is given bywhile in the momentum-conserving (efficiently cooling) regime, it is given byThus, the momentum-conserving bubble will have a smaller age for a given radius and velocity. This can be used to resolve various discrepancies pointed out in the literature.Nazé et al. [40] compared the expansion dynamics of interstellar bubbles in N180B and N11B with the Weaver et al. [10] PD solution, and found that it leads to wind luminosities that are at least an order of magnitude lower than expected.The bubble blown by the O3-O4 star MGSD 214 in N180B has a radius of 11 pc and an expansion velocity 20 km s, giving a dynamical timescale of 3.3 × yr. With an rms density of ∼9.5 cm, using the Weaver et al. [10] solution they calculated a wind luminosity of ∼3 × erg s for MGSD 214, which is a factor of 10 lower than expected from an O3-O4 star.Using the momentum-conserving bubble solution, we obtain an age that is 1.2 times lower, ∼ yr. Using the expression in Equation (4), and assuming a wind velocity of 2000 km s, we obtain a wind luminosity of 6 × erg s, which is comparable to what is expected from an O3-O4 star.Nazé et al. [40] similarly considered the bubble blown by PGMW 3204, 3209, and 3223 in N11B. The star PGMW 3209, although dominated by an O3 III star, is in a cluster of at least 5 other O stars. Using the derived radius of 7 pc, and an expansion velocity of 10 km s, they found a dynamical timescale for this bubble to be 4.1 × yr using the Weaver et al. [10] solution. With the rms density of 15 cm for N11B, they found a wind luminosity of ∼2.5 × 10 erg s for PGMW 3209, which is almost 2 orders of magnitude lower than what is expected from an O3 III star.The momentum-conserving solution, on the other hand, gives a lifetime of 3.42 × yr. Using Equation (4), and a wind velocity of 3245 km s for an O3 III star [67], we find a bubble luminosity of 1.6 × erg s, bringing it in line with the expectation for an O3 III star, and close to two orders of magnitude higher than the value obtained by Nazé et al. [40].
- Expansion velocities of the bubbles:The velocity of a bubble in the momentum-conserving phase is given by:where is the time in years, and we use yr, km s, and a density in the surrounding medium cm. Initially, the bubble will be energy-conserving, but due to efficient cooling, it slowly transforms into a momentum-conserving bubble. The time when the momentum-conserving phase is reached will vary for different mass stars. Equation (8) applies only after the momentum-conserving stage is reached. In our simulation, this happens at around half a million years. From that time onward the velocity in our simulation (for the radius shown in Figure 2) is found to decrease, as t, which is consistent with the value for a momentum-conserving bubble. Prior to this, the bubble will have a higher velocity, being in the pressure-driven stage. Therefore, although the velocity decreases at the rate given by Equation (8) after around 500,000 years, its actual value is slightly higher than that calculated from the above equation. The equation implies that in a million years the velocity should decrease to 5.8 km s. The velocity and mass-loss rate of the stellar wind will change with time, so the above estimate is an approximation, but it clearly shows that the velocities of wind bubbles will be low throughout most of the star’s evolution. The velocities of typical wind bubbles, both on the MS and in the W-R phase, are found to be generally less than 10 km s [68], so these values are consistent. The bubble may also approach pressure equilibrium with the surrounding medium. For a higher ambient density, the bubble velocity scales as , whereas it will increase with increasing mass-loss rate and wind velocity as and , respectively.Chu et al. [44] contend that the low velocity implies weak shocks and a lack of compression of the material in the dense shell, which could account for the lack of observed MS bubbles, as it will make the bubble difficult to observe at optical wavelengths, especially if the surrounding medium is an HII region. This is debatable, as the slow shock will likely be a radiative shock, as expected in wind bubbles, with a total compression ratio larger than that for a strong shock. This will happen until the shock is close to reaching pressure equilibrium with the surrounding medium. Thus, a lack of compression cannot be the reason. Chu et al. [44] further contend that as massive stars evolve, they will ‘lose ionizing power’, and the bubbles and the ambient medium will recombine and cool, making them more detectable. There are difficulties with this argument when comparing MS and W-R bubbles. W-R stars have more ionizing photons than MS stars, so the argument that stars lose ionizing power as they age would not hold, in fact they become more powerful ionizing sources.We suggest here that the reason that W-R nebulae, formed when stars age, are more easily detectable than MS nebulae in the optical, is simply because their optical luminosity is higher. For one, the dense shell has swept up a larger amount of mass () by the W-R stage. It has also expanded outwards, and its radius has increased. The shell volume , where , the thickness of the dense shell, increases almost proportionately to the radius in self-similar evolution. Therefore, the density remains the same or decreases slightly. Due to the larger volume, the H emission resulting from recombination in the shell will be higher. Secondly, the W-R wind carries both its mass and the mass of the prior RSG wind, mixing it into the hot shocked MS wind. As pointed out in Paper 1, and in earlier sections, the W-R wind collides with the dense RSG wind, breaking it up, and forming high density clumps and filaments in the hot shocked wind region. The densest clumps are too dense to emit in X-rays but have the right temperature to emit in the optical (Figure 5). The H luminosity arising from Case B recombination is, similar to the X-ray luminosity (Section 6), a function of the square of the plasma density. Therefore, the densest clumps can emit in H, and the H luminosity in the W-R phase will be significantly higher than in the MS phase, contributing to the detectability at optical wavelengths. We therefore suggest that it is the higher optical luminosity of bubbles in the W-R phase, and not the shock compression, which makes W-R bubbles more detectable compared to MS ones.
6. X-ray Emission from Wind-Blown Bubbles
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WBB | wind-blown bubble |
| MS | main sequence |
| RSG | red supergiant |
| W-R | Wolf–Rayet |
| R-T | Rayleigh-Taylor |
References
- Sukhbold, T.; Ertl, T.; Woosley, S.E.; Brown, J.M.; Janka, H.T. Core-collapse Supernovae from 9 to 120 Solar Masses Based on Neutrino-powered Explosions. Astrophys. J. 2016, 821, 38. [Google Scholar] [CrossRef] [Green Version]
- Soker, N. The two promising scenarios to explode core collapse supernovae. Res. Astron. Astrophys. 2017, 17, 113. [Google Scholar] [CrossRef] [Green Version]
- Chevalier, R.A.; Liang, E.P. The interaction of supernovae with circumstellar bubbles. Astrophys. J. 1989, 344, 332–340. [Google Scholar] [CrossRef]
- Tenorio-Tagle, G.; Bodenheimer, P.; Franco, J.; Rozyczka, M. On the evolution of supernova remnants. I—Explosions inside pre-existing wind-driven bubbles. Mon. Not. R. Astron. Soc. 1990, 244, 563–576. [Google Scholar]
- Tenorio-Tagle, G.; Rozyczka, M.; Franco, J.; Bodenheimer, P. On the evolution of supernova remnants. II—Two-dimensional calculations of explosions inside pre-existing wind-driven bubbles. Mon. Not. R. Astron. Soc. 1991, 251, 318–329. [Google Scholar] [CrossRef] [Green Version]
- Dwarkadas, V.V. The Evolution of Supernovae in Circumstellar Wind-Blown Bubbles. I. Introduction and One-Dimensional Calculations. Astrophys. J. 2005, 630, 892–910. [Google Scholar] [CrossRef] [Green Version]
- Dwarkadas, V.V. The Evolution of Supernovae in Circumstellar Wind Bubbles. II. Case of a Wolf-Rayet Star. Astrophys. J. 2007, 667, 226–247. [Google Scholar] [CrossRef] [Green Version]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef] [Green Version]
- Avedisova, V.S. Formation of Nebulae by Wolf-Rayet Stars. Sov. Astron. 1972, 15, 708. [Google Scholar]
- Weaver, R.; McCray, R.; Castor, J.; Shapiro, P.; Moore, R. Interstellar bubbles. II. Structure and evolution. Astrophys. J. 1977, 218, 377–395. [Google Scholar] [CrossRef]
- Koo, B.C.; McKee, C.F. Dynamics of Wind Bubbles and Superbubbles. I. Slow Winds and Fast Winds. Astrophys. J. 1992, 388, 93. [Google Scholar] [CrossRef]
- Koo, B.C.; McKee, C.F. Dynamics of Wind Bubbles and Superbubbles. II. Analytic Theory. Astrophys. J. 1992, 388, 103. [Google Scholar] [CrossRef]
- Chevalier, R.A. Expansion of a Photoionized Stellar Wind. Astrophys. J. 1997, 488, 263–267. [Google Scholar] [CrossRef]
- Garcia-Segura, G.; Langer, N.; Mac Low, M.M. The hydrodynamic evolution of circumstellar gas around massive stars. II. The impact of the time sequence O star -> RSG -> WR star. Astron. Astrophys. 1996, 316, 133–146. [Google Scholar]
- Garcia-Segura, G.; Mac Low, M.M.; Langer, N. The dynamical evolution of circumstellar gas around massive stars. I. The impact of the time sequence Ostar -> LBV -> WR star. Astron. Astrophys. 1996, 305, 229. [Google Scholar]
- Frank, A.; Balick, B.; Davidson, K. The Homunculus of eta Carinae: An Interacting Stellar Winds Paradigm. Astrophys. J. 1995, 441, L77. [Google Scholar] [CrossRef]
- Dwarkadas, V.V.; Balick, B. On the Formation of the Homunculus Nebula around eta Carinae. Astron. J. 1998, 116, 829–839. [Google Scholar] [CrossRef] [Green Version]
- Frank, A.; Ryu, D.; Davidson, K. Where is the Doughnut? Luminous Blue Variable Bubbles and Aspherical Fast Winds. Astrophys. J. 1998, 500, 291–301. [Google Scholar] [CrossRef] [Green Version]
- Dwarkadas, V.V.; Owocki, S.P. Radiatively Driven Winds and the Shaping of Bipolar Luminous Blue Variable Nebulae. Astrophys. J. 2002, 581, 1337–1343. [Google Scholar] [CrossRef]
- van Marle, A.J.; Langer, N.; García-Segura, G. Constraints on gamma-ray burst and supernova progenitors through circumstellar absorption lines. Astron. Astrophys. 2005, 444, 837–847. [Google Scholar] [CrossRef] [Green Version]
- van Marle, A.J.; Langer, N.; Achterberg, A.; Garcaía-Segura, G. Forming a constant density medium close to long gamma-ray bursts. Astron. Astrophys. 2006, 460, 105–116. [Google Scholar] [CrossRef]
- Freyer, T.; Hensler, G.; Yorke, H.W. Massive Stars and the Energy Balance of the Interstellar Medium. I. The Impact of an Isolated 60 Msolar Star. Astrophys. J. 2003, 594, 888–910. [Google Scholar] [CrossRef] [Green Version]
- Freyer, T.; Hensler, G.; Yorke, H.W. Massive Stars and the Energy Balance of the Interstellar Medium. II. The 35 Msolar Star and a Solution to the “Missing Wind Problem”. Astrophys. J. 2006, 638, 262–280. [Google Scholar] [CrossRef] [Green Version]
- Dwarkadas, V.V. Hydrodynamics of Supernova Evolution in the Winds of Massive Stars. ApSS 2007, 307, 153–158. [Google Scholar] [CrossRef] [Green Version]
- Dwarkadas, V.V. Turbulence in wind-blown bubbles around massive stars. Phys. Scr. Vol. T 2008, 132, 014024. [Google Scholar] [CrossRef]
- van Marle, A.J.; Keppens, R.; Meliani, Z. 3-D simulations of shells around massive stars. arXiv 2011, arXiv:1102.0104. [Google Scholar]
- Arthur, S.J. Wind-Blown Bubbles and HII Regions around Massive Stars. Rev. Mex. Astron. Astrofis. 2007, 30, 64–71. [Google Scholar]
- Arthur, S.J. Dynamics of Bubbles in the ISM. AIP Conf. Proc. 2009, 1156, 285–294. [Google Scholar] [CrossRef]
- Toalá, J.A.; Arthur, S.J. Radiation-hydrodynamic Models of the Evolving Circumstellar Medium around Massive Stars. Astrophys. J. 2011, 737, 100. [Google Scholar] [CrossRef] [Green Version]
- Dwarkadas, V.V.; Rosenberg, D.L. Simulated X-ray spectra from ionized wind-blown nebulae around massive stars. High Energy Density Phys. 2013, 9, 226–230. [Google Scholar] [CrossRef] [Green Version]
- Dwarkadas, V.V. Ionization-Gasdynamic Simulations of Wind-Blown Nebulae around Massive Stars. Galaxies 2022, 10, 37. [Google Scholar] [CrossRef]
- Capriotti, E.R.; Kozminski, J.F. Relative Effects of Ionizing Radiation and Winds from O-Type Stars on the Structure and Dynamics of H II Regions. Publ. Astron. Soc. Pac. 2001, 113, 677–691. [Google Scholar] [CrossRef] [Green Version]
- Haid, S.; Walch, S.; Seifried, D.; Wünsch, R.; Dinnbier, F.; Naab, T. The relative impact of photoionizing radiation and stellar winds on different environments. Mon. Not. R. Astron. Soc. 2018, 478, 4799–4815. [Google Scholar] [CrossRef] [Green Version]
- Geen, S.; Bieri, R.; Rosdahl, J.; de Koter, A. The geometry and dynamical role of stellar wind bubbles in photoionized H II regions. Mon. Not. R. Astron. Soc. 2021, 501, 1352–1369. [Google Scholar] [CrossRef]
- Lancaster, L.; Ostriker, E.C.; Kim, J.G.; Kim, C.G. Efficiently Cooled Stellar Wind Bubbles in Turbulent Clouds. I. Fractal Theory and Application to Star-forming Clouds. Astrophys. J. 2021, 914, 89. [Google Scholar] [CrossRef]
- Lancaster, L.; Ostriker, E.C.; Kim, J.G.; Kim, C.G. Efficiently Cooled Stellar Wind Bubbles in Turbulent Clouds. II. Validation of Theory with Hydrodynamic Simulations. Astrophys. J. 2021, 914, 90. [Google Scholar] [CrossRef]
- Meyer, D.M.A.; Oskinova, L.M.; Pohl, M.; Petrov, M. On the ring nebulae around runaway Wolf-Rayet stars. Mon. Not. R. Astron. Soc. 2020, 496, 3906–3911. [Google Scholar] [CrossRef]
- Meyer, D.M.A. On the bipolarity of Wolf-Rayet nebulae. Mon. Not. R. Astron. Soc. 2021, 507, 4697–4714. [Google Scholar] [CrossRef]
- Mac Low, M.M.; McCray, R. Superbubbles in Disk Galaxies. Astrophys. J. 1988, 324, 776. [Google Scholar] [CrossRef]
- Nazé, Y.; Chu, Y.H.; Points, S.D.; Danforth, C.W.; Rosado, M.; Chen, C.H.R. Interstellar Bubbles in Two Young H II Regions. Astron. J. 2001, 122, 921–937. [Google Scholar] [CrossRef]
- Chu, Y. Bubbles and Superbubbles: Observations and Theory. Proc. Int. Astron. Union 2008, 250, 341–354. [Google Scholar] [CrossRef] [Green Version]
- Chu, Y. Ring nebulae around massive stars throughout the Hertzsprung-Russell diagram. Proc. Int. Astron. Union 2003, 212, 585–595. [Google Scholar] [CrossRef] [Green Version]
- Chu, Y.H.; Guerrero, M.A.; Gruendl, R.A.; García-Segura, G.; Wendker, H.J. Hot Gas in the Circumstellar Bubble S308. Astrophys. J. 2003, 599, 1189–1195. [Google Scholar] [CrossRef] [Green Version]
- Chu, Y.H.; Gruendl, R.A.; Guerrero, M.A. An Inside-Out View of Bubbles. arXiv 2002, arXiv:astro-ph/0212152. [Google Scholar]
- Wrigge, M.; Chu, Y.H.; Magnier, E.A.; Wendker, H.J. X-Ray Emission from Wind-blown Bubbles. III. ASCA SIS Observations of NGC 6888. Astrophys. J. 2005, 633, 248–256. [Google Scholar] [CrossRef] [Green Version]
- Zhekov, S.A.; Park, S. Suzaku Observations of the Prototype Wind-blown Bubble NGC 6888. Astrophys. J. 2011, 728, 135. [Google Scholar] [CrossRef] [Green Version]
- Toalá, J.A.; Guerrero, M.A.; Gruendl, R.A.; Chu, Y.H. X-ray Emission from the Wolf-Rayet Bubble NGC 6888. I. Chandra ACIS-S Observations. Astron. J. 2014, 147, 30. [Google Scholar] [CrossRef] [Green Version]
- Toalá, J.A.; Guerrero, M.A.; Chu, Y.H.; Arthur, S.J.; Tafoya, D.; Gruendl, R.A. X-ray emission from the Wolf-Rayet bubble NGC 6888—II. XMM-Newton EPIC observations. Mon. Not. R. Astron. Soc. 2016, 456, 4305–4314. [Google Scholar] [CrossRef] [Green Version]
- Toalá, J.A.; Guerrero, M.A.; Chu, Y.H.; Gruendl, R.A. On the diffuse X-ray emission from the Wolf-Rayet bubble NGC 2359. Mon. Not. R. Astron. Soc. 2015, 446, 1083–1089. [Google Scholar] [CrossRef] [Green Version]
- Toalá, J.A.; Marston, A.P.; Guerrero, M.A.; Chu, Y.H.; Gruendl, R.A. Hot Gas in the Wolf-Rayet Nebula NGC 3199. Astrophys. J. 2017, 846, 76. [Google Scholar] [CrossRef] [Green Version]
- Toalá, J.A.; Guerrero, M.A.; Todt, H.; Sabin, L.; Oskinova, L.M.; Chu, Y.H.; Ramos-Larios, G.; Gómez-González, V.M.A. The Bubble Nebula NGC 7635 - testing the wind-blown bubble theory. Mon. Not. R. Astron. Soc. 2020, 495, 3041–3051. [Google Scholar] [CrossRef]
- Chu, Y.H.; Gruendl, R.A.; Guerrero, M.A. Hot Gas in Wind-Blown Bubbles. In Proceedings of the The X-ray Universe, Madrid, Spain, 26–30 September 2005; Wilson, A., Ed.; ESA Publications Division ESTEC: Noordwijk, The Netherlands, 2006; Volume 604, p. 363. [Google Scholar]
- Chevalier, R.A.; Dwarkadas, V.V. The Presupernova H II Region around SN 1987A. Astrophys. J. 1995, 452, L45. [Google Scholar] [CrossRef]
- El-Badry, K.; Ostriker, E.C.; Kim, C.G.; Quataert, E.; Weisz, D.R. Evolution of supernovae-driven superbubbles with conduction and cooling. Mon. Not. R. Astron. Soc. 2019, 490, 1961–1990. [Google Scholar] [CrossRef] [Green Version]
- Lamers, H.J.; Cassinelli, J.P. Introduction to Stellar Winds; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Treffers, R.R.; Chu, Y.H. Galactic ring nebulae associated with Wolf-rayet stars. V. The stellar wind blown bubbles. Astrophys. J. 1982, 254, 569–577. [Google Scholar] [CrossRef]
- van Marle, A.J.; Keppens, R. Multi-dimensional models of circumstellar shells around evolved massive stars. Astron. Astrophys. 2012, 547, A3. [Google Scholar] [CrossRef] [Green Version]
- Dwarkadas, V.V.; Balick, B. The Morphology of Planetary Nebulae: Simulations with Time-evolving Winds. Astrophys. J. 1998, 497, 267–275. [Google Scholar] [CrossRef]
- Smith, L.M.; Yakhot, V. Onset of intermittency in two-dimensional decaying turbulence. PRevE 1997, 55, 5458–5464. [Google Scholar] [CrossRef]
- Danilov, S.D.; Gurarie, D. REVIEWS OF TOPICAL PROBLEMS: Quasi-two-dimensional turbulence. Phys. Uspekhi 2000, 43, 863–900. [Google Scholar] [CrossRef] [Green Version]
- Delbende, I.; Gomez, T.; Josserand, C.; Nore, C.; Rossi, M. Various aspects of fluid vortices. Comptes Rendus Mec. 2004, 332, 767–781. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Scalo, J. Interstellar Turbulence I: Observations and Processes. Annu. Rev. Astron. Astrophys. 2004, 42, 211–273. [Google Scholar] [CrossRef] [Green Version]
- Scalo, J.; Elmegreen, B.G. Interstellar Turbulence II: Implications and Effects. Annu. Rev. Astron. Astrophys. 2004, 42, 275–316. [Google Scholar] [CrossRef] [Green Version]
- Bruneau, C.H.; Fischer, P.; Kellay, H. The structures responsible for the inverse energy and the forward enstrophy cascades in two-dimensional turbulence. Europhys. Lett. 2007, 78, 34002. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Nath, B.B.; Sharma, P. Constraining cosmic ray acceleration in young star clusters using multi-wavelength observations. Mon. Not. R. Astron. Soc. 2018, 479, 5220–5234. [Google Scholar] [CrossRef] [Green Version]
- Georgy, C.; Walder, R.; Folini, D.; Bykov, A.; Marcowith, A.; Favre, J.M. Circumstellar medium around rotating massive stars at solar metallicity. Astron. Astrophys. 2013, 559, A69. [Google Scholar] [CrossRef] [Green Version]
- Prinja, R.K.; Crowther, P.A. HSTUV measurements of wind structure and velocities in Local Group OB stars. Mon. Not. R. Astron. Soc. 1998, 300, 828–836. [Google Scholar] [CrossRef] [Green Version]
- Cappa, C.E.; Arnal, E.M.; Cichowolski, S.; Goss, W.M.; Pineault, S. Radio observations of interstellar bubbles surrounding massive stars. Proc. Int. Astron. Union 2003, 212, 596–603. [Google Scholar] [CrossRef] [Green Version]
- Houck, J.C.; Denicola, L.A. ISIS: An Interactive Spectral Interpretation System for High Resolution X-Ray Spectroscopy. In Proceedings of the Astronomical Data Analysis Software and Systems IX; Manset, N., Veillet, C., Crabtree, D., Eds.; Astronomical Society of the Pacific Conference Series; ASP: San Francisco, CA, USA, 2000; Volume 216, p. 591. [Google Scholar]
- Anders, E.; Grevesse, N. Abundances of the elements—Meteoritic and solar. Geochim. Cosmochim. Acta 1989, 53, 197–214. [Google Scholar] [CrossRef]
- Steigman, G.; Strittmatter, P.A.; Williams, R.E. The Copernicus observations: Interstellar or circumstellar material? Astrophys. J. 1975, 198, 575–582. [Google Scholar] [CrossRef]
- Silich, S.; Tenorio-Tagle, G. How Significant is Radiation Pressure in the Dynamics of the Gas around Young Stellar Clusters? Astrophys. J. 2013, 765, 43. [Google Scholar] [CrossRef] [Green Version]
- Mackey, J.; Gvaramadze, V.V.; Mohamed, S.; Langer, N. Wind bubbles within H ii regions around slowly moving stars. Astron. Astrophys. 2015, 573, A10. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Nath, B.B.; Sharma, P.; Shchekinov, Y. How radiation affects superbubbles: Through momentum injection in early phase and photo-heating thereafter. Mon. Not. R. Astron. Soc. 2016, 462, 4532–4548. [Google Scholar] [CrossRef] [Green Version]
- Parizot, E.; Marcowith, A.; van der Swaluw, E.; Bykov, A.M.; Tatischeff, V. Superbubbles and energetic particles in the Galaxy. I. Collective effects of particle acceleration. Astron. Astrophys. 2004, 424, 747–760. [Google Scholar] [CrossRef] [Green Version]
- Vieu, T.; Gabici, S.; Tatischeff, V.; Ravikularaman, S. Cosmic ray production in superbubbles. Mon. Not. R. Astron. Soc. 2022, 512, 1275–1293. [Google Scholar] [CrossRef]
- Morlino, G.; Blasi, P.; Peretti, E.; Cristofari, P. Particle acceleration in winds of star clusters. Mon. Not. R. Astron. Soc. 2021, 504, 6096–6105. [Google Scholar] [CrossRef]
- Chita, S.M.; Langer, N.; van Marle, A.J.; García-Segura, G.; Heger, A. Multiple ring nebulae around blue supergiants. Astron. Astrophys. 2008, 488, L37–L41. [Google Scholar] [CrossRef] [Green Version]
- van Marle, A.J.; Langer, N.; Yoon, S.C.; García-Segura, G. The circumstellar medium around a rapidly rotating, chemically homogeneously evolving, possible gamma-ray burst progenitor. Astron. Astrophys. 2008, 478, 769–778. [Google Scholar] [CrossRef] [Green Version]
- Maeder, A.; Desjacques, V. The shape of eta Carinae and LBV nebulae. Astron. Astrophys. 2001, 372, L9–L12. [Google Scholar] [CrossRef] [Green Version]
- Weis, K. Nebulae around Luminous Blue Variables - large bipolar variety. Proc. Int. Astron. Union 2011, 272, 372–377. [Google Scholar] [CrossRef] [Green Version]
- Gvaramadze, V.V.; Menten, K.M. Discovery of a parsec-scale bipolar nebula around MWC 349A. Astron. Astrophys. 2012, 541, A7. [Google Scholar] [CrossRef] [Green Version]
- Gvaramadze, V.V.; Kniazev, A.Y.; Bestenlehner, J.M.; Bodensteiner, J.; Langer, N.; Greiner, J.; Grebel, E.K.; Berdnikov, L.N.; Beletsky, Y. The blue supergiant MN18 and its bipolar circumstellar nebula. Mon. Not. R. Astron. Soc. 2015, 454, 219–237. [Google Scholar] [CrossRef] [Green Version]
- Weis, K.; Bomans, D.J. Luminous Blue Variables. Galaxies 2020, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- Blondin, J.M.; Lundqvist, P. Formation of the Circumstellar Shell around SN 1987A. Astrophys. J. 1993, 405, 337. [Google Scholar] [CrossRef]
- Toalá, J.A.; Arthur, S.J. On the X-ray temperature of hot gas in diffuse nebulae. Mon. Not. R. Astron. Soc. 2018, 478, 1218–1230. [Google Scholar] [CrossRef]
- Steffen, M.; Schönberner, D.; Warmuth, A. The evolution of planetary nebulae. V. The diffuse X-ray emission. Astron. Astrophys. 2008, 489, 173–194. [Google Scholar] [CrossRef] [Green Version]
- Toalá, J.A.; Arthur, S.J. Formation and X-ray emission from hot bubbles in planetary nebulae—II. Hot bubble X-ray emission. Mon. Not. R. Astron. Soc. 2016, 463, 4438–4458. [Google Scholar] [CrossRef] [Green Version]
- Soker, N.; Kastner, J.H. On the Luminosities and Temperatures of Extended X-Ray Emission from Planetary Nebulae. Astrophys. J. 2003, 583, 368–373. [Google Scholar] [CrossRef] [Green Version]
- Akashi, M.; Meiron, Y.; Soker, N. X-ray emission from jet wind interaction in planetary nebulae. NewAstro 2008, 13, 563–568. [Google Scholar] [CrossRef] [Green Version]
- Nordon, R.; Behar, E.; Soker, N.; Kastner, J.H.; Yu, Y.S. Narrow Radiative Recombination Continua: A Signature of Ions Crossing the Contact Discontinuity of Astrophysical Shocks. Astrophys. J. 2009, 695, 834–843. [Google Scholar] [CrossRef] [Green Version]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dwarkadas, V.V. On the Evolution of, and Hot Gas in, Wind-Blown Bubbles around Massive Stars - Wind Bubbles Are Not Energy-Conserving. Galaxies 2023, 11, 78. https://doi.org/10.3390/galaxies11030078
Dwarkadas VV. On the Evolution of, and Hot Gas in, Wind-Blown Bubbles around Massive Stars - Wind Bubbles Are Not Energy-Conserving. Galaxies. 2023; 11(3):78. https://doi.org/10.3390/galaxies11030078
Chicago/Turabian StyleDwarkadas, Vikram V. 2023. "On the Evolution of, and Hot Gas in, Wind-Blown Bubbles around Massive Stars - Wind Bubbles Are Not Energy-Conserving" Galaxies 11, no. 3: 78. https://doi.org/10.3390/galaxies11030078
APA StyleDwarkadas, V. V. (2023). On the Evolution of, and Hot Gas in, Wind-Blown Bubbles around Massive Stars - Wind Bubbles Are Not Energy-Conserving. Galaxies, 11(3), 78. https://doi.org/10.3390/galaxies11030078




