Baryonic Mass Inventory for Galaxies and Rarefied Media from Theory and Observations of Rotation and Luminosity
Abstract
:1. Introduction
- The galactic mass inventory rests on an ambiguous mass–luminosity correlation (Figure 2). The fits underestimate hydrogen (HI) mass for large galaxies from their luminosity. This defect is problematic because large galaxies are thought to disproportionately control the distribution function of baryonic mass used in the inventory [5]. Section 1.1 provides further discussion.
- Revisiting the inventory of baryons, particularly in the Local Group, is warranted not only by the greatly expanded database, but moreover by recent advances in how mass is deduced from the measured rotation curves (RC = tangential velocity vs. equatorial radius: see Section 1.1). Not only do recent data probe CGM, but a recently developed inverse model further permits addressing the gradation of CGM density into IGM (Section 2.1).
- Distribution functions of galactic luminosity merit revisiting, due to growth of observational data. Roughly 10 times the luminosity data exist today than in 1999 (e.g., the NED website [26]).
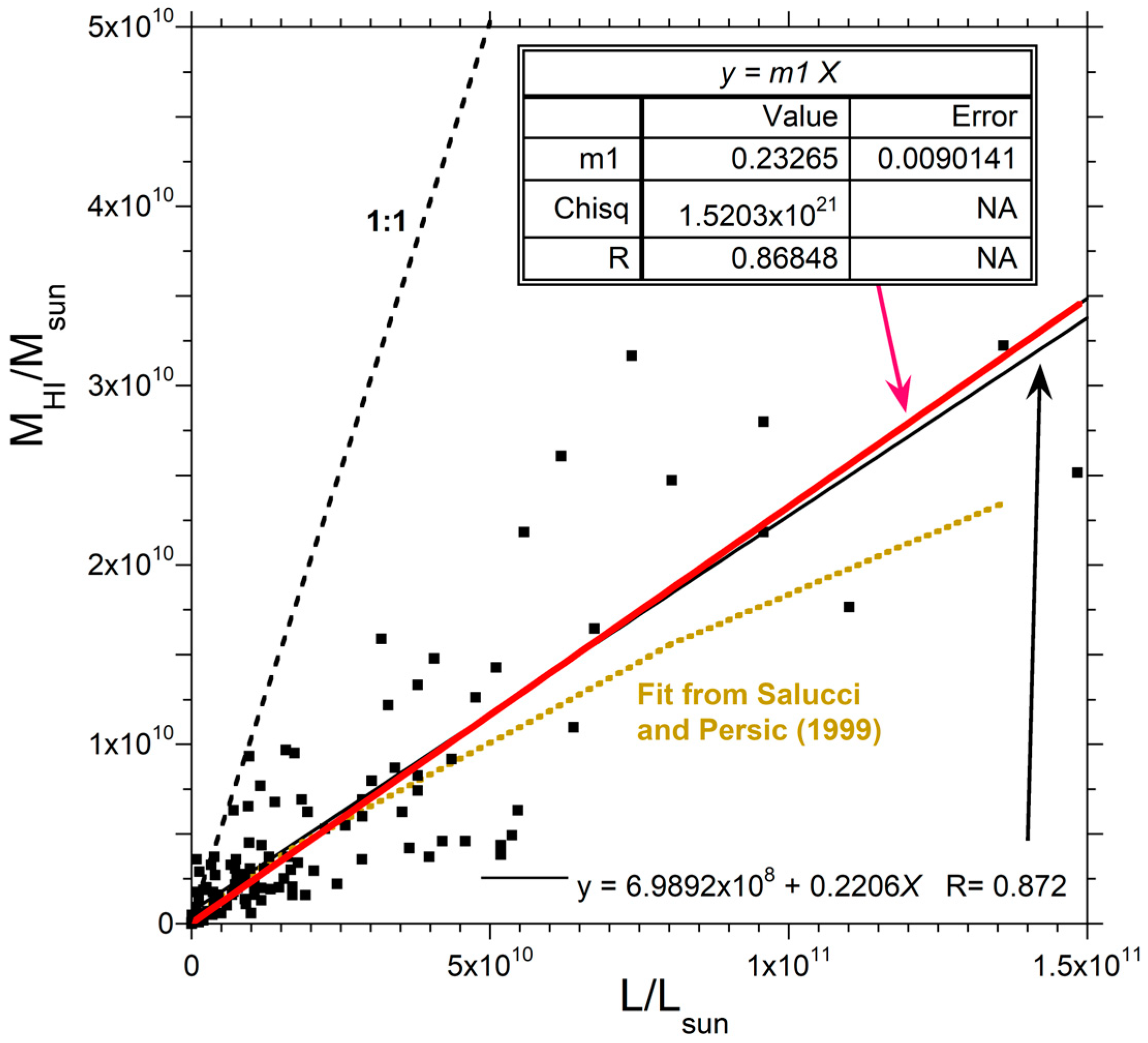
1.1. Background on Mass Determinations of Galaxies
1.1.1. Analysis of RC through Multiparameter Fitting Models with Halos
1.1.2. Recent Inverse Models for RC Analysis
1.2. Organization of the Present Paper
2. Gravitational Assessment of Baryonic Mass and Density in and near Galaxies
2.1. Summary of a Parameter-Free Inverse Model of Differentially Rotating Oblate Sphereoids
- Half of Andromeda’s known 27 dwarf satellite galaxies orbit in a plane with a radius of nearly 400 kpc, which is slightly more than halfway to the proximal Milky Way (MW). This plane is tilted ~23° from Andromeda’s equatorial plane [43] and includes the center of the MW. Hence, the additional force from the MW stabilizes these tilted orbits.
- Dwarf satellite galaxies around the MW occupy polar orbits [58] rather than having the equatorial orientation expected around an isolated oblate spheroid. Hence, the force from larger, nearby Andromeda influences orientations of MW satellite orbits.
- Rarely, isolated spiral galaxies exhibit polar structures [59] or have outer rings that rotate nearly perpendicularly to the inner discoid [60,61]. In contrast, counter-rotating galaxies are fairly common, whose orientation can be attributed to a tilted ring being pulled to the equatorial plane of the central body.
2.1.1. Mathematical Construct
2.2. Parameter-Free Analysis of 72 Galaxies
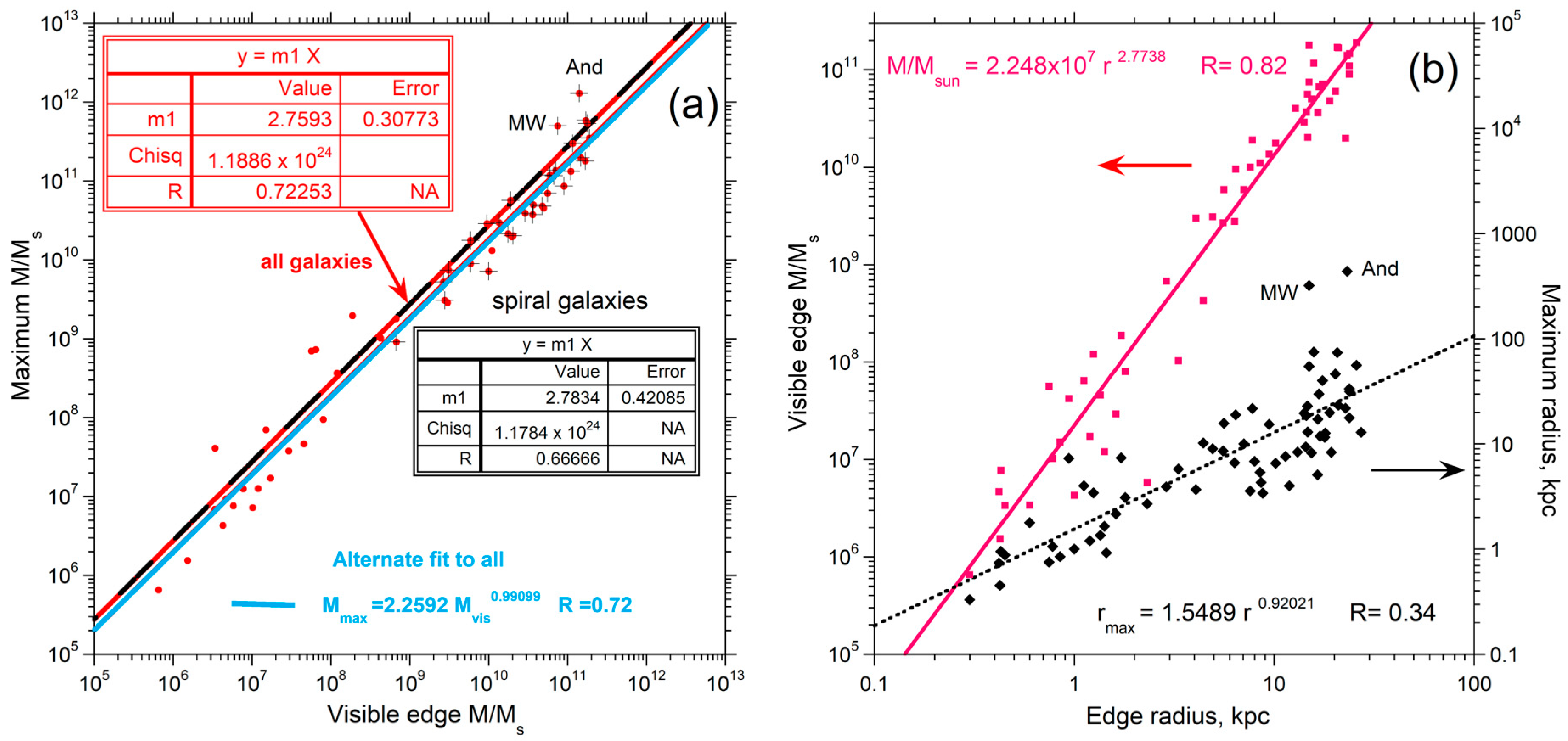
2.2.1. Dependence of Mass on Galaxy Size
2.2.2. Uncertainties from Comparison to Other Inverse Models and Shape Effects
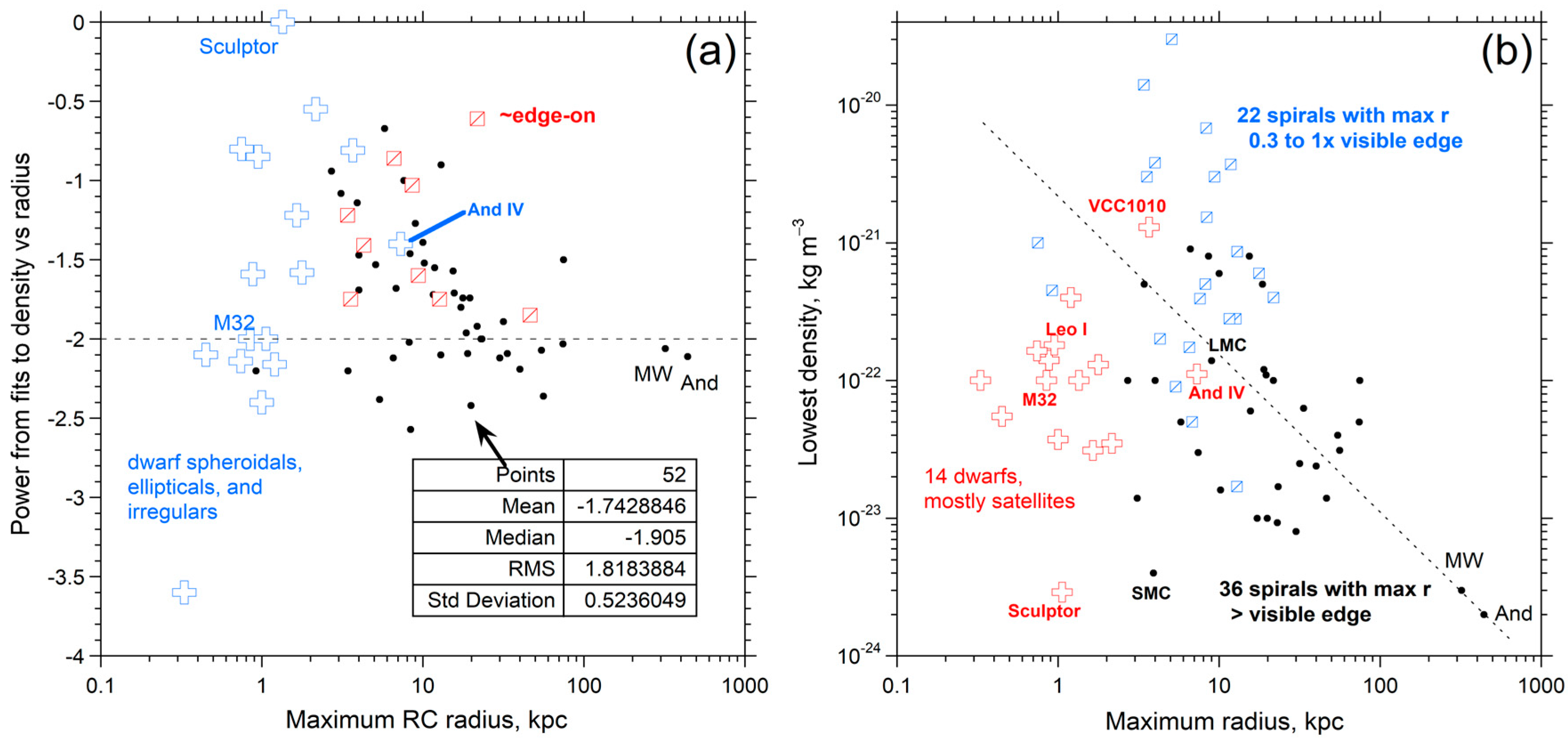
2.2.3. Dependence of Density on Radius and Inclination
2.2.4. Physics Underlying Our ρ(r) Formula
2.2.5. Calculated Density at the Visible Edge and of CGM and IGM
2.2.6. Validation via Comparison with Direct, Independent Measurements of Baryon Densities
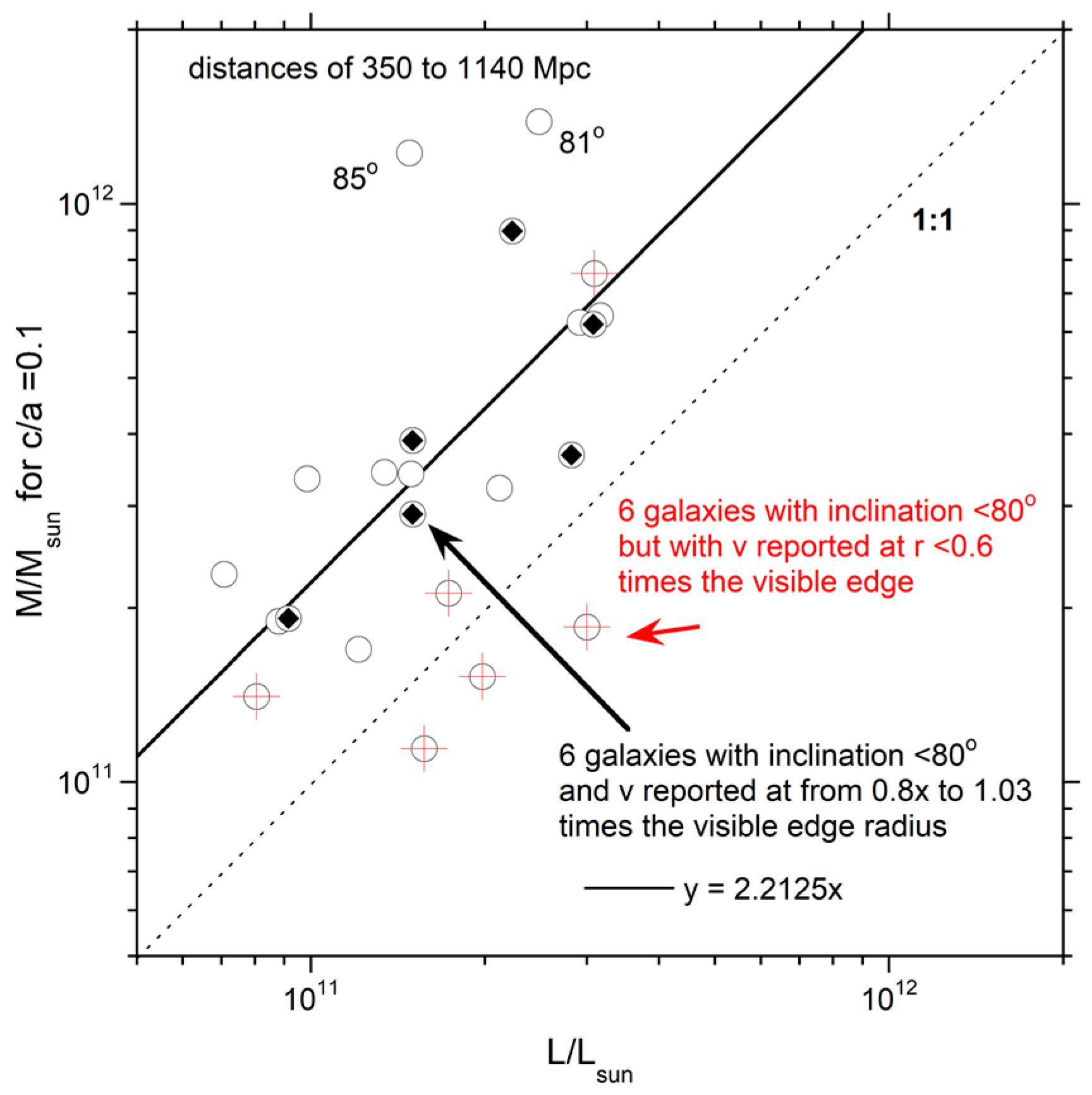
2.2.7. Dependence of Mass, including CGM, on Luminosity
2.2.8. Large, Very Distant Galaxies Behave in the Same Manner as Small, Close Galaxies
3. Galactic Luminosity Data
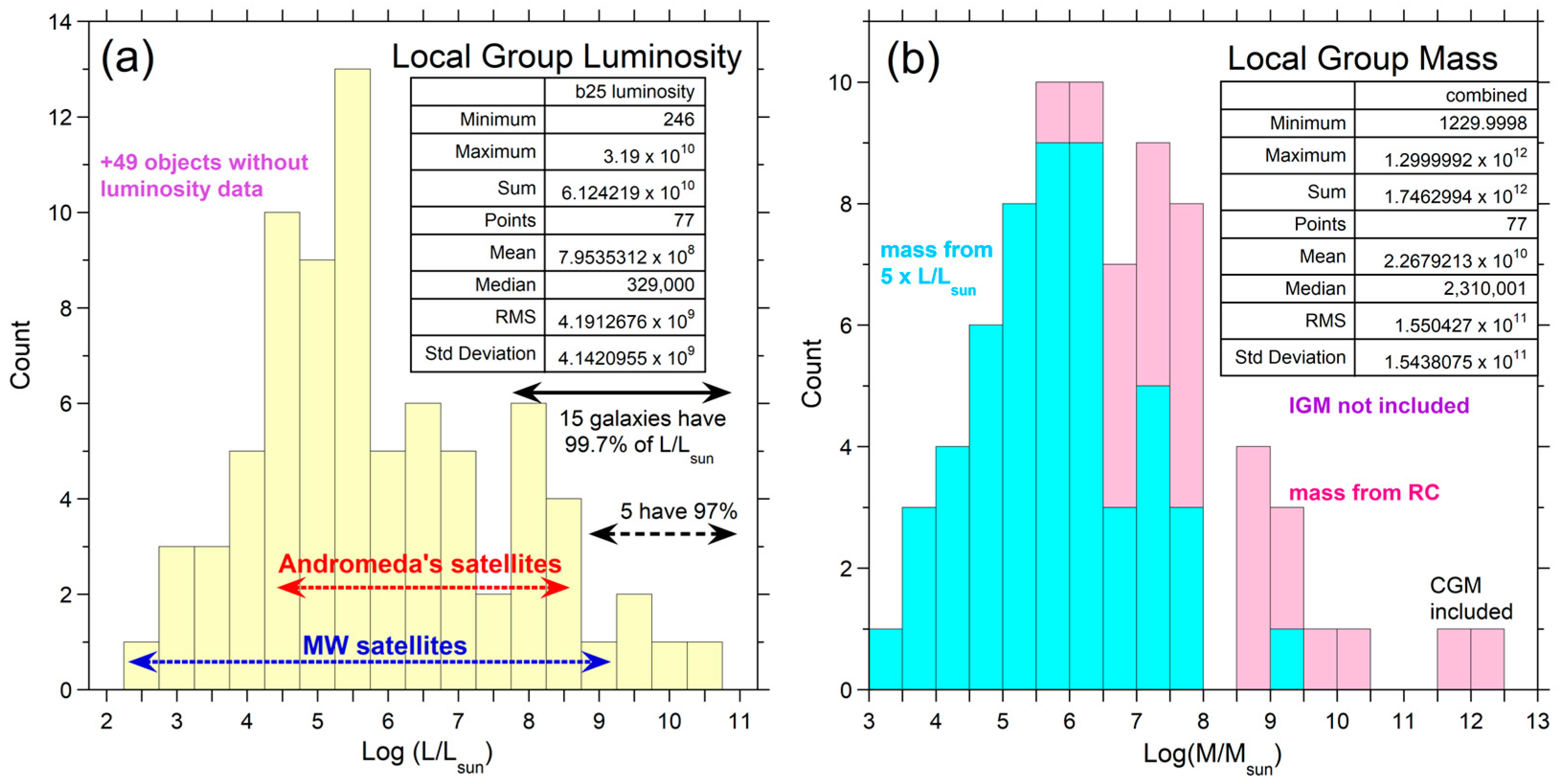
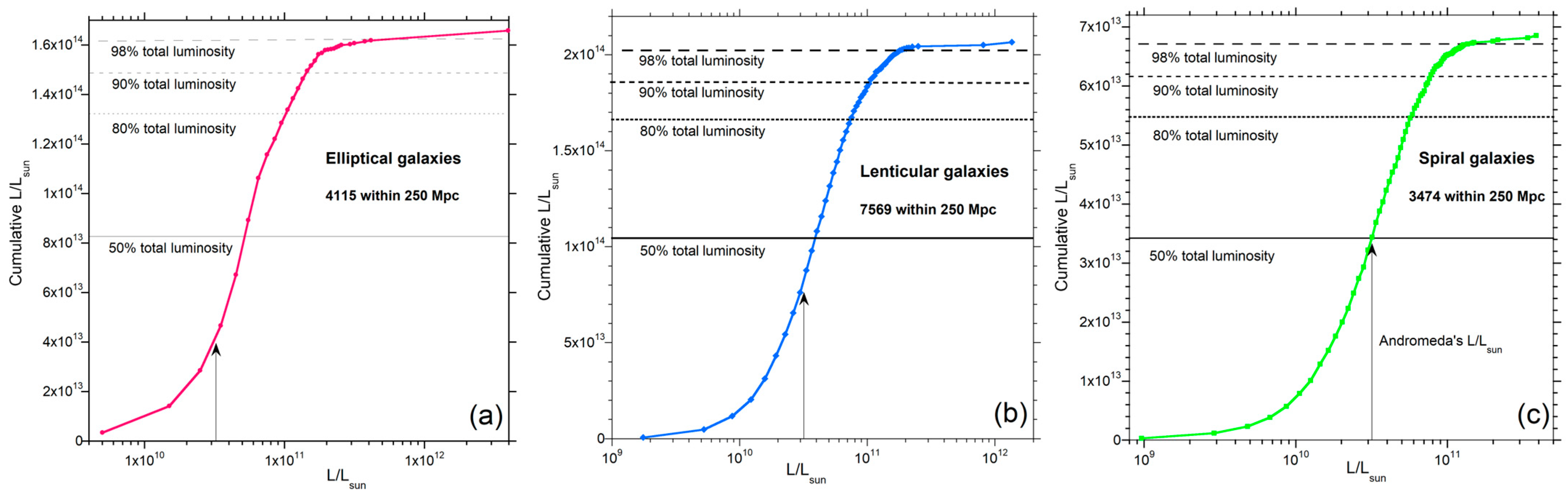
3.1. Luminosity of Galaxies in the Local Group
3.2. Luminosity of Galaxies in the Virgo Cluster with Comparison to the Local Group
3.3. Luminosity of Near and Far Galaxies
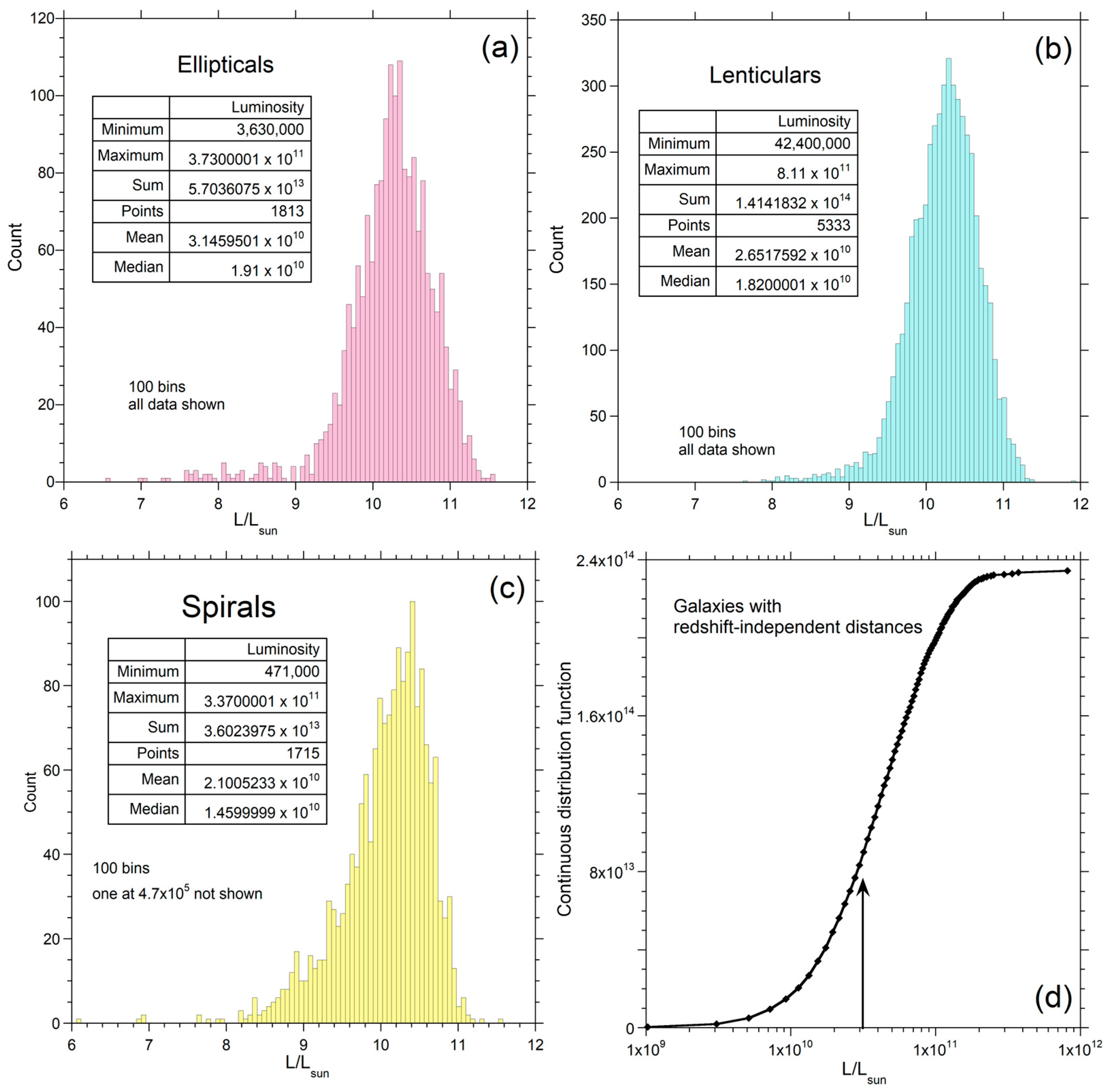
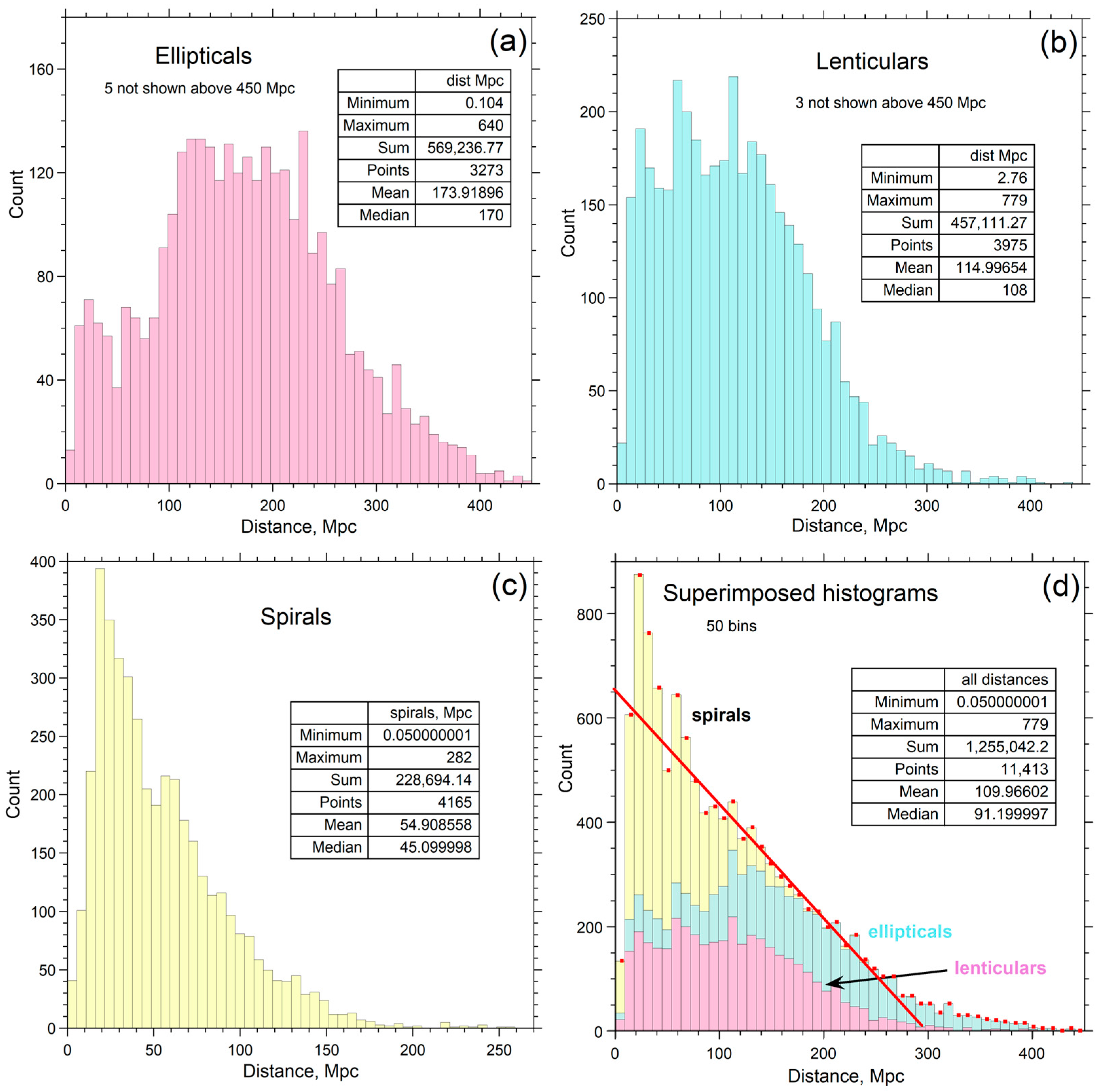
3.3.1. Distribution Functions for Redshift-Independent Distances
3.3.2. Distribution Functions at Larger Distances
3.4. Effect of Distance on Galactic Distribution Functions
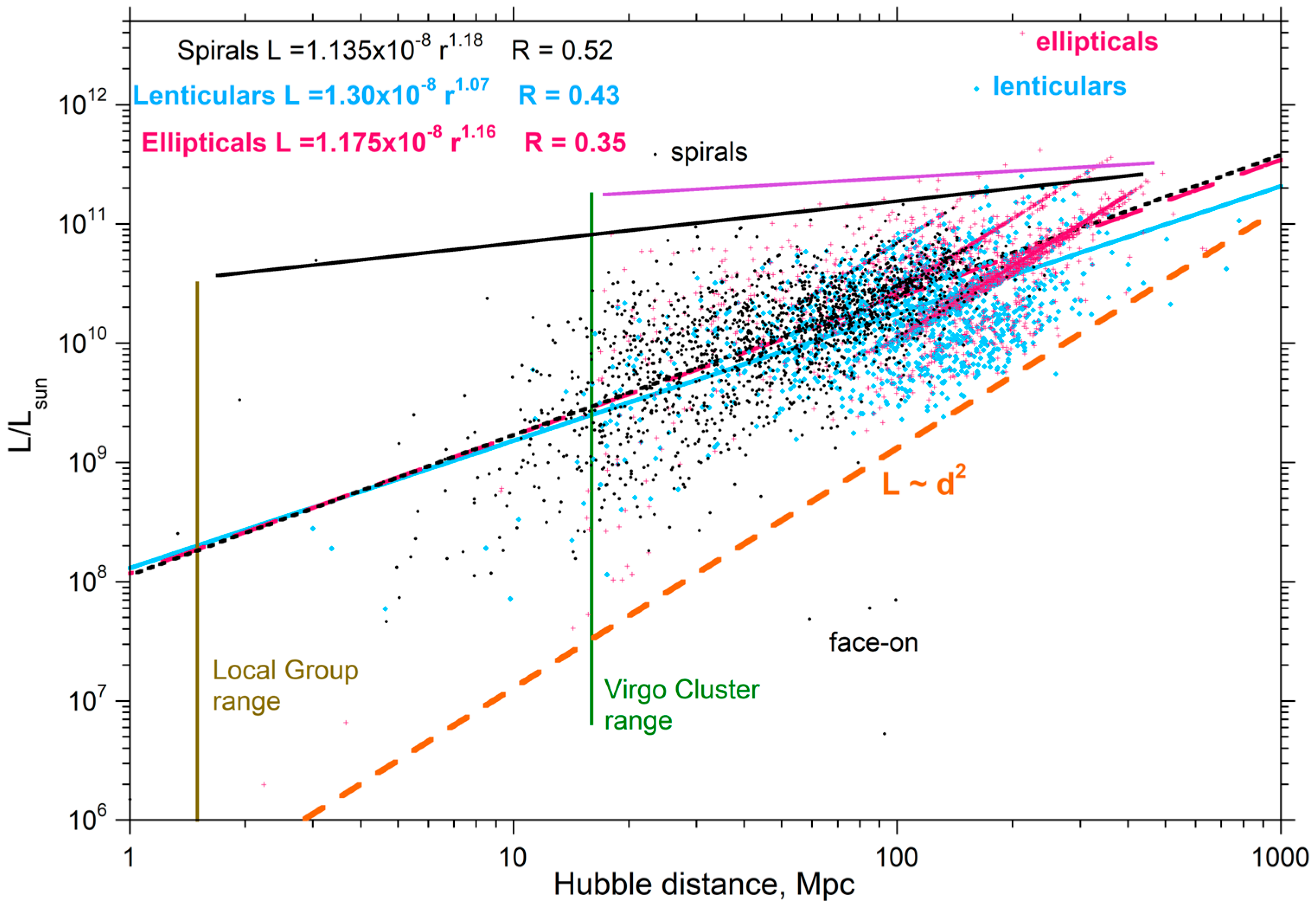
3.4.1. Dependence of Luminosity of the Objects on Hubble Distance
3.4.2. Dependence of the Number of Galaxies Observed on Distance
4. Gravitationally Derived Estimates of Baryonic Mass in the Universe
4.1. The Local and Nearby Universe
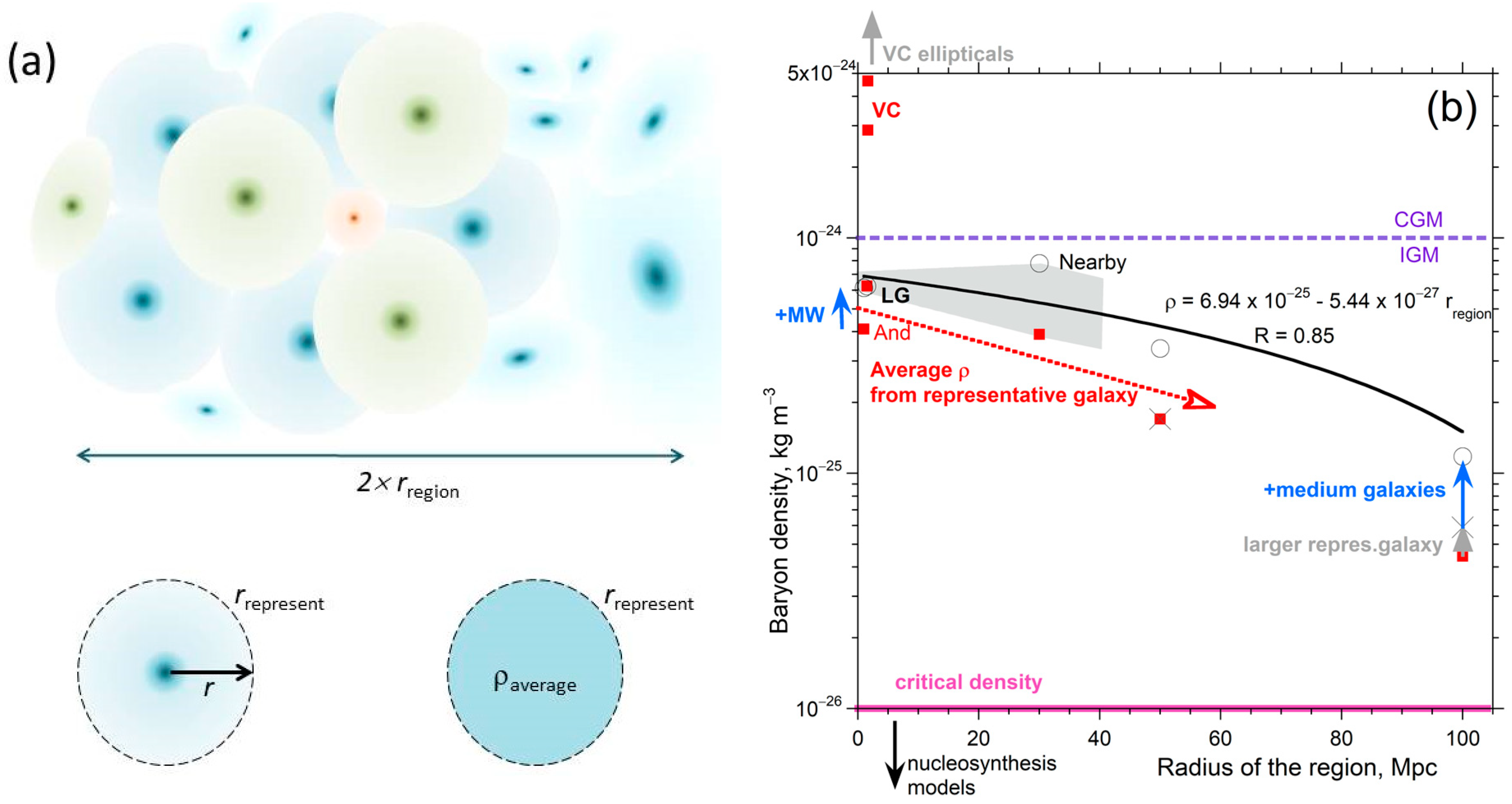
4.1.1. Concept of a Representative Galaxy
4.1.2. Density and Number in the Volume Surrounding a Representative Galaxy
- Neglecting mass concentrations within 1 kpc of galactic centers (and possible central blackholes) would provide a small addition.
- In contrast, the potentially significant contributions of the smaller galaxies within rrepresentative can be ascertained from the PDFs and CDFs (Section 4.1.2).
- More importantly, rrepresentative from Equation (8) is overestimated, as this depends on the number observed, which is strongly attenuated as distance increases beyond ~30 Mpc. This is the main reason that ρaverage in Table 3 for large distances is underestimated.
4.1.3. Effect of Small Galaxies and Count on the Average Mass Density
4.1.4. Baryon Inventory with and without IGM
4.2. Extrapolation of Trends to 1000 Mpc
4.3. Galaxy Count Estimates for the Universe
4.4. Calculation of Universe Mass and Density from an Energy Balance
4.5. Estimates of Critical Density
5. Discussion
5.1. Uncertainties in Our Estimates
5.1.1. Calculations Based on Rotation Curves and the NED Database
5.1.2. Calculation Based on Models of Galaxy Count
- The curves shown in [80] are consistent with the parabolic form implied by the above dimensional analysis, but their shape is unrelated to any dependence of M on distance.
5.1.3. Energy Balance Calculation and Critical Densities
5.2. Inventoried Density of Baryons in the Universe
5.2.1. Previous Inventories Underestimate Baryon Density
5.2.2. Comparison of Our Results to Cosmological Models for Baryons
6. Conclusions and Implications
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

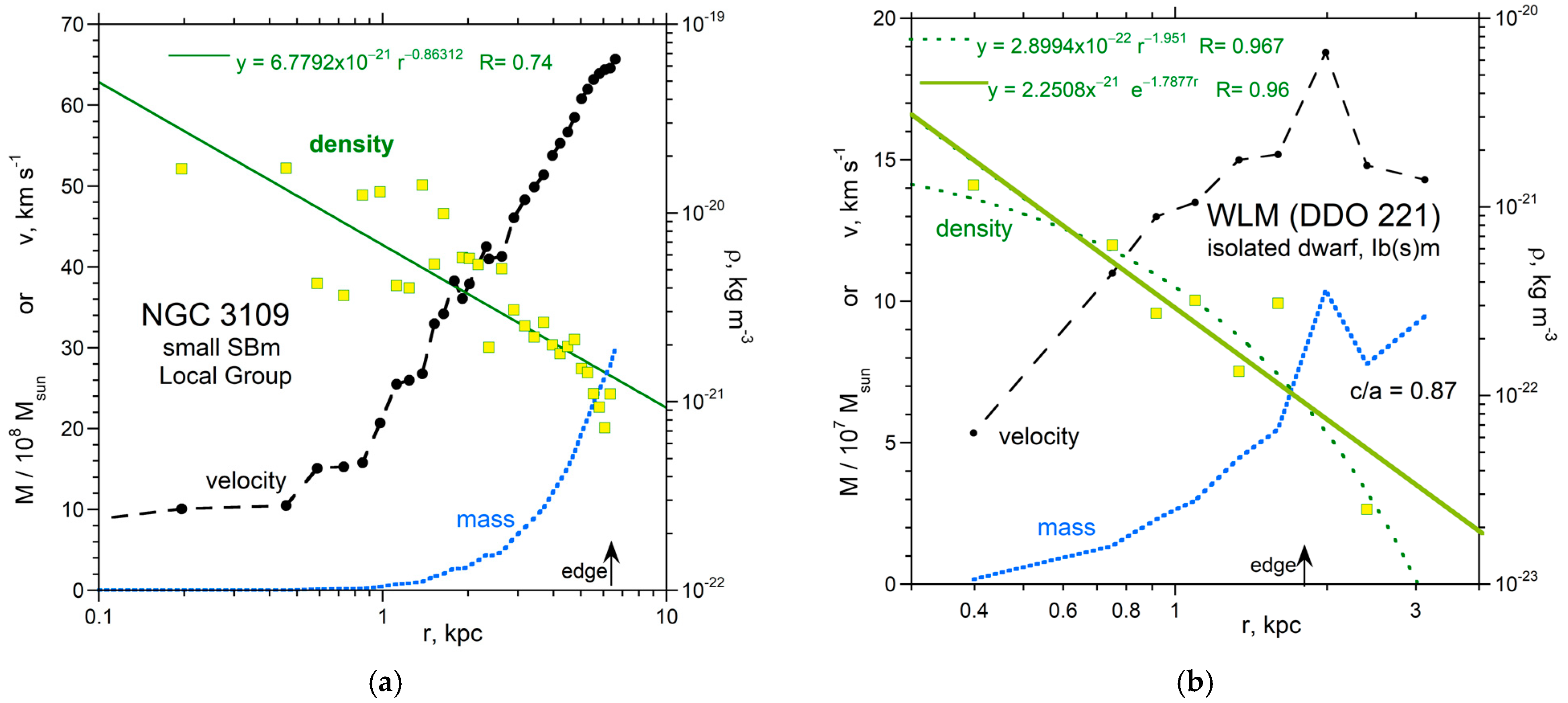
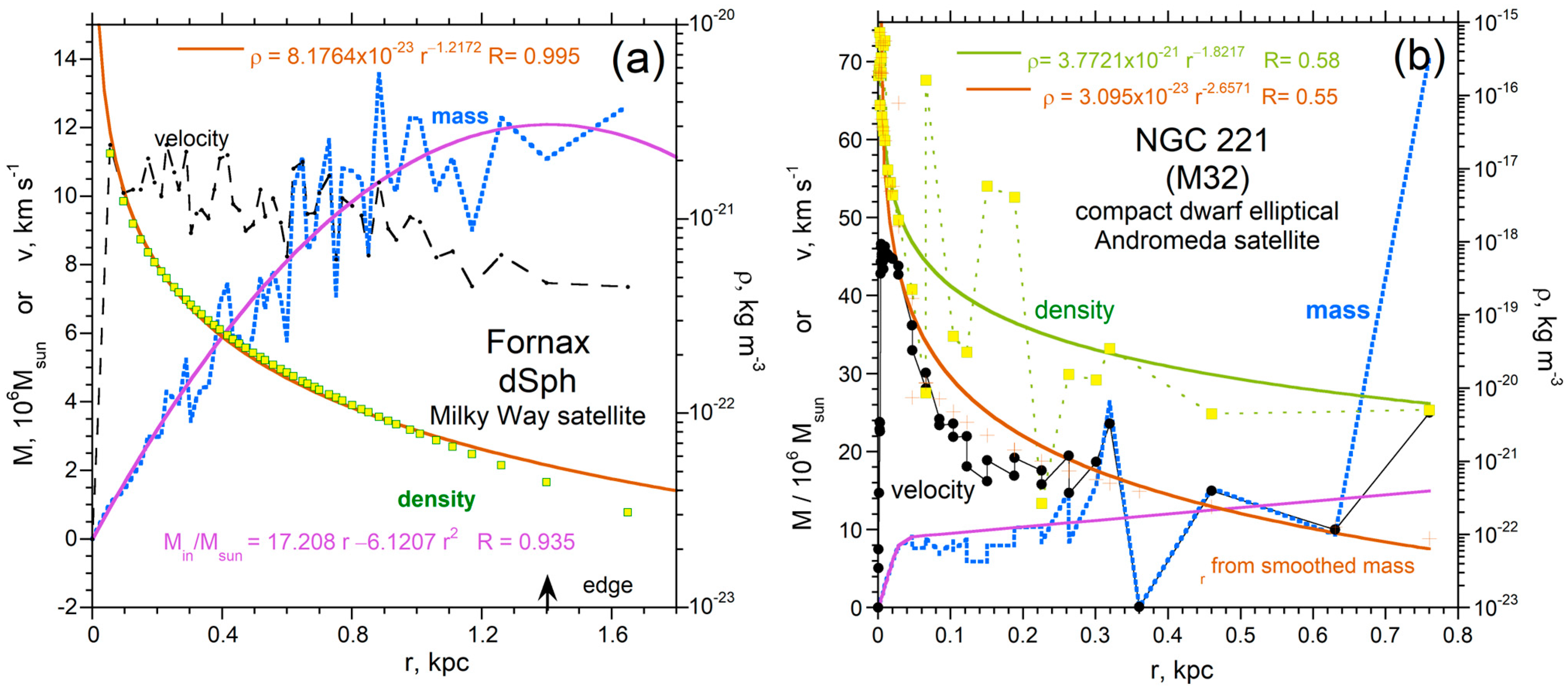
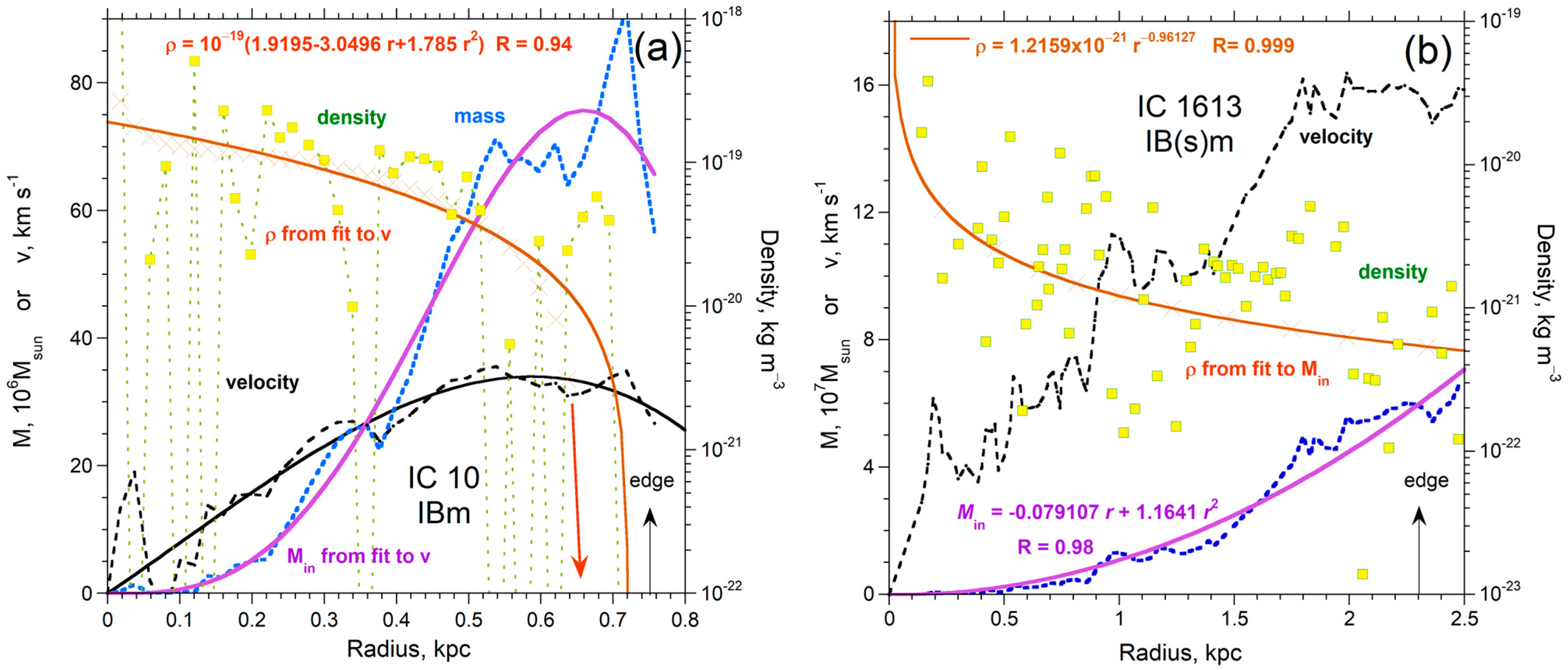

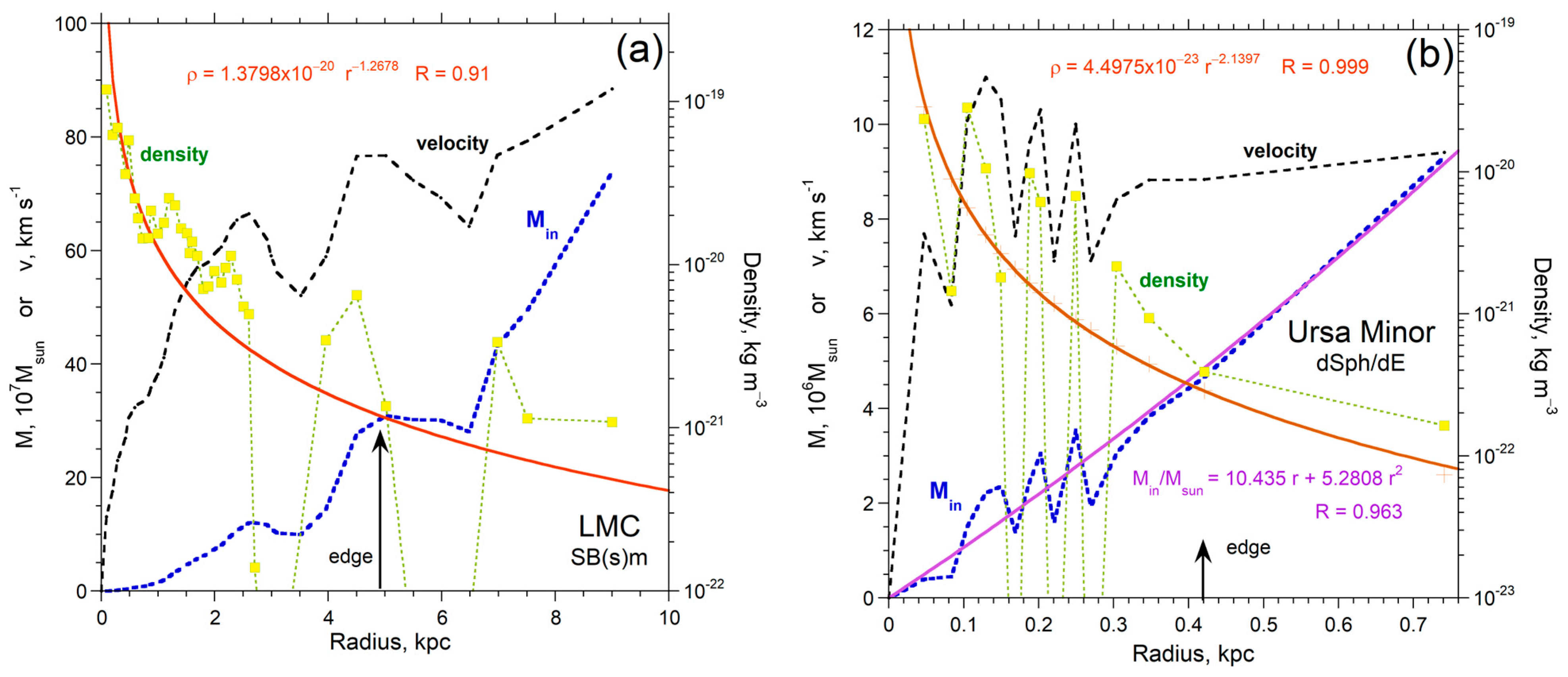
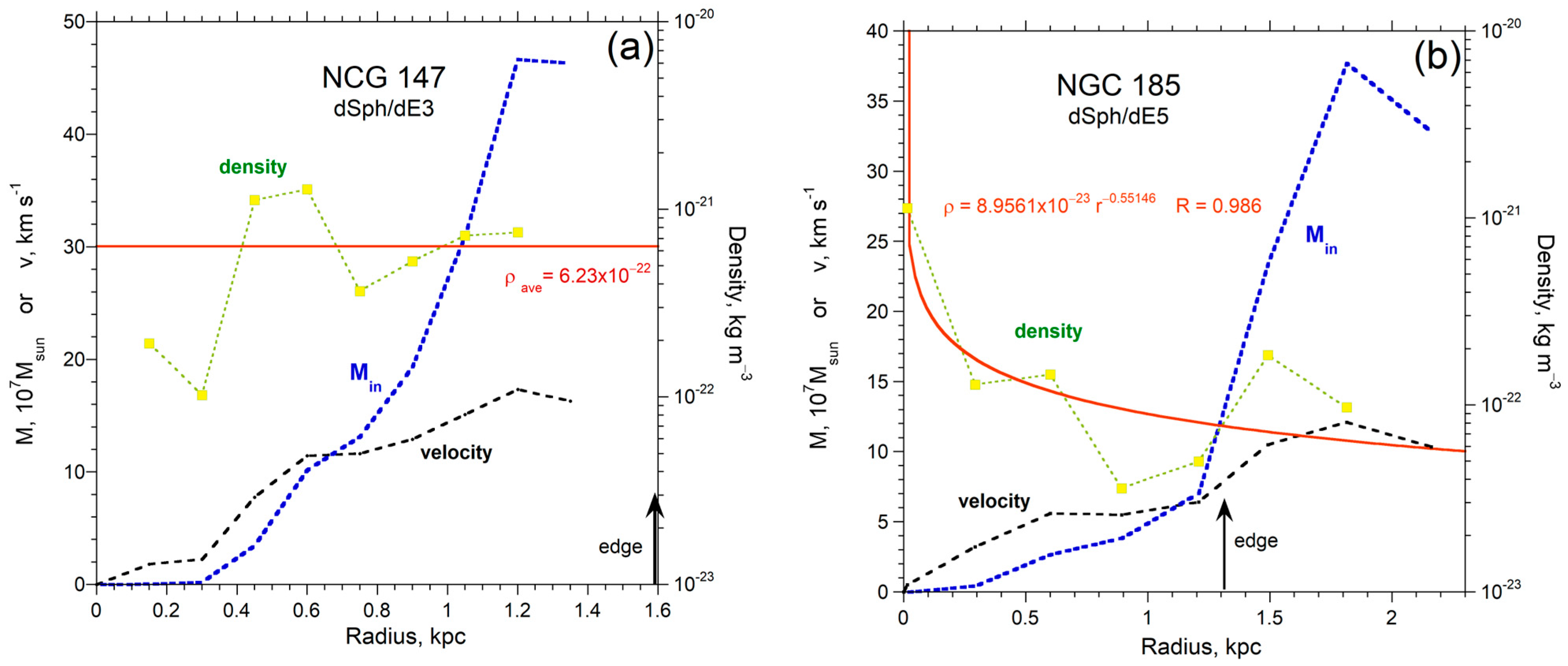
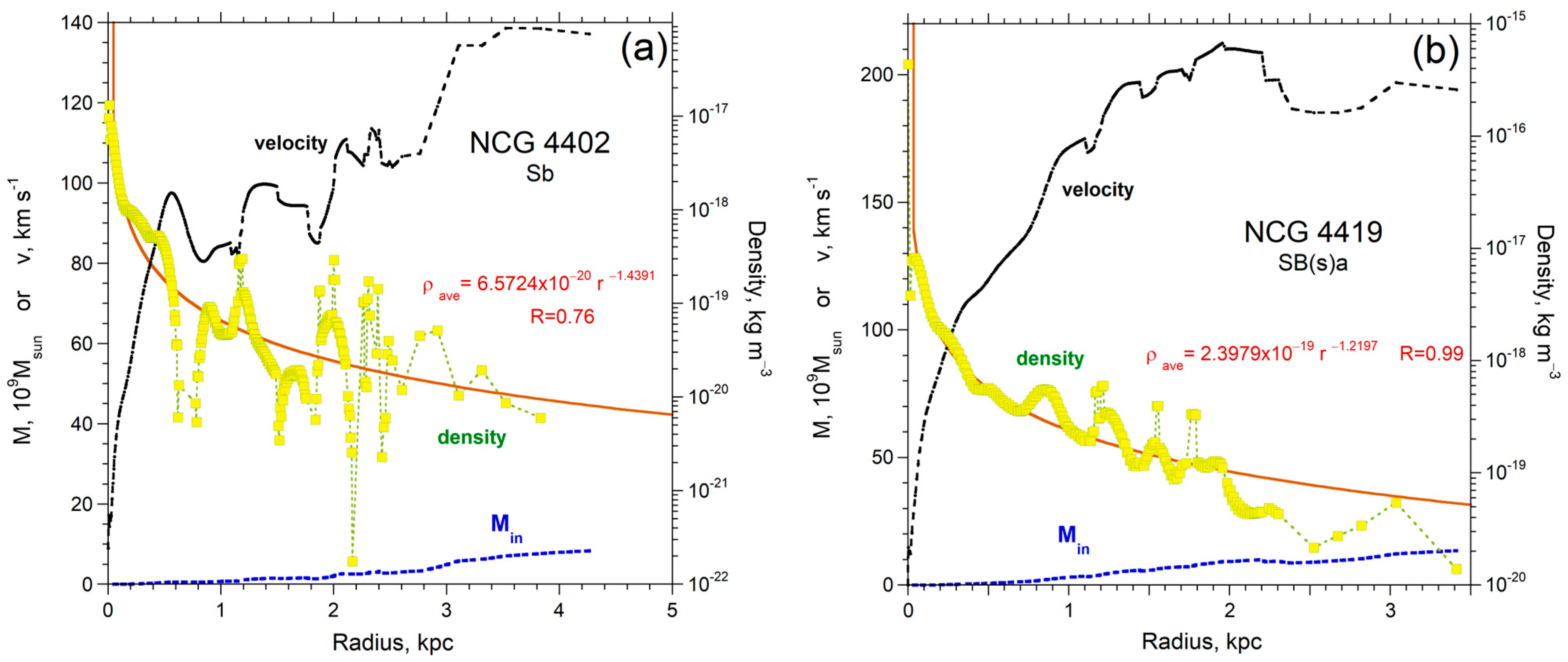
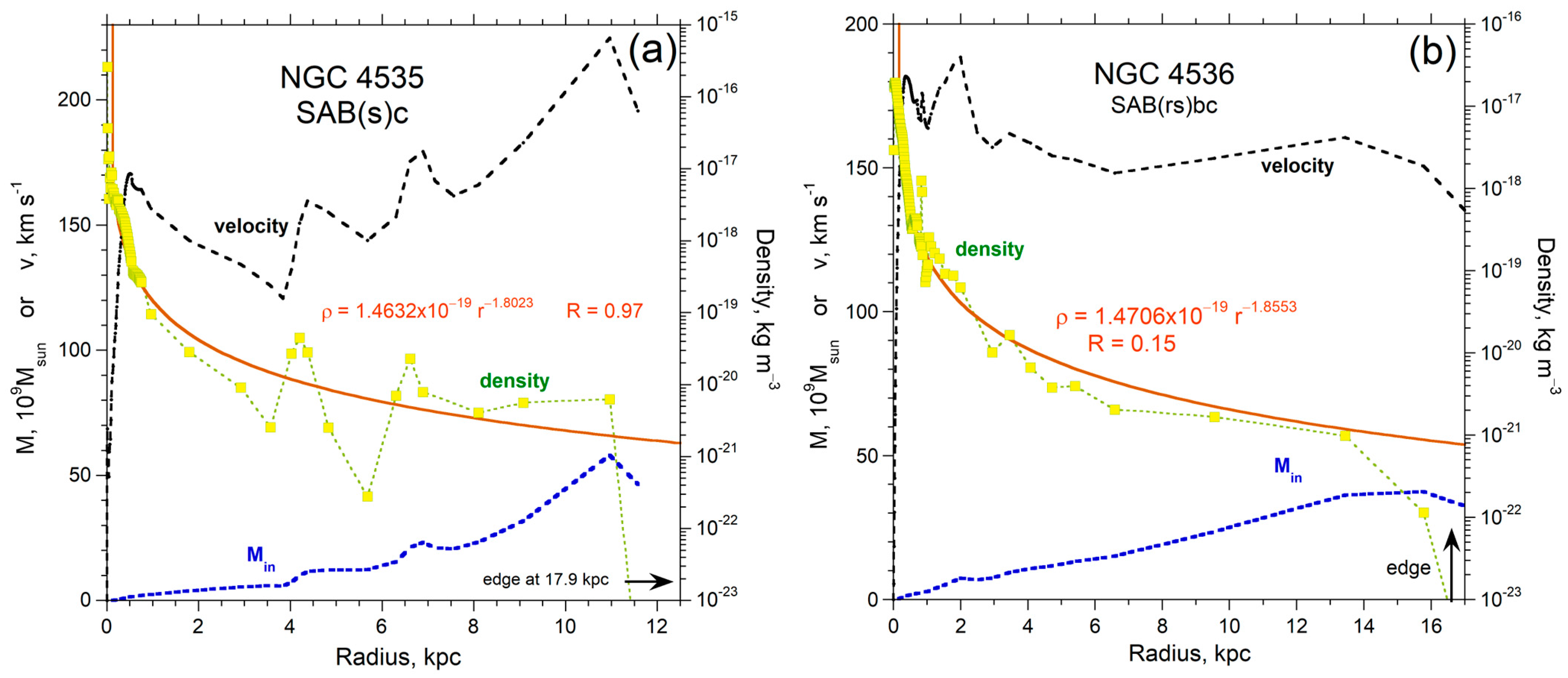
| Name | Type | Ref. RC | Lvis (LSun) | redge (kpc) | Medge (MSun) | Density (kg m−3) | Lowest ρ (kg m−3) | Power | rmax (kpc) | Mmax (MSun) |
|---|---|---|---|---|---|---|---|---|---|---|
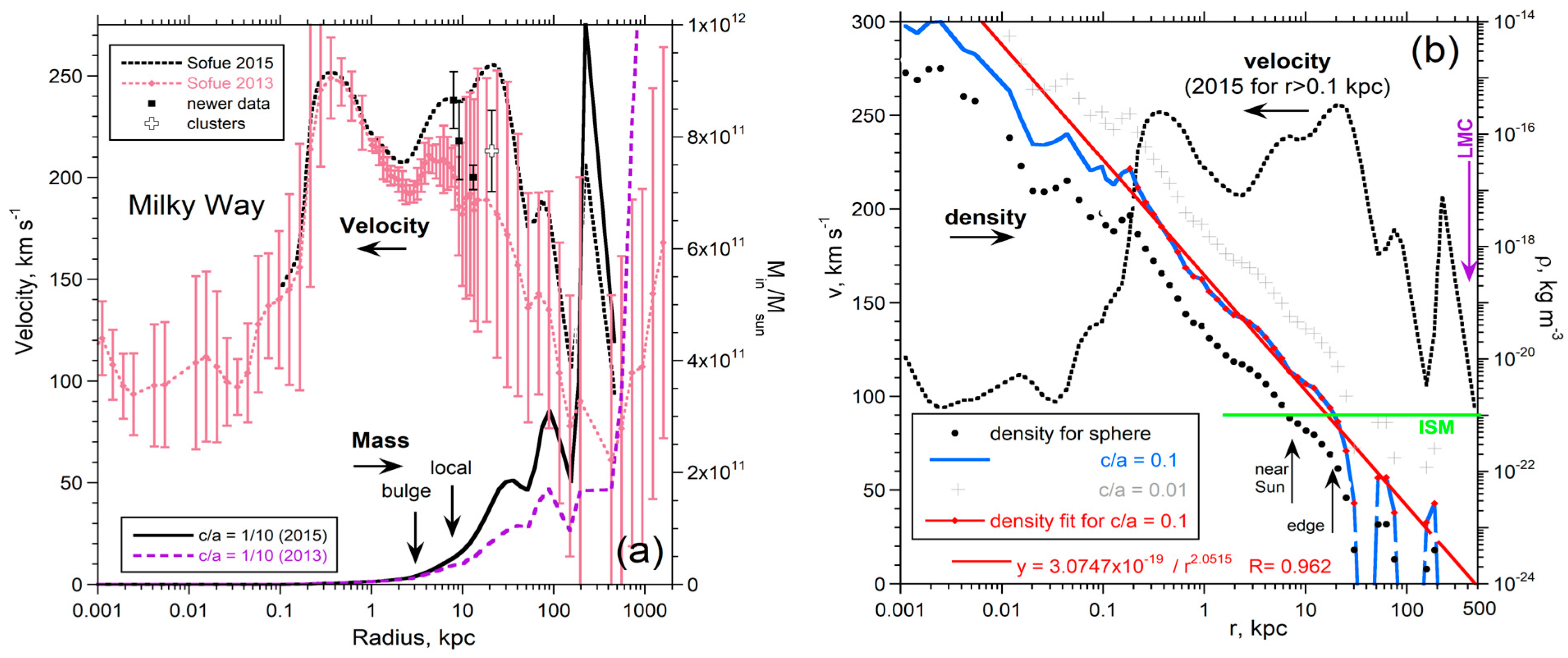
| Milky Way * | SBc | [64,65] | ~1.7 × 1010 | 15 | 7.5 × 1010 | † | ~3.0 × 10−24 | −2.06 | ~330 | ~4.5 × 1011 |
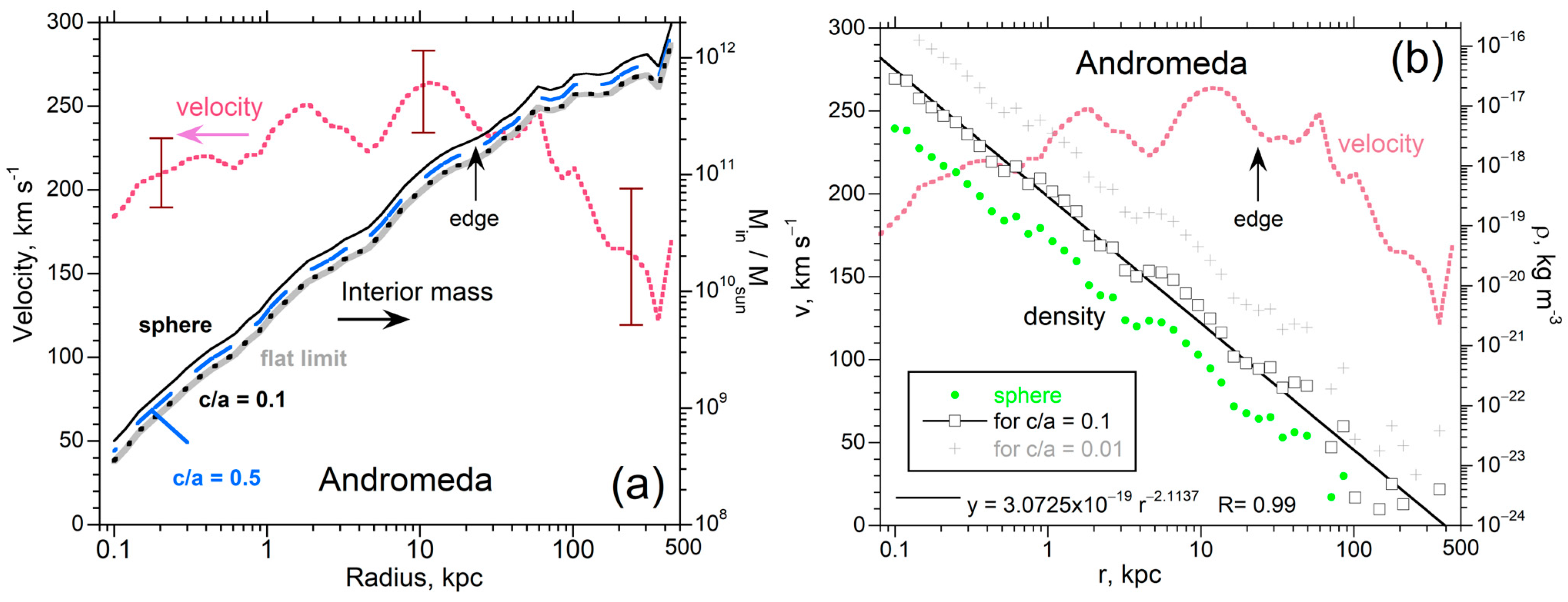
| Andromeda * | SA(s)b | [64] | 3.19 × 1010 | 23 | 1.41 × 1011 | 4.29 × 10−22 | 2.0 × 10−24 | −2.11 | 440 | 1.30 × 1012 |
| Triangulum * | SA(s)cd | [86,90,91] | 3.65 × 109 | 9.45 | 1.36 × 1010 | 1.00 × 10−21 | 8.0 × 10−22 | −1.57 | 15 | 2.96 × 1010 |
| NGC 3109 * | SB(s)m | [72] | 2.51 × 108 | 6.35 | 2.77 × 109 | 9.00 × 10−22 | 7.0 × 10−22 | −0.86 | 6.62 | 3.08 × 109 |
| Sextans A | IBm | [102] | 3.58 × 107 | 1.25 | 1.20 × 108 | 6.80 × 10−21 | 5.0 × 10−22 | −2.20 | 3.43 | 3.64 × 108 |
| Sextans B | IBm | [102] | 5.69 × 107 | 1.12 | 6.44 × 107 | 8.80 × 10−21 | 1.0 × 10−22 | −1.47 | 4.00 | 8.26 × 108 |
| WLM * | IB(s)m | [92] | 5.83 × 107 | 1.8 | 8.00 × 107 | 9.20 × 10−23 | 1.4 × 10−23 | −1.08 | 3.1 | 9.47 × 107 |
| IC 10 | IBm | [97] | 5.53 × 109 | 0.75 | 5.64 × 107 | 3.00 × 10−21 | 1.0 × 10−21 | −0.80 | 0.74 | 7.00 × 108 |
| IC 1613 | IB(s)m | [97] | 7.06 × 107 | 2.32 | 5.80 × 106 | 7.00 × 10−22 | 1.0 × 10−22 | −0.94 | 2.7 | 7.67 × 107 |
| DDO 210 | dIrr | [97] | 1.39 × 107 | 0.3 | 6.56 × 105 | 1.00 × 10−22 | 1.0 × 10−22 | −3.60 | 0.33 | 6.56 × 105 |
| DDO 216 | Im/dSph | [97] | 3.93 × 107 | 1.2 | 1.72 × 107 | 4.00 × 10−22 | 4.0 × 10−22 | −2.16 | 1.20 | 1.72 × 107 |
| NGC 6822 | IB(s)m | [98] | 1.03 × 108 | 3.32 | 6.70 × 108 | 2.00 × 10−21 | 5.0 × 10−23 | −0.67 | 5.80 | 1.80 × 109 |
| Satellites of the Milky Way | ||||||||||
| LMC | SB(s)m | [100] | 1.31 × 109 | 4.93 | 3.10 × 109 | 1.80 × 10−21 | 1.39 × 10−22 | −1.27 | 9.00 | 7.39 × 109 |
| SMC | SB(s)m pec | [103] | 3.95 × 108 | 2.89 | 6.77 × 108 | 1.00 × 10−21 | 4.0 × 10−24 | −1.14 | 3.90 | 9.17 × 108 |
| Carina * | dSph, dE3 | [93] | 2.95 × 105 | 0.45 | 3.38 × 106 | 6.50 × 10−22 | 1.4 × 10−22 | −1.59 | 0.88 | 6.88 × 106 |
| Draco * | dSph, Epec | [93] | 2.95 × 105 | 0.60 | 3.40 × 106 | 1.00 × 10−21 | 1.3 × 10−22 | −1.58 | 1.78 | 4.10 × 107 |
| Fornax * | dSph, dE4 | [93] | 1.30 × 107 | 1.42 | 1.20 × 107 | 1.00 × 10−21 | 2.0 × 10−23 | −1.56 | 1.65 | 1.27 × 107 |
| Leo I * | dSph, dE3 | [93] | 4.99 × 106 | 0.43 | 7.74 × 106 | 1.00 × 10−21 | 1.8 × 10−22 | −0.85 | 0.95 | 1.26 × 107 |
| Leo II | dSph/dE0 | [93] | 4.67 × 105 | 0.426 | 1.53 × 106 | 5.47 × 10−23 | 5.47 × 10−23 | −2.1 | 0.45 | 1.54 × 106 |
| Sculptor | dSph | [93] | 1.50 × 106 | 0.78 | 1.02 × 107 | 2.90 × 10−24 | 2.9 × 10−24 | −1.0 | 1.06 | 7.24 × 106 |
| Sextans | dSph | [93] | 3.07 × 105 | 1.0 | 4.30 × 106 | 3.71 × 10−23 | 3.71 × 10−23 | −2.4 | 1.00 | 4.30 × 106 |
| Ursa Minor | dSph/dE | [93] | 1.84 × 105 | 0.42 | 4.67 × 106 | 2.87 × 10−22 | 1.64 × 10−22 | −2.1 | 0.74 | 9.35 × 106 |
| Satellites of Andromeda | ||||||||||
| M32 * | cE2 | [71] | 2.61 × 108 | 0.85 | 1.5 × 107 | 1.0 × 10−22 | 1.0 × 10−22 | −2.00 | 0.85 | 1.5 × 107 |
| NGC 147 | dSph/dE3 | [101] | 1.21 × 108 | 1.62 | 2.92 × 107 | 1.0 × 10−22 | 1.13 × 10−21 | −0.55 | 2.16 | 3.77 × 107 |
| NGC 185 | dSph/dE5 | [101] | 9.27 × 107 | 1.35 | 4.57 × 107 | 7.5 × 10−22 | 1.20 × 10−21 | 0 | 1.35 | 4.67 × 107 |
| Small, low surface brightness, extensive RC | ||||||||||
| And IV | dIrr | [99] | 2.08 × 107 | 0.94 | 4.21 × 107 | 1.09 × 10−20 | 1.11 × 10−22 | −1.4 | 7.3 | 1.62 × 109 |
| Virgo Cluster | ||||||||||
| NGC 4402 | Sb | [23] | 3.57 × 109 | 8.61 | 8.41 × 109 | 4.84 × 10−21 | 2.00 × 10−22 | −1.41 | 4.30 | 8.41 × 109 |
| NGC 4419 | SB(s)a | “ | 8.11 × 109 | 8.77 | 1.35 × 1010 | 1.40 × 10−20 | 1.40 × 10−20 | −1.22 | 3.41 | 1.35 × 1010 |
| NGC 4535 | SAB(s)c | “ | 1.87 × 1010 | 17.90 | 4.65 × 1010 | 2.55 × 10−21 | 2.80 × 10−22 | −1.72 | 11.6 | 4.65 × 1010 |
| NGC 4536 | SAB(rs)bc | “ | 1.33 × 1010 | 16.59 | 3.63 × 1010 | 5.0 × 10−23 | 1.00 × 10−23 | −1.8 | 17.2 | 3.76 × 1010 |
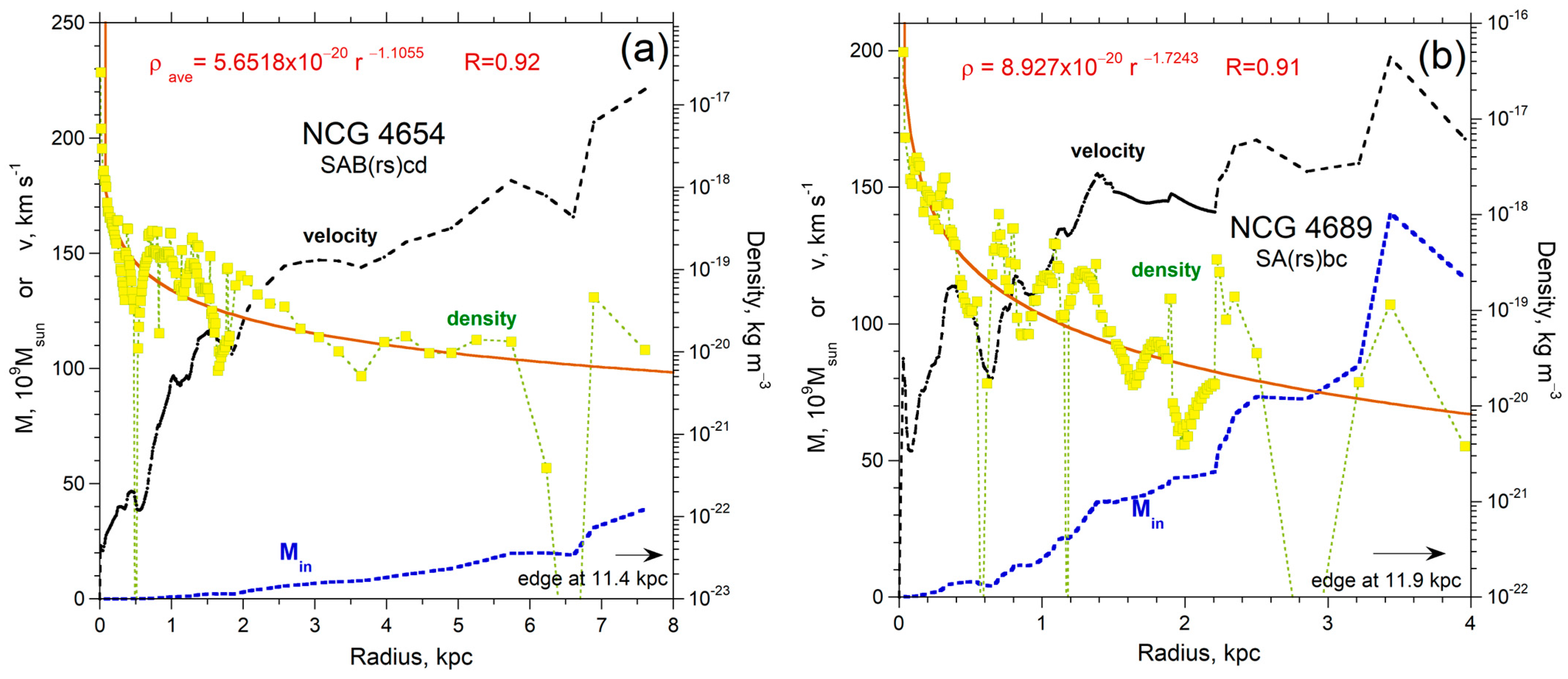
| NGC 4654 | SAB(rs)cd | “ | 1.27 × 1010 | 11.42 | 3.90 × 1010 | 1.06 × 10−20 | 3.92 × 10−22 | −1.1 | 7.60 | 3.90 × 1010 |
| NGC 4689 | SA(rs)bc | “ | 9.16 × 109 | 11.94 | 1.41 × 1010 | 1.0 × 10−20 | 3.8 × 10−21 | −1.69 | 4.00 | 1.41 × 1010 |

References
- Nicastro, F.; Kaastra, J.; Krongold, Y.; Borgani, S.; Branchini, E.; Cen, R.; Dadina, M.; Danforth, C.W.; Elvis, M.; Fiore, F.; et al. Observations of the missing baryons in the warm–hot intergalactic medium. Nature 2018, 558, 406–409. [Google Scholar] [CrossRef] [PubMed]
- Shull, J.M.; Smith, B.D.; Danforth, C.W. The baryon census in a multiphase intergalactic medium: 30% of the baryons may still be missing. Astrophys. J. 2012, 759, 23. [Google Scholar] [CrossRef]
- Kirkman, D.; Tytler, D.; Suzuki, N.; O’Meara, J.M.; Lubin, D. The cosmological baryon density from the deuterium-to-hydrogen ratio in QSO absorption systems: D/H toward Q1243+3047. Astrophys. J. Suppl. Ser. 2003, 149, 1–28. [Google Scholar] [CrossRef]
- Bregman, J.N.; Lloyd-Davies, E.J. X-ray absorption from the Milky Way halo and the local group. Astrophys. J. 2007, 669, 990–1002. [Google Scholar] [CrossRef]
- Salucci, P.; Persic, M. The baryonic mass function of spiral galaxies: Clues to galaxy formation. Mon. Not. R. Ast. Soc. 1999, 309, 923–928. [Google Scholar] [CrossRef]
- Fukugita, M.; Peebles, P.J. The cosmic energy inventory. Astrophys. J. 2004, 616, 643–668. [Google Scholar] [CrossRef]
- Cen, R.; Ostriker, J.P. Where are the baryons? Astrophys. J. 1999, 514, 1. [Google Scholar] [CrossRef]
- Davé, R.; Cen, R.; Ostriker, J.P.; Bryan, G.L.; Hernquist, L.; Katz, N.; Weinberg, D.H.; Norman, M.L.; O’Shea, B. Baryons in the warm–hot intergalactic medium. Astrophys. J. 2001, 552, 473–483. [Google Scholar] [CrossRef]
- Wijers, N.A.; Schaye, J.; Oppenheimer, B.D. The warm-hot circumgalactic medium around EAGLE-simulation galaxies and its detection prospects with X-ray and UV line absorption. Mon. Not. R. Ast. Soc. 2020, 498, 574–598. [Google Scholar] [CrossRef]
- Tuominen, T.; Nevalainen, J.; Tempel, E.; Kuutma, T.; Wijers, N.; Schaye, J.; Heinämäki, P.; Bonamente, M.; Veena, P.G. An EAGLE view of the missing baryons. Astron. Astrophys. 2021, 646, A156. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, F.; Feng, L.L. Profiles of cosmic filaments since z = 4.0 in cosmological hydrodynamical simulation. Astrophys. J. 2021, 920, 2. [Google Scholar] [CrossRef]
- Bykov, A.M.; Paerels, F.B.S.; Petrosian, V. Equilibration processes in the warm-hot intergalactic medium. Space Sci. Rev. 2008, 134, 141–153. [Google Scholar] [CrossRef]
- Bertone, S.; Schaye, J.; Dolag, K. Numerical Simulations of the Warm-Hot Intergalactic Medium. Space Sci. Rev. 2008, 134, 295–310. [Google Scholar] [CrossRef]
- Richter, P.; Paerels, F.B.S.; Kaastra, J.S. FUV and X-Ray absorption in the Warm-Hot Intergalactic Medium. Space Sci. Rev. 2008, 134, 25–49. [Google Scholar] [CrossRef]
- Cen, R.; Ostriker, J.P. Where are the baryons? II. Feedback effects. Astrophys. J. 2006, 650, 560–572. [Google Scholar] [CrossRef]
- Fresco, A.Y.; P´eroux, C.; Merloni, A.; Hamanowicz, A.; Szakacs, R. Tracing the 107 K warm–hot intergalactic medium with UV absorption lines. Mon. Not. R. Astron. Soc. 2008, 499, 5230–5240. [Google Scholar] [CrossRef]
- Reeves, J.; Done, C.; Pounds, K.; Terashima, Y.; Hayashida, K.; Anabuki, N.; Uchino, M.; Turner, M. On why the iron K-shell absorption in AGN is not a signature of the local warm/hot intergalactic medium. Mon. Not. R. Astron. Soc. 2008, 385, L108–L112. [Google Scholar] [CrossRef]
- Wiegert, T.; Irwin, J.; Miskolczi, A.; Schmidt, P.; Carolina Mora, S.; Damas-Segovia, A.; Stein, Y.; English, J.; Rand, R.J.; Santistevan, I.; et al. CHANG-ES IV: Radio continuum emission of 35 edge-on galaxies observed with the Karl, G. Jansky very large array in D configuration—Data release 1. Astronom. J. 2015, 150, 81. [Google Scholar] [CrossRef]
- Higgs, C.R.; McConnachie, A.W. Solo dwarfs IV: Comparing and contrasting satellite and isolated dwarf galaxies in the Local Group. Mon. Not. R. Astron. Soc. 2008, 506, 2766–2779. [Google Scholar] [CrossRef]
- McConnachie, A.W. The observed properties of dwarf galaxies in and around the Local Group. Astronom. J. 2012, 144, 4. [Google Scholar] [CrossRef]
- Tsai, C.W.; Eisenhardt, P.R.; Wu, J.; Stern, D.; Assef, R.J.; Blain, A.W.; Bridge, C.R.; Benford, D.J.; Cutri, R.M.; Griffith, R.L.; et al. The most luminous galaxies discovered by WISE. Astrophys. J. 2015, 805, 90. [Google Scholar] [CrossRef]
- Ogle, P.M.; Jarrett, T.; Lanz, L.; Cluver, M.; Alatalo, K.; Appleton, P.N.; Mazzarella, J.M. A break in spiral galaxy scaling relations at the upper limit of galaxy mass. Astrophys. J. Lett. 2019, 884, L11. [Google Scholar] [CrossRef]
- Sofue, Y.; Koda, J.; Nakanishi, H.; Onodera, S. The Virgo high-resolution CO survey, II. Rotation curves and dynamical mass distributions. Publ. Astron. Soc. Jpn. 2003, 55, 59–74. [Google Scholar] [CrossRef]
- Continuum Changes in Nearby Galaxies. Available online: https://www.queensu.ca/changes/ (accessed on 28 December 2022).
- Irwin, J.; Beck, R.; Benjamin, R.A.; Dettmar, R.J.; English, J.; Heald, G.; Henriksen, R.N.; Johnson, M.; Krause, M.; Li, J.T.; et al. Continuum Halos in Nearby Galaxies: An EVLA Survey (CHANG-ES). I. Introduction to the Survey. Astronom. J. 2012, 144, 43. [Google Scholar] [CrossRef]
- NASA/IPAC. Extragalactic Database. Available online: https://ned.ipac.caltech.edu/ (accessed on 1 February 2020).
- Rhee, M.-H. A Physical Basis of the Tully-Fisher Relation. Ph.D. Thesis, University Groningen, Groningen, Germany, 1996. [Google Scholar]
- Hoffman, G.L.; Salpeter, E.E.; Farhat, B.; Roos, T.; Williams, H.; Helou, G. Arecibo HI mapping of a large sample of dwarf irregular galaxies. Astrophys. J. Supp. 1996, 105, 269–301. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Debated Models for Galactic Rotation Curves: A Review and Mathematical Assessment. Galaxies 2020, 8, 47. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K. Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 1970, 159, 379–403. [Google Scholar] [CrossRef]
- Burbidge, G. On the masses and relative velocities of galaxies. Astrophys. J. 1975, 196, L7–L10. [Google Scholar] [CrossRef]
- Ackermann, M.; Albert, A.; Anderson, B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Bissaldi, E.; et al. Dark matter constraints from observations of 25 Milky Way satellite galaxies with the Fermi Large Area Telescope. Phys. Rev. D 2014, 89, 042001. [Google Scholar] [CrossRef]
- Giagu, S. WIMP dark matter searches with the ATLAS detector at the LHC. Front. Phys. 2019, 7, 75. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- McGaugh, S.S. A tale of two paradigms, the mutual incommensurability of LCDM and MOND. Can. J. Phys. 2015, 93, 250–259. [Google Scholar] [CrossRef]
- Gauss, C.F. Determinatio Attractionis quam in punctum quodvis positionis datae ejus massa per totam orbitam ratione temporis quo singulae partes describuntur esset dispertita. In Werke; Königlichen Gesellschaft der Wissenschaften: Göttingen, Germany, 1866; Volume 3, pp. 331–357. [Google Scholar]
- Hill, G.W. The secular perturbations of the planets. Am. J. Math. 1901, 23, 317–336. [Google Scholar] [CrossRef]
- Criss, R.E.; Hofmeister, A.M. Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves. Galaxies 2020, 8, 19. [Google Scholar] [CrossRef]
- Wang, Q.D.; Nowak, M.A.; Markoff, S.B.; Baganoff, F.K.; Nayakshin, S.; Yuan, F.; Cuadra, J.; Davis, J.; Dexter, J.; Fabian, A.C.; et al. Dissecting X-ray–emitting gas around the center of our galaxy. Science 2013, 341, 981–983. [Google Scholar] [CrossRef]
- What Does the Milky Way Weigh? Hubble and Gaia Investigate. Available online: https://www.nasa.gov/feature/goddard/2019/what-does-the-milky-way-weigh-hubble-and-gaia-investigate (accessed on 18 July 2023).
- Groetsch, C.W. Inverse Problems: Activities for Undergraduates; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Halliday, D.; Resnick, R. Physics; John Wiley and Sons: New York, NY, USA, 1966. [Google Scholar]
- Ibata, R.; Lewis, G.F.; Martin, N.F.; Bellazzini, M.; Correnti, M. Does the Sagittarius stream constrain the Milky Way halo to be triaxial? Astrophys. J. Lett. 2013, 765, L155. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E.; Criss, E.M. Verified solutions for the gravitational attraction to an oblate spheroid: Implications for planet mass and satellite orbits. Planet. Space Sci. 2018, 152, 68–81. [Google Scholar] [CrossRef]
- Sipols, A.; Pavlovich, A. Dark matter dogma: A study of 214 galaxies. Galaxies 2020, 8, 36. [Google Scholar] [CrossRef]
- Sipols, A.; Pavlovich, A. Surface Brightness Plateau in S4G Galaxies. Galaxies 2020, 8, 48. [Google Scholar] [CrossRef]
- Gallo, C.F.; Feng, J.Q. A thin-disk gravitational model for galactic rotation. In Proceedings of the 2nd Crisis Cosmology Conference, Washington, DC, USA, 7–11 September 2009; Volume 413, pp. 289–303. [Google Scholar]
- Feng, J.Q.; Gallo, C.F. Mass distribution in rotating thin-disk galaxies according to Newtonian dynamics. Galaxies 2014, 2, 199–222. [Google Scholar] [CrossRef]
- Feng, J.Q. Rotating Disk Galaxies without Dark Matter Based on Scientific Reasoning. Galaxies 2020, 8, 9. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. The physics of galactic spin. Can. J. Phys. 2017, 95, 156–166. [Google Scholar] [CrossRef]
- Craig, I.J.D.; Brown, J.C. Inverse Problems in Astronomy; Adam Hilger Ltd.: Bristol, UK, 1986. [Google Scholar]
- Criss, R.E.; Hofmeister, A.M. Galactic density and evolution based on the virial theorem, energy minimization, and conservation of angular momentum. Galaxies 2018, 6, 115–135. [Google Scholar] [CrossRef]
- Criss, R.E. Analytics of planetary rotation: Improved physics with implications for the shape and super-rotation of Earth’s Core. Earth Sci. Rev. 2019, 192, 471–479. [Google Scholar] [CrossRef]
- Kellogg, O.D. Foundations of Potential Theory; Dover Publications: New York, NY, USA, 1953. [Google Scholar]
- MacMillan, W.D. The Theory of the Potential; McGraw-Hill: New York, NY, USA, 1930. [Google Scholar]
- Moulton, F.R. An Introduction to Celestial Mechanics; MacMillan: New York, NY, USA, 1914. [Google Scholar]
- Perek, L. Heterogeneous spheroids with Gaussian and exponential density laws. Bull. Astron. Inst. Czechoslov. 1958, 9, 208–212. [Google Scholar]
- Pawlowski, M.S.; Pflamm-Altenburg, J.; Kroupa, P. The VPOS: A vast polar structure of satellite galaxies, globular clusters and streams around the Milky Way. Mon. Not. R. Ast. Soc. 2012, 423, 1109–1126. [Google Scholar] [CrossRef]
- Moiseev, A.V.; Smirnova, K.I.; Smirnova, A.A.; Reshetnikov, V.P. A new catalogue of polar-ring galaxies selected from the Sloan Digital Sky Survey. Mon. Not. R. Ast. Soc. 2011, 418, 244–257. [Google Scholar] [CrossRef]
- Finkelman, I.; Funes, J.G.; Brosch, N. Polar ring galaxies in the Galaxy Zoo. Mon. Not. Royal Ast. Soc. 2012, 422, 2386–2398. [Google Scholar] [CrossRef]
- Khoperskov, S.A.; Moiseev, A.V.; Khoperskov, A.V.; Saburova, A.S. To be or not to be oblate: The shape of the dark matter halo in polar ring galaxies. Mon. Not. R. Ast. Soc. 2014, 441, 2650–2662. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Dankova, T.; Rosensteel, G. Triaxial bifurcations of rapidly rotating spheroids. Am. J. Phys. 1998, 66, 1095–1100. [Google Scholar] [CrossRef]
- Sofue, Y. Rotation curve and mass distribution in the galactic center—From black hole to entire galaxy. Pub. Astron. Soc. Jpn. 2013, 65, 118. [Google Scholar] [CrossRef]
- Sofue, Y. Dark halos of M 31 and the Milky Way. Publ. Astron. Soc. Jpn. 2015, 67, 759. [Google Scholar] [CrossRef]
- Nakanishi, H.; Sakai, N.; Kurayama, T.; Matsuo, M.; Imai, H.; Burns, R.A.; Ozawa, T.; Honma, M.; Shibata, K.; Kawaguchi, N. Outer rotation curve of the Galaxy with VERA. II. Annual parallax and proper motion of the star-forming region IRAS 21379+5106. Pub. Astr. Soc. Jpn. 2015, 67, 68. [Google Scholar] [CrossRef]
- Watkins, L.L.; Van Der Marel, R.P.; Sangmo, S.T.; Evans, N.W. Evidence for an intermediate-mass Milky Way from Gaia DR2 halo globular cluster motions. Astrophys. J. 2019, 873, 118. [Google Scholar] [CrossRef]
- Romanowsky, A.J.; Douglas, N.G.; Arnaboldi, M.; Kuijken, K.; Merrifield, M.R.; Napolitano, N.R.; Capaccioli, M.; Freeman, K. A dearth of dark matter in ordinary elliptical galaxies. Science 2003, 301, 1696–1698. [Google Scholar] [CrossRef]
- Geha, M.; Guhathakurta, P.; Rich, R.M.; Cooper, M.C. Local Group dwarf elliptical galaxies. I. Mapping the dynamics of NGC 205 beyond the tidal radius. Astrophys. J. 2006, 131, 332–342. [Google Scholar] [CrossRef]
- Wiegert, T.; English, J. Kinematic classification of non-interacting spiral galaxies. New Astron. 2014, 26, 40–61. [Google Scholar] [CrossRef]
- Howley, K.M.; Guhathakurta, P.; van der Marel, R.; Geha, M.; Kalirai, J.; Yniguez, B.; Kirby, E.; Cuillandre, J.-C.; Gilbert, K. Internal stellar kinematics of M32 from the SPLASH survey, dark halo constraints. Astrophys. J. 2013, 765, 65. [Google Scholar] [CrossRef]
- Bottema, R.; Pestaña, J.L.G. The distribution of dark and luminous matter inferred from extended rotation curves. Mon. Not. R. Astron. Soc. 2015, 448, 2566–2593. [Google Scholar] [CrossRef]
- Ferrière, K. The interstellar environment of our galaxy. Rev. Mod. Phys. 2011, 73, 1031–1066. [Google Scholar] [CrossRef]
- LeDrew, G. The real starry sky. J. R. Astron. Soc. Can. 2011, 95, 322–324. [Google Scholar]
- Luyten, W.J. A new determination of the luminosity function. Mon. Not. R. Astron. Soc. 1968, 139, 221–224. [Google Scholar] [CrossRef]
- Fang, T.; Buote, D.A.; Humphrey, P.J.; Canizares, C.R.; Zappacosta, L.; Maiolino, R.; Tagliaferri, G.; Gastaldello, F. Confirmation of X-ray absorption by warm-hot intergalactic medium in the Sculptor wall. Astrophys. J. 2010, 714, 1715–1724. [Google Scholar] [CrossRef]
- Nicastro, F.; Mathur, S.; Elvis, M. Missing baryons and the warm-hot intergalactic medium. Science 2008, 319, 55–57. [Google Scholar] [CrossRef] [PubMed]
- The Virgo Cluster. Available online: http://www.atlasoftheuniverse.com/galgrps/vir.html (accessed on 10 January 2023).
- Binggeli, B.; Sandage, A.; Tarenghi, M. Studies of the Virgo Cluster. I-Photometry of 109 galaxies near the cluster center to serve as standards. Astron. J. 1984, 89, 64–82. [Google Scholar] [CrossRef]
- Conselice, C.J.; Wilkinson, A.; Duncan, K.; Mortlock, A. The evolution of galaxy number density at z < 8 and its implications. Astrophys. J. 2016, 830, 83. [Google Scholar]
- Dodelson, S. Modern Cosmology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Carroll, B.W.; Ostlie, D.A. An Introduction to Modern Astrophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; Chapter 29. [Google Scholar]
- Friedmann Equations. Available online: https://en.wikipedia.org/wiki/Friedmann_equations#Density_parameter (accessed on 18 July 2023).
- Copi, C.J.; Schramm, D.S.; Turner, M.S. Big-Bang Nucleosynthesis and the Baryon Density of the Universe. Science 1995, 267, 192–199. [Google Scholar] [CrossRef]
- Galaxy Filaments. Available online: https://en.wikipedia.org/wiki/Galaxy_filament (accessed on 27 July 2023).
- Criss, R.E.; Hofmeister, A.M. Thermodynamic Cosmology. Geochim. Cosmochim. Acta 2001, 65, 4077–4085. [Google Scholar] [CrossRef]
- Schechter, P. An analytic expression for the luminosity function for galaxies. Astrophys. J. 1976, 203, 297–306. [Google Scholar] [CrossRef]
- Yasuda, N.; Fukugita, M.; Narayanan, V.K.; Lupton, R.H.; Strateva, I.; Strauss, M.A.; Ivezić, Ž.; Kim, R.S.J.; Hogg, D.W.; Weinberg, D.H.; et al. Galaxy number counts from the sloan digital sky survey commissioning data. Astron. J. 2001, 122, 1104–1124. [Google Scholar] [CrossRef]
- Kam, Z.S.; Carignan, C.; Chemin, L.; Amram, P.; Epinat, B. Kinematics and mass modelling of M33, Hα observations. Mon. Not. R. Astron. Soc. 2015, 449, 4048–4070. [Google Scholar] [CrossRef]
- Sofue, Y.; Tutui, Y.; Honma, M.; Tomita, A.; Takamiya, T.; Koda, J.; Takeda, Y. Central rotation curves of spiral galaxies. Astrophys. J. 1999, 523, 136–146. [Google Scholar] [CrossRef]
- Corbelli, E.; Salucci, P. The extended rotation curve and the dark matter halo of M33. Mon. Not. R. Ast. Soc. 2000, 311, 441–447. [Google Scholar] [CrossRef]
- Leaman, R.; Venn, K.A.; Brooks, A.M.; Battaglia, G.; Cole, A.A.; Ibata, R.A.; Irwin, M.J.; McConnachie, A.W.; Mendel, J.T.; Tolstoy, E. The resolved structure and dynamics of an isolated dwarf galaxy, A VLT and Keck spectroscopic survey of WLM. Astrophys. J. 2012, 750, 33. [Google Scholar] [CrossRef]
- Salucci, P.; Wilkinson, M.I.; Walker, M.G.; Gilmore, G.F.; Grebel, E.K.; Koch, A.; Frigerio Martins, C.; Wyse, R.F.G. Dwarf spheroidal galaxy kinematics and spiral galaxy scaling laws. Mon. Not. R. Ast. Soc. 2012, 420, 2034–2041. [Google Scholar] [CrossRef]
- Walker, M.G.; Mateo, M.; Olszewski, E.W.; Gnedin, O.Y.; Wang, X.; Sen, B.; Woodroofe, M. Velocity dispersion profiles of seven dwarf spheroidal galaxies. Astrophys. J. 2007, 667, L53–L56. [Google Scholar] [CrossRef]
- Walker, M.G.; Mateo, M.; Olszewski, E.W. Stellar velocities in the Carina, Fornax, Sculptor, and Sextans dSph galaxies, data from the Magellan/MMFS survey. Astronom. J. 2009, 137, 3100. [Google Scholar] [CrossRef]
- Mateo, M.; Olszewski, E.W.; Walker, M.G. The velocity dispersion profile of the remote dwarf spheroidal galaxy Leo I, A tidal hit and run? Astrophys. J. 2008, 675, 20. [Google Scholar] [CrossRef]
- Oh, S.H.; Hunter, D.A.; Brinks, E.; Elmegreen, B.G.; Schruba, A.; Walter, F.; Rupen, M.P.; Young, L.M.; Simpson, C.E.; Johnson, M.C.; et al. High-resolution mass models of dwarf galaxies from LITTLE THINGS. Astronom. J. 2015, 149, 180. [Google Scholar] [CrossRef]
- Weldrake, D.T.; De Blok, W.J.; Walter, F. A high-resolution rotation curve of NGC 6822: A test-case for cold dark matter. Mon. Not. R. Astron. Soc. 2003, 340, 12–28. [Google Scholar] [CrossRef]
- Karachentsev, I.D.; Chengalur, J.N.; Tully, R.B.; Makarova, L.N.; Sharina, M.E.; Begum, A.; Rizzi, L. Andromeda IV, a solitary gas-rich dwarf galaxy. Astron. Nach. 2016, 337, 306–314. [Google Scholar] [CrossRef]
- Alves, D.R.; Nelson, C.A. The rotation curve of the Large Magellanic cloud and the implications for Microlensing. Astrophys. J. 2000, 542, 789. [Google Scholar] [CrossRef]
- Geha, M.; Van der Marel, R.P.; Guhathakurta, P.; Gilbert, K.M.; Kalirai, J.; Kirby, E.N. Local Group dwarf elliptical galaxies. II. Stellar kinematics to large radii in NGC 147 and NGC 185. Astrophys. J. 2010, 711, 361–373. [Google Scholar] [CrossRef]
- Namumba, B.; Carignan, C.; Passmoor, S. HI observations of Sextans A and B with the SKA pathfinder KAT-7. Mon. Not. R. Astron. Soc. 2018, 478, 487–500. [Google Scholar] [CrossRef]
- Di Teodoro, E.M.; McClure-Griffiths, N.M.; Jameson, K.E.; Denes, H.; Dickey, J.M.; Stanimirović, S.; Staveley-Smith, L.; Anderson, C.; Bunton, J.D.; Chippendale, A.; et al. On the dynamics of the Small Magellanic Cloud through high-resolution ASKAP HI observations. Mon. Not. R. Astron. Soc. 2019, 483, 392–406. [Google Scholar] [CrossRef]



| Density | Reference | This Work * | ||
|---|---|---|---|---|
| Object or Region | kg m−3 | kg m−3 | Figure No. | |
| Solar neighborhood | ~3 × 10−21 | [74,75] | 5 × 10−21 | Figure 4 |
| Interstellar medium | ~10−21 | [73] † | 10−21 | Figure 3 and Figure 4 |
| Circumgalactic medium | 2 × 10−24 to 5 × 10−26 | [76] ‡ | 10−22 to 10−24 | Figure 3 and Figure 6b |
| Intergalactic medium | 1.9 × 10−28 § | Figure 6b § | ||
| WHIM absorptions | 1.7 × 10−26 to 1.7 × 10−27 | [77] § | 1.9 × 10−28 § | Figure 6b § |
| Cutoff | Ellipticals | Lenticulars | Spirals | All Types | ||||
|---|---|---|---|---|---|---|---|---|
| Mpc | Number | Mean L/Lsun | Number | Mean L/Lsun | Number | Mean L/Lsun | Number | Mean L/Lsun |
| 250 * | 4515 | 4.02 × 1010 | 7569 | 2.73 × 1010 | 3474 | 1.97 × 1010 | 15,558 | 2.93 × 1010 |
| 100 | 2210 | 3.06 × 1010 | 5492 | 2.55 × 1010 | 3101 | 2.17 × 1010 | 10,803 | 2.55 × 1010 |
| 50 | 1956 | 3.04 × 1010 | 5483 | 2.60 × 1010 | 2518 | 2.18 × 1010 | 9957 | 2.58 × 1010 |
| ~30 † | 1813 | 3.14 × 1010 | 5333 | 2.65 × 1010 | 1719 | 2.69 × 1010 | 8865 | 2.76 × 1010 |
| Region | rregion (Mpc) | Number of Large Galaxies | Data | rrepresentative (Mpc) | ρaverage * (kg m−3) | Enclosed ρ (kg m−3) |
|---|---|---|---|---|---|---|
| LG | 1.5 | 2 | Figure 9 | 1.2 | 6.24 × 10−25 | 6.24 × 10−25 |
| LG | 1.5 | 1 | Figure 9 | 1.5 | 4.11 × 10−25 | 6.15 × 10−25 † |
| VC | 1.65 | 4 (L > 1011 Lsun) | Figure 10 | 1.0 | >9 × 10−25 § | (60 to 1000) × 10−25 % |
| VC | 1.65 | 26 (L > 2 × 1010 Lsun) | Figure 10 | 0.56 | 2.88 × 10−24 # | 300 × 10−25 % |
| VC | 1.65 | 52 (L > 1010 Lsun) | Figure 10 | 0.44 | 4.65 × 10−24 # | 50 × 10−25 |
| VC dispersed to LG | 16 | 54(L > 1010 Lsun) | as above | 4.2 | 5.0 × 10−26 | 1 × 10−25 % |
| Inside 30 Mpc ‡ | ~30 ‡ | 8865 | Figure 11 | 1.5 | 3.9 × 10−25 | 7.8 × 10−25 † |
| Inside 50 Mpc | 50 | 9912 | not shown | 2.3 | 1.7 × 10−25 | 3.4 × 10−25 † |
| Inside 100 Mpc | 10 | 10,803 | not shown | 4.5 | 4.5 × 10−26 | 1.2 × 10−25 † |
| Inside 250 Mpc | 250 | 15,158 | Figure A11 | 10 | 9 × 10−27 | 0.34 × 10−25 † % |
| Extrapolated trends | 1000 | >384,000 | Section 4.2 | <7 | >1.86 × 10−27 | See Section 4.2 |
| Universe (Z < 0.8) | 7500 | 2 × 1012(L > 106 Lsun) | Section 4.3 | 0.6–2 | (2 to 24) × 10−25 | (2 to 24) × 10−25 |
| Method or Region | Baryon Density kg m−3 | ρ (Neglects IGM) # kg m−3 |
|---|---|---|
| Local Group † | 6.2 × 10−25 | 0.042 × 10−25 |
| Distance directly determined (<30 Mpc) | 7.8 × 10−25 | 0.034 × 10−25 |
| Nearby (<50 Mpc) | 3.4 × 10−25 | 0.01 × 10−25 |
| Universe Count ‡ | (2 to 24) × 10−25 | ~0.5 × 10−25 |
| Energy Balance § | 0.2 × 10−25 | n.a. |
| Expansionary critical density & | 0.09 × 10−25 | n.a. |
| Cosmology models of baryon density | 0.003 × 10−25 | n.a. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmeister, A.M.; Criss, R.E.; Chou, H. Baryonic Mass Inventory for Galaxies and Rarefied Media from Theory and Observations of Rotation and Luminosity. Galaxies 2023, 11, 100. https://doi.org/10.3390/galaxies11050100
Hofmeister AM, Criss RE, Chou H. Baryonic Mass Inventory for Galaxies and Rarefied Media from Theory and Observations of Rotation and Luminosity. Galaxies. 2023; 11(5):100. https://doi.org/10.3390/galaxies11050100
Chicago/Turabian StyleHofmeister, Anne M., Robert E. Criss, and Hugh Chou. 2023. "Baryonic Mass Inventory for Galaxies and Rarefied Media from Theory and Observations of Rotation and Luminosity" Galaxies 11, no. 5: 100. https://doi.org/10.3390/galaxies11050100
APA StyleHofmeister, A. M., Criss, R. E., & Chou, H. (2023). Baryonic Mass Inventory for Galaxies and Rarefied Media from Theory and Observations of Rotation and Luminosity. Galaxies, 11(5), 100. https://doi.org/10.3390/galaxies11050100







