From the s-Process to the i-Process: A New Perspective on the Chemical Enrichment of Extrinsic Stars
Abstract
:1. Introduction
- The site of the s-process for nuclei is well-identified as low- and intermediate-mass ( 3–4M⊙) thermally-pulsing asymptotic giant branch (TP-AGB) stars [3,4,7,8]. Stars producing their s-process elements are classified as intrinsic S or carbon stars, whereas stars polluted by s-process material originating from a companion are tagged extrinsic S, barium, CH, or CEMP-s stars (CEMP stands for ‘carbon-enriched metalpoor’), by order of decreasing metallicity.
- The site of the r-process is still debated: the decompression of neutron–star matter ejected during a binary neutron star merger [9] provides, since the observation of GW170817 [10], a promising alternative to core-collapse supernovae [11] or magnetorotational supernovae (e.g., [12]). Whether the neutron star merger site is the only one contributing to the r-process is still highly debated [13,14]. r-process-enriched stars are found among the CEMP-r stellar class, subdivided into the classes r-I ( [Eu/Fe] and [Ba/Eu]), r-II ([Eu/Fe] > 0.7 and [Ba/Eu] < 0), and r-III ([Eu/Fe] > 2) ([15] and references therein). We adopt the usual notation: [A/B] , where is the number density of the X element and
- Some stars are enriched in both r- and s-elements; they are also carbon-enriched and have been initially detected among metal-poor stars (they are thus tagged CEMP-rs) and among CH stars. However, some of them have been found in more metal-rich ([Fe/H] = −0.5) carbon-enriched objects (see e.g., [16,17,18,19,20]).
2. Isotopic Ratio Determination
2.1. Materials and Methods
2.2. Results
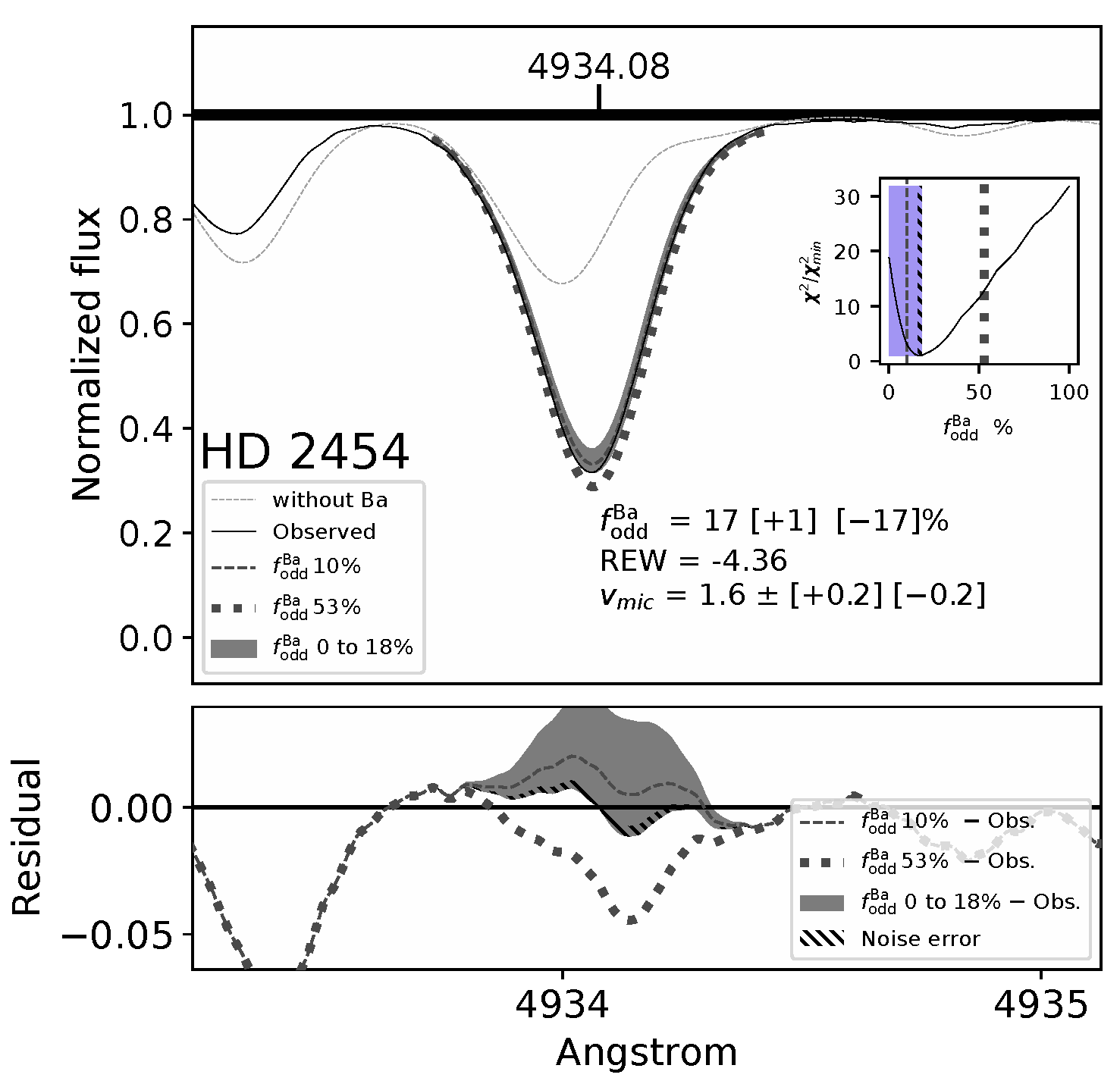
- HD 2454: Both the signed and RMS distances exceed 0.7, indicating that the s-process is responsible for the measured chemical peculiarities. The analysis also strongly supports the s-process. Furthermore, the low value of is consistent only with the s-process.
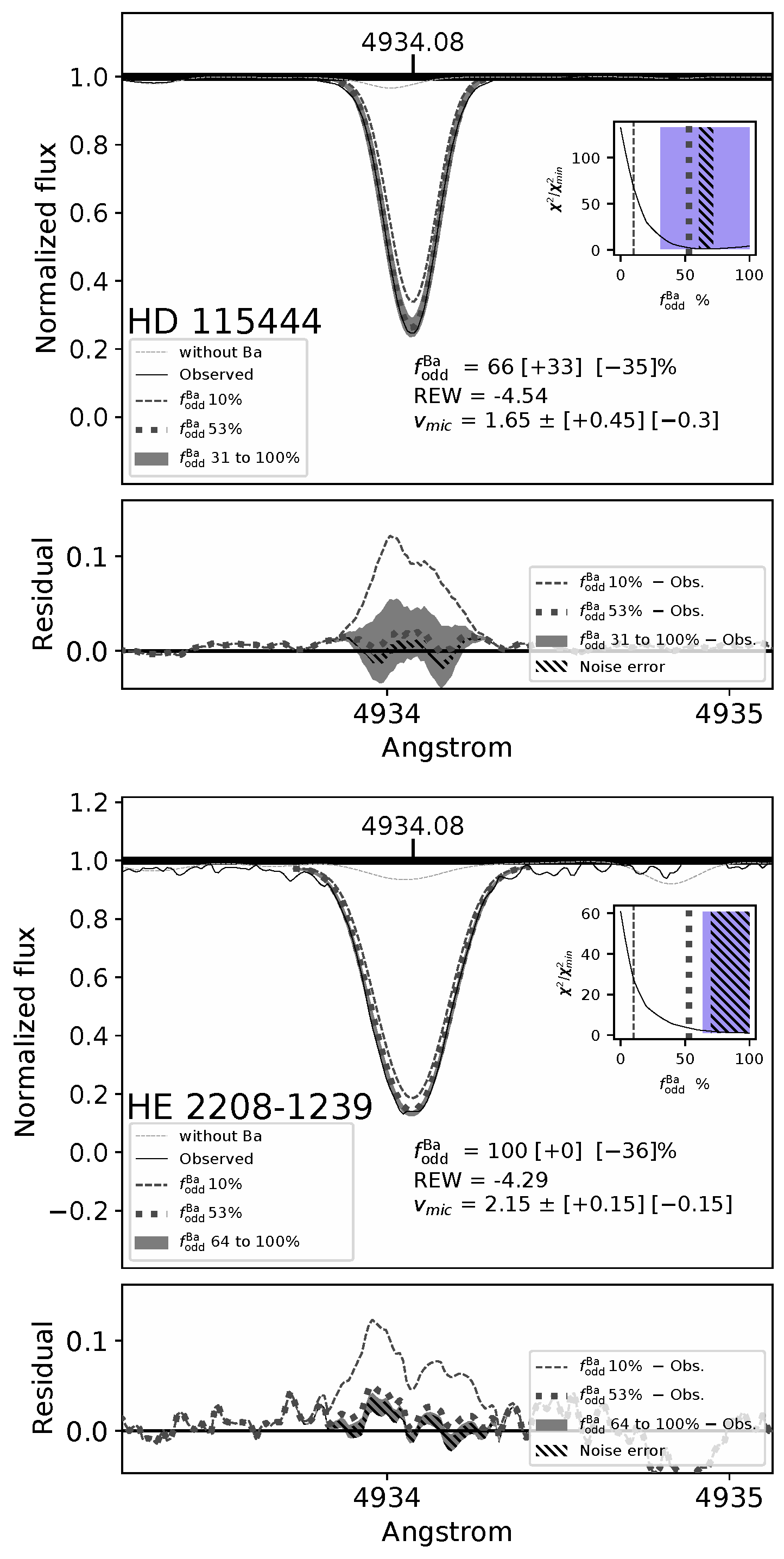
- HD 115444: The signed and RMS distances are very small or even zero, as expected for a pure r-process abundance profile. The analysis also favors the r-process. The isotopic fraction rules out the s-process but cannot distinguish between pollution by an i- or r-process.
- HE 2208-1239: The signed distance is below the threshold of 0.7, pointing to an i-process, while the RMS distance suggests the s-process. The analysis offers a clearer conclusion, strongly supporting the i-process, likely due to the inclusion of more chemical elements. Finally, suggests an i- or r-process origin.
3. Extrinsic Stars in Surveys: Searching for a Needle in a Haystack
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TP-AGB | Thermally-Pulsing Asymptotic Giant Branch |
| (N)LTE | (Non)-Local Thermal Equilibrium |
References
- Arnould, M.; Goriely, S. Astronuclear Physics: A tale of the atomic nuclei in the skies. Prog. Part. Nucl. Phys. 2020, 112, 103766. [Google Scholar] [CrossRef]
- Käppeler, F.; Gallino, R.; Bisterzo, S.; Aoki, W. The s process: Nuclear physics, stellar models, and observations. Rev. Mod. Phys. 2011, 83, 157–193. [Google Scholar] [CrossRef]
- Karakas, A. Updated stellar yields from asymptotic giant branch models. Mon. Not. R. Astron. Soc. 2010, 403, 1413. [Google Scholar] [CrossRef]
- Goriely, S.; Siess, L. Sensitivity of the s-process nucleosynthesis in AGB stars to the overshoot model. Astron. Astrophys. 2018, 609, A29. [Google Scholar] [CrossRef]
- Arnould, M.; Goriely, S.; Takahashi, K. The r-process of stellar nucleosynthesis: Astrophysics and nuclear physics achievements and mysteries. Phys. Repts. 2007, 450, 97–213. [Google Scholar] [CrossRef]
- Cowan, J.; Sneden, C.; Lawler, J.; Aprahamian, A.; Wiescher, M.; Langanke, K.; Martínez-Pinedo, G.; Thielemann, F.K. Origin of the heaviest elements: The rapid neutron-capture process. Rev. Mod. Phys. 2021, 93, 015002. [Google Scholar] [CrossRef]
- Gallino, R.; Arlandini, C.; Busso, M.; Lugaro, M.; Travaglio, C.; Straniero, O.; Chieffi, A.; Limongi, M. Evolution and Nucleosynthesis in Low-Mass Asymptotic Giant Branch Stars. II. Neutron Capture and the s-Process. Astrophys. J. 1998, 497, 388. [Google Scholar] [CrossRef]
- Cristallo, S.; Straniero, O.; Gallino, R.; Piersanti, L.; Domínguez, I.; Lederer, M.T. Evolution, Nucleosynthesis, and Yields of Low-Mass Asymptotic Giant Branch Stars at Different Metallicities. Astrophys. J 2009, 696, 797–820. [Google Scholar] [CrossRef]
- Goriely, S.; Bauswein, A.; Janka, H.T. r-process Nucleosynthesis in Dynamically Ejected Matter of Neutron Star Mergers. Astrophys. J. Lett. 2011, 738, L32. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Janka, H.T. Explosion Mechanisms of Core-Collapse Supernovae. Annu. Rev. Nucl. Part. Sci. 2012, 62, 407–451. [Google Scholar] [CrossRef]
- Kobayashi, C.; Karakas, A.I.; Lugaro, M. The Origin of Elements from Carbon to Uranium. Astrophys. J. 2020, 900, 179. [Google Scholar] [CrossRef]
- Kobayashi, C.; Mandel, I.; Belczynski, K.; Goriely, S.; Janka, T.H.; Just, O.; Ruiter, A.J.; Vanbeveren, D.; Kruckow, M.U.; Briel, M.M.; et al. Can Neutron Star Mergers Alone Explain the r-process Enrichment of the Milky Way? Astrophys. J. Lett. 2023, 943, L12. [Google Scholar] [CrossRef]
- Lian, J.; Storm, N.; Guiglion, G.; Serenelli, A.; Cote, B.; Karakas, A.I.; Boardman, N.; Bergemann, M. Observational constraints on the origin of the elements - VI. Origin and evolution of neutron-capture elements as probed by the Gaia-ESO survey. Mon. Not. R. Astron. Soc. 2023, 525, 1329–1341. [Google Scholar] [CrossRef]
- Holmbeck, E.M.; Hansen, T.T.; Beers, T.C.; Placco, V.M.; Whitten, D.D.; Rasmussen, K.C.; Roederer, I.U.; Ezzeddine, R.; Sakari, C.M.; Frebel, A.; et al. The R-Process Alliance: Fourth Data Release from the Search for R-process-enhanced Stars in the Galactic Halo. Astrophys. J. Suppl. Ser. 2020, 249, 30. [Google Scholar] [CrossRef]
- Cui, W.Y.; Zhang, B.; Shi, J.R.; Zhao, G.; Wang, W.J.; Niu, P. Possible discovery of the r-process characteristics in the abundances of metal-rich barium stars. Astron. Astrophys. 2014, 566, A16. [Google Scholar] [CrossRef]
- Karinkuzhi, D.; Van Eck, S.; Jorissen, A.; Goriely, S.; Siess, L.; Merle, T.; Escorza, A.; Van der Swaelmen, M.; Boffin, H.M.J.; Masseron, T.; et al. When binaries keep track of recent nucleosynthesis. The Zr-Nb pair in extrinsic stars as an s-process diagnostic. Astron. Astrophys. 2018, 618, A32. [Google Scholar] [CrossRef]
- Karinkuzhi, D.; Van Eck, S.; Goriely, S.; Siess, L.; Jorissen, A.; Merle, T.; Escorza, A.; Masseron, T. Low-mass low-metallicity AGB stars as an efficient i-process site explaining CEMP-rs stars. Astron. Astrophys. 2021, 645, A61. [Google Scholar] [CrossRef]
- den Hartogh, J.W.; Yagüe López, A.; Cseh, B.; Pignatari, M.; Világos, B.; Roriz, M.P.; Pereira, C.B.; Drake, N.A.; Junqueira, S.; Lugaro, M. Barium stars as tracers of s-process nucleosynthesis in AGB stars. II. Using machine learning techniques on 169 stars. Astron. Astrophys. 2023 2023, 672, A143. [Google Scholar] [CrossRef]
- Karinkuzhi, D.; Van Eck, S.; Goriely, S.; Siess, L.; Jorissen, A.; Choplin, A.; Escorza, A.; Shetye, S.; Van Winckel, H. Does the i-process operate at nearly solar metallicity? Astron. Astrophys. 2023, 677, A47. [Google Scholar] [CrossRef]
- Beers, T.C.; Christlieb, N. The Discovery and Analysis of Very Metal-Poor Stars in the Galaxy. Annu. Rev. Astron. Astrophys. 2005, 43, 531–580. [Google Scholar] [CrossRef]
- Masseron, T.; Johnson, J.A.; Plez, B.; van Eck, S.; Primas, F.; Goriely, S.; Jorissen, A. A holistic approach to carbon-enhanced metal-poor stars. Astron. Astrophys. 2010, 509, A93. [Google Scholar] [CrossRef]
- Hansen, C.J.; Hansen, T.T.; Koch, A.; Beers, T.C.; Nordström, B.; Placco, V.M.; Andersen, J. Abundances and kinematics of carbon-enhanced metal-poor stars in the Galactic halo. A new classification scheme based on Sr and Ba. Astron. Astrophys. 2019, 623, A128. [Google Scholar] [CrossRef]
- Hansen, T.T.; Andersen, J.; Nordström, B.; Beers, T.C.; Placco, V.M.; Yoon, J.; Buchhave, L.A. The role of binaries in the enrichment of the early Galactic halo. III. Carbon-enhanced metal-poor stars - CEMP-s stars. Astron. Astrophys. 2016, 588, A3. [Google Scholar] [CrossRef]
- Gull, M.; Frebel, A.; Cain, M.G.; Placco, V.M.; Ji, A.P.; Abate, C.; Ezzeddine, R.; Karakas, A.I.; Hansen, T.T.; Sakari, C.; et al. The R-Process Alliance: Discovery of the First Metal-poor Star with a Combined r- and s-process Element Signature. Astrophys. J. 2018, 862, 174. [Google Scholar] [CrossRef]
- Hampel, M.; Stancliffe, R.J.; Lugaro, M.; Meyer, B.S. The Intermediate Neutron-capture Process and Carbon-enhanced Metal-poor Stars. Astrophys. J. 2016, 831, 171. [Google Scholar] [CrossRef]
- Iben, I., Jr.; Renzini, A. Asymptotic giant branch evolution and beyond. Annu. Rev. Astron. Astrophys. 1983, 21, 271–342. [Google Scholar] [CrossRef]
- Jonsell, K.; Barklem, P.S.; Gustafsson, B.; Christlieb, N.; Hill, V.; Beers, T.C.; Holmberg, J. The Hamburg/ESO R-process enhanced star survey (HERES). III. HE 0338-3945 and the formation of the r + s stars. Astron. Astrophys. 2006, 451, 651–670. [Google Scholar] [CrossRef]
- Cowan, J.J.; Rose, W.K. Production of 14C and neutrons in red giants. Astrophys. J. 1977, 212, 149–158. [Google Scholar] [CrossRef]
- Serenelli, A. Nucleosynthesis in Low Mass Very Metal Poor AGB Stars. In Chemical Abundances and Mixing in Stars in the Milky Way and Its Satellites; Randich, S., Pasquini, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; p. 322. [Google Scholar] [CrossRef]
- Choplin, A.; Siess, L.; Goriely, S. The intermediate neutron capture process. I. Development of the i-process in low-metallicity low-mass AGB stars. Astron. Astrophys. 2021, 648, A119. [Google Scholar] [CrossRef]
- Choplin, A.; Siess, L.; Goriely, S. The intermediate neutron-capture process in AGB stars. Eur. Phys. J. Web Conf. 2023, 279, 07001. [Google Scholar] [CrossRef]
- Choplin, A.; Siess, L.; Goriely, S. The intermediate neutron capture process III. The i-process in AGB stars of different masses and metallicities without overshoot. Astron. Astrophys. 2022, 667, A155. [Google Scholar] [CrossRef]
- Martinet, S.; Choplin, A.; Goriely, S.; Siess, L. The intermediate neutron capture process. IV. Impact of nuclear model and parameter uncertainties. Astron. Astrophys. 2024, 684, A8. [Google Scholar] [CrossRef]
- Choplin, A.; Goriely, S.; Siess, L.; Martinet, S. Synthesis of actinides and short-lived radionuclides during i-process nucleosynthesis in AGB stars. Eur. Phys. J. 2025; in press. [Google Scholar]
- Goriely, S. Uncertainties in the solar system r-abundance distribution. Astron. Astrophys. 1999, 342, 881–891. [Google Scholar]
- Bisterzo, S.; Travaglio, C.; Gallino, R.; Wiescher, M.; Kaeppeler, F. Galactic Chemical Evolution and Solar s-process Abundances: Dependence on the 13C-pocket Structure. Astrophys. J 2014, 787, 10. [Google Scholar] [CrossRef]
- Prantzos, N.; Abia, C.; Cristallo, S.; Limongi, M.; Chieffi, A. Chemical evolution with rotating massive star yields II. A new assessment of the solar s- and r-process components. Mon. Not. R. Astron. Soc. 2020, 491, 1832. [Google Scholar] [CrossRef]
- Mashonkina, L.; Gehren, T.; Bikmaev, I. Barium abundances in cool dwarf stars as a constraint to s- and r-process nucleosynthesis. Astron. Astrophys. 1999, 343, 519–530. [Google Scholar]
- Mashonkina, L.; Gehren, T. Heavy element abundances in cool dwarf stars: An implication for the evolution of the Galaxy. Astron. Astrophys. 2001, 376, 232–247. [Google Scholar] [CrossRef]
- Mashonkina, L.; Zhao, G. Barium even-to-odd isotope abundance ratios in thick disk and thin disk stars. Astron. Astrophys. 2006, 456, 313–321. [Google Scholar] [CrossRef]
- Mashonkina, L.; Christlieb, N. The Hamburg/ESO R-process Enhanced Star survey (HERES). IX. Constraining pure r-process Ba/Eu abundance ratio from observations of r-II stars. Astron. Astrophys. 2014, 565, A123. [Google Scholar] [CrossRef]
- Magain, P.; Zhao, G. Barium isotopes in the very metal-poor star HD 140283. Astron. Astrophys. 1993, 268, L27–L29. [Google Scholar]
- Lambert, D.L.; Allende Prieto, C. The isotopic mixture of barium in the metal-poor subgiant HD 140283. Mon. Not. R. Astron. Soc. 2002, 335, 325–334. [Google Scholar] [CrossRef]
- Collet, R.; Asplund, M.; Nissen, P.E. The Barium Isotopic Abundance in the Metal-Poor Star HD140283. Publ. Astron. Soc. Aust. 2009, 26, 330–334. [Google Scholar] [CrossRef]
- Gallagher, A.J.; Ryan, S.G.; García Pérez, A.E.; Aoki, W. The barium isotopic mixture for the metal-poor subgiant star HD 140283. Astron. Astrophys. 2010, 523, A24. [Google Scholar] [CrossRef]
- Gallagher, A.J.; Ludwig, H.G.; Ryan, S.G.; Aoki, W. A three-dimensional hydrodynamical line profile analysis of iron lines and barium isotopes in HD 140283. Astron. Astrophys. 2015, 579, A94. [Google Scholar] [CrossRef]
- Meng, X.Y.; Cui, W.Y.; Shi, J.R.; Jiang, X.H.; Zhao, G.; Zhang, B.; Li, J. The odd-isotope fractions of barium in CEMP-r/s star HE 0338-3945 and r-II star CS 31082-001. Astron. Astrophys. 2016, 593, A62. [Google Scholar] [CrossRef]
- Wenyuan, C.; Xiaohua, J.; Jianrong, S.; Gang, Z.; Bo, Z. The Odd Isotope Fractions of Barium in the Strongly r-process-enhanced (r-II) Stars. Astrophys. J. 2018, 854, 131. [Google Scholar] [CrossRef]
- Short, C.I.; Hauschildt, P.H. NLTE Strontium and Barium in Metal-poor Red Giant Stars. Astrophys. J. 2006, 641, 494–503. [Google Scholar] [CrossRef]
- Raskin, G.; van Winckel, H.; Hensberge, H.; Jorissen, A.; Lehmann, H.; Waelkens, C.; Avila, G.; de Cuyper, J.P.; Degroote, P.; Dubosson, R.; et al. HERMES: A high-resolution fibre-fed spectrograph for the Mercator telescope. Astron. Astrophys. 2011, 526, A69. [Google Scholar] [CrossRef]
- Tomkin, J.; Lambert, D.L.; Edvardsson, B.; Gustafsson, B.; Nissen, P.E. HR 107—An F-type mild barium dwarf star. Astron. Astrophys. 1989, 219, L15–L18. [Google Scholar]
- Sneden, C.; Lawler, J.E.; Cowan, J.J.; Ivans, I.I.; Den Hartog, E.A. New Rare Earth Element Abundance Distributions for the Sun and Five r-Process-Rich Very Metal-Poor Stars. Astrophys. J. Suppl. Ser. 2009, 182, 80–96. [Google Scholar] [CrossRef]
- Hansen, T.; Hansen, C.J.; Christlieb, N.; Beers, T.C.; Yong, D.; Bessell, M.S.; Frebel, A.; García Pérez, A.E.; Placco, V.M.; Norris, J.E.; et al. An Elemental Assay of Very, Extremely, and Ultra-metal-poor Stars. Astrophys. J. 2015, 807, 173. [Google Scholar] [CrossRef]
- Amarsi, A.M.; Nordlander, T.; Barklem, P.S.; Asplund, M.; Collet, R.; Lind, K. Effective temperature determinations of late-type stars based on 3D non-LTE Balmer line formation. Astron. Astrophys. 2018, 615, A139. [Google Scholar] [CrossRef]
- Giribaldi, R.E.; Ubaldo-Melo, M.L.; Porto de Mello, G.F.; Pasquini, L.; Ludwig, H.G.; Ulmer-Moll, S.; Lorenzo-Oliveira, D. Accurate effective temperature from Hα profiles. Astron. Astrophys. 2019, 624, A10. [Google Scholar] [CrossRef]
- Giribaldi, R.E.; Van Eck, S.; Merle, T.; Jorissen, A.; Krynski, P.; Planquart, L.; Valentini, M.; Chiappini, C.; Van Winckel, H. TITANS metal-poor reference stars. II. Red giants and CEMP stars. Astron. Astrophys. 2023, 679, A110. [Google Scholar] [CrossRef]
- Gerber, J.M.; Magg, E.; Plez, B.; Bergemann, M.; Heiter, U.; Olander, T.; Hoppe, R. Non-LTE radiative transfer with Turbospectrum. Astron. Astrophys. 2023, 669, A43. [Google Scholar] [CrossRef]
- Contursi, G.; de Laverny, P.; Recio-Blanco, A.; Spitoni, E.; Palicio, P.A.; Poggio, E.; Grisoni, V.; Cescutti, G.; Matteucci, F.; Spina, L.; et al. The cerium content of the Milky Way as revealed by Gaia DR3 GSP-Spec abundances. Astron. Astrophys. 2023, 670, A106. [Google Scholar] [CrossRef]
- McClure, R.D.; Woodsworth, A.W. The Binary Nature of the Barium and CH Stars. III. Orbital Parameters. Astrophys. J. 1990, 352, 709. [Google Scholar] [CrossRef]

| Star ID | Type | [Fe/H] | LTE/NLTE | R | SNR | Ref. | |
|---|---|---|---|---|---|---|---|
| HE 0338-3945 | CEMP-rs | 0.23 ± 0.12 | NLTE | 35,000 | ≥70 | [48] | |
| CS 31082-001 | CEMP-rII | 0.43 ± 0.09 | NLTE | 75,000 | ≥250 | [48] | |
| CS 29491-069 | CEMP-rII | 0.46 ± 0.08 | NLTE | 60,000 | 70–50 | [49] | |
| HE 1219-0312 | CEMP-rII | 0.51±0.09 | NLTE | 70,000 | 110–111 | [49] | |
| HE 2327-5642 | CEMP-rII | 0.50±0.13 | NLTE | 60,000 | 50–100 | [49] | |
| HE 2252-4225 | CEMP-rII | 0.48±0.12 | NLTE | 50,000 | 70–60 | [49] | |
| HD 140283 | CEMP-rI | 0.38 ±0.1 | 3D, LTE | 95,000 | 1100 * | [47] |
| Star | Type | Reference | Spectrograph | SNR |
|---|---|---|---|---|
| HD 2454 | Dwarf Ba (s) | [52] | HERMES | 330 |
| HD 115444 | CEMP-r | [53] | HERMES | 350 |
| HE 2208-1239 | CEMP-r/s | [54] | UVES | 40–100 |
| Star | log g | [Fe/H]NLTE | |||
|---|---|---|---|---|---|
| (K) | (dex) | (dex) | (km/s) | (km/s) | |
| HD 2454 | not required | ||||
| HD 115444 | |||||
| HE 2208-1239 |
| Star | Type | Signed | RMS | ||||
|---|---|---|---|---|---|---|---|
| Distance | Distance | ||||||
| HD 2454 | Dwarf Ba (s) | 0.83 | 0.90 | 1.38 | 1.56 | 4.47 | |
| HD 115444 | CEMP-r | 0.00 | 0.14 | 4.46 | 2.35 | 0.79 | |
| HE 2208-1239 | CEMP-r/s | 0.56 | 0.80 | 13.14 | 2.05 | 7.37 |
| Extrinsic Sample Proportion (%) | Extrinsic Sample Number (Total: 82 Stars) | Reference Sample Proportion (%) | Reference Sample Number (Total: 4161 Stars) | Golden Sample Proportion (%) | Golden Sample Number (Total: 28 Stars) | ||
|---|---|---|---|---|---|---|---|
| Variable radial velocity | Yes | 45.12 ± 5.49 | 37 ± 4.51 | 14.59 ± 0.55 | 607 ± 22.77 | 57.14 ± 9.35 | 16 ± 2.62 |
| No | 51.22 ± 5.52 | 42 ± 4.53 | 80.72 ± 0.61 | 3359 ± 25.45 | 39.29 ± 9.23 | 11 ± 2.58 | |
| Undetermined | 3.66 ± 0.23 | 3 ± 0.19 | 4.69 ± 0.33 | 195 ± 13.64 | 3.57 ± 0.68 | 1 ± 0.19 | |
| Gaia binarity flags | Non binary (NSS = 0) | 69.51 ± 5.08 | 57 ± 4.17 | 88.18 ± 0.50 | 3669 ± 20.83 | 46.43 ± 9.42 | 13 ± 2.64 |
| Astrometric binary (NSS = 1) | 10.98 ± 3.45 | 9 ± 2.83 | 3.58 ± 0.29 | 149 ± 11.98 | 17.86 ± 7.23 | 5 ± 2.02 | |
| Spectroscopic binary (NSS = 2) | 9.76 ± 3.28 | 8 ± 2.69 | 5.19 ± 0.34 | 216 ± 14.31 | 17.86 ± 7.23 | 5 ± 2.02 | |
| Astrometric and spectroscopic binary (NSS = 3) | 9.76 ± 3.28 | 8 ± 2.69 | 3.05 ± 0.27 | 127 ± 11.09 | 17.86 ± 7.23 | 5 ± 2.02 | |
| Re-normalized error | RUWE ≥ 1.4 | 41.46 ± 5.44 | 34 ± 4.46 | 16.46 ± 0.57 | 685 ± 23.92 | 50.00 ± 9.45 | 14 ± 2.65 |
| RUWE < 1.4 | 58.54 ± 5.44 | 48 ± 4.46 | 83.49 ± 0.58 | 3474 ± 23.95 | 50.00 ± 9.45 | 14 ± 2.65 | |
| Union of all binarity indicators | 52.44 ± 5.51 | 43 ± 4.52 | 21.68 ± 0.64 | 902 ± 26.58 | 62.50 ± 9.15 | 18 ± 2.56 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Eck, S.; Giribaldi, R.; Merle, T.; Lambotte, A.; Karinkuzhi, D.; Goriely, S.; Choplin, A.; Storm, N.; Gerber, J.; Siess, L.; et al. From the s-Process to the i-Process: A New Perspective on the Chemical Enrichment of Extrinsic Stars. Galaxies 2024, 12, 89. https://doi.org/10.3390/galaxies12060089
Van Eck S, Giribaldi R, Merle T, Lambotte A, Karinkuzhi D, Goriely S, Choplin A, Storm N, Gerber J, Siess L, et al. From the s-Process to the i-Process: A New Perspective on the Chemical Enrichment of Extrinsic Stars. Galaxies. 2024; 12(6):89. https://doi.org/10.3390/galaxies12060089
Chicago/Turabian StyleVan Eck, Sophie, Riano Giribaldi, Thibault Merle, Adrian Lambotte, Drisya Karinkuzhi, Stéphane Goriely, Arthur Choplin, Nicholas Storm, Jeffrey Gerber, Lionel Siess, and et al. 2024. "From the s-Process to the i-Process: A New Perspective on the Chemical Enrichment of Extrinsic Stars" Galaxies 12, no. 6: 89. https://doi.org/10.3390/galaxies12060089
APA StyleVan Eck, S., Giribaldi, R., Merle, T., Lambotte, A., Karinkuzhi, D., Goriely, S., Choplin, A., Storm, N., Gerber, J., Siess, L., Bergemann, M., & Jorissen, A. (2024). From the s-Process to the i-Process: A New Perspective on the Chemical Enrichment of Extrinsic Stars. Galaxies, 12(6), 89. https://doi.org/10.3390/galaxies12060089







