A Nested Inverted Pendulum as a Possible Pre-Isolator for the ET-LF Seismic Isolation System
Abstract
1. Introduction
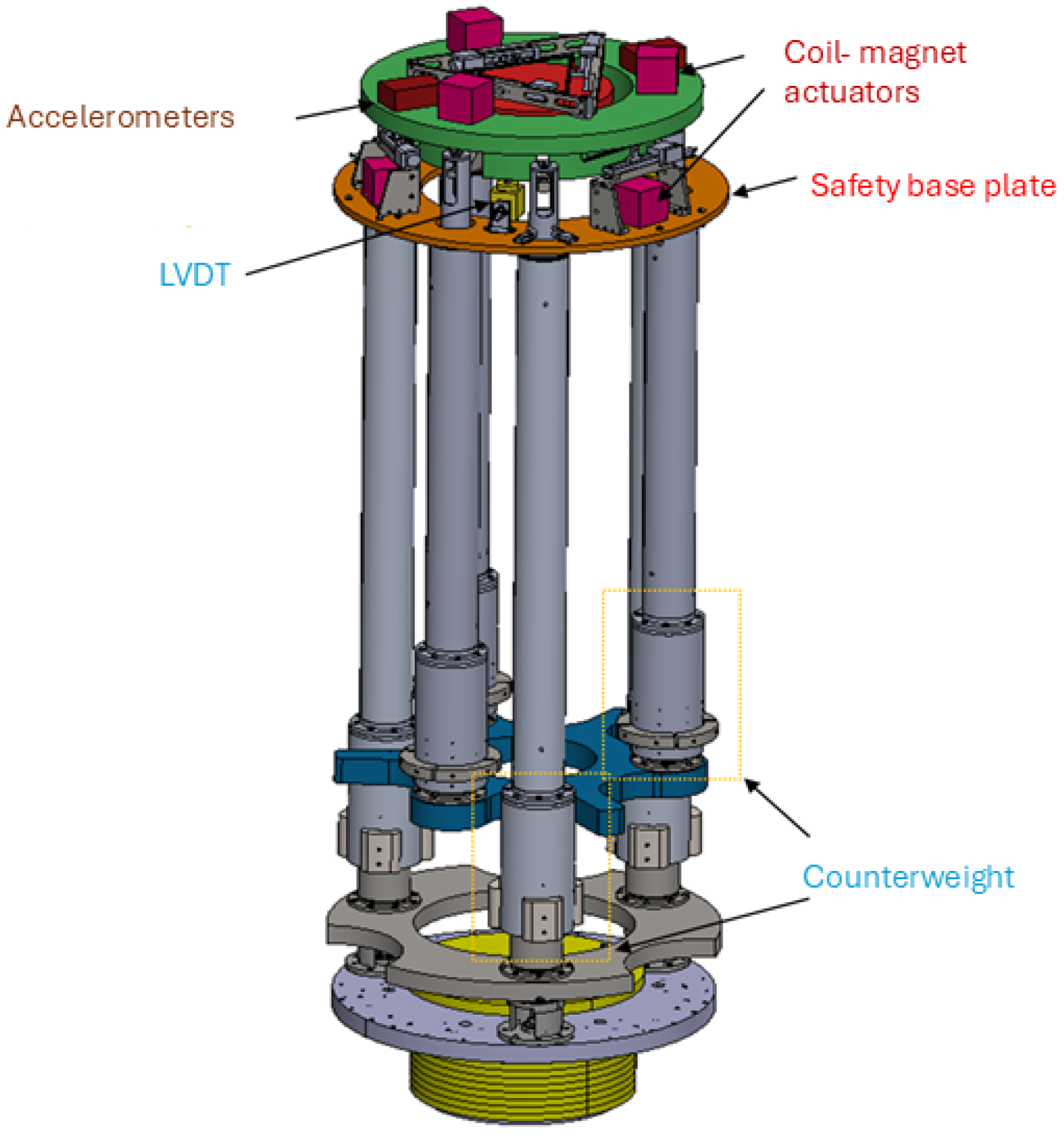
2. The NIP Prototype
Modeling an NIP Prototype
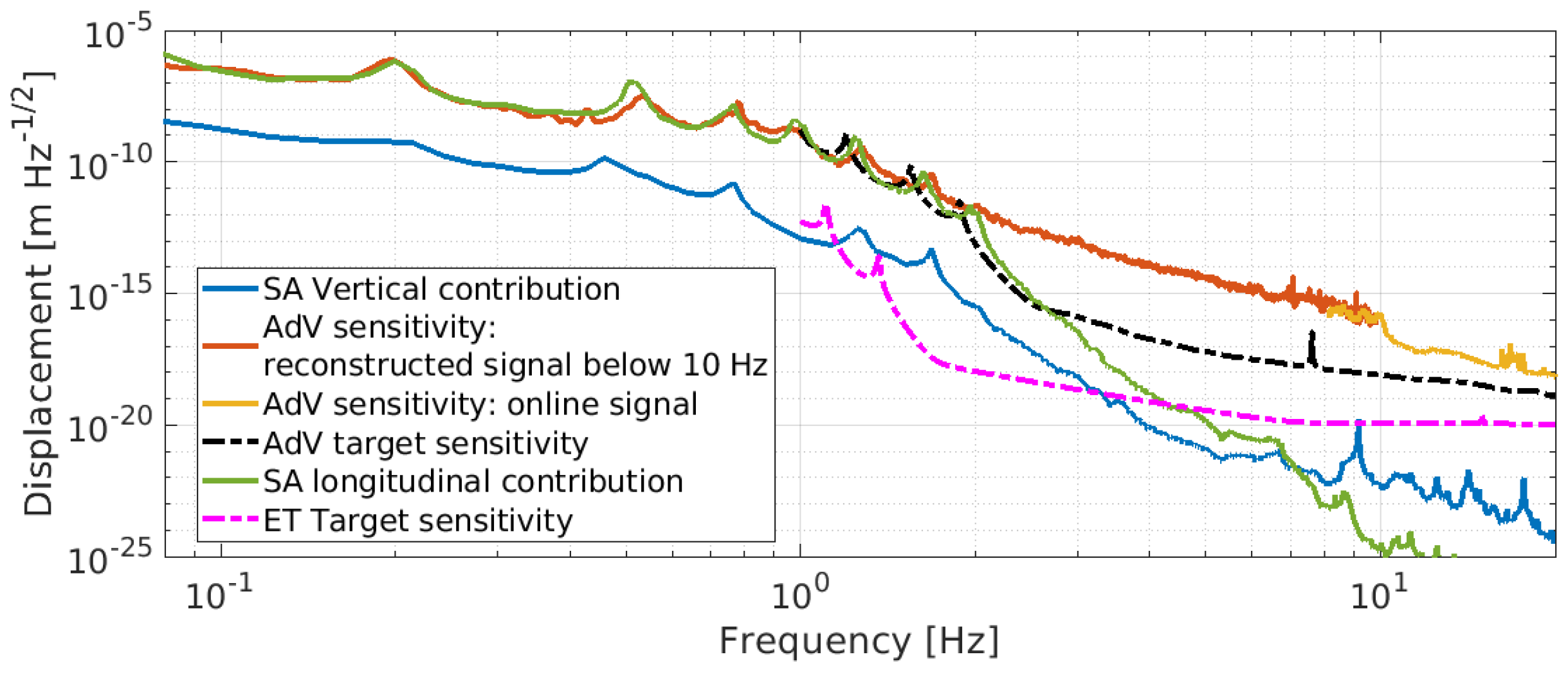
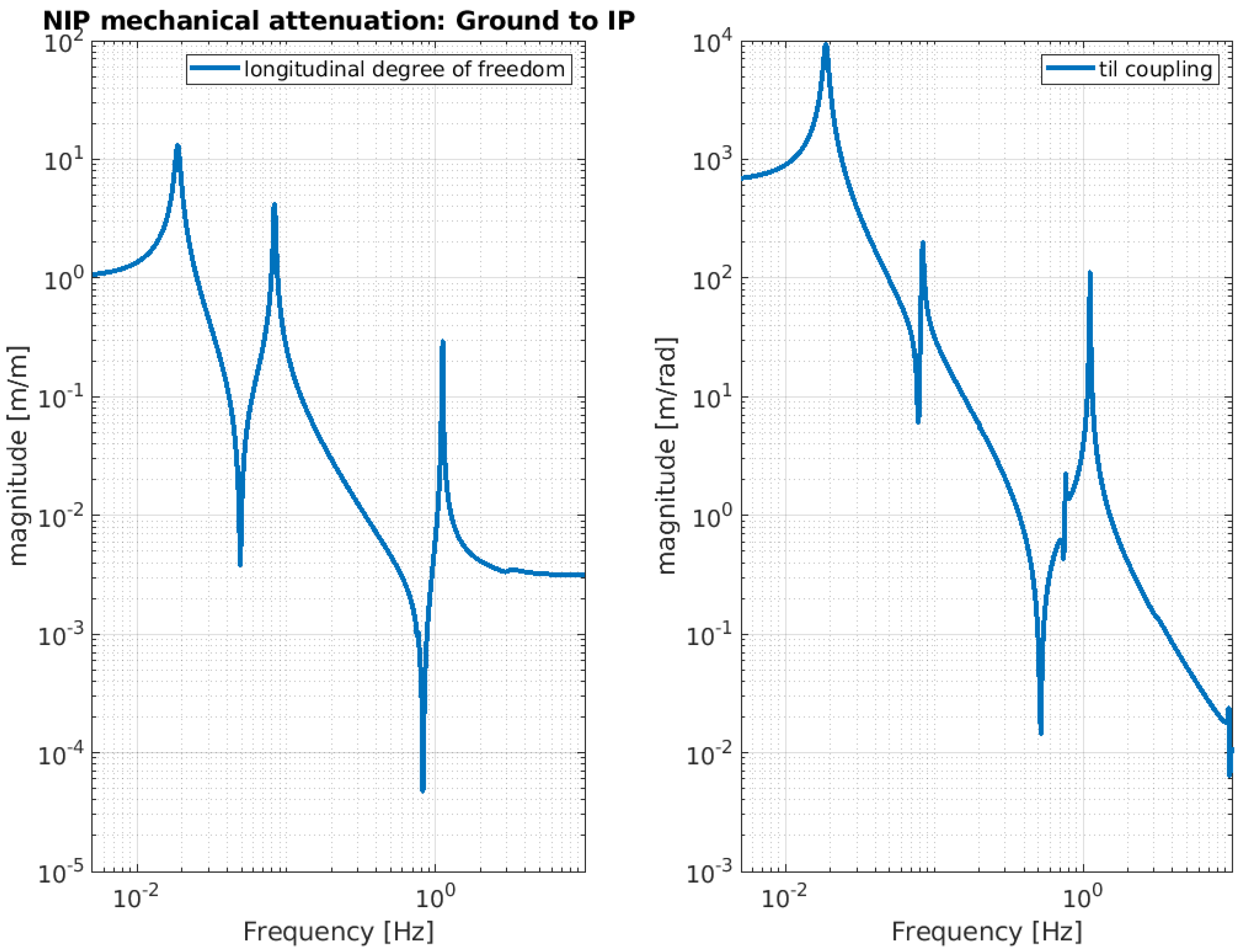
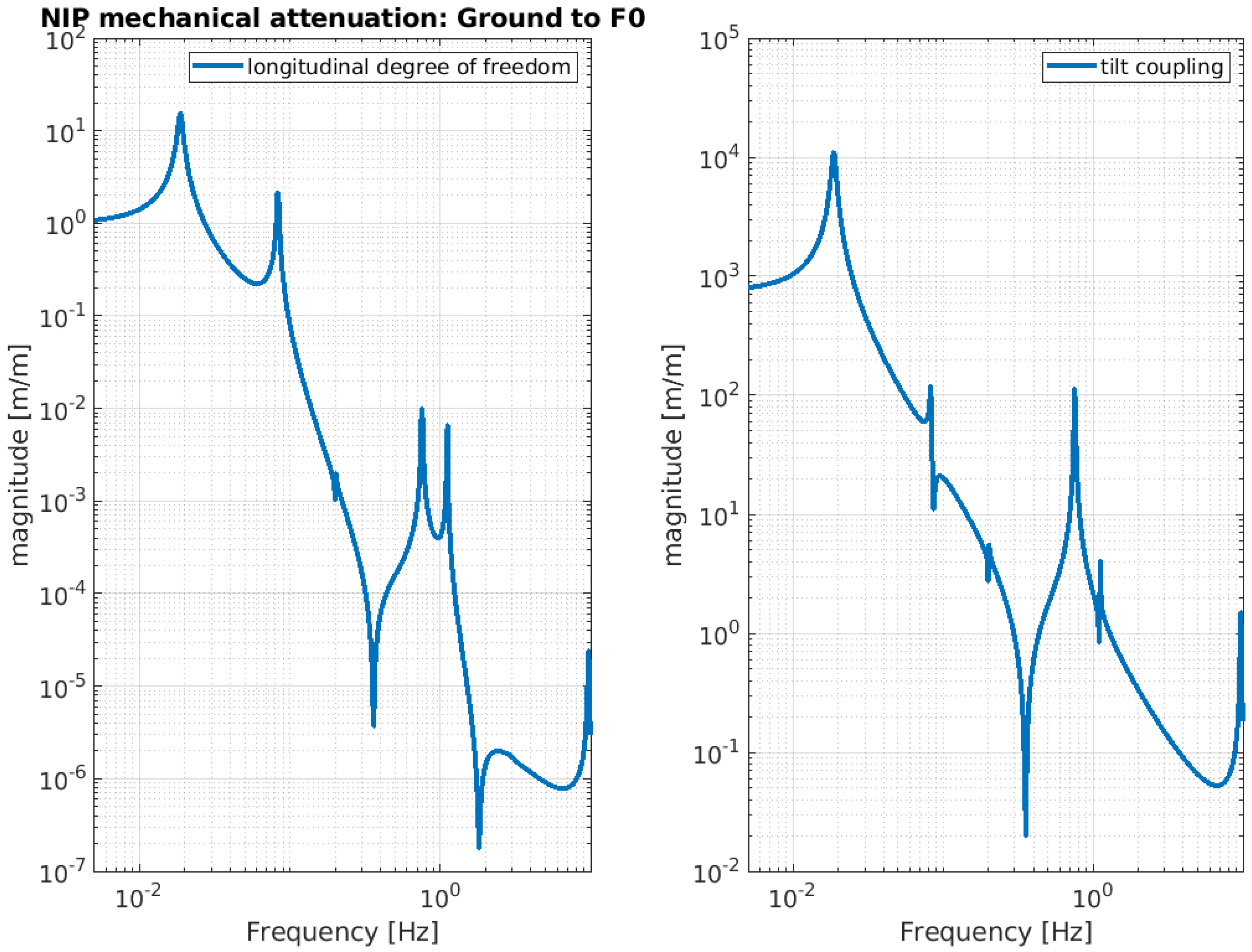
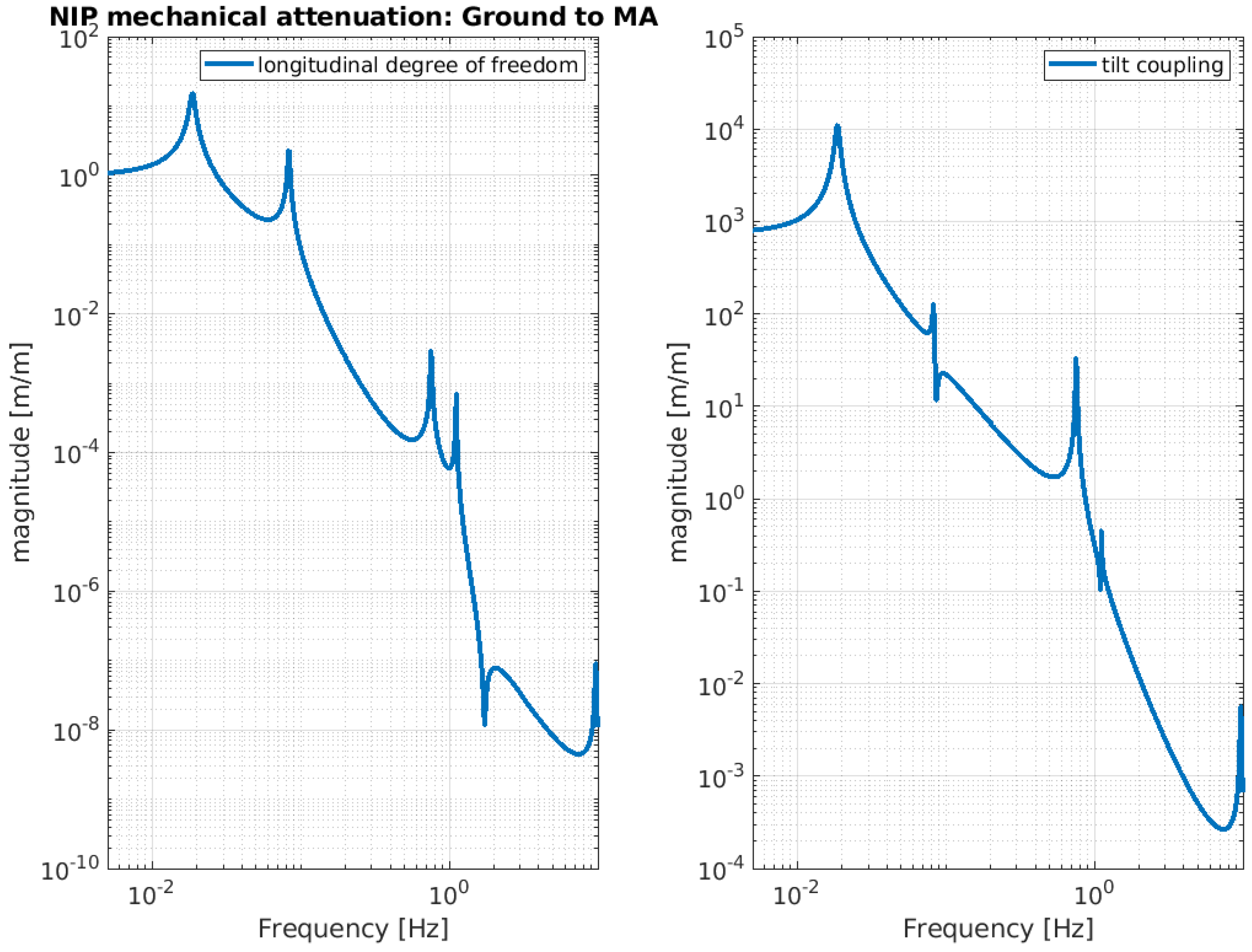
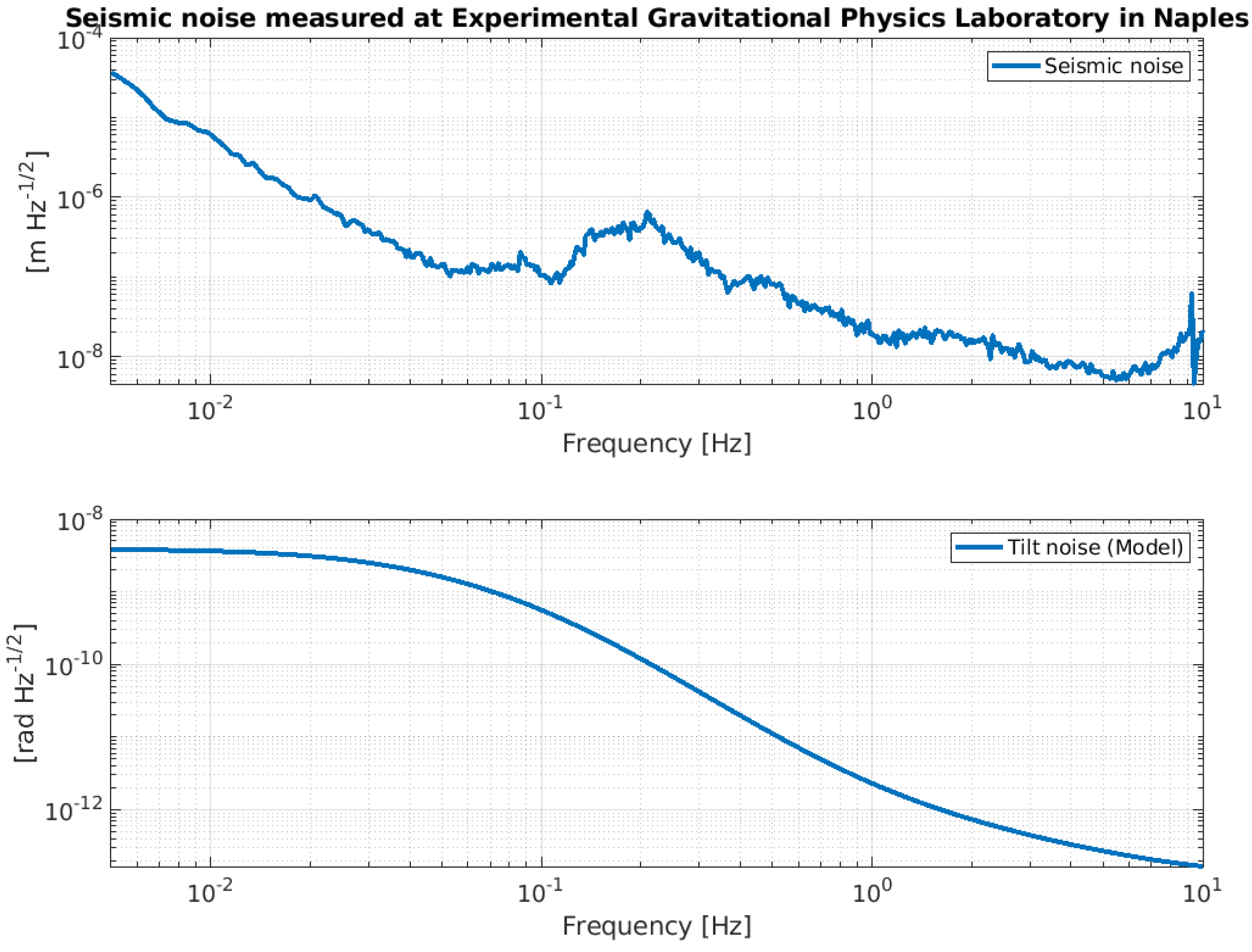
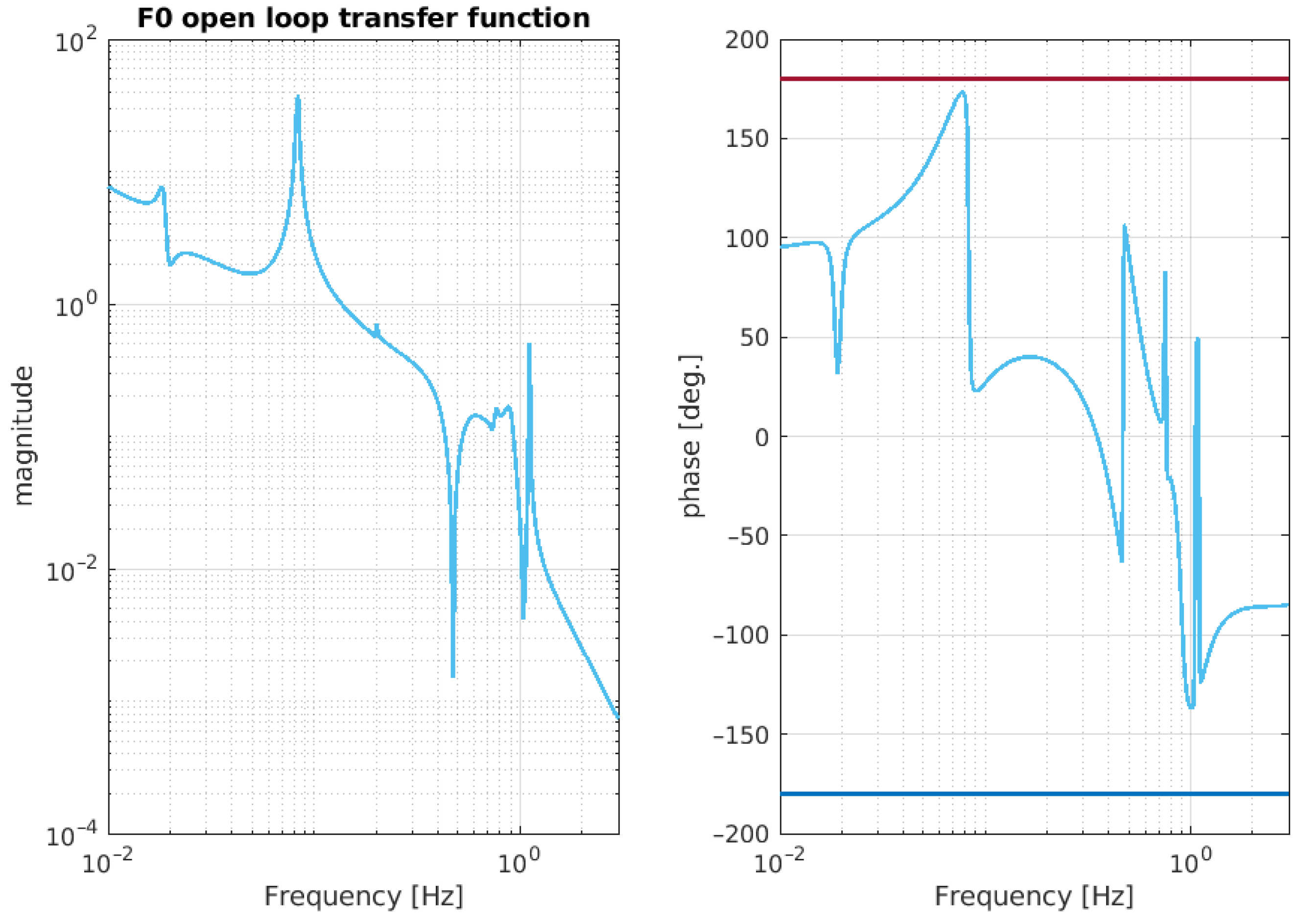
3. Expected Behavior of the NIP Prototype
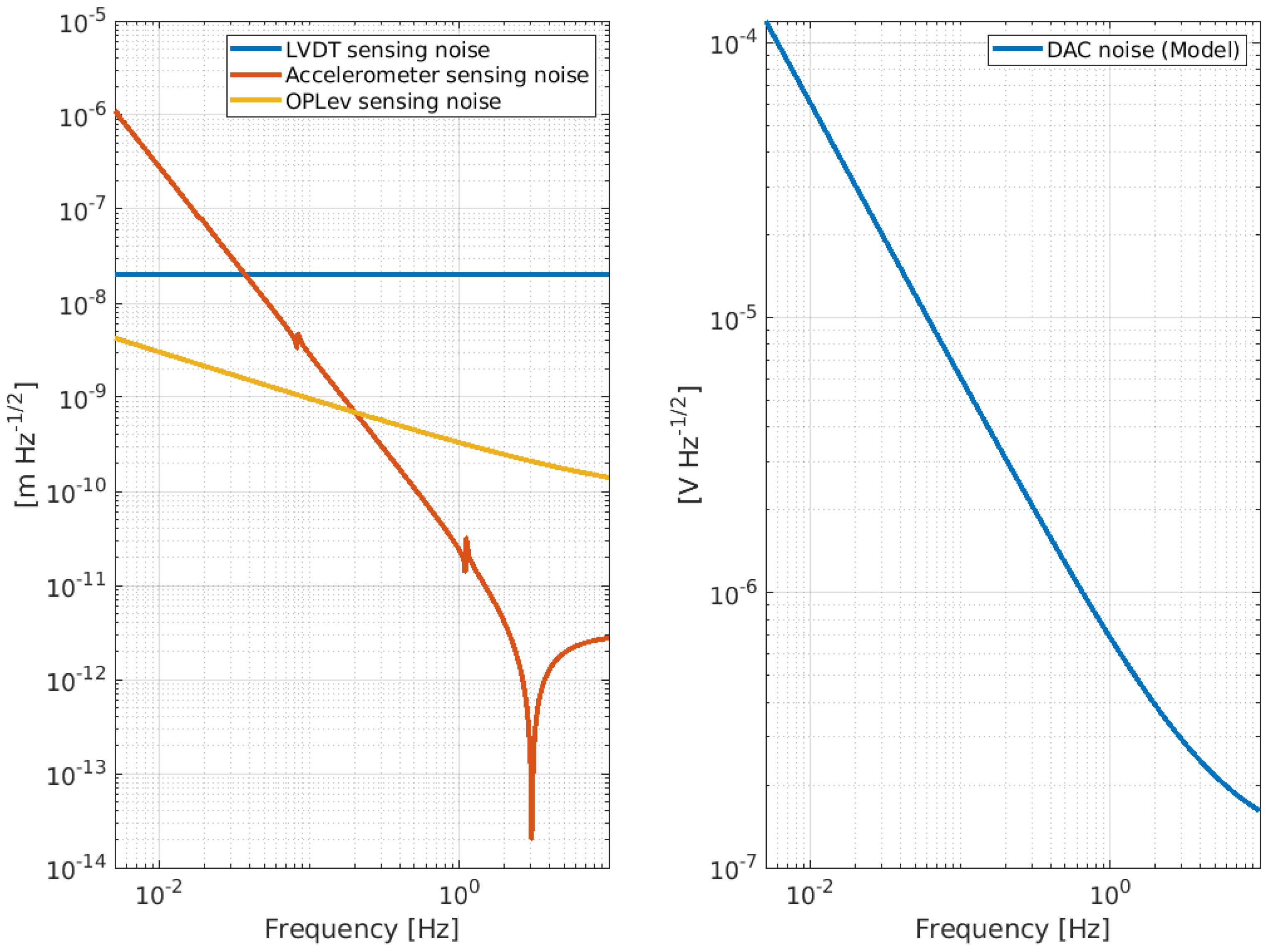
Noise Budget of the NIP
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASD | Amplitude spectral density |
| DAC | Digital-to-analog converter |
| ET | Einstein Telescope |
| IP | Inverted pendulum |
| LVDT | Linear variable displacement transducer |
| OpLev | Optical levers |
| NIP | Nested inverted pendulum |
| SA | Super-attenuator |
References
- Trozzo, L.; Badaracco, F. Seismic and Newtonian Noise in the GW Detectors. Galaxies 2022, 10, 20. [Google Scholar] [CrossRef]
- ET Steering Committee Editorial Team. Design Report Update 2020 for the Einstein Telescope. Available online: https://gwic.ligo.org/3Gsubcomm/docs/ET-0007B-20_ETDesignReportUpdate2020.pdf (accessed on 1 December 2024).
- Hild, S.; Abernathy, M.; Acernese, F.E.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Sensitivity studies for third generation gravitational waves observatories. Class. Quantum Gravity 2011, 28, 094013. [Google Scholar] [CrossRef]
- Update on Suspension Design for Advanced LIGO. 2012. Available online: https://dcc.ligo.org/public/0001/G0900367/002/G0900367v2.pdf (accessed on 1 December 2024).
- Matichard, F.; Lantz, B.; Mittleman, R.; Mason, K.; Kissel, J.; Abbott, B.; Biscans, S.; McIver, J.; Abbott, R.; Abbott, S.; et al. Seismic isolation of Advanced LIGO: Review of strategy, instrumentation and performance. Class. Quantum Gravity 2015, 32, 185003. [Google Scholar] [CrossRef]
- Robertson, N.A.; Cagnoli, G.; Crooks, D.R.M.; Elliffe, E.; Faller, J.E.; Fritschel, P.; Goßler, S.; Grant, A.; Heptonstall, A.; Hough, J.; et al. Quadruple suspension design for Advanced LIGO. Class. Quantum Gravity 2002, 19, 4043. [Google Scholar] [CrossRef]
- Driggers, J.C.; Evans, M.; Pepper, K.; Adhikari, R. Active noise cancellation in a suspended interferometer. Rev. Sci. Instrum. 2019, 83, 024501. [Google Scholar] [CrossRef] [PubMed]
- Driggers, J.C.; Vitale, S.; Lundgren, A.P.; Evans, M.; Kawabe, K.; Dwyer, S.E.; Izumi, K.; Schofield, R.M.; Effler, A.; Sigg, D.; et al. Improving astrophysical parameter estimation via offline noise subtraction for Advanced LIGO. Phys. Rev. D 2019, 99, 042001. [Google Scholar] [CrossRef]
- DeRosa, R.; Driggers, J.C.; Atkinson, D.; Miao, H.; Frolov, V.; Landry, M.; Giaime, J.A.; Adhikari, R.X. Global feed-forward vibration isolation in a km scale interferometer. Class. Quantum Gravity 2012, 29, 215008. [Google Scholar] [CrossRef]
- Giaime, J.A.; Daw, E.J.; Weitz, M.; Adhikari, R.; Fritschel, P.; Abbott, R.; Bork, R.; Heefner, J. Feedforward reduction of the microseism disturbance in a long-base-line interferometric gravitational-wave detector. Rev. Sci. Instrum. 2003, 74, 218–224. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Aso, Y.; Bae, S.; Bae, Y.; et al. Overview of KAGRA: Detector design and construction history. Prog. Theor. Exp. Phys. 2021, 74, 05A101. [Google Scholar] [CrossRef]
- Ballardin, G.; Bracci, L.; Braccini, S.; Bradaschia, C.; Casciano, C.; Calamai, G.; Cavalieri, R.; Cecchi, R.; Cella, G.; Cuoco, E.; et al. Measurement of the Virgo Superattenuator performance for seismic noise suppression. Rev. Sci. Instrum. 2001, 72, 3643–3652. [Google Scholar] [CrossRef]
- Acernese, F.; Antonucci, F.; Aoudia, S.; Arun, K.G.; Astone, P.; Ballardin, G.; Barone, F.; Barsuglia, M.; Bauer, T.S.; Beker, M.G.; et al. Measurements of Superattenuator seismic isolation by Virgo interferometer. Astropart. Phys. 2010, 33, 182–189. [Google Scholar] [CrossRef]
- Trozzo, L. Low Frequency Optimization and Performance of Advanced Virgo Seismic Isolation System. Ph.D. Thesis, Università di Siena, Siena, Italy, 2018. [Google Scholar]
- Bertocco, A.; Bruno, M.; De Rosa, R.; Di Fiore, L.; D’Urso, D.; Frasconi, F.; Gennai, A.; Lucchesi, L.; Refat, M.; Pilo, F.; et al. New Generation of Superattenuator for Einstein Telescope: Preliminary studies. Class. Quantum Gravity 2024, 41, 117004. [Google Scholar] [CrossRef]
- Ruggi, P.; Pinto, M.; Trozzo, L.; Cella, G.; Losurdo, G.; Chessa, P.; Longo, A.; Vicerè, A.; MAjorana, E. A mechanical simulation tool based on impedance matrices. Phys. Rev. D, submitted to PRD and under review.
- Bove, A.; Di Fiore, L.; Calloni, E.; Grado, A. Optimization of multi-pendular seismic suspensions for interferometric gravitational-wave detectors. Europhys. Lett. 1997, 40, 601–606. [Google Scholar] [CrossRef]
- De Rosa, R.; Di Fiore, L.; Garufi, F.; Grado, A.; La Rana, A.; Milano, L. An optical readout system for the drag free control of the LISA spacecraft. Astropart. Phys. 2011, 34, 394–400. [Google Scholar] [CrossRef]







| Transfer Function | Longitudinal [m/m] | Tilt Coupling [m/rad] |
|---|---|---|
| Ground to IP | ||
| Ground to F0 | ||
| Ground to MA |
| Frequency [Hz] | Q | Zero (Z) or Pole (P) |
| 0 | 0 | P |
| 0.02 | 0.5 | Z |
| 20 | 0 | P |
| 100 | 0.5 | P |
| Gain [N/m] | Frequency Gain [Hz] | Delay |
| 7666 | 1 | 0 |
| Frequency [Hz] | Q | Zero (Z) or Pole (P) |
| 0 | 0 | P |
| 0.07 | 1.1 | Z |
| 0.5 | 1.5 | P |
| 0.5 | 1.5 | P |
| 0.752 | 100 | Z |
| 0.9 | 10 | P |
| 1.1 | 2.5 | Z |
| Gain [N/m] | Frequency Gain [Hz] | Delay |
| 125 | 1 | 0 |
| Noise Source | Transfer Function: IP to MA | Transfer Function: F0 to MA | Branch |
|---|---|---|---|
| LVDT sensing | In: Force to IP Out: MA displacement | IP Control | |
| Accelerometer sensing | In: Force to IP Out: MA displacement | IP Control | |
| Oplev sensing | In: Force to F0 Out: MA displacement | ||
| DAC noise | In: Force to IP Out: MA displacement | In: Force to F0 Out: MA displacement | IP and F0 Control |
| Ground noise (z-z) | In: IP displacement Out: MA displacement | Ground | |
| Ground tilt (z-tx) | In: IP displacement (tx) Out: MA displacement (z) | Ground |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trozzo, L.; Bertocco, A.; Bruno, M.; De Rosa, R.; Di Fiore, L.; D’Urso, D.; Frasconi, F.; Gennai, A.; Lucchesi, L.; Nacca, M.; et al. A Nested Inverted Pendulum as a Possible Pre-Isolator for the ET-LF Seismic Isolation System. Galaxies 2025, 13, 21. https://doi.org/10.3390/galaxies13020021
Trozzo L, Bertocco A, Bruno M, De Rosa R, Di Fiore L, D’Urso D, Frasconi F, Gennai A, Lucchesi L, Nacca M, et al. A Nested Inverted Pendulum as a Possible Pre-Isolator for the ET-LF Seismic Isolation System. Galaxies. 2025; 13(2):21. https://doi.org/10.3390/galaxies13020021
Chicago/Turabian StyleTrozzo, Lucia, Alcide Bertocco, Matteo Bruno, Rosario De Rosa, Luciano Di Fiore, Domenico D’Urso, Franco Frasconi, Alberto Gennai, Leonardo Lucchesi, Moreno Nacca, and et al. 2025. "A Nested Inverted Pendulum as a Possible Pre-Isolator for the ET-LF Seismic Isolation System" Galaxies 13, no. 2: 21. https://doi.org/10.3390/galaxies13020021
APA StyleTrozzo, L., Bertocco, A., Bruno, M., De Rosa, R., Di Fiore, L., D’Urso, D., Frasconi, F., Gennai, A., Lucchesi, L., Nacca, M., Pilo, F., Prosperi, P., Rozza, D., Ruggi, P., Sipala, V., & Spada, F. (2025). A Nested Inverted Pendulum as a Possible Pre-Isolator for the ET-LF Seismic Isolation System. Galaxies, 13(2), 21. https://doi.org/10.3390/galaxies13020021







