HR 4049: A Spectroscopic Analysis of a Post-AGB Object
Abstract
:1. Introduction
2. Observations and Data Reduction
3. Methods
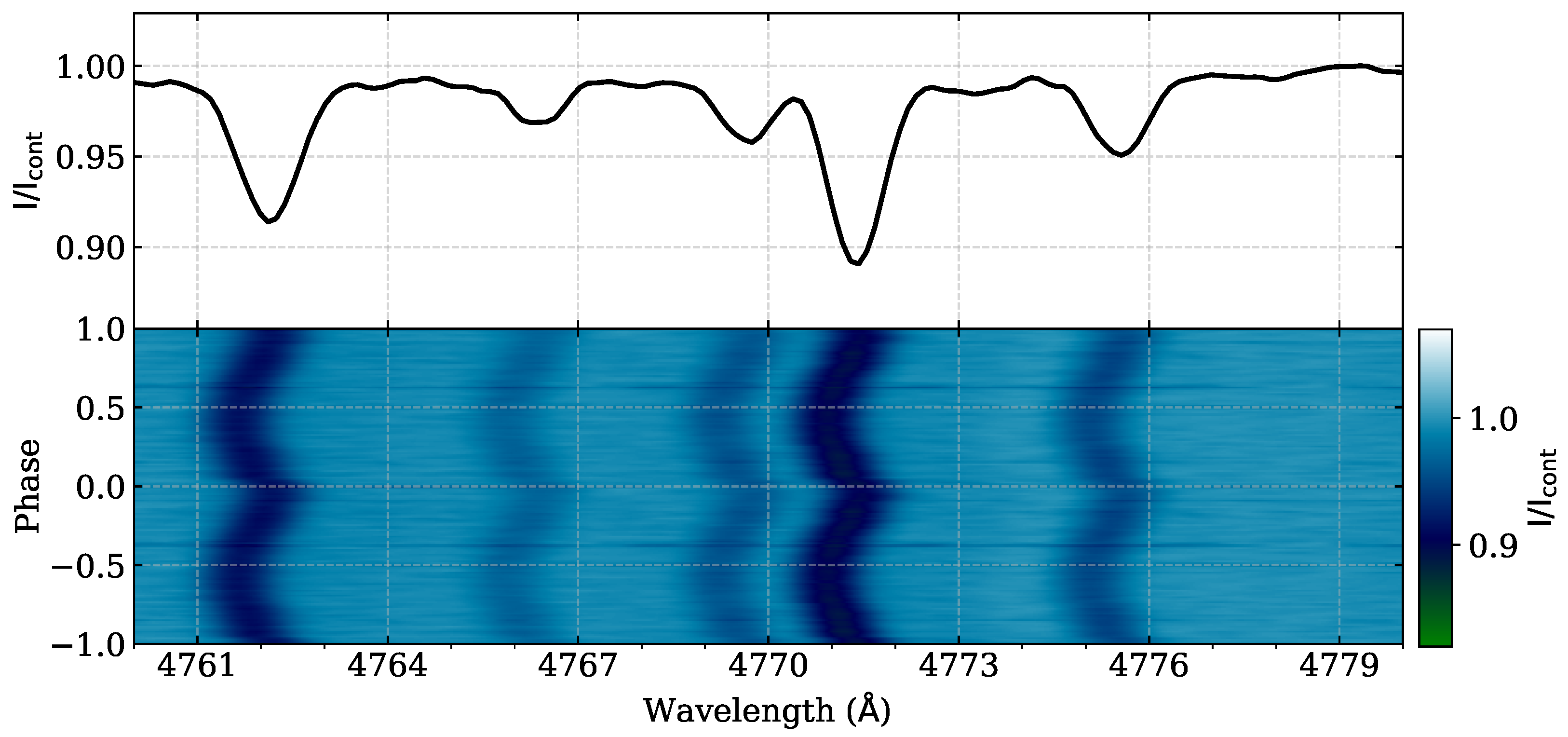
3.1. Cross-Correlation
3.2. Orbital Parameters
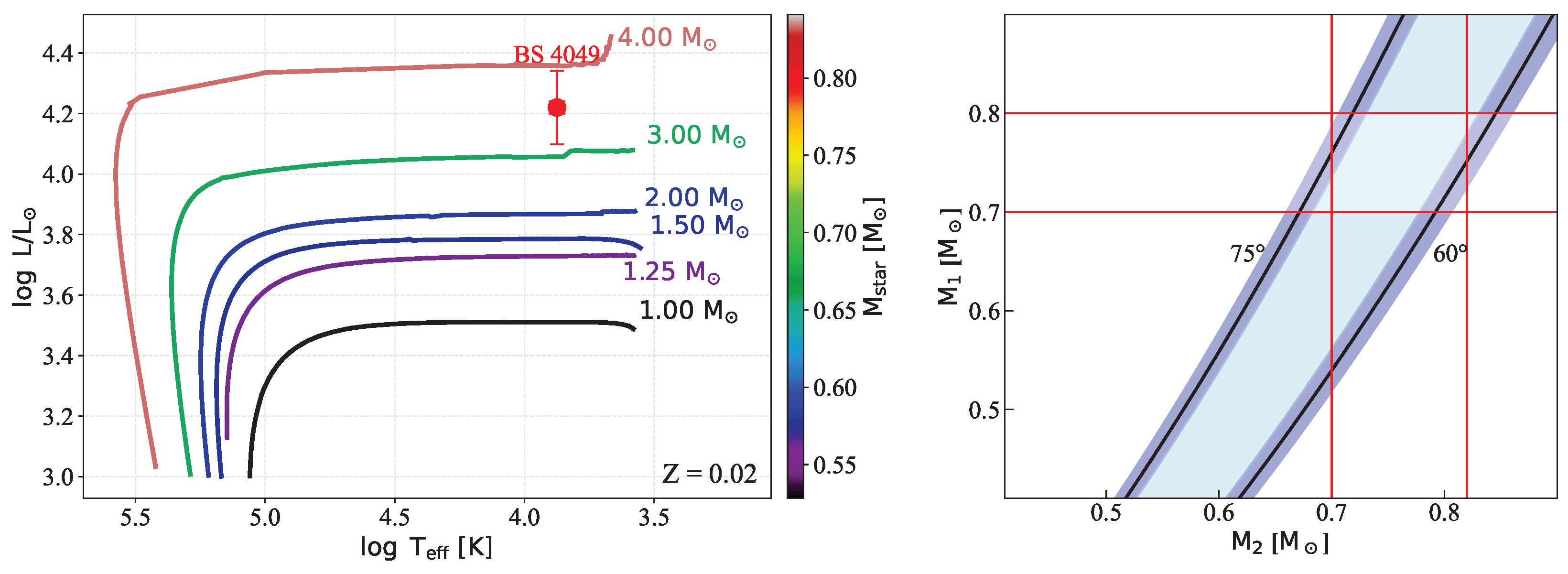
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RV | radial velocity |
| R | spectral resolving power |
| TCO | Three College Observatory |
| SED | spectral energy distribution |
| IRAF | Image Reduction and Analysis Facility |
| 1 | Shelyak Instruments: https://www.shelyak.com (accessed on 18 February 2025). |
| 2 | Research Center “Data Science in Astrophysics”: https://astro.kaznu.info/Computingcluster.html (accessed on 18 February 2025). |
References
- Miller Bertolami, M.M. New models for the evolution of post-asymptotic giant branch stars and central stars of planetary nebulae. Astron. Astrophys. 2016, 588, A25. [Google Scholar] [CrossRef]
- Bakker, E.J.; Lambert, D.L.; Van Winckel, H.; McCarthy, J.K.; Waelkens, C.; Gonzalez, G. Spectral variability of the binary HR 4049. Astron. Astrophys. 1998, 336, 263–275. [Google Scholar] [CrossRef]
- Van Winckel, H.; Waelkens, C.; Waters, L.B.F.M. The extremely iron-deficient “Post-AGB” stars and binaries. Astron. Astrophys. 1995, 293, L25–L28. Available online: https://ui.adsabs.harvard.edu/abs/1995A&A...293L..25V (accessed on 18 February 2025).
- Acke, B.; Degroote, P.; Lombaert, R.; de Vries, B.L.; Smolders, K.; Verhoelst, T.; Lagadec, E.; Gielen, C.; Van Winckel, H.; Waelkens, C. Amorphous carbon in the disk around the post-AGB binary HR 4049. Discerning dust species with featureless opacity curves. Astron. Astrophys. 2013, 551, A76. [Google Scholar] [CrossRef]
- Malek, S.E.; Cami, J. The Gas-rich Circumbinary Disk of HR 4049. II. A Detailed Study of the Near-infrared Spectrum. Astrophys. J. 2014, 794, 113. [Google Scholar] [CrossRef]
- Andrych, K.; Kamath, D.; Kluska, J.; Van Winckel, H.; Ertel, S.; Corporaal, A. Second-generation protoplanetary discs around evolved binaries: A high-resolution polarimetric view with SPHERE/IRDIS. Mon. Not. R. Astron. Soc. 2023, 524, 4168. [Google Scholar] [CrossRef]
- Gorlova, N.; Van Winckel, H.; Gielen, C.; Raskin, G.; Prins, S.; Pessemier, W.; Waelkens, C.; Frémat, Y.; Hensberge, H.; Dumortier, L.; et al. Time-resolved spectroscopy of BD + 46°442: Gas streams and jet creation in a newly discovered evolved binary with a disk. Astron. Astrophys. 2012, 542, A27. [Google Scholar] [CrossRef]
- Oomen, G.M.; Van Winckel, H.; Pols, O.; Nelemans, G. Modelling depletion by re-accretion of gas from a dusty disc in post-AGB stars. Astron. Astrophys. 2019, 629, A49. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Chari, R.; Danford, S.; Prendergast, P.; Aarnio, A.N.; Andronov, I.L.; Chinarova, L.L.; Lytle, A.; Amantayeva, A.; Gabitova, I.A.; et al. Searching for Phase-Locked Variations of the Emission-Line Profiles in Binary Be Stars. Galaxies 2023, 11, 83. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Zharikov, S.V.; Manset, N.; Khokhlov, S.A.; Nodyarov, A.S.; Klochkova, V.G.; Danford, S.; Kuratova, A.K.; Mennickent, R.; Chojnowski, S.D.; et al. Recent Progress in Finding Binary Systems with the B[e] Phenomenon. Galaxies 2023, 11, 36. [Google Scholar] [CrossRef]
- Mink, J.D.; Kurtz, M. RVSAO 2.0: Digital Redshifts and Radial Velocities. Publ. Astron. Soc. Pac. 1998, 110, 934. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in Astronomical Time Series Analysis. II. Statistical Aspects of Spectral Analysis of Unevenly Spaced Data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- VanderPlas, J.T. Understanding the Lomb–Scargle Periodogram. Astrophys. J. Suppl. Ser. 2018, 236, 16. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Oomen, G.M.; Van Winckel, H.; Pols, O.; Nelemans, G.; Escorza, A.; Manick, R.; Kamath, D.; Waelkens, C. Orbital properties of binary post-AGB stars. Astron. Astrophys. 2018, 620, A85. [Google Scholar] [CrossRef]
- Trams, N.R.; Waters, L.B.F.M.; Waelkens, C.; Lamers, H.J.G.L.M.; van der Veen, W.E.C.J. The effect of mass loss on the evolution of low-mass post-AGB stars. Astron. Astrophys. 1989, 218, L1–L4. Available online: https://ui.adsabs.harvard.edu/abs/1989A&A...218L...1T (accessed on 18 February 2025).
- Waelkens, C.; Lamers, H.J.G.L.M.; Waters, L.B.F.M.; Rufener, F.; Trams, N.R.; Le Bertre, T.; Ferlet, R.; Vidal-Madjar, A. Variability of the post-AGB star HR 4049: Dust obscuration in a binary system. Astron. Astrophys. 1991, 242, 433. Available online: https://ui.adsabs.harvard.edu/abs/1991A&A...242..433W (accessed on 18 February 2025).
- Vickers, S.B.; Frew, D.J.; Parker, Q.A.; Bojičić, I.S. New light on Galactic post-asymptotic giant branch stars—I: First distance catalogue. MNRAS 2015, 447, 1673–1691. [Google Scholar] [CrossRef]
- Oudmaijer, R.D.; Jones, E.R.M.; Vioque, M. A census of post-AGB stars in Gaia DR3: Evidence for a substantial population of Galactic post-RGB stars. MNRAS 2022, 516, L61–L65. [Google Scholar] [CrossRef]
- Rufener, F.; Bartholdi, P. List of 333 variable microvariable or suspected variable stars detected in the Geneva photometry. Astron. Astrophys. 1982, 48, 503–511. Available online: https://ui.adsabs.harvard.edu/abs/1982A&AS...48..503R (accessed on 18 February 2025).
- Lake, R. Photoelectric magnitudes and colours for bright southern stars (sixth list). Mon. Notes Astron. Soc. South. Afr. (MNASSA) 1965, 24, 41. Available online: https://journals.co.za/doi/pdf/10.10520/AJA00248266_953 (accessed on 18 February 2025).
- Monier, R.; Parthasarathy, M. The ultraviolet variations of the post-AGB star HD 89353. Astron. Astrophys. 1999, 341, 117–120. Available online: https://ui.adsabs.harvard.edu/abs/1999A&A...341..117M (accessed on 18 February 2025).
- Green, G.M.; Schlafly, E.F.; Zucker, C.; Speagle, J.S.; Finkbeiner, D.P. A 3D Dust Map Based on Gaia, Pan-STARRS 1 and 2MASS. Astrophys. J. 2019, 887, 93. [Google Scholar] [CrossRef]
- Bailer-Jones, C.A.L.; Rybizki, J.; Fouesneau, M.; Demleitner, M.; Andrae, R. Estimating Distances from Parallaxes. V. Geometric and Photogeometric Distances to 1.47 Billion Stars in Gaia Early Data Release 3. Astron. J. 2021, 161, 147. [Google Scholar] [CrossRef]
- Pecaut, M.J.; Mamajek, E.E. Intrinsic Colors, Temperatures, and Bolometric Corrections of Pre-Main-Sequence Stars. Astrophys. J. Suppl. Ser. 2013, 208, 9. [Google Scholar] [CrossRef]
- Schoenberner, D. Late stages of stellar evolution. II—Mass loss and the transition of asymptotic giant branch stars into hot remnants. Astrophys. J. 1983, 272, 708–714. Available online: https://ui.adsabs.harvard.edu/abs/1983ApJ...272..708S (accessed on 18 February 2025). [CrossRef]
- Blöcker, T. Stellar evolution of low- and intermediate-mass stars. II. Post-AGB evolution. Astron. Astrophys. 1995, 299, 755. Available online: https://ui.adsabs.harvard.edu/abs/1995A&A...299..755B (accessed on 18 February 2025).
- Van Winckel, H. Post-AGB Stars. Annu. Rev. Astron. Astrophys. 2003, 41, 391–427. [Google Scholar] [CrossRef]
- Dominik, C.; Dullemond, C.P.; Cami, J.; van Winckel, H. The dust disk of HR 4049. Another brick in the wall. Astron. Astrophys. 2003, 397, 595–609. [Google Scholar] [CrossRef]
- Bollen, D.; Van Winckel, H.; Kamath, D. Jet creation in post-AGB binaries: The circum-companion accretion disk around BD + 46°442. Astron. Astrophys. 2017, 607, A60. [Google Scholar] [CrossRef]


| HJD | RV | Error | HJD | RV | Error | HJD | RV | Error |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 8562.6602 | −4.3 | 0.6 | 9249.7985 | −18.1 | 0.7 | 9959.8392 | −18.9 | 0.7 |
| 8566.6351 | −4.6 | 0.7 | 9251.7624 | −17.0 | 0.4 | 9979.8027 | −22.0 | 0.4 |
| 8590.5823 | −7.7 | 0.4 | 9253.7630 | −16.0 | 0.5 | 9989.7342 | −23.6 | 0.6 |
| 8902.7197 | 0.2 | 0.5 | 9262.7311 | −12.4 | 0.7 | 9994.7277 | −23.8 | 0.6 |
| 8907.7189 | 0.9 | 0.6 | 9265.7342 | −11.6 | 0.7 | 10,027.6705 | −28.1 | 0.6 |
| 8916.6736 | 0.1 | 0.8 | 9270.7083 | −9.6 | 0.5 | 10,031.6577 | −29.7 | 0.5 |
| 8934.6116 | −0.2 | 0.6 | 9277.7172 | −7.2 | 0.6 | 10,037.6349 | −29.3 | 0.6 |
| 8942.5858 | −2.4 | 0.6 | 9280.7031 | −6.7 | 1.1 | 10,039.6059 | −30.2 | 0.5 |
| 9189.9058 | −31.8 | 1.3 | 9282.7137 | −6.7 | 0.6 | 10,048.5852 | −31.0 | 0.6 |
| 9191.9035 | −31.3 | 0.5 | 9284.7008 | −5.5 | 0.9 | 10,323.8246 | −10.4 | 0.6 |
| 9193.8931 | −31.5 | 0.5 | 9295.6691 | −4.6 | 0.4 | 10,326.8121 | −10.5 | 0.8 |
| 9194.9040 | −31.1 | 0.7 | 9298.6341 | −4.0 | 0.6 | 10,341.8154 | −13.5 | 0.5 |
| 9202.8910 | −30.9 | 0.9 | 9303.6276 | −3.2 | 0.9 | 10,347.7567 | −13.9 | 1.3 |
| 9206.8769 | −30.8 | 0.6 | 9308.6002 | −2.6 | 0.5 | 10,354.7510 | −13.9 | 0.5 |
| 9210.8649 | −29.9 | 0.6 | 9317.5736 | 0.1 | 0.5 | 10,361.7125 | −14.5 | 0.5 |
| 9219.8376 | −29.4 | 0.5 | 9587.8278 | −27.8 | 0.4 | 10,381.7052 | −18.2 | 0.7 |
| 9221.8288 | −29.3 | 0.5 | 9606.8234 | −29.5 | 0.5 | 10,390.6720 | −19.9 | 0.9 |
| 9227.8067 | −27.2 | 0.5 | 9609.7550 | −30.5 | 0.4 | 10,398.6533 | −20.3 | 0.6 |
| 9229.8317 | −25.3 | 0.5 | 9619.7540 | −32.0 | 0.5 | 10,401.6297 | −21.2 | 0.5 |
| 9231.8307 | −25.1 | 0.4 | 9625.7243 | −30.2 | 0.6 | 10,723.7618 | −6.5 | 0.5 |
| 9232.8106 | −25.2 | 0.6 | 9639.7301 | −29.7 | 0.6 | 10,727.7388 | −7.7 | 0.5 |
| 9233.7879 | −23.9 | 0.7 | 9709.5371 | −8.3 | 0.6 | 10,731.7746 | −9.5 | 0.6 |
| 9234.8066 | −23.0 | 0.7 | 9939.8485 | −16.2 | 1.1 | 10,737.7341 | −10.1 | 0.6 |
| 9238.8181 | −21.8 | 0.6 | 9943.8899 | −16.7 | 0.3 | |||
| 9243.7729 | −20.2 | 0.4 | 9952.8155 | −17.8 | 0.8 |
| Parameter | [2] | [15] | Our Data |
|---|---|---|---|
| P (days) | |||
| (HJD) | 2,446,746.6 ± 2.4 | 2,447,176.6 ± 3.8 | 2,458,383.2 ± 0.6 |
| e | |||
| (degrees) | |||
| (km s−1) | −30.12 ± 0.09 * | ||
| (km s−1) | |||
| , M⊙ | |||
| N | 60 | 86 | 73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nurmakhametova, S.T.; Vaidman, N.L.; Miroshnichenko, A.S.; Khokhlov, A.A.; Agishev, A.T.; Yermekbayev, B.S.; Danford, S.; Aarnio, A.N. HR 4049: A Spectroscopic Analysis of a Post-AGB Object. Galaxies 2025, 13, 26. https://doi.org/10.3390/galaxies13020026
Nurmakhametova ST, Vaidman NL, Miroshnichenko AS, Khokhlov AA, Agishev AT, Yermekbayev BS, Danford S, Aarnio AN. HR 4049: A Spectroscopic Analysis of a Post-AGB Object. Galaxies. 2025; 13(2):26. https://doi.org/10.3390/galaxies13020026
Chicago/Turabian StyleNurmakhametova, Shakhida T., Nadezhda L. Vaidman, Anatoly S. Miroshnichenko, Azamat A. Khokhlov, Aldiyar T. Agishev, Berik S. Yermekbayev, Stephen Danford, and Alicia N. Aarnio. 2025. "HR 4049: A Spectroscopic Analysis of a Post-AGB Object" Galaxies 13, no. 2: 26. https://doi.org/10.3390/galaxies13020026
APA StyleNurmakhametova, S. T., Vaidman, N. L., Miroshnichenko, A. S., Khokhlov, A. A., Agishev, A. T., Yermekbayev, B. S., Danford, S., & Aarnio, A. N. (2025). HR 4049: A Spectroscopic Analysis of a Post-AGB Object. Galaxies, 13(2), 26. https://doi.org/10.3390/galaxies13020026







