Magnetic Fields and Halos in Spiral Galaxies
Abstract
:1. Introduction
2. Faraday Rotation and Depolarization Effects
3. Magnetic Field Strength and Star Formation
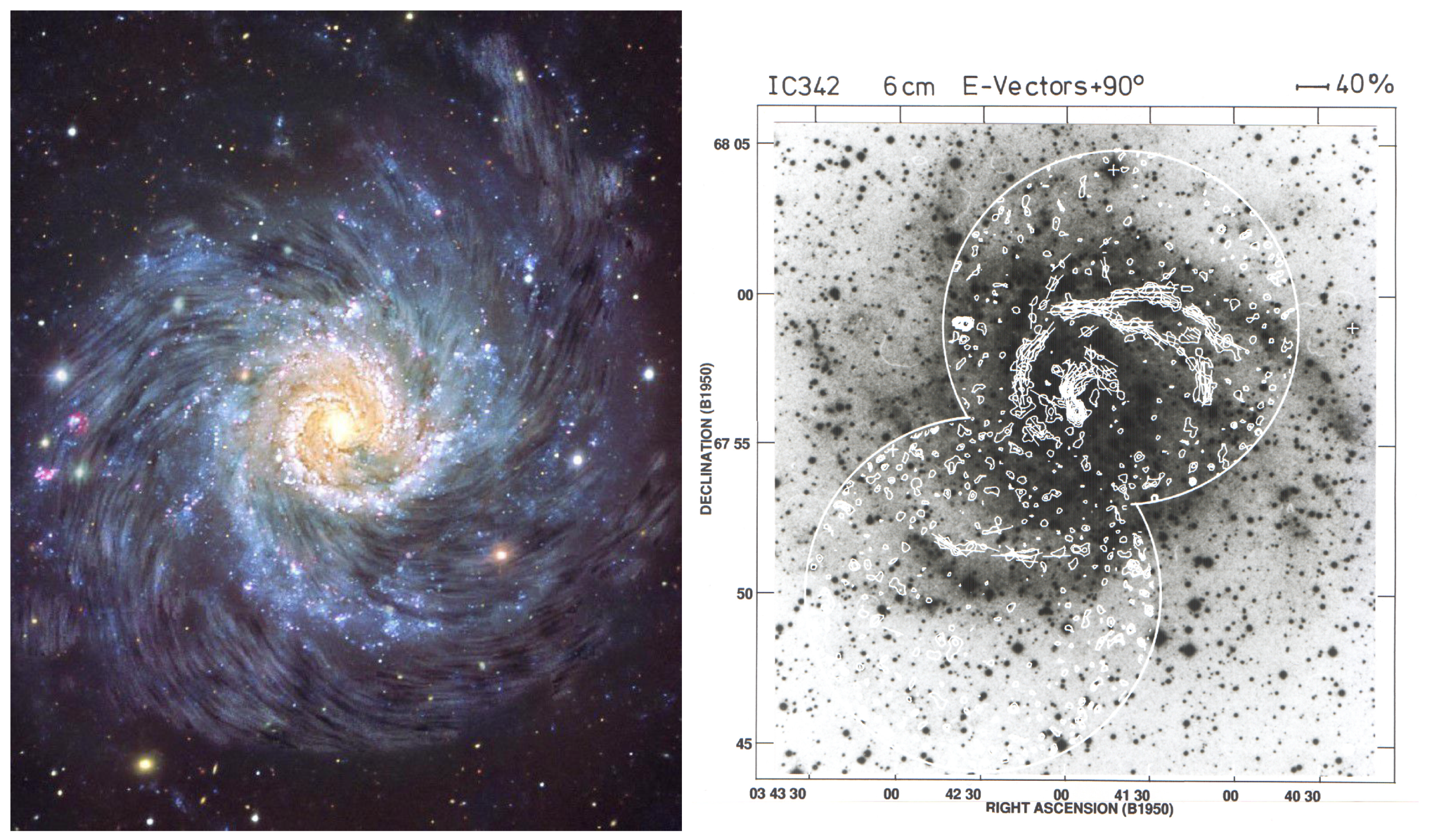
4. Magnetic Field Structure in Spiral Galaxies
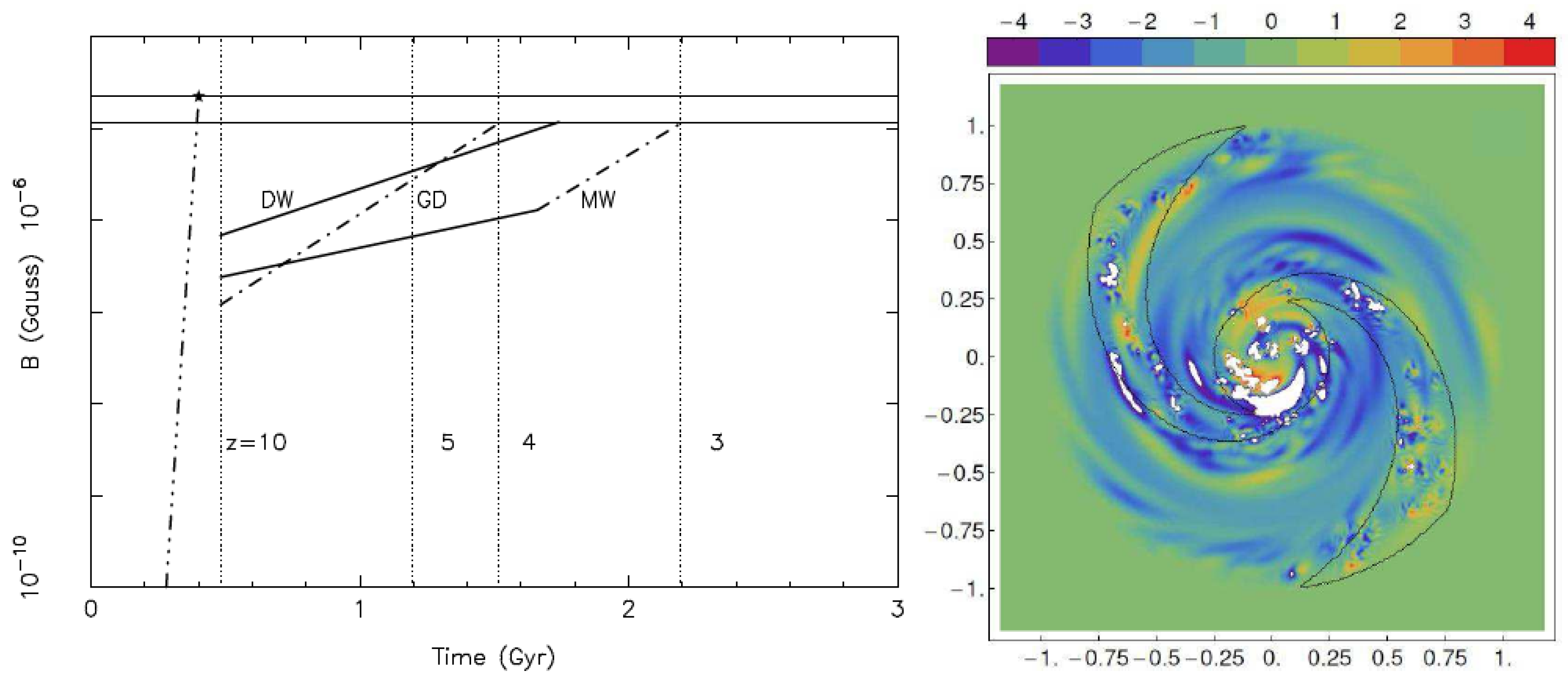
5. Dynamo Action and the Evolution of the Large-Scale Magnetic Field
6. Vertical Scale Heights and Galactic Wind
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Avillez, M.A.; Breitschwerdt, D. Global Dynamical Evolution of the ISM in Star Forming Galaxies. I. High Resolution 3D Simulations: Effect of the magnetic Field. Astron. Astrophys. 2019, 436, 585–600. [Google Scholar] [CrossRef]
- Korpi, M.J.; Brandenburg, A.; Shukurov, A.; Tuominen, I.; Nordlund, A. A Supernova-regulated Interstellar Medium: Simulations of the turbulent multiphase Medium. Astrophys. J. 1999, 514, L99–L102. [Google Scholar] [CrossRef]
- Pakmor, R.; Springel, V. Simulations of Magnetic Fields in isolated Disc Galaxies. Mon. Not. R. Astron. Soc. 2013, 432, 176–193. [Google Scholar] [CrossRef]
- Beck, R. Magnetism in the Spiral Galaxy NGC 6946: Magnetic Arms, depolarization Rings, dynamo Modes, and helical Fields. Astron. Astrophys. 2007, 470, 539–556. [Google Scholar] [CrossRef]
- Tabatabaei, F.S.; Krause, M.; Fletcher, A.; Beck, R. High-resolution radio continuum Survey of M 33. III. Magnetic Fields. Astron. Astrophys. 2008, 490, 1005–1017. [Google Scholar] [CrossRef]
- Marinacci, F.; Vogelsberger, M.; Pakmor, V.; Torrey, P.; Springel, V.; Hernquist, L.; Nelson, D.; Weinerger, R.; Pillepich, A.; Naiman, J.; et al. First Results from the IllustrisTNG Simulations: Radio Haloes and magnetic Fields. Mon. Not. R. Astron. Soc. 2018, 480, 5113–5139. [Google Scholar] [CrossRef]
- Grand, R.J.J.; Gómez, F.A.; Marinacci, F.; Pakmor, R.; Springel, V.; Campbell, D.J.R.; Frenk, C.S.; Jenkins, A.; White, S.D.M. The Auriga Project: The Properties and Formation Mechanisms of Disc Galaxies across cosmic Time. Mon. Not. R. Astron. Soc. 2017, 467, 179–207. [Google Scholar] [CrossRef]
- Pakmor, R.; Gómez, F.A.; Grand, R.J.J.; Marinacci, F.; Simpson, C.M.; Springel, V.; Campbell, D.J.R.; Frenk, C.S.; Guillet, T.; Pfrommer, C.; et al. Magnetic field Formation in the Milky Way like disc Galaxies of the Auriga Project. Mon. Not. R. Astron. Soc. 2017, 469, 3185–3199. [Google Scholar] [CrossRef]
- Burn, B.J. On the Depolarization of discrete Radio Sources by Faraday Dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67–83. [Google Scholar] [CrossRef]
- Sokoloff, D.D.; Bykov, A.A.; Shukurov, A.; Berkhuijsen, E.M.; Beck, R.; Poezd, A.D. Depolarization and Faraday Effects in Galaxies. Mon. Not. R. Astron. Soc. 1998, 299, 189–206. [Google Scholar] [CrossRef]
- Mora, S.C.; Krause, M. Magnetic Field Structure and Halo in NGC 4631. Astron. Astrophys. 2013, 560, A42. [Google Scholar] [CrossRef]
- Brentjens, M.A.; de Bruyn, A.G. Faraday Rotation Measure Synthesis. Astron. Astrophys. 2005, 441, 1217–1228. [Google Scholar] [CrossRef]
- Heald, G.; Braun, R.; Edmonds, R. The Westerbork SINGS Survey. II Polarization, Faraday Rotation, and magnetic Fields. Astron. Astrophys. 2009, 503, 409–435. [Google Scholar] [CrossRef]
- Beck, R.; Krause, M. Revised Equipartition and minimum Energy Formula for magnetic Field Strength Estimates from radio Synchrotron Observations. Astron. Nachr. 2005, 326, 414–427. [Google Scholar] [CrossRef]
- Niklas, S. Eigenschaften von Spiralgalaxien im hochfrequenten Radiokontinuum. Ph.D. Thesis, University Bonn, Bonn, Germany, 1995. [Google Scholar]
- Fletcher, A.; Beck, R.; Shukurov, A.; Berkhuijsen, E.M.; Horrelou, C. Magnetic Fields and spiral Arms in the Galaxy M51. Mon. Not. R. Astron. Soc. 2011, 412, 2396–2416. [Google Scholar] [CrossRef]
- Mulcahy, D.D.; Beck, R.; Heald, G.H. Resolved magnetic Structures in the disk-halo Interface of NGC 628. Astron. Astrophys. 2017, 600, A6. [Google Scholar] [CrossRef]
- Krause, M. High Resolution Observations of the Magnetic Field in IC 342. In The Cosmic Dynamo, Proceedings of IAU Symposium; Cambridge University Press: Cambridge, UK, 1993; pp. 305–310. [Google Scholar]
- Beck, R. Magnetic Fields in the nearby spiral Galaxy IC 342: A multi-frequency radio polarization Study. Astron. Astrophys. 2015, 578, A93. [Google Scholar] [CrossRef]
- Beck, R.; Brandenburg, A.; Moss, D.; Shukurov, A.; Sokoloff, D. Galactic Magnetism: Recent Developments and Perspectives. Annu. Rev. Astron. Astrophys. 1996, 34, 155–206. [Google Scholar] [CrossRef]
- Niklas, S.; Beck, R. A new Approach to the radio-far infrared Correlation for non-calorimeter Galaxies. Astron. Astrophys. 1997, 320, 54–64. [Google Scholar]
- Krause, M. Magnetic Fields and Star Formation in Spiral Galaxies. Rev. Mex. Astron. Astrofis. 2009, 36, 25–29. [Google Scholar]
- Stil, J.M.; Krause, M.; Beck, R.; Taylor, A.R. The integrated Polarization of spiral Galaxy Disks. Astrophys. J. 2009, 693, 1392–1403. [Google Scholar] [CrossRef]
- Chyży, K.T. Magnetic Fields and Gas in the cluster-influenced spiral Galaxy NGC 4254. II. Structures of magnetic Fields. Astron. Astrophys. 2008, 482, 755–769. [Google Scholar] [CrossRef]
- Frick, P.; Stepanov, R.; Beck, R.; Sokoloff, D.; Shukurov, A.; Ehle, M.; Lundgren, A. Magnetic and gaseous spiral Arms in M83. Astron. Astrophys. 2016, 585, A21. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Urbanik, M.; Beck, R.; Han, J.L. Radio Polarization and magnetic Field Structure in M 101. Astron. Astrophys. 2016, 588, A114. [Google Scholar] [CrossRef]
- Ruzmaikin, A.A.; Shukurov, A.M.; Sokoloff, D.D. Magnetic Fields of Galaxies; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Seigar, M.S.; Kennefick, D.; Kennefick, J.; Lacy, C.H.S. Discovery of a Relationship between Spiral Arm Morphology and Supermassive Black Hole Mass in Disk Galaxies. Astrophys. J. 2008, 678, L93–L96. [Google Scholar] [CrossRef]
- Soida, M.; Krause, M.; Dettmar, R.-J.; Urbanik, M. The large scale magnetic Field Structure of the Spiral Galaxy NGC 5775. Astron. Astrophys. 2011, 531, A127. [Google Scholar] [CrossRef]
- Mora-Partiarroyo, S.C.; Krause, M.; Basu, A.; Beck, R.; Wiegert, T.; Irwin, J.; Henriksen, R.; Stein, Y.; Vargas, C.J.; Heesen, V.; et al. CHANG-ES XIV: Cosmic-Ray Propagation and Magnetic Field Strengths in the Radio Halo of NGC 4631. Astron. Astrophys. 2019, submitted. [Google Scholar]
- Irwin, J.; Beck, R.; Benjamin, R.A.; Dettmar, R.-J.; English, J.; Heald, G.; Henriksen, R.N.; Johnson, M.; Krause, M.; Li, J.-T.; et al. Continuum Halos in Nearby Galaxies: An EVLA Survey (CHANG-ES). I. Introduction to the Survey. Astron. J. 2012, 144, 43. [Google Scholar] [CrossRef]
- Irwin, J.; Damas-Segovia, A.; Krause, M.; Miskolczi, A.; Li, J.-T.; Stein, Y.; English, J.; Henriksen, R.; Beck, R.; Wiegert, T.; et al. CHANG-ES: XVIII—The CHANG-ES survey and relected results. Galaxies 2019, 7, 42. [Google Scholar] [CrossRef]
- Krause, M.; Mora-Partiarroyo, S.C.; Schmidt, P. Magnetic Fields and CR Propagation in the Halos of Spiral Galaxies. In Proceedings of the Focus Meeting 8 at the XXXth IAU General Assembly, Vienna, Austria, 29–31 August 2018; pp. 127–128. [Google Scholar]
- Mora-Partiarroyo, S.C.; Krause, M.; Basu, A.; Beck, R.; English, J.; Wiegert, T.; Irwin, J.; Henriksen, R.; Stein, Y.; Vargas, C.J.; et al. CHANG-ES XV: Large-Scale Magnetic Field Reversal in the Halo of NGC 4631. Astron. Astrophys. 2019, submitted. [Google Scholar]
- Woodfinden, A.; Henriksen, R.N.; Irwin, J.; Mora-Partiarroyo, S.C. Evolving Galactic Dynamos and Fits to the Reversing Magnetic Field in the Halo of NGC 4631. Mon. Not. R. Astron. Soc. 2019, submitted. [Google Scholar]
- Moss, D.; Sokoloff, D. Magnetic Fields around galactic Discs. Galaxies 2019, 7, 36. [Google Scholar] [CrossRef]
- Seta, A.; Beck, R. Revisiting the Equipatition Assumption in star-forming Galaxies. Galaxies 2019, 7, 45. [Google Scholar] [CrossRef]
- Heesen, V.; Beck, R.; Krause, M.; Dettmar, R.-J. Cosmic Rays and the magnetic Field in the nearby Starburst Galaxy NGC 253. I. The Distribution and Transport of Cosmic Rays. Astron. Astrophys. 2009, 494, 563–577. [Google Scholar] [CrossRef]
- Schmidt, P.; Krause, M.; Heesen, V.; Basu, A.; Beck, R.; Wiegert, T.; Irwin, J.A.; Heald, J.; Rand, R.J.; Li, J.-T.; et al. CHANG-ES XVI: An in-depth View of the Cosmic-Ray Transport in the edge-on Spiral Galaxies NGC 891 and NGC 4565. Astron. Astrophys. 2019. submitted. [Google Scholar]
- Stein, Y.; Dettmar, R.-J.; Irwin, J.; Beck, R.; Weżgowiec, M.; Miskolczi, A.; Krause, M.; Heesen, V.; Wiegert, T.; Heald, G.; et al. CHANG-ES XIII: Transport Processes and the magnetic Fields of NGC 4666—Indication of a reversing Disk magnetic Field. Astron. Astrophys. 2019, 623, A33. [Google Scholar] [CrossRef]
- Stein, Y.; Dettmar, R.-J.; Weżgowiec; Irwin, J.; Beck, R.; Wiegert, T.; Krause, M.; Li, J.-T.; Heesen, V.; Miskolczi, A.; et al. CHANG-ES XIX: The Galaxy NGC 4013—A Diffusion-dominated Radio Halo with Plane-parallel Disk and Vertical Halo Magnetic Fields. Astron. Astrophys. 2019. submitted. [Google Scholar]
- Beck, R.; Poezd, A.D.; Sukurov, A.; Sokoloff, D.D. Dynamos in evolving Galaxies. Astron. Astrophys. 1994, 289, 94–100. [Google Scholar]
- Chamandy, L.; Taylor, A.R. Non-linear galactic Dynamos and the magnetic pitch Angle. Astrophys. J. 2015, 808, 28. [Google Scholar] [CrossRef]
- Fletcher, A. Magnetic Fields in Nearby Galaxies. Dynamoc Interstellar Medium Celebr. Can. Glactic Plane Surv. 2010, 438, 197–210. [Google Scholar]
- Beck, R. Magnetic Fields in spiral Galaxies. Astron. Astrophys. Rev. 2016, 24, 4. [Google Scholar] [CrossRef]
- Arshakian, T.G.; Beck, R.; Krause, M.; Sokoloff, D. Evolution of magnetic Fields in Galaxies and future observational Tests with the Square Kilometre Array. Astron. Astrophys. 2009, 494, 21–32. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Chamandy, L.; Shukurov, A.; Baugh, C.M.; Taylor, A.R. Evolution of galactic magnetic Fields. Mon. Not. R. Astron. Soc. 2019, 483, 2424–2440. [Google Scholar] [CrossRef]
- Moss, D.; Beck, R.; Sokoloff, D.; Stepanov, R.; Krause, M.; Arshakian, T.G. The Relation between magnetic and material Arms in Models for Spiral Galaxies. Astron. Astrophys. 2013, 556, A147. [Google Scholar] [CrossRef]
- Arshakian, T.G.; Stepanov, R.; Beck, R.; Krause, M.; Sokoloff, D. Modeling the total and polarized Emission in evolving Galaxies: “Spotty” magnetic Structures. Astron. Nachr. 2011, 332, 524–536. [Google Scholar] [CrossRef]
- Moss, D.; Stepanov, R.; Arshakian, T.; Beck, R.; Krause, M.; Sokoloff, D. Multiscale magnetic Fields in Spiral Galaxies: Evolution and Reversals. Astron. Astrophys. 2012, 537, A68. [Google Scholar] [CrossRef]
- Chamandy, L.; Shukurov, A.; Subramanian, K. Magnetic spiral Arms and galactic Outflows. Mon. Not. R. Astron. Soc. 2015, 446, L6–L10. [Google Scholar] [CrossRef]
- Heesen, V.; Krause, M.; Beck, R.; Adebahr, B.; Bomans, D.J.; Carretti, E.; Dumke, M.; Heald, G.; Irwin, J.; Koribalski, B.; et al. Radio Haloes in nearby Galaxies modelled with 1D Cosmic Ray Transport using SPINNAKER. Mon. Not. R. Astron. Soc. 2018, 476, 158–183. [Google Scholar] [CrossRef]
- Heesen, V.; Dettmar, R.-J.; Krause, M.; Beck, R. Advective and diffusive Cosmic Ray Transport in galactic Haloes. Mon. Not. R. Astron. Soc. 2016, 458, 332–353. [Google Scholar] [CrossRef]
- Dumke, M.; Krause, M. Radio and Polarization Properties in the Disk and Halo of edge-on Spirals. In IAU Colloq. 166: The Lokal Bubble and Beyond; Lecture Notes in Physics; Springer: Berlin, Germany, 1998; pp. 555–558. [Google Scholar]
- Krause, M.; Irwin, J.; Wiegert, T.; Miskoczi, A.; Damas-Segovia, A.; Beck, R.; Li, J.-T.; Heald, G.; Müller, P.; Stein, Y.; et al. CHANG-ES. IX. Radio Scale Heights and Scale Lengths of a consistent Sample of 13 Spiral Galaxies seen edge-on and their Correlations. Astron. Astrophys. 2018, 611, A72. [Google Scholar] [CrossRef]
- Dumke, M.; Krause, M.; Wielebinski, R.; Klein, U. Polarized Radio Emission at 2.8cm from a selected Sample of edge-on Galaxies. Astron. Astrophys. 1995, 302, 691–703. [Google Scholar]
- Müller, P.; Krause, M.; Beck, R. The NOD3 Software Package: A graphical user Interface-supported Reduction Package for Single-Dish Radio Continuum and Polarisation Observations. Astron. Astrophys. 2017, 606, A41. [Google Scholar] [CrossRef]
- Vargas, C.J.; Walterbos, R.A.M.; Rand, R.J.; Stil, J.M.; Krause, M.; Li, J.-T.; Irwin, J. CHANG-ES XVII: Hα Imaging of Nearby Edge-on Galaxies, New SFRs, and an Extreme Star Formation Region—Data Release 2. Astrophys. J. 2019, submitted. [Google Scholar]
- Brandenburg, A.; Donner, K.J.; Moss, D.; Shukurov, A.; Sokoloff, D.; Tuaminen, I. Vertical magnetic Fields above the Discs of Spiral Galaxies. Astron. Astrophys. 1993, 271, 36–50. [Google Scholar]
- Moss, D.; Sokoloff, D.; Beck, R.; Krause, M. Galactic Winds and the Symmetry Properties of galactic magnetic Fields. Astron. Astrophys. 2010, 512, A61. [Google Scholar] [CrossRef]
- Gressel, O.; Elstner, D.; Ziegler, U.; Rüdiger, G. Direct Simulations of a Supernova-driven galactic Dynamo. Astron. Astrophys. 2008, 486, L35–L38. [Google Scholar] [CrossRef]
- Hanasz, M.; Otmianowska-Mazur, K.; Kowal; Lesch, H. Cosmic-Ray-driven Dynamo in galactic Disks. A Parameter Study. Astron. Astrophys. 2009, 498, 335–346. [Google Scholar] [CrossRef]
- Hanasz, M.; Wóltánski, D.; Kowalik, K. Global galactic Dynamo driven by Cosmic Rays and exploding magnetized Stars. Astrophys. J. 2009, 706, L155–L159. [Google Scholar] [CrossRef]
- Sur, S.; Shukurov, A.; Subramanian, K. Galactic Dynamos supported by magnetic Helicity Fluxes. Mon. Not. R. Astron. Soc. 2007, 377, 874–882. [Google Scholar] [CrossRef]




© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krause, M. Magnetic Fields and Halos in Spiral Galaxies. Galaxies 2019, 7, 54. https://doi.org/10.3390/galaxies7020054
Krause M. Magnetic Fields and Halos in Spiral Galaxies. Galaxies. 2019; 7(2):54. https://doi.org/10.3390/galaxies7020054
Chicago/Turabian StyleKrause, Marita. 2019. "Magnetic Fields and Halos in Spiral Galaxies" Galaxies 7, no. 2: 54. https://doi.org/10.3390/galaxies7020054
APA StyleKrause, M. (2019). Magnetic Fields and Halos in Spiral Galaxies. Galaxies, 7(2), 54. https://doi.org/10.3390/galaxies7020054



