Abstract
After one year of data taking, the observing run three (O3), we are preparing for an improved version of the system, named the Advanced Virgo plus. One of the major upgrades will be the installation of the signal recycling mirror to form an additional optical cavity and improve the sensitivity of the interferometer. This also requires a change in the lock acquisition strategy. In particular, the arms will be locked at the beginning with lasers at a different wavelength from the main one. Such a strategy has already been implemented and tested in LIGO and KAGRA, and in this paper we will present how it has been conceived in Virgo.
1. Introduction
The Advanced Virgo+ (AdV+) working principle is the one of a Michelson interferometer. However, this configuration does not allow the detection of such a small signal as that of gravitational waves, which have a strain amplitude of the order of . Several optical cavities were added in order to increase sensitivity and in particular two Fabry–Perot cavities were placed in the arms of the Michelson and an additional mirror was placed between the laser source and Beam Splitter (BS) creating another optical cavity, called the Power Recycling cavity (PRC), to recycle the power reflected back towards the laser. In this way the optical length is increased (the optical gain of the Fabry Perot cavities being 300), and the effective input power is also increased by the optical gain of the PR cavity, which in Advanced Virgo is 38.
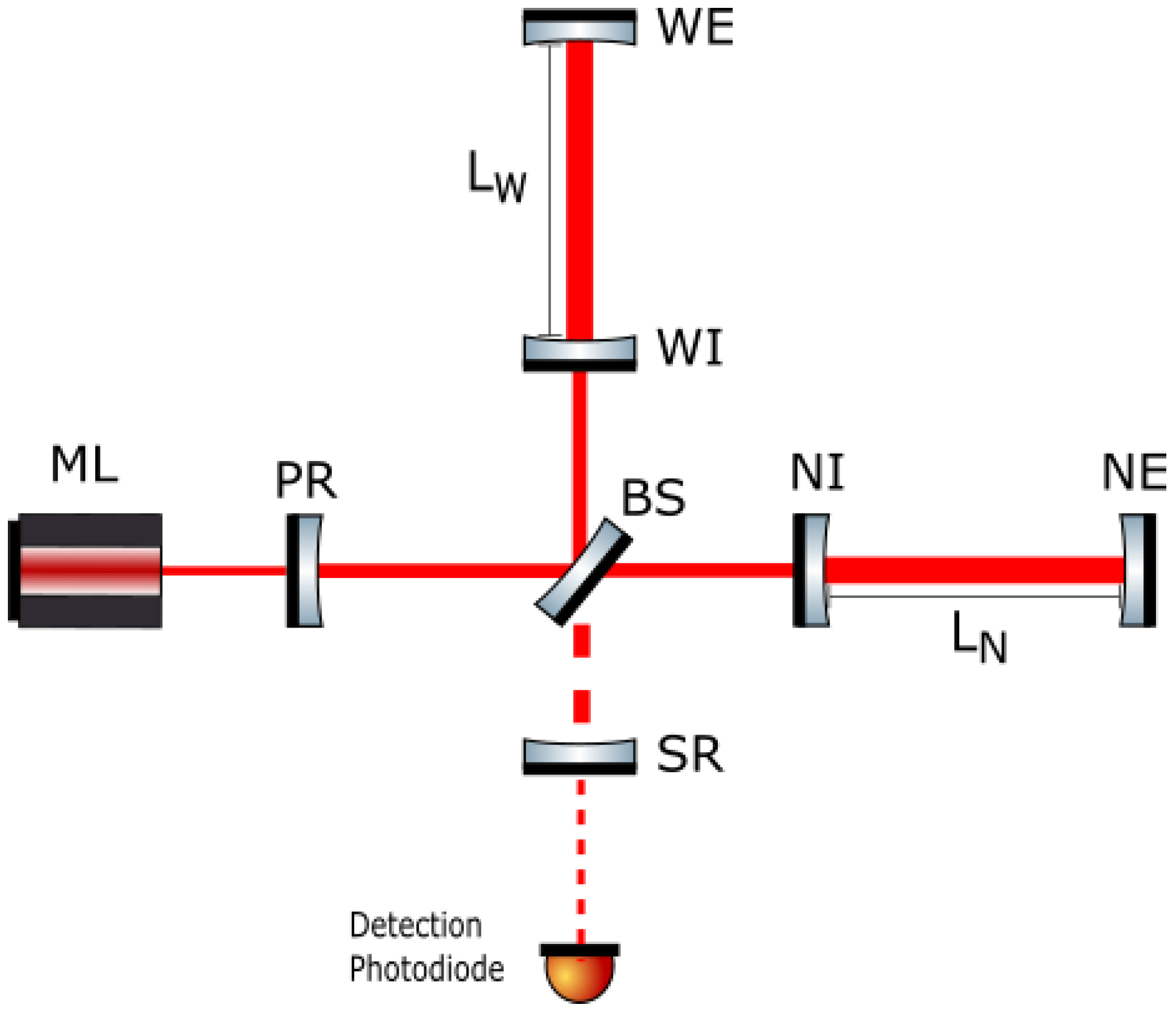
This optical design, shown in Figure 1, allowed for the detection of gravitational waves by the Advanced Virgo detector for the first time on 14 August 2017 [1].
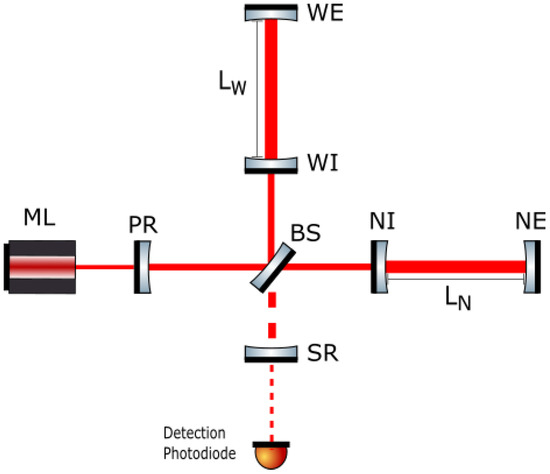
Figure 1.
Optical configuration of Advanced Virgo+. The laser light provided by an amplified master laser (ML) is transmitted by the power recycling mirror (PR) and split into two by the beam splitter (BS). The two beams are then injected into the 3 km long arm cavities, where the input mirrors (NI and WI) and the end mirrors (NE and WE) form two stable resonators whose lengths are indicated as and respectively. At the dark port an additional recycling cavity is added thanks to the Signal Recycling mirror (SR).
For AdV+ another optical cavity was added in order to further increase the detector sensitivity. A new mirror was placed between the BS (beam splitter) and the output port of the detector, and its role is to recycle the signal originated from the passage of a gravitational wave. This optical cavity is also called the Signal Recycling cavity (SRC) [2].
In order to reach the best sensitivity of the detector, all the optical cavities need to be locked on their resonance and the Michelson (MICH) needs to be locked in an almost destructive interference (homodyne detection [3]). The process of bringing all degrees of freedom (DOFs) to their working point in a controlled and repeatable way is called lock acquisition.
The lock acquisition developed for the Advanced Virgo detector is called the Variable Finesse technique [4], which is based on the acquisition of the lock passing through increasingly complex configurations up to the lock of all the longitudinal DOFs at the final working point.
The presence of an additional cavity, such as the SR cavity, makes the implementation of the Variable Finesse technique too difficult and uncertain. For this reason it has been chosen to adapt the lock acquisition used in LIGO and KAGRA for the Advanced Virgo+ configuration.
In order to begin the lock in a simpler configuration, this particular lock acquisition foresees to reduce the number of DOFs to be controlled by using lasers at a different wavelength with respect to the main one. These auxiliary lasers are green and their wavelength is half of the main laser wavelength, which is in the infrared (IR) range, at 1064 nm.
In this way two DOFs can be removed from the global locking scheme and the controls of the remaining three can be then engaged at the same time, until the arm cavities are brought to the main laser resonance, reaching the final working point.
This lock strategy has been proposed [5], demonstrated [6], and already implemented in the LIGO [7] and KAGRA [8] gravitational waves detectors, with different optical setups. In this article the innovative experimental setup designed for the Advanced Virgo+ will be presented. The main difference with respect to the present ones is that, instead of using independent green sources, locked in phase with the main laser, it is foreseen to generate a different wavelength from a pick off from the main laser which will be brought through a fiber toward the end mirrors, the terminal test masses of the long arm cavities, and then doubled in frequency before being injected in the arms, as shown in Figure 2. This solution results to be effective and reliable as the LIGO scheme but less expensive and more robust since no additional laser sources nor phase locking loops are used.
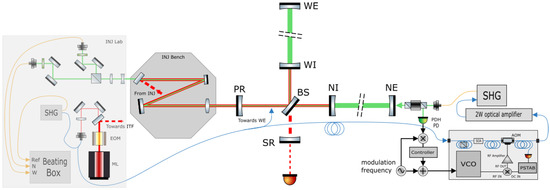
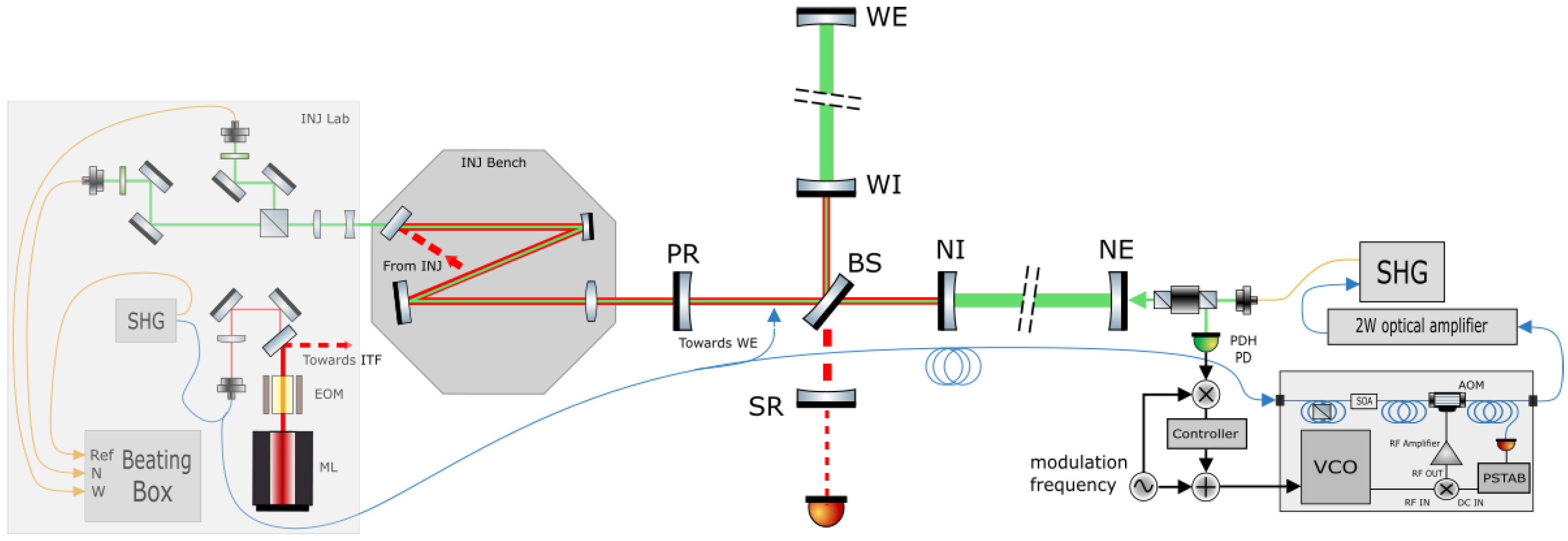
Figure 2.
General scheme of the Auxiliary Lasers System implemented in Virgo. The pick-off of the main infrared beam is taken after the corrections of the frequency stabilization, done by acting on the temperature of the crystal of the ML, by applying a stress on this crystal thanks to a piezoelectric transducer and with an EOM at higher frequencies. The beam is then fibered and split into three parts: Two are brought to the end buildings and frequency-doubled in the SHG boxes, the third one, which is the reference beam (indicated as Ref in the beating box), is doubled in the INJ lab. In the north and west end buildings, before being doubled the infrared seed is frequency shifted while passing through a fibered AOM. The control of this frequency shift thanks to the VCO allows us to keep the arms locked with the green light. The transmitted light from the arms is recombined with the reference at the level of the beating box.
2. Auxiliary Laser System Implemented in AdV+
As mentioned in the introduction, the Auxiliary Laser System (ALS) of Virgo follows the same scheme as LIGO and KAGRA. The main difference is that in Virgo, the green beam is directly obtained from doubling a pick off of the main laser, while in LIGO and KAGRA a commercial laser at 532 nm is used, locked in phase with the main one.
2.1. Overview of the Optics of the Green Locking System
The Virgo ALS (see Figure 2) consists of three green sources: Two are located in the end buildings (NE and WE) and a third one in the laboratory, named injection (INJ) lab, close to the main laser setup. A pick-off of the main laser is taken from the injection lab after the actuators for the frequency stabilization, which are an Electro-Optic Modulator (EOM) plus the piezoelectric and thermal corrections directly applied on the master laser (ML), and split into three parts. One part is directly amplified and frequency-doubled, and it will be used to build the error signals for the control of the common and differential lengths of the arm cavities CARM = and DARM = , see Figure 1, the two others are delivered to the end buildings through 3 km-long telecom optical fibers, amplified, doubled, and shaped to be injected into the arms cavities through the end mirrors. The system has been fully tested and pre-commissioned thanks to several experimental measurements performed both in a table-top experiment and in the final location, such as along the Virgo long arms. Five essential parts can be identified, which will be described below:
- -
- The fiber delivery;
- -
- The power amplification and stabilization;
- -
- The frequency shift;
- -
- The second harmonic generator;
- -
- The arm locking.
2.2. Fiber Delivery
When designing the system, fibered components were used as much as possible in order to minimize the alignment errors and to ease its maintenance. The optics for the green generation are in fact mounted on small benches and inserted into boxes, onto which the fibers delivering the beam are plugged. These boxes are easily installed in racks together with the electronics, protecting the optics from acoustic noise and air flows. In this sense the system can be defined as ‘plug and play’. The target is to generate 50 mW of green light, which is the amount of light necessary to have enough power in transmission of the cavity, not to be limited by the shot noise of the photodetectors that build the error signals to control the arm cavities together (CARM and DARM). Moreover, the phase noise and frequency stability has to be enough to lock the arm cavities [9], more details in Section 3. For this reason, the infrared seed used as an input for the SHG is a pick-off of the main laser beam.
This pick-off will be routed from the Advanced Virgo laser bench to the end buildings, where the end mirrors are located, through the telecom fiber network of the Virgo interferometer, which has a 1319 nm wavelength. In this way, there is requirement for installing new fibers along the length of the long arms. However using such a fiber introduces three main problems that we address.
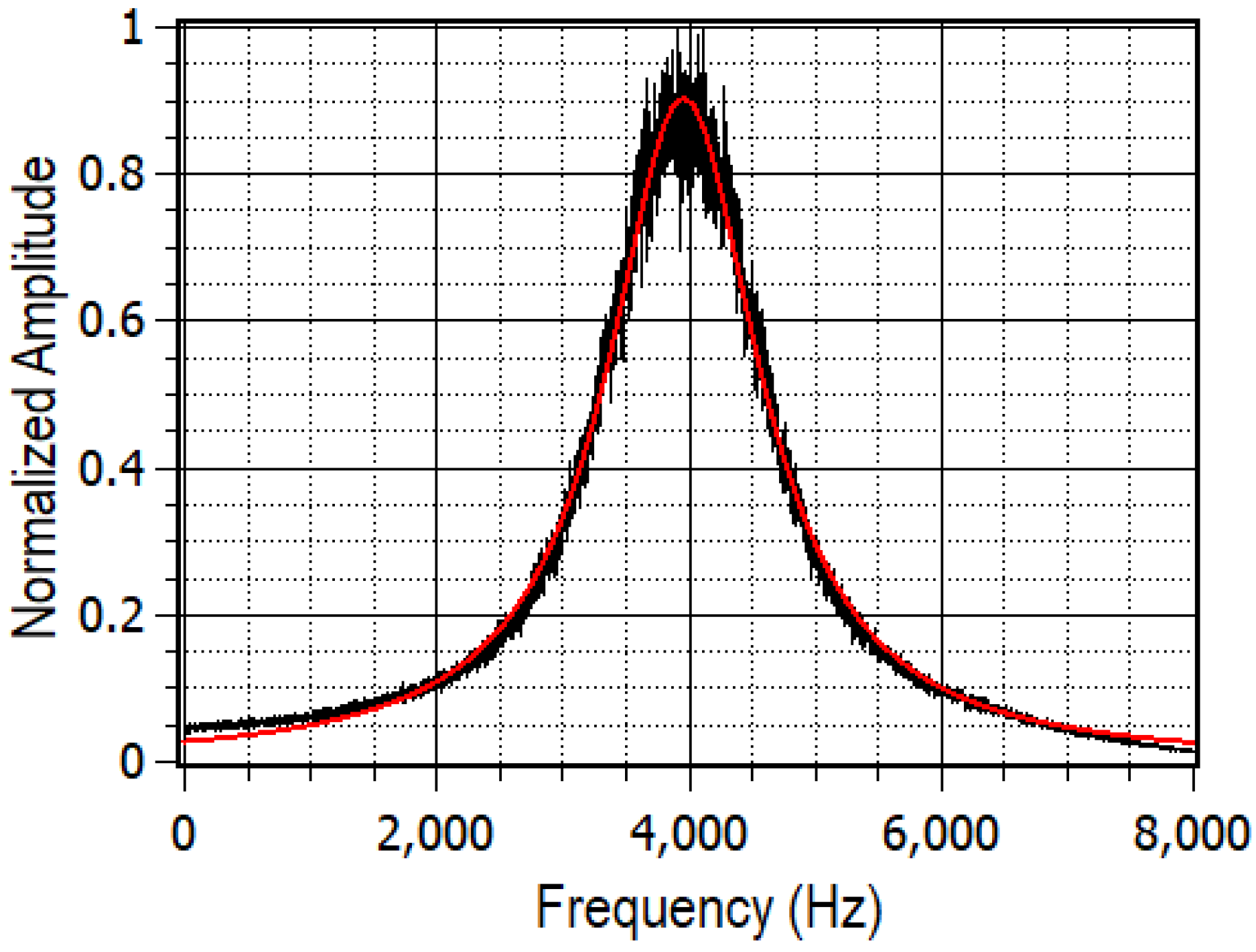
The first one is about the phase noise that is introduced by the fiber itself. A measurement of the phase noise over 6 km of this fiber has been done as reported in [9]. It allowed us to give an upper limit of 1.5 kHz, as shown in Figure 3. This result is analyzed in the noise studies shown in Section 3.1.
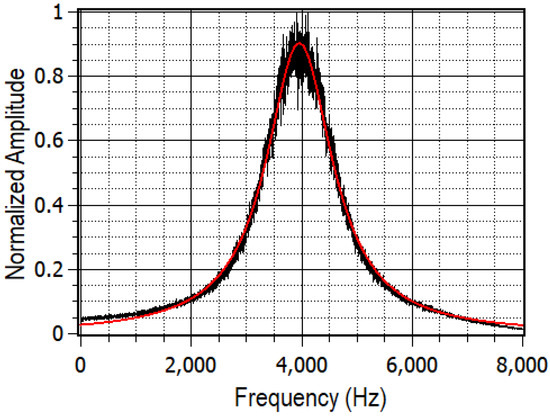
Figure 3.
Induced phase noise from 6 km of telecom fiber [9]. The black line shows the beat note measured over 100 s between a reference of the input beam shifted by 80 MHz and the beam at the output of 6 km of telecom fiber. The signal is demodulated in order to center it at 4 kHz. In red, the Lorentzian fit of the beat note is shown, it has a FWHM = 1.48 kHz, = 0.993.
The other problem while working with a narrow linewidth laser in such a long fiber is the Stimulated Brillouin Scattering (SBS). Brillouin Scattering is a spontaneous effect due to the interaction between the light and medium in which it propagates. The refractive index of the fiber is locally and periodically modified, resulting in an acoustic wave propagating inside the fiber that acts as an oscillating diffraction grating on which part of the incoming light is back reflected. While going above a certain amount of input power, this phenomenon becomes self stimulated and most of the power is back reflected, thus limiting the maximum power that can be sent into the fiber. There is no easy formula to compute this threshold but a good approximation is given in [10]. Using this formula we found a theoretical SBS threshold of about 8 mW. A measurement in situ was completed and it was found that with up to 12 mW of input power we could not measure any back reflected light. Another known effect of SBS is the increase of Relative Intensity Noise (RIN). In order to avoid to a further increase, 8 mW at the input of the telecom fibers was kept.
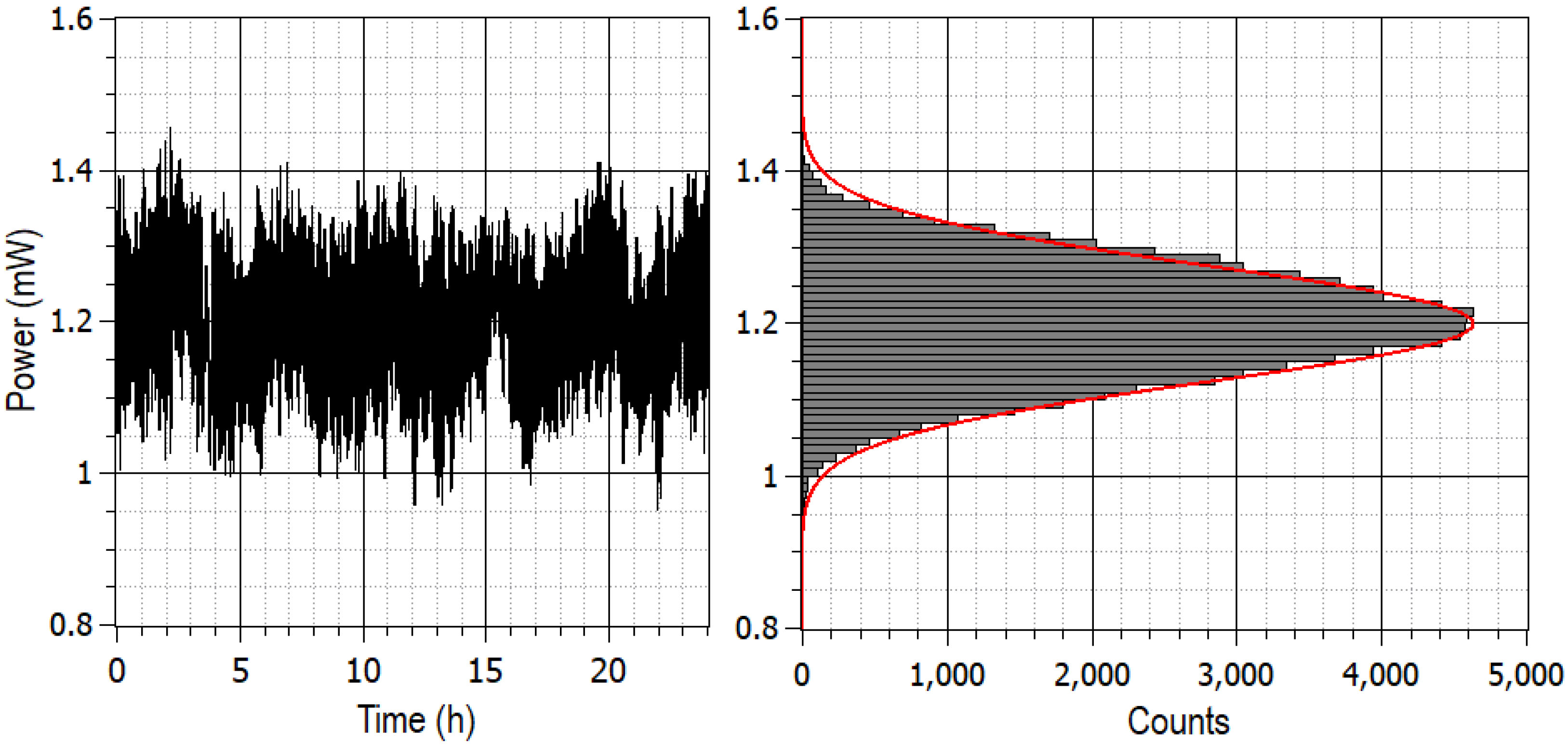
Finally because of the attenuation of the fiber at 1064 nm and because of the different fiber connections, it was possible to achieve 2.5 mW at the end buildings. Since the telecom fibers do not maintain the polarization of the beam, those 2.5 mW of power are unpolarized. In order to get back to a linear polarization, the beam passes through a fibered in-line polarizer. However, this results into power fluctuations at the output of the polarizer. In order to study this effect, measurements were performed over several days to evaluate the change in power due to these slow polarization fluctuations. The results over 24 h are shown in Figure 4.
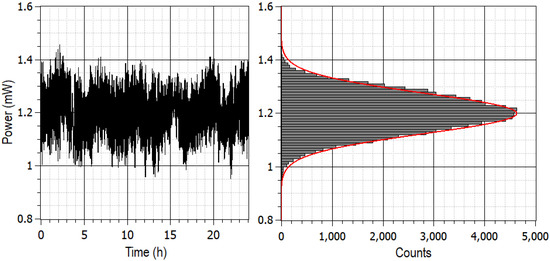
Figure 4.
Power fluctuations at the output of a fibered polarizer placed after the 3 km-long telecom fiber. Left: Power measured at the output of the fibered polarizer for 8 mW linearly polarized light injected at the input of the telecom fiber. Right: Statistical distribution of this power and its gaussian fit. The average is 1.2 mW, FWHM is 0.152 mW, and is 0.998.
2.3. Power Amplification and Stabilization
The beam is amplified in two stages: The preamplification is made with a Semiconductor Optical Amplifier (SOA), then the power is stabilized thanks to an Acousto Optics Modulator, and a commercial fibered amplifier allows one to reach enough power for a second harmonic generation process. More details are described hereafter.
The seed beam brought thanks to the telecom fiber is shaped in the so-called electronic (ELEC) box. A scheme of the optical setup of this box is given in Figure 5. At the output of the in-line polarizer, the remaining 1.2 mW are preamplified with a SOA [11]. The SOA is formed by two layers of semiconductor material having inside an active layer through which the laser beam passes. An electrical current is applied to the device to excite the electrons which will emit photons in the de-excitation phase. The incoming photons will stimulate the excited electrons, so the new generated photons will be matched to the incoming ones, amplifying the beam. It is used to amplify the seed by a factor 5 and get about 6 mW at its output. The SOA could allow us to get up to 20 mW at the output but this would imply more spontaneous emission and thus a degradation of the Optical Signal to Noise Ratio (OSNR). After the SOA, the power of the beam is stabilized at 1.5 mW with a fibered Acousto-Optic Modulator (AOM), whose functioning is explained in detail in Section 2.4. By acting on the amplitude of the driving signal, the ratio between the power into the order 0 (no frequency shift, dumped inside the AOM) and the first diffracted order (beam shifted in frequency) can be modified. We use for this purpose a double balanced frequency mixer: The output signal of the VCO is injected into the RF IN port of the frequency mixer while a direct current (DC) power is applied on the DC IN port, as shown in Figure 5. The result is a radio-frequency (RF) signal at the frequency of the RF IN port whose amplitude is proportional to the amplitude of the (DC) power of the DC IN port. Thus by taking a pick-off of the power going out of the box, a simple loop to stabilize the power fluctuations was designed.
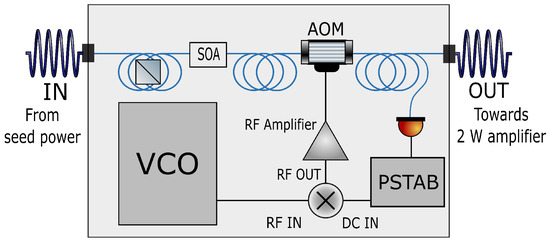
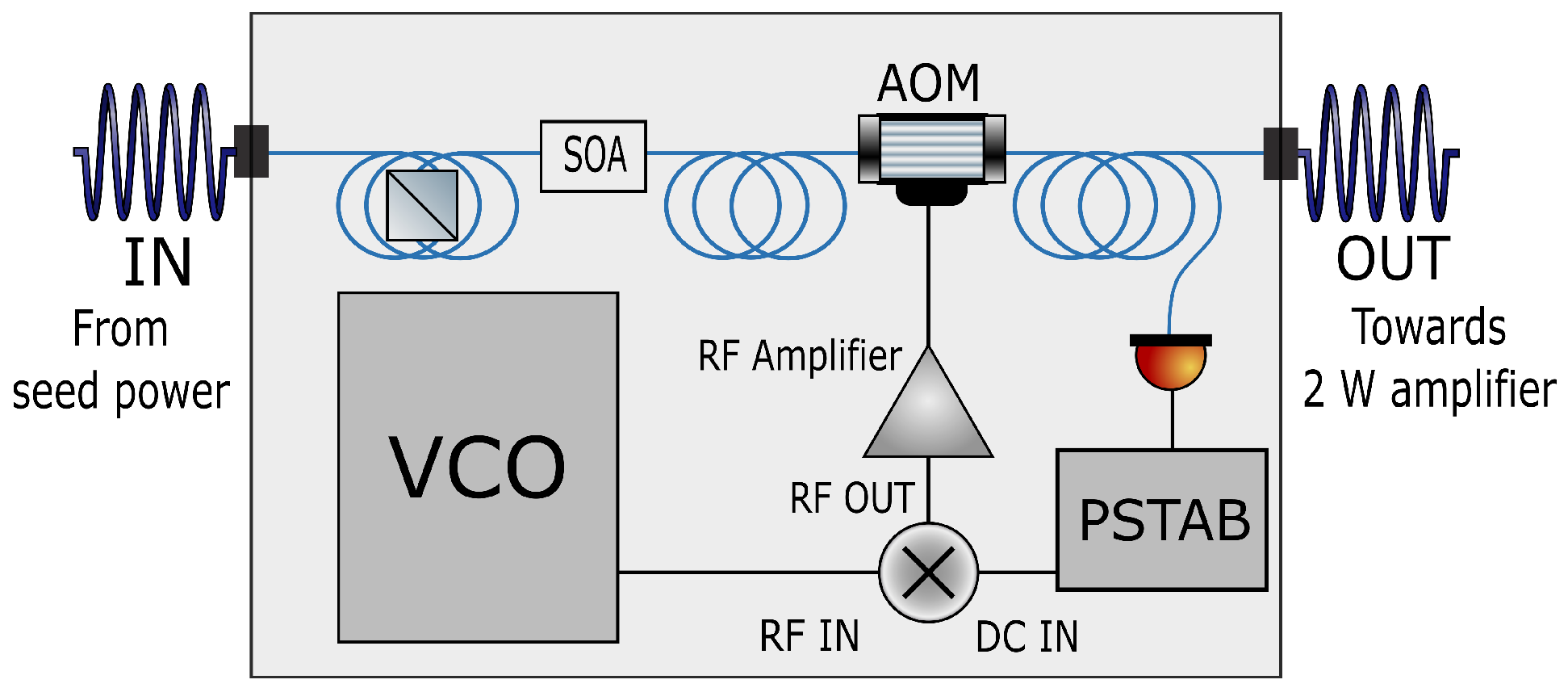
Figure 5.
Sketch of the Electronic box. The polarization of the beam is cleaned thanks to a fibered polarizer, and is then amplified with a SOA and passes through a fibered AOM where only the 1st diffracted order is coupled into the fiber, so that at its output the beam is shifted in frequency by 80 MHz. The RF to drive the AOM is given by a VCO (Voltage-Controlled Oscillator) and the amount of diffracted light can be set thanks to a DC IN offset coming from a power stabilization loop (PSTAB).
At the output of the electronic box, the beam is then sent towards a 2 W fibered amplifier [12]. The phase noise was measured to verify that both the 2 W amplifier and the SOA were not introducing additional phase noise with respect to the one introduced by the propagation into the telecom fiber.
2.4. Frequency Shift
As mentioned in the introduction, the Auxiliary Laser System will be used to control the frequency of the laser of the green beam with respect to the length of the Fabry–Perot cavities in the arms. Since the SHG process (which will be presented in Section 2.5) is a passive process, all the controls needed to lock the cavity can be done on the IR seed beforehand. The frequency of the beam will be shifted to keep the cavity on resonance thanks to an Acousto-Optical Modulator (see Figure 5). This component uses acoustic waves to diffract part of the light which is going through it. In our application, the first diffracted order is coupled into the output fiber [13], so the frequency of the laser beam passing through is shifted by the frequency of the acoustic wave. The control of this frequency is done thanks to a Voltage-Controlled Oscillator (VCO), acting on the voltage at its input. Not only does it shift the frequency by 80 MHz but it is also used as an actuator to apply the frequency corrections needed to keep the arms locked. After the frequency doubling, the green beam in transmission of the arm cavities is shifted by 160 MHz with respect to the green reference in the INJ lab, and their beating will be used as an error signal for controlling CARM and DARM. Moreover, in order to distinguish which information comes from which arm, the frequency shift is slightly different for the North arm cavity and the West arm one.
The VCO chosen has a frequency tuning constant of 4 MHz/V. For the green beam, the Finesse of the Fabry–Perot arm cavities is lower than for the infrared, 150 for one arm, and 190 for the other, resulting in a linewidth of 260 Hz and 330 Hz respectively. Considering the smallest one of 260 Hz, it is necessary to make frequency shifts of at least a factor of 10 lower than this value in order to achieve good control in the lock acquisition phase of each arm cavity independently. In practice, the corrections calculated by the control filter will be sent to the VCO through a Digital-to-Analog Converter (DAC), which has its own noise.
This DAC has 16 effective bits and an actuation range of ±10 V so the smallest step it can do is 300 V, which means that the maximum precision that can be achieved with it is only 1200 Hz, much higher than our target.
Specific electronics have been designed in order to decrease by a factor 100 the amount of voltage that can be delivered to the VCO, so that the frequency tuning constant at the end is 40 kHz/V, so that the minimum frequency shift will be Hz, which is around 20 times smaller than the linewidth, thus fulfilling the required specifications [14].
2.5. Second Harmonic Generation Process
Second Harmonic Generation or frequency doubling is a nonlinear optical process in which two photons at the same wavelength interact within a particular material to get a new photon at half the wavelength [15]. Due to the relative simplicity of the SHG process, the wavelength chosen for the auxiliary lasers is 532 nm. In Virgo, it is done with a homemade optical setup that amplifies and doubles a pick-off of the main 1064 nm laser beam [16]. The doubling setup is the only part which is in free space and the optics are mounted in a 40 × 50 cm breadboard, inserted into a box and installed into a rack together with the needed electronics, as shown in Figure 6.

Figure 6.
Second Harmonic Generation (SHG) bench. On the left, a picture of one of the three frequency-doubling setups realized in EGO, on the right, an optical scheme of the setup. The Polarized Beam Splitter (PBS) and the Half-Wave Plate (HWP) ensure the correct polarization and allow one to tune the power. The lenses L1 and L2 form a telescope to focus the beam into the crystal and the lense L3 collimates it at the output. M3, M4, and M5 are dichroic mirrors, transmittive for the infrared and reflective for the green. With M5 and M6 the beam is coupled into the fiber and the HWP2 adjusts its polarization to the axis of the output fiber. PD1 and PD2 are monitoring photodiodes for the infrared and the green powers respectively.
In order to have good conversion efficiency, defined as the ratio between the power of the green beam and the square of the infrared seed power, , at the output of the SHG material a constructive interference with the previously generated green photons is needed.
For this, the SHG material chosen is a periodically poled magnesium doped lithium niobate (MgO-PPLN) crystal [17]. This means that its orientation is periodically inverted (poled) in order to generate photons with a phase difference of compared to the case of a photon created at the same point of the crystal without poling. The whole crystal is actually composed by five poled channels called gratings, each one 0.5 mm wide and having a different periodicity, from m to m by steps of m. This allows one to choose the best periodicity to obtain the previously mentioned constructive interference. Another important parameter to reach the maximum conversion efficiency is to choose the optimal value for the waist of the input beam. This optimal value has been calculated according to the Boyd and Kleinmann theory on SHG of focused beams [18] and corresponds to a waist of m in the crystal [19].
In order to ensure the stability of the conversion efficiency, it is necessary to keep the temperature of the SHG material constant, since its refractive index strongly depends on it. For this purpose the crystal is inserted into an oven, whose temperature is controlled at C from near-ambient to C [20].
The typical conversion efficiency that was reached is ∼0.02 W in a single pass. Giving the relative simplicity of the fibered amplification technology, a single pass solution with a preamplification of the beam chosen with respect to an intra cavity doubling that would have required a locking loop. Since the target was to generate 50 mW of green light at the output of the fiber, a 2 W fibered amplifier was chosen. This allows one to produce up to 80 mW of green light ( W). The setup used to double in frequency the infrared seed is shown in Figure 6.
Concerning the stability, it has been estimated that less than of power fluctuations over 20 min are needed [21], which is the amount of time needed for the locking of the cavities. This requirement is fulfilled since the power fluctuations are over two days, as seen in Figure 7.
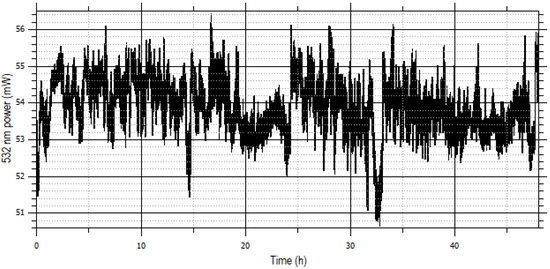
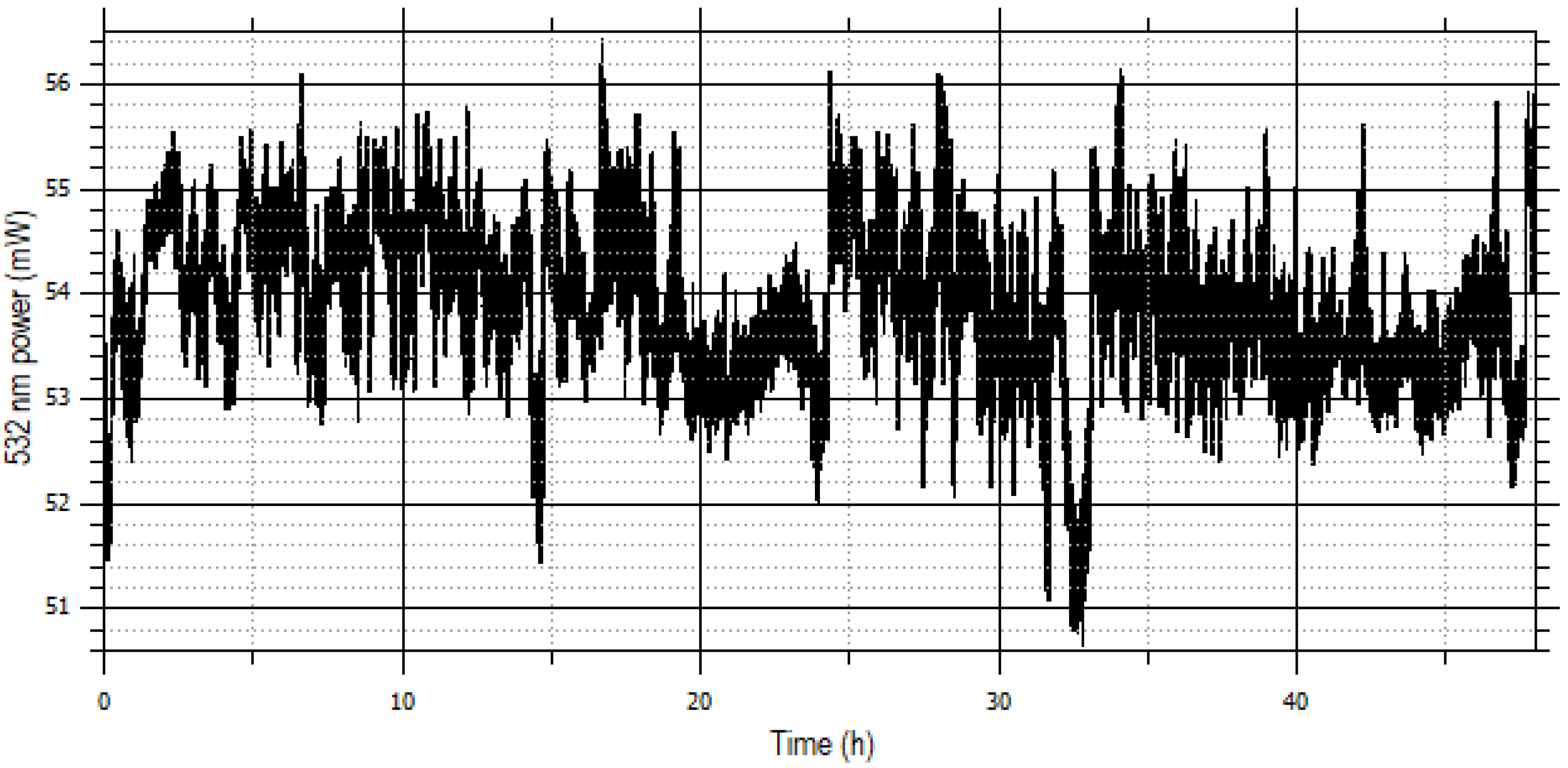
Figure 7.
Trend of the power of the 532 nm beam over two days. The average value is 53.9 mW with a FWHM of 1.5 mW.
Thus, about 80 mW of a 532 nm laser beam containing the same phase information of the 2 W of 1064 nm seeder are generated and coupled into a fiber. This fiber will then both deliver the beam at the end stations where it will be shaped by a telescope, stabilized and injected into the arms, and to a box located in the injection laboratory (see Figure 8), to make the beating with the other two green beams come from the arms.
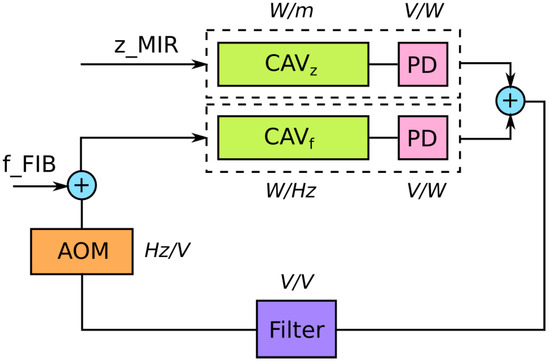
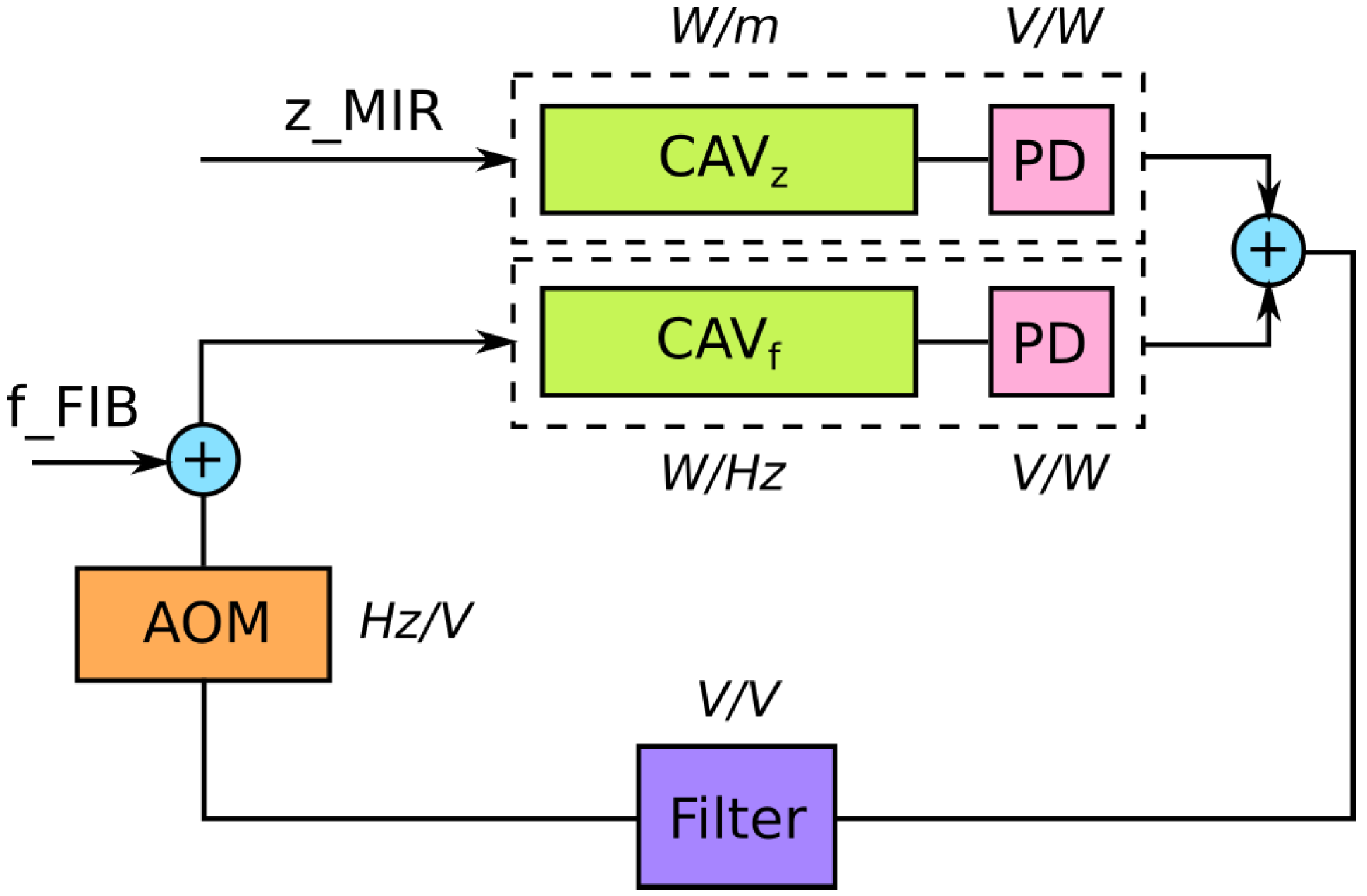
Figure 8.
Scheme of the arm cavity control loop. The green boxes represent the transfer function of the optical cavity both for a frequency and a length change. The pink boxes represent the transfer function of the photodetectors (PD), the purple one the control filter, and the orange one the transfer function of the actuator (AOM). In the scheme the noises are explicitly shown at their entrance point: Through the mirrors of the cavity (z) and through the laser beam itself (f).
2.6. The Control Error Signal
The arm cavities are locked with the Pound Drever Hall (PDH) [22] technique, and this requires the laser beam to be phase modulated. This is done by modulating the amplitude of the signal driving the VCO at the desired modulation frequency. In turns, it modulates in phase the carrier of the laser beam [23]. This modulation is done at 35 kHz and it is interesting to notice that, while the carrier frequency is doubled, the sidebands remain at the same frequency in the green beam. This can be explained by the fact that the doubling process is statistical: There are much more photons in the carrier than in the sidebands, so there is a very low probability for photons from the upper and lower sidebands to interact together.
3. Controls
In order to design a feedback loop there are several elements that need to be taken into account. First of all it is necessary to know the behavior of the system that needs to be controlled, in our case the long Fabry–Perot cavities. Their optical Transfer Function is well known: A simple pole at a frequency that depends on their Finesse and length (3 km). As already mentioned, for the green beam, the Finesse of the cavities is lower than for the infrared, 150 for one arm and 190 for the other, resulting in a cavity pole of 167 and 131 Hz, respectively.
Then an error signal to monitor the deviation with respect to the working point is needed. As presented in the previous sections, a standard PDH technique [22] is used, with the sidebands being generated using the AOM. Finally an actuator is needed to apply the corresponding corrections to bring the system to the working point. The same AOM is used for this purpose with the help of the VCO presented in Section 2.4. The behavior in the frequency domain of these two elements do not contribute significantly to the design of the control filter, since it is flat in the region of interest: A simple pole at 30 kHz for the couple VCO and AOM. Finally, the photodiode used for building the error signal also has a flat transfer function up to a simple pole in the MHz region. A scheme of the control system is shown in Figure 8.
With this information it is possible to design a control filter that keeps the cavity on resonance, as required. However, in order to properly tune it, it is necessary to also study the noises that bring the cavity out of its working point. In the present case the two noise sources to consider are: The frequency noise present on the green beam, and the seismic noise that cause a longitudinal movement of the mirrors. In Figure 8, they are called f and z respectively and it is shown how they couple into the system.
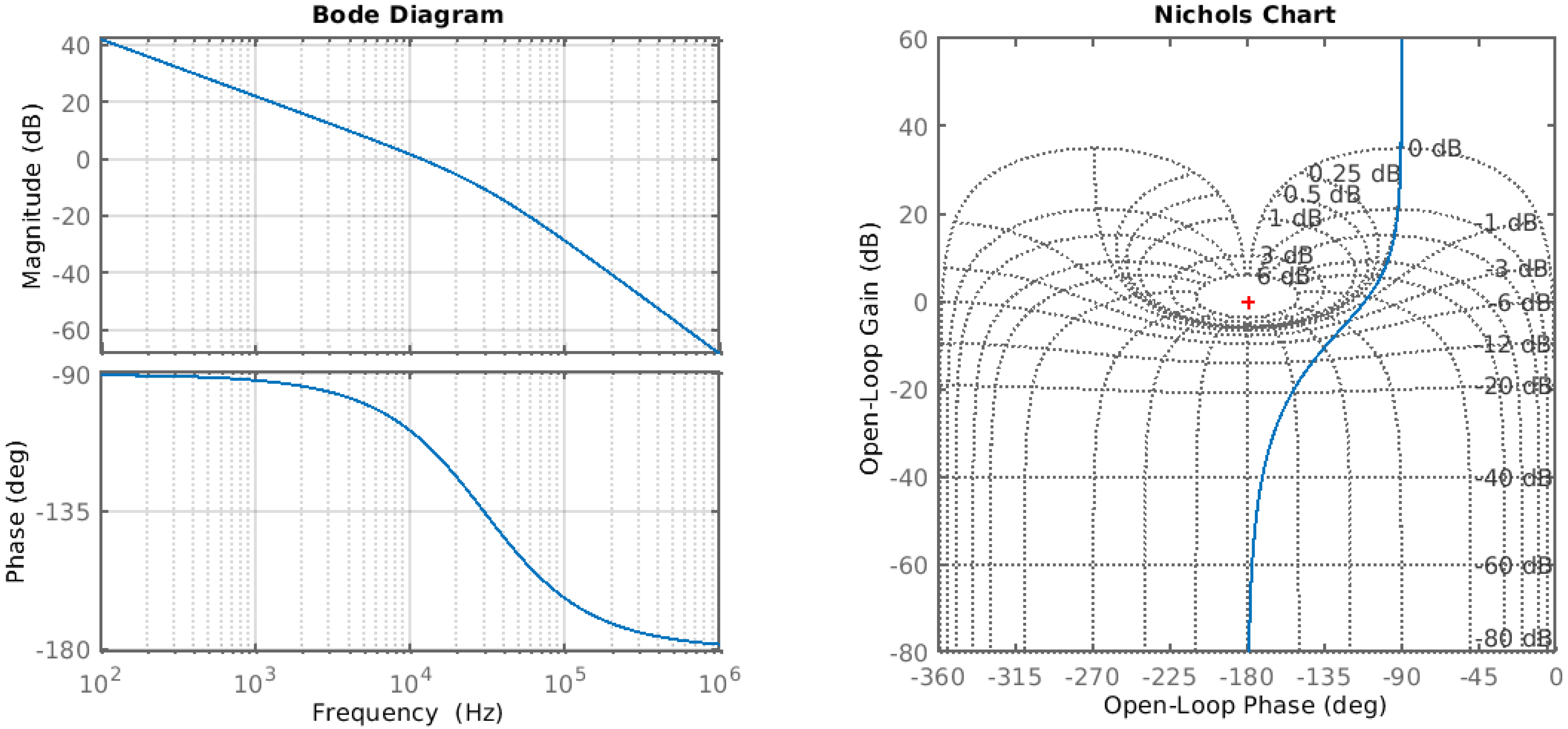
The latter one is well known, since it is the same for all the mirrors in the interferometer. It is shown as Ground Noise in Figure 9, with a typical rms value of 1 m. It has a f shape so it is very suppressed above 100 Hz. For the frequency noise of the green beam, an upper limit has been measured [9], also shown in Figure 9. This noise contributes up to higher frequencies. For this reason it is necessary to design a control loop with a high bandwidth, of the order of 10 kHz. The total Open Loop Transfer Function including all the elements described in this section is shown in Figure 10.

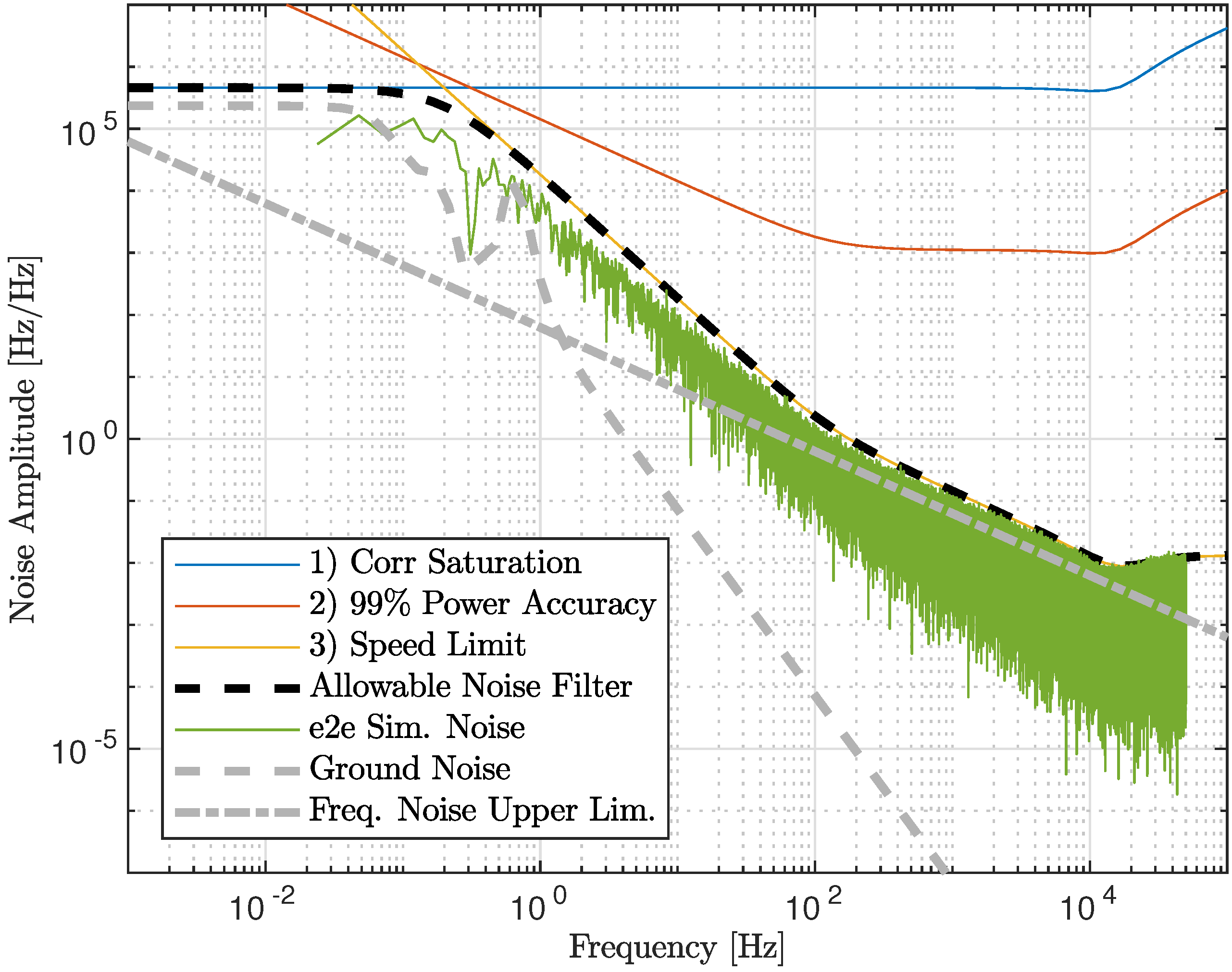
Figure 9.
Maximum allowable noise filter defined as the minimum magnitude of anticipated constraining performance parameters. Also shown are the known ground and frequency noise levels.
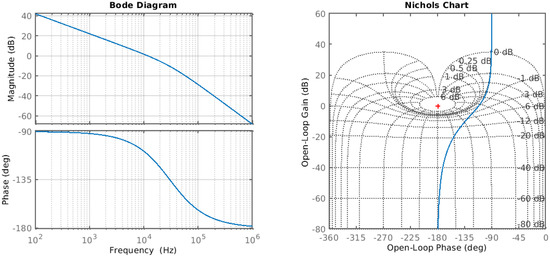
Figure 10.
The left plot shows the Bode plot of the Open Loop Transfer Function of the control of the arm cavity. The Unity Gain Frequency is around 10 kHz. The plot in the right shows the Nichols plot of the same system, and it shows that the control is stable and it is far from the overshoot region (1–6 dB).
The control presented here, using only one actuator (the AOM), corresponds to the lock acquisition of the arm cavities. Once the cavities will be kept in resonance, the mirrors will also be used as actuators, in order to reduce the frequency band of each actuator, allowing one to increase the corrections without saturating them. The precision that can be reached this way will be improved (a rms value of 7 Hz is required for the global lock acquisition) [24].
3.1. Maximum Allowable Noise
Beyond the identified noise sources, it is necessary to determine the maximum allowable noise to ensure the ability to lock the green cavity with necessary accuracy using the frequency actuator. For this analysis it is assumed that noise enters the control loop between the frequency actuator and cavity. The transfer functions that are necessary to propagate the noise limits are developed in Brooks et al. [25]. The maximum allowable noise is limited by three performance requirements:
- 1.
- Avoid actuator saturation at 10 V correction signal [24];
- 2.
- Maintain 99% intracavity power, which corresponds to 1/10 FWHM around the resonance [25];
- 3.
- Limit the cavity speed to allow time for power to build above the threshold to engage linear lock [25].
Figure 9 plots the allowable noise level due to each of the constraints listed above. The maximum allowable noise is calculated as the minimum of these curves and shown as the black dashed line. Also shown in the gray lines in Figure 9 are the noise magnitude from known sources: Seismic disturbances [26] and noise fluctuations due to the fiber optic [9]. The ground noise is close to the allowable noise limit. However, this is not a concern as there is also the magnetic coil pair actuators (whose transfer function is not included in the plot) which can supplement the frequency actuator if needed. The frequency noise remains at least a factor of two below the allowable noise limit for all frequencies. Low frequency noise is not a large concern for ALS as the system is only active on the order of 10 min while the Central Interferometer is locking.
The ability of the cavity to lock while subjected to the theoretical maximum allowable noise was simulated in [25] with the time-domain End-to-End (e2e) software [27] for one minute. Figure 9 shows the amplitude spectrum density of the noise injected into the simulation to verify that it conforms to the maximum noise curve. The results of the simulation show that the accuracy of the lock is well above 99% as listed in the performance requirements, with the value at % of the maximum transmitted DC power. Furthermore, the actuator correction voltage was well below the saturation limit for the minute-long simulation. Based on the e2e simulation results, the theoretical maximum allowable noise has been validated for the ability of lock and locking accuracy.
4. Conclusions
One of the major upgrades of AdV+ is the installation of an additional mirror, which forms a cavity to recycle the interferometer output signal. This requires a new control strategy, already implemented on LIGO and KAGRA, which locks the arm cavities in the first step with green beams at 532 nm. This paper presented on how this system is designed for AdV+ and the requirements in terms of stability and noise performance to ensure the lock.
This auxiliary laser system is innovative with respect to the ones already implemented in LIGO and KAGRA, it is simpler since it can be considered as ’plug and play’, and less expensive since no additional lasers sources are needed. Moreover, experimental measurements and simulation results verified that it fulfills all the requirements for lock acquisition.
ReftitleReferences
Author Contributions
Writing original draft preparation, C.D.R., J.B., J.C.D., A.C., M.G., M.M., writing review and editing E.G., N.L., B.M., F.N. and G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work have been supported by the fundings of European Gravitational Observatory.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbot, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rew. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Virgo Collaboration; Advanced Virgo Technical Design Report, VIR-0128A-12. April 2012. Available online: https://tds.virgo-gw.eu/ql/?c=8940 (accessed on 8 December 2020).
- Hild, S.; Grote, H.; Degallaix, J.; Chelkowski, S.; Danzmann, K.; Freise, A.; Hewitson, M.; Hough, J.; Lück, H.; Prijatelj, M. DC-readout of a signal-recycled gravitational wave detector. Class. Quantum Gravity 2009, 26, 5. [Google Scholar] [CrossRef]
- Acernese, F.; Amico, P.; Al-Shourbagy, M.; Aoudia, S.; Avino, S.; Babusci, D.; Ballardin, G.; Barille, R.; Barone, F.; Barsotti, L.; et al. The variable finesse locking technique. Proceedings of the Amaldi 6 Conference, Okinawa (Japan). Class. Quantum Grav. 2006, 23, S85–S89. [Google Scholar] [CrossRef]
- Mullavey, A.J.; Slagmolen, B.J.J.; Miller, J.; Evans, M.; Fritschel, P.; Sigg, D.; Waldman, S.J.; Shaddock, D.A.; McClelland, D.E. Arm-length stabilisation for interferometric gravitational-wave detectors using frequency-doubled auxiliary lasers. Opt. Express 2012, 20, 81. [Google Scholar] [CrossRef] [PubMed]
- Izumi, K.; Arai, K.; Barr, B.; Betzwieser, J.; Brooks, A.; Dahl, K.; Doravari, S.; Driggers, J.C.; Korth, W.Z.; Miao, H.; et al. Multicolor cavity metrology. J. Opt. Soc. Am. A 2012, 29, 2092. [Google Scholar] [CrossRef] [PubMed]
- Staley, A.; Martynov, D.; Abbott, R.; Adhikari, R.X.; Arai, K.; Ballmer, S.; Barsotti, L.; Brooks, A.F.; DeRosa, R.T.; Dwyer, S.; et al. Achieving resonance in the Advanced LIGO gravitational-wave interferometer. Class. Quantum Grav. 2014, 31, 245010. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Aso, Y.; Bae, S.; et al. An arm length stabilization system for KAGRA and future gravitational-wave detectors. Class. Quantum Grav. 2020, 37, 035004. [Google Scholar] [CrossRef]
- Casanueva, J.; Pillant, G.; Genin, E.; Leroy, N. Auxiliary Laser System: Fiber Phase Noise Measurement and Cavity Lock Requirements, VIR-0540B-16. 2016. Available online: https://tds.virgo-gw.eu/ql/?c=11857 (accessed on 8 December 2020).
- Gangwar, R.; Singh, S.P.; Singh, N. Nonlinear scattering effects in optical fibers. Prog. Electromagn. Res. 2007, 74, 379–405. [Google Scholar]
- Available online: https://www.superlumdiodes.com/pdf/soa542.pdf (accessed on 8 December 2020).
- Available online: https://www.lasercomponents.com/fileadmin/user_upload/home/Datasheets/keopsys/ytterbium-pre-booster-amplifier-cyfa-pb.pdf (accessed on 8 December 2020).
- Available online: http://www.aaoptoelectronic.com/wp-content/uploads/2018/08/MT80-MT110-MT200-MT250-IR-Fio-VSF-ed1-18.pdf (accessed on 8 December 2020).
- Casanueva, J.; Chiummo, A.; Gosselin, M.; Leroy, N.; Masserot, A.; Montanari, B.; Nocera, F.; de Rossi, C.; Vardaro, M. ALS Test 1: Arm Cavities Actuation Chain. VIR-0381B-20. (2020). Available online: https://tds.virgo-gw.eu/ql/?c=15505 (accessed on 8 December 2020).
- Boyd, R. The Nonlinear Optical Susceptibility. Nonlinear Opt. 2007, 1–67. [Google Scholar] [CrossRef]
- Khan, I.; Genin, E.; Fafone, V.; Pillant, G.; Magazzu, A.; Casanueva, J.; Chiummo, A.; Leroy, N. Auxiliary lasers for Advanced Virgo Gravitational Wave detector using single pass Second Harmonic Generation in Periodically Poled Lithium Niobate crystal. J. Phys. Conf. Ser. 2020, 1548, 012025. Available online: https://hal.archives-ouvertes.fr/hal-02886865 (accessed on 8 December 2020). [CrossRef]
- Available online: https://www.covesion.com/assets/downloads/MSHG1064-1.0.pdf (accessed on 8 December 2020).
- Boyd, G.D.; Kleinmann, D.A. Parametric Interaction of Focused Gaussian Light Beams. J. Appl. Phys. 1968, 39, 3597–3639. [Google Scholar] [CrossRef]
- Jahn, W. Development and Characterization of a Second Harmonic Generator for the Advanced Virgo Project, VIR-0436A-14. 2014. Available online: https://tds.virgo-gw.eu/ql/?c=10486 (accessed on 8 December 2020).
- Available online: https://www.covesion.com/assets/downloads/PV%20oven%20series.pdf (accessed on 8 December 2020).
- Mantovani, M.; Brooks, J.; Casanueva, J. Alignment Requirements for the Advanced Virgo+ Arm Cavity Using the Green Laser, VIR-1165A-19. 2019. Available online: https://tds.virgo-gw.eu/ql/?c=14999 (accessed on 8 December 2020).
- Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. Lasers Opt. 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Chiummo, A.; Genin, E.; Leroy, N.; Magazzù, A.; Mantovani, M.; Paoletti, F.; Pillant, G. All Fibered 532 nm Laser Source for AdV Auxiliary Lasers, VIR-0542A-16. 2016. Available online: https://tds.virgo-gw.eu/ql/?c=11859 (accessed on 8 December 2020).
- Casanueva, J.; Leroy, N. Auxiliary Laser System: Study of the Lock Acquisition Strategy, VIR-0327A-19. 2019. Available online: https://tds.virgo-gw.eu/ql/?c=14154 (accessed on 8 December 2020).
- Brooks, J.; Casanueva, J.; Mantovani, M. Green Arm Cavity Length Noise Requirement, VIR-0461A-20. 2020. Available online: https://tds.virgo-gw.eu/ql/?c=15586 (accessed on 8 December 2020).
- Brooks, J.; Casanueva, J.; Mantovani, M. Time Domain Simulation of the Green Cavity Lock in Advanced Virgo+, VIR-0527A-20. 2020. Available online: https://tds.virgo-gw.eu/ql/?c=15652 (accessed on 8 December 2020).
- Bhawal, B.; Evans, M.; Maros, E.; Rahman, M.; Yamamoto, H. Getting Started with End-to-End Model, LIGO-T980051-00-E. 1998. Available online: https://dcc.ligo.org/public/0029/T980051/000/T980051-00.pdf (accessed on 8 December 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).