Optical Characteristics of Electromagnetic Radiation, Emitted by Particles or Stars Moving near Supermassive Black Hole

Abstract

The general problem of calculating of the propagation of electromagnetic radiation from particles or stars moving in the vicinity of a supermassive black hole is considered in geometrical optics approximation within the framework of the general theory of relativity. Different approaches that can be used to calculate certain characteristics of radiation, including redshift, the intensity and rotation of the plane of polarization, which have been presented in the literature are analysed herein. The inverse problem—the calculation of the parameters of the motion of the source (star or particle) from the data of the redshift, the intensity and the plane of polarization—is also considered.

1. Introduction

Recent discoveries in the field of gravity (gravitational waves [1,2], black hole images [3,4], microgravity [5], active galactic nuclei [6,7,8], motion of the stars near Galactic Centre black hole [9,10,11,12,13,14,15,16,17,18,19,20]) show the great importance of such studies. The investigation all of these phenomena directly or indirectly uses properties of the electromagnetic radiation that propagates in the external gravitational field. As such, the problem of studying radiation propagation through space–time in the framework of the general theory of relativity seems very important.

In the present paper, we briefly review certain optical characteristics of electromagnetic radiation in the external gravitational field and theoretical methods for its calculation and study. There is a large number of studies in which certain aspects of the considered issue have been discussed (see, e.g., [21,22,23,24,25,26]). However, our aim was to present a self-consistent review of the problem. We consider the fundamental properties of electromagnetic radiation in classical general relativity and show how it can be used for obtaining information about the source of radiation.

The electromagnetic radiation characteristics of stars moving in the external gravitational field of a black hole have been considered in many papers (see, e.g., [13,14,15,16,17,18,19,20,27,28,29]). In [18,20], the calculation of the redshift of the star is considered. Furthermore, the inverse problem—calculating the parameters of the motion of the star from the redshift—is solved. The redshift function is calculated in the first Newtonian approximation. The problem of calculating radiation from pulsars in the external gravitational field was considered in the papers [28,29]. In these papers, the influence of the external gravitational field on the precession of the pulsar was taken into account. However, the influence of the gravitational field on the propagation of light was neglected. In our previous paper [30], we showed that the last effect must also generally be taken into account. Unlike the cited papers, our works use fully generally relativistic approaches in calculations. Therefore, our results can be used not only in cases of weak external gravitational field, but also in cases of a strong gravitational field (for example, in the immediate vicinity of a black hole). The main approximation used in our study is that of the possibility of using classical physics and geometrical optics approximation ($\omega \to \infty$, where $\omega$ is the electromagnetic wave frequency).

In our notations, Latin indices run from 1 to 4; Greek indices run from 1 to 3; and the signature of the space–time metric $g_{lm}$ is +2.

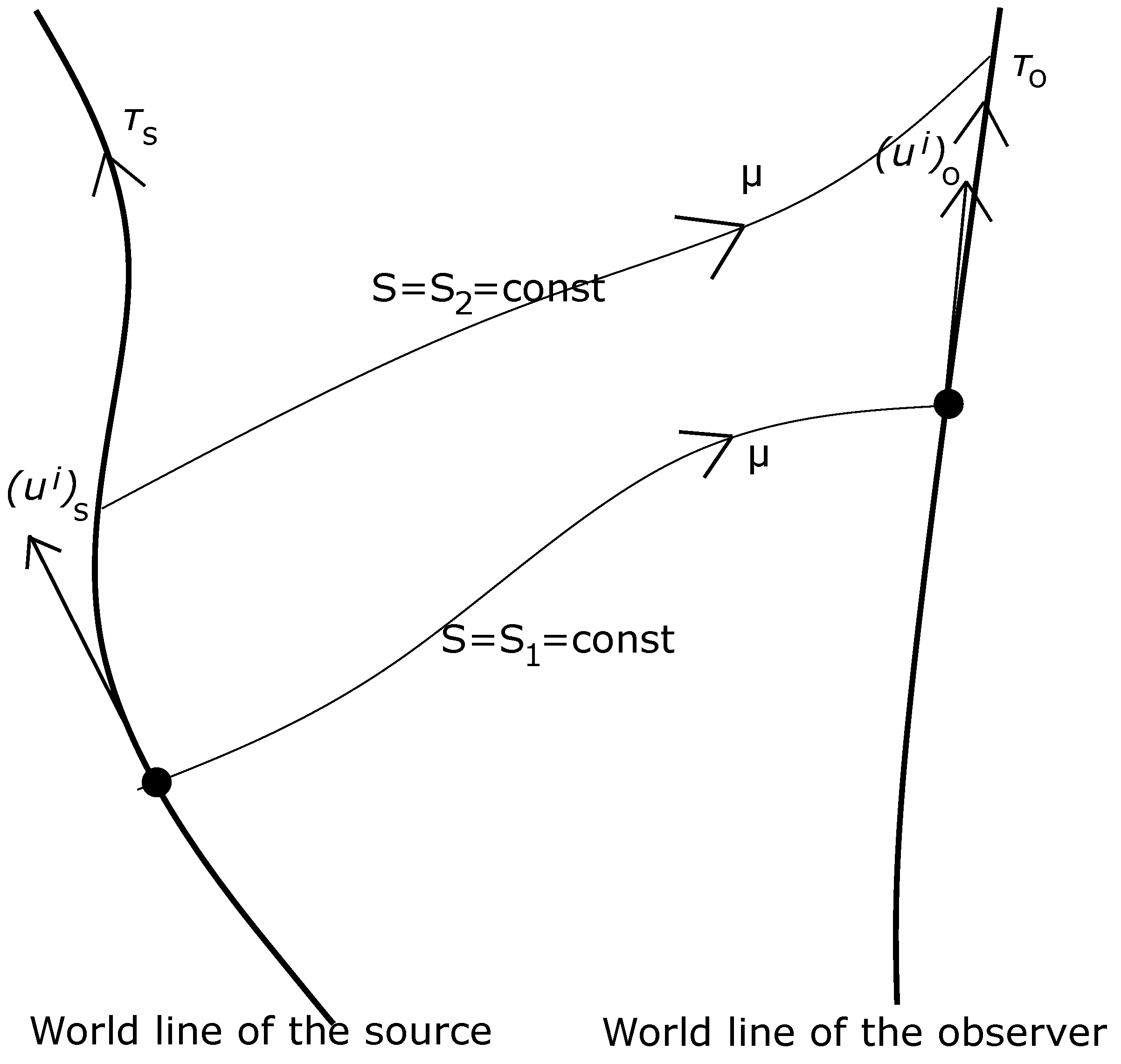
2. Geometrical Optics

In general, the electromagnetic field in curved space–time satisfies the Maxwell equation (see, e.g., [31]):

$$F_{lm}{}^{;m}=j_l,$$

(1)

where $j_l$ is the four-vector electromagnetic current. The tensor of the electromagnetic field $F_{lm}$ constructed from the electromagnetic potential $A_l$ is as follows:

$$F_{lm}=A_{l;m}-A_{m;l}.$$

(2)

Furthermore, we use the Lorentz condition:

$$A^l{}_{;l}=0.$$

(3)

We are only interested in the region where the electromagnetic field propagates in vacuum. Then, we have $j_l=0$. Geometrical optics’ approximation of the solution of Equation (1) can be obtained using the ansatz [31]:

$$A_l\left(x\right)=\widetilde{A_l}\left(x\right)e^{i\omega S\left(x\right)}.$$

(4)

Here, x denotes a space–time point, $\widetilde{A_l}\left(x\right)$ denotes the amplitude of the electromagnetic wave, $\omega S\left(x\right)$ denotes its phase, and $\omega$ denotes its frequency. In terms of geometrical optic limit, $\omega \to \infty$, while $\widetilde{A_l}\left(x\right)$, $\omega S\left(x\right)$, and their derivatives have finite values. In the formula (4), i denotes the imaginary unit. Due to the linearity of Maxwell equations, the physical values of potentials can be obtained by taking the real part from the mathematical solution (4). Taking into account that $e^{i\omega S\left(x\right)}\ne 0$ for all space–time points x, from the Lorentz condition (3) we obtain:

$$i\omega S_{,l}\left(x\right){\tilde{A}}^l\left(x\right)+{\tilde{A}}^l{}_{;l}=0.$$

(5)

Equation (5) must be satisfied in the geometrical optics limit $\omega \to \infty$. Therefore, we obtain:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\tilde{A}}^l{}_{;l}=0,\hfill \\ S_{,l}\left(x\right){\tilde{A}}^l\left(x\right)=0.\hfill \end{array}\right.\end{array}$$

(6)

By substituting the ansatz (4) into Maxwell Equation (1), another system of equations obtains in vacuum:

$$\begin{array}{ccc}\hfill & \hfill & -{\omega }^2{S}_{,m}{S}^{,m}{\tilde{A}}_l+{\omega }^2{S}_{,l}{S}^{,m}{\tilde{A}}_m-i\omega S_{,l}{}^{;m}{\tilde{A}}_m+i\omega S_{,m}{}^{;m}{\tilde{A}}_l+2i\omega S_{,m}{\tilde{A}}_l{}^{;m}-i\omega S^{,m}{\tilde{A}}_{m;l}-\hfill \\ \hfill & \hfill & i\omega S_{,l}{\tilde{A}}_m{}^{;m}+{\left({\tilde{A}}_{l;m}-{\tilde{A}}_{m;l}\right)}^{;m}=0.\hfill \end{array}$$

(7)

Taking into account geometrical optics approximation, we concluded that terms for all pours of $\omega$ on the left-hand side are equal to zero. We also used Equation (6). Then, we obtain the following equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{S}_{,m}{S}^{,m}=0,\hfill \\ S_{,m}{}^{;m}{\tilde{A}}_l+2S_{,m}{\tilde{A}}_l{}^{;m}=0,\hfill \\ {\left({\tilde{A}}_{l;m}-{\tilde{A}}_{m;l}\right)}^{;m}=0.\hfill \end{array}\right.\end{array}$$

(8)

It follows from the first equation in (8) that the vector field $k_m=\omega S_{,m}$ is isotropic. By differentiating this equation with respect to $x^l$, we obtain the equation:

$$S_{,m;l}{S}^{,m}+S^{,m}{S}_{,l;m}=0,$$

from which it follows that the vector field $k_m$ represents vectors tangent to the certain congruence of isotropic geodesics: $k_{l;m}{k}^m=0$. Physically, this congruence consists of rays of light that propagate through the gravitational field. $k_m$ is the wave vector of light.

The second equation in (8) can be rewritten in the form:

$${\left({\tilde{A}}_m{\tilde{A}}^m{k}_l\right)}^{;l},$$

which represents a certain conservation law with the current ${\tilde{A}}_m{\tilde{A}}^m{k}_l$. Physically, it means that of the conservation of the “numbers of photons” along the ray [31].

3. Redshift of the Spectrum of Electromagnetic Radiation

In the previous section, we saw that the solution (4) of the Maxwell equations in vacuum describes the wave that propagates along the null geodesic with the tangent vector $k_m=\omega S_{,m}$. A very important characteristic of the electromagnetic wave in astronomy and astrophysics is the redshift of the spectrum of radiation z. It can be defined by the following formula (see, e.g., [18]):

$$z=\frac{\delta \lambda }{\lambda }.$$

(9)

Here, $\lambda$ is the wavelength of emitted light, and $\delta \lambda$ is the difference between the wavelengths of received and emitted light.

Consider a source of the electromagnetic field and an observer. They are both moving in the external gravitational field along certain world lines that are parametrized by proper times ${\tau }_s$ and ${\tau }_o$, respectively, (see Figure 1). We parametrize isotropic geodesics by the affine parameter $\mu$, such that $k^m=\mathrm{d}{x}^m/\mathrm{d}\mu$. An isotropic geodesic describing the propagation of radiation must lie on the surface $S\left(x\right)=const$. Indeed:

$$\frac{\mathrm{d}}{\mathrm{d}\mu }S=S_{,m}{k}^m=0.$$

Consider a set of such surfaces $S=S_1$, $S=S_2$…, for which $e^{i\omega S\left(x\right)}$ has a maximum. This corresponds to the maximum value of the electromagnetic field. Part of the world line of the source/observer between two nearest surfaces (for example, $S=S_1$ and $S=S_2$) will correspond to the emission/registration of one wave of electromagnetic radiation. Let $\mathsf{\Delta }{\tau }_s$ be the proper time of the emission of the whole electromagnetic wave and $\mathsf{\Delta }{\tau }_o$ be the proper time of the detection of the whole electromagnetic wave. Therefore, we obtain:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\lambda =c\mathsf{\Delta }{\tau }_s,\hfill \\ \lambda +\delta \lambda =c\mathsf{\Delta }{\tau }_o.\hfill \end{array}\right.\end{array}$$

(10)

From (9) and (10), we obtain:

$$z=\frac{\mathsf{\Delta }{\tau }_o}{\mathsf{\Delta }{\tau }_s}-1.$$

(11)

Consider all isotropic geodesics which intersect the world lines of the source and the observer. Phase $\omega S$ is a monotonic function of proper time ${\tau }_s$. Due to this, we can parametrize while considering points by an affine parameter along the geodesic $\mu$ and parameter S that are proportional to the phase, characterizing the geodesic in congruence (see also Figure 1). From the general properties of derivatives in the Riemannian manifold, we obtain:

$$\frac{D}{DS}{\displaystyle {\displaystyle \frac{\mathrm{d}{x}^j}{\mathrm{d}\mu }}}=\frac{D}{D\mu }{\displaystyle {\displaystyle \frac{\mathrm{d}{x}^j}{\mathrm{d}S}}},$$

therefore:

$${\displaystyle {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mu }}}\left({\displaystyle {\displaystyle \frac{\mathrm{d}{x}_j}{\mathrm{d}S}}}{\displaystyle {\displaystyle \frac{\mathrm{d}{x}^j}{\mathrm{d}\mu }}}\right)={\displaystyle {\displaystyle \frac{\mathrm{d}{x}^j}{\mathrm{d}\mu }}}\frac{D}{DS}{\displaystyle {\displaystyle \frac{\mathrm{d}{x}_j}{\mathrm{d}\mu }}}=\frac{1}{2}{\displaystyle {\displaystyle \frac{\mathrm{d}}{\mathrm{d}S}}}\left({\displaystyle {\displaystyle \frac{\mathrm{d}{x}^j}{\mathrm{d}\mu }}}{\displaystyle {\displaystyle \frac{\mathrm{d}{x}_j}{\mathrm{d}\mu }}}\right)=0.$$

(12)

We introduce the following abbreviation:

$$\mathsf{\Delta }{x}^j={\displaystyle {\displaystyle \frac{\mathrm{d}{x}_j}{\mathrm{d}S}}}\left(S_2-S_1\right).$$

(13)

From (12):

$$k_j\mathsf{\Delta }{x}^j=const\mathrm{along}\mathrm{the}\mathrm{isotropic}\mathrm{geodesic}.$$

(14)

In the geometrical optics limit ($\omega \to \infty$), the period of the emitted wave $\delta {\tau }_s$ and the period of the observed wave tend towards zero. Due to this, the mentioned finite increments will become the differentials: $\mathsf{\Delta }{\tau }_s\to \mathrm{d}{\tau }_s$, $\mathsf{\Delta }{x}^j\to \mathrm{d}{x}^j$, …

${\left(k_j\right)}_s$ and ${\left(k_j\right)}_o$ denote the wave vector in the points of radiation and the observer receiving the radiation, respectively. Furthermore, ${\left(u_j\right)}_o$ and ${\left(u_j\right)}_s$ denote the four-velocity vector of the observer and of the star, respectively. From Figure 1 and relation (14), we obtain:

$${\left(k_j\right)}_s{\left(u^j\right)}_s\mathsf{\Delta }{\tau }_s={\left(k_j\right)}_o{\left(u^j\right)}_o\mathsf{\Delta }{\tau }_o.$$

(15)

From (11) and (15), it follows that:

$$z=\frac{{\left(k_j\right)}_s{\left(u^j\right)}_s}{{\left(k_l\right)}_o{\left(u^l\right)}_o}-1.$$

(16)

Comparing this result with (11) and using the relation $\omega =2\pi /\mathsf{\Delta }\tau$, with an appropriate choice of affine parameter $\mu$, we find:

$${\left(k_l\right)}_s{\left(u^l\right)}_s={\omega }_s,{\left(k_j\right)}_o{\left(u^j\right)}_o={\omega }_o.$$

(17)

4. Luminous Intensity

Another important optical characteristic of electromagnetic radiation is luminous intensity. As in the paper [32], we define this characteristic as

$$I=\frac{\mathrm{d}E}{\mathrm{d}\tau \delta \mathsf{\Omega }},$$

(18)

where $\mathrm{d}E$ is the energy emitted during a period of time $\mathrm{d}\tau$ per solid angle $\delta \mathsf{\Omega }$. For astrophysical purposes, it is interesting to know the magnification coefficient K. It is the detected to emitted luminous intensity ratio:

$$K=\frac{I_o}{I_s},$$

(19)

where indexes o and s relate to quantities at the point of the observer and of the source, respectively. Then, we obtain:

$$K=\frac{\mathrm{d}{E}_o}{\mathrm{d}{E}_s}\frac{\mathrm{d}{\tau }_s}{\mathrm{d}{\tau }_o}\frac{\delta {\mathsf{\Omega }}_s}{\delta {\mathsf{\Omega }}_o}.$$

(20)

We assume for a moment that radiation consists of photons with a frequency of $\omega$. Then, $\mathrm{d}E=\hslash \omega \mathrm{d}N$, where $\mathrm{d}N$ is the number of emitted photons and ℏ is the Plank constant. We find that:

$$\frac{\mathrm{d}{E}_o}{\mathrm{d}{E}_s}=\frac{{\omega }_o}{{\omega }_s}=\frac{1}{z+1},$$

(21)

and:

$$\frac{{\tau }_s}{{\tau }_o}=\frac{1}{z+1}.$$

(22)

Consider the elementary solid angle $\delta \mathsf{\Omega }$ that is formed by wave vectors $k^i$, $k^i+\delta k^i$, $k^i+\delta {\tilde{k}}^i$, $k^i+\delta k^i+\delta {\tilde{k}}^i$. In the flat space–time solid angle, $\mathrm{d}\mathsf{\Omega }$ has the following expression:

$$\delta \mathsf{\Omega }=\mathbf{n}·\left(\delta \mathbf{n}\times \delta \tilde{\mathbf{n}}\right),$$

(23)

where $\mathbf{n}=c\mathbf{k}/\omega$. The generally relativistic generalization of formula (23) has the form [32]:

$$\delta \mathsf{\Omega }=\frac{c^3}{{\omega }^3}\sqrt{-g}{e}_{ijml}{u}^l{k}^i\delta k^j\delta {\tilde{k}}^m.$$

(24)

Here, $g=\det g_{lm}$ and $e_{ijml}$ is the Levi–Civita symbol, $e_{1234}=1$.

Consider the external gravitational field of a Schwarzschild black hole. The metric of the Schwarzschild black hole has the form (as can be seen, e.g., in [33]):

$$\mathrm{d}{s}^2=\frac{\mathrm{d}{r}^2}{1-2M/r}+r^2\mathrm{d}{\theta }^2+r^2{sin}^2\theta \mathrm{d}{\phi }^2-\left(1-\frac{2M}{r}\right)c^2\mathrm{d}{t}^2.$$

(25)

Here, $x^i=\{ct,r,\theta ,\phi \}$ are Schwarzschild coordinates. In $M=G{m}_{BH}/c^2$, G is the gravitational constant and $m_{BH}$ is the mass of the black hole. Electromagnetic radiation propagates from the source to the observer between two space–time points. Choosing coordinate frame $\tilde{F}:\{ct,r,\tilde{\theta },\tilde{\phi }\}$ such that the observer resides on the axis $\tilde{\theta }=0,$$\tilde{\phi }=0$, we obtain that the trajectory of the ray of light lies in the plane $\tilde{\phi }=const$ and (see, e.g., [33]):

$$\begin{array}{ccc}\hfill & & k^1=\frac{\mathrm{d}r}{\mathrm{d}\mu }=e_r\frac{{\omega }_i}{c}\sqrt{1-(1-2M/r)D^2/r^2};\hfill \\ & & k^2=\frac{\mathrm{d}\tilde{\theta }}{\mathrm{d}\mu }=-\frac{D}{r^2}\frac{{\omega }_i}{c};\hfill \\ & & k^3=\frac{\mathrm{d}\tilde{\phi }}{\mathrm{d}\mu }=0;\hfill \\ & & k^4=c\frac{\mathrm{d}t}{\mathrm{d}\mu }=\frac{{\omega }_i}{c(1-2M/r)},\hfill \end{array}$$

(26)

where D is the impact parameter. Factor $e_s=\pm 1$ takes into account either the receding or approaching part of the trajectory of light under consideration. From (17), we find that ${\omega }_i$ is the frequency registered by the resting observer at infinity.

From (26) and the boundary condition $r\to \infty$ for $\tilde{\theta }=0$, we obtain the following analytical expression for the trajectory of the ray:

$$\begin{array}{ccc}& & \frac{1}{r}=\frac{1}{r_r(\tilde{\theta },D)}=\hfill \\ & & \frac{1}{P}-\frac{Q{k}^2}{2PM}{cn}^2\left[\frac{\tilde{\theta }}{2}\sqrt{\frac{Q}{P}}+F\left[arccos\left(\sqrt{\frac{2M}{Q{k}^2}}\right),k\right],k\right],\hfill \end{array}$$

(27)

where $r_r=r$ for the points of the world line of the ray:

$$\begin{array}{ccc}& & Q=\sqrt{P^2+4PM-12M};\hfill \end{array}$$

(28)

$$\begin{array}{ccc}& & k=\sqrt{\frac{Q-P+6M}{2Q}},\hfill \end{array}$$

(29)

$cn\left[\phi ,k\right]$ and $F\left[\phi ,k\right]$ are the Jacobi cosine and the elliptic integral of the first kind, respectively, (for which the definition can be found in [34]). For the real values, P has the physical meaning of the closest distance approached (see, e.g., [35]). However, in all cases (complex or real value), P can be expressed through the impact parameter D as follows:

$$P=-\frac{2}{\sqrt{3}}Dsin\left[\frac{1}{3}arcsin\left(\frac{3\sqrt{3}M}{D}\right)-\frac{\pi }{3}\right].$$

We define $\delta k^j$ as the deviation of the wave vector due to deviation of the impact parameter $\delta D$:

$$\begin{array}{c}\hfill \delta k^j=\frac{{\omega }_i}{c}\left\{\frac{-e_r(1-2M/r)D\delta D}{r^2\sqrt{1-(1-2M/r)D^2/r^2}},-\frac{\delta D}{r^2},0,0\right\}.\end{array}$$

(30)

Another deviation $\delta {\tilde{k}}^j$ is defined as the deviation due to the rotation of the plane of light propagation in the direction of $\tilde{\varphi }$ [32]:

$$\begin{array}{c}\hfill \delta {\tilde{k}}^j=\frac{{\omega }_i}{c}\left\{0,0,\frac{D}{r^2}\delta \tilde{\varphi },0\right\}.\end{array}$$

(31)

We find that $\delta {\mathsf{\Omega }}_o=sin\theta \delta \tilde{\varphi }\delta \theta$ and use the relations (24), (30) and (31). We obtain:

$$\frac{\delta {\mathsf{\Omega }}_s}{\delta {\mathsf{\Omega }}_o}=\frac{1}{{(1+z)}^{2}sin\tilde{\theta }}\frac{e_{r}D}{r^2\sqrt{1-(1-2M/r)D^2/r^2}}\frac{\partial D}{\partial \tilde{\theta }}.$$

(32)

Here, D is the solution of the equation:

$$r_r(\tilde{\theta },D)=r,$$

(33)

from which follows the solution of the boundary value problem for an isotropic geodesic. Therefore, we can find D to be a function of r and $\tilde{\theta }$. From (20)–(22) and (32), we obtain:

$$K=\frac{1}{{(1+z)}^{4}sin\tilde{\theta }}\frac{e_{r}D}{r^2\sqrt{1-(1-2M/r)D^2/r^2}}\frac{\partial D}{\partial \tilde{\theta }}.$$

(34)

5. Polarization Plane

The polarization plane of electromagnetic radiation can be determined by two vectors: the wave vector $k^i$ and the vector of electric field $E^i$. It is known that Lorentz force is directed in parallel to four-vector electric field. Therefore, the direction of the mentioned plane is measured by polarimeters. We studied the evolution of the wave vector in Section 2. The electromagnetic field is defined as (see, e.g., [31]):

$$E_l=F_{lm}{\left(u^m\right)}_o.$$

(35)

It is obvious from formula (35) that the vector $E^i$ is dependent on the velocity ${\left(u^i\right)}_o$ of the observer’s reference frame in which it is measured. In keeping with the work of [36], we introduce the following unit vectors:

$$a^m=\frac{{\tilde{A}}^m}{A};e^m=\frac{E^m}{E}.$$

Here, $A=\sqrt{A^m{\left(A_m\right)}^{*}}$ and $E=\sqrt{E^m{\left(E_m\right)}^{*}}$. The asterisk in formulas denotes complex conjugation. From Equation (8), it is easy to show that:

$$\frac{D{a}^j}{D\mu }=0.$$

(36)

In order to determine the evolution of the polarization plane, we find the evolution equation for vector $e^j$ alongside the isotropic geodesic. For this purpose, we obtain, in the geometrical optics limit, that:

$$E_l=i\omega e^{i\omega S}\left({\omega }_o{\tilde{A}}_l-k_l{\tilde{A}}_m{\left(u^m\right)}_o\right).$$

(37)

For the norm, we obtain:

$$E=\sqrt{{\omega }^2{\left({\omega }_o\right)}^2{A}^2}=\omega {\omega }_{o}A,$$

(38)

and:

$$e_l=i{a}_l-i\frac{a_m{\left(u^m\right)}_o}{{\omega }_o}{k}_l.$$

(39)

Differentiating (39) gives:

$$\frac{D{e}_l}{D\mu }=-i\frac{a_m{k}_l}{{\omega }_o}\frac{D{\left(u^m\right)}_o}{D\mu }.$$

(40)

Here, we also take into account that $a_m{\left(u^m\right)}_o=0$. The main consequence of this formula is the dependence of the evolution of a polarization plane on the motion of the set of observers.

6. Inverse Problem

6.1. General Approaches

In previous sections, we considered the main optical characteristics of electromagnetic radiation in the external gravitational field and several approaches for its calculations. However, for astrophysical purposes, it is more important to solve the inverse problem: determining the motion of the source using the known data of its electromagnetic radiation. For example, such a problem appears when we determine the motion of S-stars in the vicinity of the Galactic Centre. For the solution of this problem, the redshift and astrometric positions of the stars can be used. For the solution of the inverse problem, it is necessary to consider the ${\chi }^2$ function [17,18,20]:

$$\begin{array}{cc}\hfill & {\chi }^2={\chi }_P^2+{\chi }_Z^2,\hfill \\ \hfill \\ \hfill & {\chi }_P^2=\sum _{j=1}^N\left[\frac{{({\alpha }_j-{\alpha }_{\mathrm{obs},j})}^2+{({\beta }_j-{\beta }_{\mathrm{obs},j})}^2}{{\sigma }_P^2}\right],{\chi }_Z^2=\sum _{j=1}^N\left[\frac{{(z_j-z_{\mathrm{obs},j})}^2}{{\sigma }_Z^2}\right],\hfill \end{array}$$

(41)

where N is the number of observations, $({\alpha }_j,{\beta }_j)$ and $({\alpha }_{\mathrm{obs},j},{\beta }_{\mathrm{obs},j})$ are the angle coordinates of the source in the jth observation, calculated from the theoretical model and obtained from observations, respectively. $z_j$ and $z_{\mathrm{obs},j}$ are the redshift in the jth observation, calculated from the theoretical model and obtained from observations, respectively; ${\sigma }_P$ and ${\sigma }_Z$ are the root mean square deviations for the astrometric position and redshift, respectively. In these cases in which only one type of data exists, we obtain ${\chi }^2={\chi }_Z^2$ or ${\chi }^2={\chi }_P^2$, respectively.

All observational data are denoted by $\mathfrak{D}$, and the set of all possible parameters is denoted by $\mathsf{ƒ}$. From the Bayes theorem, we obtain:

$$\begin{array}{c}\hfill P\left(\mathsf{ƒ}\right|\mathfrak{D})=P\left(\mathfrak{D}\right|\mathsf{ƒ})P\left(\mathsf{ƒ}\right)=e^{-{\chi }^2/2}P\left(\mathsf{ƒ}\right).\end{array}$$

(42)

Assume that $P\left(\mathsf{ƒ}\right)$ has a uniform distribution. Then, the maximization of the probability $P\left(\mathsf{ƒ}\right|\mathfrak{D})$ is reduced to the minimization of ${\chi }^2$. Due to the complexity of obtaining expressions in practice, this minimization is usually performed using statistical algorithms such as the Metropolis–Hastings method [37].

6.2. Reconstruction of the Motion of the Source Using Redshift and Luminous Intensity

An approach to the solution of the inverse problem in the case of an external gravitational field of a Schwarzschild black hole is presented in [32]. This approach does not need any a priori known equations of motion of the source while the assumption of light propagation along isotropic geodesics in Riemannian space–time is used. It creates possibilities of independently finding all four coordinates and four components of the velocity vector of the source ${\left(u^j\right)}_s$. Therefore, the mentioned approach that is most useful for testing certain theories of gravity and for the study of the distribution of sources near a black hole distorts the metric. The approach proposed in [32] is based on the solution to the following system of equations:

$$\begin{array}{cc}\hfill & \frac{K_{-1}^{geom}(\varphi ,r)}{K_0^{geom}(\varphi ,r)}=\frac{I_{-1}^{obs}\left(\tau \right){(1+z^{obs}\left(\tau \right))}^4}{I_0^{obs}\left(\tau \right){(1+z^{obs}\left(\tau \right))}^4};\hfill \\ \hfill & \frac{K_1^{geom}(\varphi ,r)}{K_0^{geom}(\varphi ,r)}=\frac{I_1^{obs}\left(\tau \right){(1+z^{obs}\left(\tau \right))}^4}{I_0^{obs}\left(\tau \right){(1+z^{obs}\left(\tau \right))}^4}.\hfill \end{array}$$

(43)

Here, the geometrical magnification $K^{geom}$ can be found from magnification coefficient $K_n$ (see Section 4):

$$\begin{array}{c}\hfill K_n=\frac{I_{o,n}}{I_{s,n}}=\frac{K_n^{geom}(\varphi ,r)}{{(1+z)}^4},\end{array}$$

(44)

where $I_{s,n}$ and $I_{o,n}$ are the luminous intensity of the emitted and registered radiation, respectively. Index n is the order of the ray (see, e.g., [32,38]), $K_n$ is the radiation magnification of the order n, the calculation of which is described in Section 4. z is the redshift. Index $obs$ is related to the values that are obtained from observations. Therefore, (43) provide us with possibilities of finding $\varphi$ and r for the proper time $\tau$ (due to the axial symmetry of the problem, it is possible to find only one angle coordinate of the source). This method can only be used in cases when more than one image of the source is observed (with indexes $n=-1,n=1$).

6.3. Reconstruction of the Motion of the Components of a Binary Star That Moves in the Vicinity of a Black Hole

In this subsection, we consider the problem of the reconstruction of the motion of the binary star in the vicinity of a black hole using the redshift function only. Based of the research in [39], we consider the relative motion of the component of the binary in Fermi coordinates [33,40,41]. Consider the world line $x^i={\xi }^i\left(\tau \right)$ of a certain observer and $\tau$ their proper time. Along ${\xi }^i\left(\tau \right)$, we define the co-moving tetrad (or vierbein) $h_{\left(m\right)}{}^i$:

$$h_{\left(4\right)}{}^i=\frac{1}{c}{u}^i,h_{\left(i\right)}{}^k{h}_{\left(j\right)k}={\eta }_{\left(i\right)\left(j\right)},$$

(45)

where $u^i=\mathrm{d}{\xi }^i/\mathrm{d}\tau$ is the four velocities of the observer, ${\eta }_{\left(m\right)\left(n\right)}=\mathrm{diag}(1,1,1,-1)$.

Any point in the vicinity of world line ${\xi }^i\left(\tau \right)$ can be given coordinates $\left\{x^{\widehat{i}}\right\}$ in the following way. At first, we construct a space-like geodesic hypersurface that is orthogonal to the world line ${\xi }^i\left(\tau \right)$ at the point O which belongs to ${\xi }^i\left(\tau \right)$. All points on this hypersurface have a coordinate $x^{\widehat{4}}=c\tau$. Then, we find a geodesic line which goes through O and any point P lying on the hypersurface. At the point O, we construct a vector tangent to the geodesic. Finally, we assign to P three coordinates $X^{\left(\alpha \right)}={\sigma }_P{h}^{\left(\alpha \right)}{}_i{\eta }^i$, where ${\sigma }_P$ is the canonical parameter of the geodesic, evaluated at point P.

The equation of the relative motion of the components of the binary in co-moving Fermi coordinates for ${\xi }^i\left(\tau \right)$ that coincides with the world line of the centre of mass of the binary has the following form [42]:

$$\begin{array}{cc}\hfill & \frac{d{v}^{\left(\kappa \right)}}{d\tau }={\left(\frac{G(m_1+m_2)}{r}\right)}_{,\left(\kappa \right)}-2{\epsilon }^{\left(\kappa \right)}{}_{\left(\alpha \right)\left(\tau \right)}{\omega }^{\left(\alpha \right)}{v}^{\left(\tau \right)}-\hfill \\ \hfill & \frac{2c(m_2-m_1)}{(m_1+m_2)}{R}^{\left(\kappa \right)}{}_{\left(\nu \right)\left(\mu \right)\left(4\right)}{x}^{\left(\mu \right)}{v}^{\left(\nu \right)}+2D^{\left(\kappa \right)}{}_{\left(\nu \right)}{x}^{\left(\nu \right)}.\hfill \end{array}$$

(46)

Here, $m_{1,2}$ are the masses of the components of the binary, and $x^{\left(\alpha \right)}=X_2^{\left(\alpha \right)}-X_1^{\left(\alpha \right)}$, $X_{1,2}^{\left(\alpha \right)}$ are the Fermi coordinates of the components of the binary with respect to its centre of mass, $v_{1,2}^{\alpha }$ are their velocities, and $v^{\left(\alpha \right)}=v_2^{\left(\alpha \right)}-v_1^{\left(\alpha \right)}$, ${\omega }^{\left(\alpha \right)}$ is the angular velocity of the tetrad:

$${\omega }^{\left(\alpha \right)}=\frac{1}{2}{\epsilon }^{\left(\alpha \right)\left(\kappa \right)\left(\tau \right)}{h}_{\left(\tau \right)i}\frac{D{h}_{\left(\kappa \right)}{}^i}{D\tau }.$$

Furthermore, the following abbreviation is introduced:

$$D_{\left(\mu \right)\left(\nu \right)}=-\frac{c^2}{2}{R}_{\left(4\right)\left(\mu \right)\left(4\right)\left(\nu \right)}+\frac{1}{2}({\delta }_{\left(\mu \right)\left(\nu \right)}{\omega }^2-{\omega }_{\left(\mu \right)}{\omega }_{\left(\nu \right)}).$$

${\epsilon }^{\left(\alpha \right)}{}_{\left(\beta \right)\left(\gamma \right)}$ is the Levi–Civita symbol and the tetrad components of the curvature tensor $R_{ijkl}$ can be calculated as $R_{\left(m\right)\left(n\right)\left(p\right)\left(q\right)}=h^i{}_{\left(m\right)}{h}^j{}_{\left(n\right)}{h}^k{}_{\left(p\right)}{h}^l{}_{\left(q\right)}{R}_{ijkl}$. For the source in a binary system, the following relation holds (see [42]):

$$\begin{array}{c}\hfill z\left(\tau \right)=(1+z_0\left(\tau \right))\left(1-\frac{1}{c}{\displaystyle {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\tau }}}\left(n_{\left(\alpha \right)}{X}_1^{\left(\alpha \right)}\right)\right)-1+\mathrm{O}\left(\frac{{\varrho }^2}{M^2},\frac{v^2}{c^2}\right),\end{array}$$

(47)

where $\varrho$ is the order of relative distance between the components of the binary; v is their relative velocity; $z_0\left(\tau \right)$ is the redshift of the light of the imagined source that is located at the centre of mass of the binary; $\tau$ is the proper time of the centre of mass of the binary; and $n^{\left(\alpha \right)}=k^{\left(\alpha \right)}/\sqrt{k_{\left(\beta \right)}{k}^{\left(\beta \right)}}$ is the normalised three-wave vector of the light ray at the point of radiation.

The proper time of the star can be expressed by

$$t\left(\tau \right)=\underset{0}{\overset{\tau }{\int }}(1+z\left({\tau }^{\prime }\right))\mathrm{d}{\tau }^{\prime }.$$

(48)

Assume that only the function $z\left(t\right)$ is known from the observation. It consists of two parts: the slowly changing part $z_0\left(t\right)$ and the quickly oscillating part $z_r\left(t\right)=\mathrm{d}\left(n_{\left(\alpha \right)}{X}_1^{\left(\alpha \right)}\right)/\left(c\mathrm{d}\tau \right).$ In the paper [39], an approach that allows one to determine each part of redshift independently is presented. Consider the case when radiation from only one component (with mass $m_1$) of the binary system can be received by the observer on Earth. In order to use the formulas (46) and (47) for the motion of the stars and the redshift, it is necessary to introduce a Fermi basis that satisfies the standard relations [33,40,41].

The following abbreviations denote the parameters of the orbit relative to the picture plane—the two-dimensional plane that is orthogonal to vector $n^{\left(\alpha \right)}$:

• $i\in [0,\pi ]$—orbital inclination is the angle between the picture plane and the plane of the orbit;
• ${\omega }_r\in [0,\pi ]$—pericentre longitude, counted along the orbital plane;
• $\zeta \in [0.2\pi ]$—position angle, counted along the picture plane.

The period of the relative motion of the components can be found with very good accuracy by considering the function $(1+z(\tau \left)\right)/f\left(t\right(\tau \left)\right)$ that is approximately periodic:

$$T\approx \frac{\mathsf{\Delta }{T}_N}{(N-1)}$$

(49)

where $\mathsf{\Delta }{T}_N$ is the interval of proper time that is bounded by the local maxima of the function that consists of N maxima. Consider function $z_r\left(\tau \right)$ through time interval $T.$ The local maximum of the function $z_r\left(\tau \right)$ is denoted by $z_a$ (the corresponding proper time ${\tau }_a$) and the following local minimum is denoted by $z_c$ (the corresponding proper time ${\tau }_c$). Then, ${\tau }_a<{\tau }_c$. Furthermore, times ${\tau }_b,$${\tau }_d$ are denoted such that $z_r\left({\tau }_b\right)=0,$$z_r\left({\tau }_d\right)=0,$${\tau }_a<{\tau }_b<{\tau }_c<{\tau }_d$ and ${\tau }_d-{\tau }_a=T.$ We define:

$$h_1=\underset{{\tau }_a}{\overset{{\tau }_b}{\int }}{z}_r\left(\tau \right)\mathrm{d}\tau ;h_2=-\underset{{\tau }_c}{\overset{{\tau }_d}{\int }}{z}_r\left(\tau \right)\mathrm{d}\tau .$$

(50)

Using the Lemann–Files method (see, e.g., [43]), we obtain:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\omega }_r=1\left[\frac{2\sqrt{-z_a{z}_c}}{z_a-z_c}\frac{(h_1-h_2)}{(h_1+h_2)}\right];\hfill \\ e=\frac{z_a+z_c}{z_a-z_c}\frac{1}{cos{\omega }_r}.\hfill \end{array}\right.\end{array}$$

Here, e is the eccentricity of the orbit. In the Newtonian limit, it is possible to find only one more parameter of motion—that of the mass function $M_2$:

$$M_2=\frac{m_{2}sini}{{(m_1+m_2)}^{2/3}}=c{\left(\frac{T}{16\pi G}\right)}^{1/3}(z_a-z_b)\sqrt{1-e^2}.$$

(51)

The presence of an external gravitational field decrees the symmetry of the system relative to the considered approximation (Newtonian motion in flat space–time). Due to this, it is possible to anticipate that the addition parameters can be found as a result of the more detailed investigation of the inverse problem for the relative motion [39]. Finally, the obtained results can be used as starting values for the minimization of the ${\chi }^2$ function (see Section 6.1).

7. Conclusions

The presented theoretical investigation of electromagnetic radiation in an external gravitational field offers possibilities for calculating registered optical characteristics. It was shown that these characteristics depend on the external gravitational field and on the motion of the source. It is thus possible, in principle, to determine the motion of the source from the known optical characteristics of radiation. On the other hand, the presented approach can be used for testing the general theory of relativity.

The existing approaches that offer the possibility of reconstructing the motion of the source were presented. It was shown that we can have a simpler form of the solution, from a theoretical point of view, if two or more characteristics of radiation are known. For example, these can be redshift, the observation position and luminous intensity. However, luminous intensity and astrometric position can usually be measured with much less accuracy than the redshift. It is therefore interesting to study approaches that use redshift only. Such an approach was presented in Section 6.3 for the case of the source in the binary star that moves in the external gravitational field of a supermassive black hole.

Another example is that of polarization plane evolution (see Section 5). These characteristics can also be measured with quite good accuracy. We believe that the future theoretical development of this approach may enable the study of the motion of the sources of polarized radiation in an external gravitational field from the observation data of the plane of polarization. For example, such sources may be pulsars in the vicinity of the Galactic Centre black hole.

The presented approach for studying the propagation of an electromagnetic field is only valid in classical (non-quantum) theory. However, it has certain benefits relative to methods where radiation propagation is considered a motion of massless particles. For example, the presented approach offers the possibility of using the properties of the congruences of isotropic geodesics, but not solutions for each geodesic separately.

The presented approaches were formulated for the case of the general theory of relativity. However, apart from the approaches in Section 6.3, they can immediately be used in the case of all metric theories of gravity.