Experimental and Numerical Study on Mixed Lubrication Performance of Journal Bearing Considering Misalignment and Thermal Effect
Abstract
:1. Introduction
2. Modeling
2.1. Misaligned Journal Geometry Model
2.2. Average Flow Generalized Reynolds Equation
2.3. Energy Equation and Boundary Conditions
2.4. Viscosity–Temperature and Viscosity–Pressure Model
2.5. Asperity Contact Model
2.6. Bearing Performances
2.6.1. Load Capacity
2.6.2. Attitude Angle
2.6.3. Side Leakage Flow
2.6.4. Frictional Force
2.7. Convergence Criterion
3. Numerical Solving Procedure and Validation
3.1. Numerical Solving Procedure
- (a)
- Mesh the oil film and bearing and input the node coordinates. Initialize the film temperature, pressure, and viscosity.
- (b)
- Calculate the film thickness with journal misalignment and asperity contact pressure.
- (c)
- Solve the integral of the viscosity function.
- (d)
- Obtain the oil film pressure by solving the average flow generalized Reynolds Equation (4) using the finite difference method. In the meantime, determine whether formula (19) is satisfied.
- (e)
- Calculate the coefficient velocity term and velocity derivative term in the energy Equation (6).
- (f)
- Obtain the film temperature by solving the energy Equation (6) and solid heat conduction Equation (7) and decide whether expression (19) satisfies the convergence condition.
- (g)
- Solve the viscosity temperature–viscosity pressure equation (8) and obtain the viscosity field of film.
- (h)
- Repeat steps (b)~(g) until both the pressure and temperature meet the convergence conditions.
- (i)
- Compute the bearing capacity and complete the iteration of the attitude angle. Then, calculate the bearing performance parameters.
3.2. Validation
4. Analysis and Discussion
4.1. The Effect of Journal Misalignment on Lubrication States
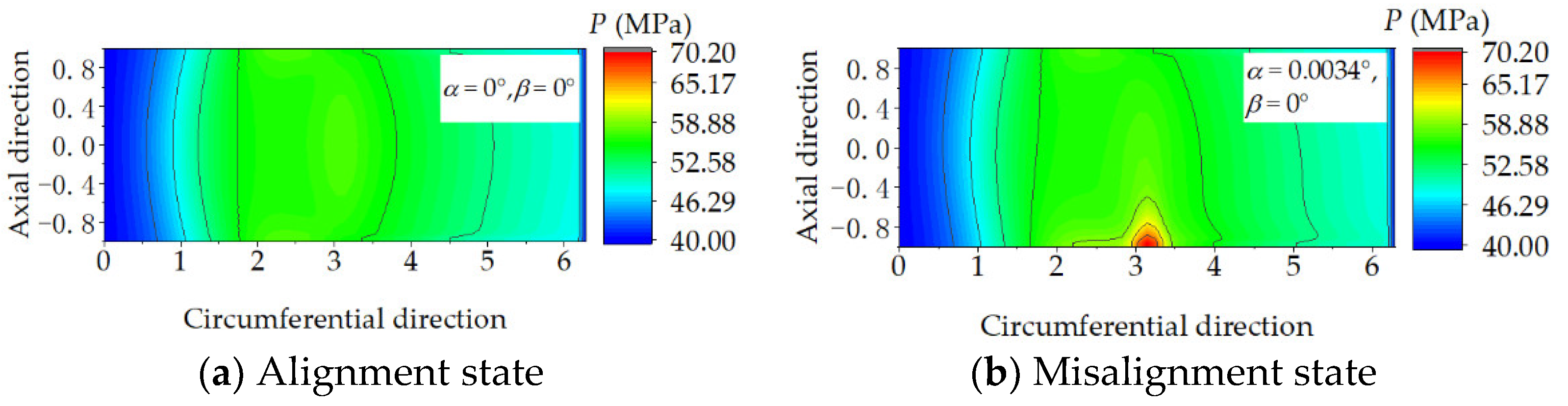
4.2. The Effect of Journal Misalignment on Geometry Clearance and Pressure Field
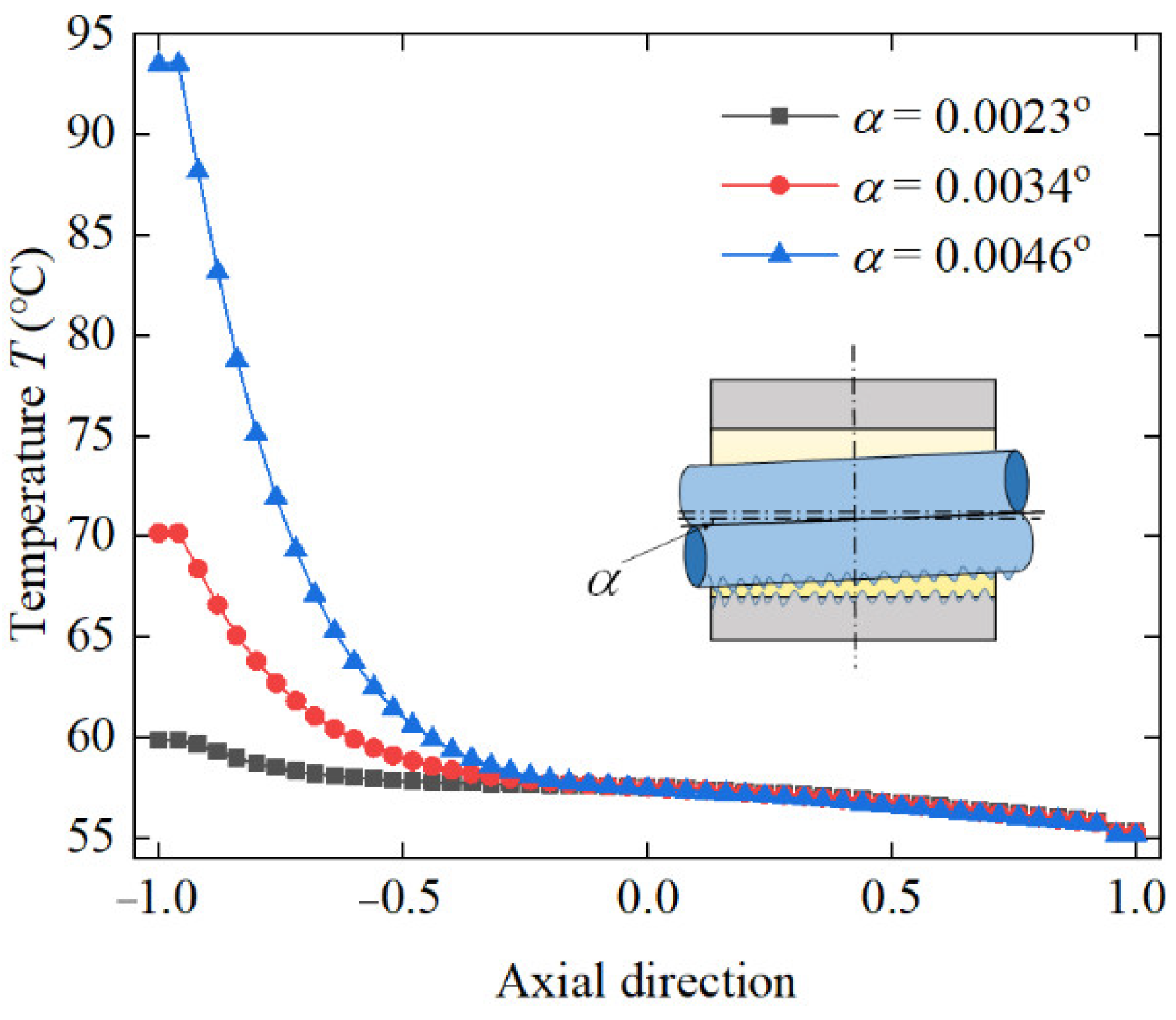
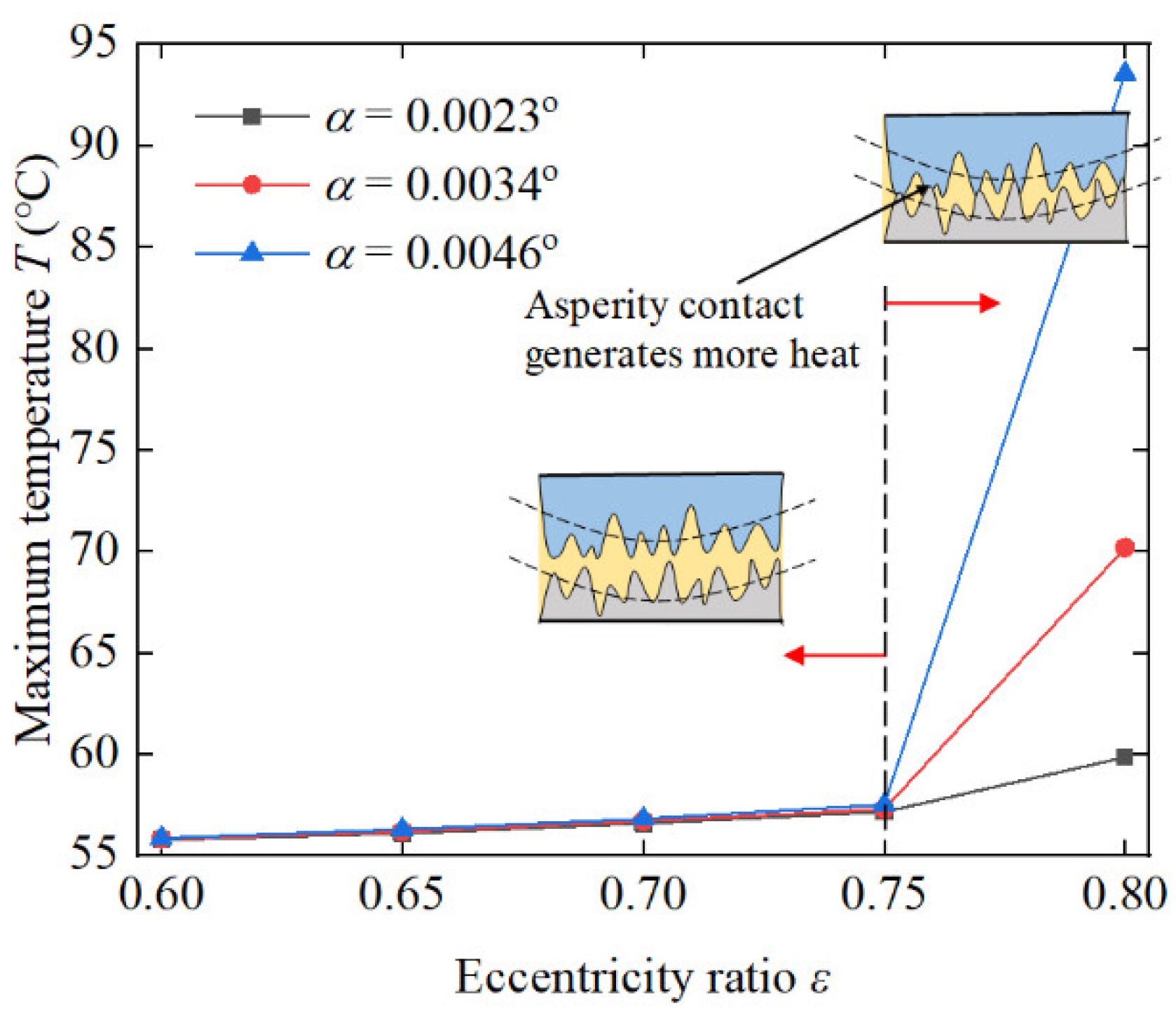
4.3. The Effect of Journal Misalignment on Thermal Performances
4.4. Performance Parameter Analysis of Misaligned Journal Bearing
4.4.1. Attitude Angle
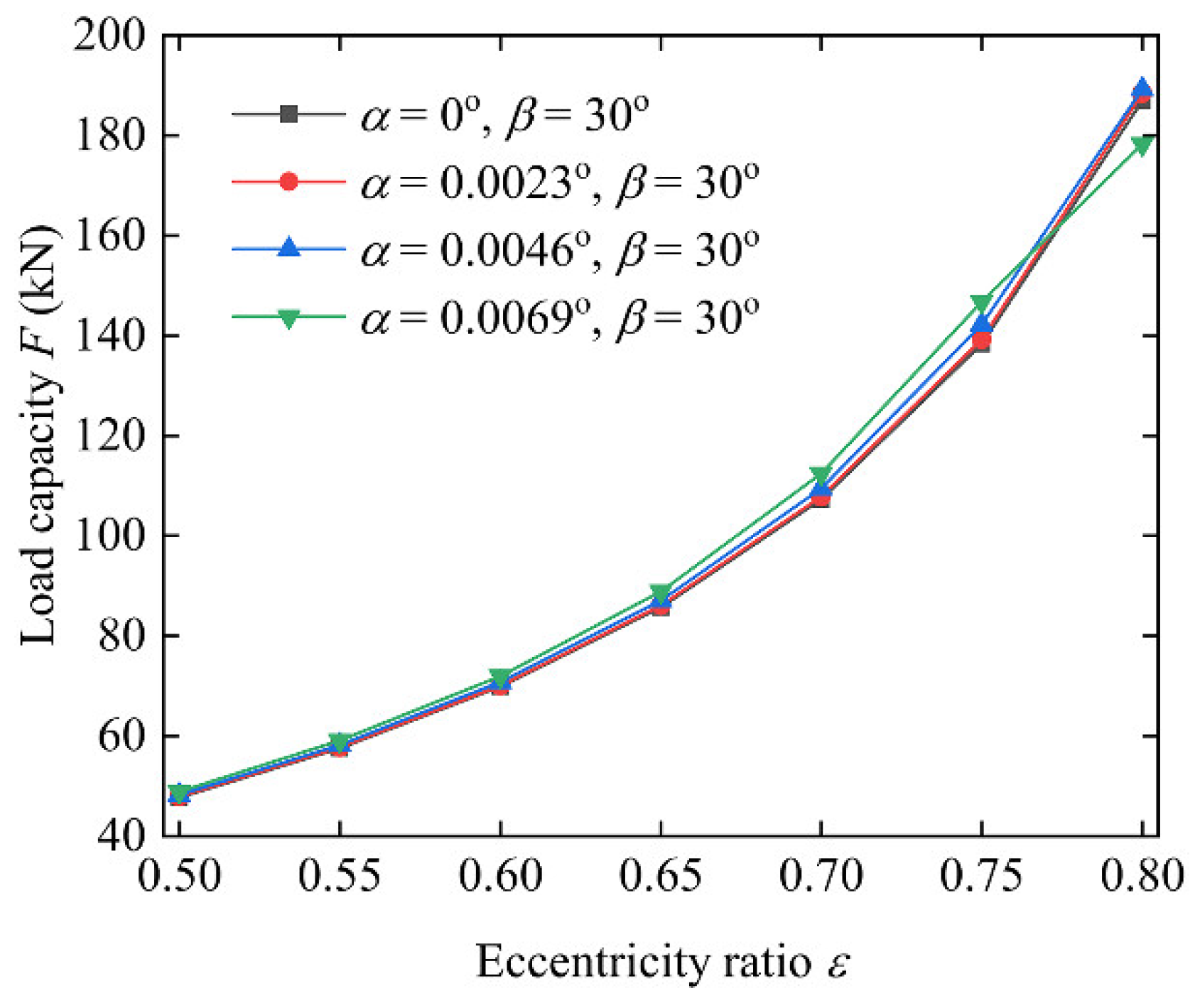
4.4.2. Load Capacity
4.4.3. Frictional Force
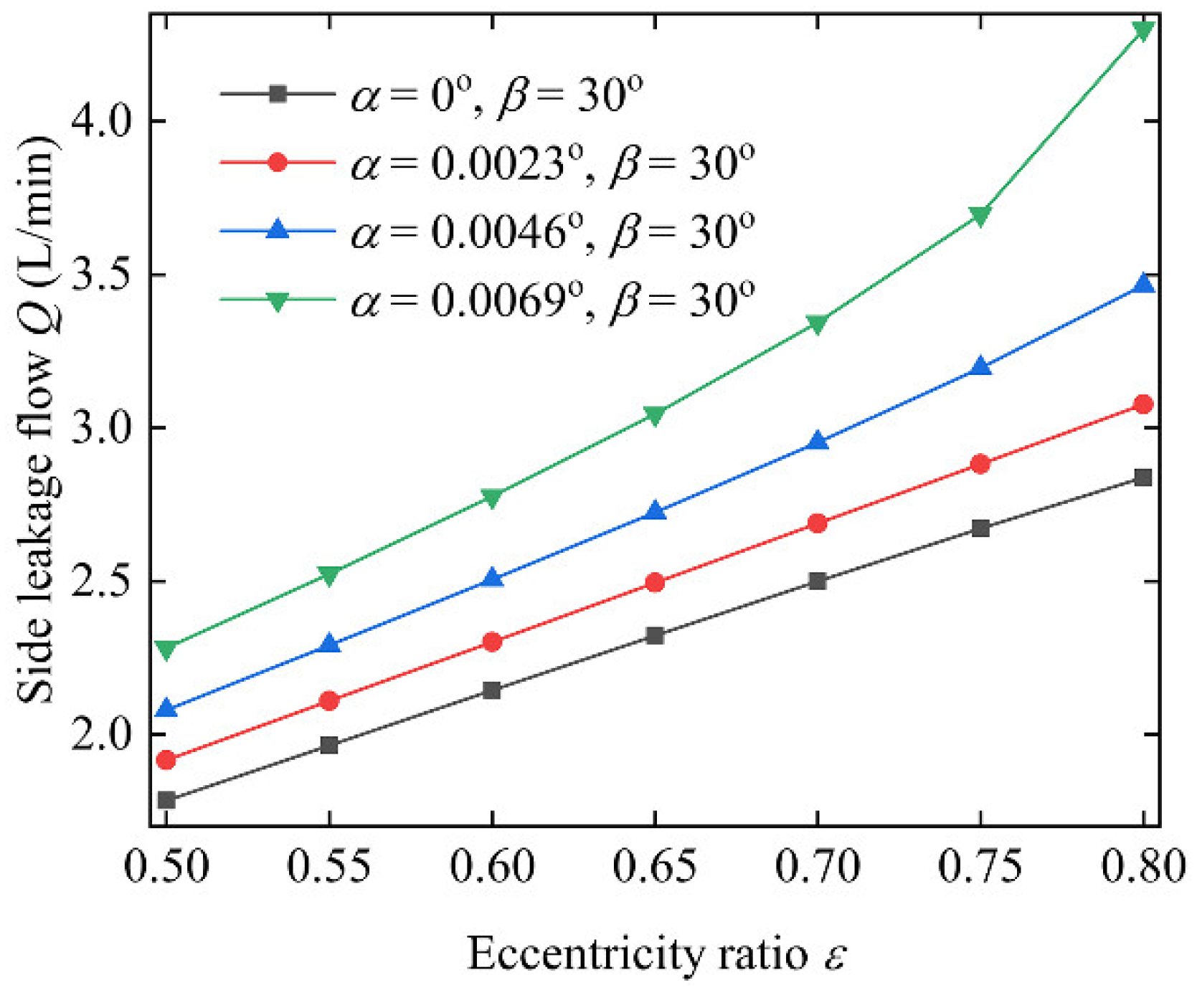
4.4.4. Side Leakage Flow
5. Experiment Research
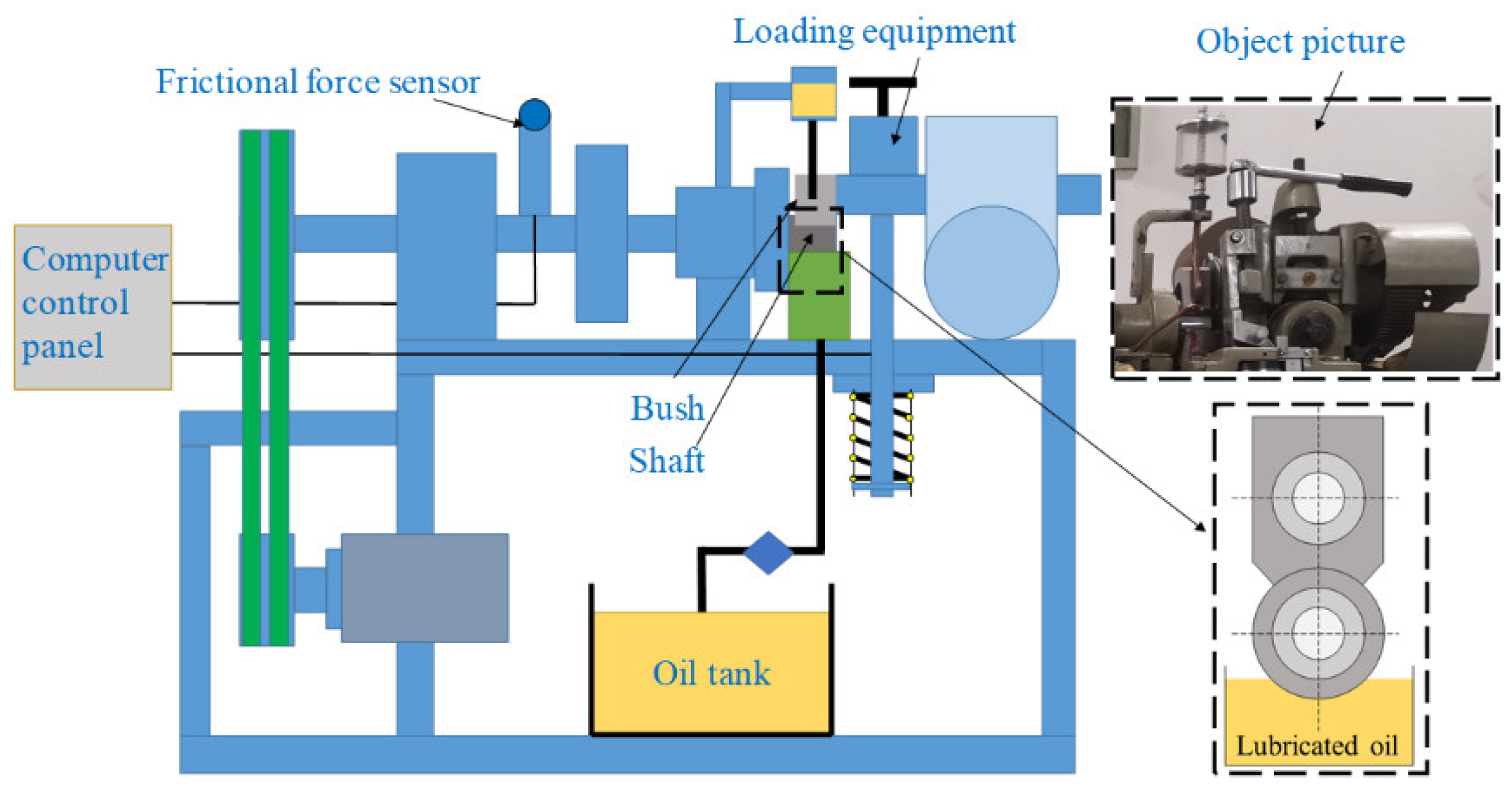
5.1. Experiment Equipment
5.2. Bush and Shaft in Experiment
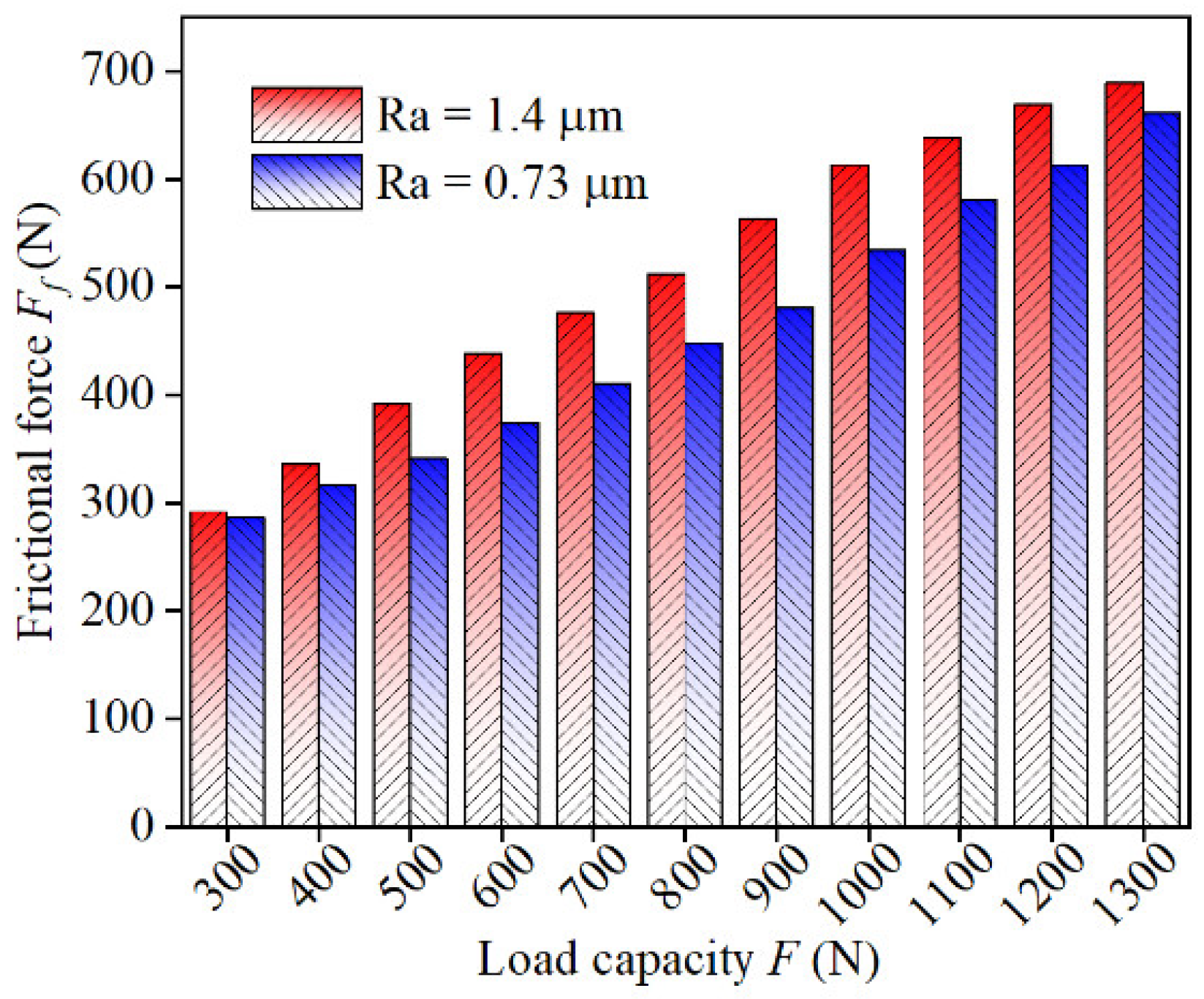
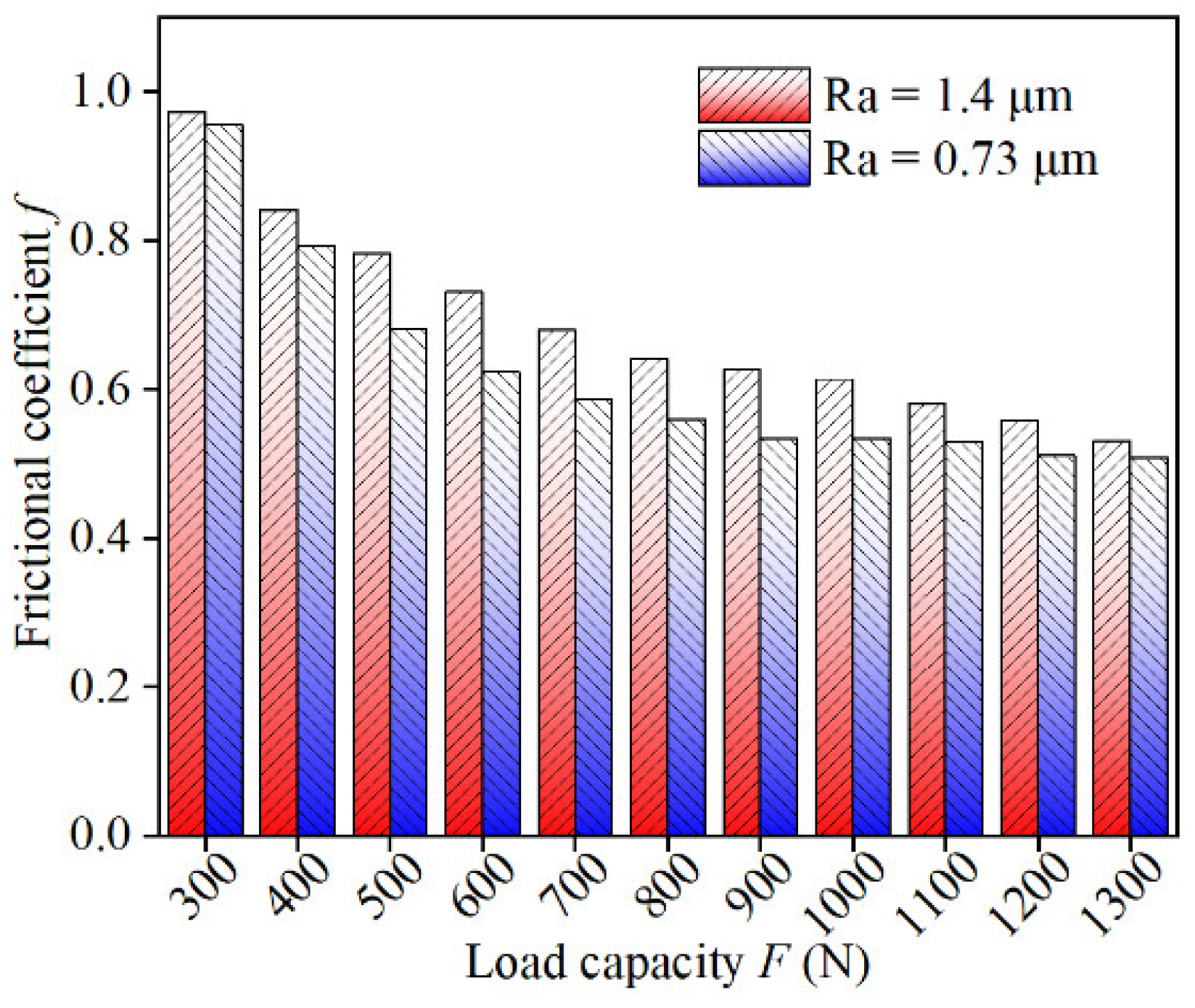
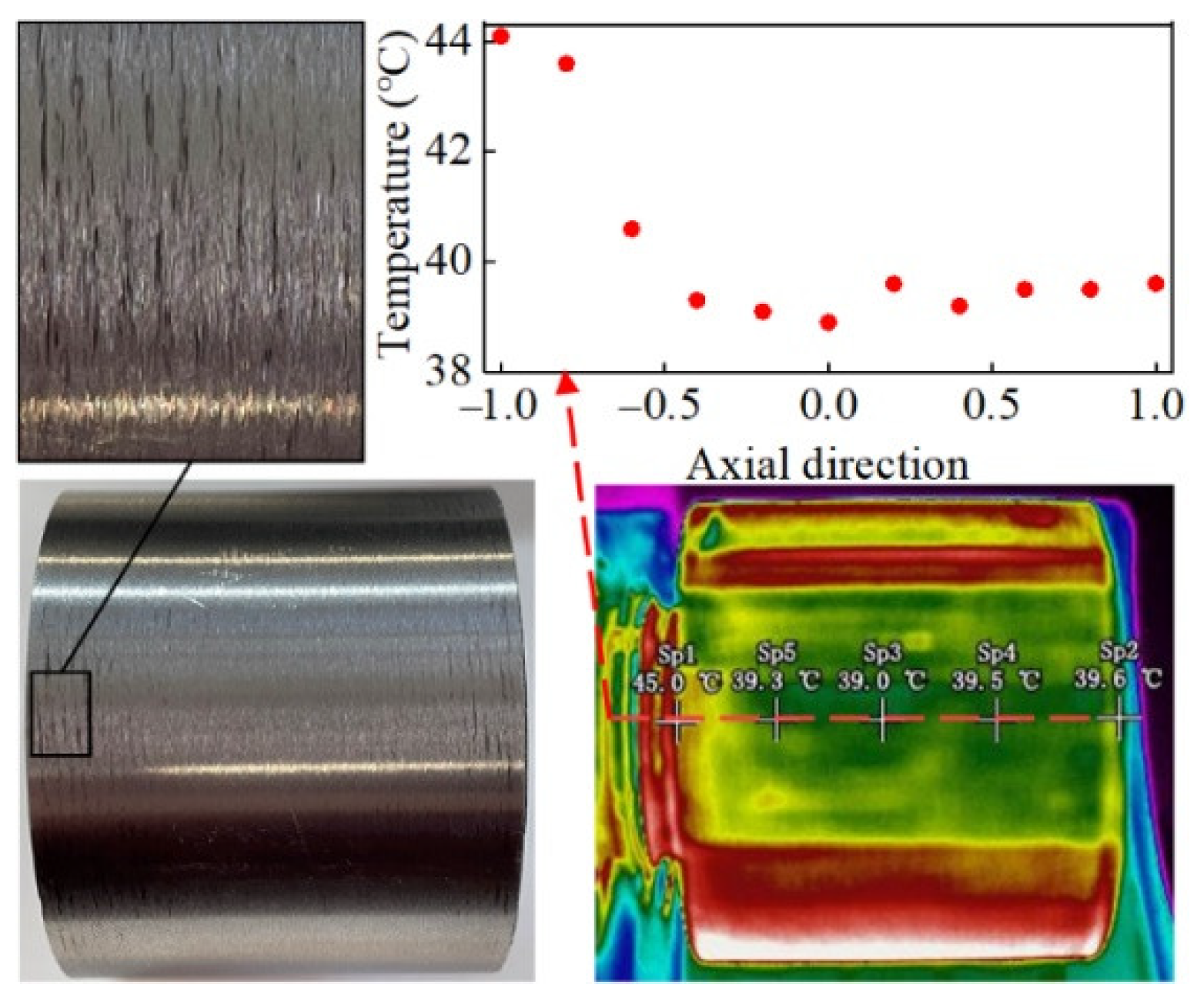
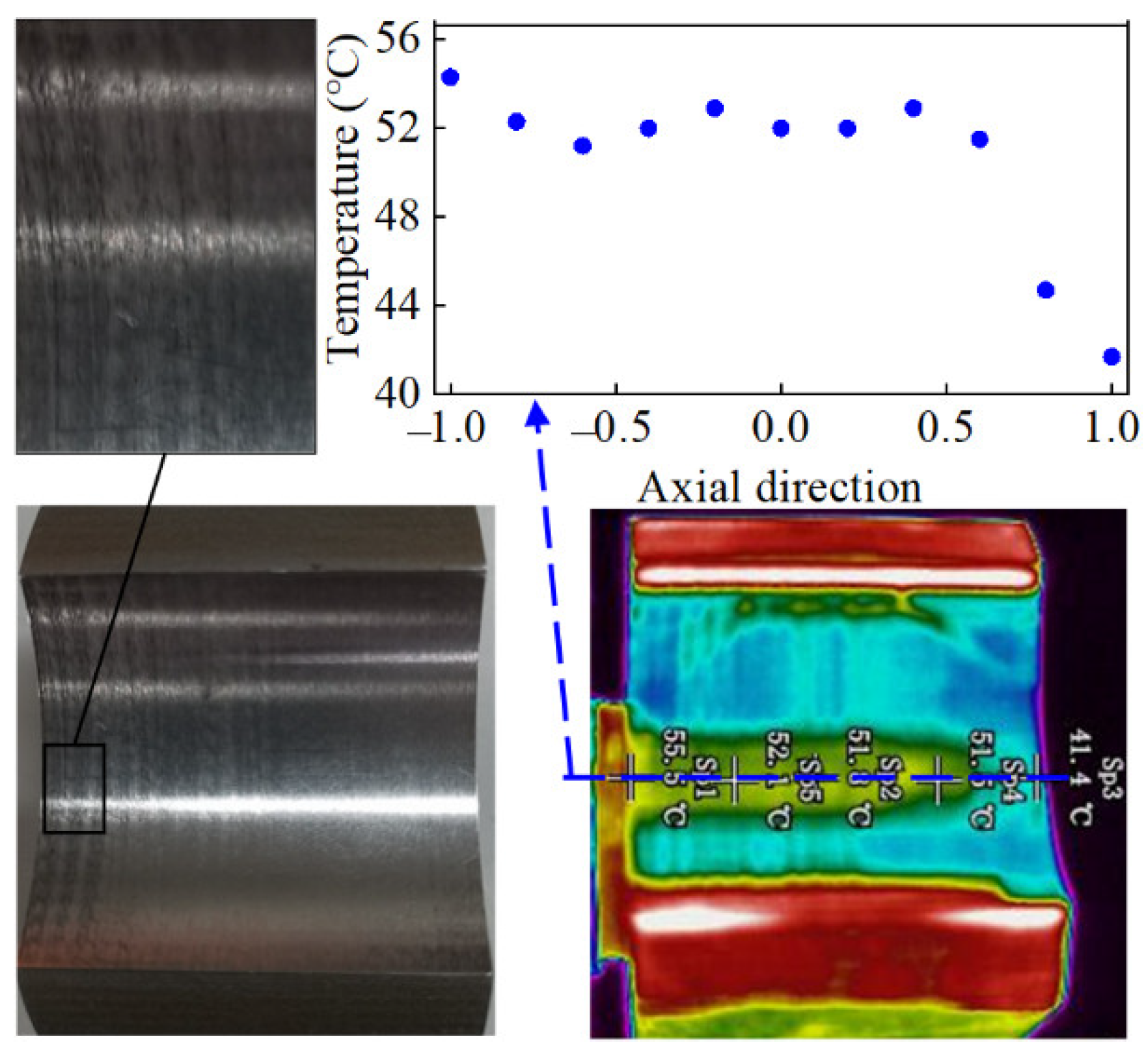
5.3. Experiment Results
6. Conclusions
- (1)
- Journal misalignment had a notable influence on the lubrication states, hydrodynamic pressure, and contact pressure. Under the aligned condition, the asperity contact pressure was larger at both sides due to the elastic deformation of the bearing. However, under the misaligned condition, the hydrodynamic pressure distribution skewed to one side, and the asperity contact pressure only occurred at one side of the bearing.
- (2)
- Temperature field distribution had a significant asymmetry along the axial direction and the temperature greatly increased with the misalignment because of the additional heat generated by asperity contact.
- (3)
- The frictional force showed a sharp rise with the increase in the misalignment angle. This also indicates that journal misalignment makes mixed lubrication occur easily. Furthermore, side leakage flow increased with the increase in the misalignment angle. The attitude angle on side-section and load capacity showed little variation within a small misalignment range.
- (4)
- The experiment results showed that the misalignment phenomenon had a notable influence on mixed lubrication between the journal and the bearing surface and caused the wear on one side.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| e | Eccentricity at axial mid-plane, (mm) |
| ε | Eccentricity ratio |
| α | Misalignment angle of axial direction, (°) |
| β | Misalignment angle of circumferential direction, (°) |
| r | Radius of shaft, (mm) |
| φ | Circumferential angle, (°) |
| R | Inner radius of bush, (mm) |
| p | Hydrodynamic pressure, (MPa) |
| t | Thickness of bearing layer, (mm) |
| h | Total nominal film thickness, (mm) |
| Average film thickness, (mm) | |
| c | Radial clearance, (mm) |
| ν0 | Poisson’s ratio |
| E | Modulus of elasticity, (GPa) |
| U | Linear velocity, (m/s) |
| l | Width of bearing, (mm) |
| φs | Shear flow factor |
| φx,φz | Pressure flow factor |
| σ | Surface roughness, (μm) |
| pc | Contact pressure, (MPa) |
| ρ | Lubricated oil density, (kg/m3) |
| κ | Thermal conductivity of oil, (W/m⋅°C) |
| cv | Specific heat of oil, (J/kg·K) |
| T | Temperature of oil, (°C) |
| T0 | Initial temperature of oil, (°C) |
| Tb | Temperature of bush, (°C) |
| fc | Boundary frictional coefficient |
| Ac | Contact area, (mm2) |
| A | Contact area, (mm2) |
| η | Viscosity of lubricant, (Pa·s) |
| rb | Radial coordinate of journal |
| Ts | Temperature of shaft, (°C) |
| kb | Thermal conductivity of bush, (W/m⋅°C) |
| Rb | Outside bearing radius, (mm) |
| Ta | Ambient temperature, (°C) |
| hb | Convection heat transfer coefficient, (W/m2⋅°C) |
| η0 | Initial viscosity of oil, (Pa·s) |
| α0 | Viscosity–pressure coefficient |
| β0 | Viscosity–temperature coefficient |
| χ | Asperity density |
| ξ | Curvature radius of asperity |
| F | Load carrying capacity, (N) |
| θ0 | Attitude angle of mid-section, (°) |
| Ff | Frictional force, (N) |
| Q | Leakage flow, (L/min) |
| Subscripts | |
| c | Contact |
| f | Friction |
| b | Bearing |
| s | Shaft |
| a | Ambient |
| E | Elastic |
| x,z | Circumferential, axial direction |
References
- Li, B.; Sun, J.; Zhu, S.; Fu, Y.; Zhao, X.; Wang, H.; Teng, Q.; Ren, Y.; Li, Y.; Zhu, G. Thermohydrodynamic lubrication analysis of misaligned journal bearing considering the axial movement of journal. Tribol. Int. 2019, 135, 397–407. [Google Scholar] [CrossRef]
- Shenoy, S.B.; Pai, R. Theoretical investigations on the performance of an externally adjustable fluid-film bearing including misalignment and turbulence effects. Tribol. Int. 2009, 42, 1088–1100. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Zhu, W.; Tian, W.; Hao, L. Theoretical and experimental investigation on the influences of misalignment on the lubrication performances and lubrication regimes transition of water lubricated bearing. Mech. Syst. Signal Process. 2021, 149, 107211. [Google Scholar] [CrossRef]
- Lv, F.; Rao, Z.; Ta, N.; Jiao, C. Mixed-lubrication analysis of thin polymer film overplayed metallic marine stern bearing considering wall slip and journal misalignment. Tribol. Int. 2017, 109, 390–397. [Google Scholar] [CrossRef]
- Pei, J.; Han, X.; Tao, Y.; Feng, S. Mixed elastohydrodynamic lubrication analysis of line contact with Non-Gaussian surface roughness. Tribol. Int. 2020, 151, 106449. [Google Scholar] [CrossRef]
- Chong, W.W.F.; Hamdan, S.H.; Wong, K.J.; Yusup, S. Modelling Transitions in Regimes of Lubrication for Rough Surface Contact. Lubricants 2019, 7, 77. [Google Scholar] [CrossRef] [Green Version]
- De Kraker, A.; van Ostayen, R.A.J.; Rixen, D.J. Calculation of Stribeck curves for (water) lubricated journal bearings. Tribol. Int. 2007, 40, 459–469. [Google Scholar] [CrossRef]
- Liang, Y.; Gao, D.; Chen, B.; Zhao, J. Friction and Wear Study on Friction Pairs with a Biomimetic Non-smooth Surface of 316L Relative to CF/PEEK under a Seawater Lubricated Condition. Chin. J. Mech. Eng. 2019, 32, 66. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Sun, J.; Li, B.; Zhu, G. Thermal turbulent lubrication analysis of rough surface journal bearing with journal misalignment. Tribol. Int. 2020, 144, 106109. [Google Scholar] [CrossRef]
- Lv, F.; Ta, N.; Rao, Z. Analysis of equivalent supporting point location and carrying capacity of misaligned journal bearing. Tribol. Int. 2017, 116, 26–38. [Google Scholar] [CrossRef]
- Abdou, K.M.; Saber, E. Effect of rotor misalignment on stability of journal bearings with finite width. Alex. Eng. J. 2020, 59, 3407–3417. [Google Scholar] [CrossRef]
- Cui, S.; Gu, L.; Fillon, M.; Wang, L.; Zhang, C. The effects of surface roughness on the transient characteristics of hydrodynamic cylindrical bearings during startup. Tribol. Int. 2018, 128, 421–428. [Google Scholar] [CrossRef]
- Guo, Z.-W.; Yuan, C.-Q.; Bai, X.-Q.; Yan, X.-P. Experimental Study on Wear Performance and Oil Film Characteristics of Surface Textured Cylinder Liner in Marine Diesel Engine. Chin. J. Mech. Eng. 2018, 31, 52. [Google Scholar] [CrossRef] [Green Version]
- Zapletal, T.; Sperka, P.; Krupka, I.; Hartl, M. The effect of surface roughness on friction and film thickness in transition from EHL to mixed lubrication. Tribol. Int. 2018, 128, 356–364. [Google Scholar] [CrossRef]
- Prölß, M.; Schwarze, H.; Hagemann, T.; Zemella, P.; Winking, P. Theoretical and Experimental Investigations on Transient Run-Up Procedures of Journal Bearings Including Mixed Friction Conditions. Lubricants 2018, 6, 105. [Google Scholar] [CrossRef] [Green Version]
- Lv, F.; Zou, D.; Ta, N.; Rao, Z. Influence of local turbulent flow on the performance of a mixed-lubrication bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 1029–1035. [Google Scholar] [CrossRef]
- Babu, P.V.; Ismail, S.; Ben, B.S. Experimental and numerical studies of positive texture effect on friction reduction of sliding contact under mixed lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 360–375. [Google Scholar] [CrossRef]
- Reddy, A.R.; Ismail, S. Tribological performance of textured parallel sliding contact under mixed lubrication condition by considering mass conservation condition and couple-stress parameter. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 410–422. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; He, T.; Wang, J.; Xiao, K.; Li, J. Transient tribo-dynamic model for journal bearings during start-up considering 3D thermal characteristic. Tribol. Int. 2020, 144, 106123. [Google Scholar] [CrossRef]
- Xie, Z.; Zhu, W. Theoretical and experimental exploration on the micro asperity contact load ratios and lubrication regimes transition for water-lubricated stern tube bearing. Tribol. Int. 2021, 164, 107105. [Google Scholar] [CrossRef]
- Sun, J.; Changlin, G. Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation. Tribol. Int. 2004, 37, 841–848. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, X.; Zhang, L.; Wang, X.; Wang, C.; Wang, H.; Zhao, X. Effect of surface roughness, viscosity-pressure relationship and elastic deformation on lubrication performance of misaligned journal bearings. Ind. Lubr. Tribol. 2014, 66, 337–345. [Google Scholar] [CrossRef]
- Jang, J.; Khonsari, M. On the Characteristics of Misaligned Journal Bearings. Lubricants 2015, 3, 27–53. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Yin, Z.; Jiang, D.; Gao, G.; Wang, Y.; Wang, X. Load carrying capacity of misaligned hydrodynamic water-lubricated plain journal bearings with rigid bush materials. Tribol. Int. 2016, 99, 1–13. [Google Scholar] [CrossRef]
- Das, S.; Guha, S.K. Numerical analysis of steady-state performance of misaligned journal bearings with turbulent effect. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 81. [Google Scholar] [CrossRef]
- Manser, B.; Belaidi, I.; Hamrani, A.; Khelladi, S.; Bakir, F. Performance of hydrodynamic journal bearing under the combined influence of textured surface and journal misalignment: A numerical survey. Comptes Rendus Mécanique 2019, 347, 141–165. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Wang, L. Thermoelastohydrodynamic analysis of misaligned bearings with texture on journal surface under high-speed and heavy-load conditions. Chin. J. Aeronaut. 2019, 32, 1331–1342. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; Wang, J.; Xiao, K.; Li, J. A transient hydrodynamic lubrication comparative analysis for misaligned micro-grooved bearing considering axial reciprocating movement of shaft. Tribol. Int. 2019, 132, 11–23. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, H.; Zhu, J.; Deng, Y. Effects of oil film thickness and viscosity on the performance of misaligned journal bearings with couple stress lubricants. Tribol. Int. 2020, 146, 106229. [Google Scholar] [CrossRef]
- Lv, F.; Jiao, C.; Ta, N.; Rao, Z. Mixed-lubrication analysis of misaligned bearing considering turbulence. Tribol. Int. 2018, 119, 19–26. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M. On the wear of dynamically-loaded engine bearings with provision for misalignment and surface roughness. Tribol. Int. 2020, 141, 105919. [Google Scholar] [CrossRef]
- Mokhiamer, U.M.; Crosby, W.A.; El-Gamal, H.A. A study of a journal bearing lubricated by fluids with couple stress considering the elasticity of the liner. Wear 1999, 224, 194–201. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol.-Trans. ASME 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Bukovnik, S.; Offner, G.; Čaika, V.; Priebsch, H.H.; Bartz, W.J. Thermo-elasto-hydrodynamic lubrication model for journal bearing including shear rate-dependent viscosity. Lubr. Sci. 2007, 19, 231–245. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
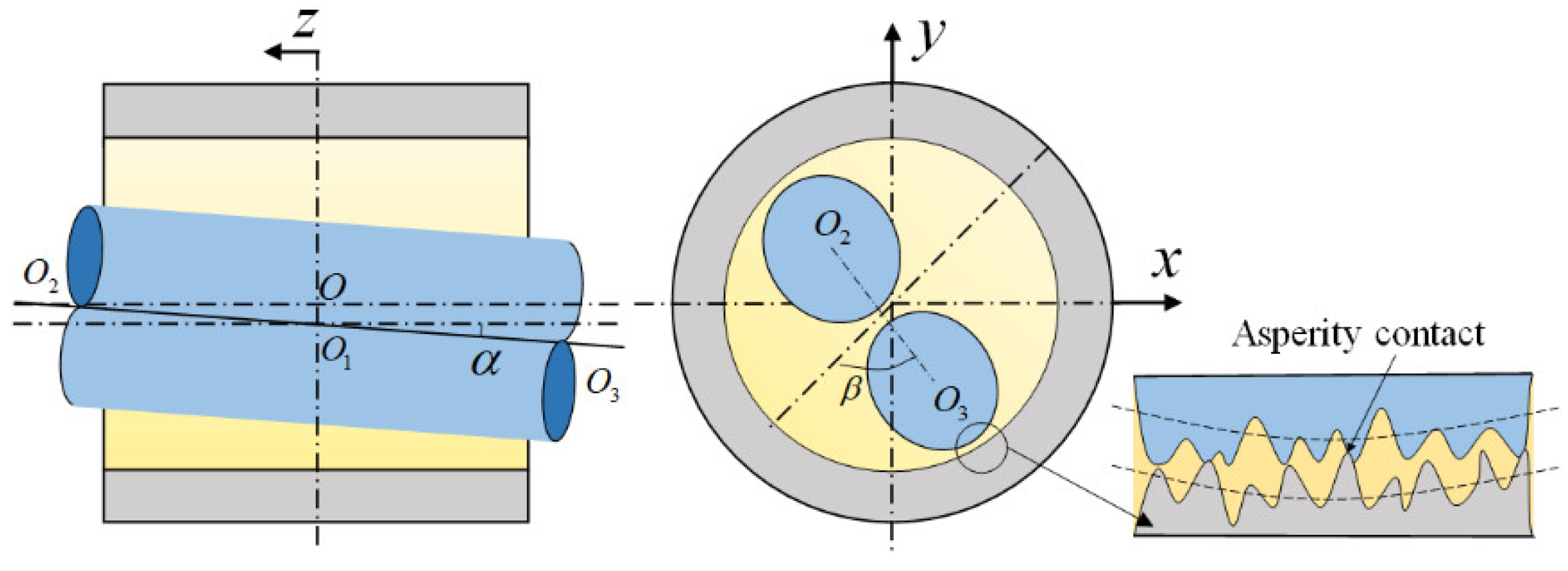
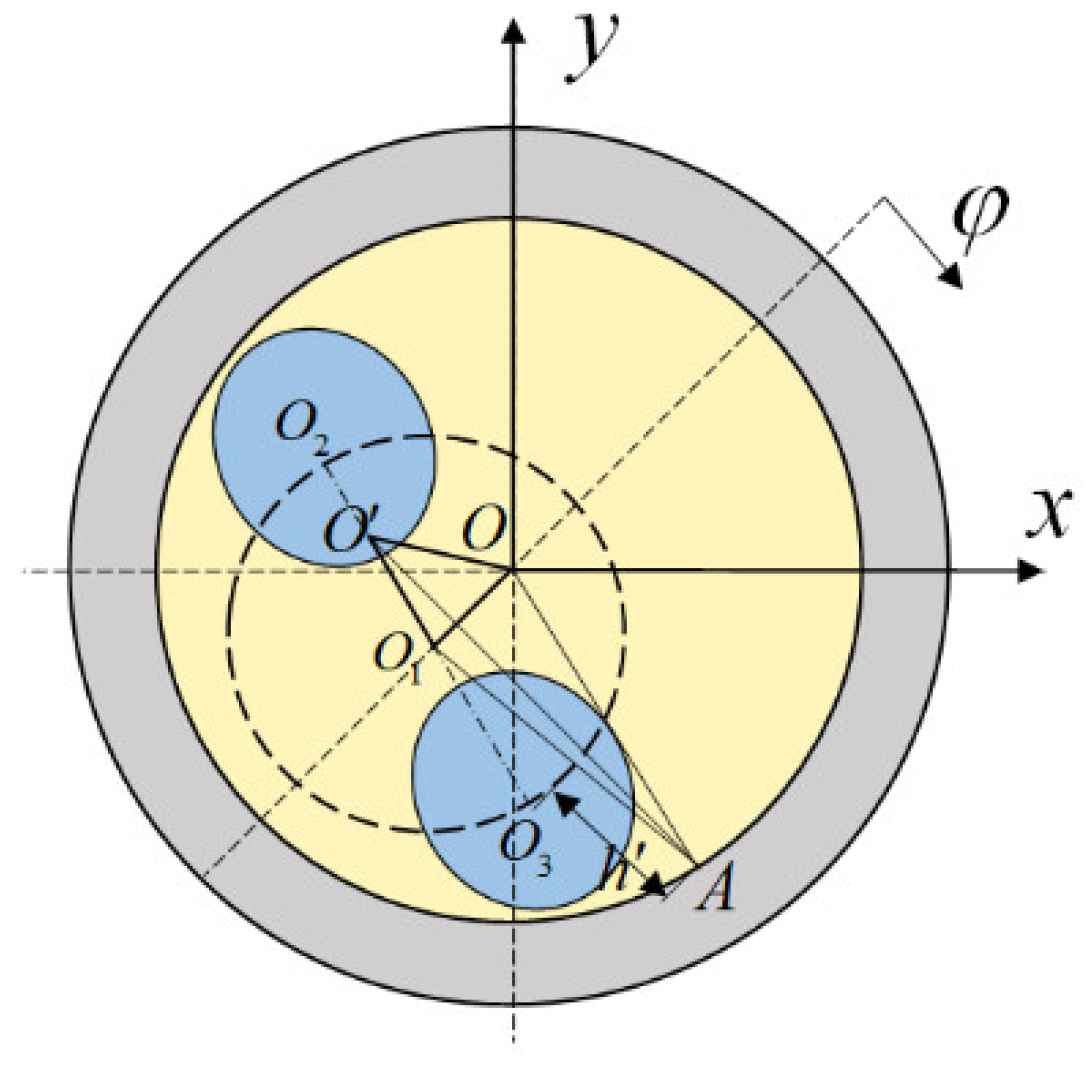




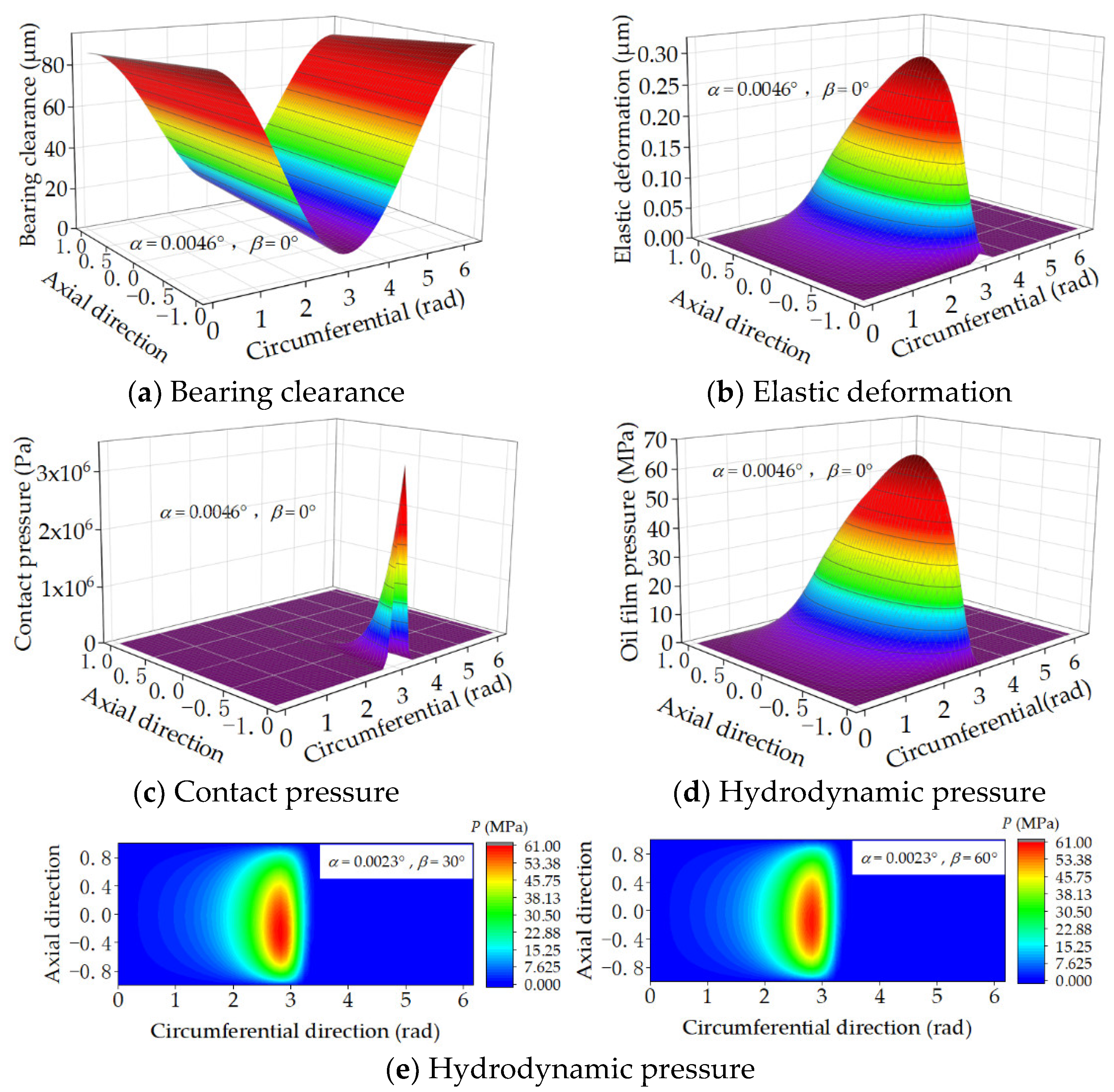
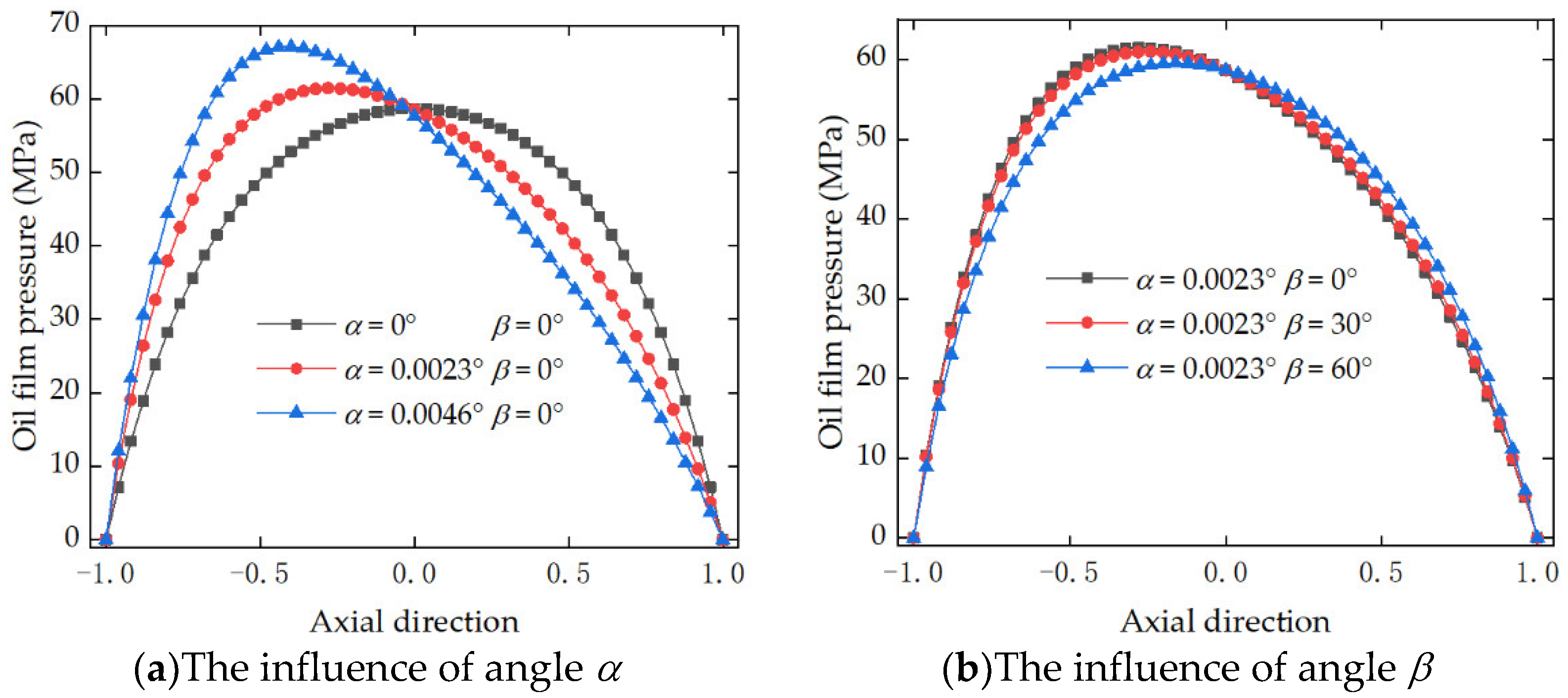




| α (Degree) | Value in Reference [21] (MPa) | Present Work (MPa) | Relative Error |
|---|---|---|---|
| 0 | 33.06 | 30.43 | 7.9% |
| 0.004 | 39.6 | 36.21 | 8.56% |
| 0.007 | 63.58 | 57.0 | 10.35% |
| Parameters | Valves | Parameters | Valves |
|---|---|---|---|
| Journal radius | 50.0 mm | Oil inlet temperature | 40 °C |
| Bush outer radius | 100.0 mm | Ambient temperature | 30 °C |
| Bearing length | 100.0 mm | Rotational speed | 3000 rpm |
| Relative clearance | 1.0‰ | Bush thermal conductivity | 250 W/m°C |
| Lubricant density | 860 kg/m3 | Lubricant specific heat | 1906 J/kg·K |
| Lubricant viscosity | 0.027 Pa·s | Convection heat transfer coefficient | 80 W/m2·°C |
| Lubricant thermal conductivity | 0.13 W/m·°C | Surface roughness | 2.4 μm |
| Viscosity–pressure coefficient | 2.2 × 10−8 | Viscosity–temperature coefficient | 0.035 |
| Integrated elasticity modulus | 210 GPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Bao, J.; Zhang, S.; Shi, M. Experimental and Numerical Study on Mixed Lubrication Performance of Journal Bearing Considering Misalignment and Thermal Effect. Lubricants 2022, 10, 262. https://doi.org/10.3390/lubricants10100262
Guo H, Bao J, Zhang S, Shi M. Experimental and Numerical Study on Mixed Lubrication Performance of Journal Bearing Considering Misalignment and Thermal Effect. Lubricants. 2022; 10(10):262. https://doi.org/10.3390/lubricants10100262
Chicago/Turabian StyleGuo, Hong, Jianqiao Bao, Shaolin Zhang, and Minghui Shi. 2022. "Experimental and Numerical Study on Mixed Lubrication Performance of Journal Bearing Considering Misalignment and Thermal Effect" Lubricants 10, no. 10: 262. https://doi.org/10.3390/lubricants10100262





