Dynamic Characteristics of Metal Seals in Roller Cone Bits
Abstract
:1. Introduction
2. Research Subject and Numerical Model
2.1. Research Subjects
2.2. Numerical Model
- The sealing system is two-dimensional axisymmetric;
- The sealing medium between the end faces is a Newtonian fluid;
- The influences of thermal hysteresis and inertial force are negligible;
- The coefficient of convective heat transfer does not change with time.
2.2.1. Lubrication Analysis
2.2.2. Heat Transfer Analysis
2.2.3. Deformation Analysis
2.2.4. Dynamic Analysis
- Periodic axial vibration
- 2.
- Instantaneous shock during periodic vibration
- 3.
- Random vibration
2.3. Calculation Process and Verification
2.3.1. Calculation Process
2.3.2. Model Verification
3. Results and Discussion
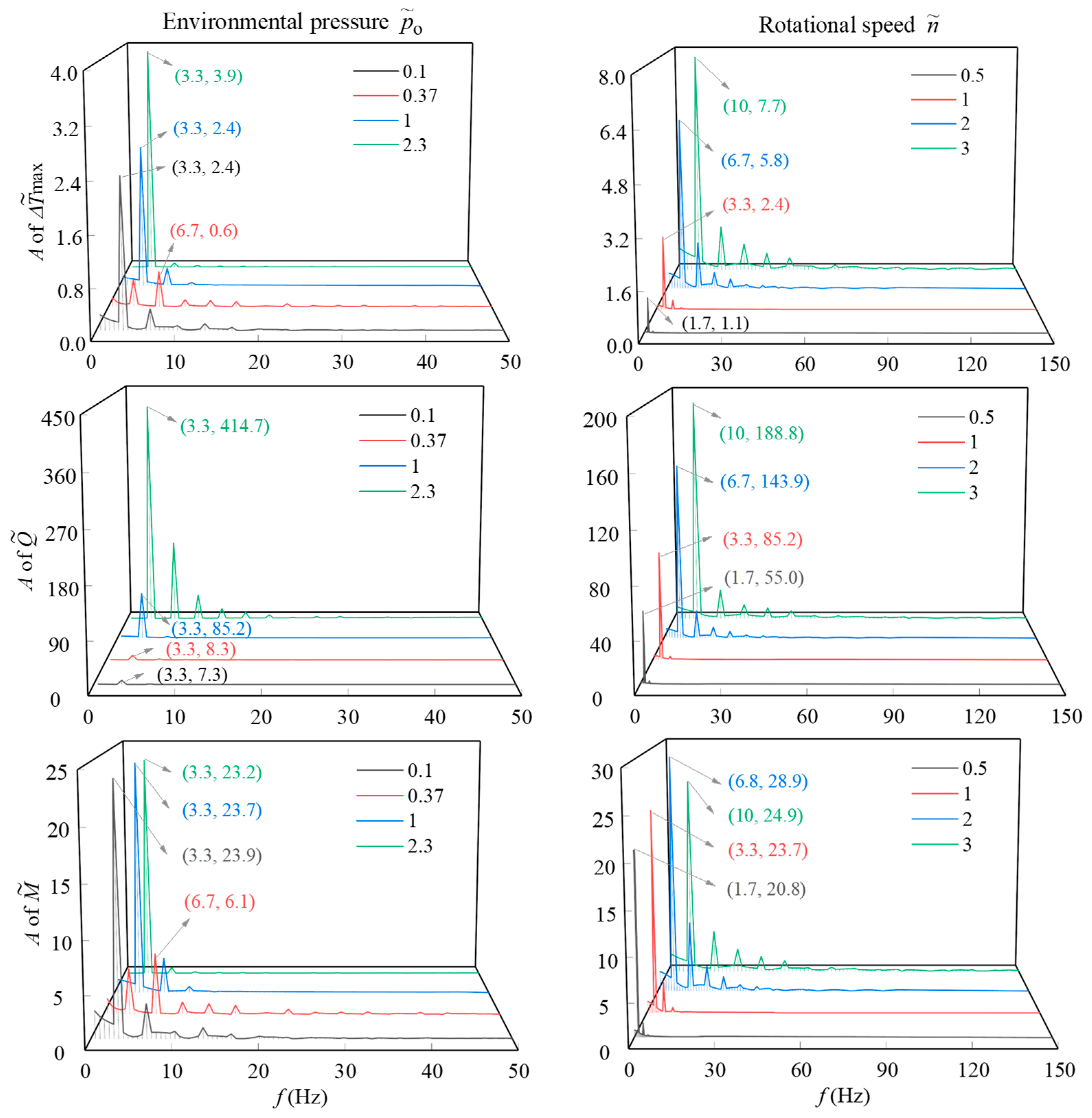
3.1. Influence of Periodic Vibrations
3.2. Influence of Instantaneous Shock
3.3. Influence of Random Vibration
4. Conclusions
- Affected by the high environmental pressure (poi = 30 MPa) and periodic excitation, the film thickness on the sealing end faces appears to have a divergent oscillating distribution along the radial direction. The vibration ranges of the maximum thickness ratio (h/σ) and interface temperature increase (Δ) reach more than two times those of the minimum values. The spectral amplitudes of the performance parameters of the SEMS2 are generated at an integer multiple of the rotation frequency (fn) of the drill bit. It is worth noting that the instantaneous leak rate () fluctuates alternately between positive and negative. When the leakage rate is negative, the mud on the OD side can easily intrude into the sealing gap, aggravating the wear on the end faces.
- When subjected to an instantaneous shock, the liquid film on the end faces of the SEMS2 is squeezed, and the maximum temperature increase (Δmax) and friction torque () change abruptly. Due to the pressure difference of the liquid film on the end faces, the negative leakage rate caused by mud intrusion increases more significantly than the positive leakage rate caused by lubricating oil escape, especially at o = 2.3. Afterwards, the sealing performance parameters oscillate and decay until stable periodic fluctuation is restored. Under quasi-real random vibration, more intense spectral oscillation and disordered amplitude distribution appear in the frequency range.
- With increasing environmental pressure (o) and rotational speed (), the fluctuation amplitudes of the maximum temperature increase (Δ) leakage rate (), and friction torque () under random vibration and instantaneous shock are significantly larger than those under periodic vibration. When o ≤ 1, random vibration has a more significant effect on the maximum interface temperature increase (Δ) friction torque () than instantaneous shock, which is the opposite when the environmental pressure is higher.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.L.; Qian, D.L.; Sun, Y.; Peng, F.F. Design of diamond bits water passage system and simulation of bottom hole fluid are applied to seafloor drill. J. Mar. Sci. Eng. 2021, 9, 1100. [Google Scholar] [CrossRef]
- Rossi, E.; Saar, M.O.; von Rohr, P.R. The influence of thermal treatment on rock-bit interaction: A study of a combined thermo-mechanical drilling (CTMD) concept. Geotherm. Energy 2020, 8, 16. [Google Scholar] [CrossRef]
- Chen, L.; Hu, C.; Yang, Y.X.; Bao, Z.J.; Niu, S.W.; Chen, X.W.; Chen, X.; Zhang, W.T. Experimental research on working principle of the composite single-cone bit. J. Petrol. Sci. Eng. 2021, 205, 108932. [Google Scholar] [CrossRef]
- Abbas, R.K.; Ghanbarzadeh, A.; Hassanpour, A. A novel method for estimating the real-time dullness of tri-cone oil drill bits. Eng. Fail. Anal. 2020, 109, 104386. [Google Scholar] [CrossRef]
- Abbas, R.K. A review on the wear of oil drill bits (conventional and the state of the art approaches for wear reduction and quantification). Eng. Fail. Anal. 2018, 90, 554–584. [Google Scholar] [CrossRef]
- Grimes, B.; Kirkpatrick, B. Step change in performance: Upgraded bit technology significantly improves drilling economics in GOM motor applications. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Suto, Y.; Takahashi, H. Effect of the load condition on frictional heat generation and temperature increase within a tri-cone bit during high-temperature formation drilling. Geothermics 2011, 40, 267–274. [Google Scholar] [CrossRef]
- de Moura, J.; Xiao, Y.J.; Yang, J.M.; Butt, S.D. An empirical model for the drilling performance prediction for roller-cone drill bits. J. Petrol. Sci. Eng. 2021, 204, 108791. [Google Scholar] [CrossRef]
- Naganawa, S. Feasibility study on roller-cone bit wear detection from axial bit vibration. J. Petrol. Sci. Eng. 2012, 82–83, 140–150. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, M.A.; Jin, Y.; Zhang, Y.K.; Zou, D.W.; Lu, Y.H. Theoretical and experimental study on the penetration rate for roller cone bits based on the rock dynamic strength and drilling parameters. J. Nat. Gas Sci. Eng. 2016, 36 Pt A, 117–123. [Google Scholar] [CrossRef] [Green Version]
- de Moraes, L.P.P.; Savi, M.A. Drill-string vibration analysis considering an axial-torsional-lateral nonsmooth model. J. Sound Vib. 2019, 438, 220–237. [Google Scholar] [CrossRef]
- Moharrami, M.J.; Martins, C.D.; Shiri, H. Nonlinear integrated dynamic analysis of drill strings under stick-slip vibration. Appl. Ocean Res. 2021, 108, 102521. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.S.; Zhang, Z.Z.; Gao, K.; Li, J.S.; Xie, X.B. The rock breaking mechanism analysis of axial ultra-high frequency vibration assisted drilling by single PDC cutter. J. Petrol. Sci. Eng. 2021, 205, 108859. [Google Scholar] [CrossRef]
- Zhang, B.S.; Chen, J.Q.; Si, R. The new-type single metal floating seal for roller bits. China Petrol. Mach. 2009, 37, 32–35. [Google Scholar]
- Zhou, Y.; Huang, Z.Q.; TAN, L.; Ma, Y.C.; Qiu, C.S.; Zhang, F.X.; Yuan, Y.; Sun, C.M.; Guo, L. Cone bit bearing seal failure analysis based on the finite element analysis. Eng. Fail. Anal. 2014, 45, 292–299. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.D.; Chang, X.P.; Wu, Q. Wear morphology analysis and structural optimization of cone bit bearing seals. Ind. Lubr. Tribol. 2018, 70, 59–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.D.; Yang, L.; Yu, X. Optimization design for downhole dynamic seal based on response surface method. Adv. Mech. Eng. 2019, 11, 1687814019828441. [Google Scholar] [CrossRef]
- Xiong, S.; Salant, R.F. A numerical model of a rock bit bearing seal. Tribol. Trans. 2000, 43, 542–548. [Google Scholar] [CrossRef]
- Xiong, S.; Salant, R.F. A non-axisymmetric steady state model of a mechanical seal for downhole tools. J. Tribol. 2002, 124, 144–150. [Google Scholar] [CrossRef]
- Ma, Y.; Yuan, Z.Y.; Ni, Y.; Meng, X.K.; Peng, X.D. Performance prediction and multi-objective optimization of metal seals in roller cone bits. J. Petrol. Sci. Eng. 2022, 208 Pt A, 109316. [Google Scholar] [CrossRef]
- Xiong, S.; Salant, R.F. A dynamic model of a contacting mechanical seal for down-hole tools. J. Tribol. 2003, 125, 391–402. [Google Scholar] [CrossRef]
- Zhang, X.D.; Zhang, Y.; Li, Y.L.; Zhang, Y.; Luo, Y. Container design and contact research of single metal seal. Mach. Design Res. 2013, 29, 132–137. [Google Scholar]
- Zhang, M.T.; Feng, Y. Numerical model of mixed lubrication and experimental study of reciprocating seal based on inverse lubrication theory. Lubricants 2022, 10, 153. [Google Scholar] [CrossRef]
- Jiang, J.B.; Zhao, W.J.; Peng, X.D.; Li, J.Y. A novel design for discrete surface texture on gas face seals based on a superposed groove model. Tribol. Int. 2020, 147, 106269. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. 1979, 101, 220–227. [Google Scholar] [CrossRef]
- Cui, S.H.; Gu, L.; Fillon, M.; Wang, L.Q.; Zhang, C.W. The effects of surface roughness on the transient characteristics of hydrodynamic cylindrical bearings during startup. Tribol. Int. 2018, 128, 421–428. [Google Scholar] [CrossRef]
- Gao, B.C.; Meng, X.K.; Li, J.Y.; Shen, M.X.; Peng, X.D. Thermal-mechanical coupled finite element model and seal performance analysis of mechanical seals. Tribology 2015, 35, 550–556. [Google Scholar]
- Abouelregal, A.E.; Marin, M. The response of nanobeams with temperature-dependent properties using state-space method via modified couple stress theory. Symmetry 2020, 12, 1276. [Google Scholar] [CrossRef]
- Henneuse, H. Surface detection of vibration and drilling optimization field experience. In Proceedings of the SPE/IADC Drilling Conference, New Orleans, LA, USA, 18–21 February 1992. [Google Scholar]
- Chen, Y.; Peng, X.D.; Jiang, J.B.; Meng, X.K.; Li, J.Y. Experimental and theoretical studies of the dynamic behavior of a spiral-groove dry gas seal at high-speeds. Tribol. Int. 2018, 125, 17–26. [Google Scholar] [CrossRef]
- Aarrestad, T.V.; Kyllingstad, A. An experimental and theoretical study of a coupling mechanism between longitudinal and torsional drillstring vibrations at the bit. SPE Drill. Eng. 1988, 3, 12–18. [Google Scholar] [CrossRef]
- Liu, J.X.; Zheng, H.L.; Kuang, Y.C.; Yu, B.; Zhou, Y.; Deng, M. A feasible model for friction-reduction investigation of drillstrings in long-horizontal wells with axial oscillation tools and analysis of key influencing factors. J. Petrol. Sci. Eng. 2020, 185, 106643. [Google Scholar] [CrossRef]
- Zhang, X.M. Research on Dynamic Characteristics of Marine Mechanical Seals; Wuhan University of Technology: Wuhan, China, 2008. [Google Scholar]
- Huang, Z.Q.; Li, G. Optimization of cone bit bearing seal based on failure analysis. Adv. Mech. Eng. 2018, 10, 1687814018767485. [Google Scholar] [CrossRef]
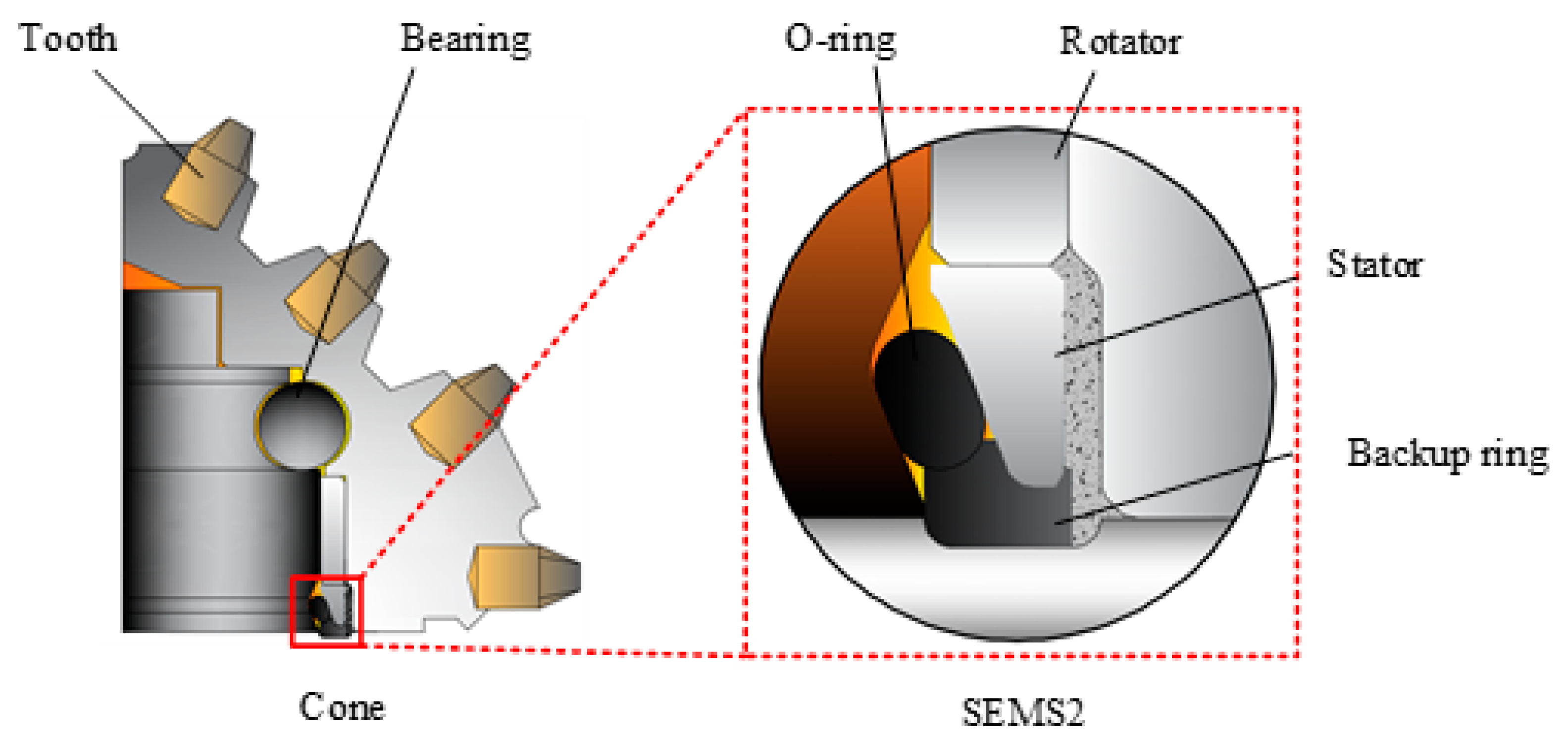














| Structural Parameters | Values | Operational Parameters | Values |
|---|---|---|---|
| Inner diameter ri (mm) | 31 | Environmental pressure poi (MPa) | 30 |
| Outer diameter ro (mm) | 34.3 | Environmental Temperature Toi (°C) | 80 |
| Contact width L (mm) | 3.3 | Rotational speed ni (r/min) | 200 |
| Incline angle of rotor β (°) | 65 | Axial stiffness coefficient k (N·m) | 5.84 × 106 |
| Wedge angle α (°) | 5 | Axial damping coefficient c (N·s·m−1) | 4183 |
| Height of rotor H (mm) | 7.5 | Exciting load A (N) | 1000 |
| Material Parameters | Medium Parameters | ||||
|---|---|---|---|---|---|
| Material Types | 20CrNiMo | FKM | Medium Types | Lubricant Oil | Drilling Mud |
| Elastic modulus (MPa) | 2.03 × 105 | 8.74 | Density (kg/m3) | 861 | 1742 |
| Poisson’s ratio | 0.3 | 0.499 | Viscosity (Pa.s) | 0.0192 | 0.0258 |
| Thermal Expansion (°C) | 4.5 × 10−6 | 115 × 10−6 | Conductivity (W/(m. °C)) | 0.1246 | 1.1619 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Xu, Y.; Chen, Y.; Meng, X.; Peng, X. Dynamic Characteristics of Metal Seals in Roller Cone Bits. Lubricants 2022, 10, 280. https://doi.org/10.3390/lubricants10110280
Ma Y, Xu Y, Chen Y, Meng X, Peng X. Dynamic Characteristics of Metal Seals in Roller Cone Bits. Lubricants. 2022; 10(11):280. https://doi.org/10.3390/lubricants10110280
Chicago/Turabian StyleMa, Yi, Yixiao Xu, Yutao Chen, Xiangkai Meng, and Xudong Peng. 2022. "Dynamic Characteristics of Metal Seals in Roller Cone Bits" Lubricants 10, no. 11: 280. https://doi.org/10.3390/lubricants10110280




