Influence of Structural and Operating Parameters on Lubrication Performance of Water-Lubricated Polymer Bearing with Journal Misalignment
Abstract
:1. Introduction
2. Modelling
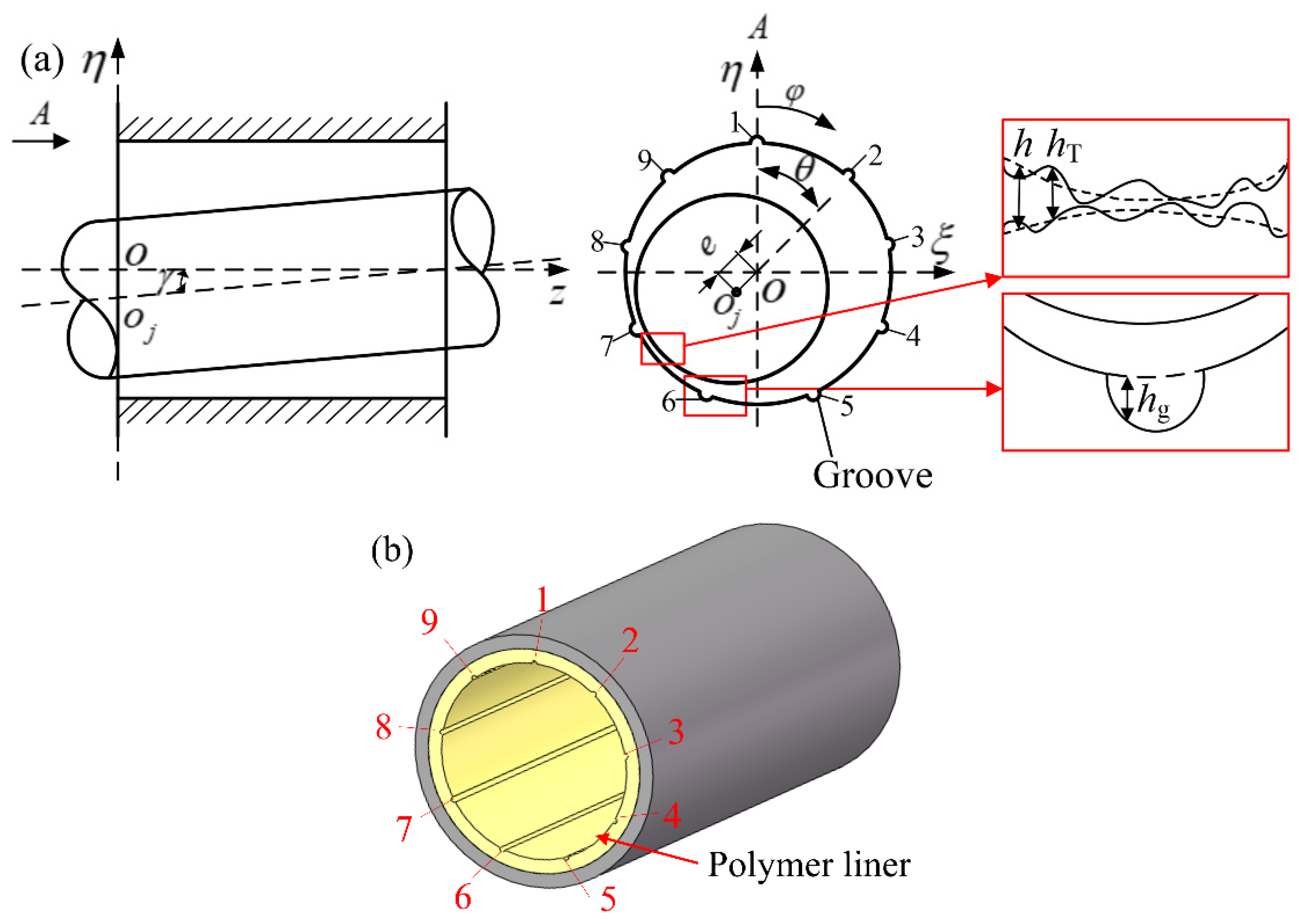
2.1. Geometry of Misaligned Water-Lubricated Polymer Bearing in Mixed Lubrication
2.2. Governing Equations for the Water Film
2.3. Asperity Contact Pressure
2.4. Bearing and Friction Forces
3. Simulation Flowchart and Verification
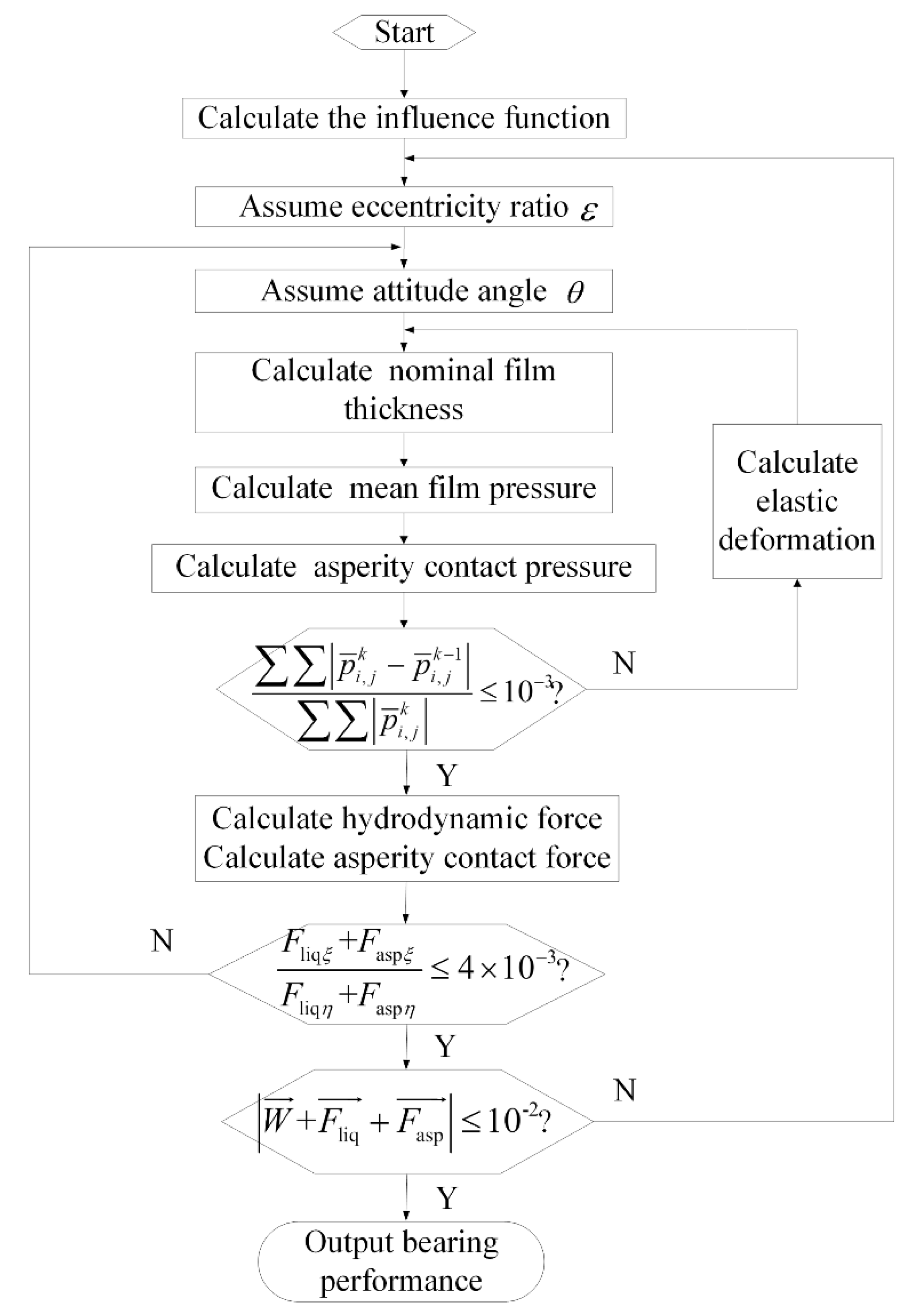
3.1. Simulation Flowchart
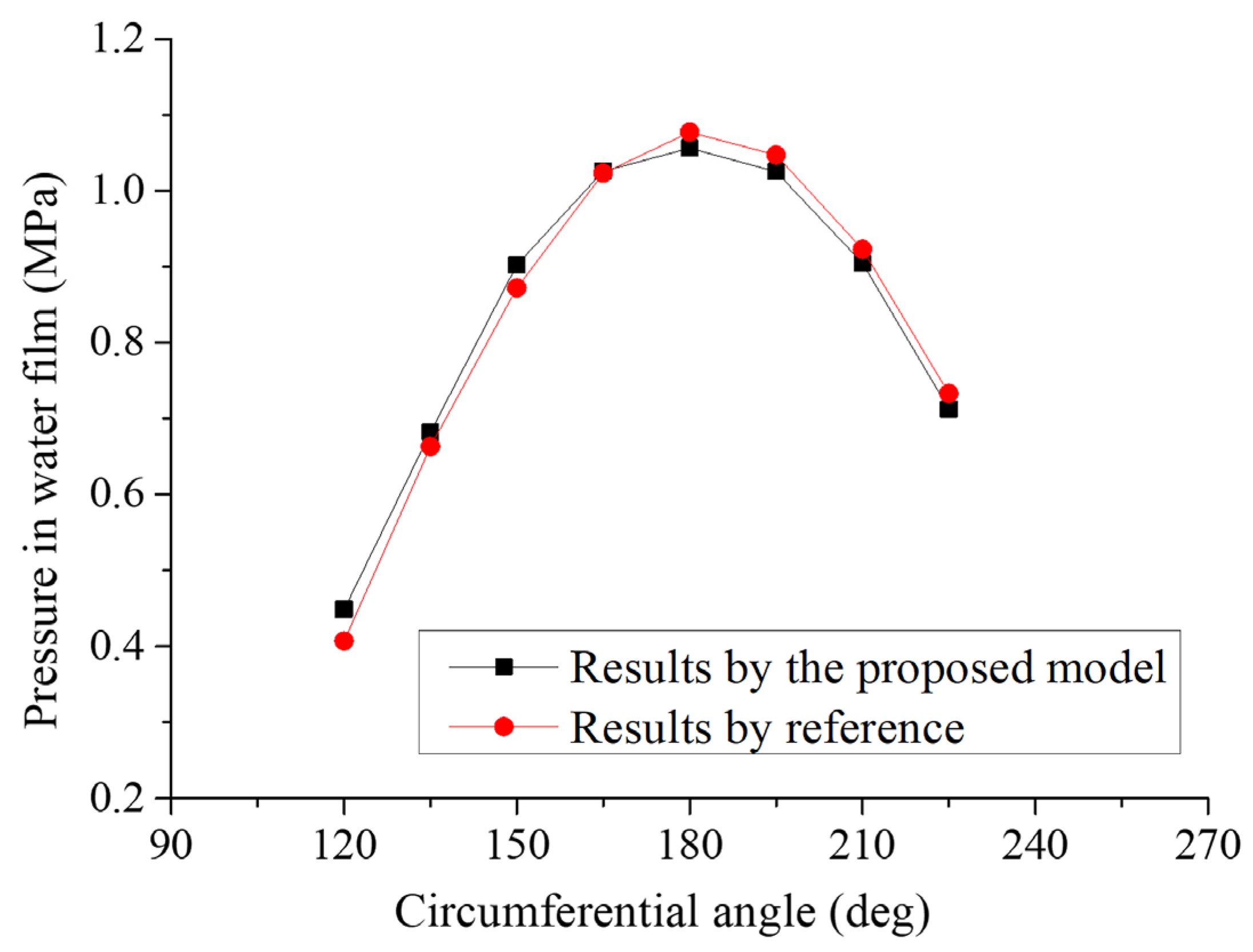
3.2. Verification
4. Results and Discussion
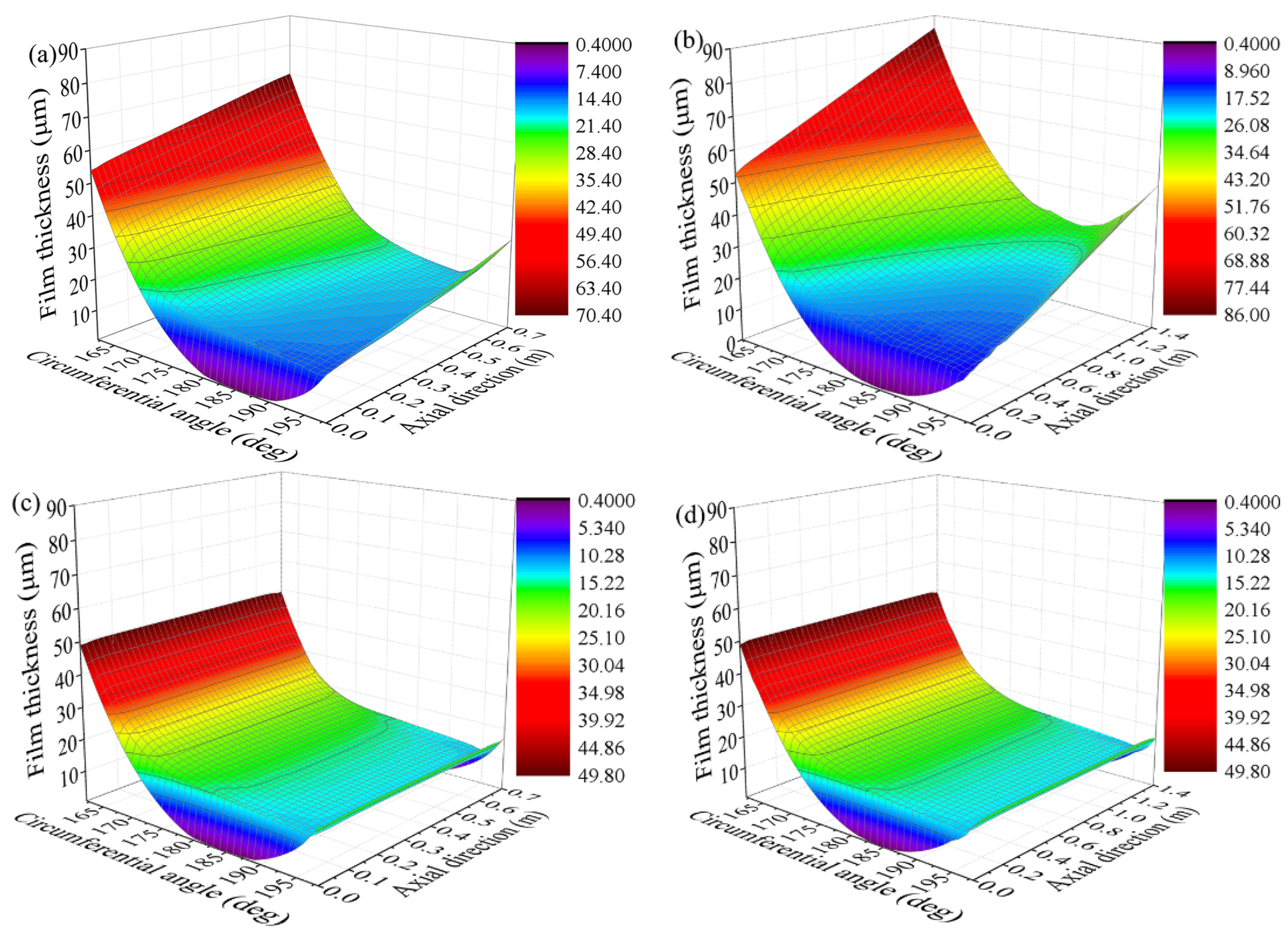
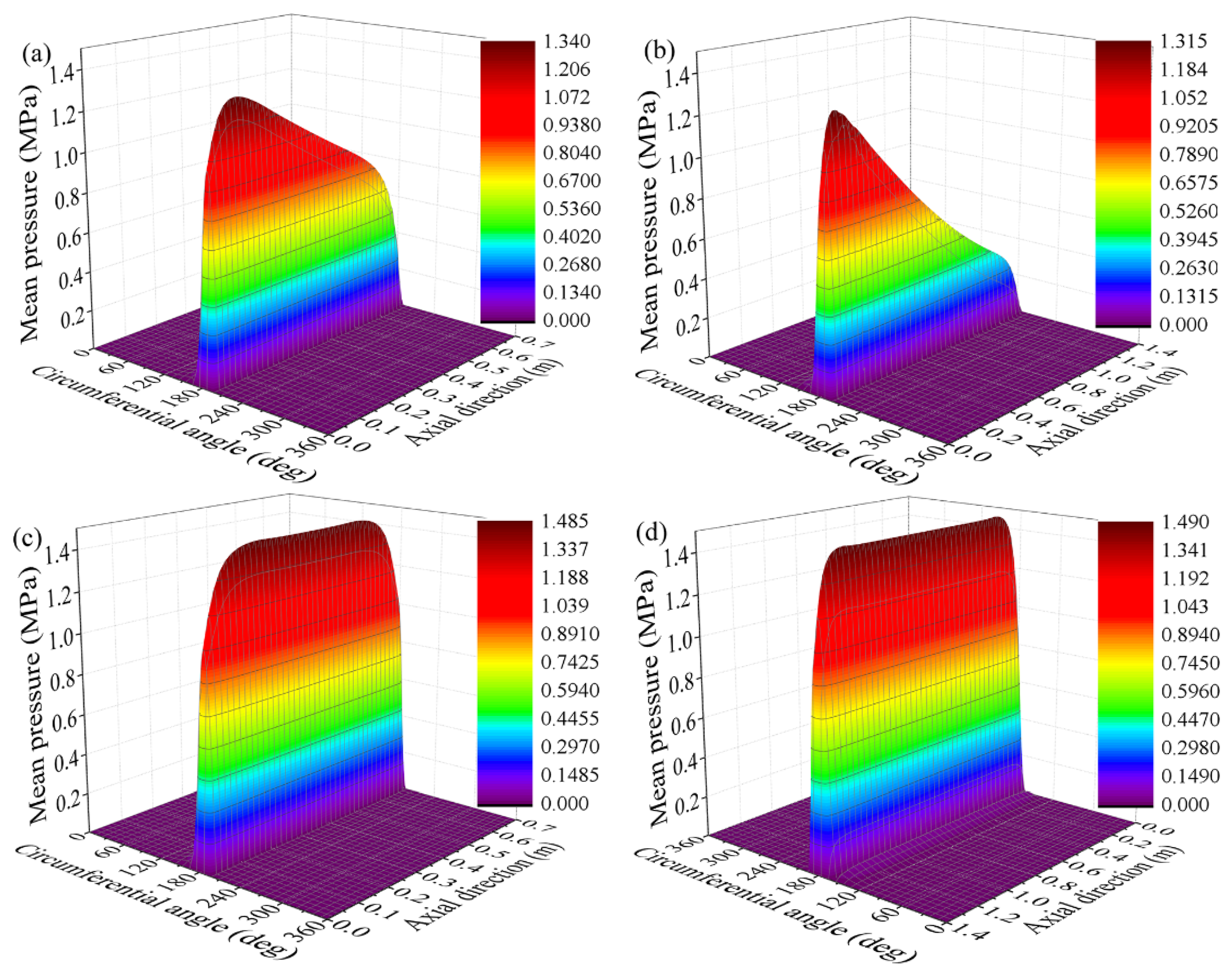
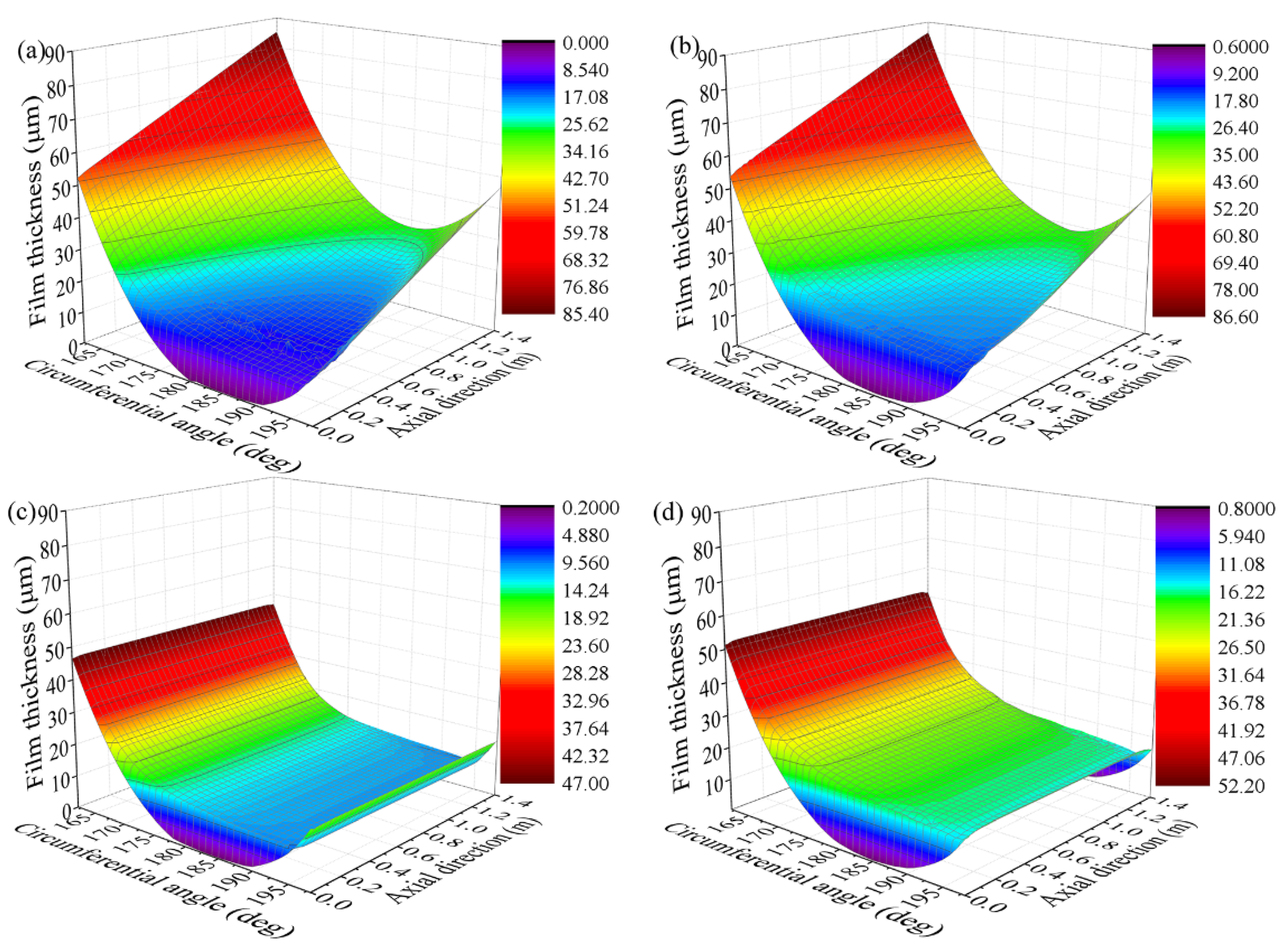
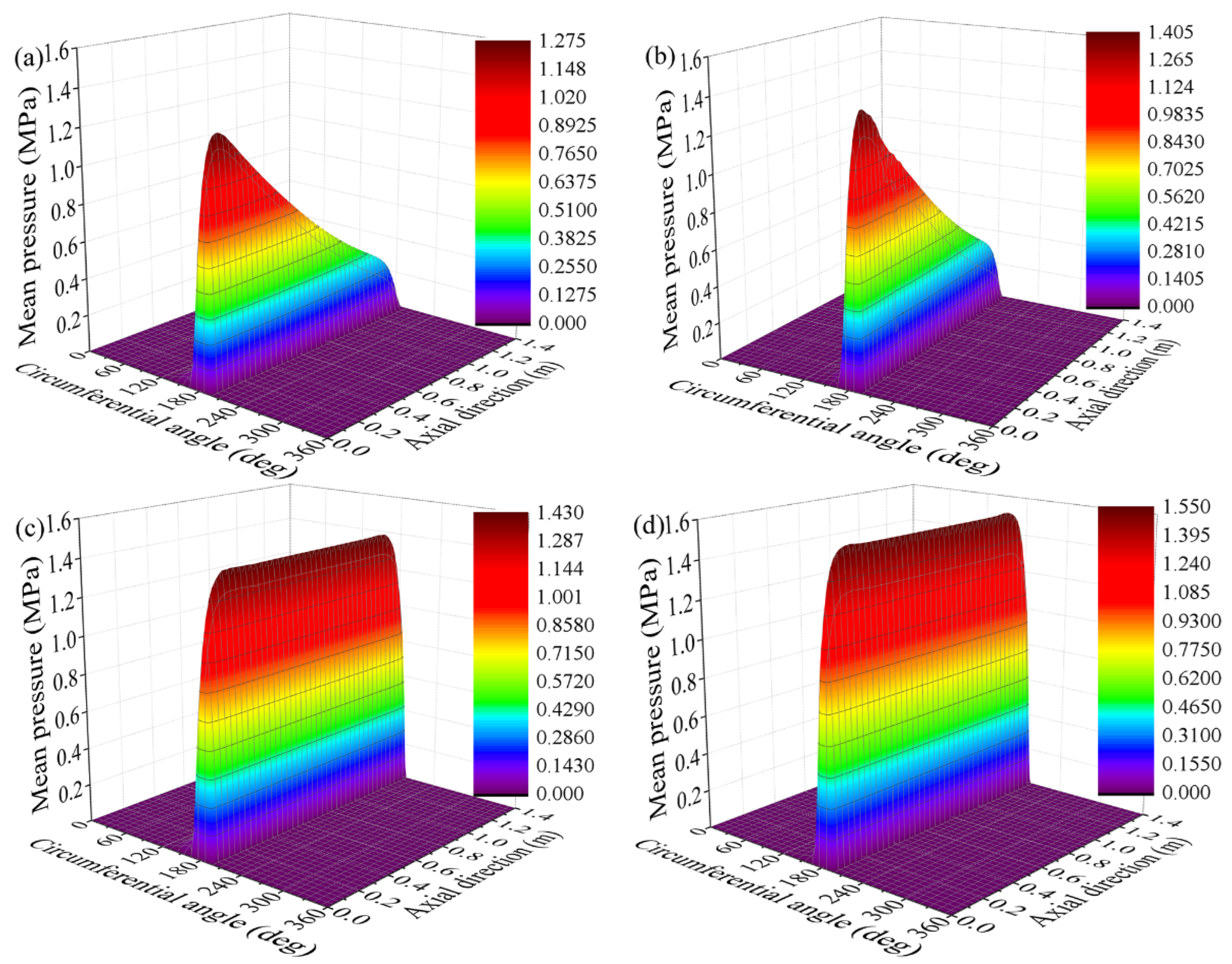
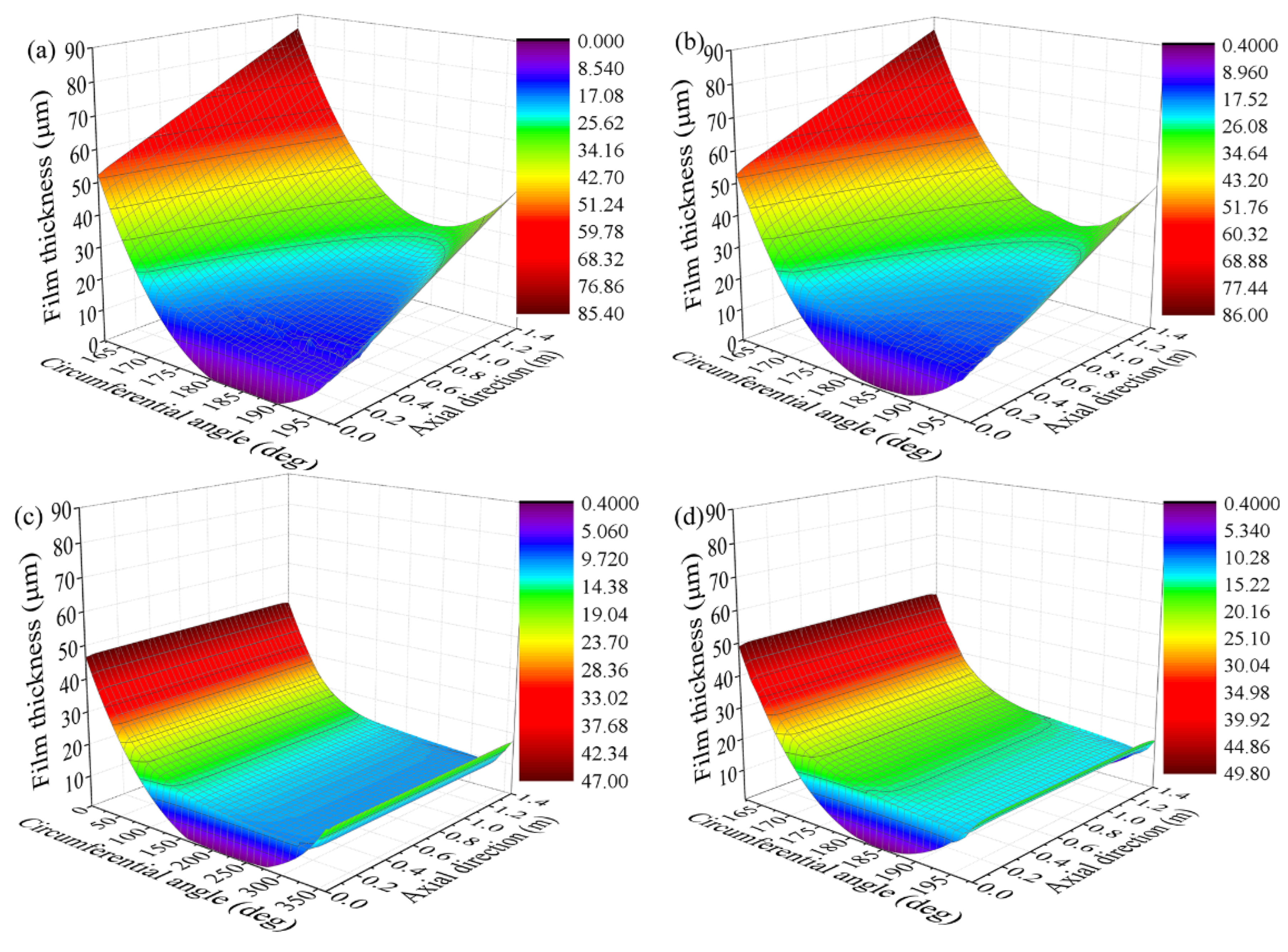
4.1. The influence of the Length-Diameter Ratio
4.2. The influence of the Liner Thickness
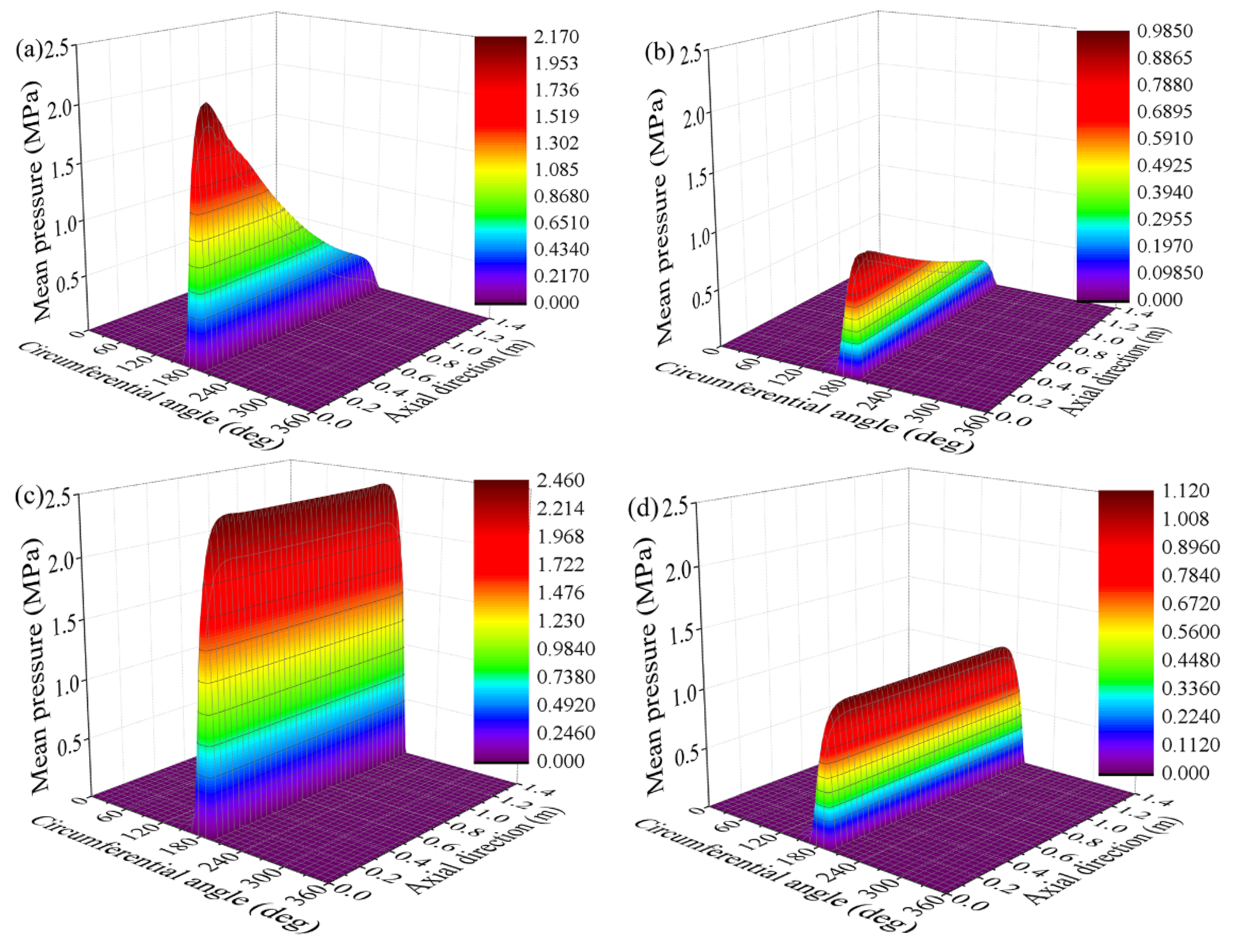
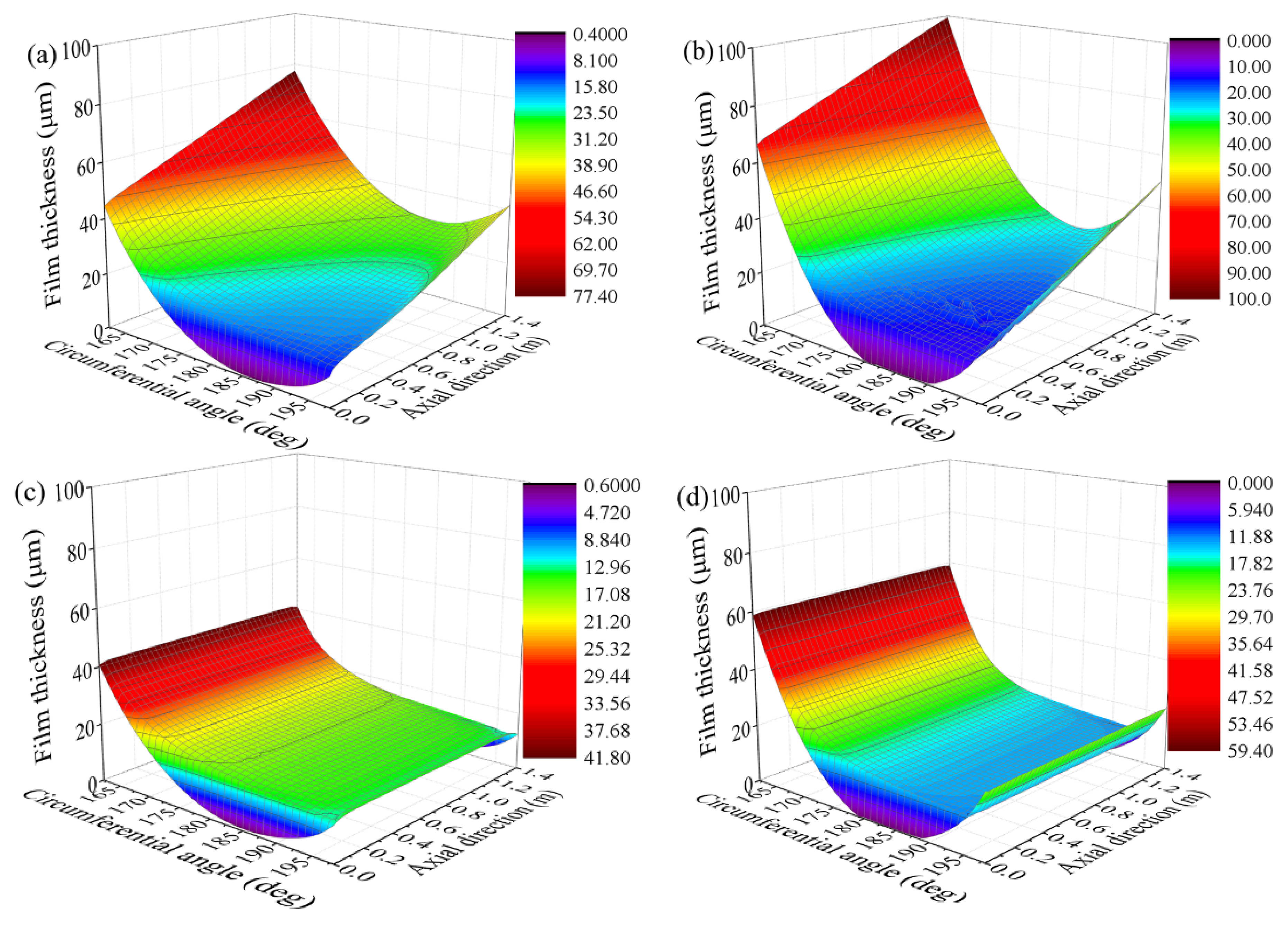
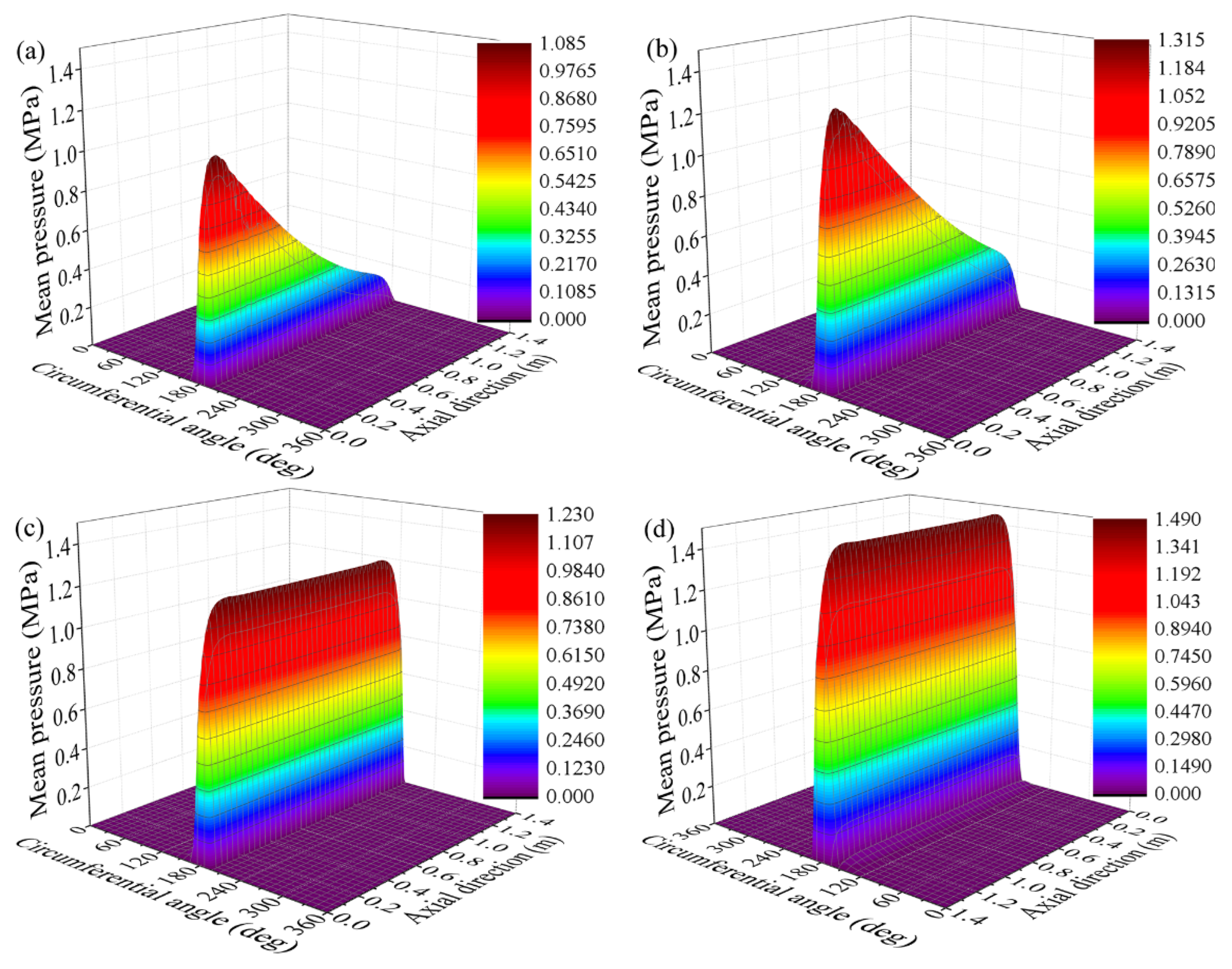
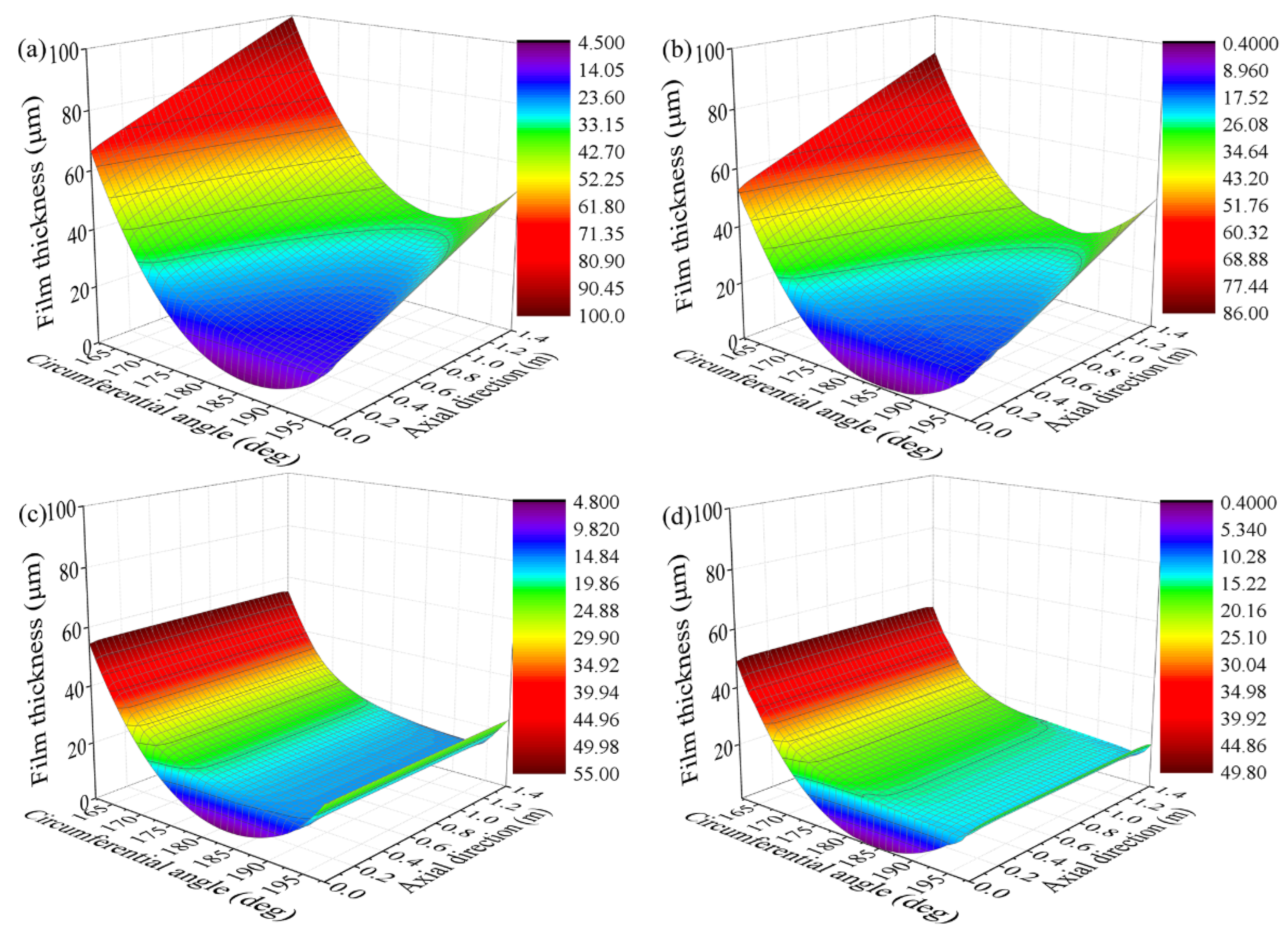
4.3. The Influence of the Clearance Ratio
4.4. The Influence of Journal Speed
4.5. The Influence of the Eccentricity Ratio
5. Conclusions
- (1)
- Journal misalignment significantly reduces the load-carrying capacity of the bearing, deteriorates its tribological characteristics, and may cause different axial sections of the bearing to be in different lubrication regimes.
- (2)
- For misaligned bearings, the load-carrying capacity is no longer proportional to the length–diameter ratio. The rate of increase of load-carrying capacity decreases with an increase in the length–diameter ratio. Therefore, the load-carrying capacity cannot be effectively increased for misaligned bearings by blindly increasing the length–diameter ratio during bearing design.
- (3)
- When the journal is misaligned, the increase in liner thickness can improve the axial uniformity of hydrodynamic pressure distribution. Therefore, the bearing pressure distribution can be improved by adjusting liner thickness during the bearing design. Selecting a liner with a relatively low elastic modulus can be inferred to improve the uniformity of pressure distribution of a bearing with journal misalignment.
- (4)
- The reduction proportion of load-carrying capacity caused by journal misalignment decreases when the eccentricity ratio increases. Accordingly, when the load increases, the influence of journal misalignment on bearing performance and axial nonuniform degree of bearing pressure distribution are both weakened for polymer bearings.
- (5)
- With an increase in the clearance ratio, the load-carrying capacity of misaligned bearing decreases slightly while the friction coefficient and the non-uniformity of the pressure increase significantly. Therefore, an excessive clearance ratio should not be selected in bearing design prone to the mixed lubrication regime.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Journal diameter (mm) | 700 | Length–diameter ratio | 2 |
| Clearance ratio | 0.22% | Groove number | 9 |
| Groove angle (°) | 4 | Contact friction coefficient | 0.2 |
| Liner surface roughness (μm) | 2.4 | Journal surface roughness (μm) | 0.8 |
| Rated speed (rpm) | 200 | Eccentricity ratio | 0.9995 |

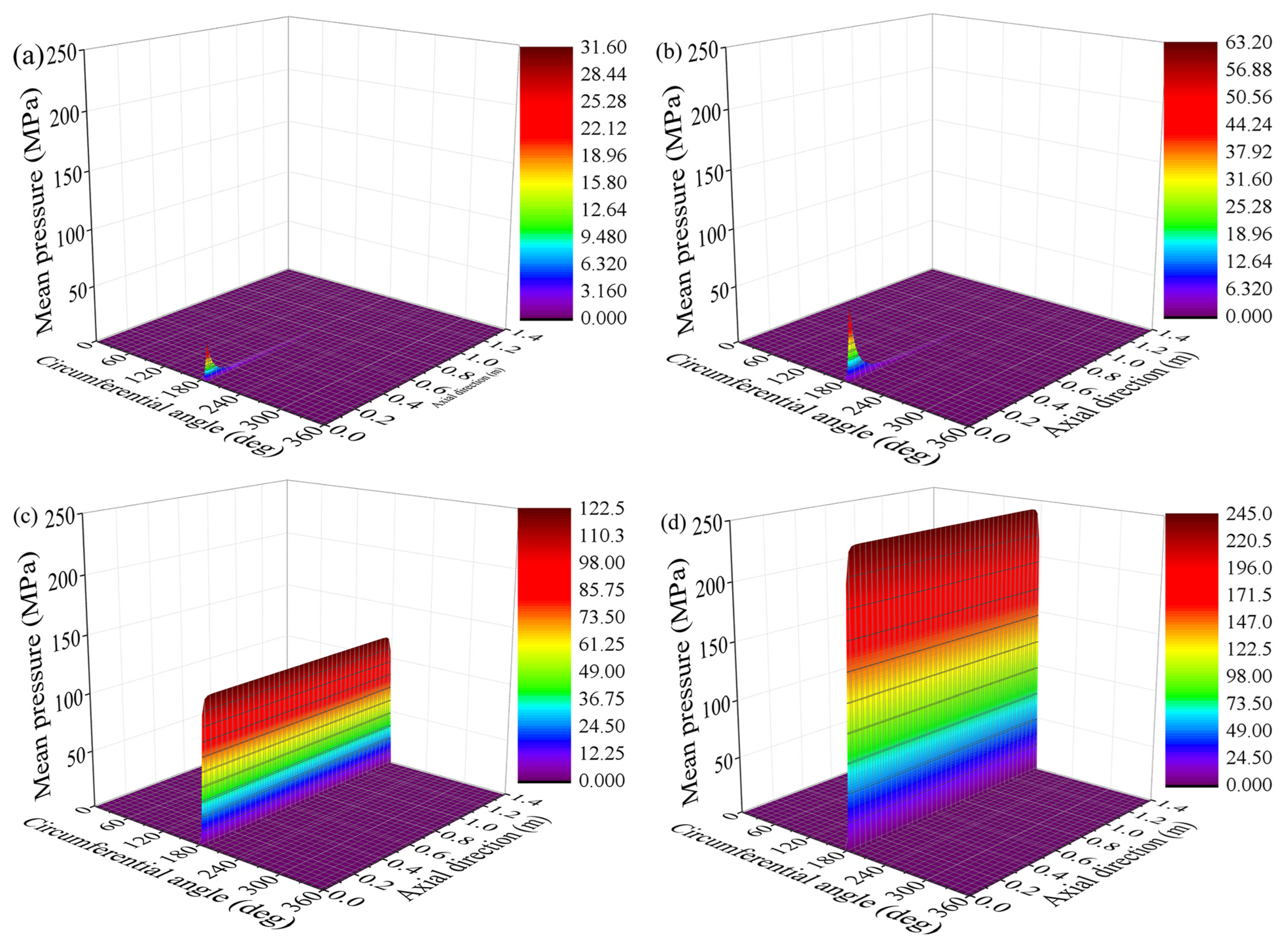
| Attitude Angle (°) | Load-Carrying Capacity (kN) | Friction Force (N) | Friction Coefficient | |
|---|---|---|---|---|
| Bearing with the rotational speed of 100 r/min and γ = 0.025 mrad | 5.62 | 115.6 | 200.2 | 0.00173 |
| Bearing with the rotational speed of 200 r/min and γ = 0.025 mrad | 5.62 | 230.6 | 263.5 | 0.00114 |
| Aligned bearing with the rotational speed of 100 r/min | 2.16 | 3128.5 | 3825.7 | 0.00122 |
| Aligned bearing with the rotational speed of 200 r/min | 2.16 | 6239.7 | 4196.9 | 0.00067 |
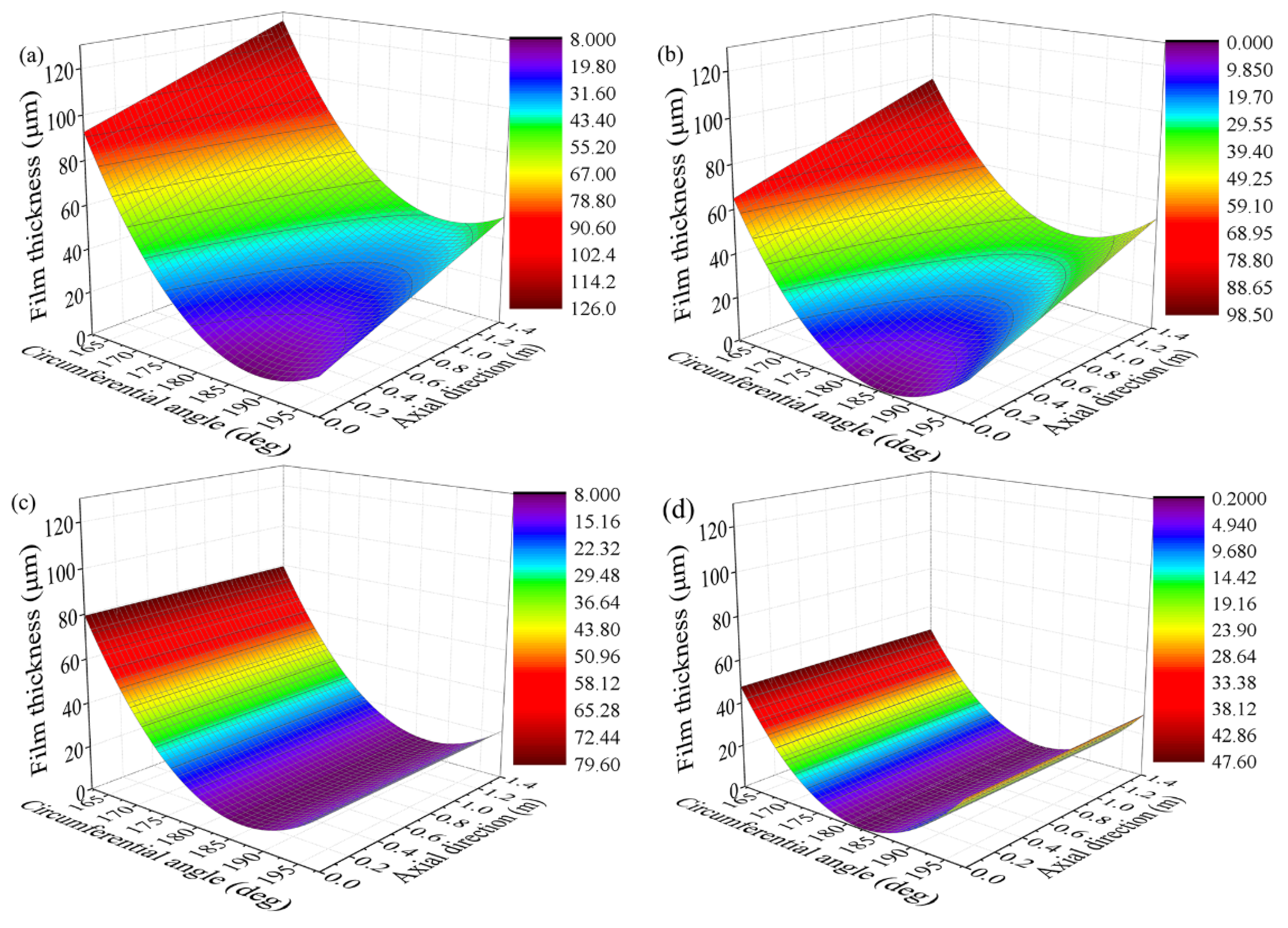
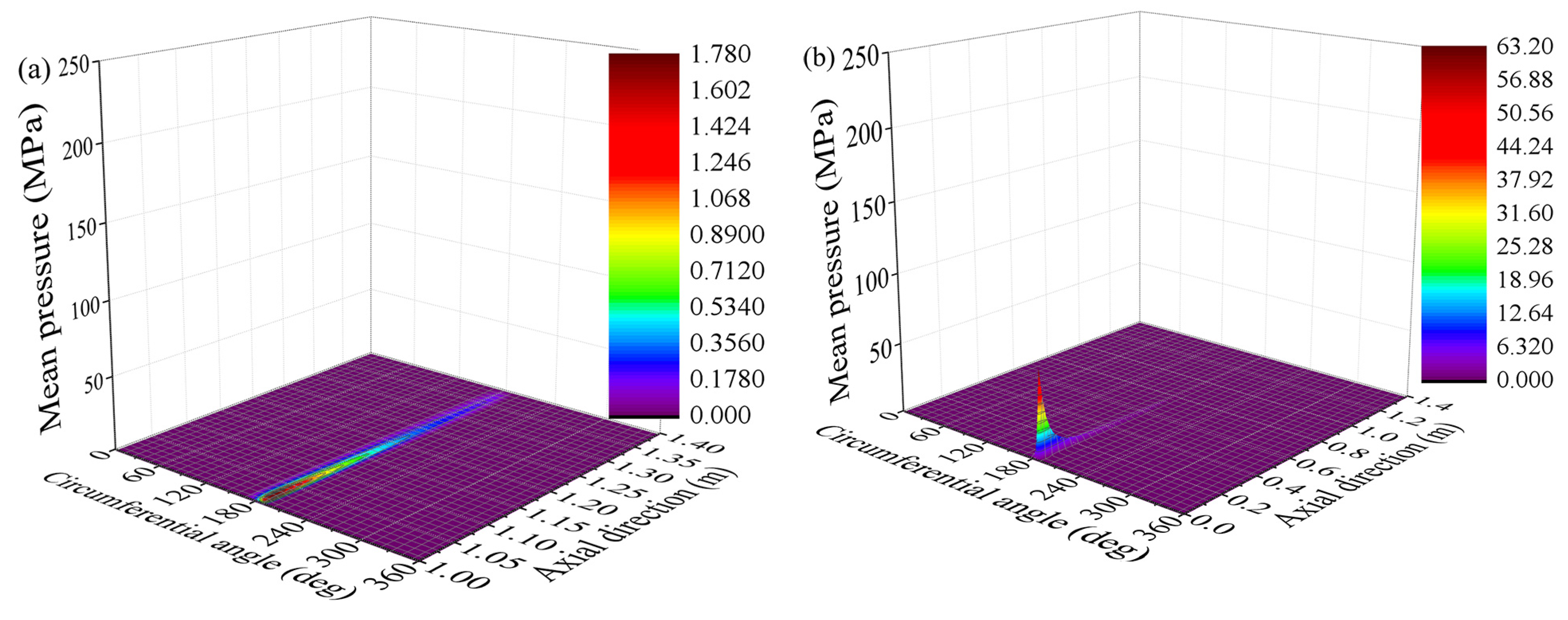
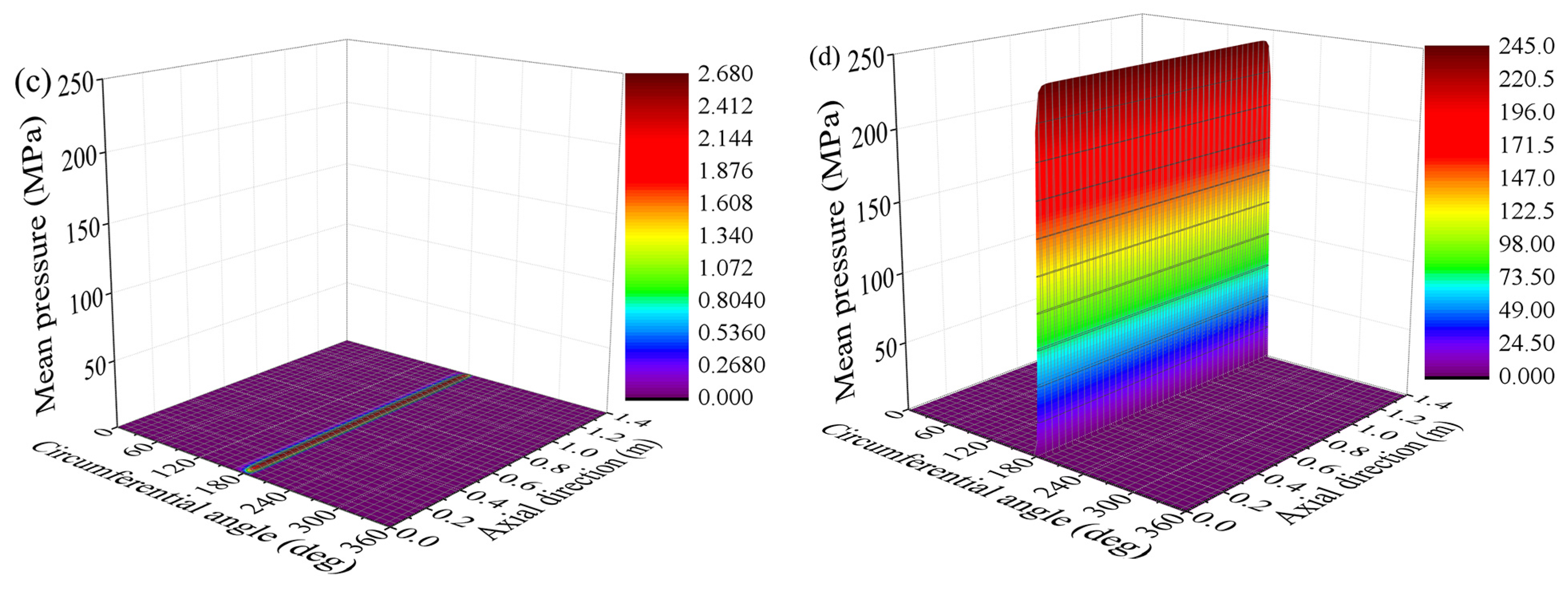
| Attitude Angle (°) | Load-Carrying Capacity (kN) | Friction Force (N) | Friction Coefficient | |
|---|---|---|---|---|
| Bearing with ε = 0.9895 and γ = 0.025 mrad | 9.22 | 75.3 | 86.3 | 0.00115 |
| Bearing with ε = 0.9995 and γ = 0.025 mrad | 5.62 | 230.6 | 263.5 | 0.00114 |
| Aligned bearing with ε = 0.9895 | 6.99 | 246.8 | 154.5 | 0.00063 |
| Aligned bearing with ε = 0.9995 | 2.16 | 6239.7 | 4196.9 | 0.00067 |
References
- Wodtke, M.; Litwin, W. Water-lubricated stern tube bearing—Experimental and theoretical investigations of thermal effects. Tribol. Int. 2021, 153, 106608. [Google Scholar] [CrossRef]
- Litwin, W. Marine propeller shaft bearings under low-speed conditions: Water vs. oil lubrication. Tribol. Trans. 2019, 62, 839. [Google Scholar] [CrossRef]
- Han, Y.; Yin, L.; Xiang, G.; Zhou, G.; Zheng, X. An experimental study on the tribological performance of water-lubricated journal bearings with three different materials. Ind. Lubr. Tribol. 2020, 72, 1159–1165. [Google Scholar] [CrossRef]
- Lin, C.; Zou, M.; Sima, C.; Liu, S.; Jiang, L. Friction-induced vibration and noise of marine stern tube bearings considering perturbations of the stochastic rough surface. Tribol. Int. 2019, 131, 661–671. [Google Scholar] [CrossRef]
- Zhang, Z.; Dai, X.; Xie, Y. Thermoelastohydrodynamic behavior of misaligned plain journal bearings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 2582–2599. [Google Scholar] [CrossRef]
- Litwin, W.; Michał, W.; Artur, O. Shaft misalignment influence on water lubricated turbine sliding bearing with various bush module of elasticity. Key Eng. Mater. 2012, 90, 128–134. [Google Scholar] [CrossRef]
- Mallya, R.; Shenoy, S.B.; Pai, R. Steady state characteristics of misaligned multiple axial groove water-lubricated journal bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 229, 712–722. [Google Scholar] [CrossRef]
- He, T.; Li, W.; Lu, X.; Zou, D.; Zhou, H. Mixed lubrication analysis of a ship stern bearing. J. Ship Mech. 2014, 18, 973–981. [Google Scholar]
- He, T.; Zou, D.; Lu, X.; Guo, Y.; Wang, Z.; Li, W. Mixed-lubrication analysis of marine stern tube bearing considering bending deformation of stern shaft and cavitation. Tribol. Int. 2014, 73, 108–116. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, Z.; Jiang, D.; Gao, G.; Wang, Y.; Wang, X. Load carrying capacity of misaligned hydrodynamic water-lubricated plain journal bearings with rigid bush materials. Tribol. Int. 2016, 99, 1–13. [Google Scholar] [CrossRef]
- Zhu, S.; Sun, J.; Li, B.; Zhu, G. Thermal turbulent lubrication analysis of rough surface journal bearing with journal misalignment. Tribol. Int. 2019, 144, 106109. [Google Scholar] [CrossRef]
- Jang, J.; Khonsari, M. On the wear of dynamically-loaded engine bearings with provision for misalignment and surface roughness. Tribol. Int. 2020, 141, 105919. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; Wang, J.; Xiao, K.; Li, J. A transient hydrodynamic lubrication comparative analysis for misaligned micro-grooved bearing considering axial reciprocating movement of shaft. Tribol. Int. 2019, 132, 11–23. [Google Scholar] [CrossRef]
- Song, X.; Wu, W.; Yuan, S. Mixed-lubrication analysis of misaligned journal bearing considering turbulence and cavitation. AIP Adv. 2022, 12, 015213. [Google Scholar] [CrossRef]
- Mallya, R.; Shenoy, S.B.; Pai, R. Static characteristics of misaligned multiple axial groove water-lubricated bearing in the turbulent regime. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 385–398. [Google Scholar] [CrossRef]
- Majumdar, B.C.; Pai, R.; Hargreaves, D. Analysis of water-lubricated journal bearings with multiple axial grooves. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2004, 218, 135–146. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; He, T.; Wang, J.; Xiao, K. A dynamic wear model for micro-grooved water-lubricated bearings under transient mixed lubrication condition. J. Tribol. 2020, 142, 071701. [Google Scholar] [CrossRef]
- Hirani, H.; Suh, N.P. Journal bearing design using multiobjective genetic algorithm and axiomatic design approaches. Tribol. Int. 2005, 38, 481–491. [Google Scholar] [CrossRef]
- Chu, H.M. Shape optimum design of slider bearings using inverse method. Tribol. Int. 2007, 40, 906–914. [Google Scholar] [CrossRef]
- Ouyang, W.; Yan, Q.; Kuang, J. Simulation and experimental investigations on water-lubricated squeeze film damping stern bearing. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 54. [Google Scholar] [CrossRef]
- Zhou, G.; Mi, X.; Wang, J.; Hu, R. Experimental comparison between the Stribeck curves of water lubricated rubber bearing with straight and spiral grooves. Ind. Lubr. Tribol. 2018, 70, 1326–1330. [Google Scholar] [CrossRef]
- Lv, F.; Zou, D.; Ta, N.; Rao, Z. Improvement of lubrication performance of water lubricated polymer bearing via enlarged axial end bearing diameter. Ind. Lubr. Tribol. 2019, 71, 564–572. [Google Scholar] [CrossRef]
- Lin, Q.; Bao, Q.; Li, K.; Khonsari, M.; Zhao, H. An investigation into the transient behavior of journal bearing with surface texture based on fluid-structure interaction approach. Tribol. Int. 2017, 118, 246–255. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Xie, Y.; Yang, Y. Effects of surface texturing on ring/liner friction under starved lubrication. Tribol. Int. 2017, 94, 591–605. [Google Scholar] [CrossRef]
- Meng, F.; Zhang, L.; Liu, Y.; Li, T. Effect of compound dimple on tribological performances of journal bearing. Tribol. Int. 2015, 91, 99–110. [Google Scholar] [CrossRef]
- Meng, F.; Yu, H.; Gui, C.; Lin, C. Experimental study of compound texture effect on acoustic performance for lubricated textured surfaces. Tribol. Int. 2019, 133, 47–54. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Zhang, D.; Xie, Y. A transient analysis of the textured journal bearing considering micro and macro cavitation during an engine cycle. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 1289–1306. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Ng, C.W.; Pan, C.H.T. A linearized turbulent lubrication theory. J. Basic Eng. 1965, 87, 675–682. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–634. [Google Scholar] [CrossRef]
- Litwin, W. Experimental research on water lubricated three layer sliding bearing with lubrication grooves in the upper part of the bush and its comparison with a rubber bearing. Tribol. Int. 2015, 82, 153–161. [Google Scholar] [CrossRef]
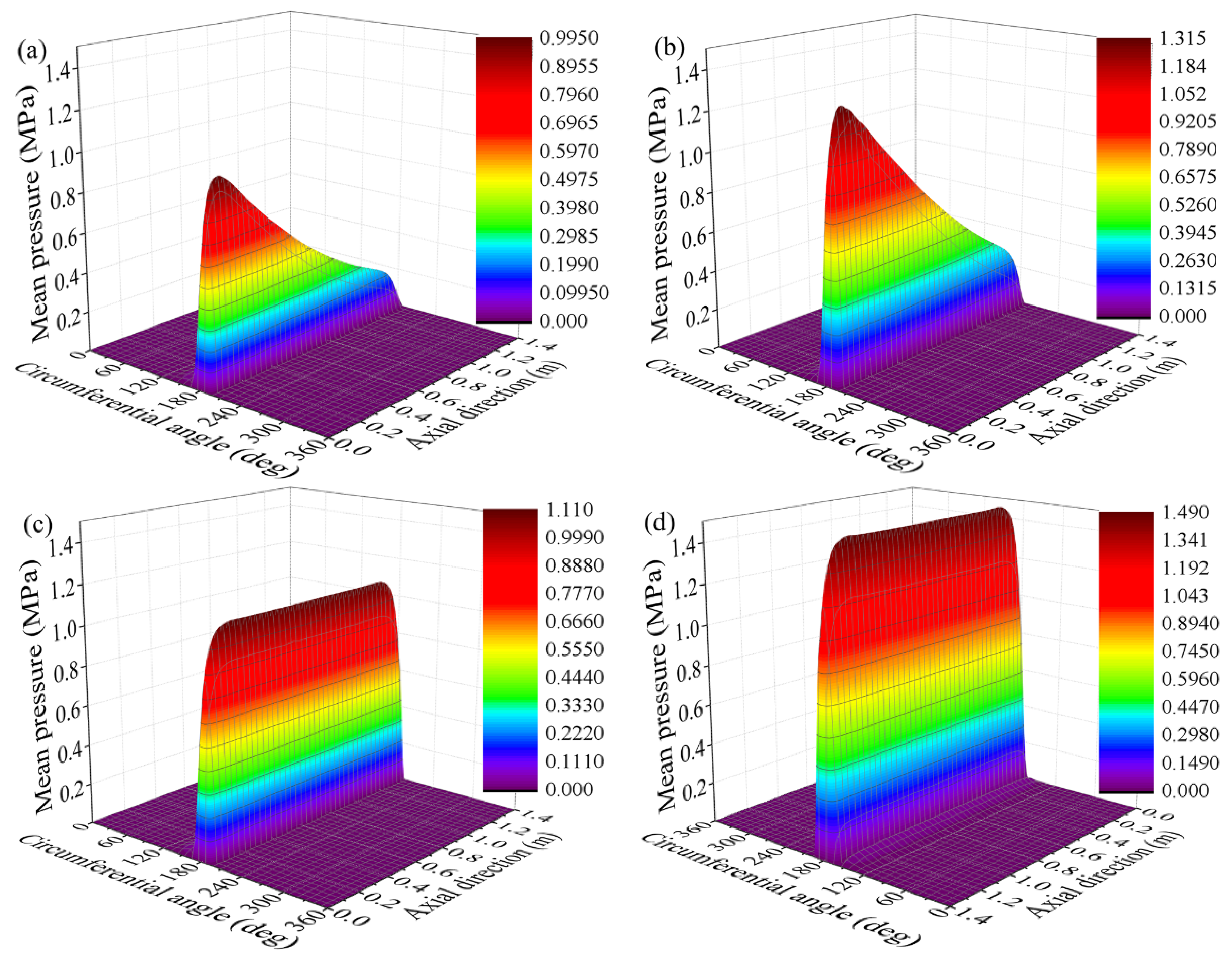
| Journal diameter (m) | 0.52 |
| Bearing length (m) | 1.20 |
| Clearance ratio | 0.23% |
| Journal speed (m/s) | 60 |
| Lubricant viscosity (Pa·s) | 0.062 |
| The roughness of the journal surface (μm) | 4.3 |
| The roughness of bearing bush (μm) | 4.3 |
| Externally applied load (kN) | 215 |
| Misalignment Angle (mrad) | Results from [8] (MPa) | Results Obtained by the Proposed Model (MPa) |
|---|---|---|
| 0.325 | 4.38 | 4.41 |
| 0.333 | 4.70 | 4.73 |
| 0.342 | 5.07 | 5.11 |
| 0.350 | 5.48 | 5.52 |
| 0.358 | 5.92 | 5.99 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Journal diameter (mm) | 700 | Length–diameter ratio | 2 |
| Clearance ratio | 0.22% | Groove number | 9 |
| Groove angle (°) | 4 | Lubricant | Water |
| Elastic modulus of the liner (Pa) | 4.4 × 108 | Elastic modulus of the journal (Pa) | 2.11 × 1011 |
| Poisson’s ratio of the liner | 0.45 | Poisson’s ratio of the journal | 0.3 |
| Liner surface roughness (μm) | 2.4 | Journal surface roughness (μm) | 0.8 |
| Liner thickness (mm) | 20 | Contact friction coefficient | 0.2 |
| Rated speed (rpm) | 200 | Eccentricity ratio | 1.01 |
| Attitude Angle (°) | Load-Carrying Capacity (kN) | Friction Force (N) | Friction Coefficient | |
|---|---|---|---|---|
| Bearing with L/D = 1 and γ = 0.025 mrad | 4.86 | 88.7 | 391.8 | 0.00442 |
| Bearing with L/D = 2 and γ = 0.025 mrad | 4.64 | 127.6 | 449.9 | 0.00353 |
| Aligned bearing with L/D = 1 | 3.86 | 127.4 | 513.3 | 0.00403 |
| Aligned bearing with L/D = 2 | 3.87 | 262.8 | 760.2 | 0.00289 |
| Attitude Angle (°) | Load-Carrying Capacity (kN) | Friction Force (N) | Friction Coefficient | |
|---|---|---|---|---|
| Bearing with liner thickness of 10 mm and γ = 0.025 mrad | 4.58 | 165.3 | 584.1 | 0.00353 |
| Bearing with liner thickness of 20 mm and γ = 0.025 mrad | 4.64 | 127.6 | 449.9 | 0.00353 |
| Bearing with liner thickness of 30 mm and γ = 0.025 mrad | 4.79 | 107.9 | 302.0 | 0.00280 |
| Aligned bearing with liner thickness of 10 mm | 3.44 | 362.6 | 1051.5 | 0.00290 |
| Aligned bearing with liner thickness of 20 mm | 3.87 | 262.8 | 760.2 | 0.00289 |
| Aligned bearing with liner thickness of 30 mm | 4.32 | 204.2 | 340.2 | 0.00167 |
| Attitude Angle (°) | Load-Carrying Capacity (kN) | Friction Force (N) | Friction Coefficient | |
|---|---|---|---|---|
| Bearing with ψ = 0.17% and γ = 0.025 mrad | 5.51 | 132.8 | 188.8 | 0.00142 |
| Bearing with ψ = 0.22% and γ = 0.025 mrad | 4.64 | 127.6 | 449.9 | 0.00353 |
| Bearing with ψ = 0.28% and γ = 0.025 mrad | 4.58 | 124.8 | 502.3 | 0.00402 |
| Aligned bearing with ψ = 0.17% | 4.58 | 266.2 | 233.5 | 0.00087 |
| Aligned bearing with ψ = 0.22% | 3.87 | 262.8 | 760.2 | 0.00289 |
| Aligned bearing with ψ = 0.28% | 3.37 | 253.5 | 910.9 | 0.00359 |
| Attitude Angle (°) | Load-Carrying Capacity (kN) | Friction Force (N) | Friction Coefficient | |
|---|---|---|---|---|
| Bearing with the rotational speed of 100 r/min and γ = 0.025 mrad | 4.58 | 84.23 | 416.5 | 0.00494 |
| Bearing with the rotational speed of 200 r/min and γ = 0.025 mrad | 4.64 | 127.6 | 449.9 | 0.00353 |
| Aligned bearing with the rotational speed of 100 r/min | 3.44 | 202.2 | 757.1 | 0.00375 |
| Aligned bearing with the rotational speed of 200 r/min | 3.87 | 262.8 | 760.2 | 0.00289 |
| Attitude Angle (°) | Load-Carrying Capacity (kN) | Friction Force (N) | Friction Coefficient | |
|---|---|---|---|---|
| Bearing with ε = 1.00 and γ = 0.025 mrad | 5.93 | 88.7 | 87.1 | 0.00098 |
| Bearing with ε = 1.01 and γ = 0.025 mrad | 4.64 | 127.6 | 449.9 | 0.00353 |
| Aligned bearing with ε = 1.00 | 3.57 | 184.4 | 116.7 | 0.00063 |
| Aligned bearing with ε = 1.01 | 3.87 | 262.8 | 760.2 | 0.00289 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, F.; Jiao, C.; Jia, Q.; Xia, K. Influence of Structural and Operating Parameters on Lubrication Performance of Water-Lubricated Polymer Bearing with Journal Misalignment. Lubricants 2022, 10, 336. https://doi.org/10.3390/lubricants10120336
Lv F, Jiao C, Jia Q, Xia K. Influence of Structural and Operating Parameters on Lubrication Performance of Water-Lubricated Polymer Bearing with Journal Misalignment. Lubricants. 2022; 10(12):336. https://doi.org/10.3390/lubricants10120336
Chicago/Turabian StyleLv, Fangrui, Chunxiao Jiao, Qian Jia, and Kang Xia. 2022. "Influence of Structural and Operating Parameters on Lubrication Performance of Water-Lubricated Polymer Bearing with Journal Misalignment" Lubricants 10, no. 12: 336. https://doi.org/10.3390/lubricants10120336
APA StyleLv, F., Jiao, C., Jia, Q., & Xia, K. (2022). Influence of Structural and Operating Parameters on Lubrication Performance of Water-Lubricated Polymer Bearing with Journal Misalignment. Lubricants, 10(12), 336. https://doi.org/10.3390/lubricants10120336




