Development of Universal Friction Calibration Curve for Ball Ironing Test
Abstract
:1. Introduction
2. Procedure to Construct the Universal FCC
3. Finite Element Modeling (FEM) Setup
4. Simulation Results
4.1. Effect on the Maximum Load (Lmax)
4.2. Effect on the Final Height (hf)
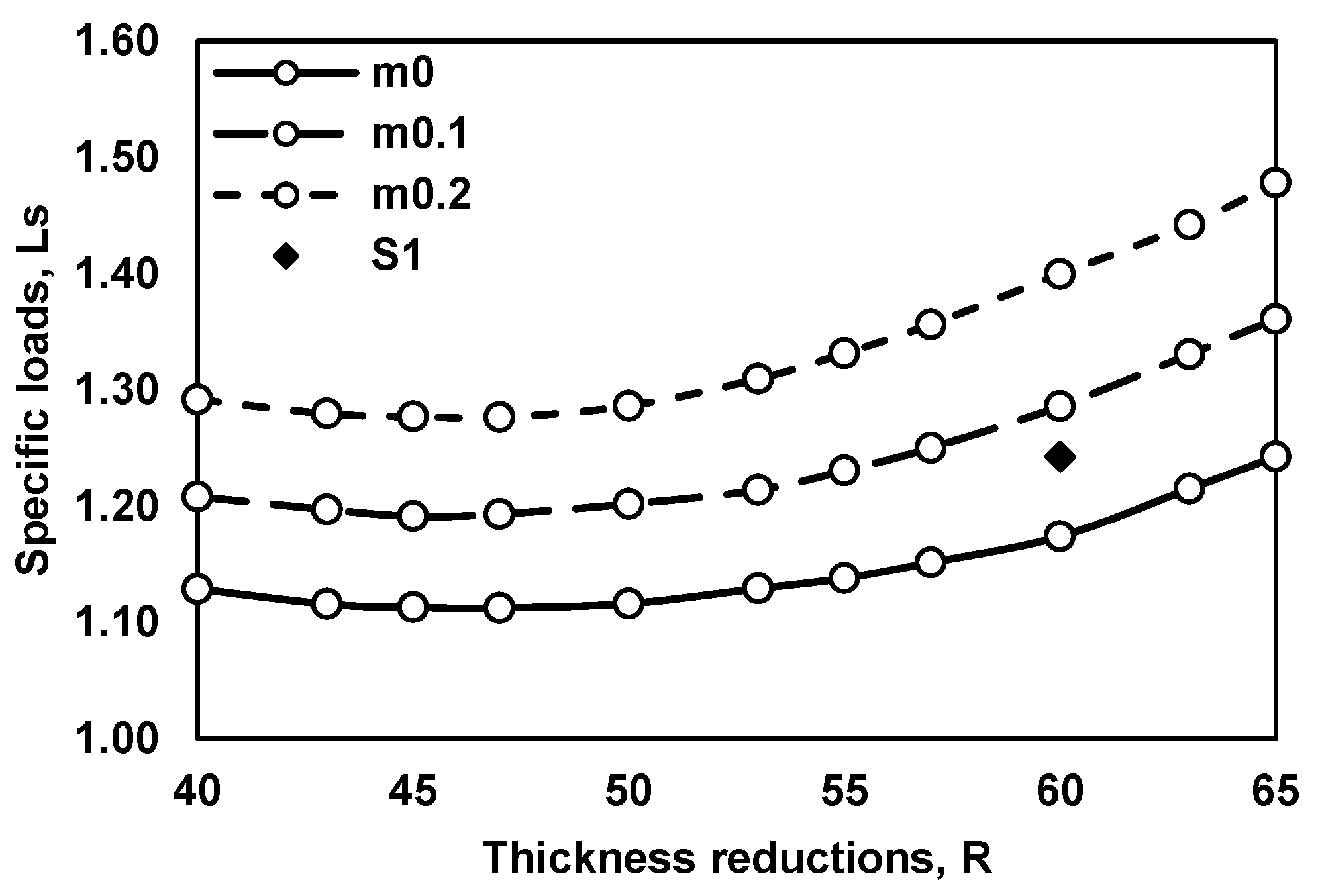
5. Development of Universal FCC
6. Experiment and Discussion
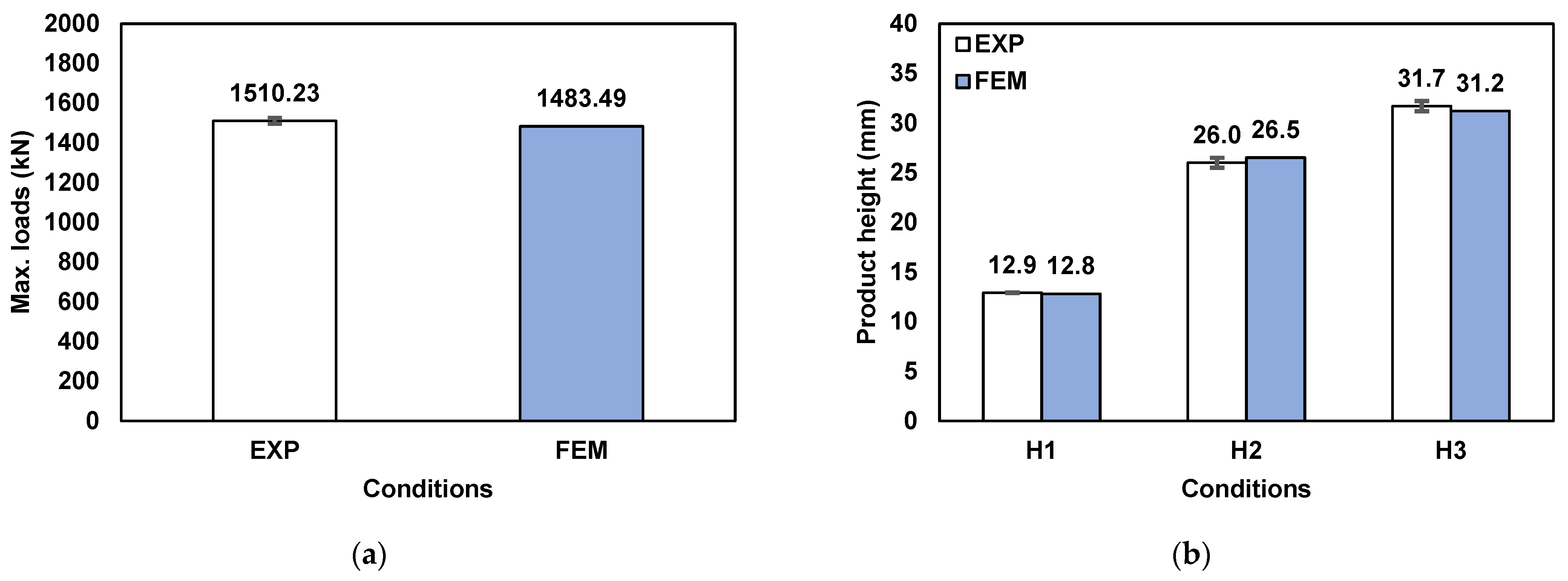
6.1. Validation of Universal FCC
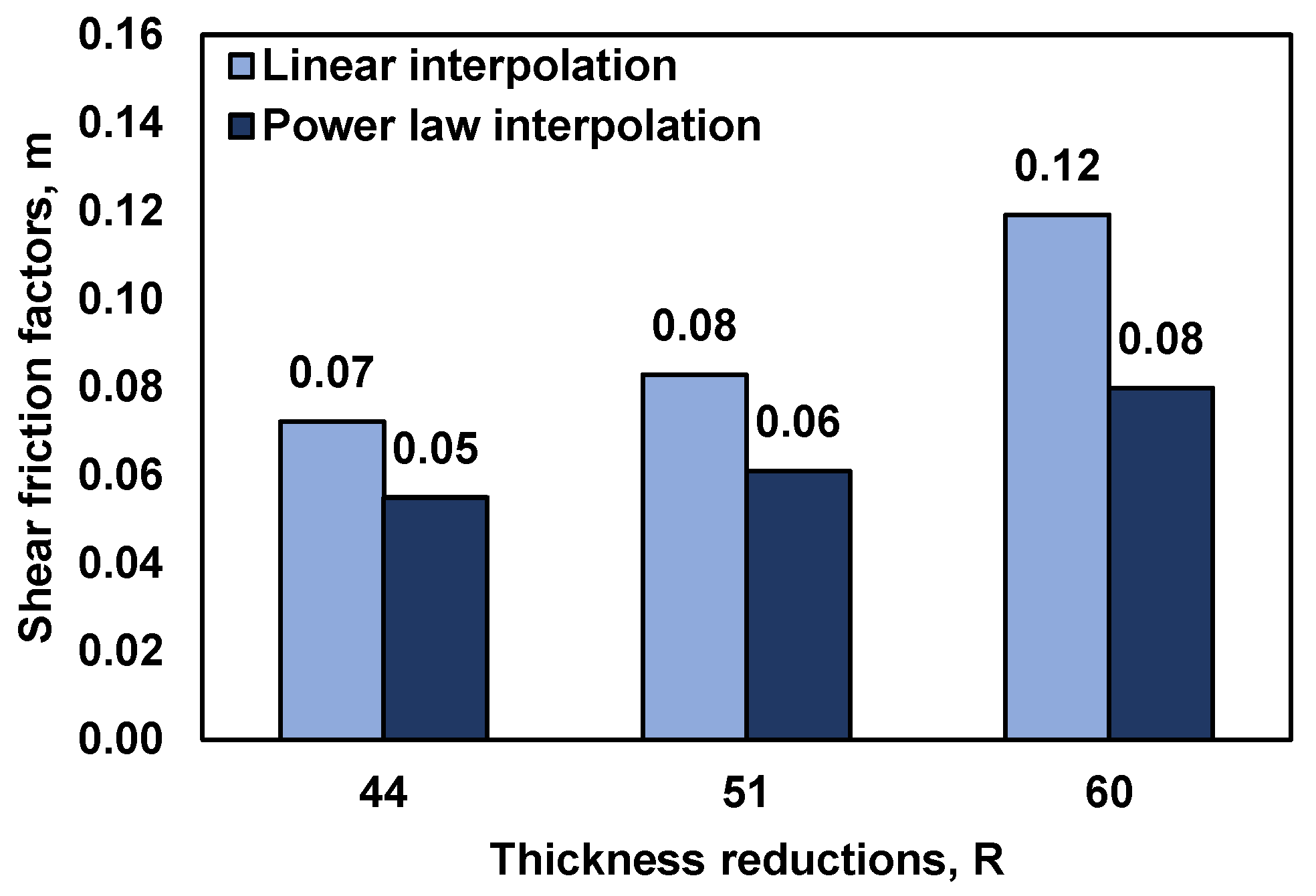
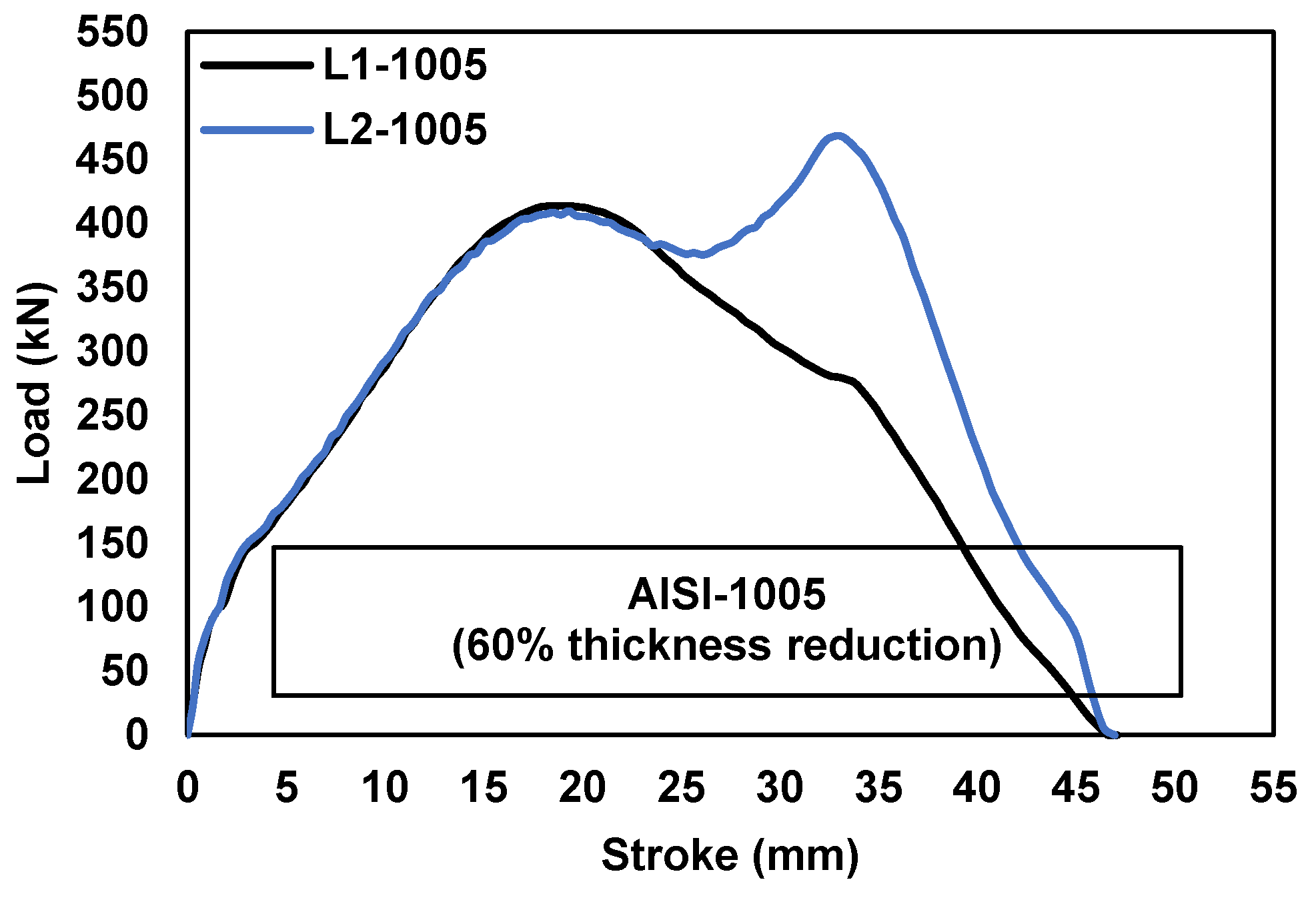
6.2. Friction Evaluation under Different Testing Conditions
6.3. Friction Evaluation in Thick-Sheet Ironing Process for Pulley Manufacturing
7. Conclusions
- A dimensionless specific load (Ls) was proposed as a new friction indicator for the BIT. It can eliminate the effect of material properties when different materials are used.
- The universal FCC, the Ls-R curve, was developed by using the relationship between the specific loads and thickness reductions under different friction values.
- The BIT with the universal FCC was used to determine the shear friction factor in the actual tribological conditions of the thick-sheet ironing process. The average shear friction factor (m) was determined as 0.06. For validation, this friction value was input into the FEM simulation model to predict the forming results. The forming load and dimension of the product from the simulation were in good agreement with the experimental results. The deviations in load and dimension were less than 2%.
- The ball ironing test with the newly developed FCC is recommended for determining the friction value of the thick-sheet ironing processes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Strain | |
| Friction sensitivity parameter | |
| Relative velocity | |
| Representative stress | |
| Normal contact pressure | |
| Shear stress | |
| Surface expansion ratio | |
| L | Load |
| Ls | Specific load |
| k | Shear strength of material |
| m | Shear friction factor |
References
- Schey, J.A. Tribology in Metalworking: Friction, Lubrication and Wear; American Society for Metals: Metals Park, OH, USA, 1983. [Google Scholar]
- Groche, P.; Kramer, P.; Bay, N.; Dubar, L.; Hayakawa, K.; Hu, C.; Kitamura, K.; Moreau, P. Friction Coefficients in Cold forging: A Global Perspective. CIRP Ann.-Manuf. Technol. 2018, 67, 261–264. [Google Scholar] [CrossRef]
- Velkavrh, I.; Lüchinger, M.; Kern, K.; Klien, S.; Ausserer, F.; Voyer, J.; Diem, A.; Schreiner, M.; Tillmann, W. Using a Standard Pin-on-disc Tribometer to Analyze Friction in a Metal Forming Process. Tribol. Int. 2017, 114, 418–428. [Google Scholar] [CrossRef]
- Trivedi, H.K.; Bhatt, D.V. Effect of Lubricating Oil on Tribological Behaviour in Pin on Disc Test Rig. Tribol. Ind. 2017, 39, 90–99. [Google Scholar] [CrossRef] [Green Version]
- Martín, F.; Martín, M.J.; Sevilla, L.; Sebastián, M.A. The Ring Compression Test: Analysis of Dimensions and Canonical Geometry. Proc. Eng. 2015, 132, 326–333. [Google Scholar] [CrossRef] [Green Version]
- Bay, N.; Azushima, A.; Groche, P.; Ishibashi, I.; Merklein, M.; Morishita, M.; Nakamura, T.; Schmid, S.; Yoshida, M. Environmentally Benign Tribo-systems for Metal Forming. CRIP Ann.-Manuf. Technol. 2010, 59, 760–780. [Google Scholar] [CrossRef] [Green Version]
- Altan, T. Cold and Hot Forging: Fundamentals and Application; ASM International: Materials Park, OH, USA, 2005. [Google Scholar]
- Hu, C.; Ou, H.; Zhao, Z. Investigation of Tribological Conditions in Cold Forging Using an Optimized Design of Spike Forging Test. Adv. Mech. Eng. 2015, 7, 1–11. [Google Scholar] [CrossRef]
- Gariety, M.; Ngaile, G.; Altan, T. Evaluation of New Cold Forging Lubricants Without Zinc Phosphate Precoat. Int. J. Mach. Tools 2007, 47, 673–681. [Google Scholar] [CrossRef]
- Zhang, Q.; Felder, E.; Bruschi, S. Evaluation of Friction Condition in Cold Forging by Using T-Shape Compression Test. J. Mater. Process. Technol. 2009, 209, 5720–5729. [Google Scholar] [CrossRef]
- Aleksandrović, S.; Đorđević, M.; Stefanović, M.; Lazić, V.; Adamović, D.; Arsić, D. Different Ways of Friction Coefficient Determination in Stripe Ironing Test. Tribol. Ind. 2014, 293–299. [Google Scholar]
- Üstünyagiz, E.; Nielsen, C.V.; Christiansen, P.; Martins, P.A.F.; Bay, N. Continuous Strip Reduction Test Simulating Tribological Conditions in Ironing. Proc. Eng. 2017, 207, 2286–2291. [Google Scholar] [CrossRef] [Green Version]
- Dubois, A.; Patalier, D.; Picart, P.; Oudin, J. Optimization of The Upsetting-sliding Test Parameters for the Determination of Friction Laws at Medium and High Contact Pressures. J. Mater. Process. Technol. 1996, 62, 140–146. [Google Scholar] [CrossRef]
- Kim, H.; Taylan, A.; Yan, Q. Evaluation of Stamping Lubricants in Forming Advanced High Strength Steels (AHSS) Using Deep Drawing and Ironing Tests. J. Mater. Process. Technol. 2009, 209, 4122–4133. [Google Scholar] [CrossRef]
- Sae-eaw, N.; Aue-u-lan, Y. Friction Evaluation for Combined Drawing and Ironing process with Thick Sheet by Ball Ironing Test. J. Manuf. Sci. Eng. 2021, 143, 061004. [Google Scholar] [CrossRef]
- Sae-eaw, N.; Aue-u-lan, Y. Evaluation of Lubricant Performance for Thick Sheet Ironing Process by Ball Ironing Test. In Proceedings of the Forming the Future: Proceedings of the 13th International Conference on the Technology of Plasticity, Online, 25–30 July 2021. [Google Scholar]
- Lin, Y.; Hsu, K.; Lee, P. The Application of Flow Stress Model to Sheet Metal Forming Simulation. China Steel Tech. Rep. 2010, 23, 31–35. [Google Scholar]
- Hering, O.; Kolpak, F.; Tekkaya, A.E. Flow Curves up to High Strains Considering Load Reversal and Damage. Int. J. Mater. Form. 2019, 12, 955–972. [Google Scholar] [CrossRef] [Green Version]
- Hosford, W.F.; Caddell, R.M. Metal Forming Mechanics and Metallurgy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Lange, K. Handbook of Metal Forming; McGraw Hill: New York, NY, USA, 1985. [Google Scholar]
- Nielsen, C.V.; Bay, N. Review of Friction Modeling in Metal Forming Processes. J. Mater. Process. Technol. 2018, 255, 231–241. [Google Scholar] [CrossRef] [Green Version]
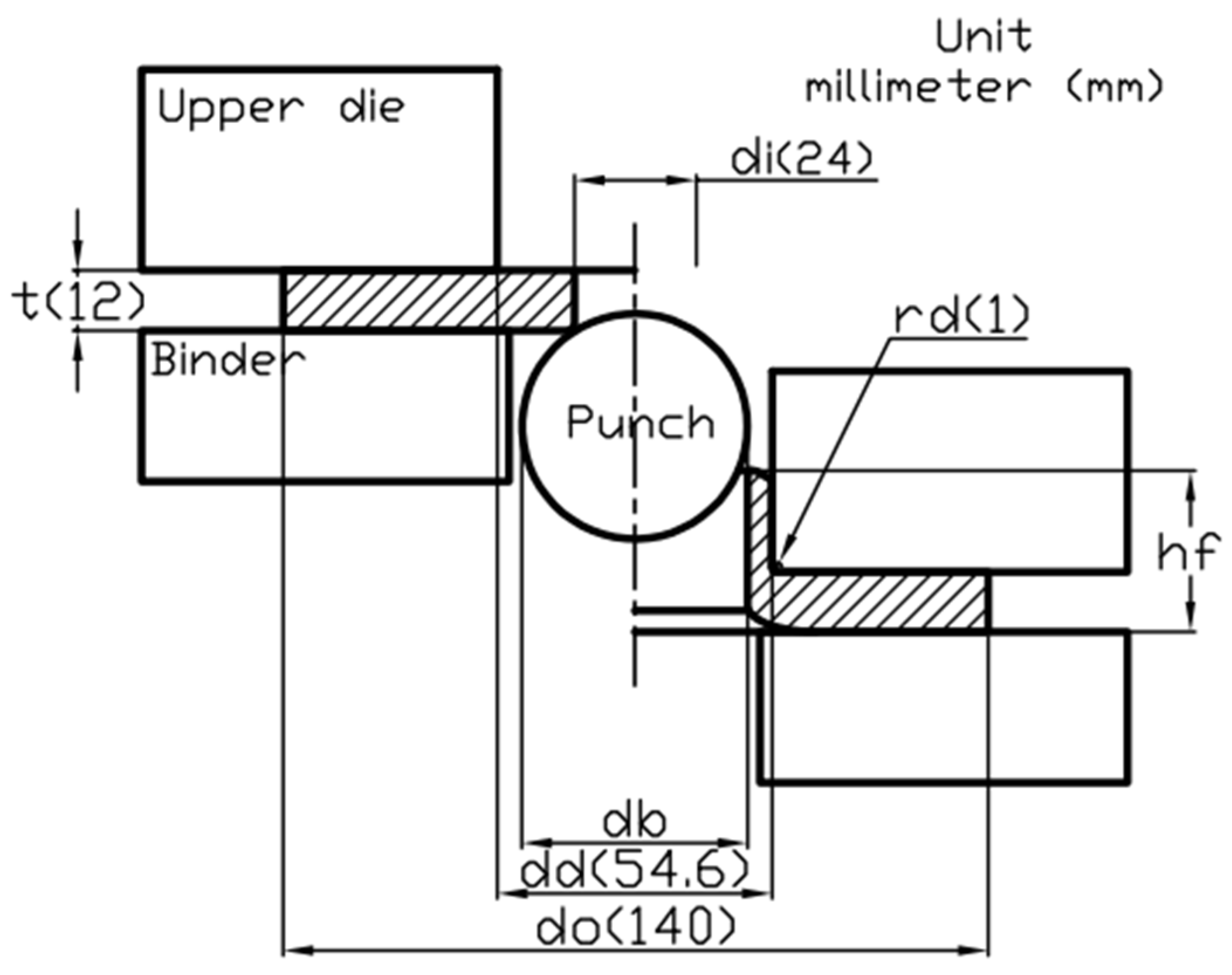
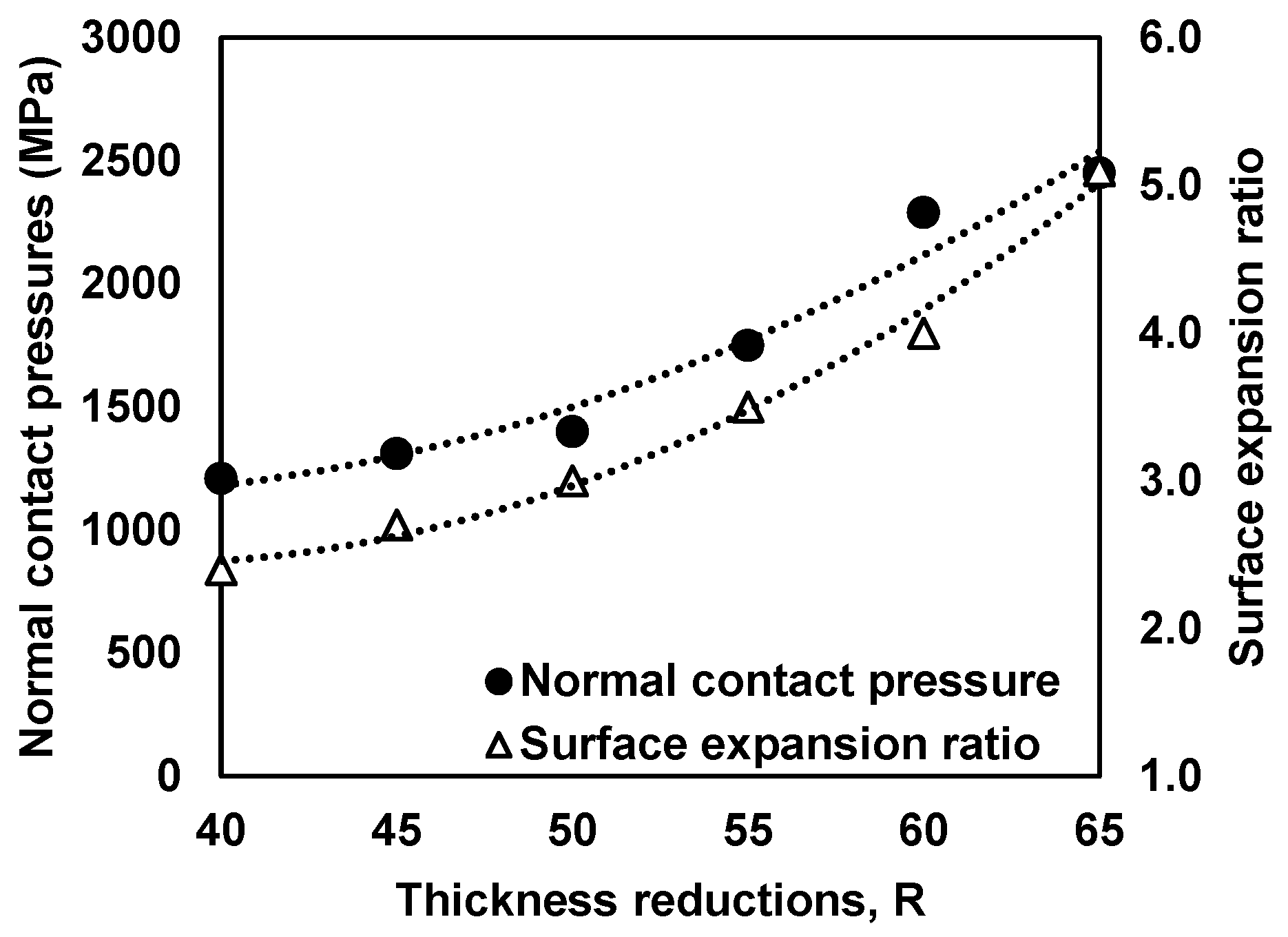
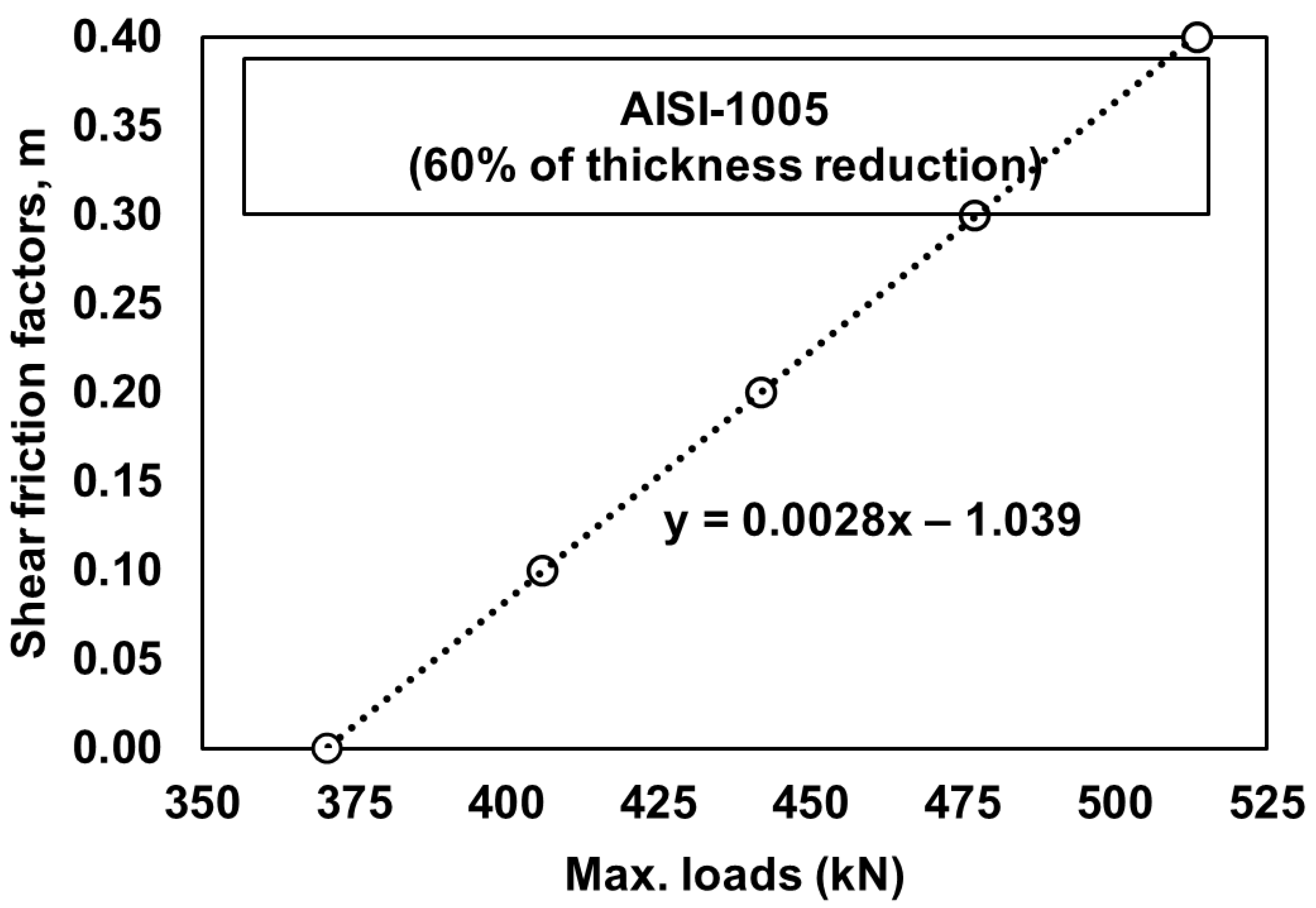
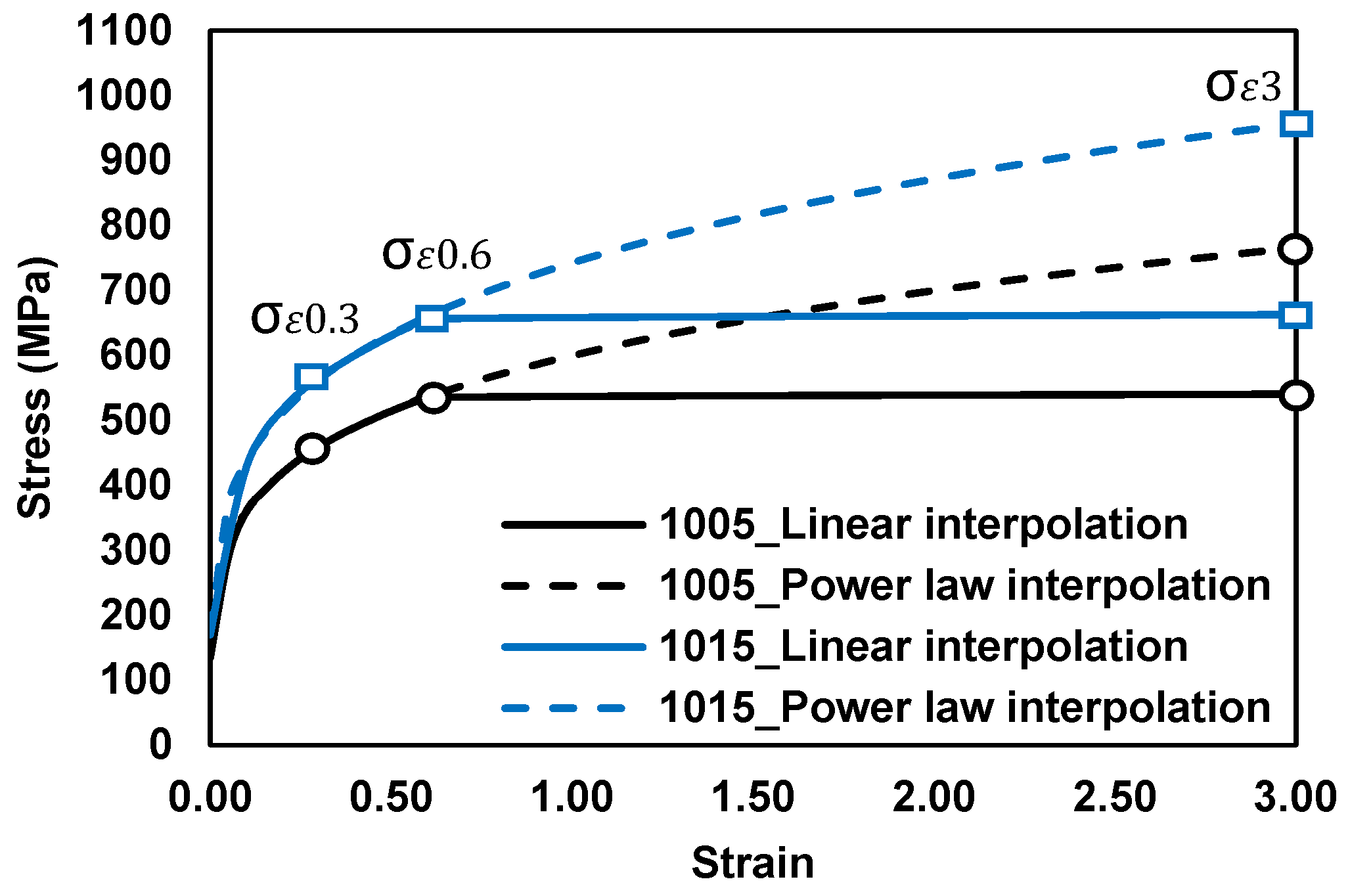

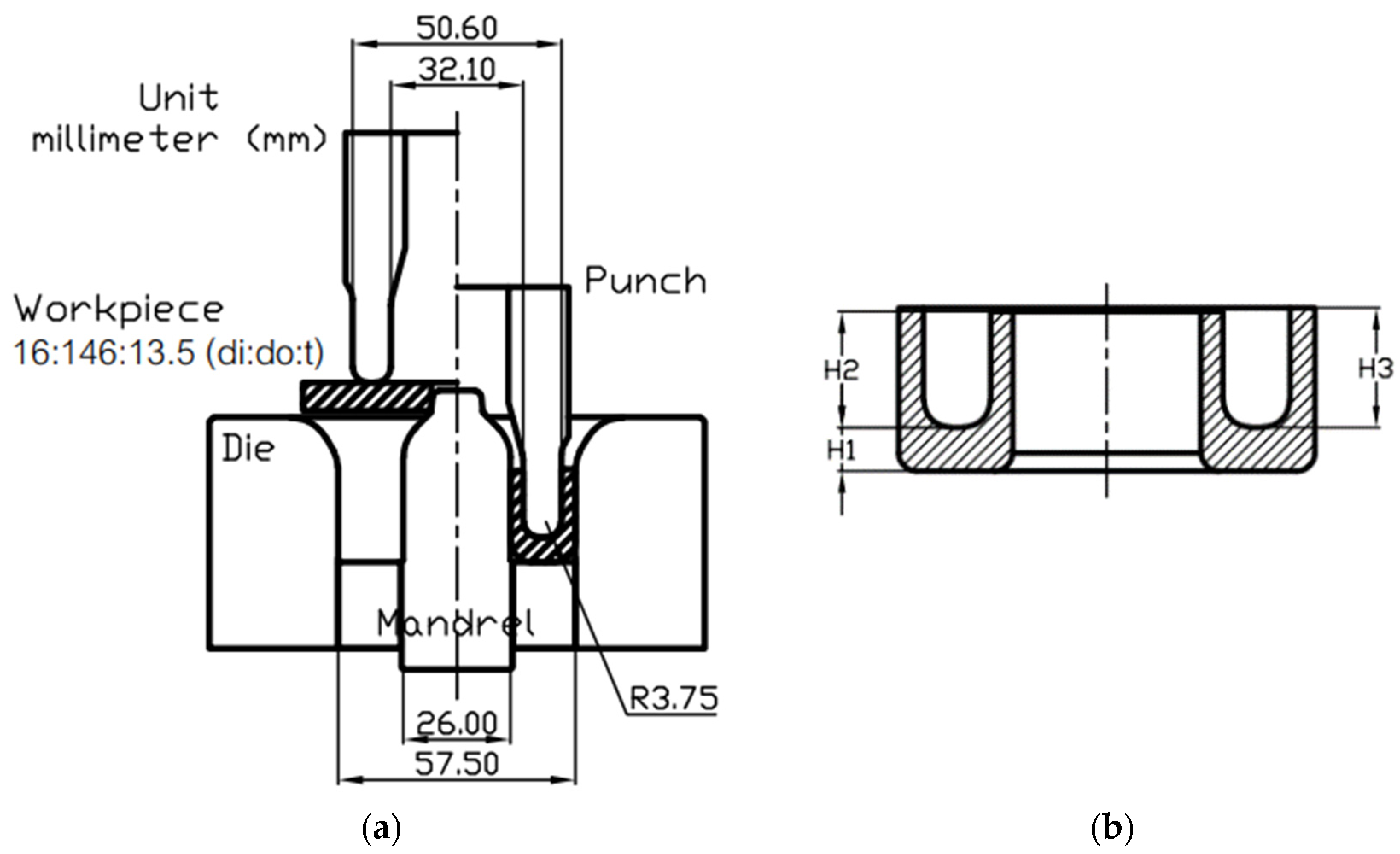

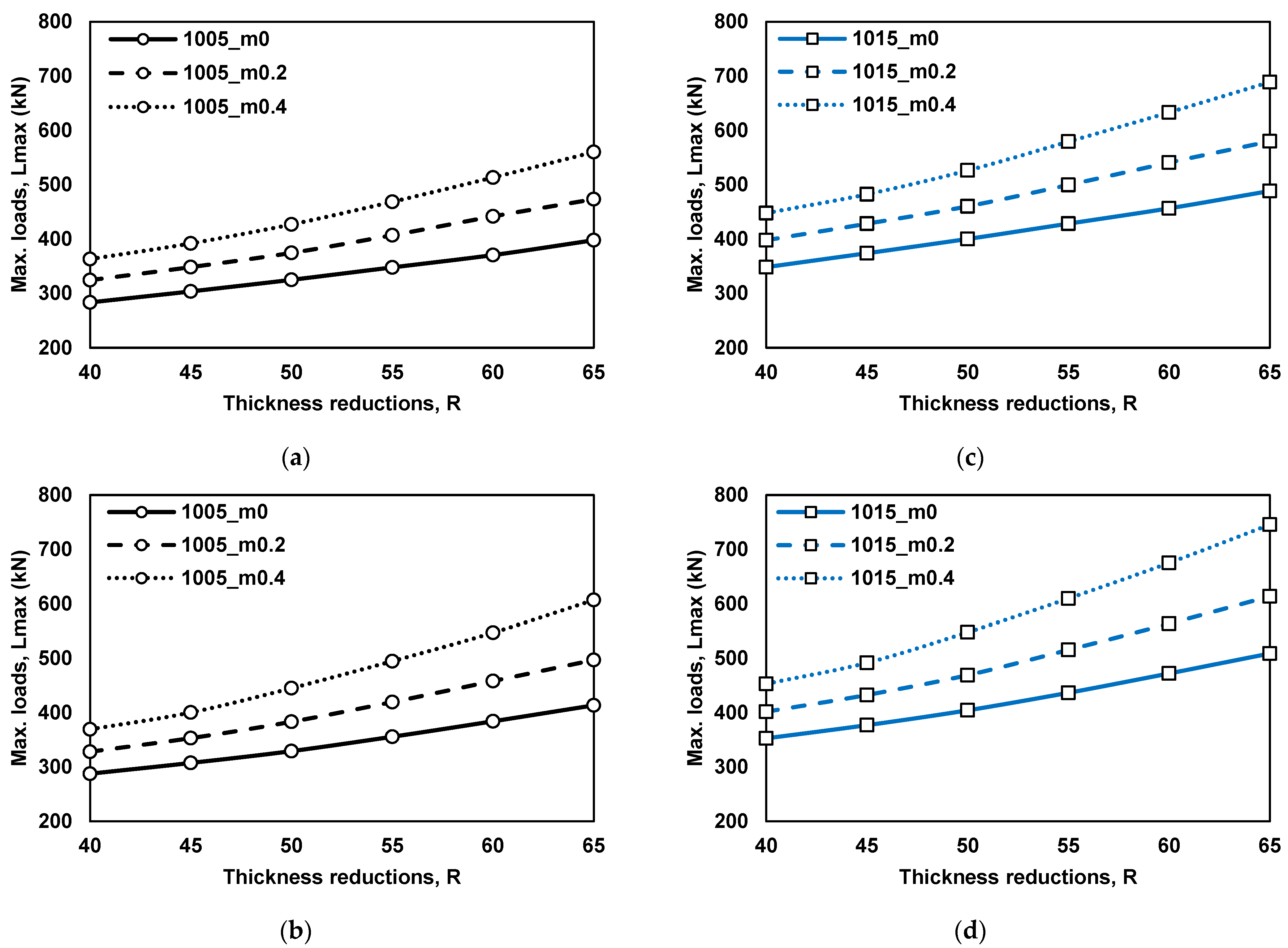
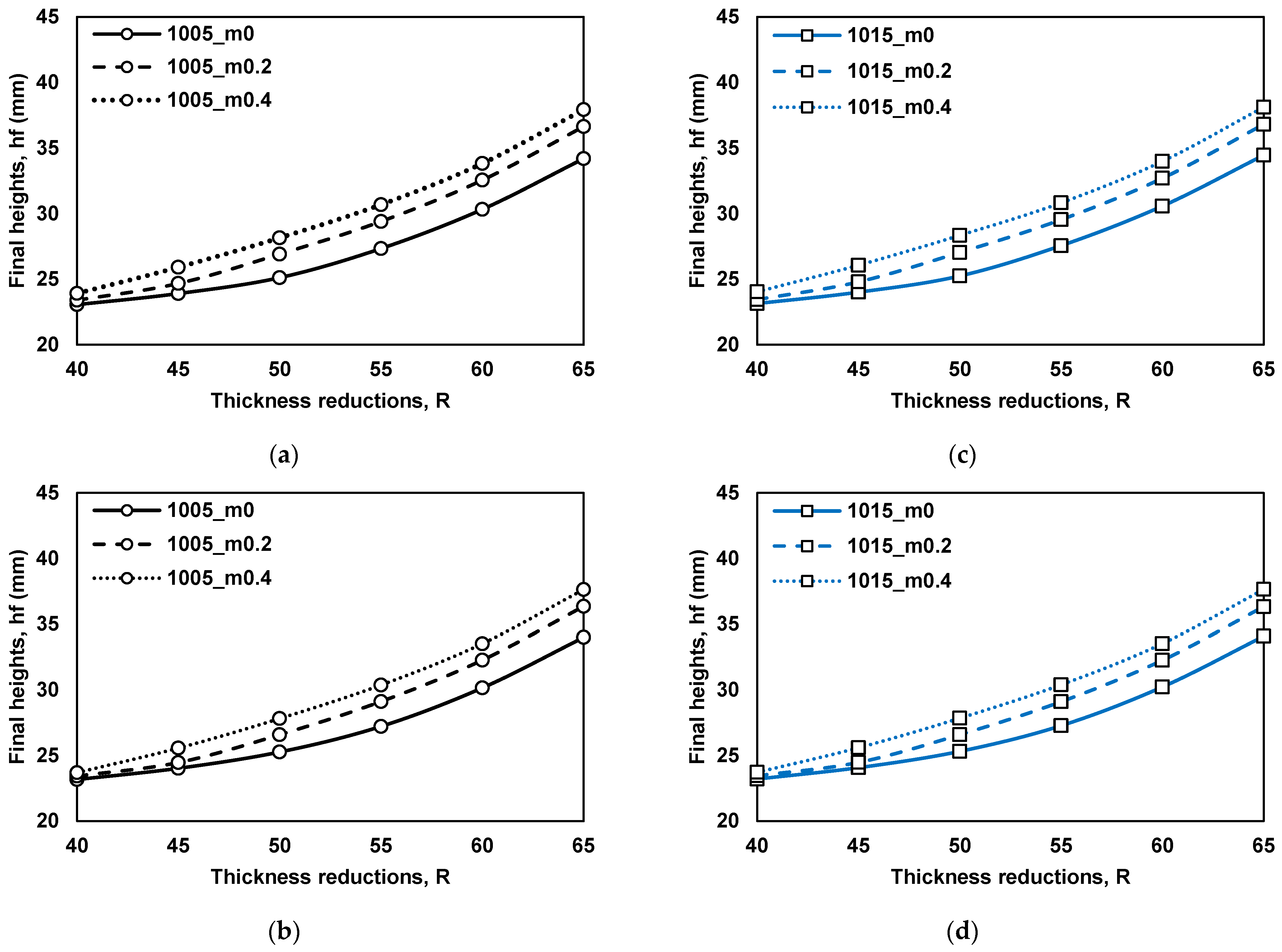




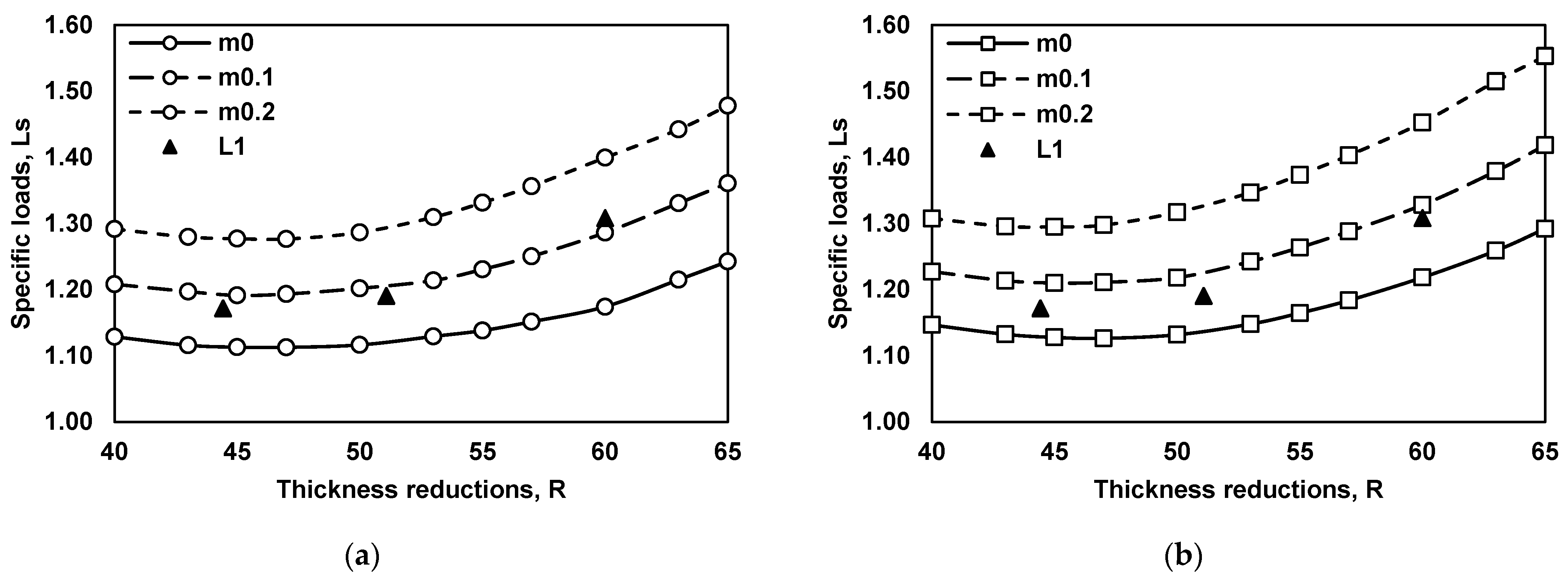





| Conditions | Details |
|---|---|
| Materials | AISI-1005, AISI-1015 |
| Thickness reduction, R (%) | R44(db41.28), R51(db42.87), R60(db45.00) |
| Lubricants | L1, L2, S1 |
| Steels | Chemical Composition (wt%) |
|---|---|
| AISI-1005 | C0.053%, Si0.004%, S0.006%, Mn0.229%, Cr0.013% |
| AISI-1015 | C0.161%, Si0.155%, S0.012%, Mn0.514%, Cr0.008% |
| Code Names | Details | |
|---|---|---|
| L1 | Liquid lubricant—additive EP Density at 30 °C (g/mm3) Kinetic viscosity at 40 °C (mm2/s) VI index Flash point temperature (°C) | 0.934 480 98 210 |
| L2 | Liquid lubricant—base oil Density at 30 °C (g/mm3) Kinetic viscosity at 40 °C (mm2/s) VI index Flash point temperature (°C) | 0.86 30 n/a 200 |
| S1 | Solid lubricant—Zn-Ph coating Combined lubrication layer weight (g/m2) | >8 |
| Parameters | Details |
|---|---|
| Representative stresses, (MPa) | , , |
| Stress–strain curve interpolation technique | Linear interpolation, power-law interpolation |
| Type of material | AISI-1005, AISI-1015 |
| Thickness reduction, R (%) | R40(db40.20)—R65(db46.20) |
| Shear friction factors, m | 0–0.4 |
| Parameters | Details |
|---|---|
| Workpiece—material type | Plastic |
| Workpiece—flow stress | Obtained from compression test |
| Workpiece—number of elements | 8000 elements |
| Tooling—material type | Rigid |
| Binder force | 16 tons |
| Punch speed | 1 mm/s |
| Total stroke | 60 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sae-eaw, N.; Olarnrithinun, S.; Premanond, V.; Aue-u-lan, Y. Development of Universal Friction Calibration Curve for Ball Ironing Test. Lubricants 2022, 10, 106. https://doi.org/10.3390/lubricants10060106
Sae-eaw N, Olarnrithinun S, Premanond V, Aue-u-lan Y. Development of Universal Friction Calibration Curve for Ball Ironing Test. Lubricants. 2022; 10(6):106. https://doi.org/10.3390/lubricants10060106
Chicago/Turabian StyleSae-eaw, Nuttakorn, Sutee Olarnrithinun, Varunee Premanond, and Yingyot Aue-u-lan. 2022. "Development of Universal Friction Calibration Curve for Ball Ironing Test" Lubricants 10, no. 6: 106. https://doi.org/10.3390/lubricants10060106
APA StyleSae-eaw, N., Olarnrithinun, S., Premanond, V., & Aue-u-lan, Y. (2022). Development of Universal Friction Calibration Curve for Ball Ironing Test. Lubricants, 10(6), 106. https://doi.org/10.3390/lubricants10060106




