1. Introduction
The occurrence of stick-slip inhibits the smooth motion of sliders and causes undesirable vibration and noise in mechanical systems. Therefore, it is important to understand the condition of stick-slip occurrence and develop design guidelines for suppressing it. Stick-slip is often observed in rubber sliding parts such as windshield wipers [
1,
2] and rubber belts [
3,
4]. In addition, stick-slip is observed in many industrial products, including automotive parts such as disc brakes and clutches [
5,
6]. Other examples of stick-slip occurrences that should be prevented are, for example, vibration isolators installed in structures [
7,
8,
9]. A historical review of stick-slip phenomena and its analysis is provided by Feeny et al. [
10].
The occurrence conditions for stick-slip are formulated using several simplified analytical models. For example, Nakano [
11] theoretically derived the occurrence criteria for stick-slip using a simplified one-degree-of-freedom vibration system with the Coulomb friction law. By extending the fundamental stick-slip theory, the impact of other parameters on stick-slip occurrence conditions were also studied, including the velocity dependence of the friction coefficient [
12], rigidity anisotropy of the support parts [
13], and tangential contact compliance [
14].
In general, actual vibration systems are often more complex than 1DOF systems, and of course, the phenomena are more complex. However, a slight change in the model from a 1-DOF system to a 2-DOF system makes it impossible to analytically derive the conditions for stick-slip occurrence. It is impossible to derive a stick-slip prediction equation that covers the entire parameter space, and an analytical treatment is possible only in q subspace with some fixed parameters [
14]. Currently, when a stick-slip analysis is performed under multi-DOF systems, the parameter range needs to be limited by considering the target system and to derive a simpler design equation within that range.
Dynamic vibration absorbers (DVAs) are effective engineering technologies for controlling vibrating systems [
15,
16,
17,
18]. Maegawa et al. [
18] quantified the stick-slip suppression effect of the DVA using a simplified analytical model based on the stick-slip theory derived by Nakano [
11] and the fundamental DVA theory [
19]. Maegawa et al. [
18] theoretically demonstrated that appropriately setting the design parameters of the DVA can narrow the stick-slip occurrence area.
In this study, we aimed to discuss the stick-slip dynamics of 2DOF systems using the DVA theory.
Figure 1 shows the analytical model used in this study. The model corresponds to the case of a sliding system with the sliding surface fixed to an elastic foundation, as shown in
Figure 2. Through numerical simulation and theoretical analysis, in this study, the following two results were obtained. First, the numerical simulation results show that a vibration system attached to an elastic foundation with optimal parameters tuned by the dynamic absorber theory has a reduced region of stick-slip conditions compared to that attached to a rigid base. The stick-slip suppression effect was quantitatively verified by analysis using an equivalent 1DOF vibration system model.
3. Numerical Results
Numerical simulations, also referred to as time variations in ξ, were performed to quantify the stick-slip suppression effect of optimally tuned elastic foundations. Using the dimensionless equations of motion, provided by Equations (19)–(27), the time variations in the dimensionless displacement of the primary mass ξ were solved numerically with the Runge–Kutta method.
Figure 7 shows the results of the numerical simulation. The parameters were set as follows: (a)
M =
Mopt,
K =
Kopt,
ζa =
ζaopt,
ζ = 0.1, and
γ = 2, and (b)
M =
Mopt,
K = 2
Kopt,
ζa =
ζaopt,
ζ = 0.1, and
γ = 2. Thus, the results in
Figure 7a,b correspond to the use of the optimally tuned DVA and the non-optimally tuned DVA systems, respectively. Previous research shows that stick-slip occurs under a large
λ condition [
11]. Considering that an increase in
λ corresponds to an increase in the normal load
W, a decrease in velocity
V, and a decrease in support stiffness
k, the observed stick-slip characteristics exhibit typical stick-slip behavior.
Figure 7 clearly shows that setting the value for the DVA parameter strongly affects the occurrence and non-occurrence of stick-slip.
As derived from the dimensionless analysis in
Section 2.3, the dynamic behavior of the analysis system shown in
Figure 1 can be determined using only the six parameters, i.e.,
M,
K,
ζa,
ζ,
λ, and
γ. Because the DVA parameters are optimally set based on Equations (28)–(30), that is,
Maopt,
Kaopt, and
ζaopt are the dependent variables of
ζ, the dynamic behavior of the present system is characterized only by the three parameters
λ,
ζ, and
γ. Because γ does not affect the occurrence and non-occurrence of stick-slip [
11], it is possible to completely determine when stick-slip occurs by investigating the occurrence and non-occurrence of stick-slip when
λ and
ζ are changed.
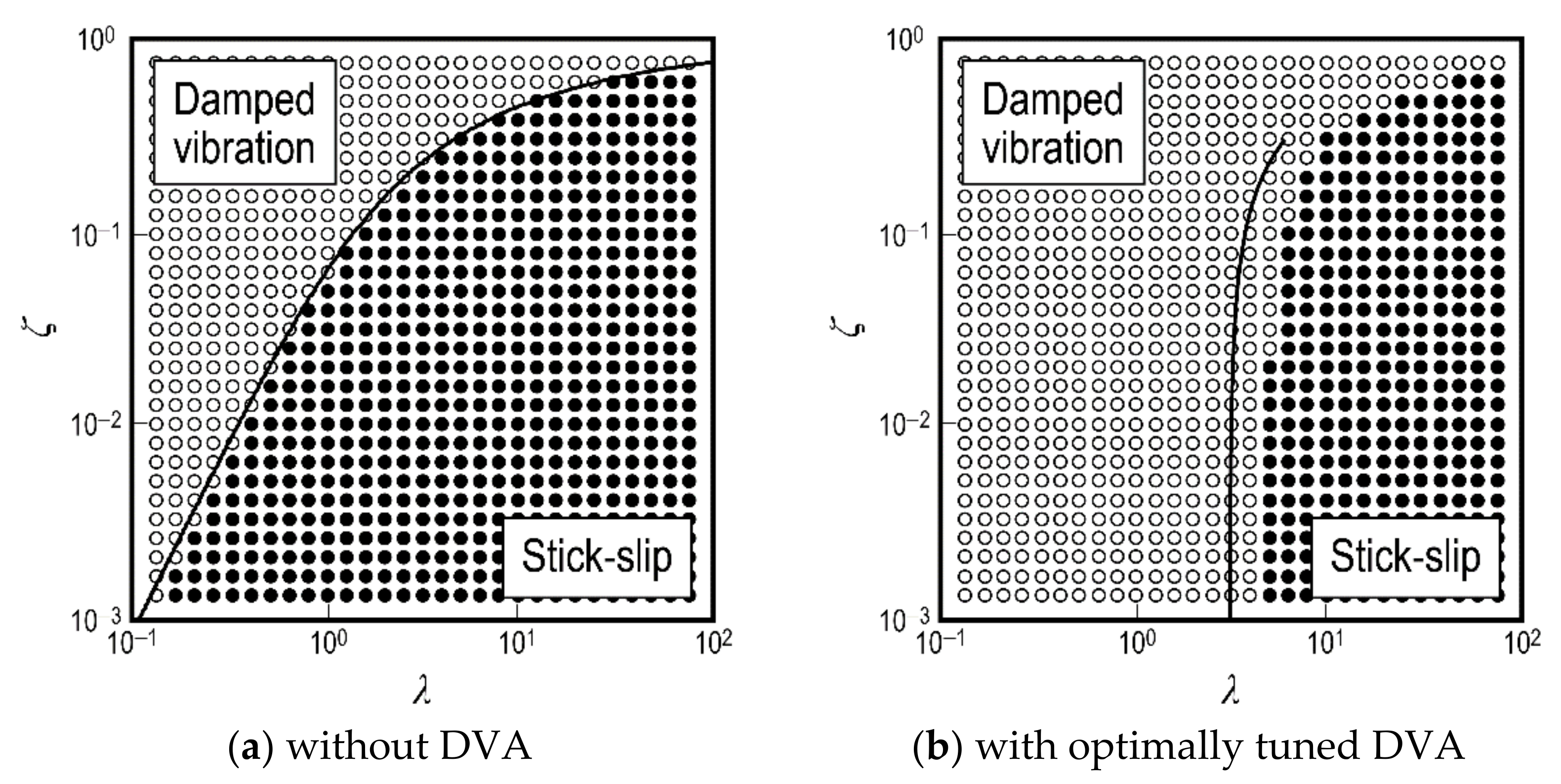
Figure 8 shows the effect of the use of the DVA on the occurrence and non-occurrence conditions of stick-slip based on the results of the numerical simulation with
γ = 2. The results shown in
Figure 8a are based on the results of the numerical simulation when the 1DOF vibration system is directly attached to the rigid base. This figure corresponds to the stick-slip occurrence/non-occurrence map for the equivalent one-degree-of-freedom vibration system shown later in
Figure 9, when
ceq = 0. Thus, this configuration corresponds to the stick-slip occurrence condition when no DVA is used. The solid line drawn in
Figure 8a is the discriminant equation of the boundary conditions for the occurrence and non-occurrence of stick-slip when not using the DVA system, based on Equation (37).
In contrast, in
Figure 8b, the stick-slip occurrence condition was determined by the numerical simulation of the optimally tuned DVA vibration system shown in
Figure 1, where the solid line in
Figure 8b is based on Equation (37). That is, it is the map of stick-slip occurrence and non-occurrence conditions when the parameters of the elastic foundation are set to optimal values based on dynamic absorber theory. Comparing
Figure 8a,b, the use of the optimized DVA works to narrow the stick-slip region under all conditions.
4. Discussion
Figure 8 demonstrates that the use of an optimized elastic foundation suppresses stick-slip occurrence. In this section, the stick-slip suppression effect is quantified.
As described above, the Harik and Issa model [
20] harmonic external force
fext (=
fsin(
ωt)) was applied to the primary mass, as shown in
Figure 3. If the frequency of the cyclic external force is in the region close to the natural frequency of the system (i.e.,
ω =
ωn) under the condition that the dynamic absorber parameters are optimized, the behavior of the system can be approximated by an equivalent 1DOF vibration system.
Figure 9 shows the equivalent 1DOF system that can replace the 2DOF DVA system shown in
Figure 1. In
Figure 9, the magnitude of
ceq represents the stick-slip suppression effect of the DVA.
The relationship between the maximum dimensionless deflection
Hmax and the damping ratio of the equivalent model
ζeq = (
c +
ceq)/(2(
mk)
0.5) is given by the following equation:
From Equations (31) and (32), the equivalent damping ratio can be written as a function of the damping ratio, as follows:
Figure 10 shows the dependence of
ζ on
ζeq. Here,
ζeq is the equivalent damping ratio including the damping effect of the optimally applied DVA, and
ζ is the damping ratio of the primary vibration system. Therefore, Equation (33) holds only when the DVA is optimally adjusted.
The black solid line in
Figure 5 shows the vibration response curve when tuned with the optimal parameters. On the other hand, the dashed line in
Figure 5 shows the vibration response curve of the equivalent 1DOF vibration system with
ζeq. From
Figure 5, it is found that the behavior of the main vibration system in the 2DOF system and the equivalent 1-DOF system are in good agreement in the range close to
ω =
ωn.
The analysis conducted by Nakano et al. shows that the vibration frequency of stick-slip approaches the natural frequency as
λ decreases [
14]. When λ is smaller than 1, the vibration frequency of the stick-slip can be approximated by the natural frequency of the system. That is, in this case, the behavior of the system vibrating due to stick-slip coincides with the behavior of the system when it is vibrated by a periodic external force. The only difference is whether the source of the vibration is an external force or the difference between static and dynamic frictional forces.
If λ is smaller than 1, the vibration frequency of stick-slip can be approximated by the natural frequency of the system. In other words, in this case, the behavior of the system vibrating due to stick-slip is consistent with the behavior of the system when it is vibrating due to periodic external forces. Although the switching between static and dynamic frictional forces excites the system, the behavior of the system is the same as when subjected to a sinusoidal external excitation force. It should be noted that the1DOF vibration system used in this study is only equivalent when
λ has relatively small values as described above. When
λ is small, the vibration waveform of the stick-slip becomes a harmonic vibration, increasing the applicability of the theory for quantifying the optimum parameter of the DVA. In the 1DOF system, the
λ dependence of the stick-slip frequency
fss and amplitude
Ass is formulated as follows
where
fn =
ωn/2π and
An =
V/
ωn.
Nakano’s [
11] boundary equation for the occurrence and non-occurrence conditions of stick-slip for the 1DOF system with Coulomb friction is applied to the equivalent model shown in
Figure 9. The boundary equation of the equivalent model can thus be written using the two dimensionless parameters,
λ and
ζeq, as follows:
Equation (36) can be expressed in the more simplified form [
11]:
From Equation (37), the criterion for preventing the occurrence of stick-slip in this configuration can be written as:
When the DVA is not installed,
ceq = 0 in the equivalent model shown in
Figure 9. Thus, the results in
Figure 8a corresponds to the results of stick-slip occurrence conditions when
ceq = 0 in
Figure 9. Therefore, by replacing
ζeq with
ζ in Equation (37), it is possible to obtain the boundary equation for the occurrence and non-occurrence of stick-slip when the DVA is not attached, as shown below:
Using Equations (33) and (37), we determined the occurrence criteria for stick-slip based on the two dimensionless parameters λ and ζ.
The procedure used to determine the stick-slip occurrence condition for a sliding surface for which ζ is known is recounted here. First, the optimum values of the dimensionless parameters (Mopt, Kopt, ζaopt) were determined using Equations (28)–(30). At the same time, the optimum value of the DVA parameters (ma_opt, ka_opt, ca_opt) were determined using Equations (28)–(30). Using the results, we were able to design a DVA for the specific situation. Based on Equation (33), we quantified the equivalent damping ratio ζeq when the optimum vibration absorber was installed. Finally, using Equation (38), we were able to quantify the values of λ at which stick-slip occurs. Because λ includes the velocity V and load W, it was possible to quantify the velocity range or normal load range in which stick-slip was expected to occur.
Figure 8b clearly shows that the stick-slip occurrence area is in good agreement with the prediction by the discriminant equation in Equation (37). In other words, the increase in the damping effect improved by the optimal tuning of the elastic foundation (DVA) is considered to have worked to suppress stick-slip. As mentioned above, Equation (37) can predict the occurrence and non-occurrence of stick-slip more accurately when
λ is relatively small. On the other hand, when
λ is relatively large, the modeling of the equivalent 1DOF vibration system is not appropriate, which may be the reason for the discrepancy between the discriminant equation and the numerical simulation results. The significance of the discriminant equation derived in this study is that it provides a theoretical basis for the fact that the stick-slip suppression effect of a vibration system mounted on an optimally tuned elastic foundation is due to the vibration suppression effect of the DVA, at least under conditions where
λ is small. The numerical simulation results show that the stick-slip occurrence region is only inside the region predicted by Equation (37), indicating that this equation can be used as a discriminant equation to predict stick-slip occurrence and non-occurrence.
The discriminant of Equation (37) is not always valid when the set values of the DVA deviate from the values found using Equations (28)–(30). This is because the equation applies an equivalent one-degree-of-freedom vibration system assuming an optimally tuned dynamic absorber is installed, which would not be appropriate if the parameters are not optimal.
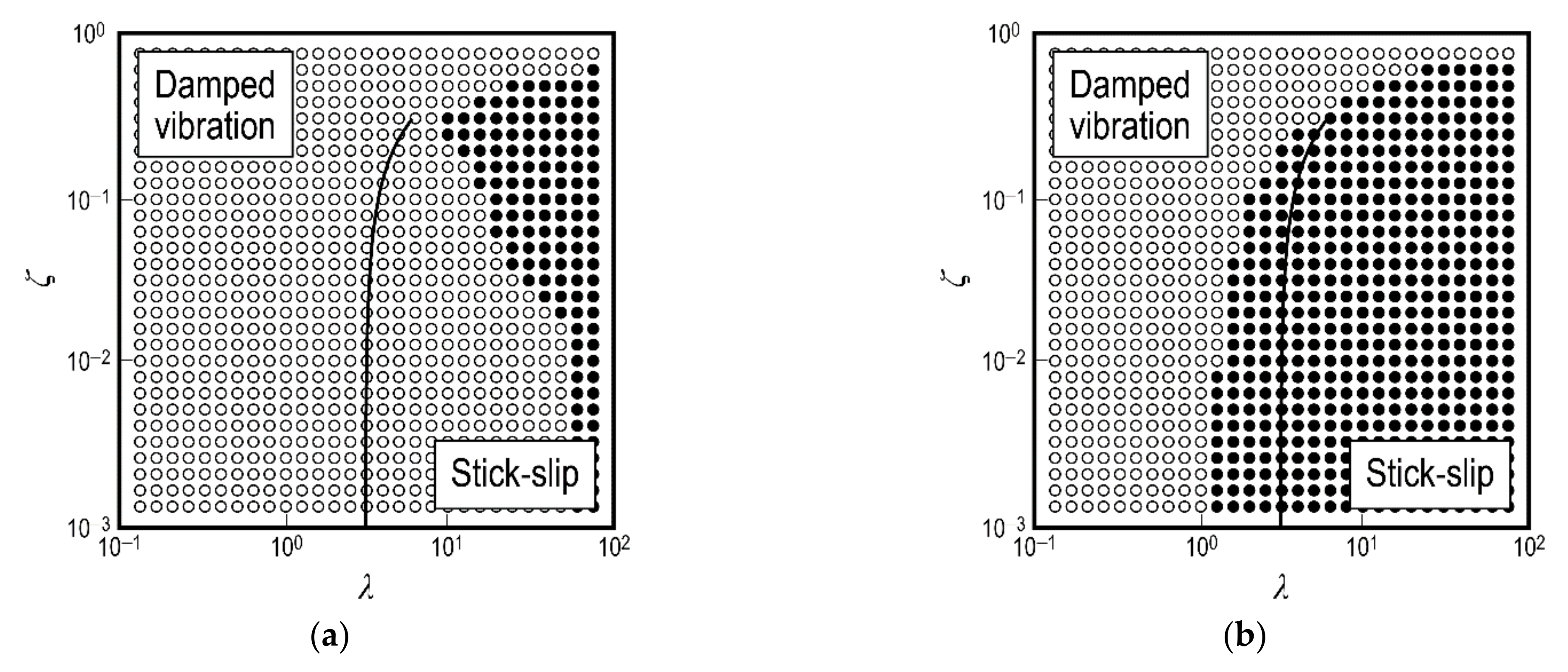
Figure 11 shows the stick-slip occurrence and non-occurrence map when a non-optimally tuned DVA system is used. The parameters were set as follows: in
Figure 11a, the parameters are set to
M =
Mopt,
K =
Kopt/2,
ζa =
ζaopt, and
γ = 2; and in
Figure 11b the parameters are set to
M =
Mopt,
K = 2
Kopt,
ζa =
ζaopt, and
γ = 2. When the parameters of the DVA diverge from those defined by Equations (28)–(30), the stick-slip occurrence region may be wider or narrower than the region predicted by Equation (37). Importantly, the discriminant of Equation (37) does not necessarily show the maximum stick-slip suppression ability of the DVA. The importance of Equation (37) is that if the parameters of the DVA are set to the values defined by Equations (28)–(30), then Equation (37) represents the region where stick-slip reliably does not occur. Thus, the theoretical prediction tool derived in this study can be utilized effectively when making a quantitative design based on theory.
Focusing on the results in
Figure 11a, it can be seen that the area of stick-slip occurrence is overwhelmingly narrower than in other conditions, which is a characteristic result.
Figure 12 shows the time variations of dimensionless displacements
ξ and
ξa and dimensionless velocities
and
under
λ = 1,
ζ = 0.01. Under these conditions, stick-slip does not occur in either case and the initial fluctuations decrease and decay with time. A closer look reveals that for
K =
Kopt/2, i.e.,
Figure 12a, the oscillations of the main vibration system (black line) and the secondary vibration (DVA) system (gray line) are nearly in opposite phases. On the other hand, in case
K =
kopt × 2, i.e.,
Figure 12b, each mass point is oscillating in perfectly in-phase.
Figure 13 shows the time variations of dimensionless displacements
ξ and
ξa and dimensionless velocities
and
under
λ = 10,
ζ= 0.01. In
Figure 13a, stick-slip does not occur, but in
Figure 13b, stick-slip is observed. This corresponds to the fact that in
Figure 11, the stick-slip region is wide for
K =
kopt × 2 and extremely narrow for
K =
Kopt/2. From the above, it can be seen that the vibration modes have a significant effect on the stick-slip suppression observed in
Figure 11a. In the case of
K =
Kopt/2, the two masses oscillate in opposite phases as a second-order mode, and their motions cancel each other out to produce the stick-slip suppression effect. In this case, stick-slip can be suppressed even at a higher λ than the condition predicted by the stick-slip occurrence discriminant formula shown in Equation (37). In other words, by setting the phases of the two masses well, it is possible to obtain a large vibration suppression effect beyond the vibration suppression effect of a general dynamic absorber. Although this effect is not discussed in depth in this study, it is considered to be an important finding for stick-slip suppression in 2DOF vibration systems.
Figure 14 and
Figure 15 show trajectories in a phase plane with
ξ and
an under
λ = 1,
ζ = 0.01 and under
λ = 10,
ζ = 0.01, respectively. Note that the calculation conditions for
Figure 14 and
Figure 15 are the same as those for
Figure 12 and
Figure 13. From the phase plane, the oscillation behavior of the main vibration system can be well understood visually. As shown in
Figure 14, under relatively small
λ conditions, the oscillations decay gradually, i.e., the orbit spirals toward the origin. On the other hand, for large
λ, the behavior changes drastically. In the case of
Figure 15a, where stick-slip does not occur, the vibration does not decay in a spiral manner as seen in
Figure 14, but instead follows a peculiar trajectory. It is clear that the behavior under the same conditions cannot be approximated by a 1DOF vibration system, and results in the second-order mode of vibration behavior described above. In
Figure 15b, where stick-slip occurs, a limit cycle is formed.
Finally,
Figure 16 shows a design flowchart for stick-slip suppression by attachment to an elastic foundation. The following seven parameters are determined by modeling into a 1DOF sliding system; further, the value of
λ and
ζ are also obtained. By substituting the estimated ζ into Equation (33) we can obtain
ζeq. Next,
λ and
ζeq are substituted into Equation (38). If the same equation holds, stick-slip suppression using an elastic foundation is possible. By substituting
ζ into Equations (28)–(30), we can then obtain
Mopt,
Kopt, and
ζaopt. From these, the optimal parameters of the elastic foundation,
ma_opt,
ka_opt, and
ca_opt, are calculated. Finally, we redesign the targeted sliding system based on the obtained design parameters of the sliding system with elastic foundation (DVA).