Numerical Model of Mixed Lubrication and Experimental Study of Reciprocating Seal Based on Inverse Lubrication Theory
Abstract
:1. Introduction
- (1)
- The established numerical simulation model for lubrication of a reciprocating seal must be improved.
- (2)
- When solving theoretical models, few solutions combine EHL and IHL Reynolds equation methods. In addition, there are few studies on sealing performance under high-pressure conditions. Research on reciprocating sealing systems is mostly limited to the field of mechanics, and there are few studies that have combined force and thermal analysis. Therefore, the influence of temperature on the sealing performance of a reciprocating seal system must be investigated, and a hybrid lubrication model of the sealing ring should be established.
- (3)
- Theoretical research is rarely combined with experimental verification, and the calculation results of numerical models are rarely verified with actual experiments. Many theoretical models have not been experimentally verified, and many experimental methods have not been guided by theory. Therefore, their results should be considered contingent on theoretical or experimental verification.
2. Numerical Model of Mixed Lubrication
- (1)
- To study the sealing performance of the seal under steady-state conditions, the transient effects and viscoelastic factors of the seal material may be ignored.
- (2)
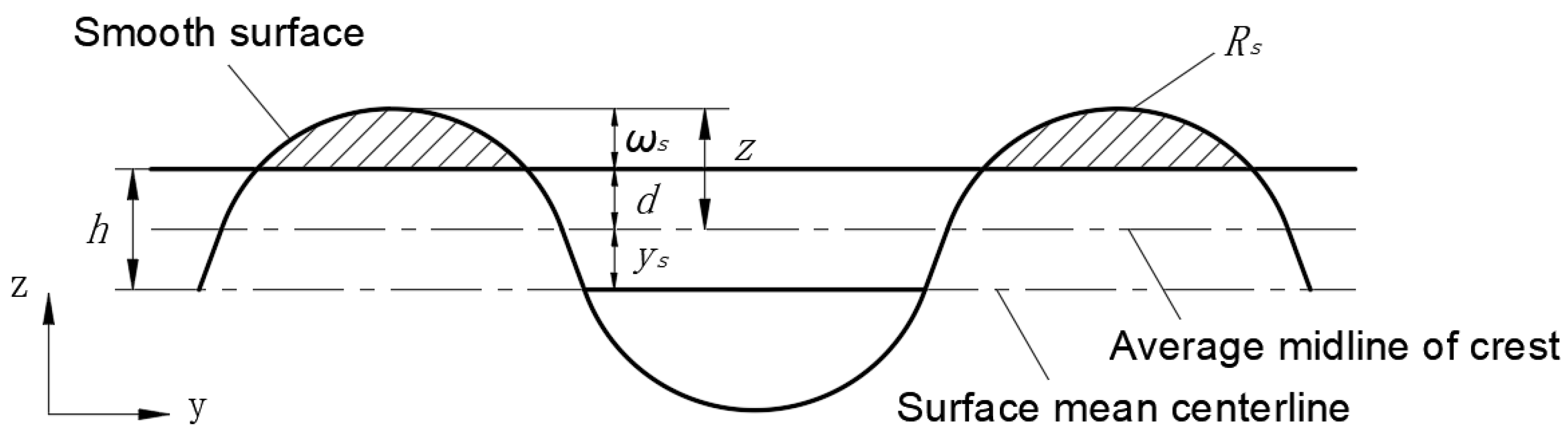
- Assuming that the surface of the piston rod is completely smooth, the empirical friction coefficient must be selected to calculate the rough peak friction force between the piston rod and the sealing ring.
- (3)
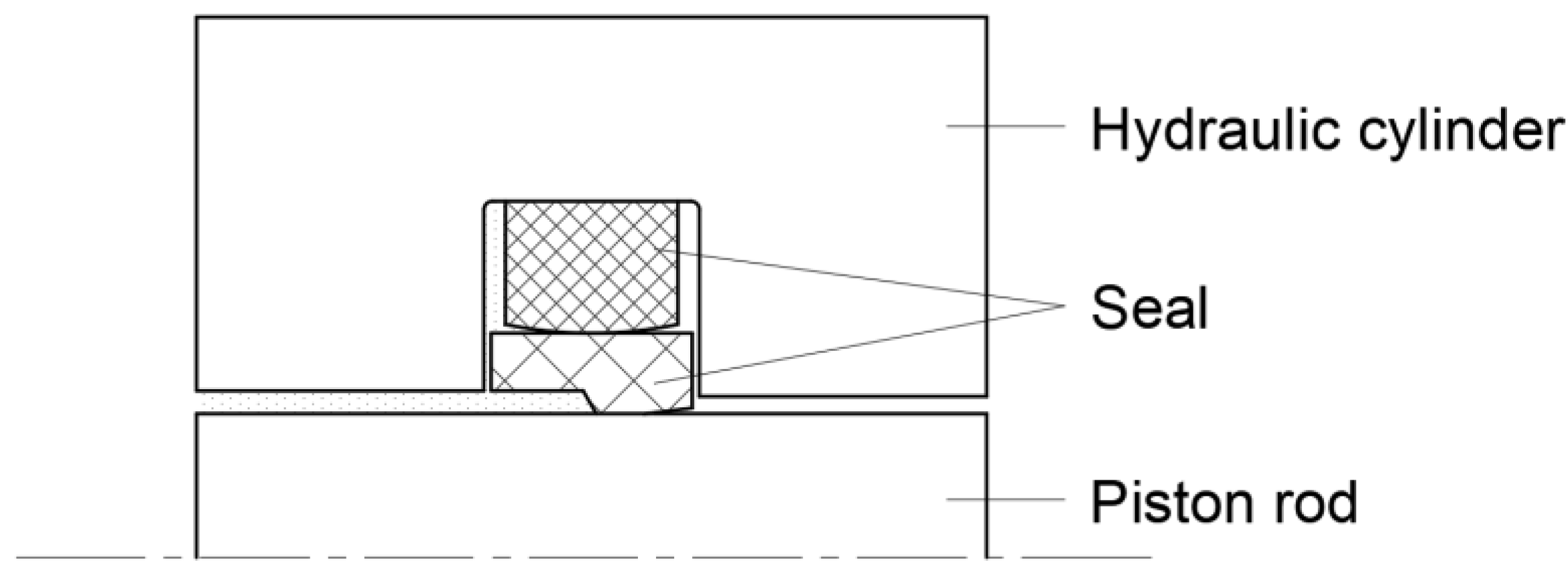
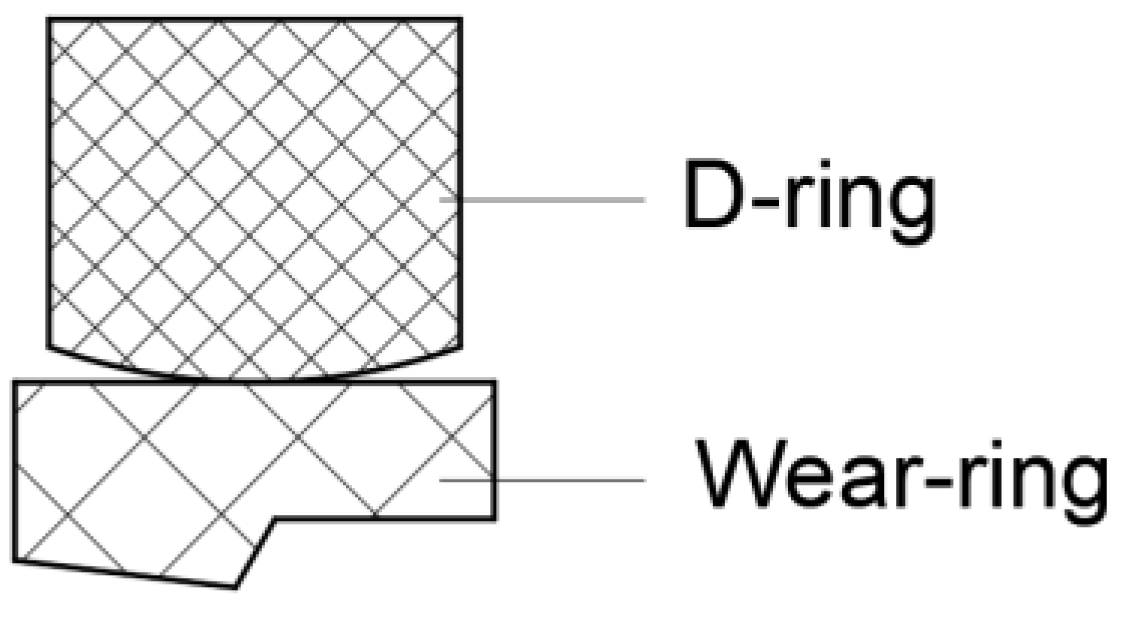
- The geometric model of the reciprocating seal is axisymmetric.
- (4)
- Assuming that there is enough oil on the air side of the lip of the seal ring, the oil flow rate during the instroke can be calculated.
- (5)
- The fluid in the contact area is assumed to be a Newtonian fluid, and the material of the sealing ring is simulated by a nonlinear elastic material model.
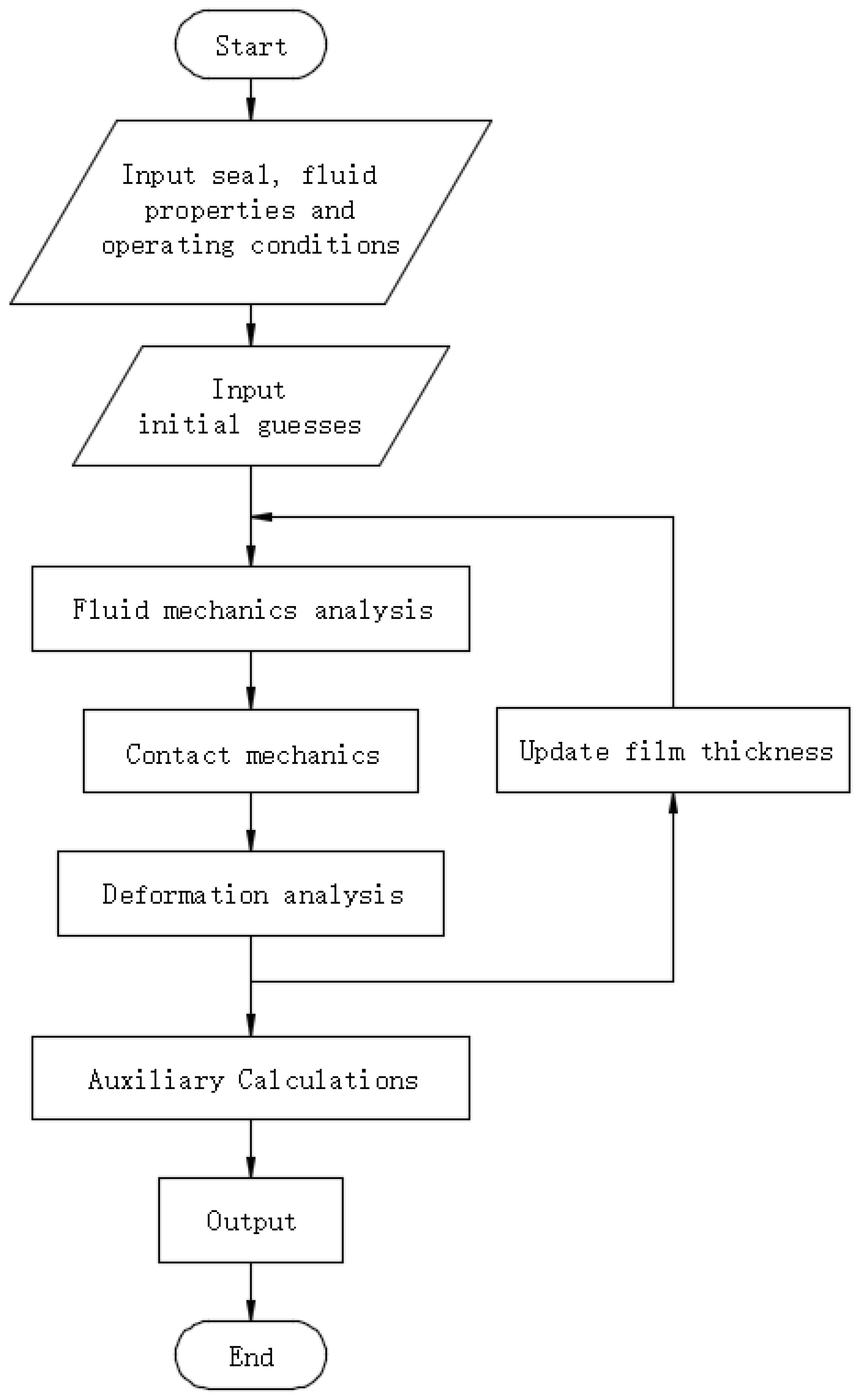
2.1. Reciprocating Seal Mixed Lubrication Model
2.2. Fluid Mechanics Analysis
2.3. Contact Mechanics Analysis
2.4. Solid Mechanics Analysis
2.5. Thermal Analysis
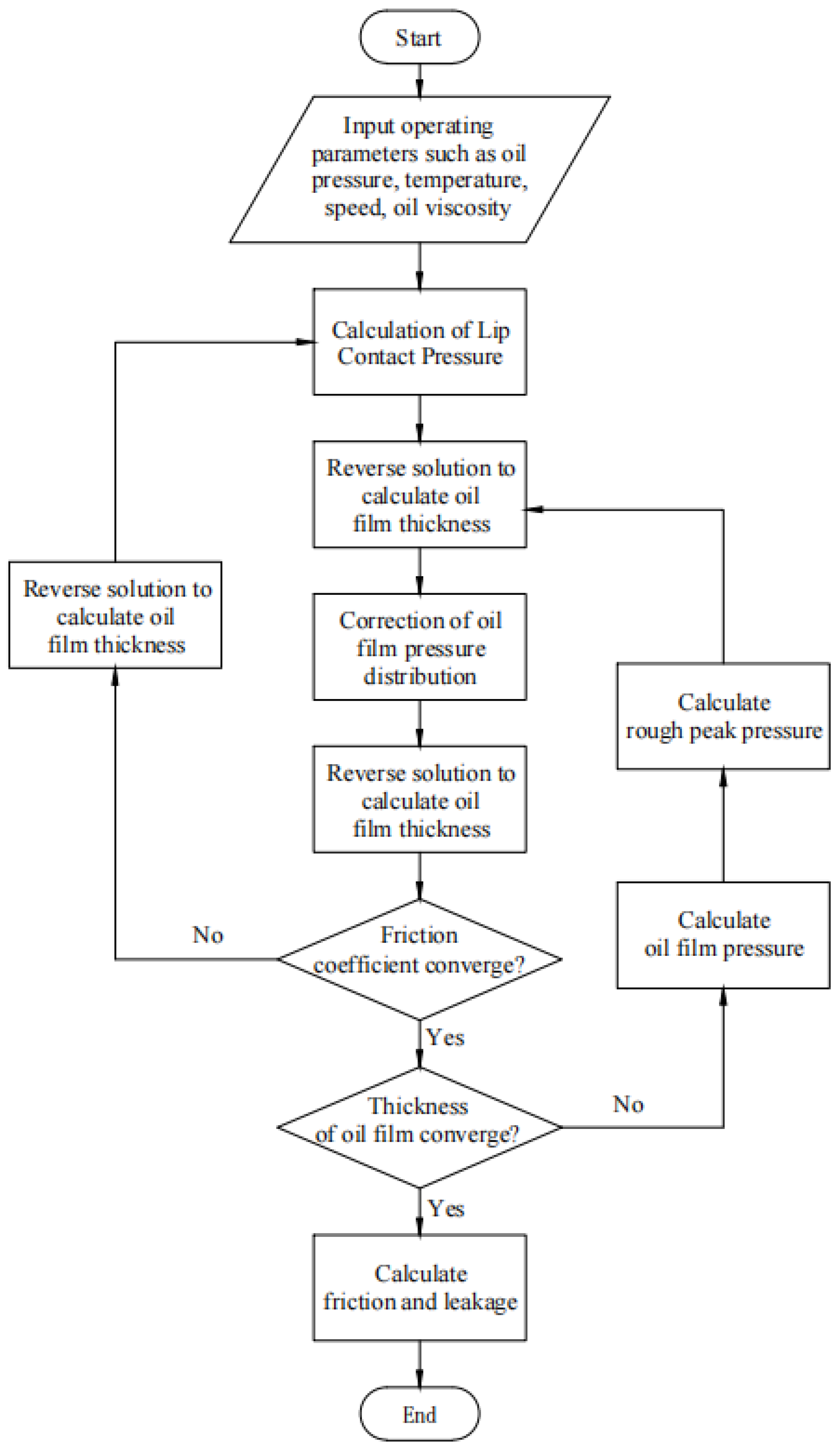
2.6. Calculation Process
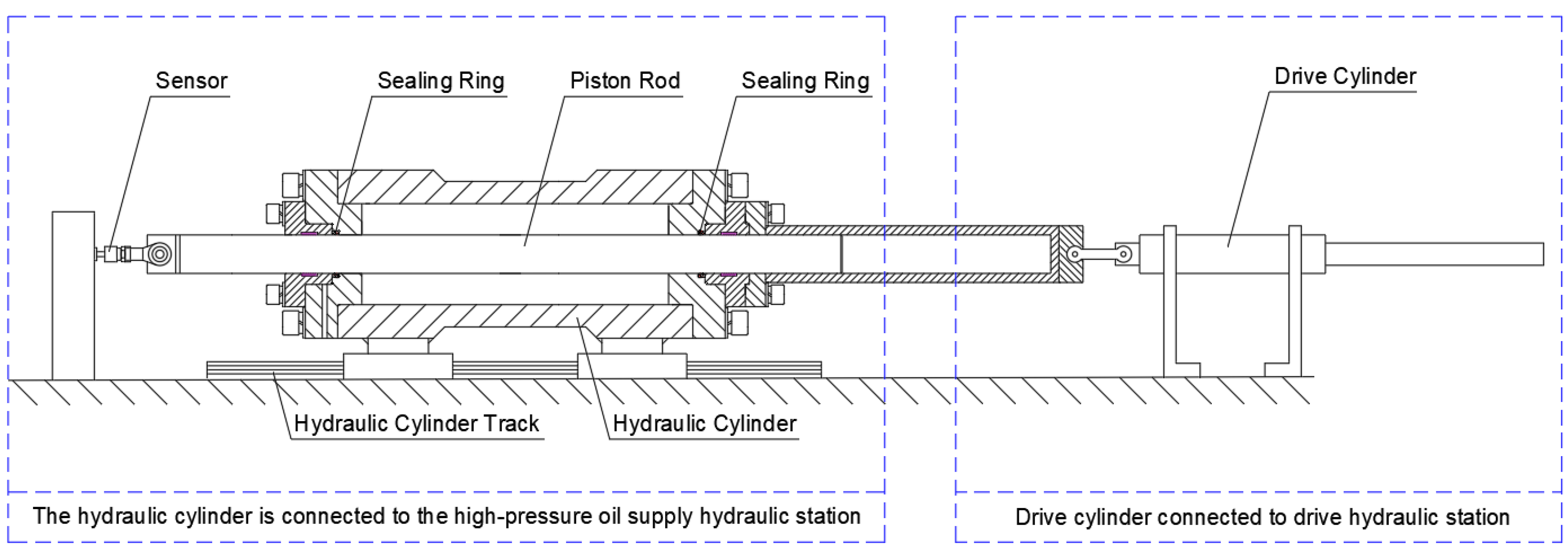
3. Reciprocating Sealing Bench Test
3.1. Reciprocating Seal Mixed Lubrication Model
3.2. Experimental Operation
- Turn on the main power supply of the test bench and turn on the high-pressure supply and pressure hydraulic and drive hydraulic stations.
- Set the direction of the hydraulic cylinder approaching the pressure sensor as the instroke and the direction of the hydraulic cylinder moving away from the pressure sensor as the outstroke.
- Set the oil pressure. Obtain the experimental hydraulic cylinder oil pressure by adjusting the pressure from the hydraulic station.
- Set the reciprocating speed. Obtain the experimental reciprocating speed of the driving hydraulic cylinder by adjusting the drive hydraulic station.
- Set the oil temperature. Set and control the oil temperature by adjusting the temperature of the oil supply hydraulic station. Set the oil temperature to 20, 40, and 100 °C.
- Set the number of reciprocations of the experiment and turn on the automatic mode to conduct the experiment and record the experimental data.
4. Results
4.1. Calculation Results of Numerical Model
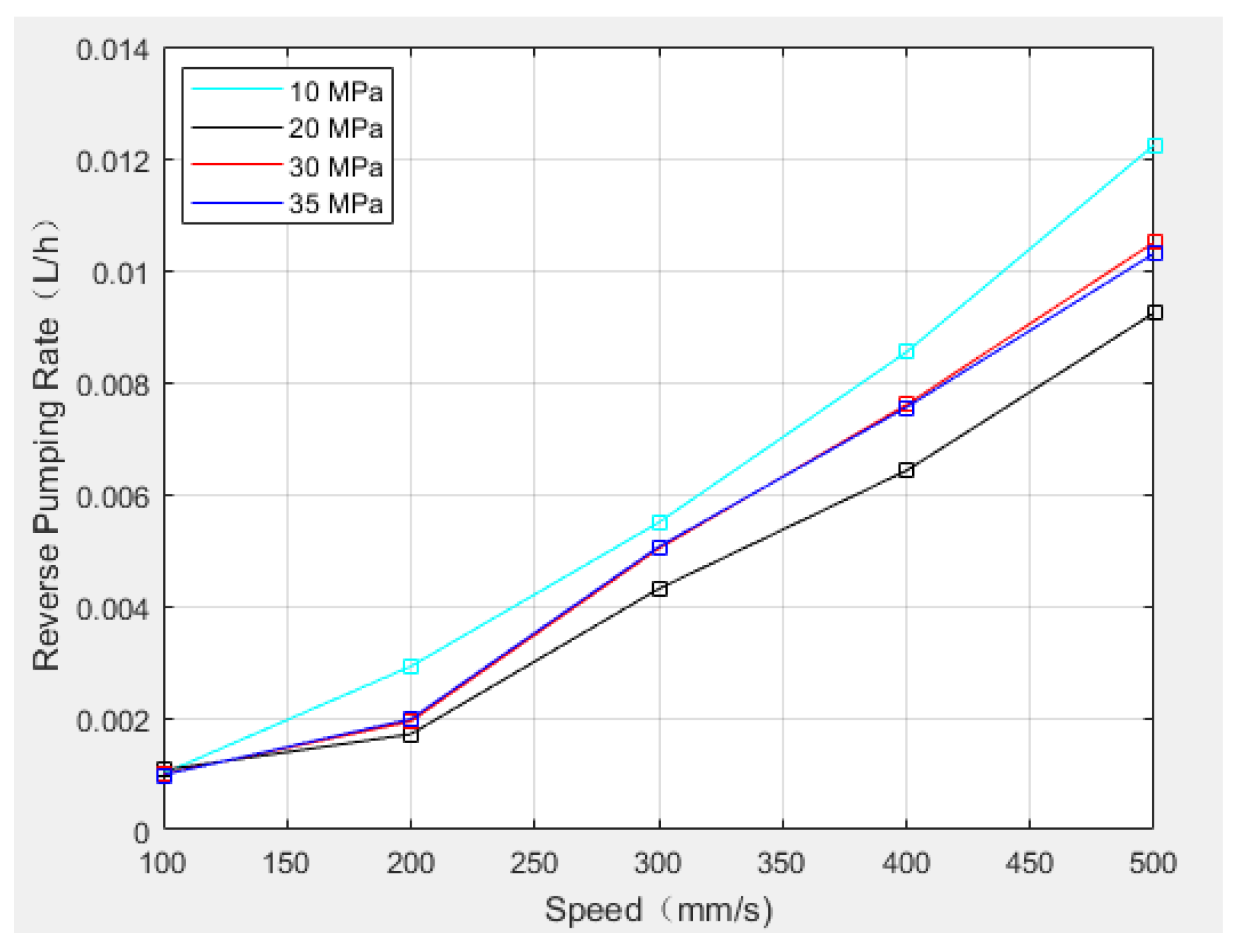
4.1.1. Reverse Pumping Rate
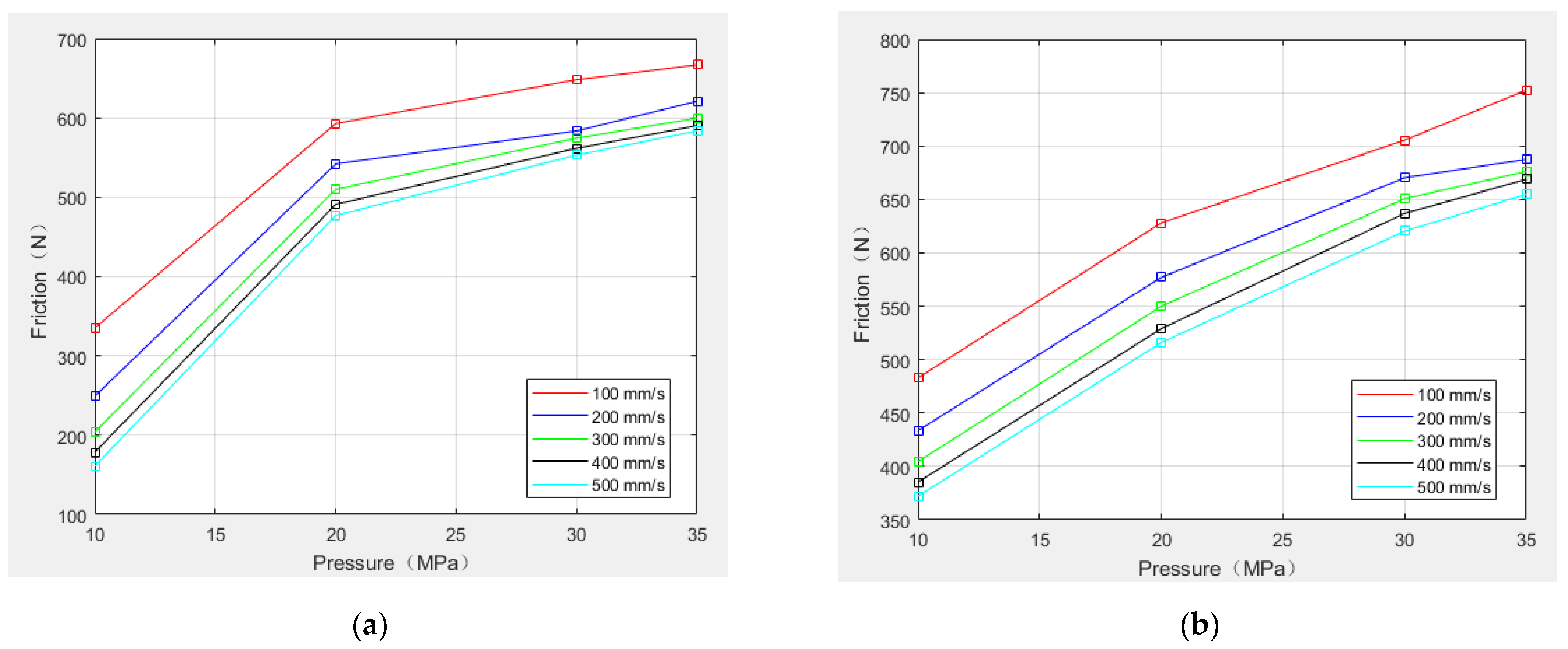
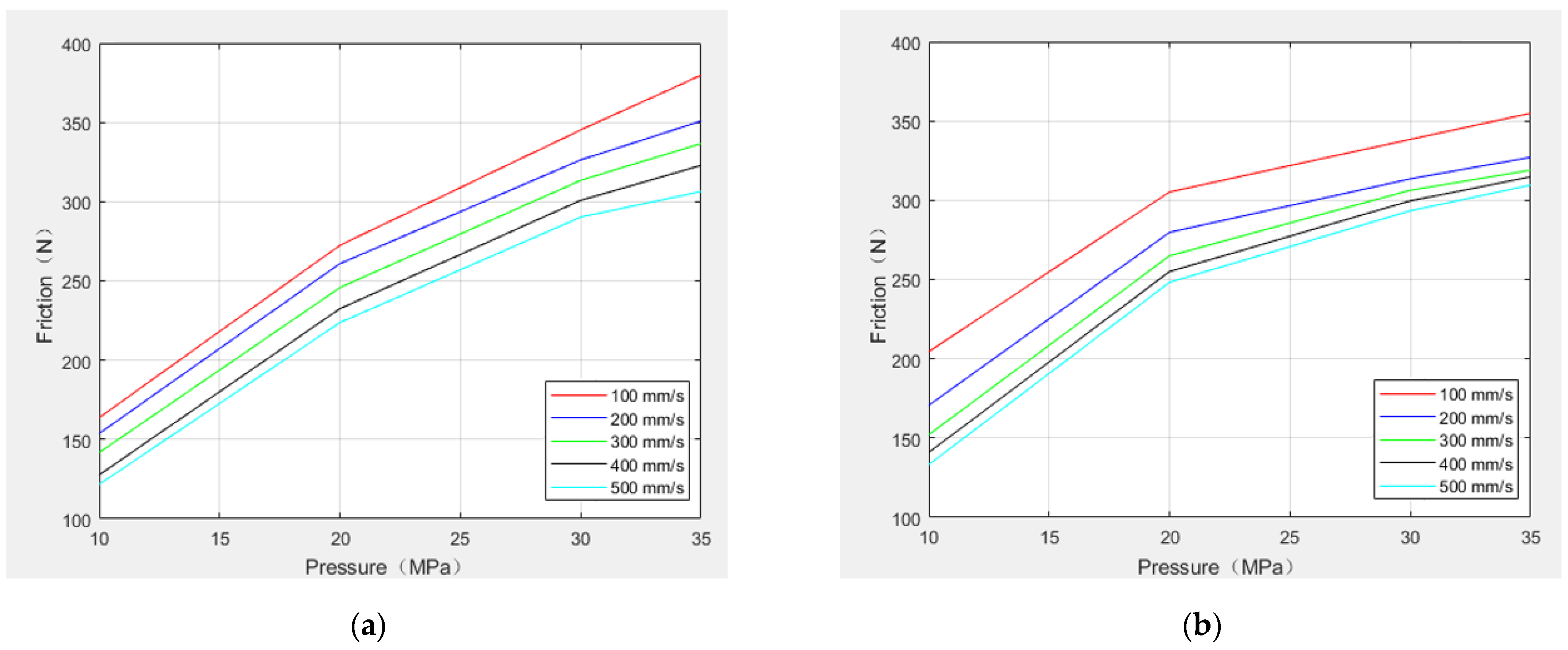
4.1.2. Friction
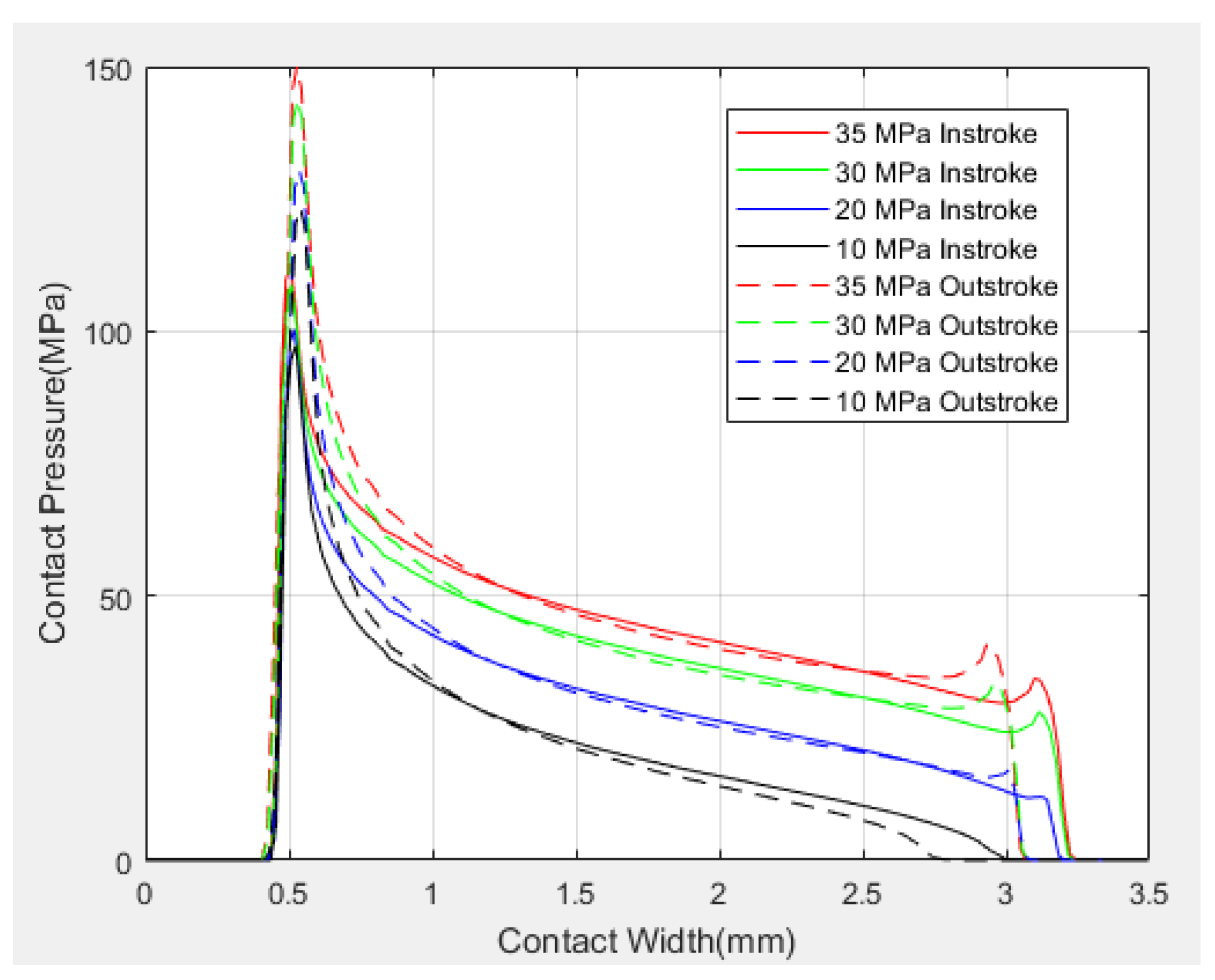
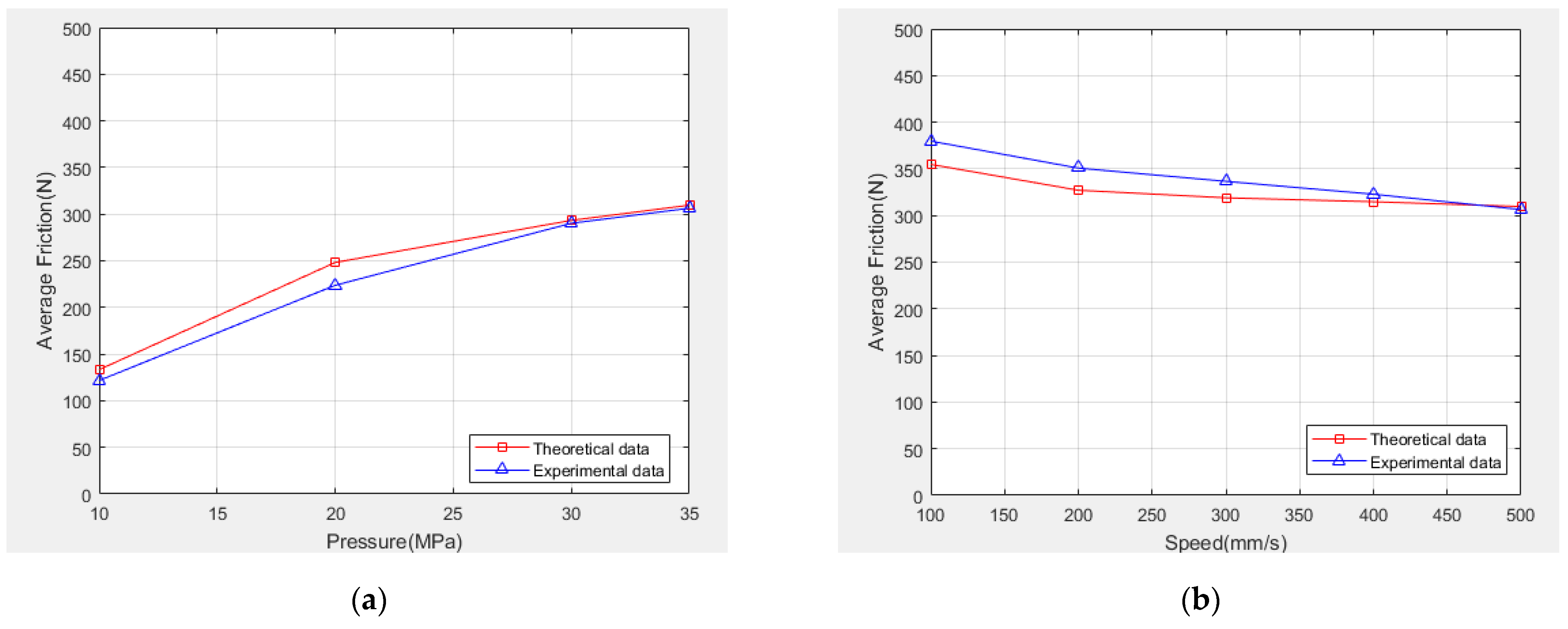
4.2. Experimental Results
5. Discussions
5.1. Reverse Pumping Rate
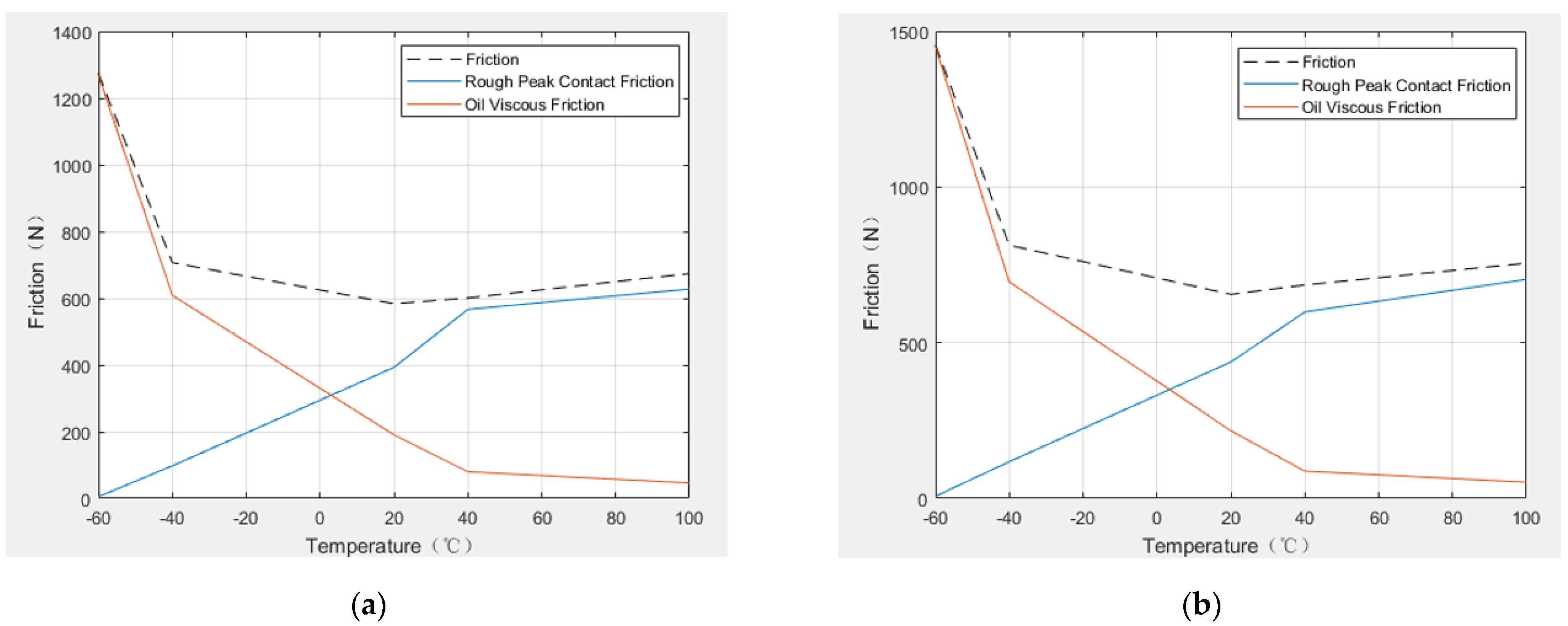
5.2. Friction
6. Conclusions
- (1)
- Based on the sealing mechanism of the reciprocating seal, EHL and IHL methods were used to solve the Reynolds equation, and a reciprocating seal mixed lubrication model was established based on the hydrodynamic analysis of the lubricating oil, contact mechanics analysis of the seal contact area, solid mechanics analysis of the seal lip, and thermal analysis of the oil temperature.
- (2)
- The reverse pumping rate (leakage) and friction force of reciprocating sealing were calculated at different temperatures. The correctness of the theoretical model was experimentally verified using a reciprocating seal bench, and a relatively complete reciprocating sealing system theory was devised.
- (3)
- Oil film stress decreases with increasing temperature, the rough peak stress increases with increasing temperature, and the oil film thickness decreases rapidly with increasing temperature owing to the viscosity–temperature effect. The flow rate of the instroke is always greater than the outer stroke, and the reverse pumping rate is always greater than zero, i.e., the leakage is less than zero. When the oil temperature is less than 0 °C, the friction in the system mainly depends on the viscous friction of the oil. However, when the oil temperature is greater than 0 °C, the friction in the system mainly depends on the contact friction of the rough peak, and the increase in the contact friction of the rough peak leads to a greater increase in system friction.
- (4)
- The hydraulic station used in the experiment is only able to heat the oil; therefore, the parameters for oil temperatures between −60 and 0 °C were not tested and verified experimentally in this study. However, low temperature has a significant influence on sealing performance, and the processing optimization and experimental testing of the experimental equipment will be the subject of future work. In addition, the reliability testing, predictive maintenance, and intelligent sealing of reciprocating seals are future development trends. It is crucial to address these factors to reduce the occurrence of catastrophic accidents. At present, there are few studies in these areas, and these are in the preliminary stages; therefore, further research into these factors is required.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.T.; Suo, S.F.; Guo, F.; Jia, X.; Meng, G. Research of Forward Design Method of Contact Dynamic Seal. Hydraul. Pneum. Seals 2018, 9, 25–27. [Google Scholar]
- Zhang, M.T.; Li, D.C.; Suo, S.F.; Shi, J.W. Piston Rod Coating Material Study of Reciprocating Sealing Experiment Based on Sterling Seal. Appl. Sci. 2021, 11, 1370. [Google Scholar] [CrossRef]
- Tan, G.; Fan, Q.; Tan, F.; Wang, D. Advances in Tribology on Elastomer Sealing and Its Future Trends for the Huge Machinery. Tribology 2016, 36, 559–666. [Google Scholar]
- Nikas, G.K. Eighty Years of Research on Hydraulic Reciprocating Seals: Review of Tribological Studies and Related Topics Since the 1930s. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 1–23. [Google Scholar] [CrossRef]
- Du, X.Q.; Chen, G.; Yab, X.L.; Zhao, Y.L. Optimization Design of Step Seal-ring Based on ISIGHT Platform. Chin. Hydraul. Pneum. 2017, 14–19. [Google Scholar] [CrossRef]
- Wu, C.; Suo, S.; Zhang, K.; Dilixiati, A. Aircraft Actuator VL Seal Finite Element Analysis Based on ABAQUS. Chin. Hydraul. Pneum. 2016, 1, 60–65. [Google Scholar]
- Shen, M.; Song, M.L.; Zhang, H. Simulation Analysis of Sealing Performance of ZHM Pneumatic Combined Sealing Ring for Reciprocating Seal Shaft. Inf. Technol. 2021, 50, 104–108. [Google Scholar]
- Nau, B.S. An historical review of studies of polymeric seals in reciprocating hydraulic systems. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1999, 213, 215–226. [Google Scholar] [CrossRef]
- Gronau, H. Investigations on Gland Packings and Sealing Rings for High Hydraulic Pressures. Ph.D. Thesis, University of Berlin, Berlin, Germany, 1935. [Google Scholar]
- White, C.M.; Denny, D.F. The Sealing Mechanism of Flexible Packings; HM Stationery Office: London, UK, 1948. [Google Scholar]
- Denny, D.F. The Friction of Rubber Sealing Rings; British Hydromechanics Research Association: Harlow, UK, 1953.
- Müller, H. Leakage and friction of flexible packings at reciprocating motion with special consideration of hydrodynamic film formation. In Proceedings of the 2nd International Conference on Fluid Sealing, Granfield, UK, April 1964; pp. 13–28. [Google Scholar]
- Ishiwata, H.; Kambayashi, H. A study of oil seal for reciprocating motion. In Proceedings of the 2nd International Conference on Fluid Sealing, Granfield, UK, April 1964. [Google Scholar]
- Dowson, D.; Swales, P. An elastohydrodynamic approach to the problem of the reciprocating seal. In Proceedings of the 3rd International Conference on Fluid Sealing, Cambridge, UK, 1967. [Google Scholar]
- Theyse, F. The inverse hydrodynamic theory and its application in the design of controlled leakage seals between moving parts. In Proceedings of the 3rd International Conference on Fluid Sealing, Cambridge, UK, 1967; pp. 17–32. [Google Scholar]
- Field, G.J.; Nau, B.S. The effects of design parameters on the lubrication of reciprocating rubber seals. In Proceedings of the 7th International Conference on Fluid Sealing, Nottingham, UK, September 1975; pp. 1–13. [Google Scholar]
- Nikas, G.K.; Sayles, R.S. Nonlinear elasticity of rectangular elastomeric seals and its effect on elastohydrodynamic numerical analysis. Tribol. Int. 2004, 37, 651–660. [Google Scholar] [CrossRef]
- Dowson, D.; Swales, P.D. The development of elastohydrodynamic conditions in a reciprocatingseal. In Proceedings of the 4th International Conference on Fluid Sealing, Cranfield, UK, 1969; pp. 2–10. [Google Scholar]
- Field, G.J.; Nau, B.S. An experiment study of reciprocating rubber seals. In Proceedings of the IMechE Symposium on Elastohydrodynamic Lubrication, Leeds, UK, 1972; pp. 29–36. [Google Scholar]
- Field, G.J.; Nau, B.S. Film thickness and friction measurements during reciprocation of a rectangular section rubber seal ring. In Proceedings of the 6th International Conference on Fluid Sealing, Munich, Germany, 27 February–2 March 1973; pp. 45–56. [Google Scholar]
- Kaneta, M.; Todoroki, H.; Nishikawa, H. Experimental investigation of friction and sealing characteristics of flexible seals for reciprocating motion. In Proceedings of the 5th International Conference on Fluid Sealing, Coventry, UK, 8–12 September 1971; pp. 33–48. [Google Scholar]
- Yang, B.; Salant, R.F. Soft EHL Simulations of U-Cup and Step Hydraulic Rod Seals. J. Tribol.-Trans. ASME 2009, 131, 021501. [Google Scholar] [CrossRef]
- Yang, B.; Salant, R.F. A numerical model of a reciprocating rod seal with a secondary lip. Tribol.-Trans. 2008, 51, 119–127. [Google Scholar] [CrossRef]
- Yang, B.; Salant, R.F. Numerical model of a tandem recipr ocating hydraulic rod seal. J. Tribol.-Trans. ASME 2008, 130, 032201. [Google Scholar] [CrossRef]
- Salant, R.F.; Maser, N.; Yang, B. Numerical model of a reciprocating hydraulic rod seal. J. Tribol.-Trans. ASME 2007, 129, 91–97. [Google Scholar] [CrossRef]
- Fatu, A.; Hajjam, M. Numerical modelling of hydraulic seals by inverse lubrication theory. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2011, 225, 1159–1173. [Google Scholar] [CrossRef]
- Li, J.X. Finite Element Analysis of Piston Seals Property of Hydraulic Cylinders. Master’s Thesis, Northeastern University, Boston, MA, USA, 2005. [Google Scholar]
- Kanters, A.F.C.; Verest, J.F.M.; Visscher, M. On reciprocating elastomeric seals: Calculation of film thicknesses using the inverse hydrodynamic lubrication theory. Tribol. Trans. 1990, 33, 301–306. [Google Scholar] [CrossRef]
- Nikas, G.K. Elastohydrodynamics and Mechanics of Rectangular Elastomeric Seals for Reciprocating Piston Rods. J. Tribol. 2003, 125, 60–69. [Google Scholar] [CrossRef]
- Nikas, G.K.; Sayles, R.S. Study of leakage and friction of flexible seals for steady motion via a numerical approximation method. Tribol. Int. 2006, 39, 921–936. [Google Scholar] [CrossRef]
- Nikas, G.K.; Sayles, R.S. Computational model of tandem rectangular elastomeric seals for reciprocating motion. Tribol. Int. 2006, 39, 622–634. [Google Scholar] [CrossRef]
- Crudu, M.; Fatu, A.; Cananau, S.; Hajjam, M.; Pascu, A.; Cristescu, C. A numerical and experimental friction analysis of reciprocating hydraulic ‘U’ rod seals. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 785–794. [Google Scholar] [CrossRef]
- Bhaumik, S.; Kumar, S.R.; Kumaraswamy, A. Experimental Investigation and FE Modelling of Contact Mechanics Phenomenon in Reciprocating Hydraulic U-Seals for Defence Applications. Appl. Mech. Mater. 2014, 592–594, 1950–1954. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Liu, H.; Liu, J.; Xing, G.C. Finite Element Analysis of Sealing Performance of Glyd-ring Seals. J. Wuhan Inst. Technol. 2014, 36, 12–15. [Google Scholar]
- Han, C.; Hu, Y.; Zhang, J.; Xie, J.X. Mechanical Properties Analysis and Structure Improvement of Tooth and Sliding Ring Combined Seals. Lubr. Eng. 2018, 43, 86–92. [Google Scholar]
- Yi, P.; Jin, Y.; Peng, Y.; Wan, B. Performance Analysis of Combined Seal Structure in Deep Sea High Pressure Environment. J. Hunan Univ. Sci. Technol. 2018, 33, 34–39. [Google Scholar]
- Wang, J.; Liao, Y.; Li, Y.; Lian, Z. Investigations on the dynamic reciprocating sealing performance with partial lubrication model. Lubr. Eng. 2020, 45, 50–55. [Google Scholar]
- Qin, Z.; Zhou, P.; Zhang, B.; Li, H.; Zhang, H.; Guo, D. Simulation and experimental study on sealing performance of PEEK rotary seal ring. Tribology 2020, 40, 330–338. [Google Scholar]
- Wen, S.; Huang, P.; Tian, Y.; Ma, L. Principles of Tribology, 5th ed.; Tsinghua University Press: Beijing, China, 2018; pp. 49–53. [Google Scholar]
- Visscher, M.; Kanters, A. Literature review and discussion on measurements of leakage, lubricantfilm thickness and friction of reciprocating elastomeric seals. Lubr. Eng. 1990, 46, 785–791. [Google Scholar]






| Parameter Name | Numerical Value |
|---|---|
| Elastic Modulus | 297 MPa |
| Poisson’s Ratio | 0.45 |
| Oil Viscosity (20 °C) | 9 × 10−8 MPa·s |
| Friction Coefficient | 0.08 |
| Piston Rod Diameter | 50 mm |
| Temperature | −60 °C | −40 °C | 20 °C | 40 °C | 100 °C |
|---|---|---|---|---|---|
| Instroke flow | 0.06278 | 0.03150 | 0.01181 | 0.005625 | 0.003425 |
| Outstroke flow | 0.06259 | 0.03142 | 0.01176 | 0.005579 | 0.003382 |
| Reverse pumping rate | 1.9 × 10−4 | 8.0 × 10−5 | 5.0 × 10−5 | 4.6 × 10−5 | 4.3 × 10−5 |
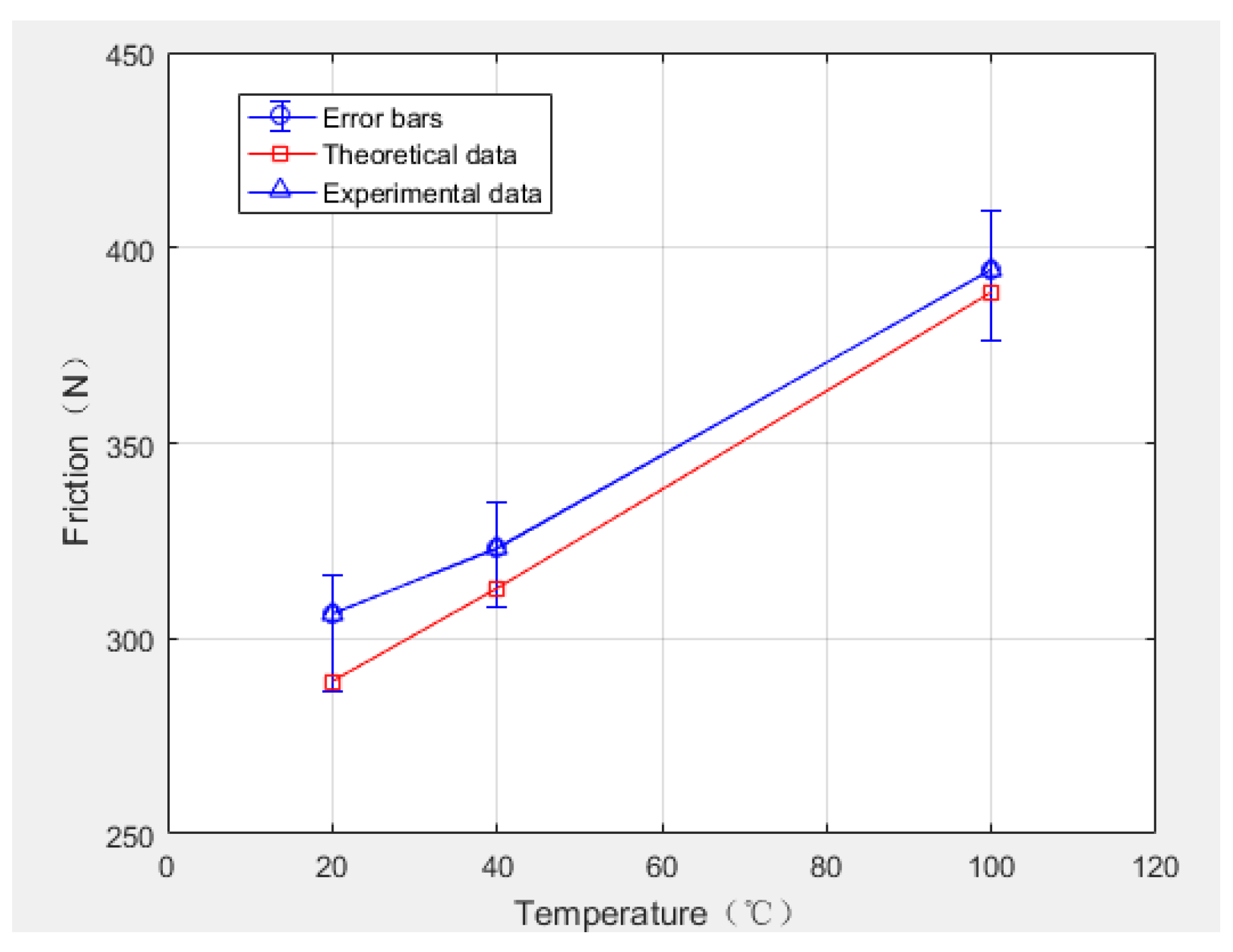
| Temperature | 20 °C | 40 °C | 100 °C |
|---|---|---|---|
| Theoretical calculation of average friction (N) | 290.0 | 312.8 | 388.6 |
| Experimental measurement of average friction (N) | 306.4 | 322.9 | 394.5 |
| Relative errors | 5.64% | 3.23% | 1.51% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Feng, Y. Numerical Model of Mixed Lubrication and Experimental Study of Reciprocating Seal Based on Inverse Lubrication Theory. Lubricants 2022, 10, 153. https://doi.org/10.3390/lubricants10070153
Zhang M, Feng Y. Numerical Model of Mixed Lubrication and Experimental Study of Reciprocating Seal Based on Inverse Lubrication Theory. Lubricants. 2022; 10(7):153. https://doi.org/10.3390/lubricants10070153
Chicago/Turabian StyleZhang, Miaotian, and Yu Feng. 2022. "Numerical Model of Mixed Lubrication and Experimental Study of Reciprocating Seal Based on Inverse Lubrication Theory" Lubricants 10, no. 7: 153. https://doi.org/10.3390/lubricants10070153
APA StyleZhang, M., & Feng, Y. (2022). Numerical Model of Mixed Lubrication and Experimental Study of Reciprocating Seal Based on Inverse Lubrication Theory. Lubricants, 10(7), 153. https://doi.org/10.3390/lubricants10070153





