Process Optimization of Automotive Brake Material in Dry Sliding Using Taguchi and ANOVA Techniques for Wear Control
Abstract
:1. Introduction
2. Methodology
2.1. Design of Experiment
2.1.1. Load
2.1.2. Sliding Distance
2.1.3. Sliding Velocity
3. Experimental Procedure
3.1. Materials
3.2. Wear Experiment
3.3. Characterization Techniques
4. Results and Discussion
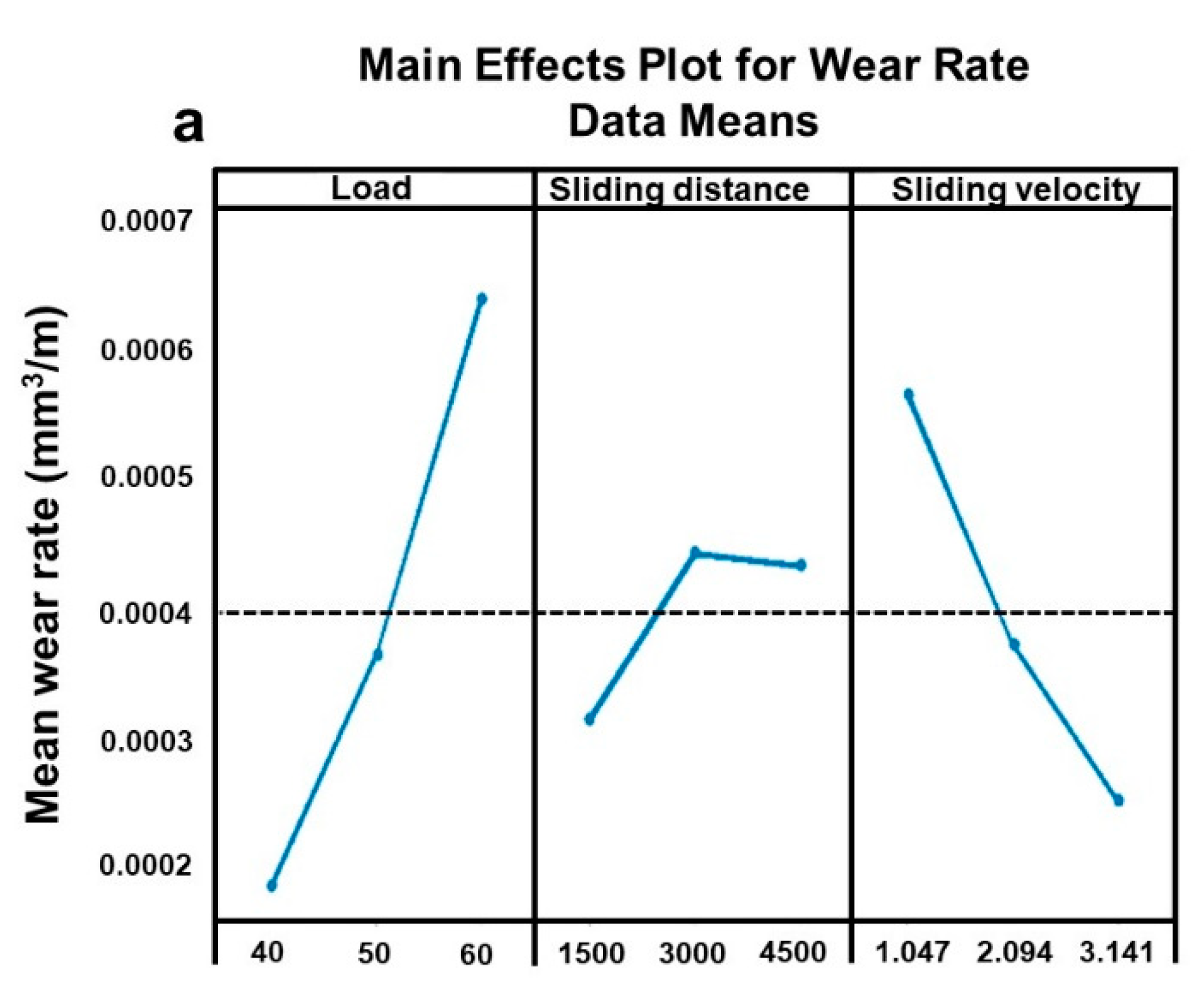
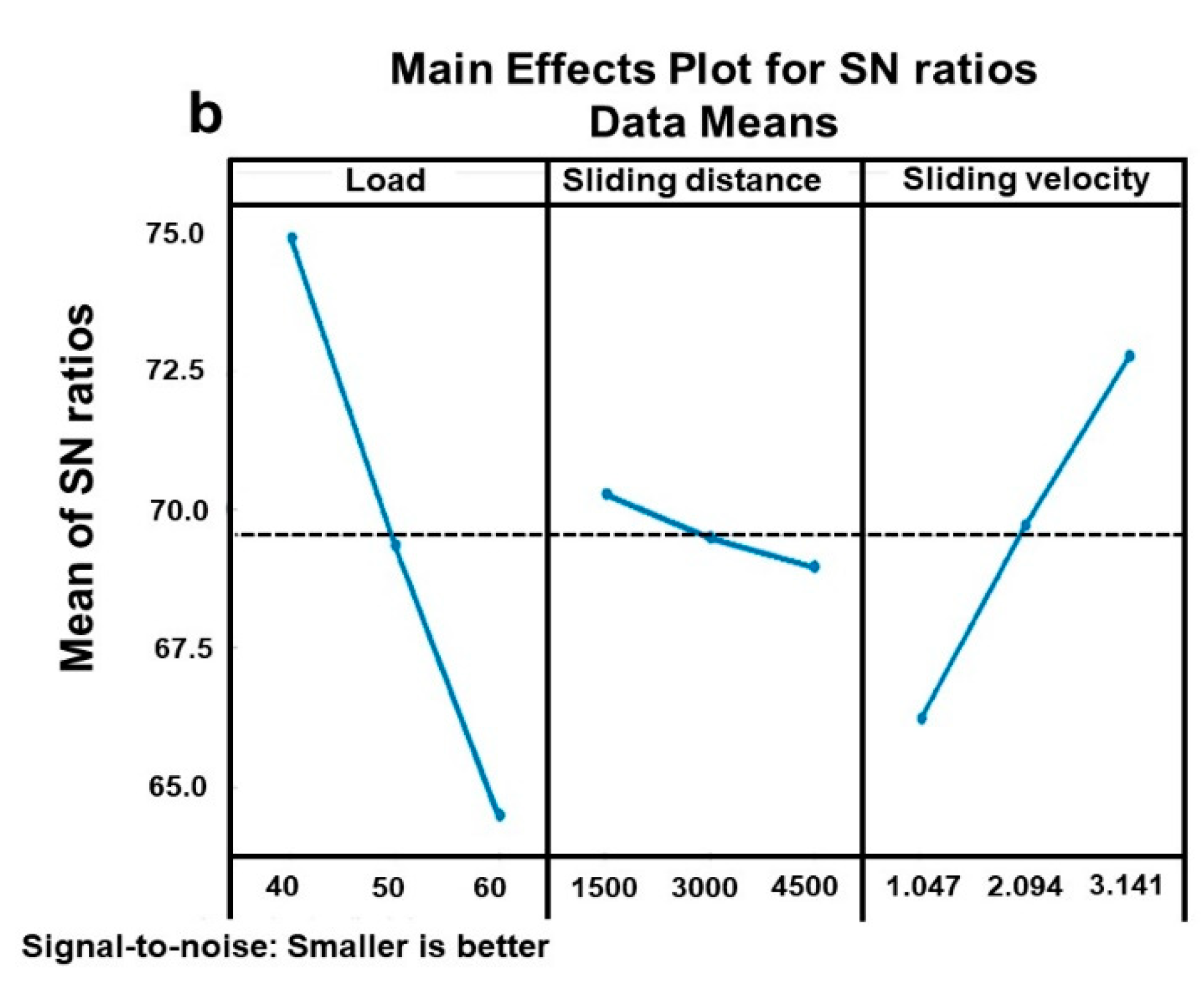
4.1. Signal to Noise (SN) Analysis of Wear
4.2. Analysis of Variance (ANOVA) of Wear
5. Multiple Linear Regression Model for Wear Rate
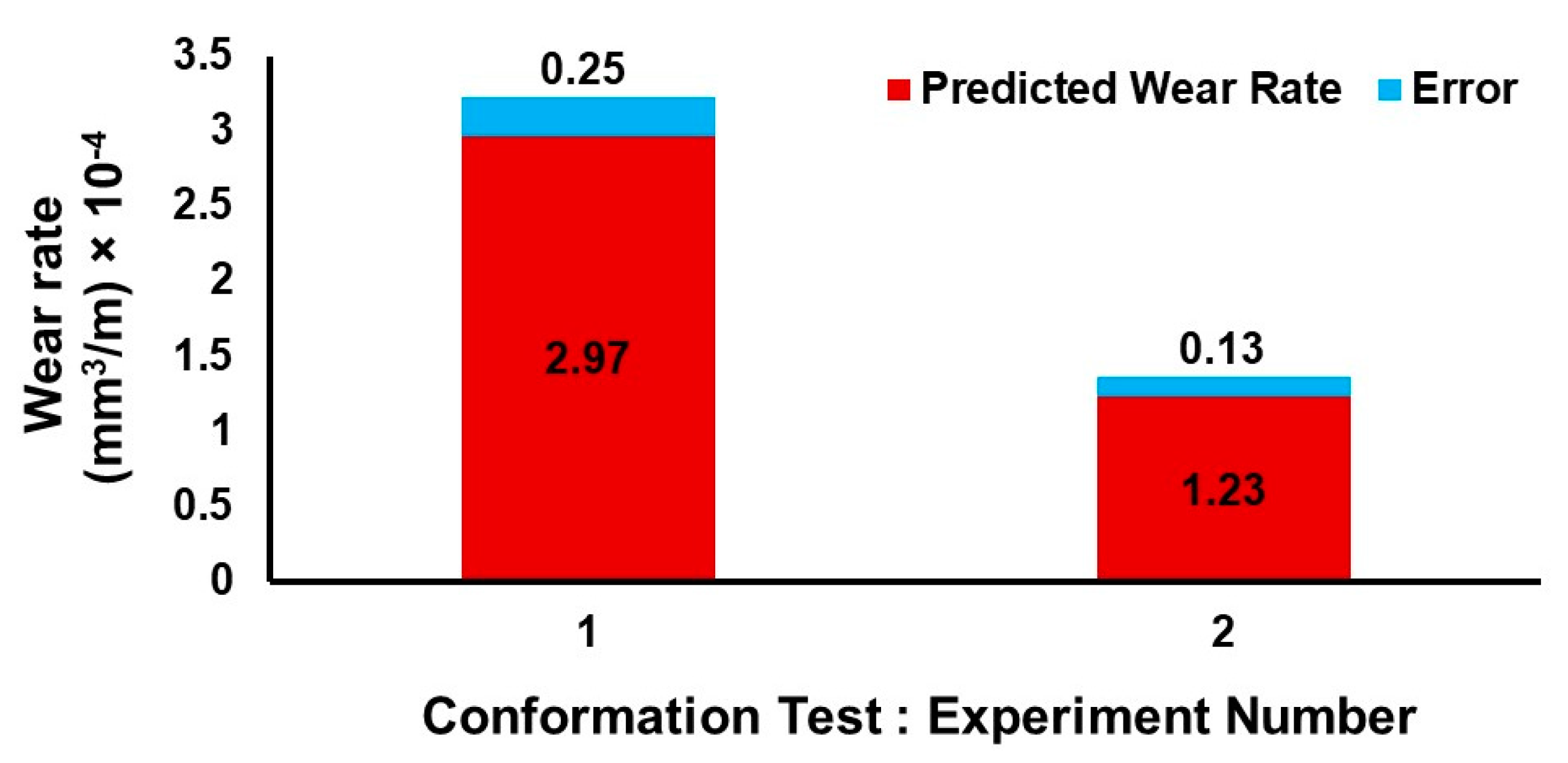
6. Validation Test and Wear Mechanism
7. Conclusions
- Normal load significantly impacts copper-free semi-metallic friction material wear rate, followed by sliding velocity and sliding distance.
- The wear rate at intermediate conditions can be calculated using the regression equation of semi-metallic friction material.
- Test results confirmed an error of less than 10% linked to the dry sliding wear rate. As a result, the wear rate estimation regression model was effectively tested.
- The normal load had the most significant impact on the wear process (71.02%), followed by sliding velocity (27.84%) and sliding distance (1.14%).
- The dynamic high wear at 60 N, 4500 m, and 1.047 m/s was confirmed by SEM analysis, and the optimal wear conditions were found at 40 N, 1500 m, and 3.141 m/s.
- At lower loading conditions, i.e., 40 N transfer of the friction layer found on the GCI disc, the adhesive wear dominance at the lower load was confirmed, whereas at 60 N, the plowing action that could be seen on the GCI disc confirmed the abrasive wear mechanism.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CoF | coefficient of friction |
| DOE | design of experiment |
| x | Sliding distance (meters) |
| d | wear track diameter (meters) |
| N | rotor speed (RPM) |
| t | time (mins) |
| v | sliding velocity (m/s) |
| D | diameter of the rotor (meters) |
| SN | signal to noise |
| N | number of observations |
| Wf | final weight of the pin (g) |
| Wi | initial weight of the pin (g) |
| ρ | density of pin (g/mm3) |
| Q | wear rate (mm3/m) |
| l | sliding distances (meters) |
| µ | arithmetic mean |
| ND | not defined |
| xi | value of ith independent variable |
| mean of independent variables | |
| SEM | scanning electron microscope |
| Bal. | balance |
| St. dev. | standard deviation |
| PQT | net-addition of squares |
| PSL | load-addition of squares |
| PSD | sliding distance addition of squares |
| PSV | sliding velocity addition of squares |
| Sdi2 | addition of the experiments at level i |
| DF | degree of freedom |
| Seq. SS | sequential sums of squares |
| Adj. SS | adjusted sum of squares |
| Adj. MS | adjusted mean squares |
| F | factor value |
| p | probability value |
| y | forecasted value |
| β | y-intercept |
| ꞓ | error |
| σ | standard deviation |
| β1 | slope parameter |
| yi | value of ith dependent variable |
| mean of dependent variables | |
| XRF | X-ray fluorescence spectroscopy |
| EDS | energy dispersive X-ray spectroscopy |
References
- Gramstat, S.; Mertens, T.; Waninger, R.; Lugovyy, D. Impacts on Brake Particle Emission Testing. Atmosphere 2020, 11, 1132. [Google Scholar] [CrossRef]
- di Confiengo, G.G.; Faga, M.G. Ecological Transition in the Field of Brake Pad Manufacturing: An Overview of the Potential Green Constituents. Sustainability 2022, 14, 2508. [Google Scholar] [CrossRef]
- Rajaei, H.; Menapace, C.; Amirabdollahian, S.; Perini, M.; Straffelini, G.; Gialanella, S. Microstructural and Tribological Evaluation of Brake Disc Refurbishing Using Fe-Based Coating via Directed Energy Deposition. Metals 2022, 12, 465. [Google Scholar] [CrossRef]
- Verma, P.C. Automotive Brake Materials: Characterization of Wear Products and Relevant Mechanisms at High Temperature. Ph.D. Thesis, University of Trento, Trento, Italy, 2016. [Google Scholar]
- Verma, P.C.; Menapace, L.; Bonfanti, A.; Ciudin, R.; Gialanella, S.; Straffelini, G. Braking Pad-Disc System: Wear Mechanisms and Formation of Wear Fragments. Wear 2015, 322–323, 251–258. [Google Scholar] [CrossRef]
- Straffelini, G.; Verma, P.C.; Metinoz, I.; Ciudin, R.; Perricone, G.; Gialanella, S. Wear Behavior of a Low Metallic Friction Material Dry Sliding against a Cast Iron Disc: Role of the Heat-Treatment of the Disc. Wear 2016, 348–349, 10–16. [Google Scholar] [CrossRef]
- Straffelini, G.; Verlinski, S.; Verma, P.C.; Valota, G.; Gialanella, S. Wear and Contact Temperature Evolution in Pin-on-Disc Tribotesting of Low-Metallic Friction Material Sliding Against Pearlitic Cast Iron. Tribol. Lett. 2016, 62, 36. [Google Scholar] [CrossRef]
- Verma, P.C.; Ciudin, R.; Bonfanti, A.; Aswath, P.; Straffelini, G.; Gialanella, S. Role of the Friction Layer in the High-Temperature Pin-On-Disc Study of a Brake Material. Wear 2016, 346–347, 56–65. [Google Scholar] [CrossRef]
- Mulani, S.M.; Kumar, A.; Shaikh, H.N.E.A.; Saurabh, A.; Singh, P.K.; Verma, P.C. A Review on recent Development and Challenges in Automotive Brake Pad-Disc System. Mater. Today Proc. 2022, 56, 447–454. [Google Scholar] [CrossRef]
- Sethupathi, P.B.; Chandradass, J.; Saibalaji, M. Comparative study of Disc Brake Pads Sold in Indian Market—Impact on Safety and Environmental Aspects. Environ. Technol. Innov. 2021, 21, 101245. [Google Scholar] [CrossRef]
- Tavangar, R.; Ansari Moghadam, H.; Khavandi, A.; Banaeifar, S. Comparison of Dry Sliding Behavior and Wear Mechanism of Low Metallic and Copper-Free Brake Pads. Tribol. Int. 2020, 151, 106416. [Google Scholar] [CrossRef]
- Shi, X.; Wen, D.; Wang, S.; Wang, G.; Zhang, M.; Li, J.; Xue, C. Investigation on Friction and Wear Performance of Laser Cladding Ni-Based Alloy Coating on Brake Disc. Optik 2021, 242, 167227. [Google Scholar] [CrossRef]
- Alves, C.; Evtyugina, M.; Vicente, A.; Conca, E.; Amato, F. Organic Profiles of Brake Wear Particles. Atmos. Res. 2021, 255, 105557. [Google Scholar] [CrossRef]
- Perricone, G.; Alemani, M.; Wahlström, J.; Olofsson, U. A Proposed Driving Cycle for Brake Emissions Investigation for Test Stand. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 122–135. [Google Scholar] [CrossRef]
- Rahimi, M.; Bortoluzzi, D.; Wahlström, J. Input Parameters for Airborne Brake Wear Emission Simulations: A Comprehensive Review. Atmosphere 2021, 12, 871. [Google Scholar] [CrossRef]
- Sinha, A.; Ischia, G.; Menapace, C.; Gialanella, S. Experimental Characterization Protocols for Wear Products from Disc Brake Materials. Atmosphere 2020, 11, 1102. [Google Scholar] [CrossRef]
- Kim, S.-H.; Jeong, M.H.; Kim, J.; Shim, W.; Kwon, S.-U.; Lee, J.-J.; Huh, S.H.; Pee, J.-H.; Kim, J.-Y. Dynamometric Investigation on Airborne Particulate Matter (PM) from Friction Materials for Automobile: Impact of Abrasive and Lubricant on PM Emission Factor. Lubricants 2021, 9, 118. [Google Scholar] [CrossRef]
- Stojanovic, N.; Abdullah, O.I.; Grujic, I.; Boskovic, B. Particles Formation Due to the Wear of Tires and Measures for the Wear Reduction: A Review. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021. [Google Scholar] [CrossRef]
- Shinde, D.; Bulsara, M.; Patil, J. Wear Analysis of Eco-Friendly Non-Asbestos Friction-Lining Material Applied in an Automotive Drum Brake: Experimental and Finite-Element Analysis. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 552–562. [Google Scholar] [CrossRef]
- Liati, A.; Schreiber, D.; Lugovyy, D.; Gramstat, S.; Eggenschwiler, P.D. Airborne Particulate Matter Emissions from Vehicle Brakes in Micro- and Nano-Scales: Morphology and Chemistry by Electron Microscopy. Atmos. Environ. 2019, 212, 281–289. [Google Scholar] [CrossRef]
- Kumar, S.; Priyadarshan; Ghosh, S.K. Statistical and Computational Analysis of an Environment-Friendly MWCNT/NiSO4 Composite Materials. J. Manuf. Process. 2021, 66, 11–26. [Google Scholar] [CrossRef]
- Luo, S.-Y.; Weng, C.-Y. A Study of the Metal Matrix Friction Materials of Hot Pressing Using Taguchi Method. Adv. Mater. Process. Technol. 2018, 4, 7–15. [Google Scholar] [CrossRef]
- Veličković, S.; Stojanović, B.; Babić, M.; Bobic, I. Optimization of Tribological Properties of Aluminum Hybrid Composites Using Taguchi Design. J. Compos. Mater. 2017, 51, 2505–2515. [Google Scholar] [CrossRef]
- Lyu, Y.; Ma, J.; Åström, A.H.; Wahlström, J.; Olofsson, U. Recycling of Worn Out Brake Pads—Impact on Tribology and Environment. Sci. Rep. 2020, 10, 8369. [Google Scholar] [CrossRef] [PubMed]
- Borawski, A. Impact of Operating Time on Selected Tribological Properties of the Friction Material in the Brake Pads of Passenger Cars. Materials 2021, 14, 884. [Google Scholar] [CrossRef]
- Mehboob, H.; Chang, S.-H. Optimal Design of a Functionally Graded Biodegradable Composite Bone Plate by Using the Taguchi Method and Finite Element Analysis. Compos. Struct. 2015, 119, 166–173. [Google Scholar] [CrossRef]
- Pattanaik, A.; Satpathy, M.P.; Mishra, S.C. Dry Sliding Wear Behavior of Epoxy Fly Ash Composite with Taguchi Optimization. Eng. Sci. Technol. Int. J. 2016, 19, 710–716. [Google Scholar] [CrossRef] [Green Version]
- Banker, V.J.; Mistry, J.M.; Thakor, M.R.; Upadhyay, B.H. Wear Behavior in Dry Sliding of Inconel 600 Alloy Using Taguchi Method and Regression Analysis. Procedia Technol. 2016, 23, 383–390. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Hao, S.; Gao, W.; Lu, Z. The Effect of Applied Load and Rotation Speed on Wear Characteristics of Al-Cu-Li Alloy. J. Mater. Eng. Perform. 2022, 31, 5875–5885. [Google Scholar] [CrossRef]
- Pai, D.; Pai, A.; Kumar, S.; Deb, A. The Response of Two-Wheeler Tires to Three-Body Wear Phenomena by Experimental Simulation of Off-Road Terrains. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 3504–3514. [Google Scholar] [CrossRef]
- Neog, S.P.; Kumar, A.R.; Das Bakshi, S.; Das, S. Understanding the Complexities of Dry Sliding Wear Behaviour of Steels. Mater. Sci. Technol. 2021, 37, 504–518. [Google Scholar] [CrossRef]
- Yun, R.; Filip, P.; Lu, Y. Performance and Evaluation of Eco-Friendly Brake Friction Materials. Tribol. Int. 2010, 43, 2010–2019. [Google Scholar] [CrossRef]
- Jerbi, A.; Ammar, A.; Krid, M.; Salah, B. Performance Optimization of a Flexible Manufacturing System Using Simulation: The Taguchi Method versus OptQuest. Simulation 2019, 95, 1085–1096. [Google Scholar] [CrossRef]
- Shah, R.; Chen, R.; Woydt, M. The Effects of Energy Efficiency and Resource Consumption on Environmental Sustainability. Lubricants 2021, 9, 117. [Google Scholar] [CrossRef]
- Reddy, V.V.; Mandava, R.K.; Rao, V.R.; Mandava, S. Optimization of Dry Sliding Wear Parameters of Al 7075 MMC’s Using Taguchi Method. Mater. Today Proc. 2022, 62, 6684–6688. [Google Scholar] [CrossRef]
- Taguchi, G.; Rafanelli, A.J. Taguchi on Robust Technology Development: Bringing Quality Engineering Upstream; ASME Press: New York, NY, USA, 1993. [Google Scholar]
- Mustapha, A.N.; Zhang, Y.; Zhang, Z.; Ding, Y.; Yuan, Q.; Li, Y. Taguchi and ANOVA Analysis for the Optimization of the Microencapsulation of a Volatile Phase Change Material. J. Mater. Res. Technol. 2021, 11, 667–680. [Google Scholar] [CrossRef]
- Schon, A.F.; Castro, N.A.; Barros, A.D.S.; Spinelli, J.E.; Garcia, A.; Cheung, N.; Silva, B.L. Multiple Linear Regression Approach to Predict Tensile Properties of Sn-Ag-Cu (SAC) Alloys. Mater. Lett. 2021, 304, 130587. [Google Scholar] [CrossRef]
- Aamir, M.; Tu, S.; Tolouei-Rad, M.; Giasin, K.; Vafadar, A. Optimization and Modeling of Process Parameters in Multi-Hole Simultaneous Drilling Using Taguchi Method and Fuzzy Logic Approach. Materials 2020, 13, 680. [Google Scholar] [CrossRef] [Green Version]
- Chan, S.N.; Wong, W.Y.; Walvekar, R.; Kadhum, A.A.H.; Khalid, M. Parametric Optimization of Pulsed Laser Ablation on Stainless Steel for Improving Corrosion Resistance by Taguchi Method. Mater. Res. Express 2018, 6, 026533. [Google Scholar] [CrossRef]
- Hora, J.; Campos, P. A Review of Performance Criteria to Validate Simulation Models. Expert Syst. 2015, 32, 578–595. [Google Scholar] [CrossRef]


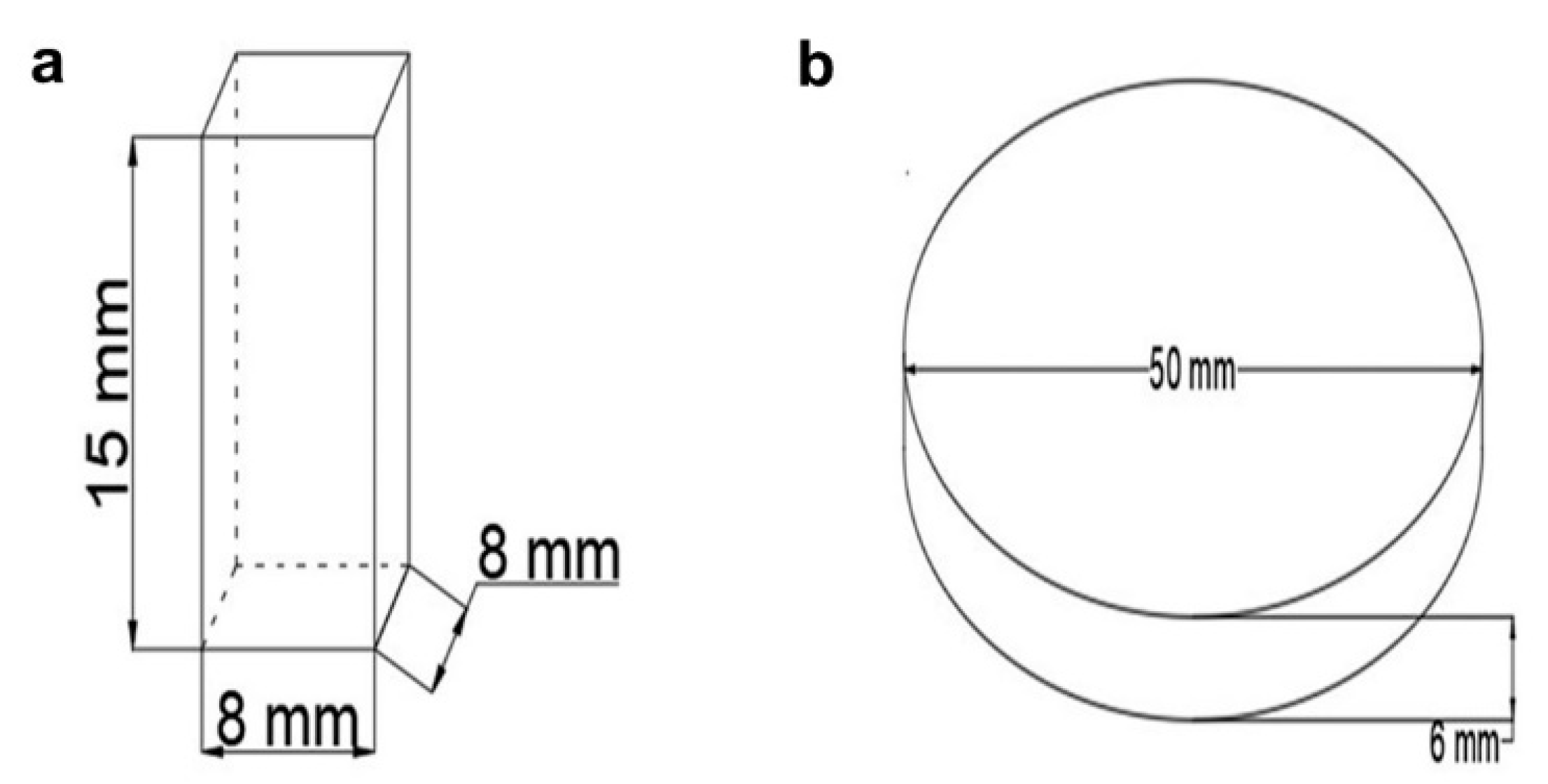








| Level | Factors | ||
|---|---|---|---|
| Load (N) | Sliding Distance (m) | Sliding Velocity (m/s) | |
| 1. | 40 | 1500 | 1.047 |
| 2. | 50 | 3000 | 2.094 |
| 3. | 60 | 4500 | 3.141 |
| SN Ratio | Objective | Meaning |
|---|---|---|
| −10 log(1/yi2) | Higher is better | Response maximization |
| 10 log (µ/σ)2 | Nominal is the best | Shifts mean to a target value |
| −10 log(yi2) | Smaller is better | Response minimization |
| S. No. | Load (N) | Sliding Distance (m) | Sliding Velocity (m/s) |
|---|---|---|---|
| 1 | 40 | 1500 | 1.047 |
| 2 | 40 | 3000 | 2.094 |
| 3 | 40 | 4500 | 3.141 |
| 4 | 50 | 1500 | 2.094 |
| 5 | 50 | 3000 | 3.141 |
| 6 | 50 | 4500 | 1.047 |
| 7 | 60 | 1500 | 3.141 |
| 8 | 60 | 3000 | 1.047 |
| 9 | 60 | 4500 | 2.094 |
| Element | Wt. (%) |
|---|---|
| Si | 0.187 |
| Ni | 1.827 |
| S | 1.013 |
| Ca | 1.229 |
| Mn | 0.448 |
| Cr | 0.258 |
| Ti | 0.133 |
| Fe | 18.063 |
| P | 0.089 |
| Zn | 0.276 |
| Ba | 3.140 |
| Bal. | ND |
| Equipment | Accuracy | Precision |
|---|---|---|
| Pin-on-disc tribometer | LVDT ± 1 μm | LVDT 10−8 μm |
| Weighing balance | ±10−4 g | 10−4 g |
| Vernier caliper | ±10−2 mm | 10−2 mm |
| Vickers hardness tester | ±10 HV60 | 10−1 HV60 |
| Surface roughness tester | ±10−2 μm | 10−3 μm |
| S. No. | Load (N) | Sliding Distance (m) | Sliding Velocity (m/s) | Wear Rate (mm3/m) ×10−4 | St. Dev. | SN Ratio |
|---|---|---|---|---|---|---|
| 1 | 40 | 1500 | 1.047 | 2.3814 | 0.00032 | 72.4633 |
| 2 | 40 | 3000 | 2.094 | 1.7933 | 0.0006 | 74.9269 |
| 3 | 40 | 4500 | 3.141 | 1.3671 | 0.00101 | 77.2839 |
| 4 | 50 | 1500 | 2.094 | 3.1752 | 0.00153 | 69.9645 |
| 5 | 50 | 3000 | 3.141 | 2.3152 | 0.00141 | 72.7080 |
| 6 | 50 | 4500 | 1.047 | 5.4243 | 0.00162 | 65.3130 |
| 7 | 60 | 1500 | 3.141 | 3.8367 | 0.00178 | 68.3208 |
| 8 | 60 | 3000 | 1.047 | 9.1288 | 0.00243 | 60.7917 |
| 9 | 60 | 4500 | 2.094 | 6.1746 | 0.00126 | 64.1877 |
| Level | Load | Sliding Distance | Sliding Velocity |
|---|---|---|---|
| 1 | 0.0001847 | 0.0003131 | 0.0005645 |
| 2 | 0.0003638 | 0.0004412 | 0.0003344 |
| 3 | 0.0006009 | 0.0003951 | 0.0002506 |
| Delta (Δ) | 0.0004162 | 0.0001281 | 0.0003139 |
| Rank | 1 | 3 | 2 |
| Level | Load | Sliding Distance | Sliding Velocity |
|---|---|---|---|
| 1 | 74.89143 | 70.24956 | 66.18937 |
| 2 | 69.32861 | 69.47563 | 70.26794 |
| 3 | 65.00826 | 69.50311 | 72.77099 |
| Delta (Δ) | 9.88317 | 0.77393 | 6.58162 |
| Rank | 1 | 3 | 2 |
| Source | DF (Degree of Freedom) | Seq. SS (Sequential Sums of Squares) | Adj. SS (Adjusted Sum of Squares) | Adj. MS (Adjusted Mean Squares) | F (Factor Value) | p (Probability Value) |
|---|---|---|---|---|---|---|
| Load | 2 | 164.277 | 164.277 | 82.1383 | 558.47 | 0.002 |
| Sliding Distance | 2 | 2.644 | 2.644 | 1.3222 | 8.99 | 0.1 |
| Sliding Velocity | 2 | 65.065 | 65.065 | 32.5327 | 221.2 | 0.005 |
| Residual Error | 2 | 0.294 | 0.294 | 0.1471 | ||
| Total | 8 | 231.281 |
| Experiment No. | Load (N) | Sliding Distance (m) | Sliding Velocity (m/s) |
|---|---|---|---|
| 1 | 40 | 3000 | 1.047 |
| 2 | 40 | 4500 | 3.141 |
| Experiment No. | Experimental Wear Rate (mm3/m) × 10−4 | Predicted Wear Rate (mm3/m) × 10−4 | % Error |
|---|---|---|---|
| 1 | 2.72 | 2.97 | 9.19 |
| 2 | 1.36 | 1.23 | 9.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saurabh, A.; Joshi, K.; Manoj, A.; Verma, P.C. Process Optimization of Automotive Brake Material in Dry Sliding Using Taguchi and ANOVA Techniques for Wear Control. Lubricants 2022, 10, 161. https://doi.org/10.3390/lubricants10070161
Saurabh A, Joshi K, Manoj A, Verma PC. Process Optimization of Automotive Brake Material in Dry Sliding Using Taguchi and ANOVA Techniques for Wear Control. Lubricants. 2022; 10(7):161. https://doi.org/10.3390/lubricants10070161
Chicago/Turabian StyleSaurabh, Ashish, Kartik Joshi, Abhinav Manoj, and Piyush Chandra Verma. 2022. "Process Optimization of Automotive Brake Material in Dry Sliding Using Taguchi and ANOVA Techniques for Wear Control" Lubricants 10, no. 7: 161. https://doi.org/10.3390/lubricants10070161
APA StyleSaurabh, A., Joshi, K., Manoj, A., & Verma, P. C. (2022). Process Optimization of Automotive Brake Material in Dry Sliding Using Taguchi and ANOVA Techniques for Wear Control. Lubricants, 10(7), 161. https://doi.org/10.3390/lubricants10070161






