Finite Element Simulation and Fretting Wear Prediction of a Tenon Connection Structure
Abstract
:1. Introduction
2. Wear Modeling
2.1. Fretting Wear Model
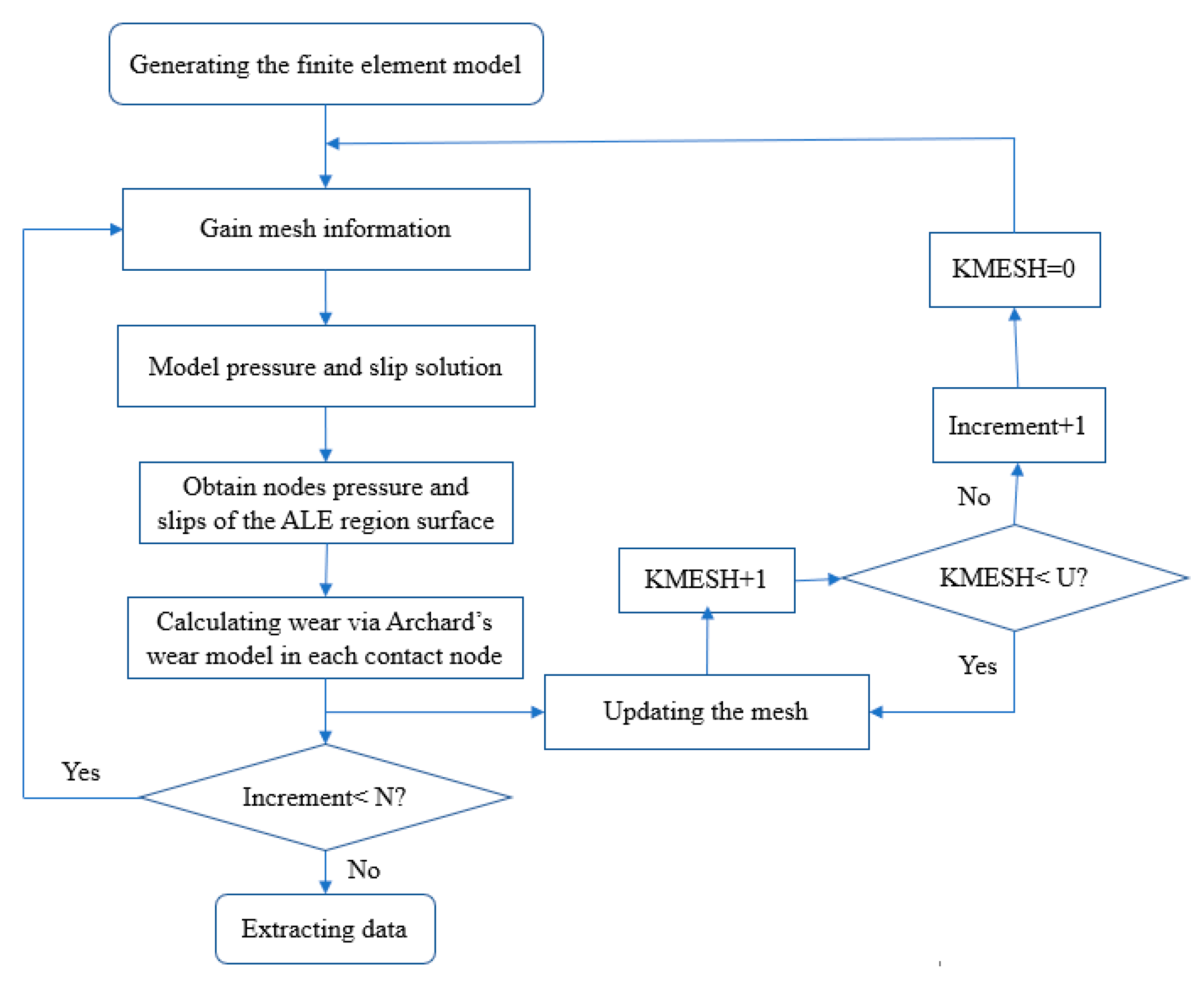
2.2. Wear Finite Element Simulation Method
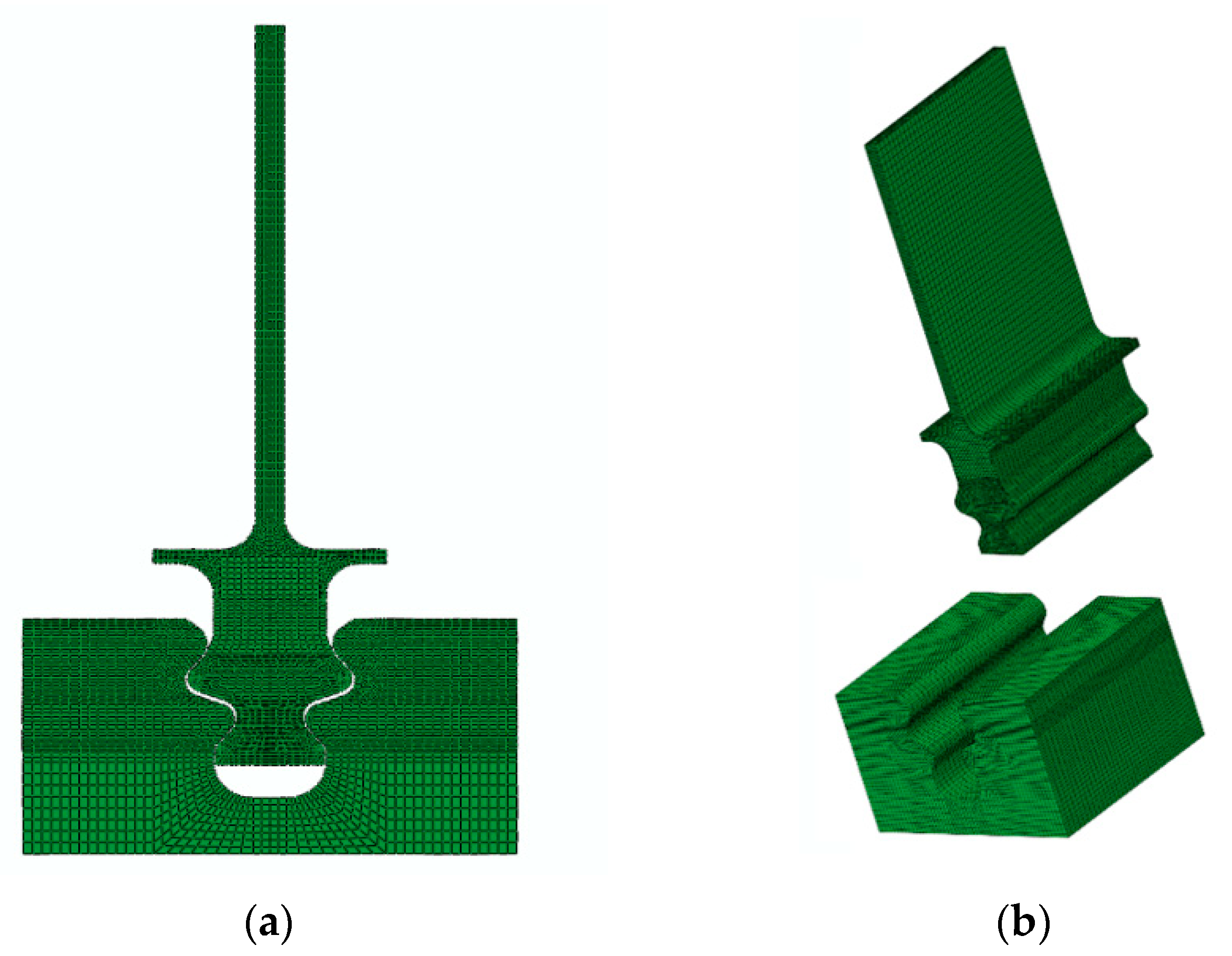
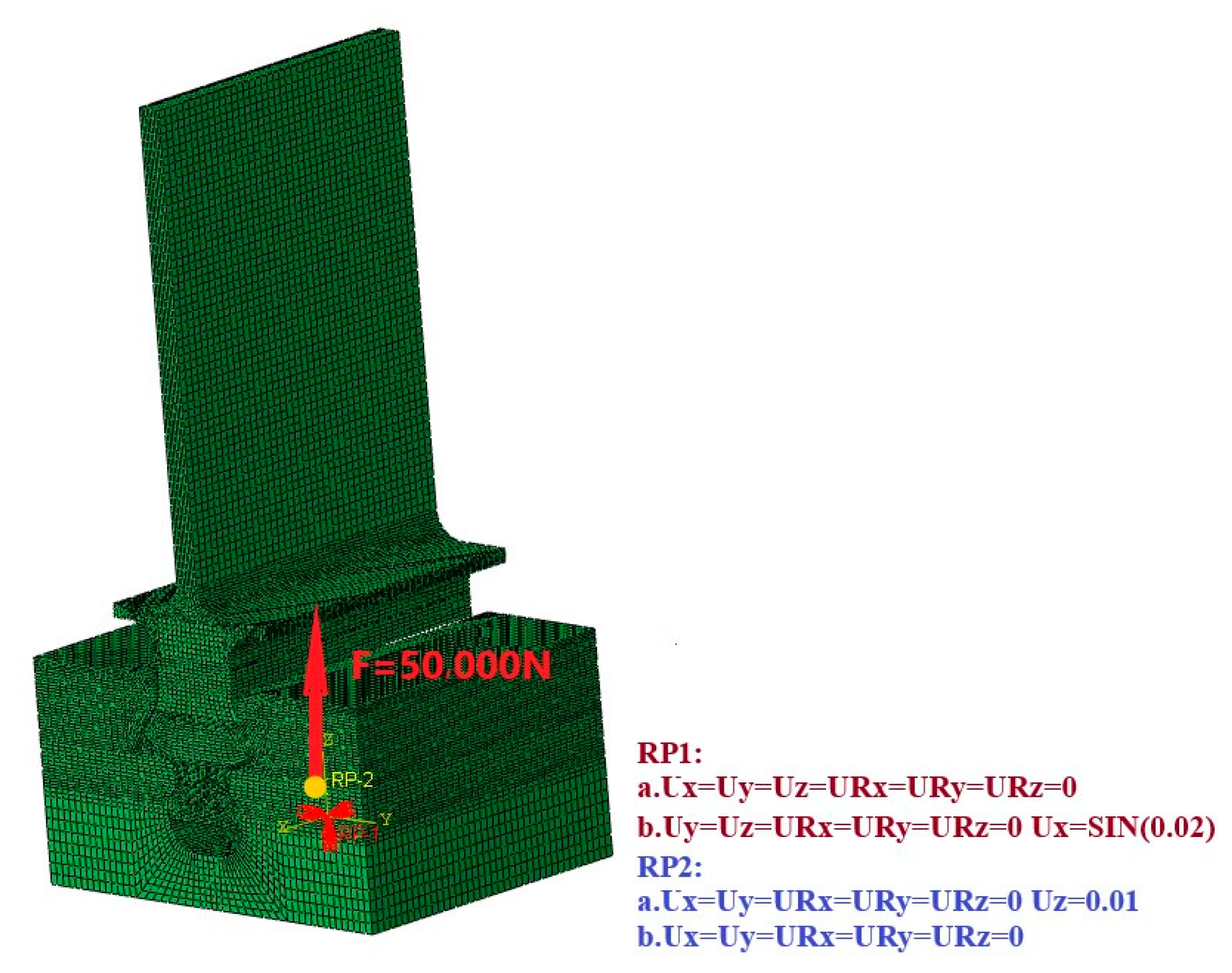
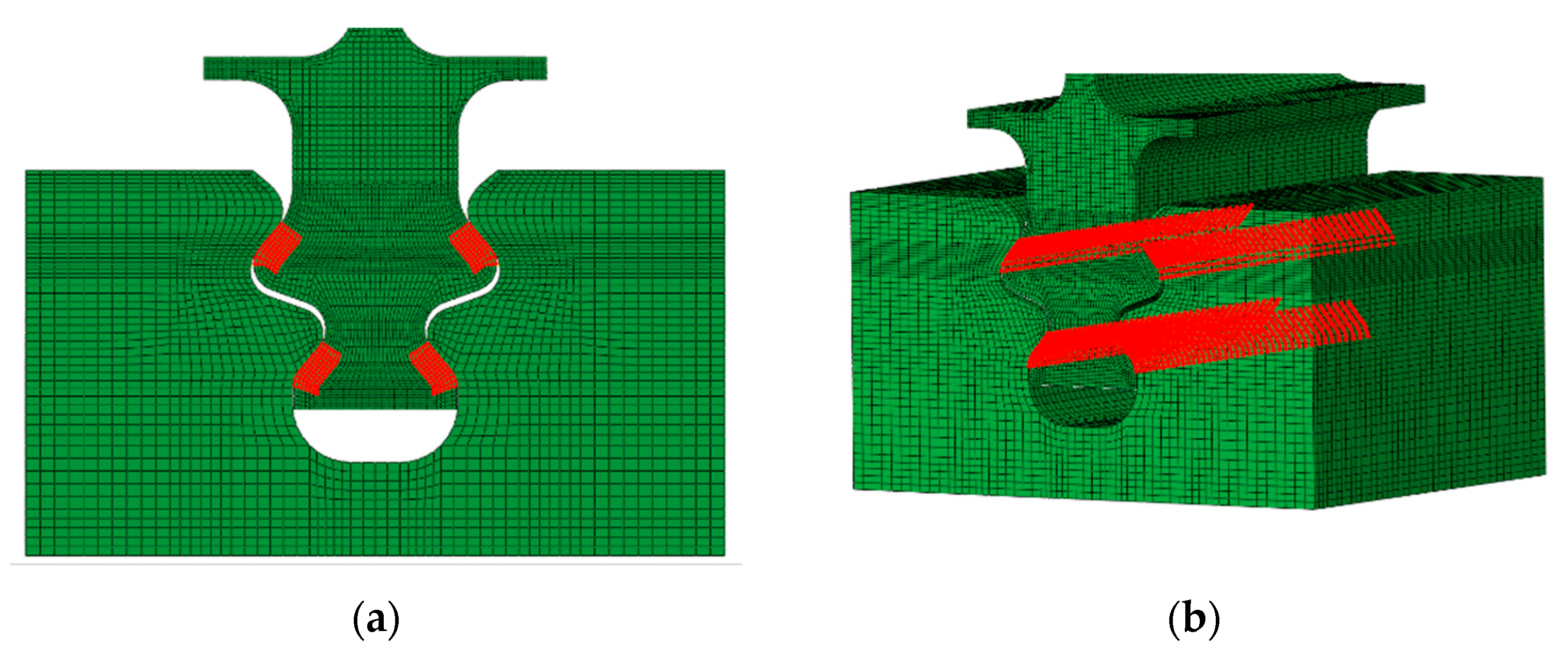
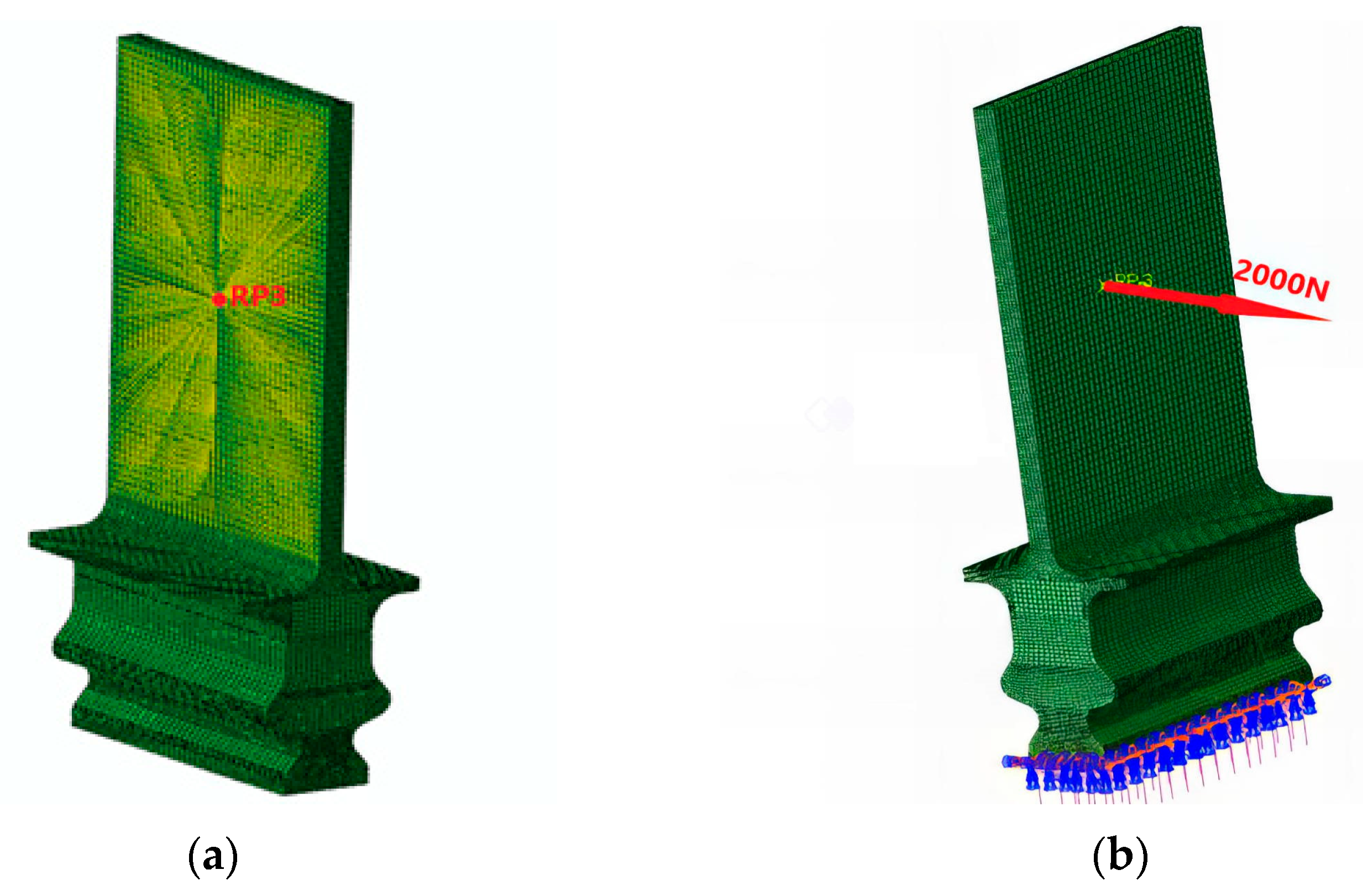
2.3. Finite Element Model
3. Results and Discussion
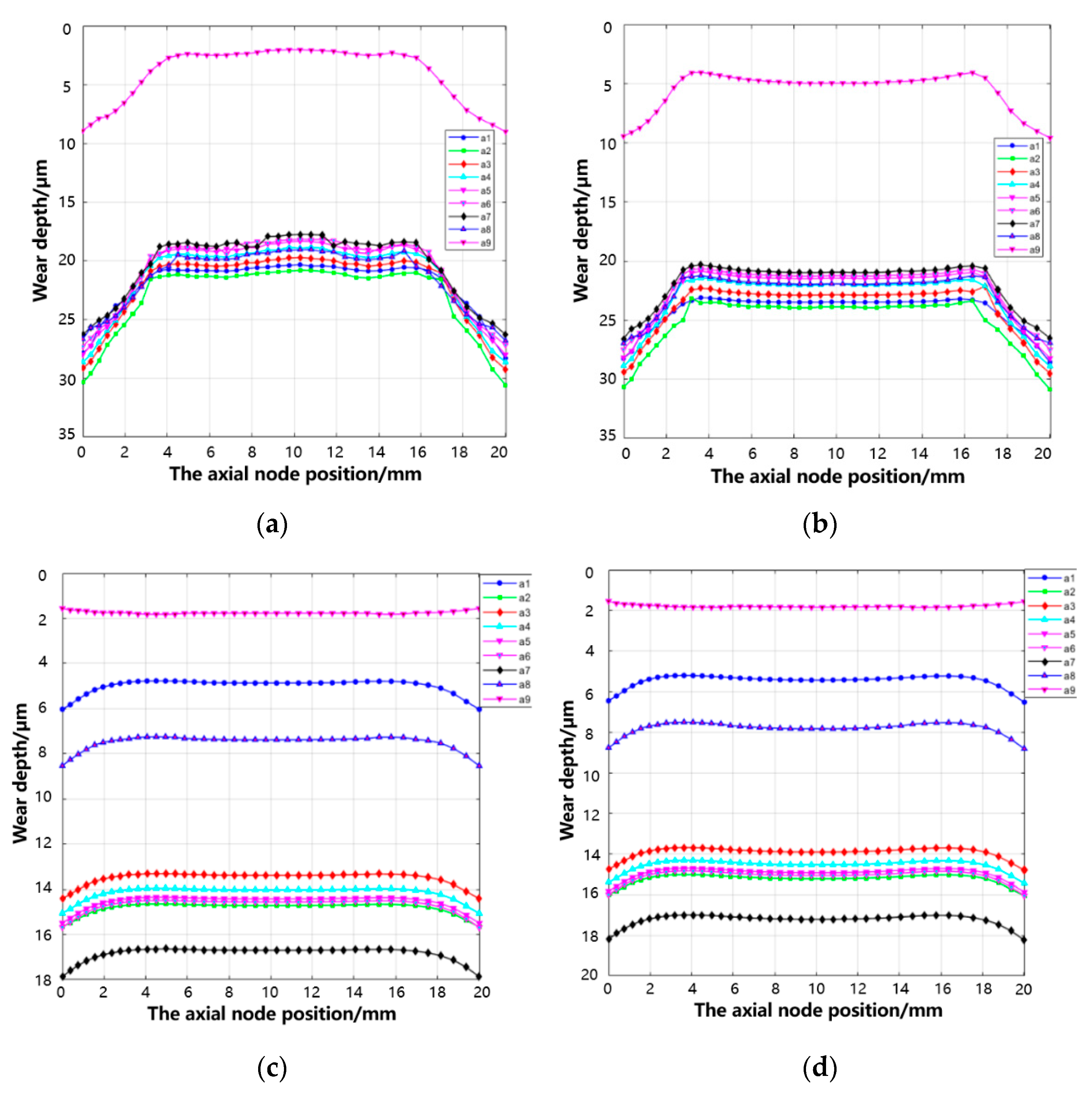
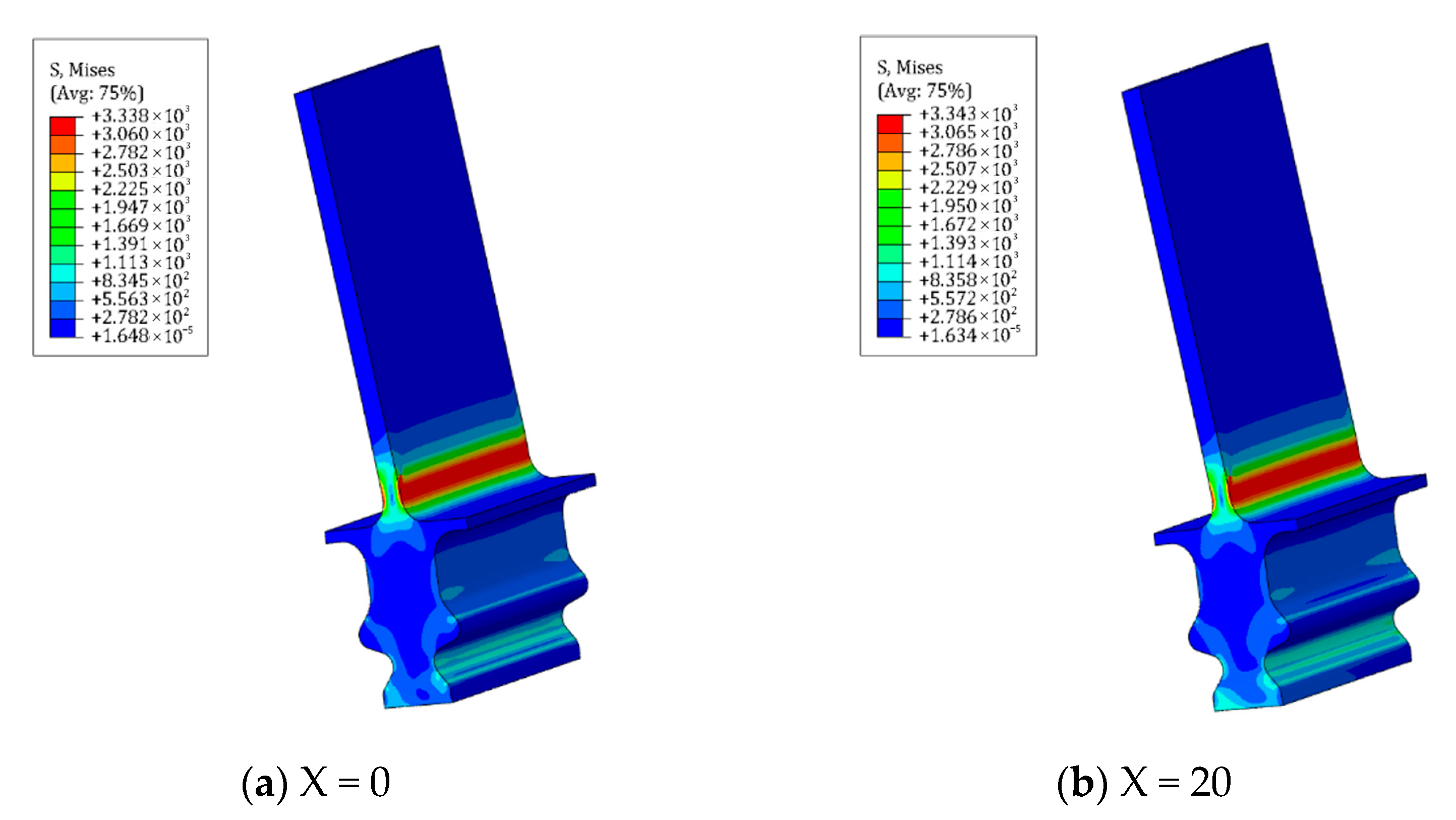
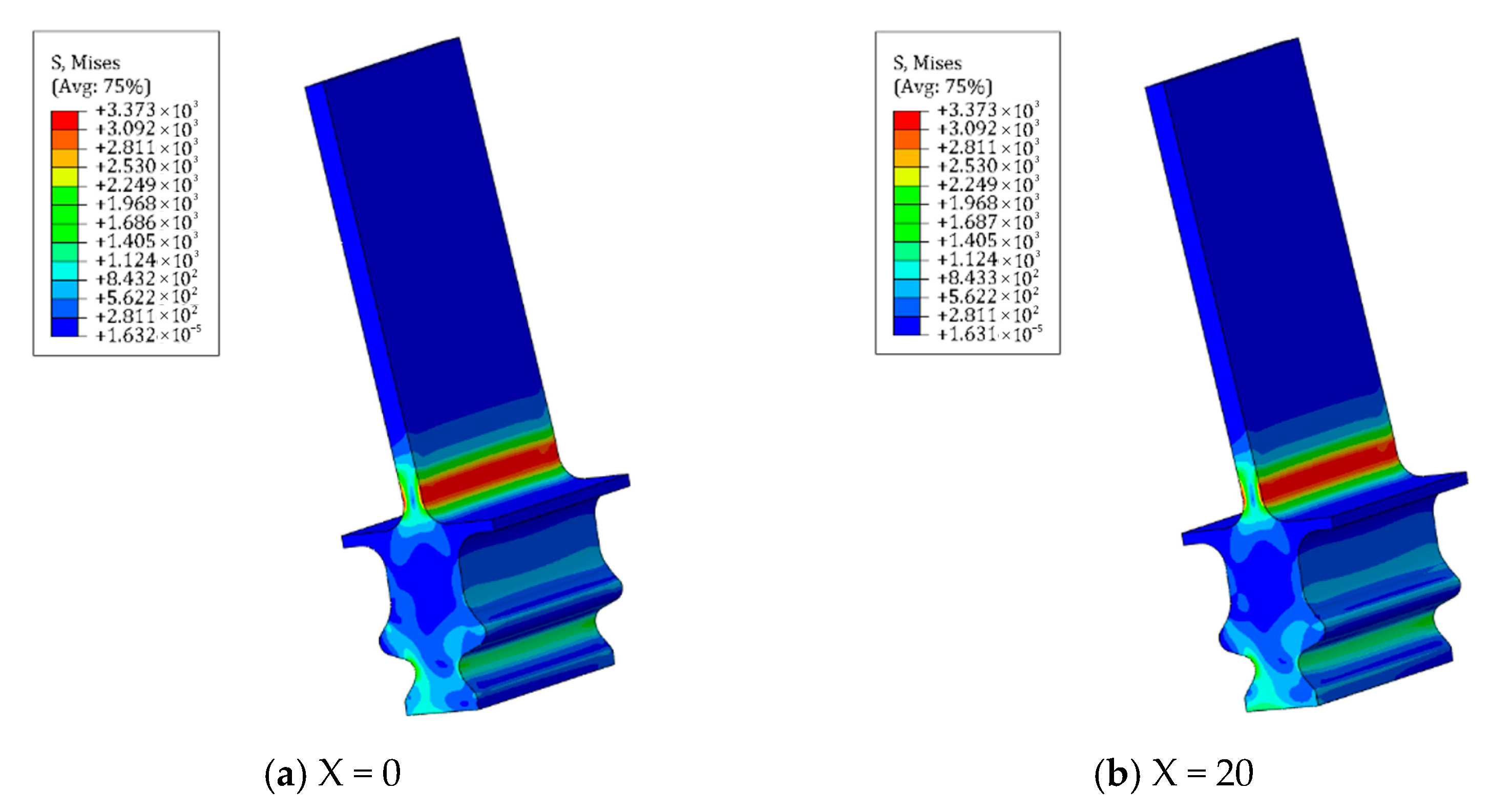
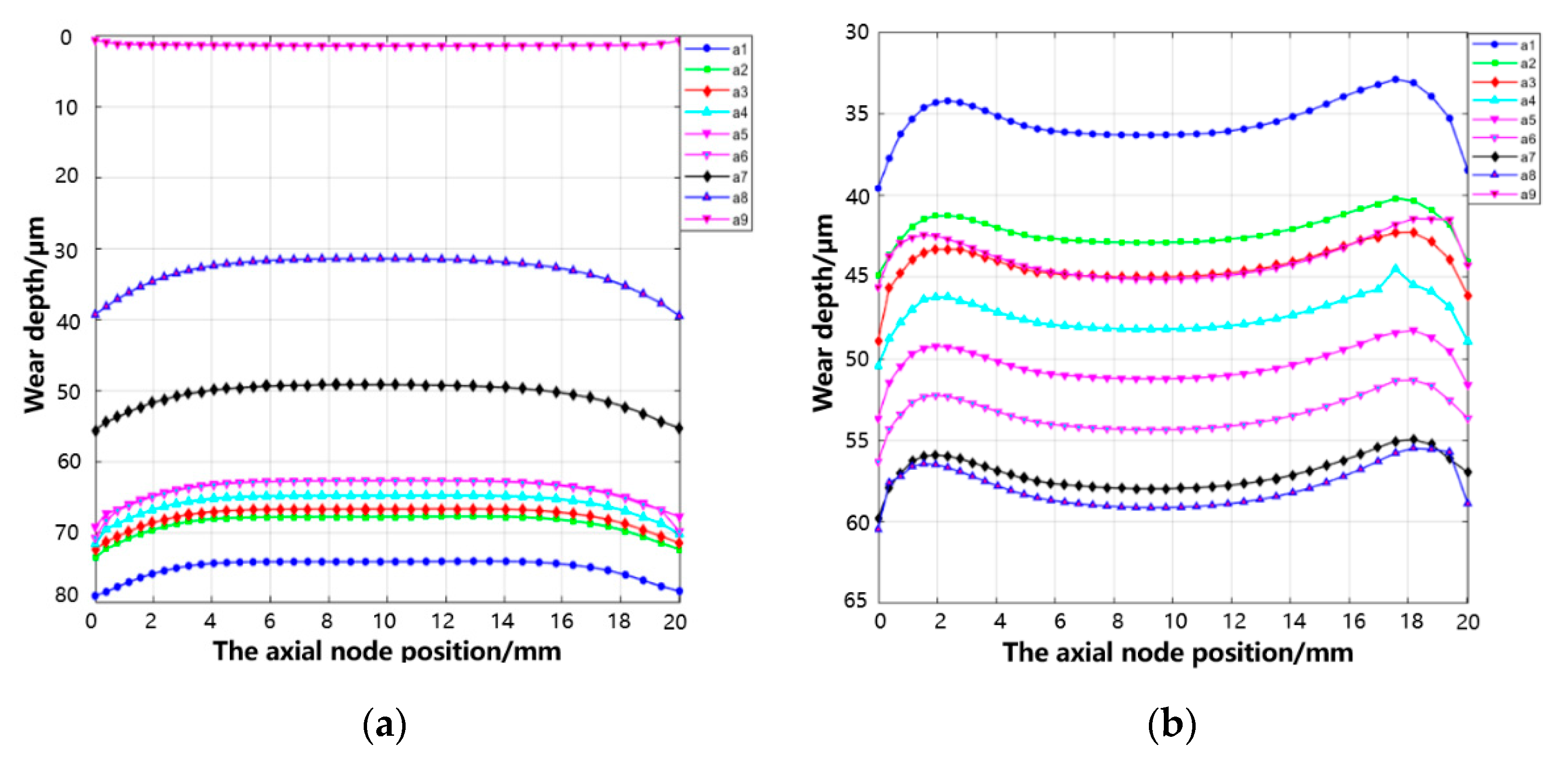
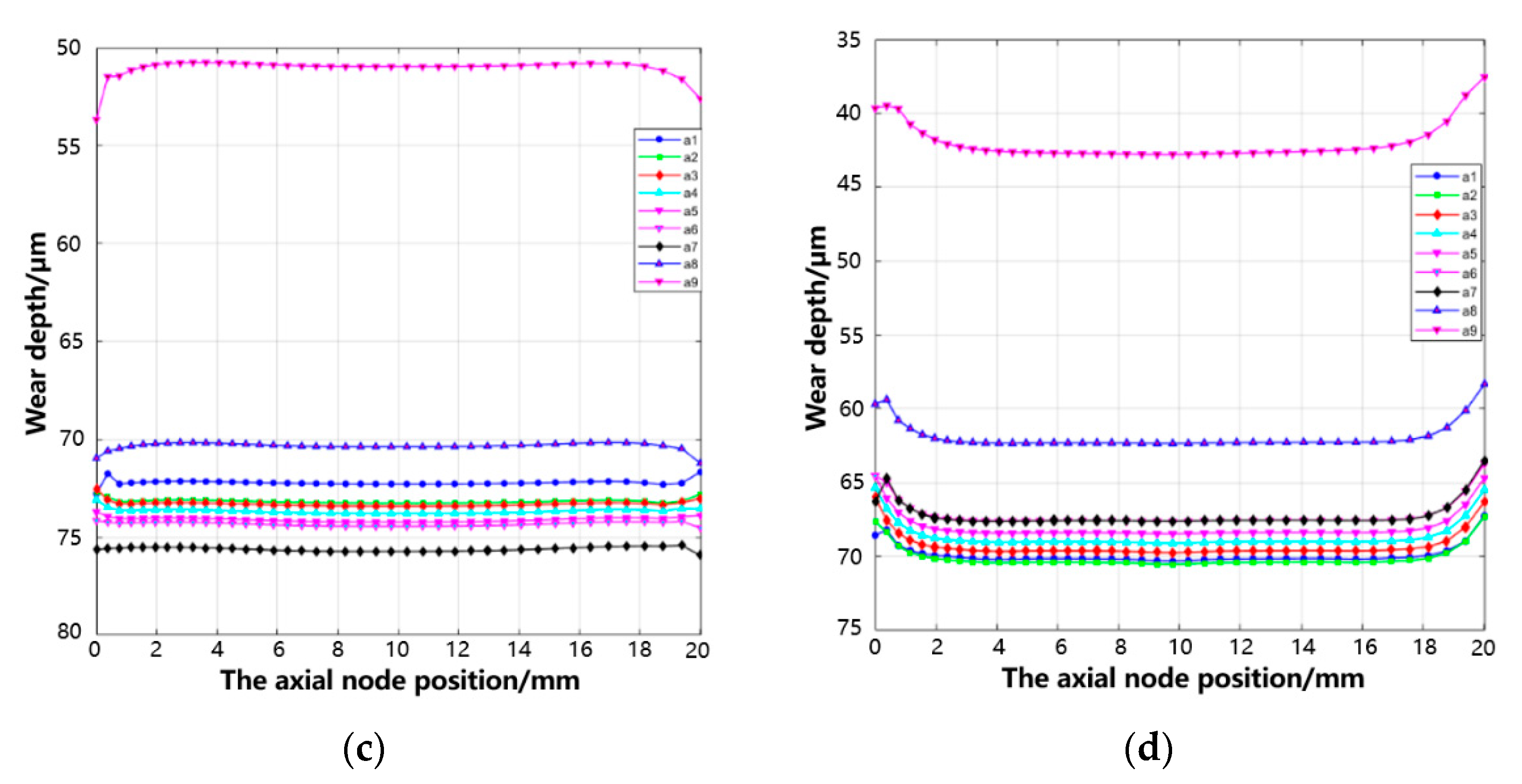
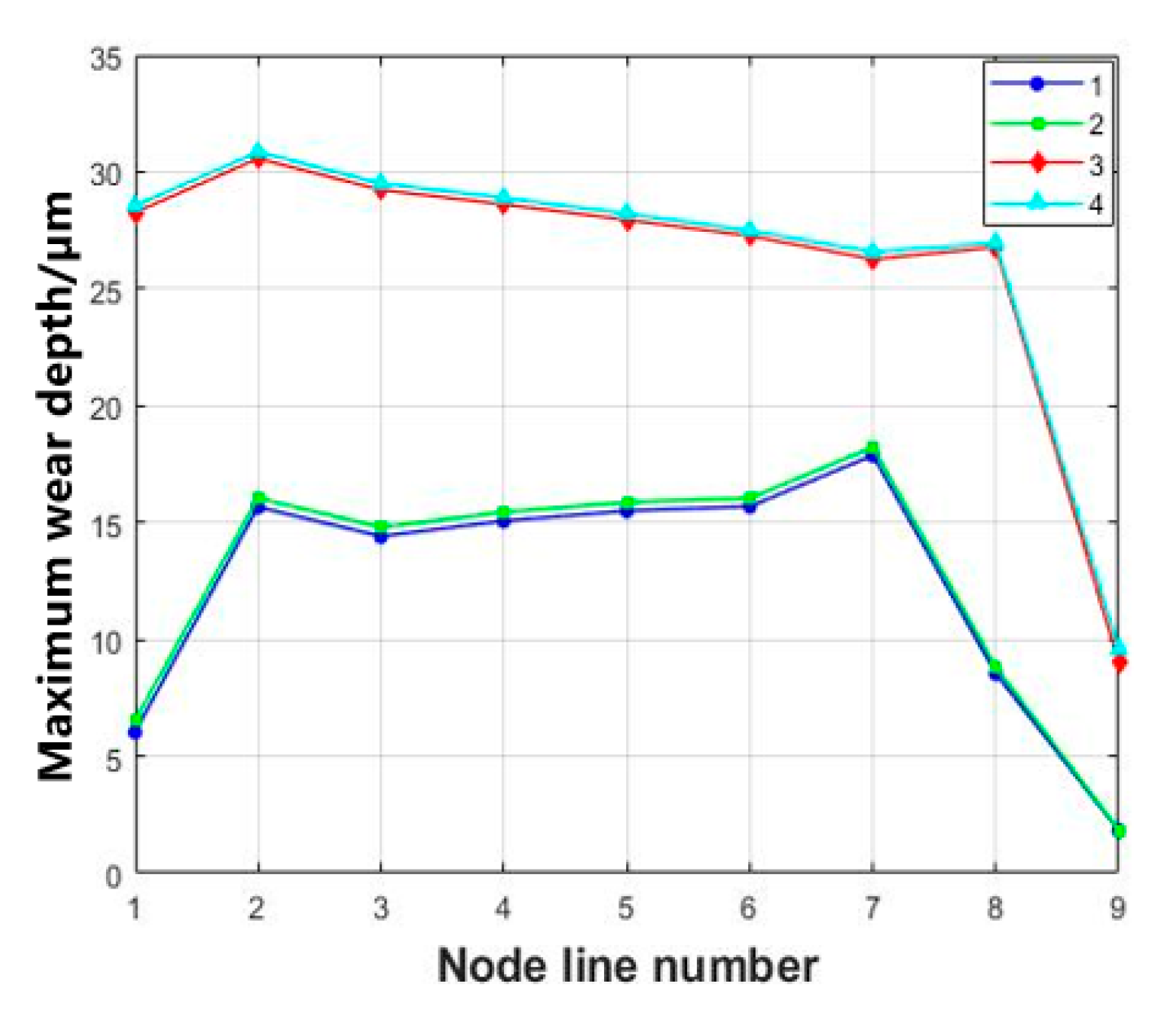
3.1. Effect of Varying Fretting Orientations on Wear Behavior
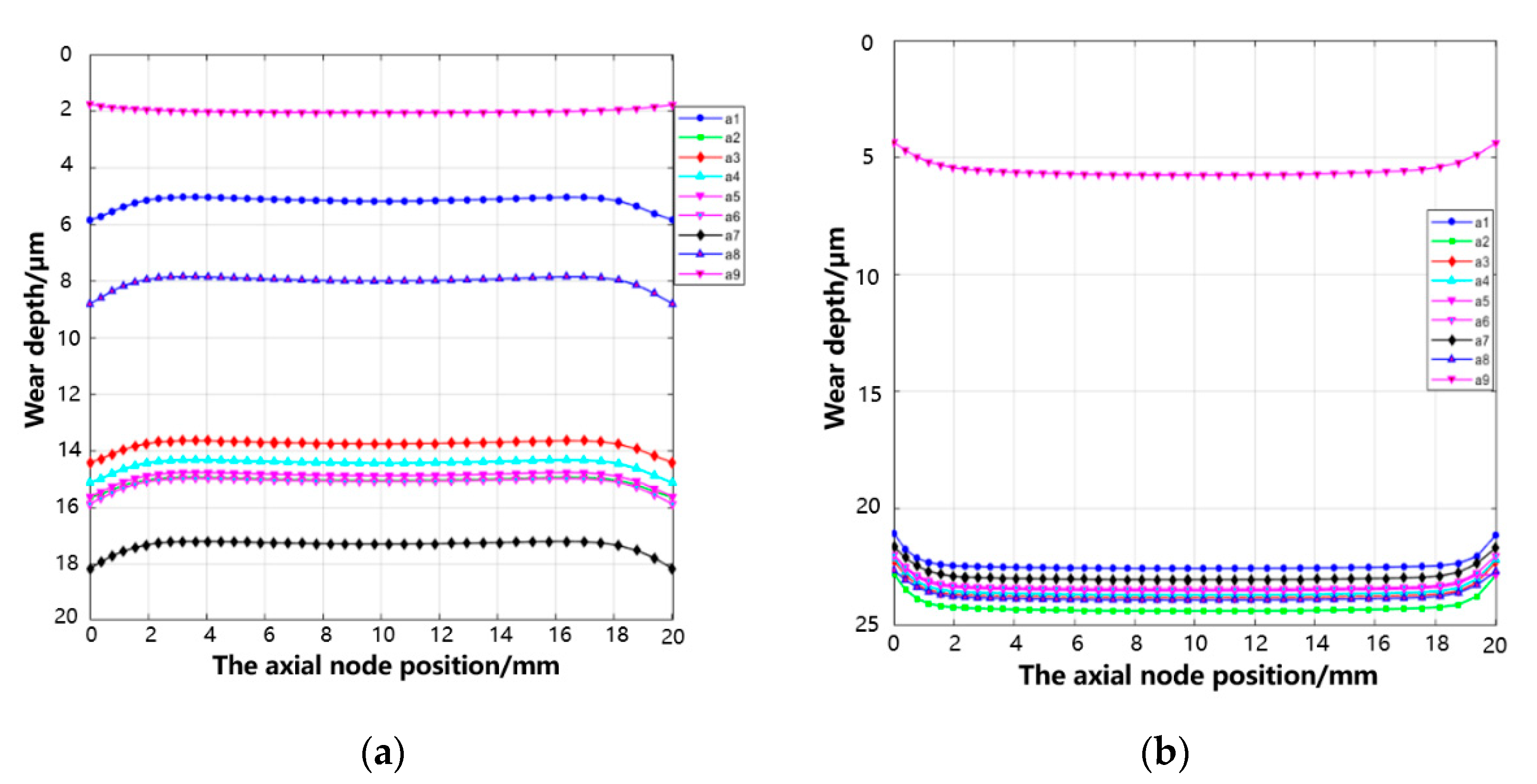
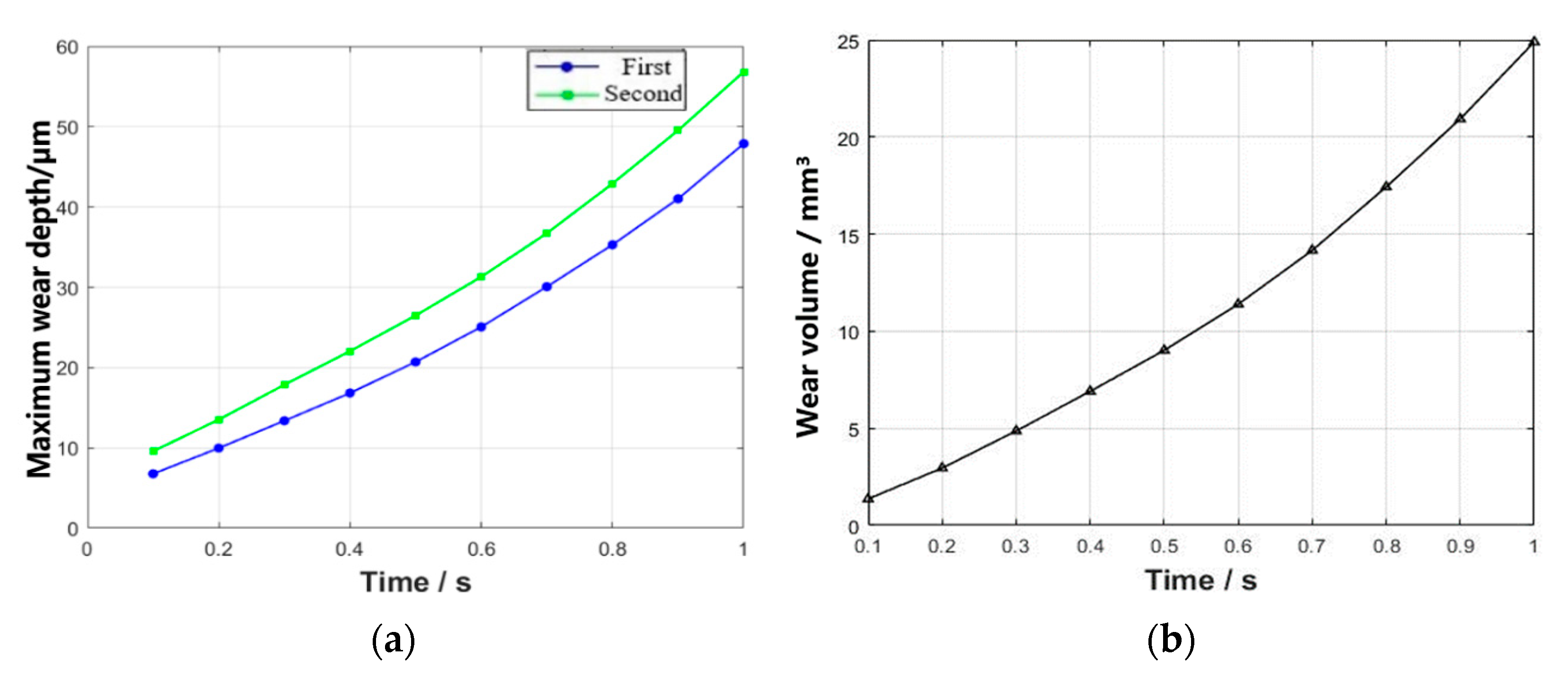
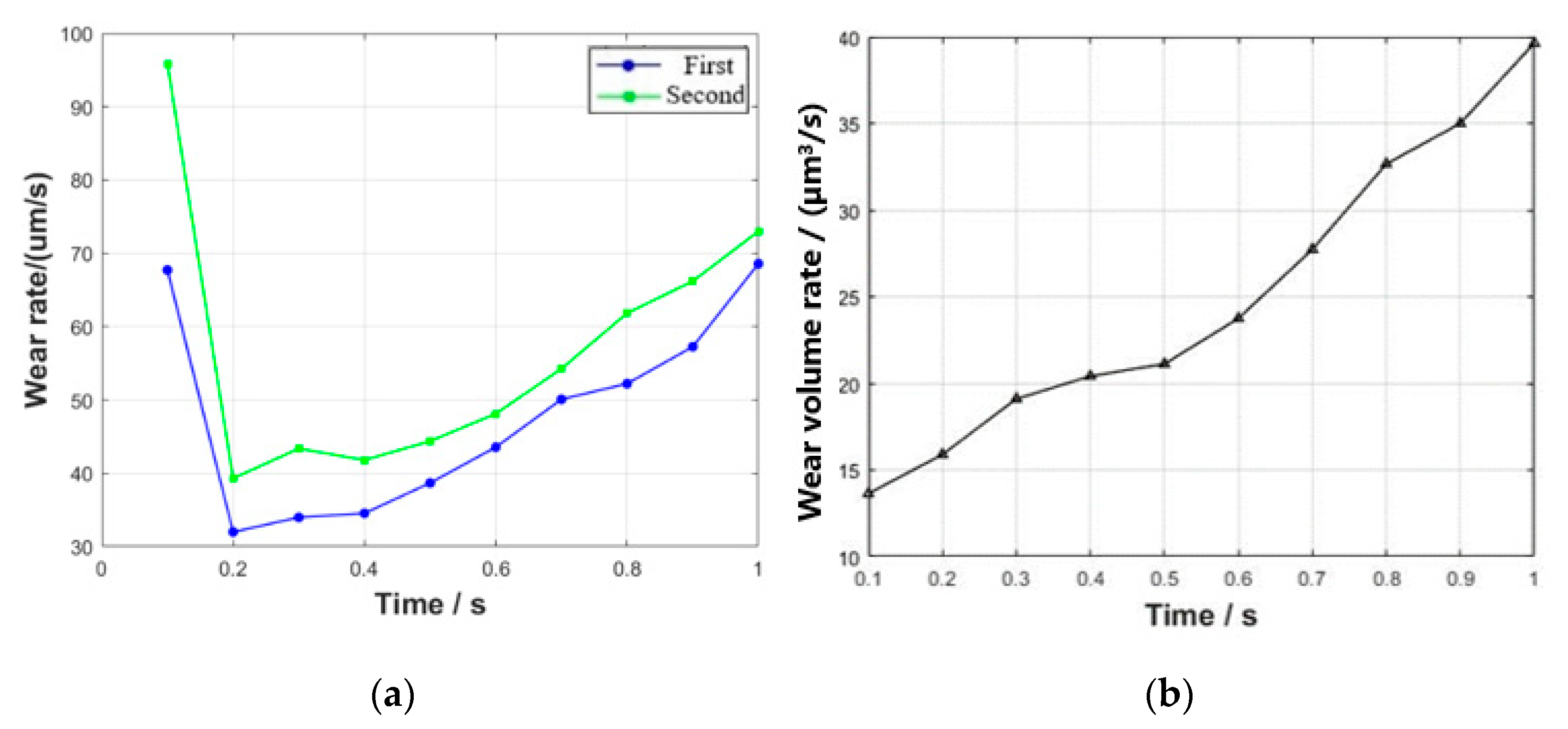
3.2. Effect of Varying Fretting Time on Wear Behavior
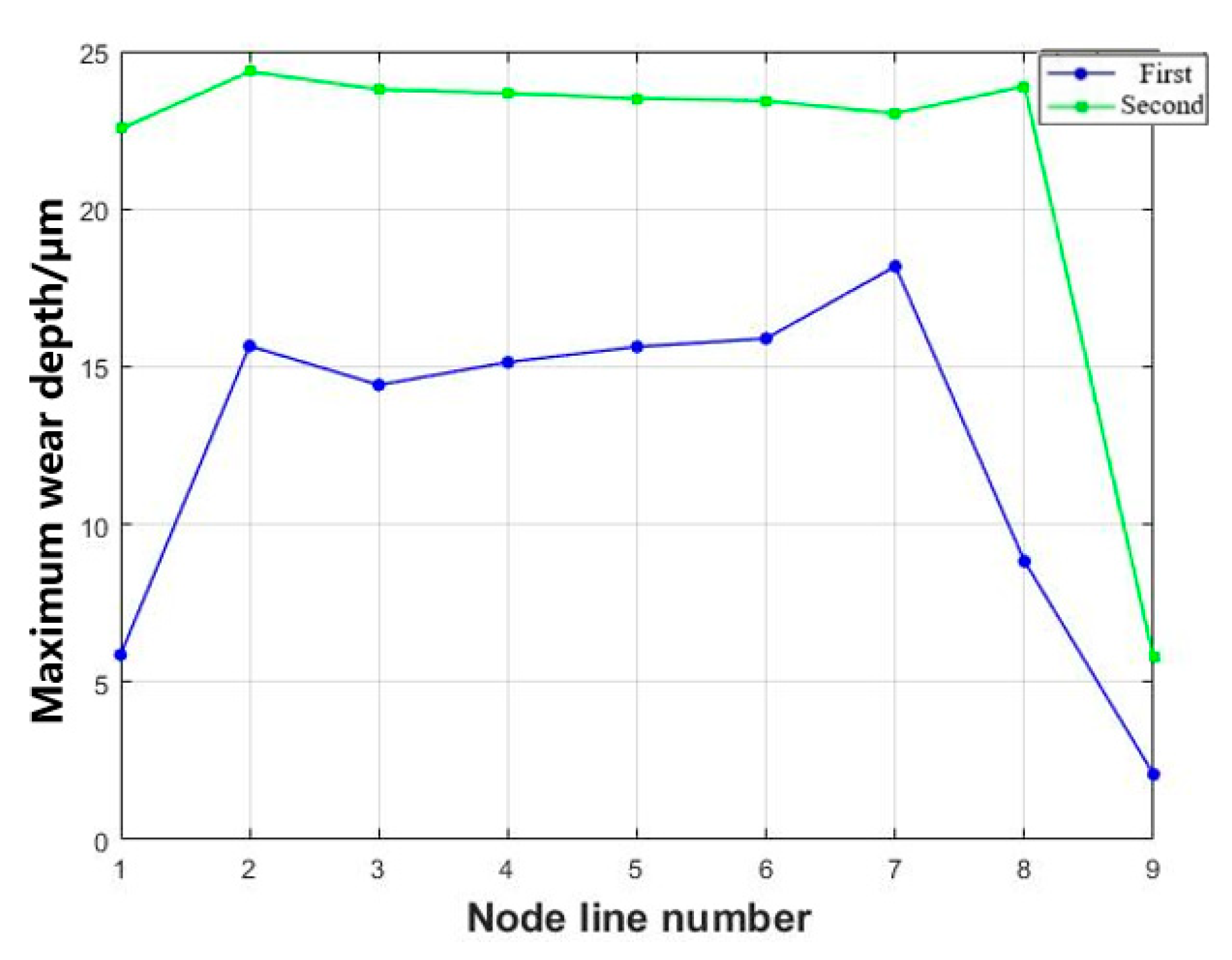
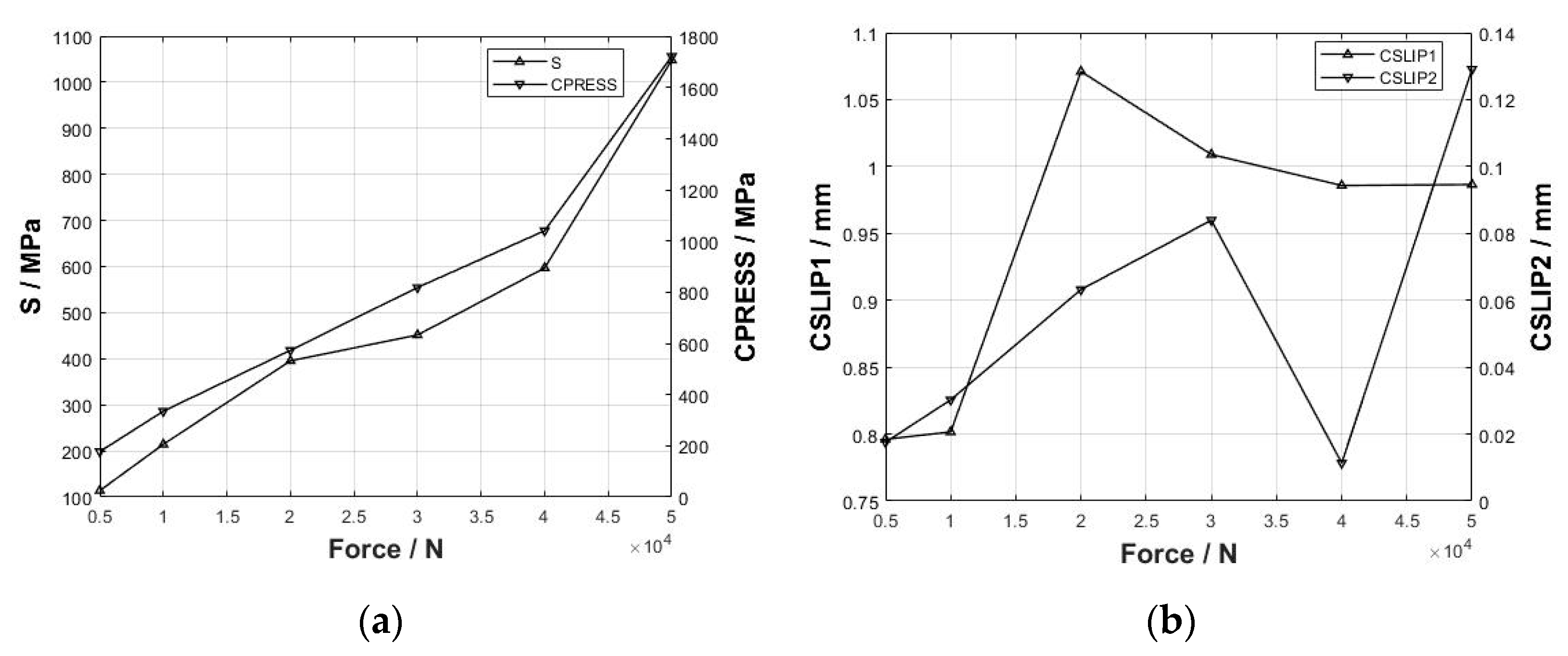
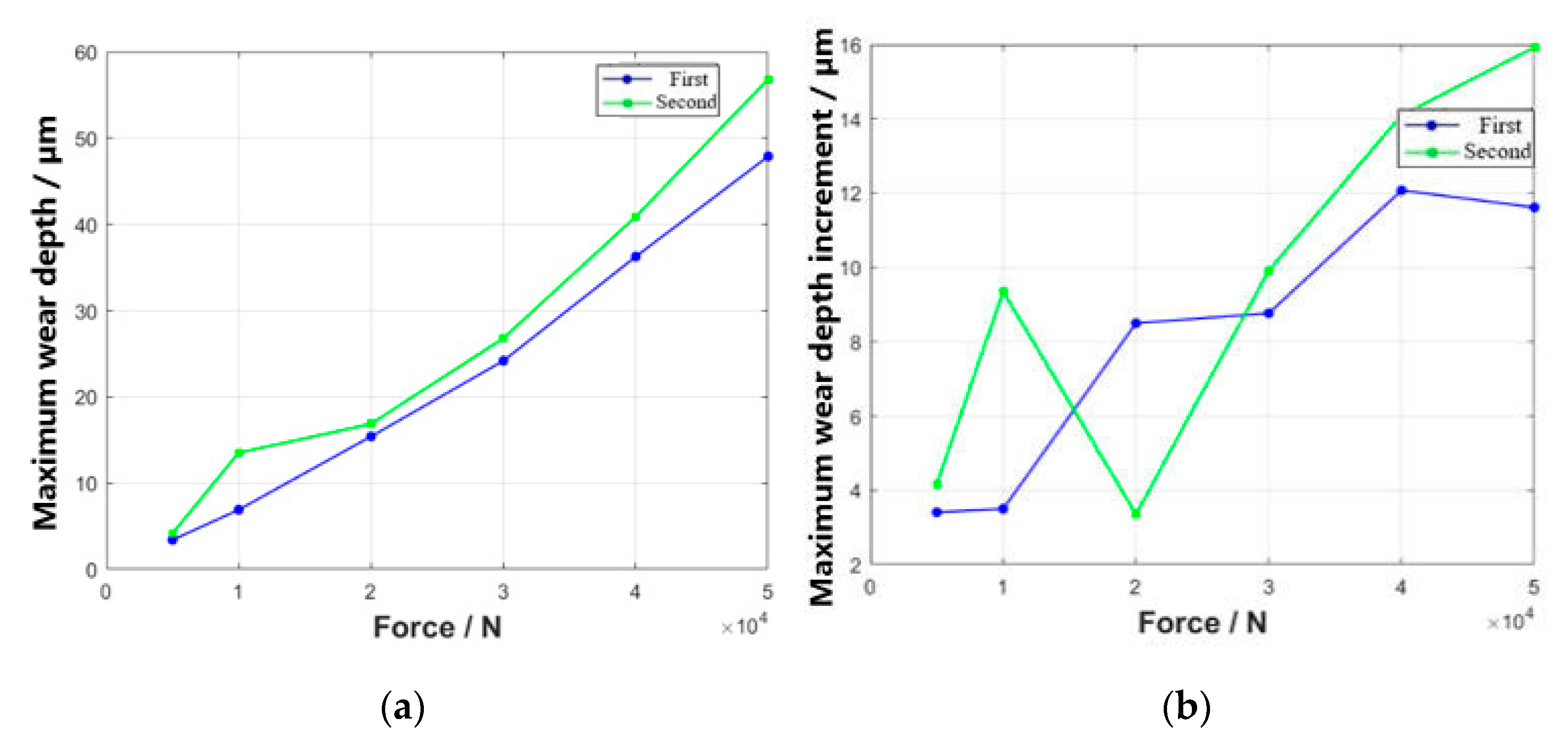
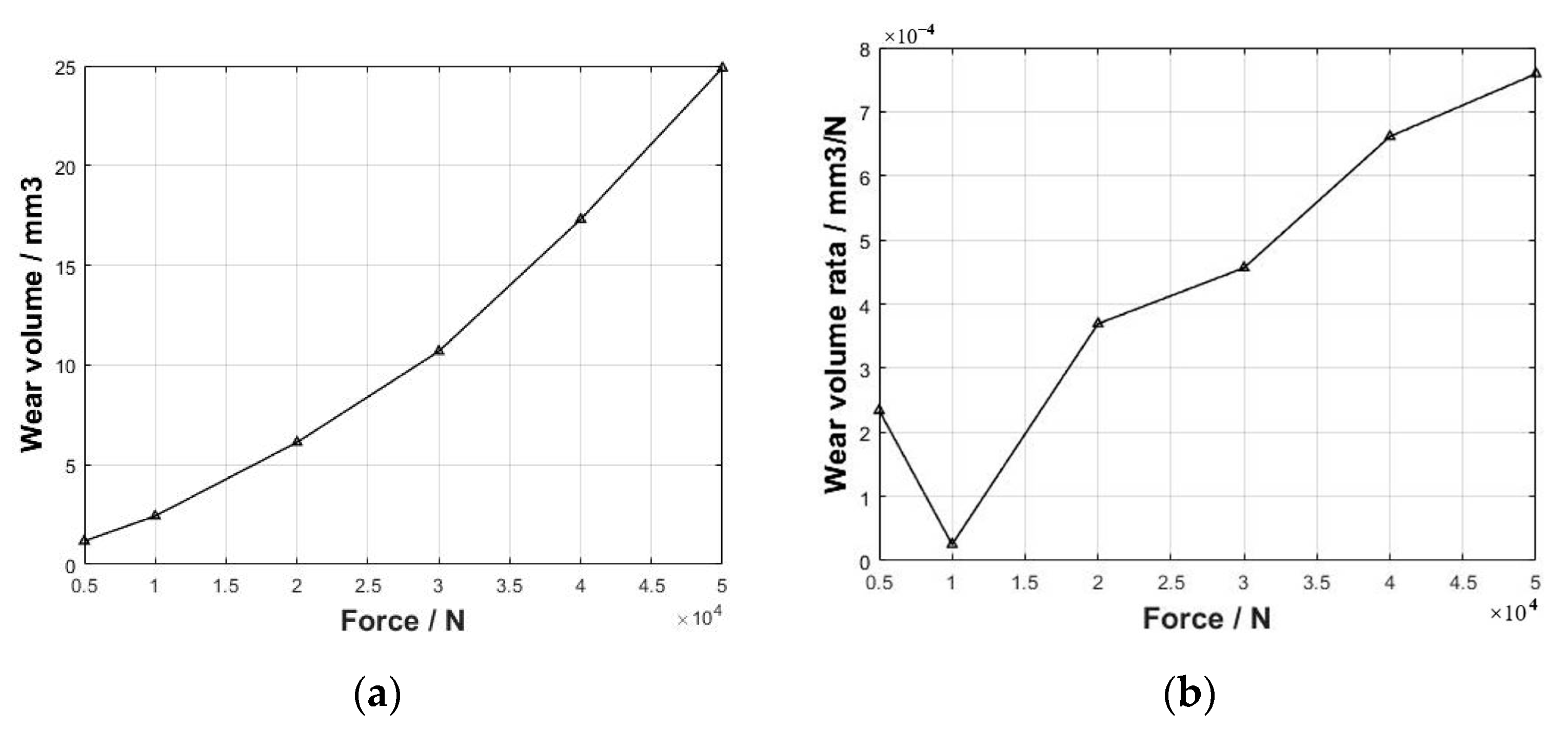
3.3. Effect of Different Loads on Wear Behavior
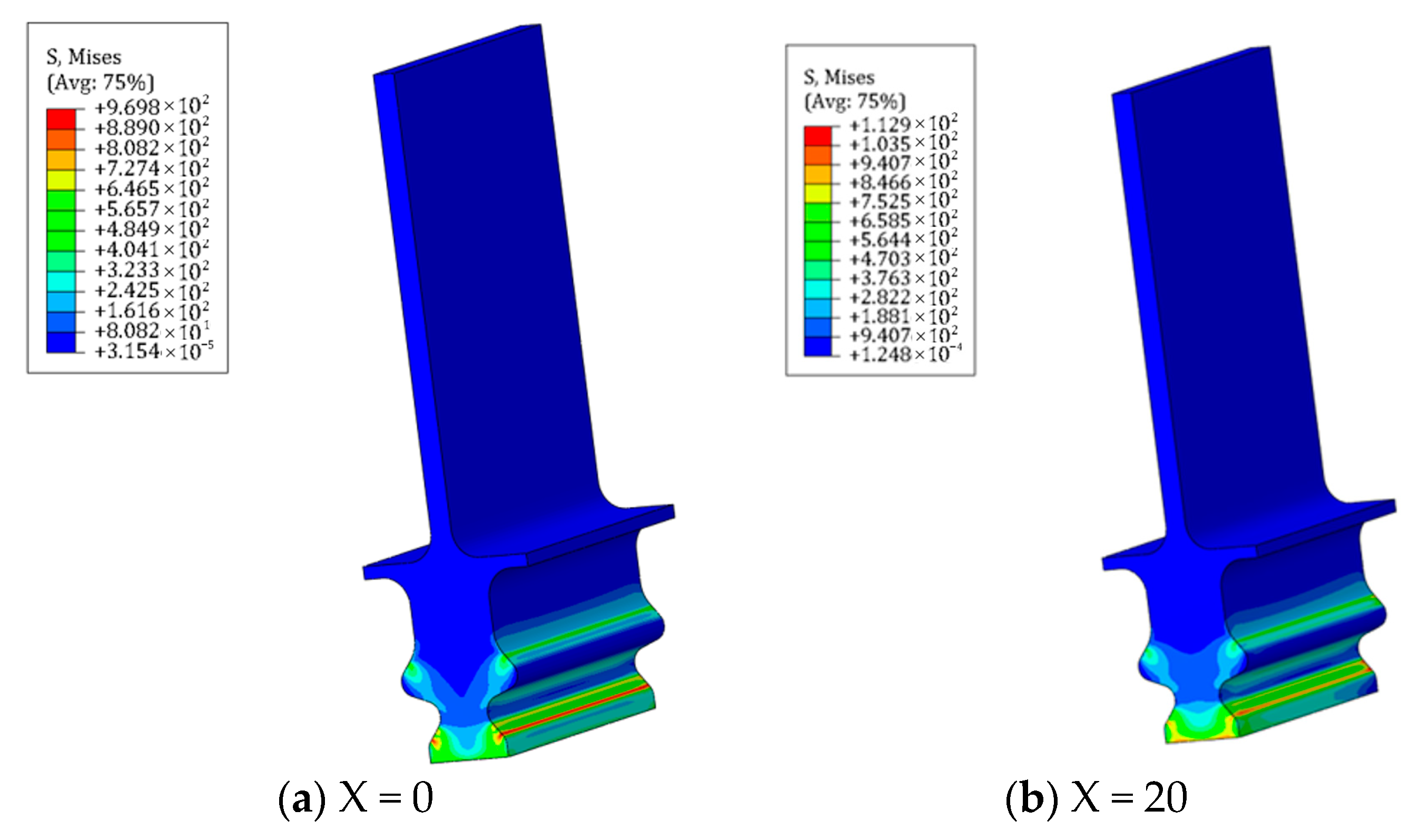
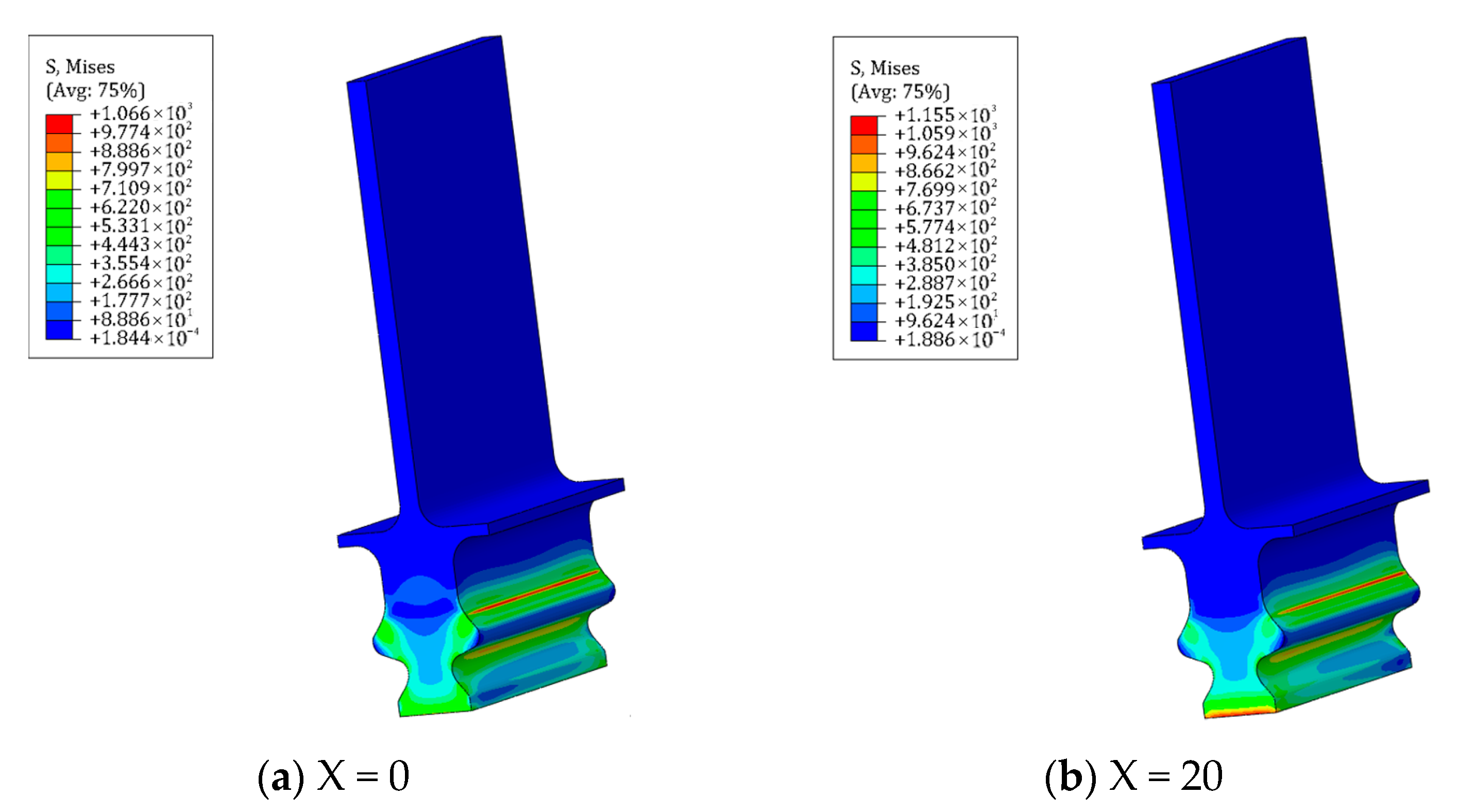
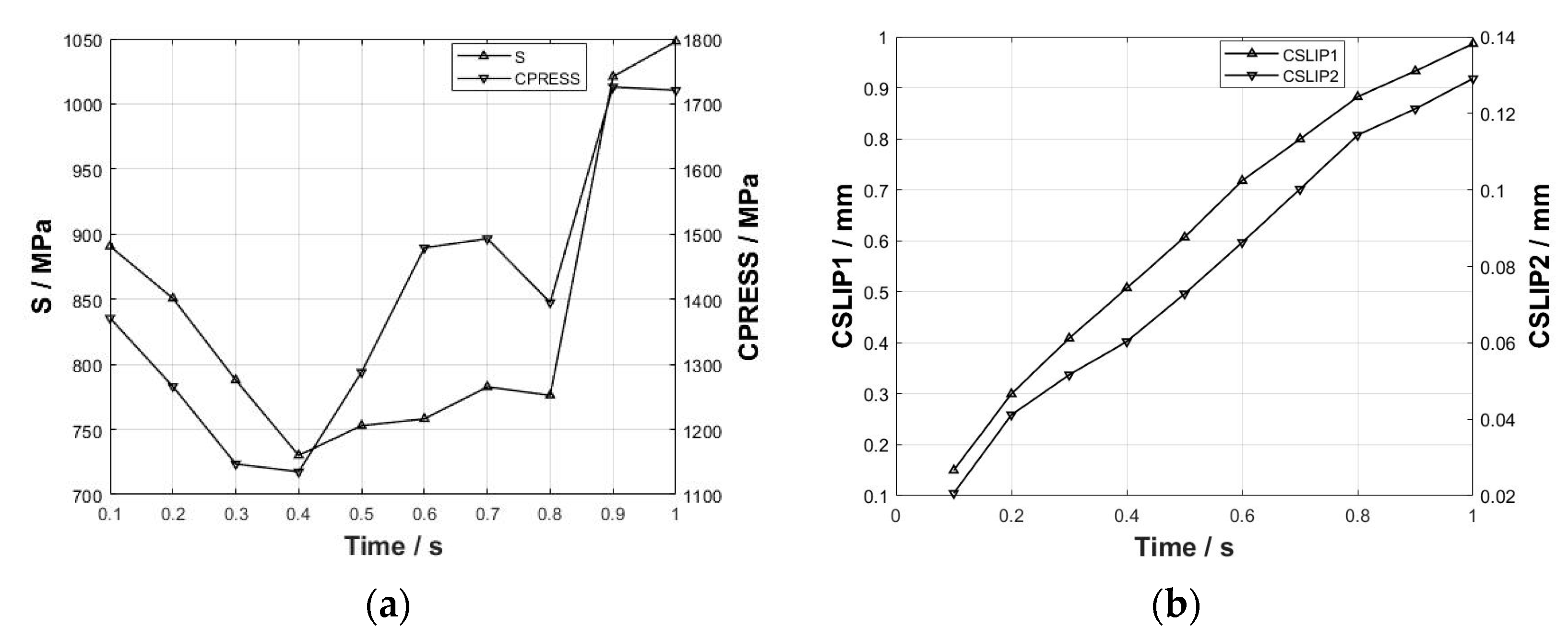
3.4. Fretting Wear under Combined Normal and Aerodynamic Loading
4. Conclusions
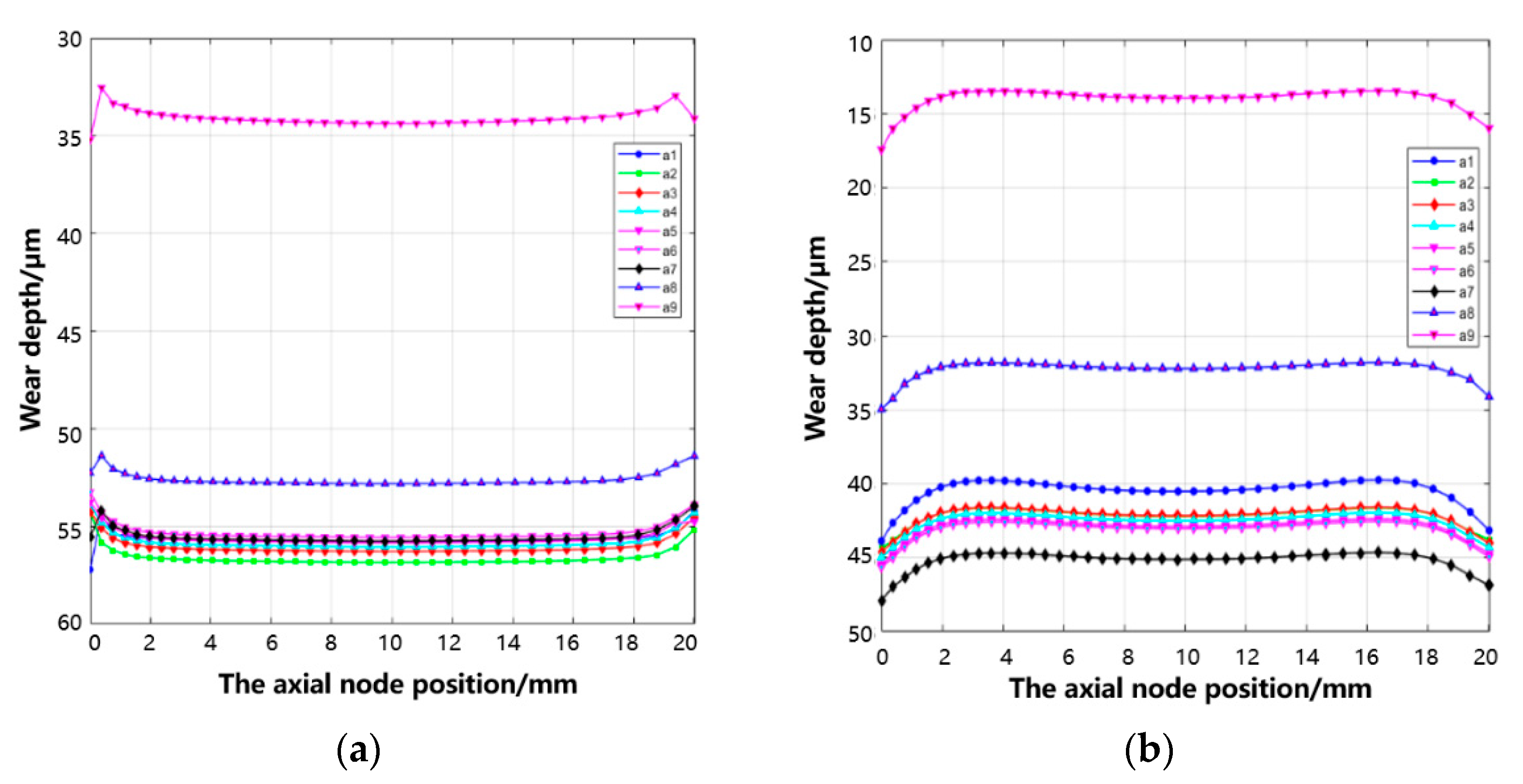
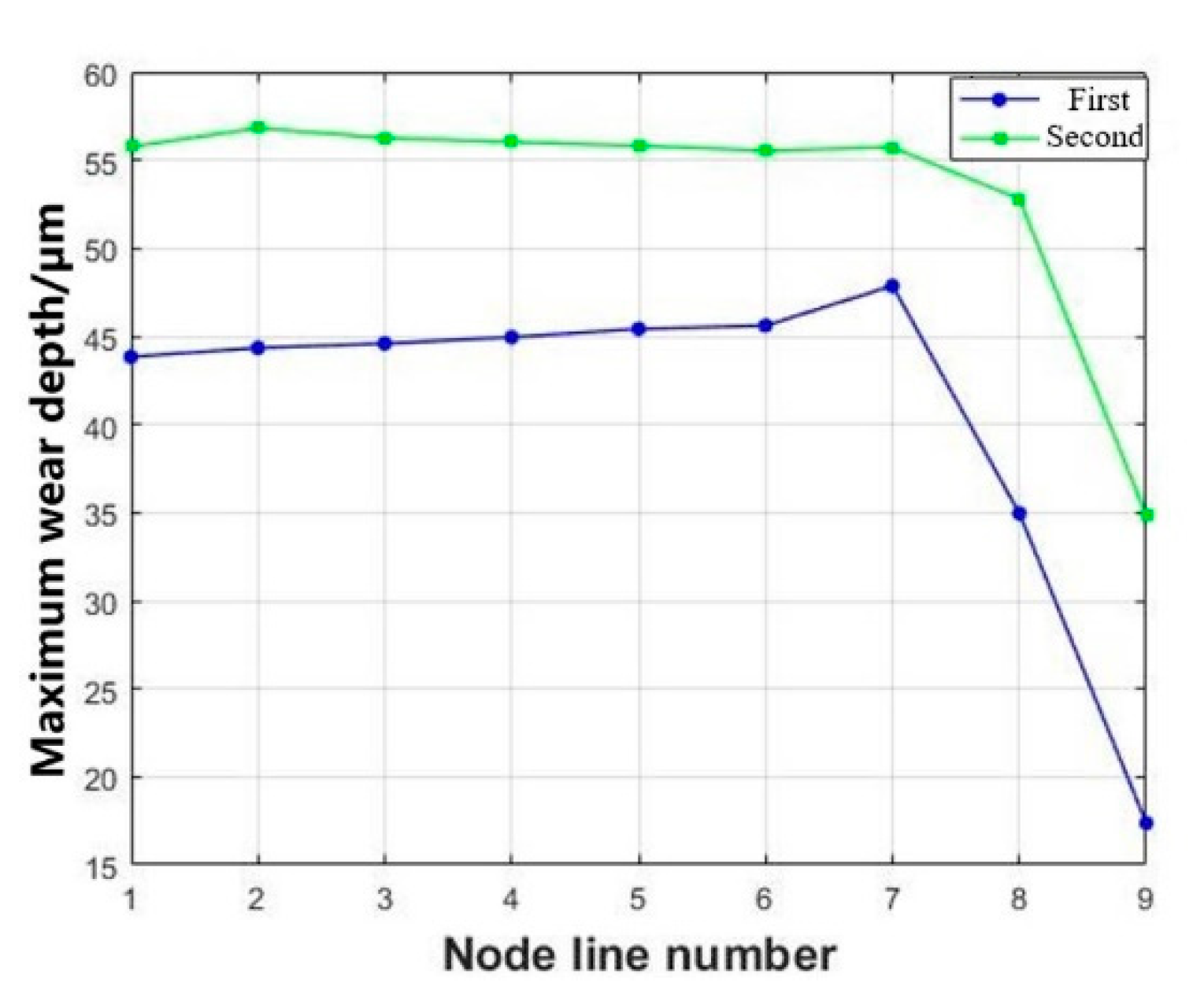
- The fretting direction exerts significant influence on the wear characteristics of the tenon connection structure. Distinct variations in wear depth and morphology are observed on each tooth surface, depending on different fretting directions. Among these, axial (x-axis) fretting exhibits the most pronounced impact on wear depth, followed by circumferential (y-axis) fretting, while radial (z-axis) fretting demonstrates a comparatively minimal influence.
- Circumferential fretting results in non-uniform wear depth on the same pair of teeth, leading to phenomena akin to rubbing and impact.
- As simulation time increases, the maximum wear depth and volume gradually increase, with an accelerating rate of wear depth growth over time. As a result of continuous wear, the contact pressure exhibits an initial decrease followed by a subsequent increase over time.
- With the increase in applied load, both the maximum wear depth and wear volume exhibit a gradual increment.
- After incorporating aerodynamic loads, the wear morphology and depth of each tooth surface in the tenon connection structure will undergo alterations, resulting in a more pronounced degree of wear on certain tooth surfaces. Notably, the maximum wear depth is observed at the lower edge of tooth one.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Q. Investigation of Fretting Fatigue Damage and Shot-Peening Palliative Mechanisms of TC4 Alloy Dovetail Joints. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Waterhouse, R.B. Fretting Fatigue; Applied Science Publishers: London, UK, 1981. [Google Scholar]
- Hoeppner, D. Mechanisms of fretting-fatigue and their impact on test methods development. ASTM STP 1992, 1159, 23–32. [Google Scholar] [CrossRef]
- Zhu, M.; Zhou, Z. On the mechanisms of various fretting wear modes. Tribol. Int. 2011, 44, 1378–1388. [Google Scholar] [CrossRef]
- Kirk, A.; Sun, W.; Bennett, C.; Shipway, P. Interaction of displacement amplitude and frequency effects in fretting wear of a high strength steel: Impact on debris bed formation and subsurface damage. Wear 2021, 482–483, 203981. [Google Scholar] [CrossRef]
- Hurricks, L.P. The mechanism of fretting wear—A review. Wear 1990, 136, 389–409. [Google Scholar]
- Vingsbo, O.; Soderberg, S. On fretting maps. Wear 1988, 126, 131–147. [Google Scholar] [CrossRef]
- Vincent, L.; Berthier, Y.; Godet, M. Testing methods in fretting fatigue: A critical appraisal. ASTM STP 1992, 1159, 33–48. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, D.; Guo, Y. Fretting friction and wear behaviors of spiral wound gasket (SWG) sealing surface. Tribol. Int. 2019, 133, 236–245. [Google Scholar] [CrossRef]
- Tang, P.; Mi, X.; Zhang, J.; Xiong, F.-R.; Zheng, B.; Shao, X.-J.; Peng, J.-F.; Zhu, M.-H. Evolution of wear damage in 690 alloy tube mated with 405 stainless steel plate due to fretting conditions. Tribol. Int. 2021, 163, 107177. [Google Scholar] [CrossRef]
- Godet, M. The third-body approach: A mechanical view of wear. Wear 1984, 100, 437–452. [Google Scholar] [CrossRef]
- Berthier, Y.; Vincent, L.; Godet, M. Velocity accommodation in fretting. Wear 1988, 125, 25–38. [Google Scholar] [CrossRef]
- Fouvry, S.; Kapsa, P.; Vincent, L. Quantification of fretting damage. Wear 1996, 200, 186–205. [Google Scholar] [CrossRef]
- Arnaud, P.; Baydoun, S.; Fouvry, S. Modeling adhesive and abrasive wear phenomena in fretting interfaces: A multiphysics approach coupling friction energy, third body and contact oxygenation concepts. Tribol. Int. 2021, 161, 107077. [Google Scholar] [CrossRef]
- Ramírez, T.D.l.M.; Cruz, I.H.; Ruiz, M.A.D.; Perrusquia, N.L.; Bustos, D.G.; Martínez, M.F. Numerical model of ultra-high molecular weight polyethylene abrasive wear tests. Model. Numer. Simul. Mater. Sci. 2020, 10, 101001. [Google Scholar] [CrossRef]
- McColl, I.R.; Ding, J.; Leen, S.B. Finite element simulation and experimental validation of fretting wear. Wear 2004, 256, 1114–1127. [Google Scholar] [CrossRef]
- Fouvry, S.; Kapsa, P.; Vincent, L. An elastic–plastic shakedown analysis of fretting wear. Wear 2001, 247, 41–54. [Google Scholar] [CrossRef]
- Fouvry, S.; Liskiewicz, T.; Kapsa, P.; Hannel, S.; Sauger, E. An energy description of wear mechanisms and its applications to oscillating sliding contacts. Wear 2003, 255, 287–298. [Google Scholar] [CrossRef]
- Shen, F.; Ke, L.-L.; Zhou, K. A debris layer evolution-based model for predicting both fretting wear and fretting fatigue lifetime. Int. J. Fatigue 2021, 142, 105928. [Google Scholar] [CrossRef]
- Wang, C.; Li, C.; Ling, Y.; Wahab, M.A. Investigation on fretting fatigue crack initiation in heterogenous materials using a hybrid of multiscale homogenization and direct numerical simulation. Tribol. Int. 2022, 169, 107470. [Google Scholar] [CrossRef]
- Kapoor, A. Re-evaluation of the life of ductile metals by cyclic plastic strain. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 201–219. [Google Scholar] [CrossRef]
- Kapoor, A.; Franklin, F. Tribological layers and the wear of ductile materials. Wear 2000, 245, 204–215. [Google Scholar] [CrossRef]
- Kapoor, A. Wear by plastic ratchetting. Wear 1997, 212, 119–130. [Google Scholar] [CrossRef]
- Yue, T.; Wahab, M.A. Finite element analysis of stress singularity in partial slip and gross sliding regimes in fretting wear. Wear 2014, 321, 53–63. [Google Scholar] [CrossRef]
- Ahmadi, A.; Sadeghi, F. A three-dimensional finite element damage mechanics model to simulate fretting wear of hertzian line and circular contacts in partial slip regime. J. Tribol. 2022, 144, 4051814. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Ding, J.; Leen, S.B.; McColl, I.R. The effect of slip regime on fretting wear-induced stress evolution. Int. J. Fatigue 2004, 26, 521–531. [Google Scholar] [CrossRef]



| Material | DD6 (Blade) | GH4720Li (Bladed Disk) |
|---|---|---|
| Density (kg/m3) | 8780 | 8140 |
| Young’s modulus (GPa) | 131 | 225 |
| Poisson’s ratio | 0.344 | 0.345 |
| Centrifugal Load/N | Aerodynamic Load/N | Fretting Direction | Maximum Wear Depth of First Pair Tooth/µm | Maximum Wear Depth of Second Pair Tooth/µm | Wear Volume/mm3 |
|---|---|---|---|---|---|
| 50,000 | 0 | X | 57.22 | 47.89 | 24.89 |
| 50,000 | 0 | Y | 30.85 | 18.23 | 7.55 |
| 50,000 | 0 | Z | 24.36 | 18.18 | 8.43 |
| 50,000 | 2000 | X | 75.93 (Tooth 1)/ 70.53 (Tooth 2) | 78.97 (Tooth 3)/ 60.44 (Tooth 4) | 39.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhao, G.; Yuan, Y.; Zhang, H.; Wu, Y. Finite Element Simulation and Fretting Wear Prediction of a Tenon Connection Structure. Lubricants 2023, 11, 421. https://doi.org/10.3390/lubricants11100421
Zhang Z, Zhao G, Yuan Y, Zhang H, Wu Y. Finite Element Simulation and Fretting Wear Prediction of a Tenon Connection Structure. Lubricants. 2023; 11(10):421. https://doi.org/10.3390/lubricants11100421
Chicago/Turabian StyleZhang, Zexin, Guang Zhao, Yunbo Yuan, Hongxiao Zhang, and Yuping Wu. 2023. "Finite Element Simulation and Fretting Wear Prediction of a Tenon Connection Structure" Lubricants 11, no. 10: 421. https://doi.org/10.3390/lubricants11100421
APA StyleZhang, Z., Zhao, G., Yuan, Y., Zhang, H., & Wu, Y. (2023). Finite Element Simulation and Fretting Wear Prediction of a Tenon Connection Structure. Lubricants, 11(10), 421. https://doi.org/10.3390/lubricants11100421




