Mathematical Analysis of Transverse Wall-Shearing Motion via Cross Flow of Nanofluid
Abstract
:1. Introduction
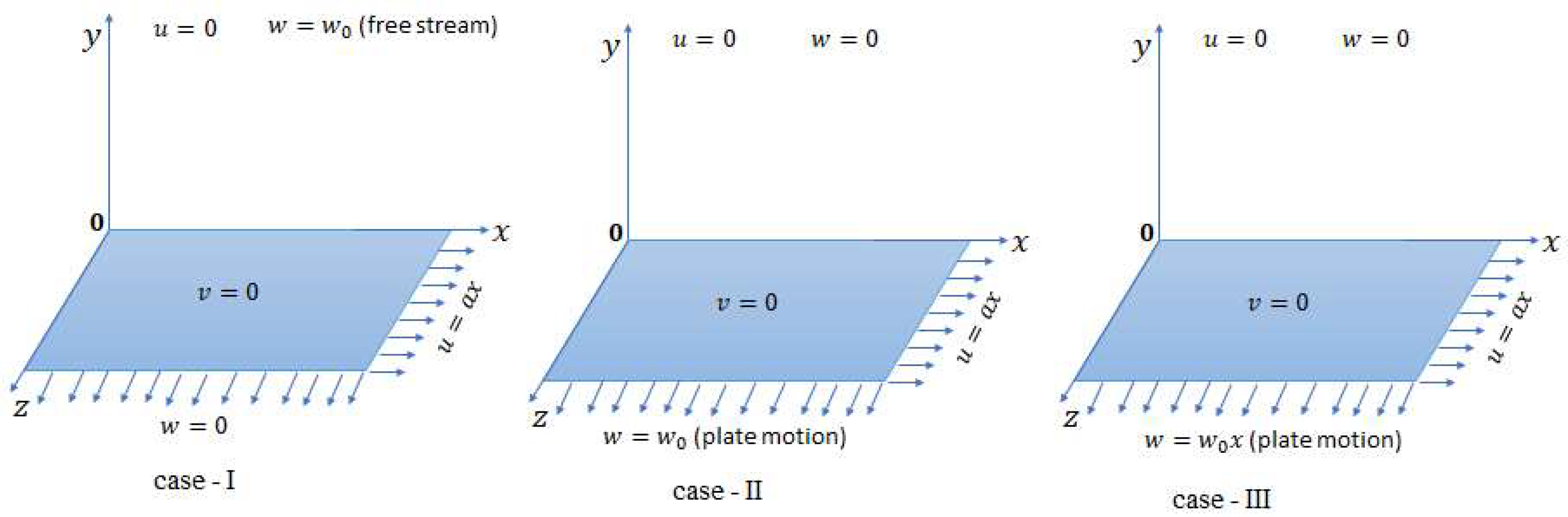
- Cross flow in the presence of a uniform free stream;
- Cross flow in the presence of a transverse moving surface;
- Cross flow in the presence of a transverse surface shearing movement.
2. Theoretical Development
2.1. Nonlinear Stretching Surfaces
2.2. Uniform Free Stream and Crosswise Plate Motion
2.3. Exceptional Cases for
2.4. Association between Two Solutions
3. Transverse Wall Shearing Motion
3.1. For Case
3.2. For Case
4. Heat Transfer
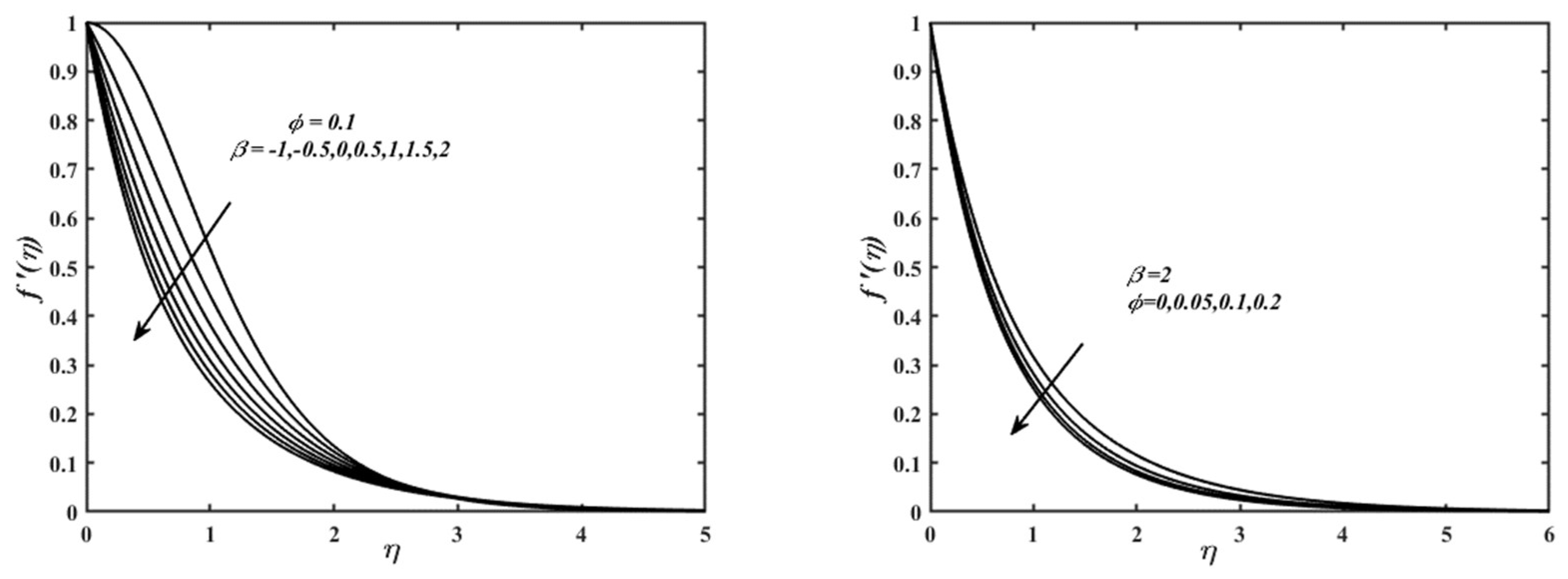
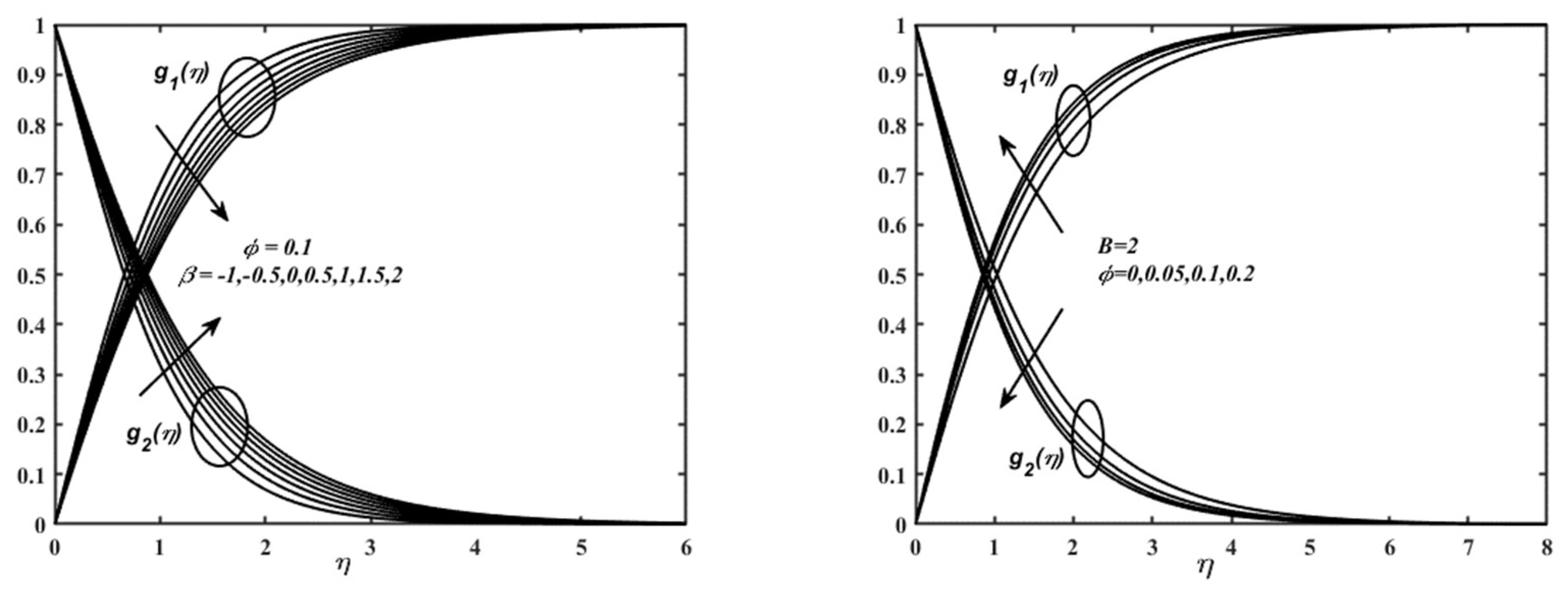
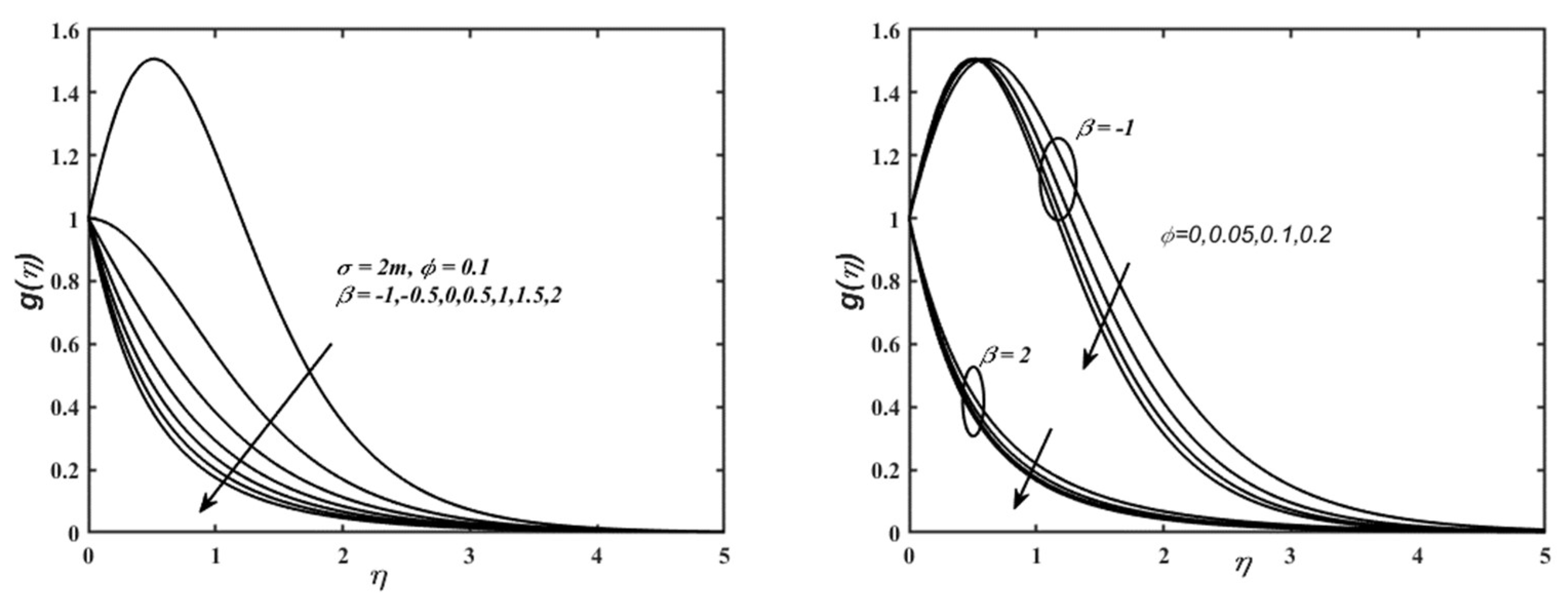
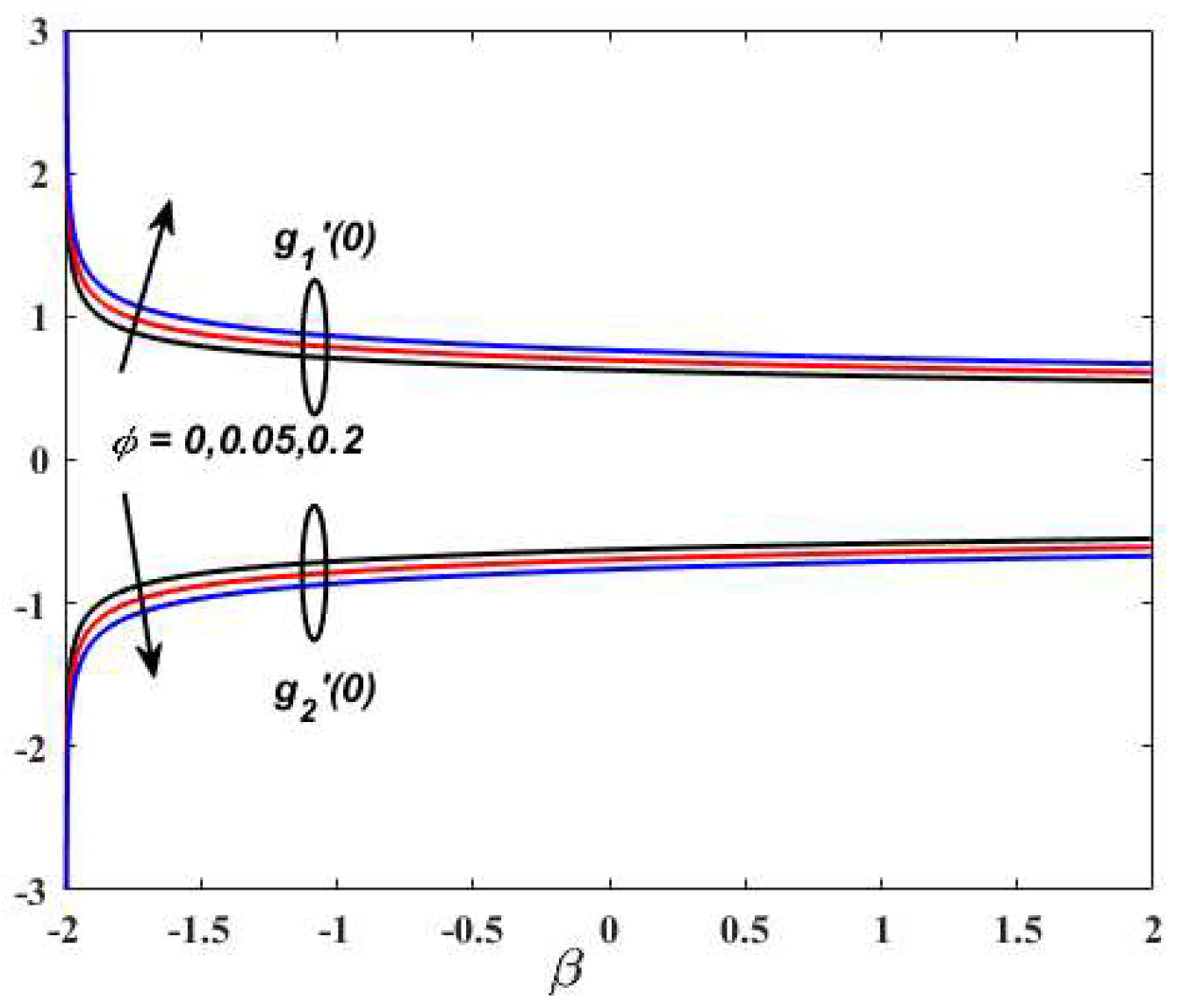
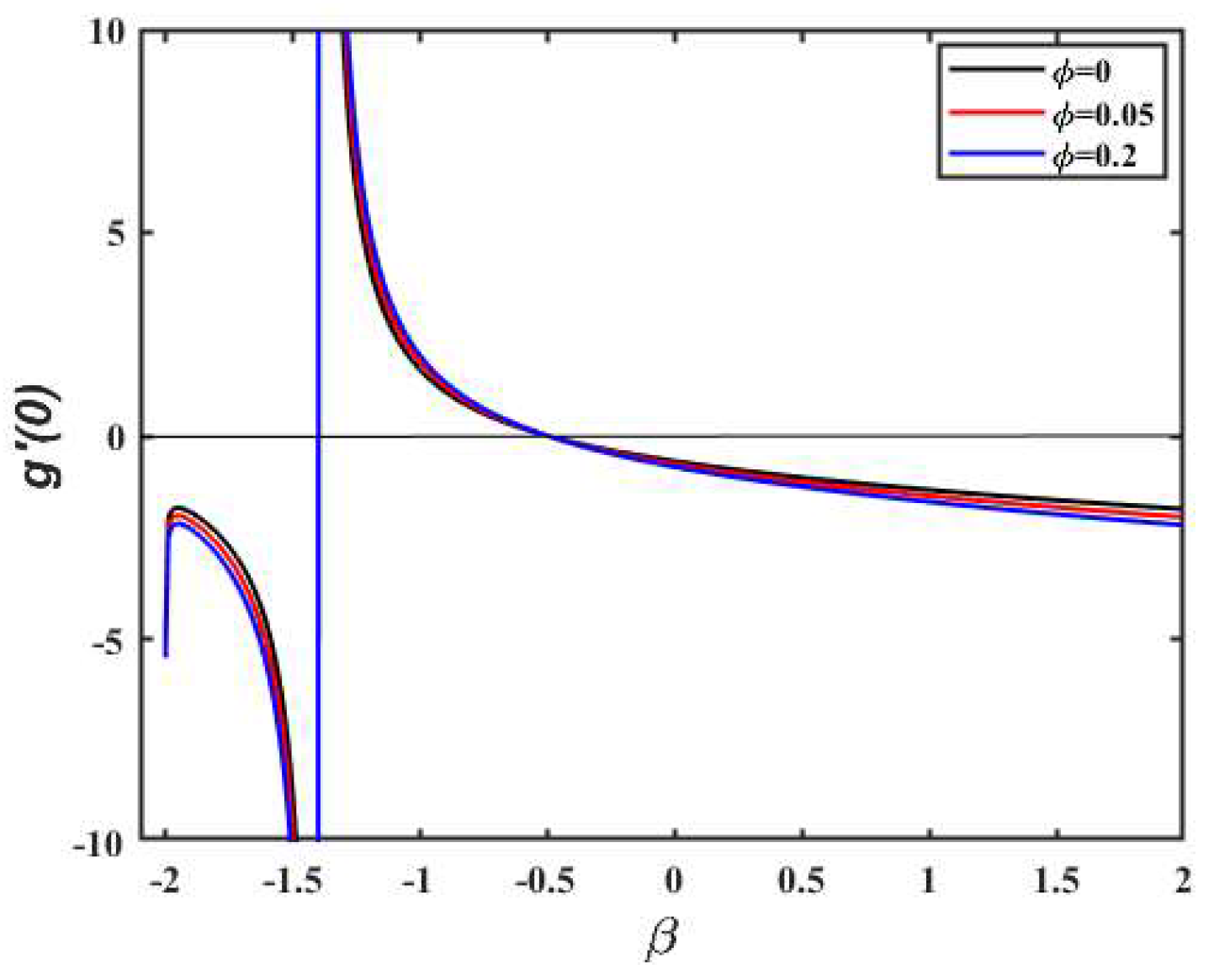
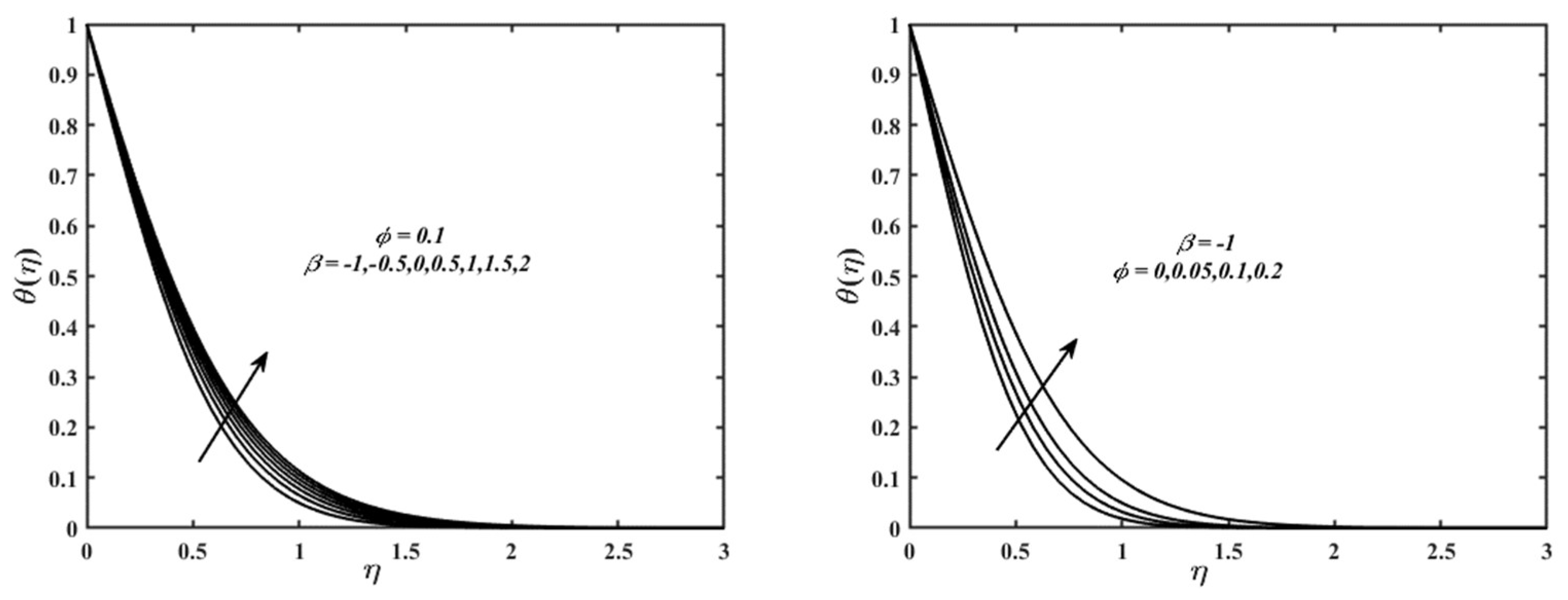
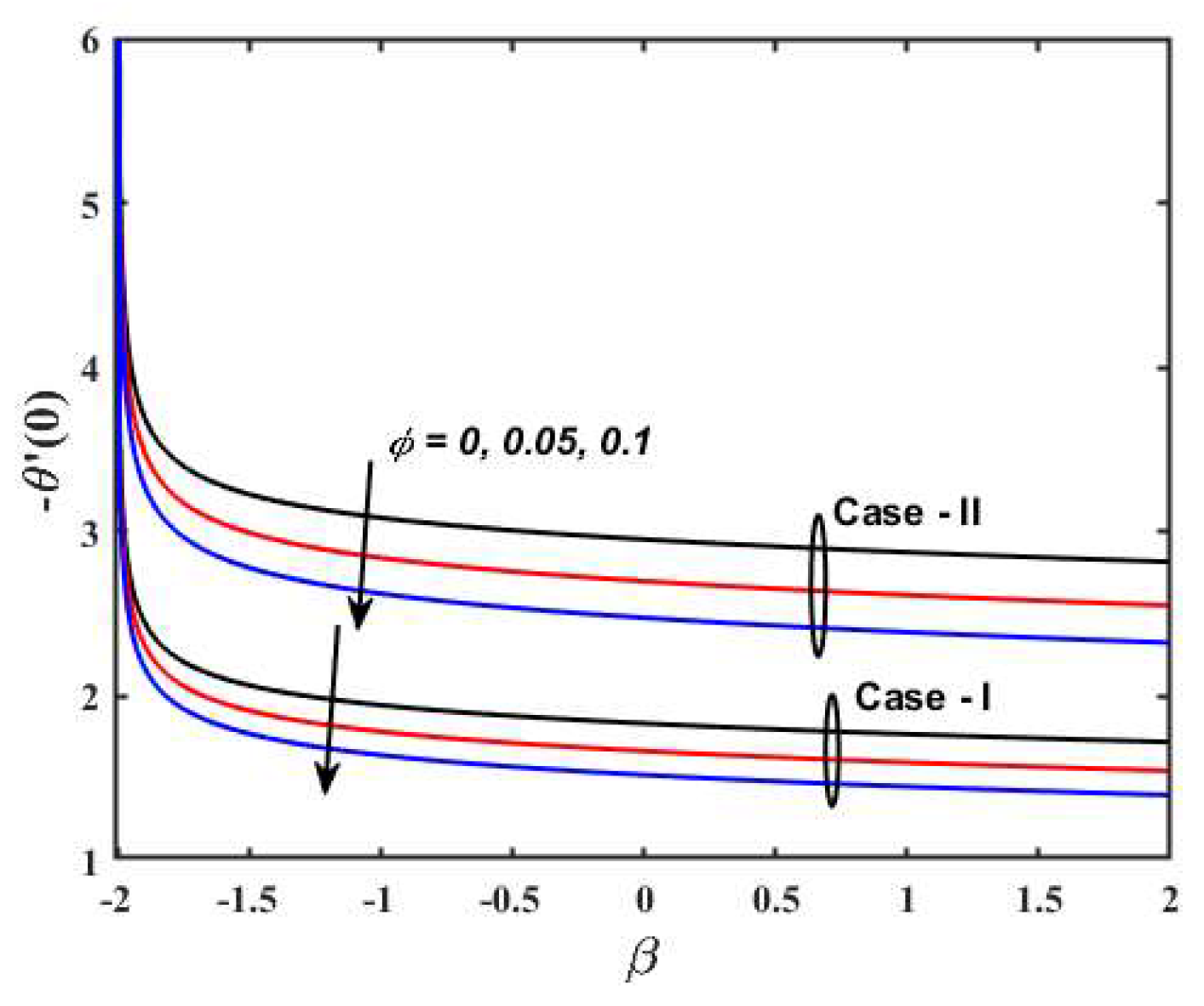
5. Result and Discussions
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Meaning and Dimension | Dimensionless Symbols |
| Cartesian coordinates | ||
| Velocity components | ||
| Temperature profile | ||
| Specific heat capacity | ||
| Greek symbols | ||
| Dynamic viscosity | ||
| Kinematic viscosity | ||
| Density | ||
| Nonlinear stretching parameter | ||
| Thermal conductivity | ||
| Nanoparticle volume fraction | ||
| Thermal diffusivity | ||
| Subscripts | ||
| Fluid | ||
| Solid fraction | ||
| Nanofluid |
References
- Blasius, H. Grenzschichten in Flüssigkeiten mit Kleiner Reibung; Druck von BG Teubner: Berlin, Germany, 1907. [Google Scholar]
- Prandtl, L. Über Flussigkeitsbewegung bei sehr kleiner Reibung. In Verhandl. III, Internat. Math.-Kong; Teubner: Heidelberg, Germany, 1904; pp. 484–491. [Google Scholar]
- Prandtl, L. On Boundary Layers in Three-Dimensional Flow. Rep. Trans. 1946, 64, 1–12. [Google Scholar]
- Vvedenskaya, N.D. Three-dimensional laminar boundary layer on a blunt body. Fluid Dyn. 1966, 1, 25–28. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. A Mathematical Study for Three-Dimensional Boundary Layer Flow of Jeffrey Nanofluid. Z. Nat. 2015, 70, 225–233. [Google Scholar] [CrossRef]
- Kumar, K.G.; Haq, R.U.; Rudraswamy, N.; Gireesha, B. Effects of mass transfer on MHD three dimensional flow of a Prandtl liquid over a flat plate in the presence of chemical reaction. Results Phys. 2017, 7, 3465–3471. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Three-dimensional flow of Prandtl fluid with Cattaneo-Christov double diffusion. Results Phys. 2018, 9, 290–296. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. Unsteady three-dimensional MHD-boundary-layer flow due to the impulsive motion of a stretching surface. Acta Mech. 2001, 146, 59–71. [Google Scholar] [CrossRef]
- Affes, H.; Xiao, Z.; Conlisk, A.T. The boundary-layer flow due to a vortex approaching a cylinder. J. Fluid Mech. 1994, 275, 33–57. [Google Scholar] [CrossRef]
- Ahmad, K.; Nazar, R.; Ishak, A.; Pop, I. Unsteady three-dimensional boundary layer flow due to a stretching surface in a micropolar fluid. Int. J. Numer. Methods Fluids 2011, 68, 1561–1573. [Google Scholar] [CrossRef]
- Weidman, P.D. New solutions for laminar boundary layers with cross flow. Z. Angew. Math. Und Phys. ZAMP 1997, 48, 341–356. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Khan, U.; Zaib, A.; Shah, S.H.A.M.; Marin, M. Numerical and Computer Simulations of Cross-Flow in the Streamwise Direction through a Moving Surface Comprising the Significant Impacts of Viscous Dissipation and Magnetic Fields: Stability Analysis and Dual Solutions. Math. Probl. Eng. 2020, 2020, 8542396. [Google Scholar] [CrossRef]
- Dauenhauer, E.C.; Majdalani, J. Exact self-similarity solution of the Navier–Stokes equations for a porous channel with orthogonally moving walls. Phys. Fluids 2003, 15, 1485–1495. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Jafarimoghaddam, A.; Pop, I. Cross flow and heat transfer past a permeable stretching/shrinking sheet in a hybrid nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 1295–1319. [Google Scholar] [CrossRef]
- Weidman, P. Further solutions for laminar boundary layers with cross flows driven by boundary motion. Acta Mech. 2017, 228, 1979–1991. [Google Scholar] [CrossRef]
- Rashidi, S.; Dehghan, M.; Ellahi, R.; Riaz, M.; Jamal-Abad, M. Study of stream wise transverse magnetic fluid flow with heat transfer around an obstacle embedded in a porous medium. J. Magn. Magn. Mater. 2015, 378, 128–137. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Pop, I. Heat transfer for boundary layers with cross flow. Chin. Phys. B 2014, 23, 024701. [Google Scholar] [CrossRef]
- Zhong, L.; Zhou, C.; Chen, S. Effects of approaching main flow boundary layer on flow and cooling performance of an inclined jet in cross flow. Int. J. Heat Mass Transf. 2016, 103, 572–581. [Google Scholar] [CrossRef]
- Yufeng, H.; Shaoxian, M.; Caihong, S. Numerical study on cross-flow transition in three-dimensional hypersonic boundary layers. Acta Aerodyn. Sin. 2019, 37, 522–529. [Google Scholar]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Und Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Makinde, O.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Slip effects on MHD boundary layer flow over an exponentially stretching sheet with suction/blowing and thermal radiation. Ain Shams Eng. J. 2013, 4, 485–491. [Google Scholar] [CrossRef]
- Mahmud, K.; Rana, S.; Al-Zubaidi, A.; Mehmood, R.; Saleem, S. Interaction of Lorentz force with cross swimming microbes in couple stress nano fluid past a porous Riga plate. Int. Commun. Heat Mass Transf. 2022, 138, 106347. [Google Scholar] [CrossRef]
- Tabassum, R.; Al-Zubaidi, A.; Rana, S.; Mehmood, R.; Saleem, S. Slanting transport of hybrid (MWCNTs-SWCNTs/H2O) nanofluid upon a Riga plate with temperature dependent viscosity and thermal jump condition. Int. Commun. Heat Mass Transf. 2022, 135, 106165. [Google Scholar] [CrossRef]
- Mahmud, K.; Mehmood, R.; Rana, S.; Al-Zubaidi, A. Flow of magnetic shear thinning nano fluid under zero mass flux and hall current. J. Mol. Liq. 2022, 352, 118732. [Google Scholar] [CrossRef]
- Rana, S.; Mehmood, R.; Muhammad, T. On homogeneous-heterogeneous reactions in oblique stagnation-point flow of Jeffrey fluid involving Cattaneo-Christov heat flux. Therm. Sci. 2021, 25, 165–172. [Google Scholar] [CrossRef]
- Rana, S.; Mehmood, R.; Bhatti, M.M.; Hassan, M. Swimming of motile gyrotactic microorganisms and suspension of nanoparticles in a rheological Jeffery fluid with Newtonian heating along elastic surface. J. Cent. South Univ. 2021, 28, 3279–3296. [Google Scholar] [CrossRef]
- Mehmood, R.; Khan, S.; Maraj, E.N.; Ijaz, S.; Rana, S. Heat transport mechanism via ion-slip and Hall current in viscoplastic flow along a porous elastic sheet. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2021, 236, 907–914. [Google Scholar] [CrossRef]
- Mehmood, R.; Rana, S.; Maraj, E.N. Transverse Transport of Polymeric Nanofluid under Pure Internal Heating: Keller Box Algorithm. Commun. Theor. Phys. 2018, 70, 106. [Google Scholar] [CrossRef]
- Navier, C. Mémoire sur les lois du mouvement des fluides. Mémoires L’académie R. Sci. L’institut Fr. 1823, 6, 389–440. [Google Scholar]
- Martin, M.J.; Boyd, I.D. Blasius boundary layer solution with slip flow conditions. AIP Conf. Proc. 2001, 585, 518–523. [Google Scholar]
- Rao, I.J.; Rajagopal, K.R. The effect of the slip boundary condition on the flow of fluids in a channel. Acta Mech. 1999, 135, 113–126. [Google Scholar] [CrossRef]
- Ellahi, R. Effects of the slip boundary condition on non-Newtonian flows in a channel. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1377–1384. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.; Ayub, M. On non-linear flows with slip boundary condition. Z. Angew. Math. Und Phys. ZAMP 2005, 56, 1012–1029. [Google Scholar] [CrossRef]
- Nandeppanavar, M.M.; Vajravelu, K.; Abel, M.S.; Siddalingappa, M. Second order slip flow and heat transfer over a stretching sheet with non-linear Navier boundary condition. Int. J. Therm. Sci. 2012, 58, 143–150. [Google Scholar] [CrossRef]
- Oyelakin, I.S.; Mondal, S.; Sibanda, P. Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alex. Eng. J. 2016, 55, 1025–1035. [Google Scholar] [CrossRef]
- Ariel, P.D.; Hayat, T.; Asghar, S. The flow of an elastico-viscous fluid past a stretching sheet with partial slip. Acta Mech. 2006, 187, 29–35. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Saffarian, M.R.; Pourrajab, R.; Ghalambaz, M. Entropy analysis for nanofluid flow over a stretching sheet in the presence of heat generation/absorption and partial slip. J. Mech. Sci. Technol. 2013, 27, 927–937. [Google Scholar] [CrossRef]
- Gupta, P.; Gupta, A. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Vajravelu, K. Viscous flow over a nonlinearly stretching sheet. Appl. Math. Comput. 2001, 124, 281–288. [Google Scholar] [CrossRef]
- Cortell, R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput. 2007, 184, 864–873. [Google Scholar] [CrossRef]
- Das, K. Nanofluid flow over a non-linear permeable stretching sheet with partial slip. J. Egypt. Math. Soc. 2015, 23, 451–456. [Google Scholar] [CrossRef]
- Seth, G.; Mishra, M. Analysis of transient flow of MHD nanofluid past a non-linear stretching sheet considering Navier’s slip boundary condition. Adv. Powder Technol. 2017, 28, 375–384. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Analysis of boundary layer flow over a porous nonlinearly stretching sheet with partial slip at the boundary. Alex. Eng. J. 2013, 52, 563–569. [Google Scholar] [CrossRef]
- Choi, S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.(ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Kang, H.U.; Kim, S.H.; Oh, J.M. Estimation of Thermal Conductivity of Nanofluid Using Experimental Effective Particle Volume. Exp. Heat Transf. 2006, 19, 181–191. [Google Scholar] [CrossRef]
- Khan, A.U.; Saleem, S.; Nadeem, S.; Alderremy, A. Analysis of unsteady non-axisymmetric Homann stagnation point flow of nanofluid and possible existence of multiple solutions. Phys. A Stat. Mech. Its Appl. 2019, 554, 123920. [Google Scholar] [CrossRef]
- Khan, A.; Hussain, S.; Nadeem, S. Existence and stability of heat and fluid flow in the presence of nanoparticles along a curved surface by mean of dual nature solution. Appl. Math. Comput. 2019, 353, 66–81. [Google Scholar] [CrossRef]
- Duraihem, F.Z.; Akbar, N.S.; Saleem, S. Mixed convective eyring-powell ferro magnetic nanofluid flow suspension towards a stretching surface with buoyancy effects through numerical analysis. Front. Mater. 2023, 10, 1109755. [Google Scholar] [CrossRef]
- Nadeem, S.; Khan, M.R.; Khan, A.U. MHD oblique stagnation point flow of nanofluid over an oscillatory stretching/shrinking sheet: Existence of dual solutions. Phys. Scr. 2019, 94, 075204. [Google Scholar] [CrossRef]
- Ali, A.; Khan, H.S.; Saleem, S.; Hussan, M. EMHD nanofluid fluid flow with radiation and variable heat flux effects along a Slandering stretching sheet. Nanomaterials 2022, 12, 3872. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S.; Khan, A.U. Rotating flow of Ag-CuO/H 2 O hybrid nanofluid with radiation and partial slip boundary effects. Eur. Phys. J. E 2018, 41, 1–9. [Google Scholar] [CrossRef]
- Sivaraj, R.; Animasaun, I.L.; Olabiyi, A.S.; Saleem, S.; Sandeep, N. Gyrotactic microorganisms and thermoelectric effects on the dynamics of 29nmCuO-water nanofluid over an upper horizontal surface of paraboloid of revolution. Multidiscip. Model. Mater. Struct. 2018, 14, 695–6721. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Saleem, S.; Wakif, A.; AlQarni, M.M. MHD Prandtl fluid flow past an isothermal sphere with slip effects: Non-Darcy porous medium. Case Stud. Therm. Eng. 2019, 14, 100447. [Google Scholar] [CrossRef]
- Nawaz, M.; Nazir, U.; Saleem, S.; Alharbi, S.O. An enhancement of thermal performance of ethylene glycol by nano and hybrid nanoparticles. Phys. A Stat. Mech. Its Appl. 2020, 551, 124527. [Google Scholar] [CrossRef]
- Weidman, P. Similarity solutions for power-law and exponentially stretching plate motion with cross flow. Int. J. Non-Linear Mech. 2017, 89, 127–131. [Google Scholar] [CrossRef]
- Banks, W. Similarity solutions of the boundary-layer equations for a stretching wall. J. Mécanique Théorique Appliquée 1983, 2, 375–392. [Google Scholar]
- Dinarvand, S.; Hosseini, R.; Damangir, E.; Pop, I. Series solutions for steady three-dimensional stagnation point flow of a nanofluid past a circular cylinder with sinusoidal radius variation. Meccanica 2012, 48, 643–652. [Google Scholar] [CrossRef]

| Thermophysical Properties | Fluid Phase (Water) | Copper |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duraihem, F.Z.; Ullah Khan, A.; Saleem, S.; Shawana. Mathematical Analysis of Transverse Wall-Shearing Motion via Cross Flow of Nanofluid. Lubricants 2023, 11, 138. https://doi.org/10.3390/lubricants11030138
Duraihem FZ, Ullah Khan A, Saleem S, Shawana. Mathematical Analysis of Transverse Wall-Shearing Motion via Cross Flow of Nanofluid. Lubricants. 2023; 11(3):138. https://doi.org/10.3390/lubricants11030138
Chicago/Turabian StyleDuraihem, Faisal Z., Arif Ullah Khan, Salman Saleem, and Shawana. 2023. "Mathematical Analysis of Transverse Wall-Shearing Motion via Cross Flow of Nanofluid" Lubricants 11, no. 3: 138. https://doi.org/10.3390/lubricants11030138
APA StyleDuraihem, F. Z., Ullah Khan, A., Saleem, S., & Shawana. (2023). Mathematical Analysis of Transverse Wall-Shearing Motion via Cross Flow of Nanofluid. Lubricants, 11(3), 138. https://doi.org/10.3390/lubricants11030138




