Impact of Ad Hoc Post-Processing Parameters on the Lubricant Viscosity Calculated with Equilibrium Molecular Dynamics Simulations
Abstract
1. Introduction
1.1. State-of-the-Art
1.2. Goal of the Paper
- To investigate the sensitivity of the viscosity to user-dependent choices and decisions in the TDM.
- To demonstrate some case studies from equilibrium MD simulations of the lubricant 2,2,4-trimethylhexane performed at different temperatures and pressures.
- To emphasize the importance of the meticulous post-simulation data analysis.
- To show how ad hoc parameters can influence the viscosity.
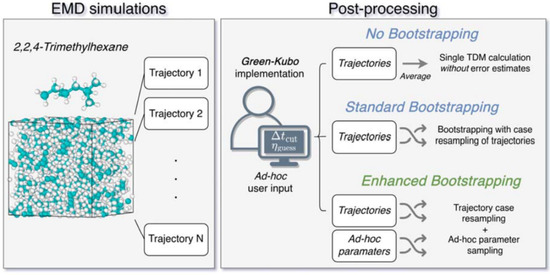
2. Materials and Methods
2.1. EMD Protocol
2.2. The Determination of Shear Viscosity from EMD Simulations
- In principle, the first decisions in the TDM are the simulation time and the number of independent MD production runs, which are difficult to determine a priori. The production runs should be sufficiently longer than the inherent correlation times in the stress tensor fluctuations, which can only be determined after the simulation. If the results are not statistically converged with a given simulation length, one should extend the trajectories or generate more until the results are satisfactory (or all resources are exhausted).
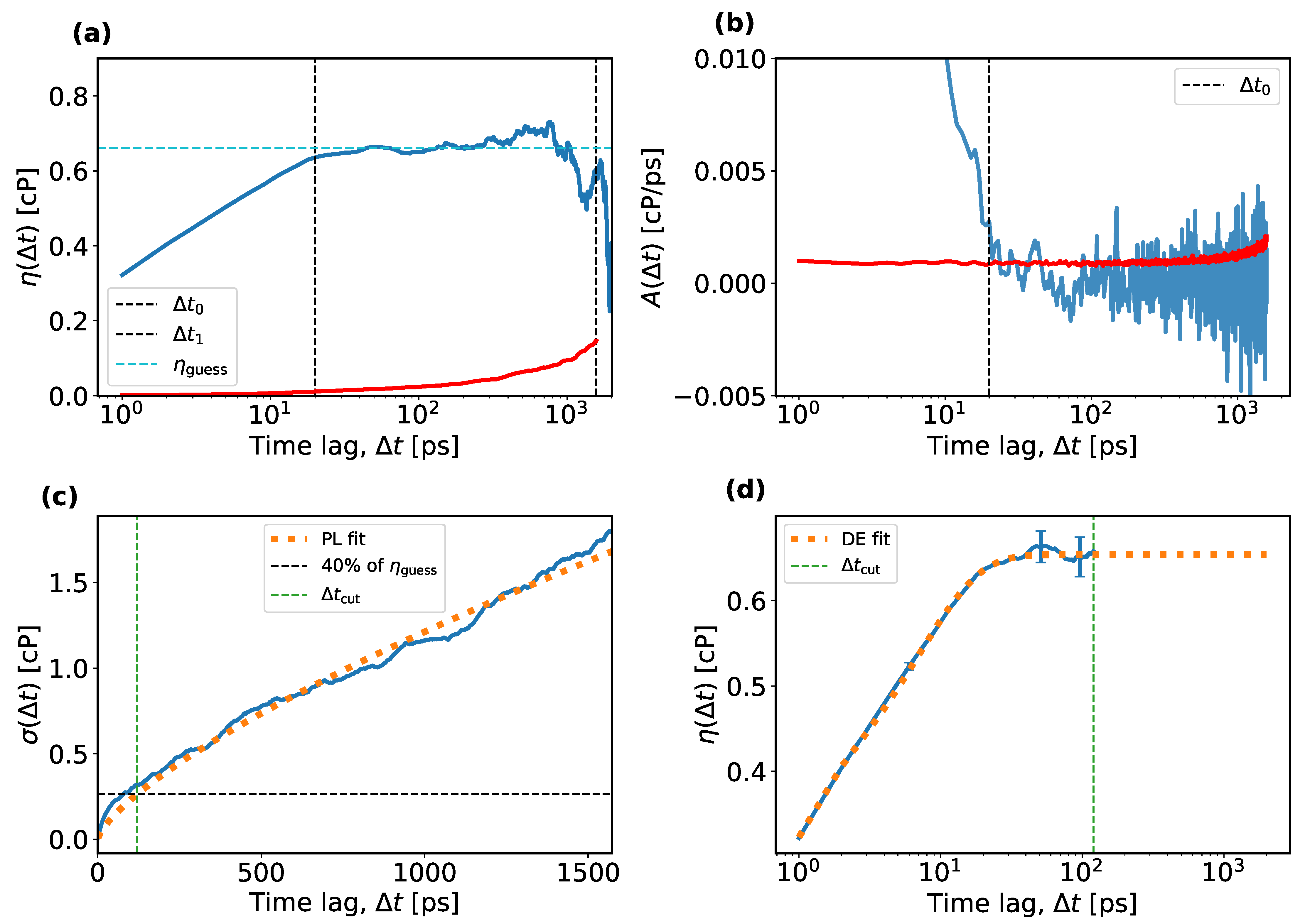
- The average running integral, ; the average autocorrelation function, ; and the standard deviation, , are calculated over N independent EMD trajectories. Typical examples are shown as solid blue curves in Figure 2a–c, respectively. Figure 2a,b also contain the standard error on the plotted average as a function of , plotted as solid red curves.
- For the TDM, one must identify a plateau-like region in and determine a reasonable guess of the viscosity in that region. Practical instructions for making this guess were not described explicitly in previous works, so it is assumed here that this guess was made by a visual inspection of a plot such as the one shown in Figure 2a. However, when making such a plot, one must decide on the range of the time lags on the horizontal axis, which entails more empirical choices. Here, an algorithmic approach is introduced to guess the viscosity, which mimics the manual guess of the TDM as closely as possible. The algorithm first selects an upper and a lower bound for the time lags to identify the plateau region and then estimates the viscosity within that region. To set an upper bound of the plateau region, the standard error of the mean is compared to the average running integral and plotted in red and blue in Figure 2a, respectively. At overly large time lags, this error increases and makes it impossible to identify any plateau. Therefore, the upper bound for the time lag, , is fixed in this work as the first point at which the standard error on the mean becomes significant compared to the average running integral, i.e., , for which is chosen. Other choices for could be considered, which is relevant for the uncertainty analysis explained later. It could be argued that any could be used instead. (The uncertainty analysis reveals that the predicted viscosity is nearly insensitive to .) The lower bound, , is set as the first time lag when the average auto-correlation function approaches zero by less than times the standard deviation of the mean over all auto-correlation functions. Both functions are shown in Figure 2b in blue and red, respectively. This corresponds to the onset of the tail of the auto-correlation function, , after which the running integral, , starts to level off and exhibit a plateau. Other values of could be considered, e.g., from the interval . Higher values of are not recommended because these would force into the interval where the auto-correlation function has not decayed to zero yet. Lower values of make more susceptible to noise in the auto-correlation function. Instead of visually estimating the viscosity in the interval , the quantile (the median) of all values in this region is used as a guess of the viscosity, . Other values in the interquartile range (IQR, ) could also be considered. The use of quantiles makes insensitive to outliers in the plateau region.
- The next step in the TDM is to fit the power law from Equation (6). One might expect the interval of the plateau region, , be suitable for estimating a and b. In some cases, however, this leads to strong parameter correlations between a and b. Instead, is fitted in the interval , which makes b less sensitive to statistical uncertainties. The time interval was not mentioned in the original TDM paper and may be specific to this work.
- Finally, the double-exponential model from Equation (4) is fitted with the curve_fit function from SciPy [59], to in the interval with a weight of , where b is taken from the power-law fit. The final viscosity is the long-term limit of the double exponential fit. See the dotted orange curve in Figure 2d. Note that other works exclude small values from the fit because the double-exponential model is not suitable for small time lags. Since the time integral of the stress tensor is stored only every picosecond, transient effects at small time lags are de facto excluded from the fits.A nonlinear regression may have multiple solutions, i.e., local minima of the least-squares cost function. To help the optimization algorithm, an initial guess can be specified, for which , and have been used. By making the values different, the symmetry of the model is effectively broken and this makes the optimizer less likely to get stuck at a saddle point. To further facilitate the regression, the parameters and are bounded to the interval . If one of the optimal parameters reaches its upper bound and the corresponding is non-zero, the solution is marked as invalid and is excluded from the remaining analysis.
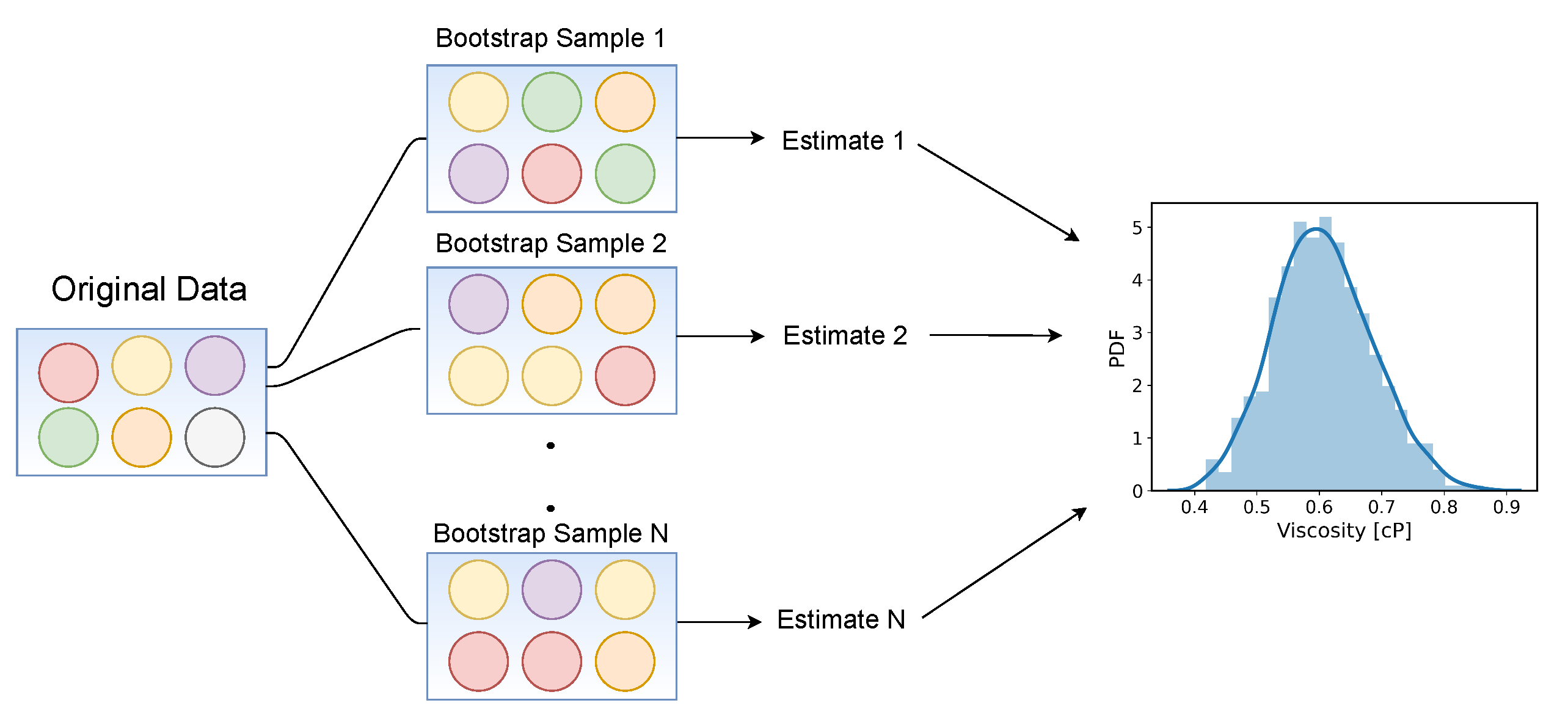
2.3. Uncertainty Quantification
3. Results and Discussion
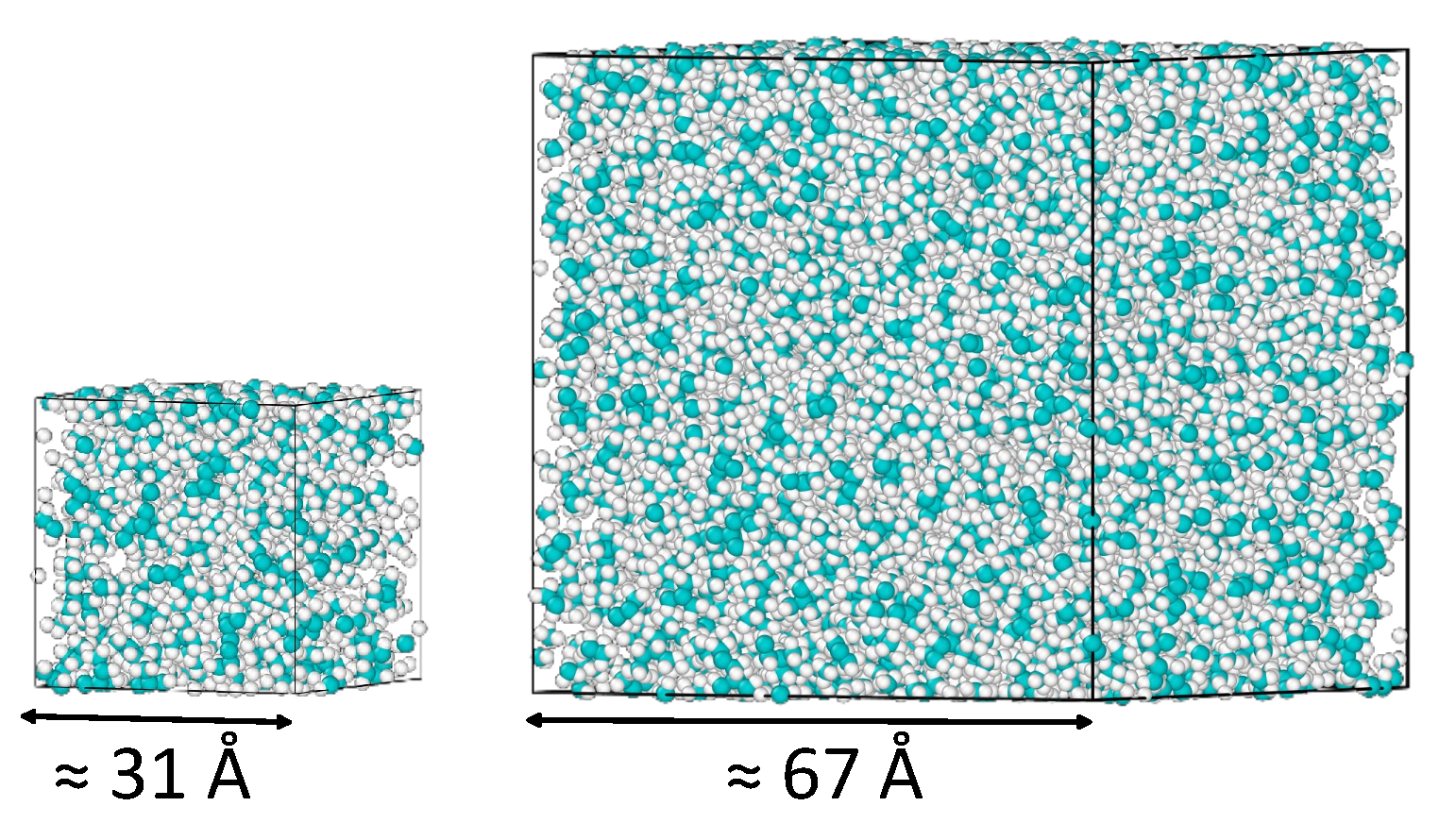
3.1. The Determination of the Viscosity of 2,2,4-Trimethylhexane at Ambient Conditions System Size Effects
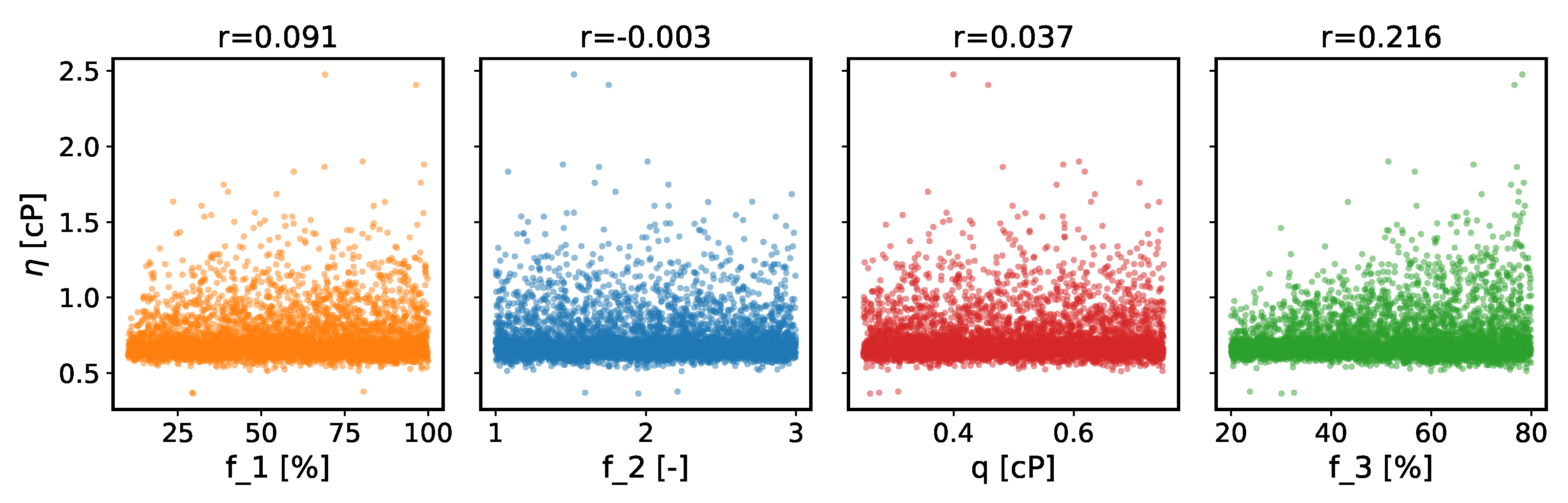
3.2. Dependence of the Viscosity on Ad Hoc Parameters
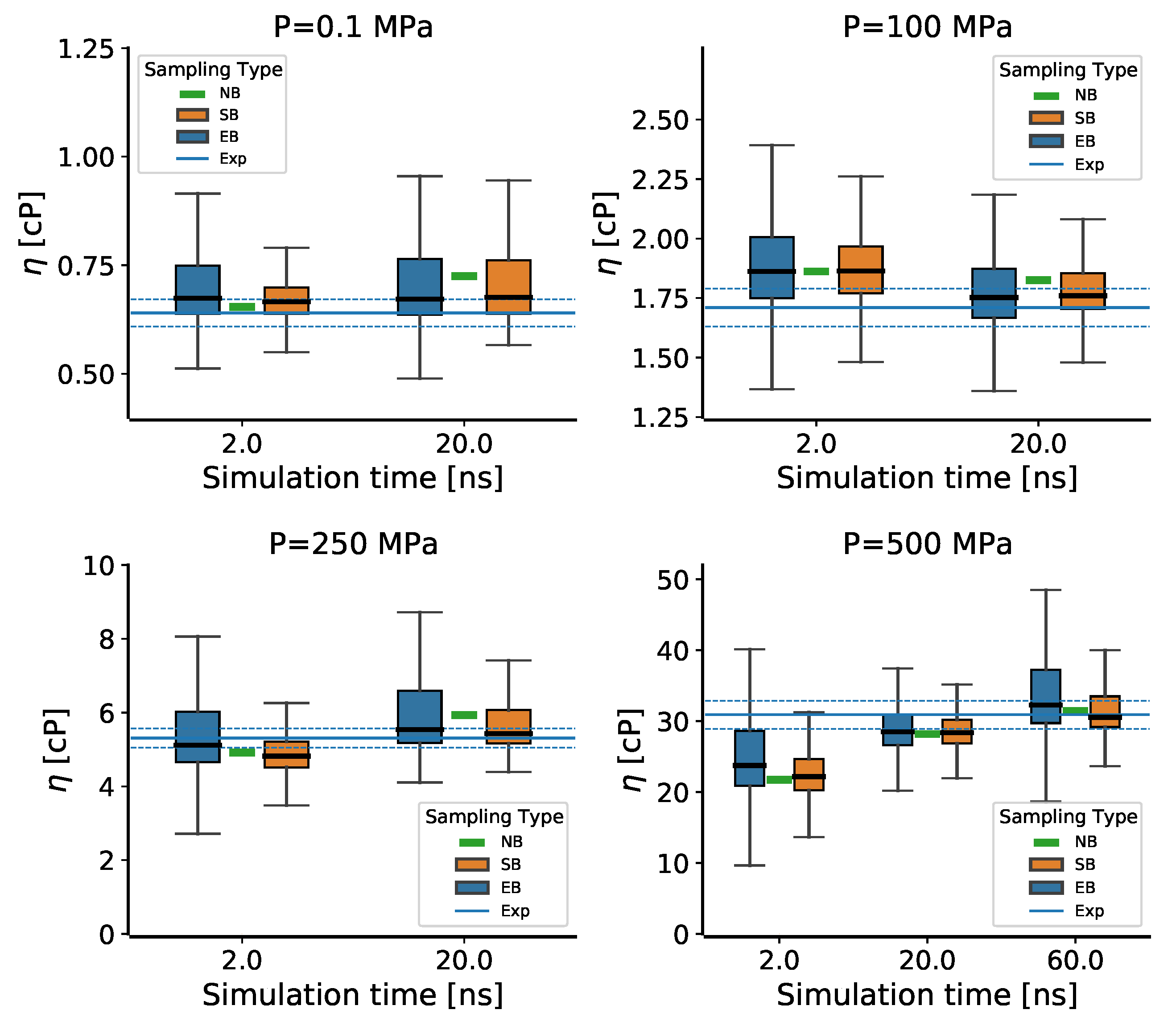
3.3. Simulation Length
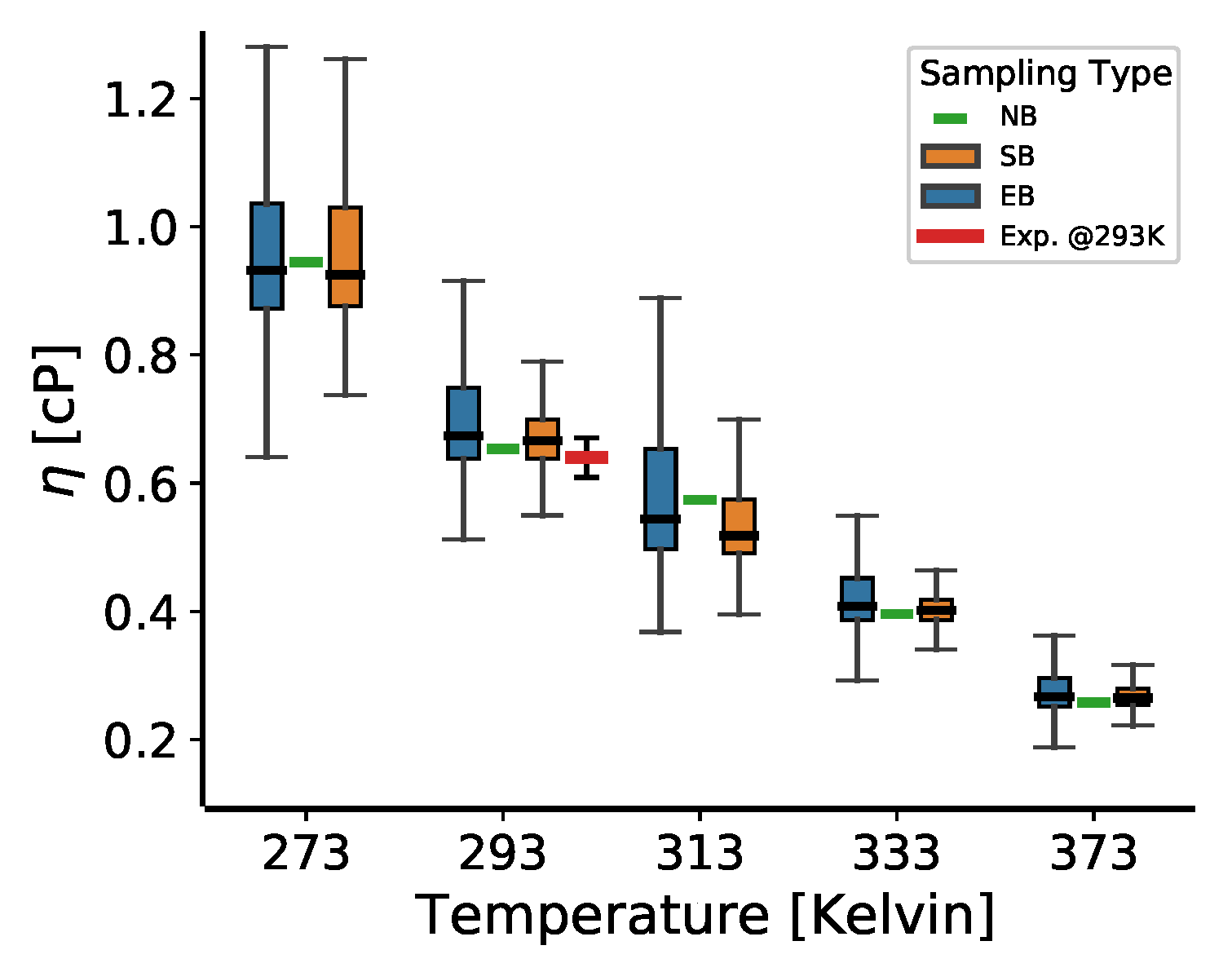
3.4. The Temperature Dependence of the Viscosity for 2,2,4-Trimethylhexane
3.5. The Pressure Dependence of the Viscosity for 2,2,4-Trimethylhexane
4. Conclusions
- An algorithmic alternative, introducing three new ad hoc parameters, was proposed to remove the subjective human guess of the viscosity from the TDM, for which three new ad hoc parameters had to be introduced. Through Monte Carlo error propagation with bootstrapping, it is shown that the new ad hoc parameters have no significant influence on the predicted viscosity.
- The proposed approach is not only convenient and robust, but it also eliminates the potentially obfuscating use of log scales, which can give the false impression that there is a stable plateau in .
- The viscosity predicted by the TDM depends on the ad hoc parameter , for which the original TDM paper recommends 40%. This is the percentage of the guessed viscosity used to estimate , up to which the double exponential is fitted. At ambient conditions, and the final have a correlation coefficient of 22%, which rises to 36% at 500 MPa. By consequence, an (un)fortunate choice of this percentage can lead to an (un)favourable comparison to the experiment. This dependence was not noticed previously, presumably because these only considered scans of one ad hoc parameter at a time, whereas in this work the enhanced bootstrapping method varied all such parameters together.
- The TDM, despite some of its limitations, still provides fairly good viscosity estimates in most cases, even without uncertainty quantification. However, when a systematic error is made due to an unfortunate choice of an ad hoc TDM parameter, only bootstrapping can clearly reveal this. Avoiding such errors becomes particularly challenging for lubricants under (T)EHL conditions, which are characterized by increased viscosity. To overcome this difficulty, it is suggested that the robustness of future improvements or alternatives to TDM should be thoroughly vetted with the enhanced bootstrapping method.
- Clear communication and meticulous analysis of trajectories and uncertainties are essential for viscosity calculations using EMD simulations.
- Future Scope
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| COMPASS | Condensed-Phase Optimized Molecular Potentials for Atomistic Simulation Studies |
| DE | Double Exponential |
| EB | Enhanced Bootstrapping |
| EMD | Equilibrium Molecular Dynamics |
| GK | Green–Kubo |
| IFPSC | International Fluid Properties Simulation Challange |
| LAMMPS | Large-scale Atomic/Molecular Massively Parallel Simulator |
| MAD | Median Absolute Deviation |
| MiPPE | Mie Potentials for Phase Equilibria |
| NB | No Bootstrapping |
| NEMD | Non-Equilibrium Molecular Dynamics |
| PL | Power law |
| SB | Standard Bootstrapping |
| TDM | Time Decomposition Method |
| TEHL | Thermo-Elasto Hydrodynamic Lubrication |
References
- Bair, S.; Martinie, L.; Vergne, P. Classical EHL Versus Quantitative EHL: A Perspective Part II—Super-Arrhenius Piezoviscosity, an Essential Component of Elastohydrodynamic Friction Missing from Classical EHL. Tribol. Lett. 2016, 63, 37. [Google Scholar] [CrossRef]
- Barus, C. Isothermals, isopiestics and isometrics relative to viscosity. Am. J. Sci. 1893, s3-45, 87–96. [Google Scholar] [CrossRef]
- Roelands, C.J.A.; Winer, W.O.; Wright, W.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. J. Lubr. Technol. 1971, 93, 209–210. [Google Scholar] [CrossRef]
- McEwen, E. The Effect of Variation of Viscosity with Pressure on the Load-Carrying Capacity of the Oil Film between Gear-Teeth. J. Inst. Petroleum 1952, 38, 646–672. [Google Scholar] [CrossRef]
- Paluch, M.; Dendzik, Z.; Rzoska, S. Scaling of high-pressure viscosity data in low-molecular-weight glass-forming liquids. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 60, 2979–2982. [Google Scholar] [CrossRef]
- Bair, S. Choosing pressure-viscosity relations. High Temp. High Press. 2015, 44, 415–428. [Google Scholar]
- Bair, S. Reference liquids for quantitative elastohydrodynamics: Selection and rheological characterization. Tribol. Lett. 2006, 22, 197–206. [Google Scholar] [CrossRef]
- Bair, S.; Yamaguchi, T.; Brouwer, L.; Schwarze, H.; Vergne, P.; Poll, G. Oscillatory and steady shear viscosity: The Cox–Merz rule, superposition, and application to EHL friction. Tribol. Int. 2014, 79, 126–131. [Google Scholar] [CrossRef]
- Bair, S. High Pressure Rheology for Quantitative Elastohydrodynamics; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Vergne, P.; Bair, S. Classical EHL versus quantitative EHL: A perspective Part i - Real viscosity-pressure dependence and the viscosity-pressure coefficient for predicting film thickness. Tribol. Lett. 2014, 54, 1–12. [Google Scholar] [CrossRef]
- Ewen, J.P.; Heyes, D.M.; Dini, D. Advances in nonequilibrium molecular dynamics simulations of lubricants and additives. Friction 2018, 6, 349–386. [Google Scholar] [CrossRef]
- Spikes, H.; Jie, Z. History, origins and prediction of elastohydrodynamic friction. Tribol. Lett. 2014, 56, 1–25. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Chen, T.; Smit, B.; Bell, A.T. Are pressure fluctuation-based equilibrium methods really worse than nonequilibrium methods for calculating viscosities? J. Chem. Phys. 2009, 131, 2005–2007. [Google Scholar] [CrossRef] [PubMed]
- Messerly, R.A.; Anderson, M.C.; Razavi, S.M.; Elliott, J.R. Improvements and limitations of Mie λ-6 potential for prediction of saturated and compressed liquid viscosity. Fluid Ph. Equilibria 2019, 483, 101–115. [Google Scholar] [CrossRef]
- Carlson, D.J.; Giles, N.F.; Wilding, W.V.; Knotts, T.A. Liquid viscosity oriented parameterization of the Mie potential for reliable predictions of normal alkanes and alkylbenzenes. Fluid Ph. Equilibria 2022, 561, 113522. [Google Scholar] [CrossRef]
- Ewen, J.P.; Spikes, H.A.; Dini, D. Contributions of Molecular Dynamics Simulations to Elastohydrodynamic Lubrication. Tribol. Lett. 2021, 69, 24. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef]
- Devereux, C.; Smith, J.S.; Huddleston, K.K.; Barros, K.; Zubatyuk, R.; Isayev, O.; Roitberg, A.E. Extending the Applicability of the ANI Deep Learning Molecular Potential to Sulfur and Halogens. J. Chem. Theory Comput. 2020, 16, 4192–4202. [Google Scholar] [CrossRef]
- Batzner, S.; Musaelian, A.; Sun, L.; Geiger, M.; Mailoa, J.P.; Kornbluth, M.; Molinari, N.; Smidt, T.E.; Kozinsky, B. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 2022, 13, 2453. [Google Scholar] [CrossRef] [PubMed]
- Maginn, E.J.; Messerly, R.A.; Carlson, D.J.; Roe, D.R.; Elliott, J.R. Best Practices for Computing Transport Properties 1. Self-Diffusivity and Viscosity from Equilibrium Molecular Dynamics [Article v1.0]. Living J. Comput. Mol. Sci. 2019, 1, 6324. [Google Scholar] [CrossRef]
- Green, M.S. Markoff Random Processes and the Statistical Mechanics of Time-Dependent Phenomena. II. Irreversible Processes in Fluids. J. Chem. Phys. 1954, 22, 398–413. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Helfand, E. Transport Coefficients from Dissipation in a Canonical Ensemble. Phys. Rev. 1960, 119, 1–9. [Google Scholar] [CrossRef]
- Kajita, S.; Kinjo, T.; Nishi, T. Autonomous molecular design by Monte-Carlo tree search and rapid evaluations using molecular dynamics simulations. Commun. Phys. 2020, 3, 77. [Google Scholar] [CrossRef]
- Zhang, Y.; Otani, A.; Maginn, E.J. Reliable Viscosity Calculation from Equilibrium Molecular Dynamics Simulations: A Time Decomposition Method. J. Chem. Theory Comput. 2015, 11, 3537–3546. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, G.; Nie, G. A molecular dynamics study of bulk and shear viscosity of liquid iron using embedded-atom potential. Phys. Chem. Miner. 2000, 27, 164–169. [Google Scholar] [CrossRef]
- Alfè, D.; Gillan, M.J. First-principles calculation of transport coefficients. Phys. Rev. Lett. 1998, 81, 5161–5164. [Google Scholar] [CrossRef]
- Danel, J.F.; Kazandjian, L.; Zérah, G. Numerical convergence of the self-diffusion coefficient and viscosity obtained with Thomas–Fermi–Dirac molecular dynamics. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2012, 85, 066701. [Google Scholar] [CrossRef]
- Mondal, A.; Balasubramanian, S. A Molecular Dynamics Study of Collective Transport Properties of Imidazolium-Based Room-Temperature Ionic Liquids. J. Chem. Eng. Data 2014, 59, 3061–3068. [Google Scholar] [CrossRef]
- Kondratyuk, N.; Ryltsev, R.; Ankudinov, V.; Chtchelkatchev, N. Can We Accurately Calculate Viscosity in Multicomponent Metallic Melts? 2022. Available online: https://arxiv.org/abs/2211.03483 (accessed on 18 April 2023). [CrossRef]
- Balyakin, I.; Yuryev, A.; Filippov, V.; Gelchinski, B. Viscosity of liquid gallium: Neural network potential molecular dynamics and experimental study. Comput. Mater. Sci. 2022, 215, 111802. [Google Scholar] [CrossRef]
- Heyes, D.M.; Smith, E.R.; Dini, D. Shear stress relaxation and diffusion in simple liquids by molecular dynamics simulations: Analytic expressions and paths to viscosity. J. Chem. Phys. 2019, 150, 174504. [Google Scholar] [CrossRef]
- Kondratyuk, N.D.; Pisarev, V.V. Calculation of viscosities of branched alkanes from 0.1 to 1000 MPa by molecular dynamics methods using COMPASS force field. Fluid Ph. Equilibria 2019, 498, 151–159. [Google Scholar] [CrossRef]
- Messerly, R.A.; Anderson, M.C.; Razavi, S.M.; Elliott, J.R. Mie 16–6 force field predicts viscosity with faster-than-exponential pressure dependence for 2,2,4-trimethylhexane. Fluid Ph. Equilibria 2019, 495, 76–85. [Google Scholar] [CrossRef]
- Zheng, L.; Trusler, J.M.; Bresme, F.; Müller, E.A. Predicting the pressure dependence of the viscosity of 2,2,4-trimethylhexane using the SAFT coarse-grained force field. Fluid Ph. Equilibria 2019, 496, 1–6. [Google Scholar] [CrossRef]
- Sun, H. Compass: An ab initio force-field optimized for condensed-phase applications - Overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Potoff, J.J.; Bernard-Brunel, D.A. Mie Potentials for Phase Equilibria Calculations: Application to Alkanes and Perfluoroalkanes. J. Phys. Chem. B 2009, 113, 14725–14731. [Google Scholar] [CrossRef] [PubMed]
- Mick, J.R.; Soroush Barhaghi, M.; Jackman, B.; Schwiebert, L.; Potoff, J.J. Optimized Mie Potentials for Phase Equilibria: Application to Branched Alkanes. J. Chem. Eng. Data 2017, 62, 1806–1818. [Google Scholar] [CrossRef]
- Kondratyuk, N.D. Comparing different force fields by viscosity prediction for branched alkane at 0.1 and 400 MPa. J. Phys. Conf. Ser. 2019, 1385, 012048. [Google Scholar] [CrossRef]
- Kondratyuk, N.D.; Pisarev, V.V.; Ewen, J.P. Probing the high-pressure viscosity of hydrocarbon mixtures using molecular dynamics simulations. J. Chem. Phys. 2020, 153, 154502. [Google Scholar] [CrossRef]
- Bair, S. The pressure dependence of viscosity for 2,2,4 trimethylhexane to 1 GPa along the 20 C isotherm. Fluid Ph. Equilibria 2019, 488, 9–12. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Sun, H.; Jin, Z.; Yang, C.; Akkermans, R.L.C.; Robertson, S.H.; Spenley, N.A.; Miller, S.; Todd, S.M. COMPASS II: Extended coverage for polymer and drug-like molecule databases. J. Mol. Model. 2016, 22, 47. [Google Scholar] [CrossRef] [PubMed]
- Moultos, O.A.; Zhang, Y.; Tsimpanogiannis, I.N.; Economou, I.G.; Maginn, E.J. System-size corrections for self-diffusion coefficients calculated from molecular dynamics simulations: The case of CO2, n-alkanes, and poly(ethylene glycol) dimethyl ethers. J. Chem. Phys. 2016, 145, 074109. [Google Scholar] [CrossRef] [PubMed]
- Daivis, P.J.; Evans, D.J. Transport coefficients of liquid butane near the boiling point by equilibrium molecular dynamics. J. Chem. Phys. 1995, 103, 4261–4265. [Google Scholar] [CrossRef]
- Jamali, S.H.; Wolff, L.; Becker, T.M.; De Groen, M.; Ramdin, M.; Hartkamp, R.; Bardow, A.; Vlugt, T.J.; Moultos, O.A. OCTP: A Tool for On-the-Fly Calculation of Transport Properties of Fluids with the Order- n Algorithm in LAMMPS. J. Chem. Inf. Model. 2019, 59, 1290–1294. [Google Scholar] [CrossRef]
- Allouche, A.R. Software News and Updates Gabedit—A Graphical User Interface for Computational Chemistry Softwares. J. Comput. Chem. 2012, 32, 174–182. [Google Scholar] [CrossRef]
- Verstraelen, T.; Adams, W.; Pujal, L.; Tehrani, A.; Kelly, B.D.; Macaya, L.; Meng, F.; Richer, M.; Hernández-Esparza, R.; Yang, X.D.; et al. IOData: A python library for reading, writing, and converting computational chemistry file formats and generating input files. J. Comput. Chem. 2021, 42, 458–464. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Chodera, J.D. A Simple Method for Automated Equilibration Detection in Molecular Simulations. J. Chem. Theory Comput. 2016, 12, 1799–1805. [Google Scholar] [CrossRef] [PubMed]
- Rey-Castro, C.; Vega, L.F. Transport properties of the ionic liquid 1-ethyl-3-methylimidazolium chloride from equilibrium molecular dynamics simulation. the effect of temperature. J. Phys. Chem. B 2006, 110, 14426–14435. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R.; Ailawadi, N.K. Statistical Error Due to Finite Time Averaging in Computer Experiments. Phys. Rev. 1969, 182, 280–283. [Google Scholar] [CrossRef]
- Schmitt, S.; Fleckenstein, F.; Hasse, H.; Stephan, S. Comparison of Force Fields for the Prediction of Thermophysical Properties of Long Linear and Branched Alkanes. J. Phys. Chem. B 2023, 127, 1789–1802. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Kim, K.S.; Kim, C.; Karniadakis, G.E.; Lee, E.K.; Kozak, J.J. Density-Dependent finite system-size effects in equilibrium molecular dynamics estimation of shear viscosity: Hydrodynamic and configurational study. J. Chem. Phys. 2019, 151, 104101. [Google Scholar] [CrossRef]
- Mathas, D.; Holweger, W.; Wolf, M.; Bohnert, C.; Bakolas, V.; Procelewska, J.; Wang, L.; Bair, S.; Skylaris, C.K. Evaluation of Methods for Viscosity Simulations of Lubricants at Different Temperatures and Pressures: A Case Study on PAO-2. Tribol. Trans. 2021, 64, 1138–1148. [Google Scholar] [CrossRef]
- Toraman, G.; Verstraelen, T.; Fauconnier, D. EMD data for the paper “Impact of ad hoc post-processing parameters on the lubricant viscosity calculated with equilibrium molecular dynamics simulations” version 0.1.1, Zenodo (accessed on 13 April 2023). [CrossRef]



| Bootstrapping Approach | |||
|---|---|---|---|
| Parameter | NB | SB | EB |
| Resampling of trajectories | No | Yes | Yes |
| 25% | 25% | [10%, 100%] | |
| 2 | 2 | [1, 3] | |
| q | 50% | 50% | [25%, 75%] |
| 40% | 40% | [20%, 80%] | |
| [cP] | |||||
|---|---|---|---|---|---|
| System | Bootstrapping Approach | ||||
| [Å] | NB | SB | EB | ||
| 100 | 30.9 | 0.721 ± 0.009 | 0.654 | 0.666 ± 0.030 | 0.674 ± 0.045 |
| 1000 | 66.6 | 0.721 ± 0.003 | 0.678 | 0.696 ± 0.047 | 0.679 ± 0.045 |
| 0.64 ± 0.031 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toraman, G.; Verstraelen, T.; Fauconnier, D. Impact of Ad Hoc Post-Processing Parameters on the Lubricant Viscosity Calculated with Equilibrium Molecular Dynamics Simulations. Lubricants 2023, 11, 183. https://doi.org/10.3390/lubricants11040183
Toraman G, Verstraelen T, Fauconnier D. Impact of Ad Hoc Post-Processing Parameters on the Lubricant Viscosity Calculated with Equilibrium Molecular Dynamics Simulations. Lubricants. 2023; 11(4):183. https://doi.org/10.3390/lubricants11040183
Chicago/Turabian StyleToraman, Gözdenur, Toon Verstraelen, and Dieter Fauconnier. 2023. "Impact of Ad Hoc Post-Processing Parameters on the Lubricant Viscosity Calculated with Equilibrium Molecular Dynamics Simulations" Lubricants 11, no. 4: 183. https://doi.org/10.3390/lubricants11040183
APA StyleToraman, G., Verstraelen, T., & Fauconnier, D. (2023). Impact of Ad Hoc Post-Processing Parameters on the Lubricant Viscosity Calculated with Equilibrium Molecular Dynamics Simulations. Lubricants, 11(4), 183. https://doi.org/10.3390/lubricants11040183