Dynamic Responses of the Planetary Gear Mechanism Considering Dynamic Wear Effects
Abstract
1. Introduction
2. Rotational Dynamic Model of Planetary Gear Mechanism
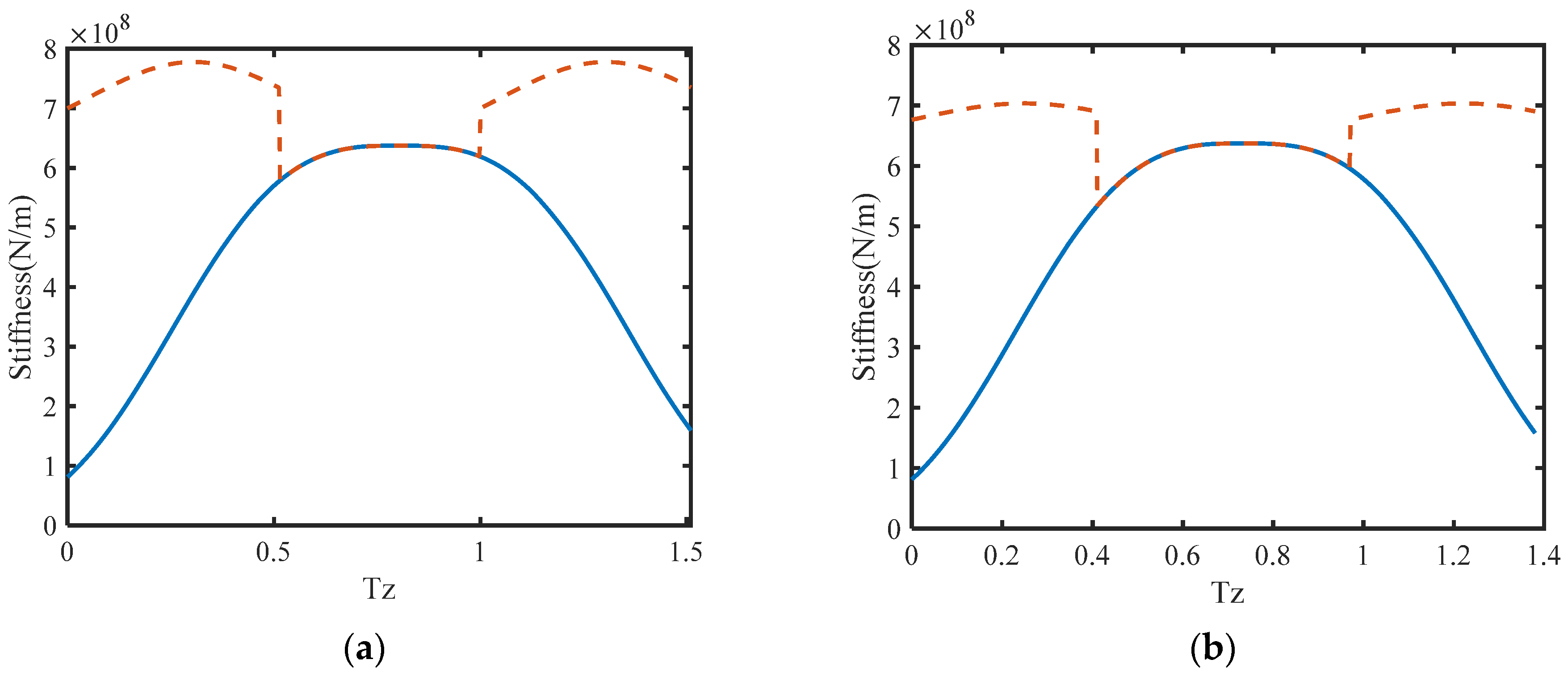
3. Modeling Gear Mesh Stiffness
4. Modeling Gear Wear
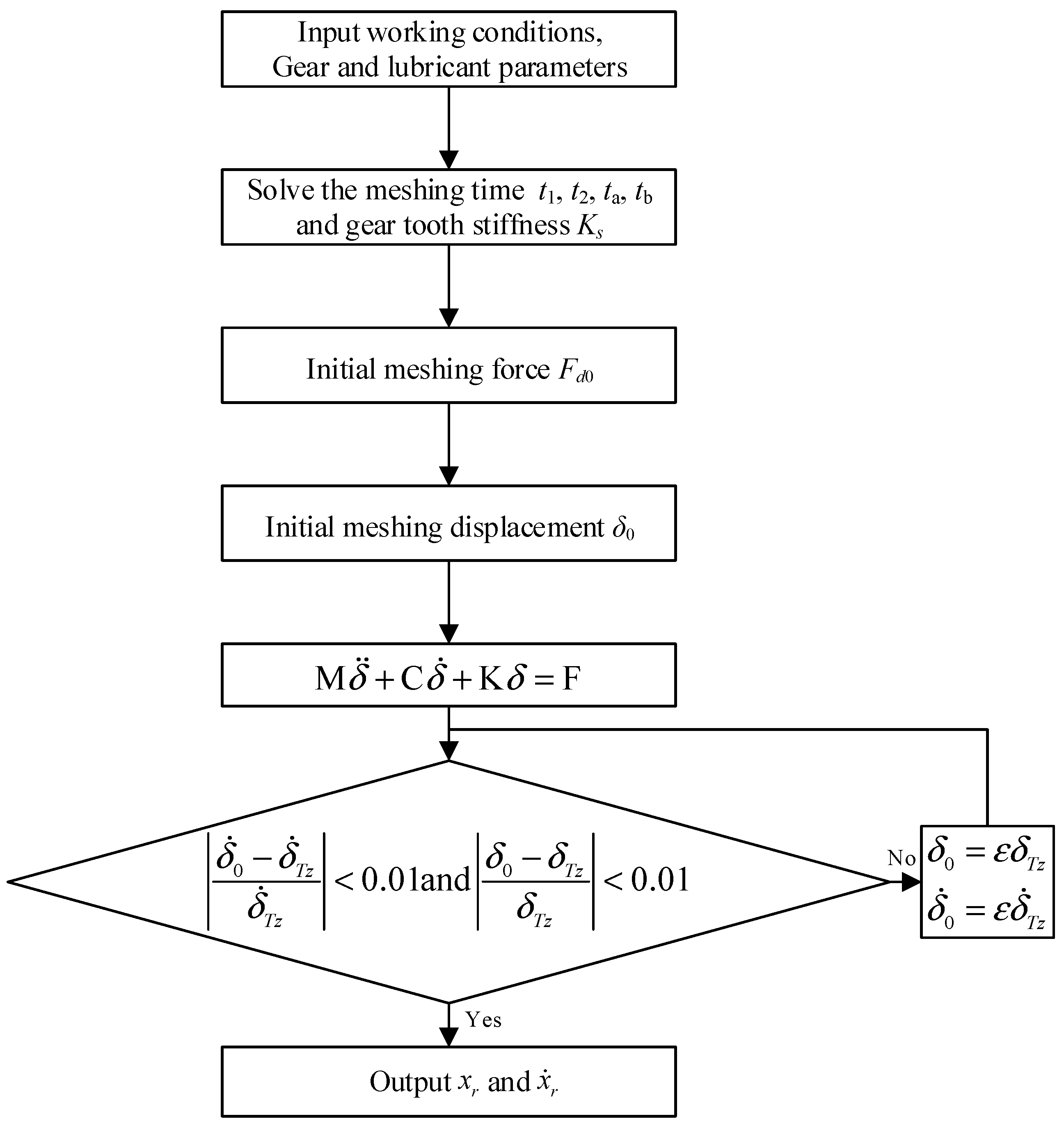
5. Wear Prediction Process
6. Numerical Results and Discussion
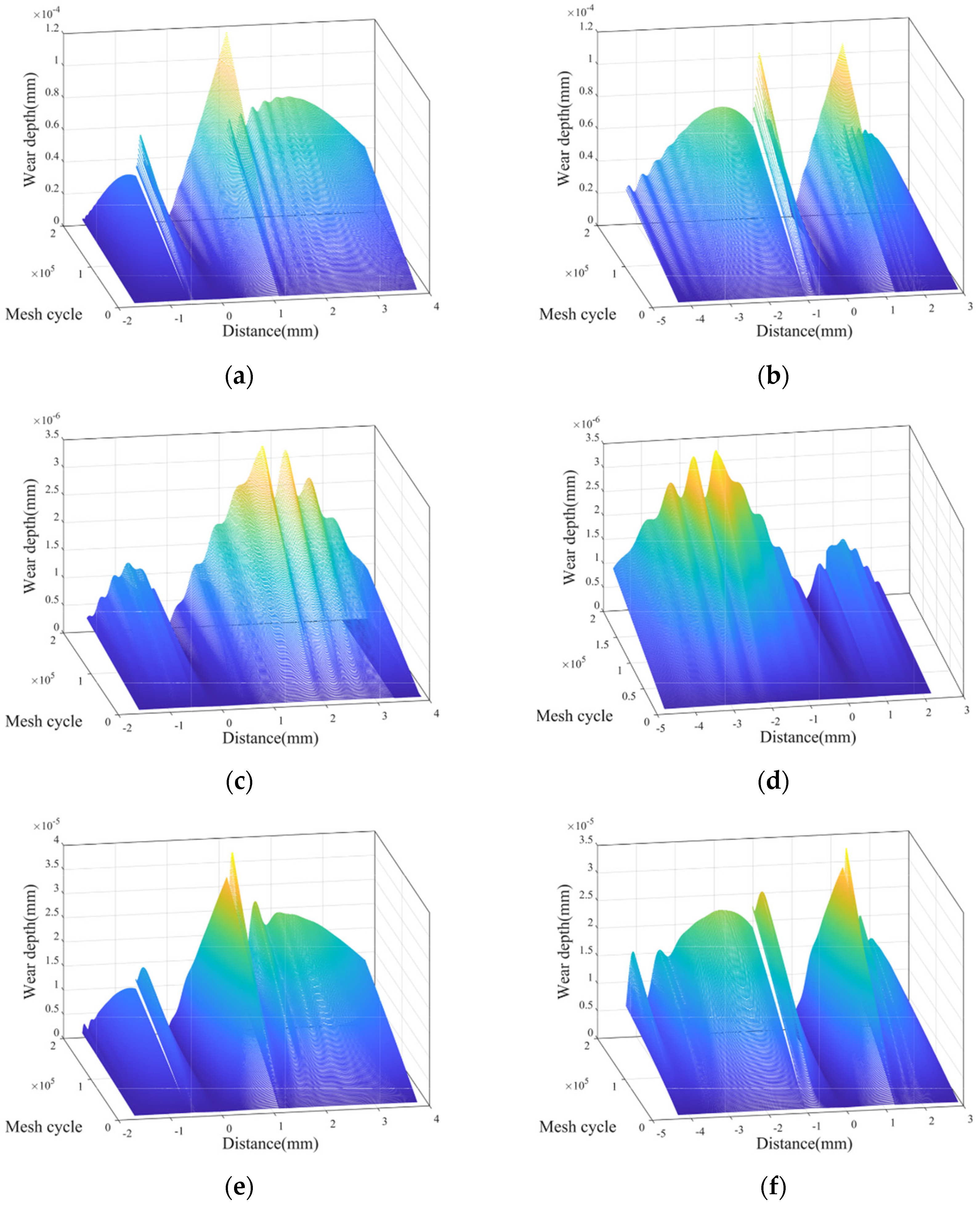
6.1. Wear Distribution
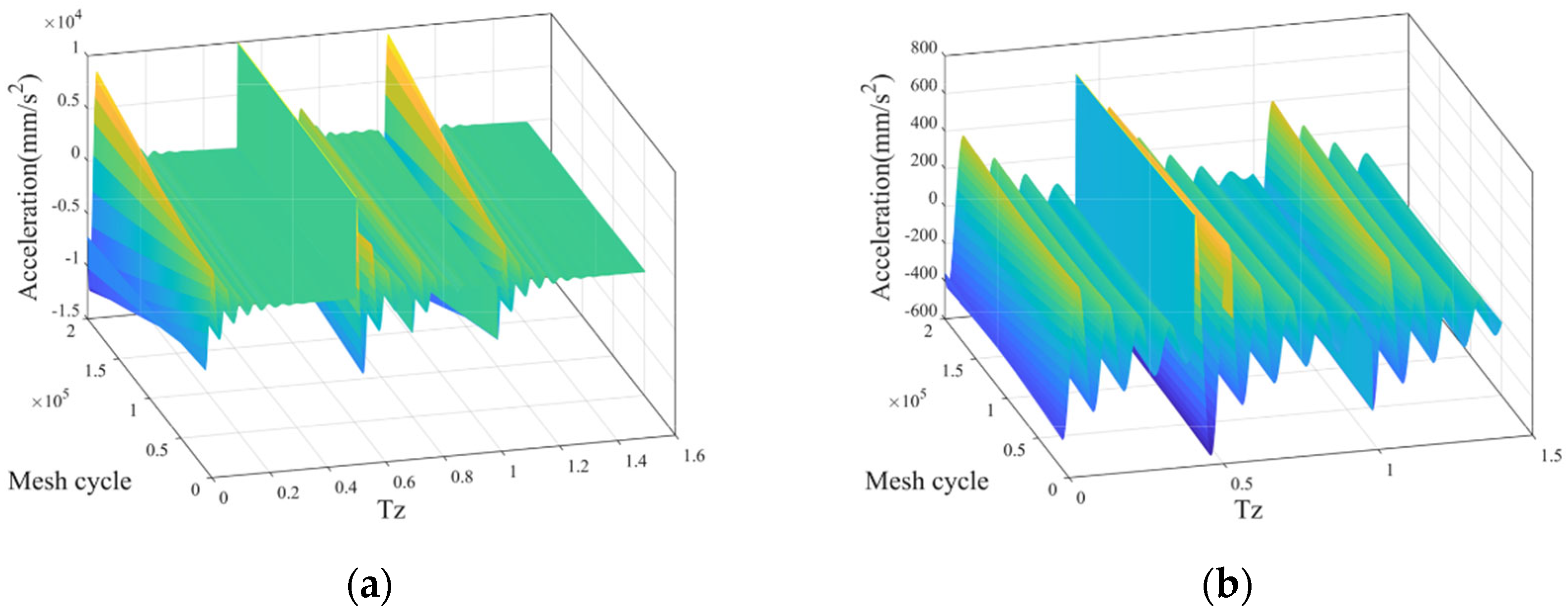
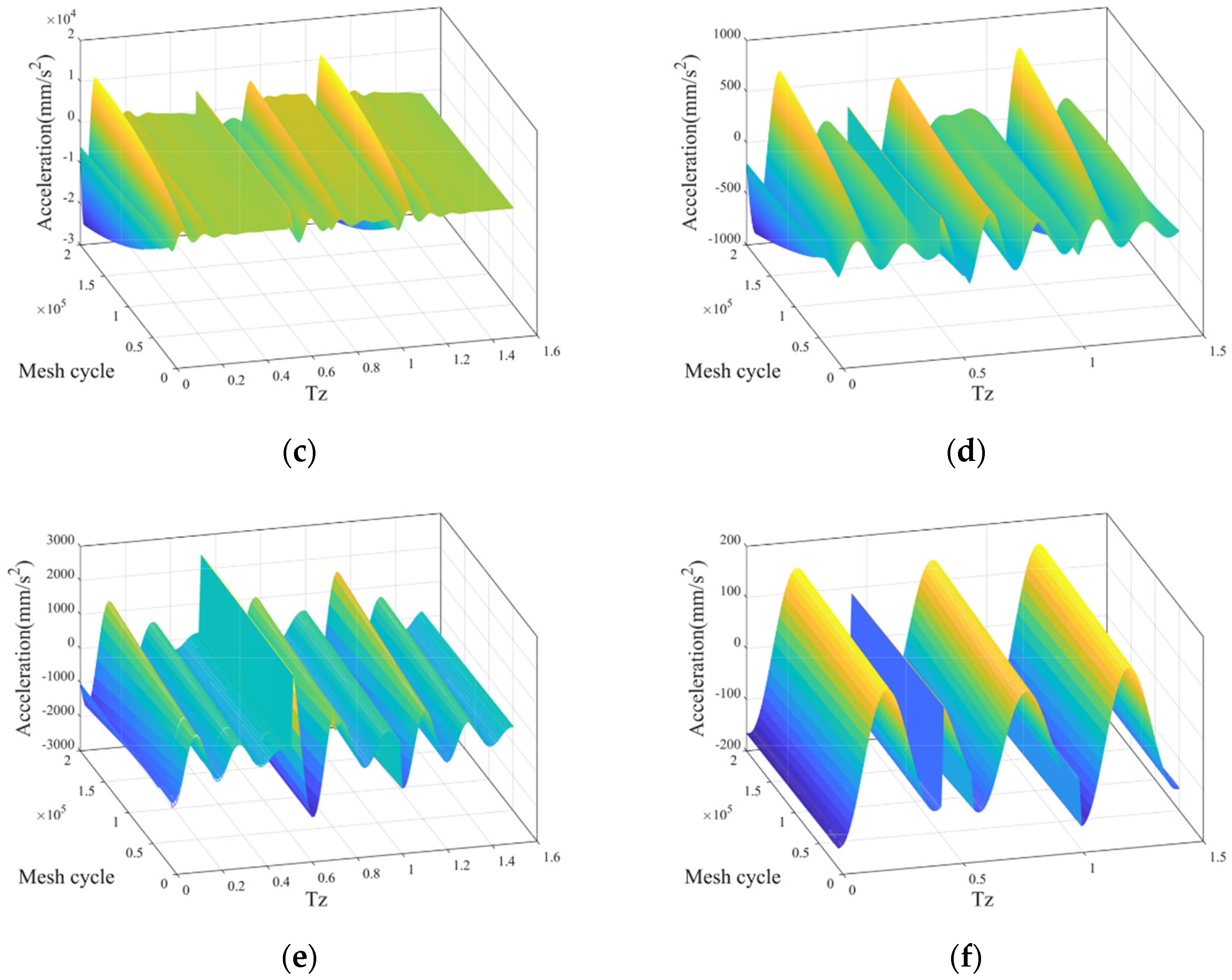
6.2. Dynamic Characteristics
6.3. Discussion
7. Conclusions
- According to the wear distribution of the planetary gear, the wear corresponding to sun–planet meshing is more severe. The wear in planet–ring meshing represents less fluctuation, which suggests better wear resistance. Because the driven gears have higher sliding speeds during meshing, the driven gears exhibit greater wear depths. The dynamic performance of the gear rapidly deteriorates as the wear depth of the tooth surface increases.
- The gear-meshing vibration at a low rotational speed exhibits a nonlinear relationship with mesh time, which is due to the coupling among the dynamic characteristics, mesh force, and sliding speed. As rotational speed increases, the nonlinear characteristic deteriorates, which is due to sliding speed becoming the main influencing factor.
- The analysis of gear wear, vibration responses, and the frequency spectra reveal that planet–ring meshing exhibits better wear and shock resistance than sun–planet meshing. This leads to frequent failure of the sun gear, which is consistent with practical engineering experience. Therefore, increasing the maintainability of the sun gear will improve the service life of the planetary gear mechanism.
- At different rotational speeds, gear wear has different effects on the amplitude of the main frequency. The adverse effects of planetary-gear wear on planetary-gear vibra-tion can be effectively mitigated by selecting an appropriate rotational speed, and the gear vibration can be improved through early gear wear.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Contact area |
| Cs | Equivalent correction factor |
| csp | Sun-planet tooth profile meshing damping |
| cpr | Planet-ring tooth profile meshing damping |
| E | Elasticity modulus |
| epr | Planet-ring meshing error |
| esp | Sun-planet meshing error |
| Fc | Damping force |
| FN | Load force |
| f | Frictional force |
| G | Shear modulus |
| H | Hardness of soft surface |
| h | Wear depth |
| Ic | Inertial moment of planet gear carrier |
| Ip | Inertial moment of the planet gear |
| Is | Inertial moment of the sun gear |
| KH | Contact stiffness |
| Ks | Mesh stiffness |
| kn | Axial compressive stiffness |
| ks | Shear stiffness |
| kx | Bending stiffness |
| LR | Load ratio |
| M | Equivalent mass |
| mc | Mass of planet gear carrier |
| mp | Mass of planet gear |
| ms | Mass of sun gear |
| p | Pressure |
| Rc | Rotation radius of planet gear carrier |
| Rp | The basic radius of planet gear |
| Rs | The basic radius of the sun gear |
| S | Equivalent curvature radius of tooth surface |
| s | Sliding distance |
| Tc | Torque of planet gear carrier |
| Ts | Torque of sun gear |
| Tp | Torque of planet gear |
| U | Gear meshing potential energy |
| V | Wear volume |
| v | Sliding velocity |
| z | Tooth number |
| α | Pressure angle |
| γp | Angle thickness at point P |
| δ | Meshing penetration depth |
| ε | Chordal thickness |
| Δt | Time step |
| ζ | Wear coefficient |
| θc | Rotational displacement of planet gear carrier |
| θp | Rotational displacement of planet gear |
| θs | Rotational displacement of sun gear |
| κ | Dimensionless wear coefficient |
References
- Kahraman, A.; Singh, R. Non-Linear Dynamics of a Spur Gear Pair. J. Sound Vib. 1990, 142, 49–75. [Google Scholar] [CrossRef]
- Kahraman, A.; Singh, R. Interactions between Time-Varying Mesh Stiffness and Clearance Non-Linearities in a Geared System. J. Sound Vib. 1991, 146, 135–156. [Google Scholar] [CrossRef]
- Kahraman, A. Free Torsional Vibration Characteristics of Compound Planetary Gear Sets. Mech. Mach. Theory 2001, 36, 953–971. [Google Scholar] [CrossRef]
- Kahraman, A. Planetary Gear Train Dynamics. J. Mech. Des. 1994, 116, 713–720. [Google Scholar] [CrossRef]
- Parker, R.G.; Vijayakar, S.M.; Imajo, T. Non-Linear Dynamic Response of a Spur Gear Pair: Modelling and Experimental Comparisons. J. Sound Vib. 2000, 237, 435–455. [Google Scholar] [CrossRef]
- Parker, R.G.; Lin, J. Mesh Phasing Relationships in Planetary and Epicyclic Gears. J. Mech. Des. 2004, 126, 365–370. [Google Scholar] [CrossRef]
- Ambarisha, V.K.; Parker, R.G. Nonlinear Dynamics of Planetary Gears Using Analytical and Finite Element Models. J. Sound Vib. 2007, 302, 577–595. [Google Scholar] [CrossRef]
- Huang, Y. Mathematical model of planetary gear sets’ vibration signal and characteristic frequency analysis. J. Mech. Eng. 2016, 52, 46. [Google Scholar] [CrossRef]
- Wang, C.C. Rotational Vibration with Backlash: Part 1. J. Mech. Des. 1978, 100, 363–373. [Google Scholar] [CrossRef]
- Wang, C.C. Rotational Vibration with Backlash: Part 2. J. Mech. Des. 1981, 103, 387–397. [Google Scholar] [CrossRef]
- Özgüven, H.N.; Houser, D.R. Mathematical Models Used in Gear Dynamics—A Review. J. Sound Vib. 1988, 121, 383–411. [Google Scholar] [CrossRef]
- Shi, J.; Gou, X.; Zhu, L. Modeling and Analysis of a Spur Gear Pair Considering Multi-State Mesh with Time-Varying Parameters and Backlash. Mech. Mach. Theory 2019, 134, 582–603. [Google Scholar] [CrossRef]
- Al-Shyyab, A.; Kahraman, A. A Non-Linear Dynamic Model for Planetary Gear Sets. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2007, 221, 567–576. [Google Scholar] [CrossRef]
- Lin, J.; Parker, R.G. Analytical Characterization of the Unique Properties of Planetary Gear Free Vibration. J. Vib. Acoust. 1999, 121, 316–321. [Google Scholar] [CrossRef]
- Lin, J.; Parker, R.G. Sensitivity of Planetary Gear Natural Frequencies and Vibration Modes to Model Parameters. J. Sound Vib. 1999, 228, 109–128. [Google Scholar] [CrossRef]
- Xiang, L.; Gao, N.; Hu, A. Dynamic Analysis of a Planetary Gear System with Multiple Nonlinear Parameters. J. Comput. Appl. Math. 2018, 327, 325–340. [Google Scholar] [CrossRef]
- Ligata, H.; Kahraman, A.; Singh, A. An Experimental Study of the Influence of Manufacturing Errors on the Planetary Gear Stresses and Planet Load Sharing. J. Mech. Des. 2008, 130, 041701. [Google Scholar] [CrossRef]
- Ligata, H.; Kahraman, A.; Singh, A. A Closed-Form Planet Load Sharing Formulation for Planetary Gear Sets Using a Translational Analogy. J. Mech. Des. 2009, 131, 021007. [Google Scholar] [CrossRef]
- He, G.; Ding, K.; Wu, X.; Yang, X. Dynamics Modeling and Vibration Modulation Signal Analysis of Wind Turbine Planetary Gearbox with a Floating Sun Gear. Renew. Energy 2019, 139, 718–729. [Google Scholar] [CrossRef]
- Dong, H.L.; Hu, J.B.; Li, X.Y. Temperature Analysis of Involute Gear Based on Mixed Elastohydrodynamic Lubrication Theory Considering Tribo-Dynamic Behaviors. J. Tribol. 2014, 136, 021504. [Google Scholar] [CrossRef]
- Yuan, S.H.; Dong, H.L.; Li, X.Y. Analysis of Lubricating Performance for Involute Gear Based on Dynamic Loading Theory. J. Mech. Des. 2012, 134, 121004. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Fang, T. On the Prediction of Friction Coefficient and Wear in Spiral Bevel Gears with Mixed TEHL. Tribol. Int. 2017, 115, 535–545. [Google Scholar] [CrossRef]
- Chen, Z.; Shao, Y. Mesh Stiffness of an Internal Spur Gear Pair with Ring Gear Rim Deformation. Mech. Mach. Theory 2013, 69, 1–12. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, X. Dynamic Load Sharing Behavior of Planetary Gear Train with Backlashes. In Proceedings of the 2009 International Conference on Engineering Computation, Hong Kong, China, 2–3 May 2009; pp. 209–212. [Google Scholar]
- Guo, Y.; Keller, J.; Parker, R.G. Nonlinear Dynamics and Stability of Wind Turbine Planetary Gear Sets under Gravity Effects. Eur. J. Mech. A. Solids 2014, 47, 45–57. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, R.G. Dynamic Modeling and Analysis of a Spur Planetary Gear Involving Tooth Wedging and Bearing Clearance Nonlinearity. Eur. J. Mech. A. Solids 2010, 29, 1022–1033. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, R.G. Analytical Determination of Mesh Phase Relations in General Compound Planetary Gears. Mech. Mach. Theory 2011, 46, 1869–1887. [Google Scholar] [CrossRef]
- Kim, W.; Lee, J.Y.; Chung, J. Dynamic Analysis for a Planetary Gear with Time-Varying Pressure Angles and Contact Ratios. J. Sound Vib. 2012, 331, 883–901. [Google Scholar] [CrossRef]
- Ma, P.; Botman, M. Load Sharing in a Planetary Gear Stage in the Presence of Gear Errors and Misalignment. J. Mech. Transm. Autom. Des. 1985, 107, 4–10. [Google Scholar] [CrossRef]
- Sánchez, M.B.; Pleguezuelos, M.; Pedrero, J.I. Calculation of Tooth Bending Strength and Surface Durability of Internal Spur Gear Drives. Mech. Mach. Theory 2016, 95, 102–113. [Google Scholar] [CrossRef]
- Sánchez, M.B.; Pleguezuelos, M.; Pedrero, J.I. Strength Model for Bending and Pitting Calculations of Internal Spur Gears. Mech. Mach. Theory 2019, 133, 691–705. [Google Scholar] [CrossRef]
- Siyu, C.; Jinyuan, T.; Caiwang, L.; Qibo, W. Nonlinear Dynamic Characteristics of Geared Rotor Bearing Systems with Dynamic Backlash and Friction. Mech. Mach. Theory 2011, 46, 466–478. [Google Scholar] [CrossRef]
- Sun, T.; Hu, H. Nonlinear Dynamics of a Planetary Gear System with Multiple Clearances. Mech. Mach. Theory 2003, 38, 1371–1390. [Google Scholar] [CrossRef]
- Tsai, S.-J.; Huang, G.-L.; Ye, S.-Y. Gear Meshing Analysis of Planetary Gear Sets with a Floating Sun Gear. Mech. Mach. Theory 2015, 84, 145–163. [Google Scholar] [CrossRef]
- Flodin, A.; Andersson, S. Simulation of Mild Wear in Spur Gears. Wear 1997, 207, 16–23. [Google Scholar] [CrossRef]
- Flodin, A.; Andersson, S. Simulation of Mild Wear in Helical Gears. Wear 2000, 241, 123–128. [Google Scholar] [CrossRef]
- Flodin, A.; Andersson, S. Wear Simulation of Spur Gears. Tribotest 1999, 5, 225–249. [Google Scholar] [CrossRef]
- Flodin, A.; Andersson, S. A Simplified Model for Wear Prediction in Helical Gears. Wear 2001, 249, 285–292. [Google Scholar] [CrossRef]
- Shen, Z.; Qiao, B.; Yang, L.; Luo, W.; Chen, X. Evaluating the Influence of Tooth Surface Wear on TVMS of Planetary Gear Set. Mech. Mach. Theory 2019, 136, 206–223. [Google Scholar] [CrossRef]
- Shen, Z.; Qiao, B.; Yang, L.; Luo, W.; Yan, R.; Chen, X. Dynamic Modeling of Planetary Gear Set with Tooth Surface Wear. Procedia Manuf. 2020, 49, 49–54. [Google Scholar] [CrossRef]
- Guerine, A.; Hami, A.E.; Walha, L.; Fakhfakh, T.; Haddar, M. Dynamic Response of a Spur Gear System with Uncertain Friction Coefficient. Adv. Eng. Softw. 2018, 120, 45–54. [Google Scholar] [CrossRef]
- Straffelini, G. Friction and Wear; Springer Tracts in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-319-05893-1. [Google Scholar]
- Li, S.; Wu, Q.; Zhang, Z. Bifurcation and Chaos Analysis of Multistage Planetary Gear Train. Nonlinear Dynam. 2014, 75, 217–233. [Google Scholar] [CrossRef]
- Li, S.; Anisetti, A. A Tribo-Dynamic Contact Fatigue Model for Spur Gear Pairs. Int. J. Fatigue 2017, 98, 81–91. [Google Scholar] [CrossRef]
- Yan, Y. Load Characteristic Analysis and Fatigue Reliability Prediction of Wind Turbine Gear Transmission System. Int. J. Fatigue 2020, 130, 105259. [Google Scholar] [CrossRef]
- Yan, Y.; Jiang, C.; Li, W. Simulation on Coupling Effects between Surface Wear and Fatigue in Spur Gear. Eng. Fail. Anal. 2022, 134, 106055. [Google Scholar] [CrossRef]
- Bajpai, P.; Kahraman, A.; Anderson, N.E. A Surface Wear Prediction Methodology for Parallel-Axis Gear Pairs. J. Tribol. 2004, 126, 597–605. [Google Scholar] [CrossRef]
- Yuksel, C.; Kahraman, A. Dynamic Tooth Loads of Planetary Gear Sets Having Tooth Profile Wear. Mech. Mach. Theory 2004, 39, 695–715. [Google Scholar] [CrossRef]
- Ding, H.; Kahraman, A. Interactions between Nonlinear Spur Gear Dynamics and Surface Wear. J. Sound Vib. 2007, 307, 662–679. [Google Scholar] [CrossRef]
- Wu, S.; Cheng, H.S. Sliding Wear Calculation in Spur Gears. J. Tribol. 1993, 115, 493–500. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, H. An Adhesive Wear Prediction Method for Double Helical Gears Based on Enhanced Coordinate Transformation and Generalized Sliding Distance Model. Mech. Mach. Theory 2018, 128, 58–83. [Google Scholar] [CrossRef]
- Choy, F.K.; Polyshchuk, V.; Zakrajsek, J.J.; Handschuh, R.F.; Townsend, D.P. Analysis of the Effects of Surface Pitting and Wear on the Vibration of a Gear Transmission System. Tribol. Int. 1996, 29, 77–83. [Google Scholar] [CrossRef]
- Wojnarowski, J.; Onishchenko, V. Tooth Wear Effects on Spur Gear Dynamics. Mech. Mach. Theory 2003, 38, 161–178. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, X. A Dynamic Tooth Wear Prediction Model for Reflecting “Two-Sides” Coupling Relation between Tooth Wear Accumulation and Load Sharing Behavior in Compound Planetary Gear Set. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1746–1763. [Google Scholar] [CrossRef]
- Feng, K.; Borghesani, P.; Smith, W.A.; Randall, R.B.; Chin, Z.Y.; Ren, J.; Peng, Z. Vibration-Based Updating of Wear Prediction for Spur Gears. Wear 2019, 426–427, 1410–1415. [Google Scholar] [CrossRef]
- Salib, J.; Kligerman, Y.; Etsion, I. A Model for Potential Adhesive Wear Particle at Sliding Inception of a Spherical Contact. Tribol. Lett. 2008, 30, 225–233. [Google Scholar] [CrossRef]
- Hanief, M.; Charoo, M.S. Archard’s Wear Law Revisited to Measure Accurate Wear Coefficient Considering Actual Sliding Velocity. Mater. Today Proc. 2021, 47, 5598–5600. [Google Scholar] [CrossRef]
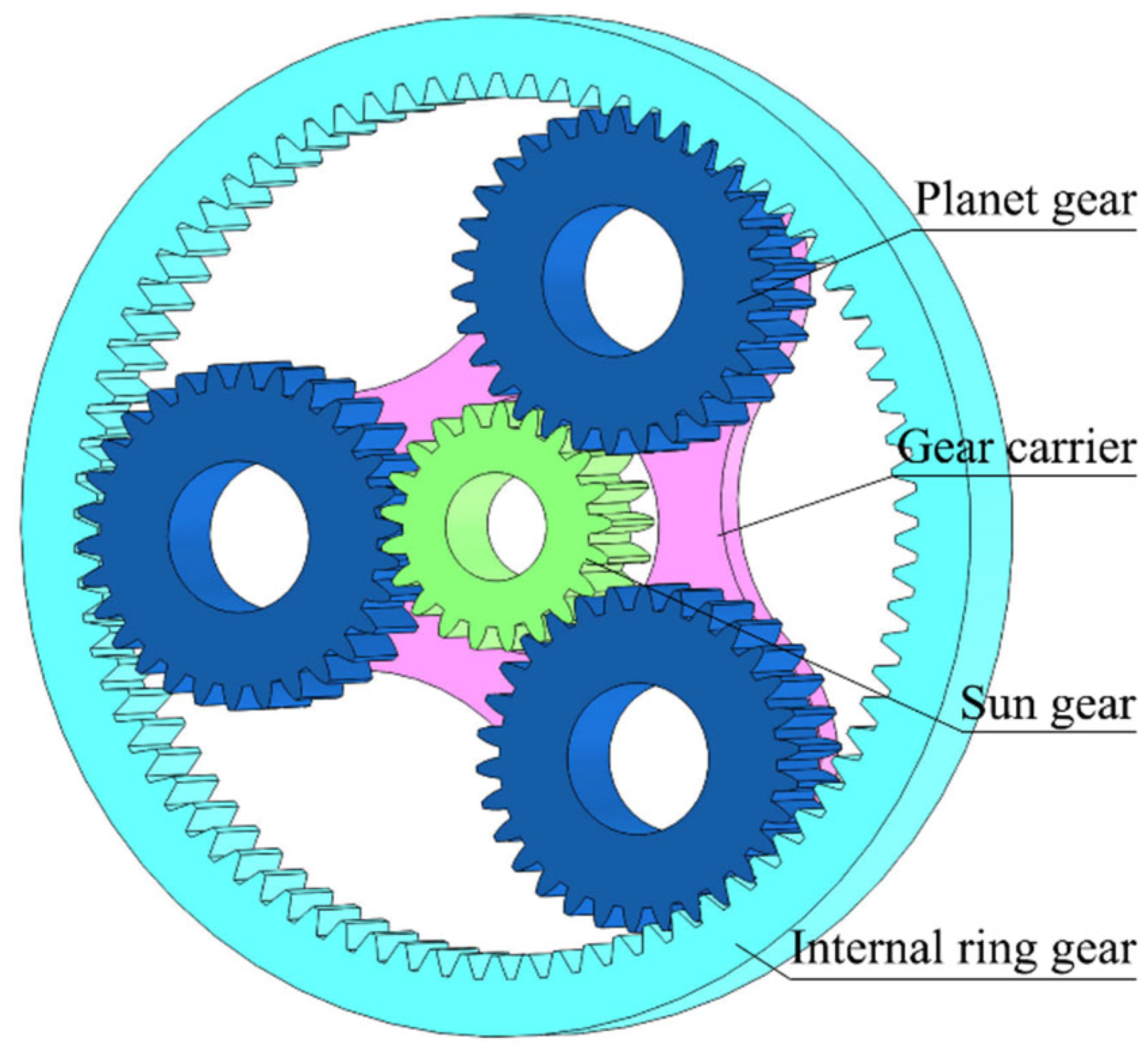


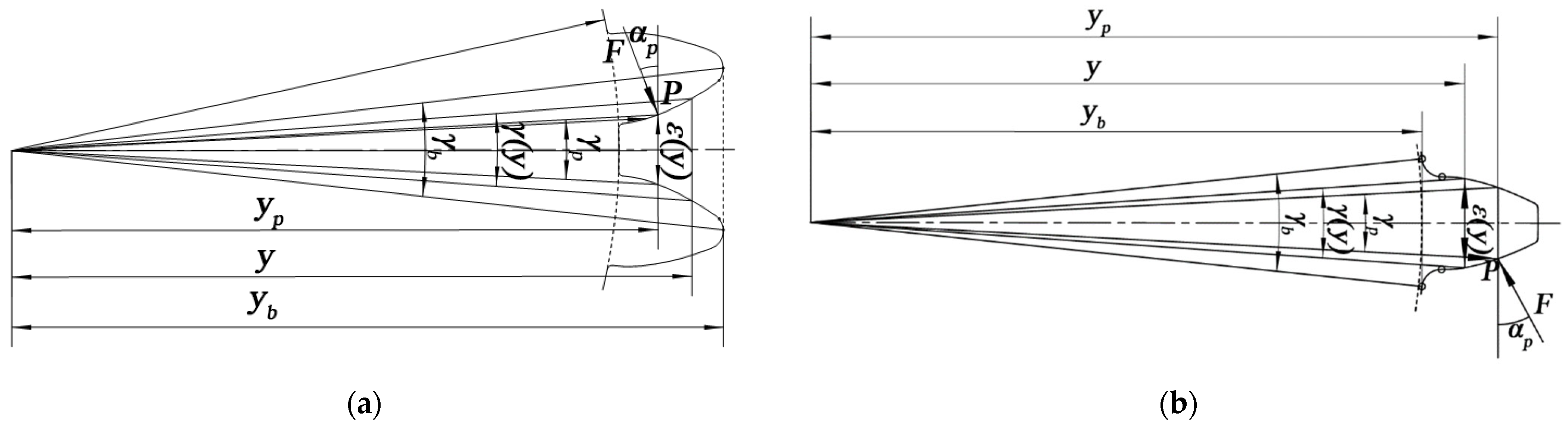
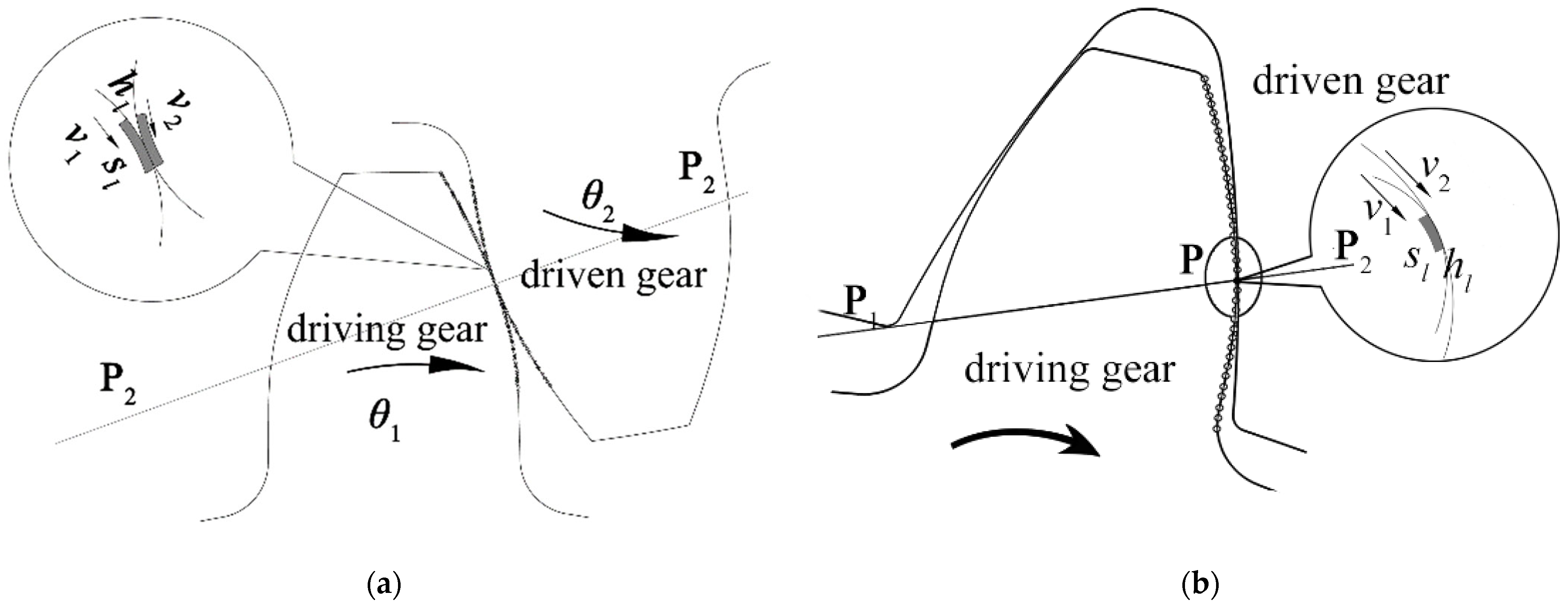
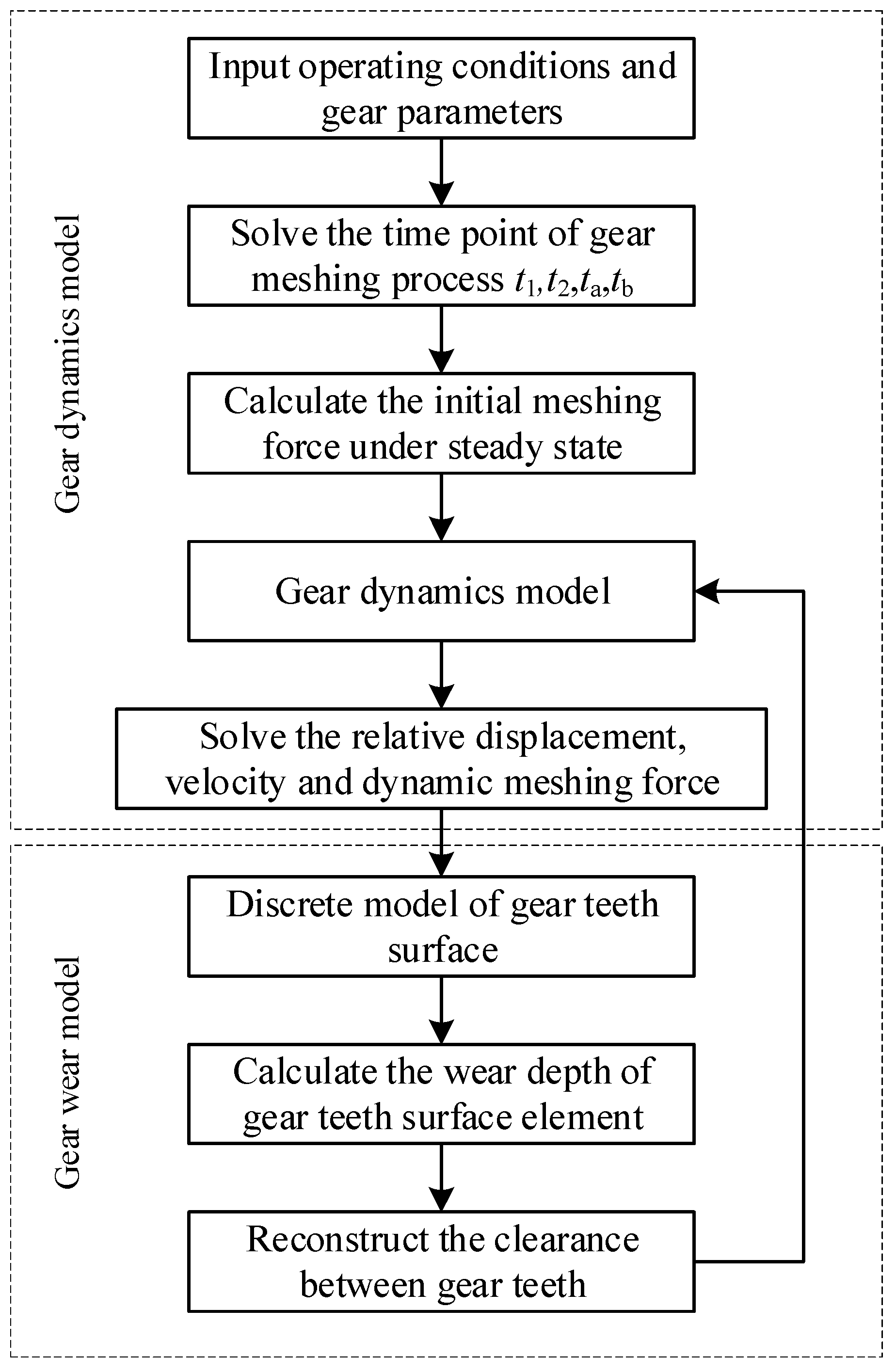




| Parameters | Value |
|---|---|
| Modules/mm | 3 |
| Tooth number of the internal ring gear | 81 |
| Tooth number of the planet gear | 30 |
| Tooth number of the sun gear | 21 |
| Meshing angle/rad | 0.349066 |
| Gear width/mm | 50 |
| Elasticity modulus of internal ring gear E1/GPa | 206 |
| Elasticity modulus of planet gear E2/GPa | 206 |
| Elasticity modulus of sun gear E3/GPa | 206 |
| Shear modulus of internal ring gear G1/GPa | 79.4 |
| Shear modulus of planet gear G2/GPa | 79.4 |
| Shear modulus of sun gear G3/GPa | 79.4 |
| Poisson ratio of internal ring gear | 0.3 |
| Poisson of planet gear | 0.3 |
| Poisson of the sun gear | 0.3 |
| Dynamic friction coefficient | 0.1 |
| Wear coefficient K | 5 × 10−11 |
| Parameter | Sun–Planet | Planet–Ring |
|---|---|---|
| Max. single stiffness | 6.372 × 106 N/m | 6.372 × 106 N/m |
| Max. general stiffness | 7.776 × 106 N/m | 7.033 × 106 N/m |
| First stiffness excitation | 1.558 × 106 N/m | 1.561 × 106 N/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Z.; Ning, Z. Dynamic Responses of the Planetary Gear Mechanism Considering Dynamic Wear Effects. Lubricants 2023, 11, 255. https://doi.org/10.3390/lubricants11060255
Bai Z, Ning Z. Dynamic Responses of the Planetary Gear Mechanism Considering Dynamic Wear Effects. Lubricants. 2023; 11(6):255. https://doi.org/10.3390/lubricants11060255
Chicago/Turabian StyleBai, Zhengfeng, and Zhiyuan Ning. 2023. "Dynamic Responses of the Planetary Gear Mechanism Considering Dynamic Wear Effects" Lubricants 11, no. 6: 255. https://doi.org/10.3390/lubricants11060255
APA StyleBai, Z., & Ning, Z. (2023). Dynamic Responses of the Planetary Gear Mechanism Considering Dynamic Wear Effects. Lubricants, 11(6), 255. https://doi.org/10.3390/lubricants11060255





