Wear and Subsurface Stress Evolution in a Half-Space under Cyclic Flat-Punch Indentation
Abstract
:1. Introduction
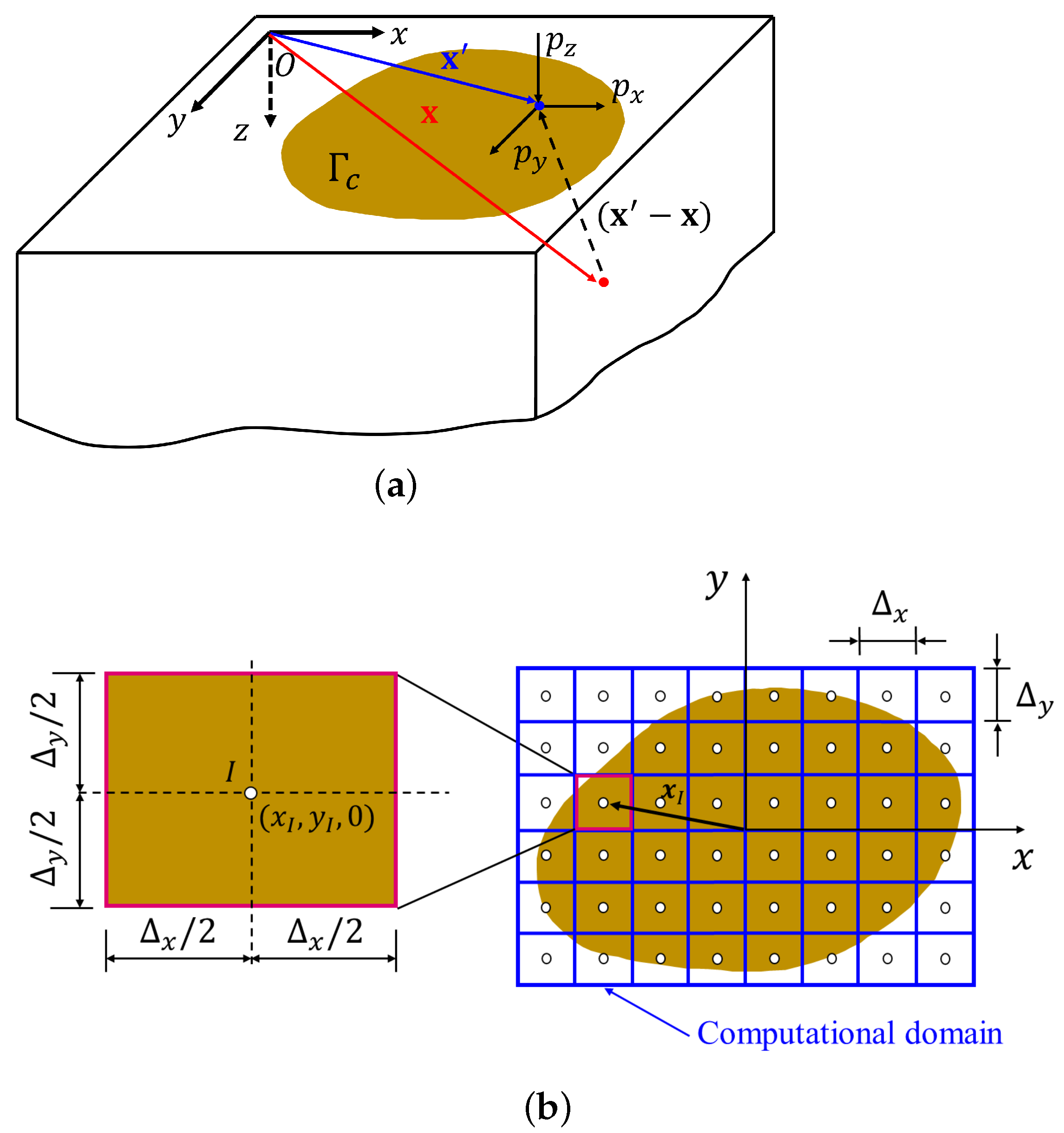
2. Frictional Contact Kinematics Including Wear
3. Boundary Element Approximation
4. Contact and Wear Laws
4.1. Normal Contact Restrictions
4.2. Tangential Contact Restrictions
4.3. Wear Law
5. Subsurface Stresses
6. Solution Scheme
7. Numerical Analysis
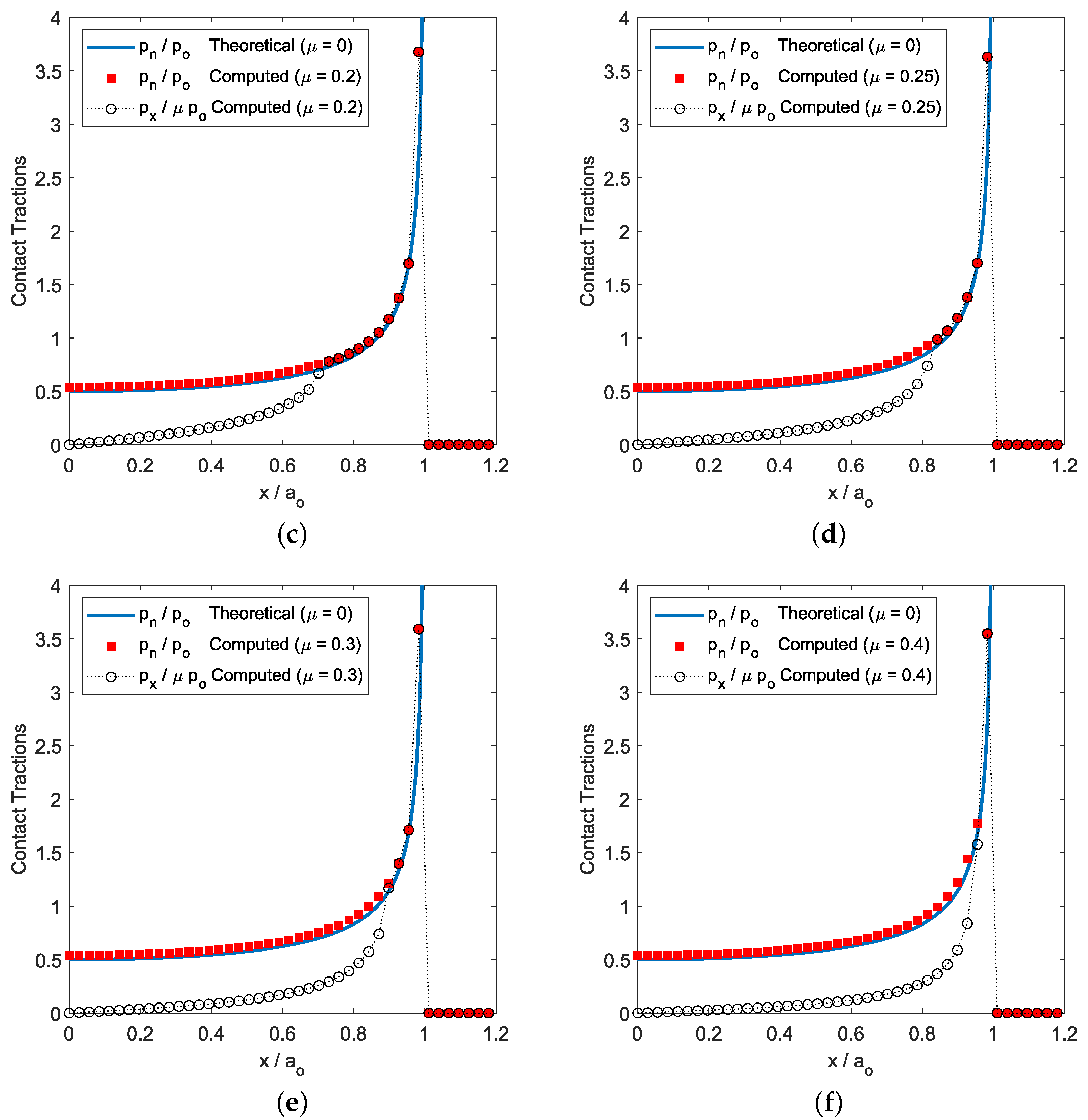
7.1. Cylindrical Flat-Punch under Static Normal Load Conditions
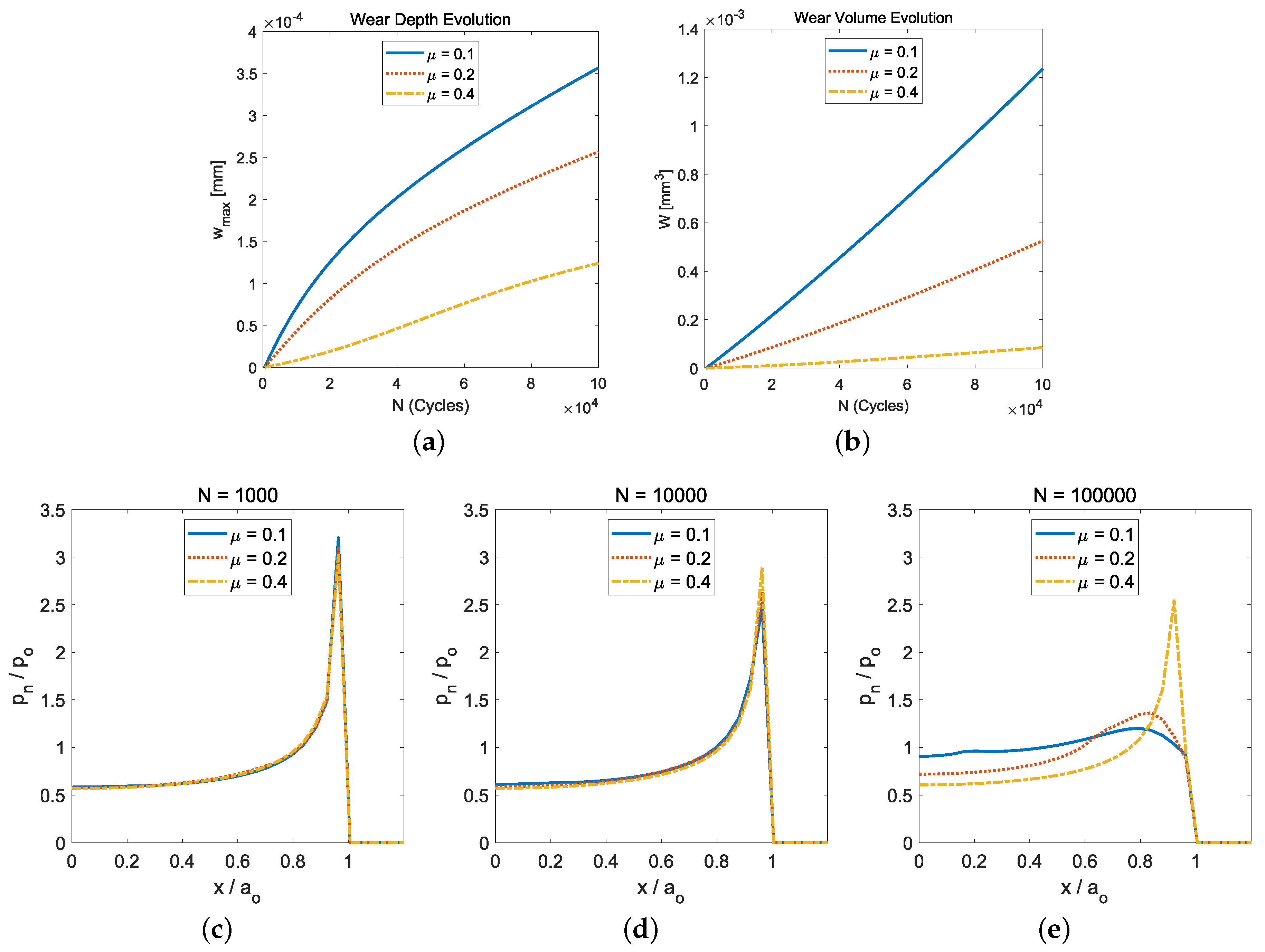
7.2. Cyclic Normal Load Conditions and Isotropic Tribological Laws
7.3. Cyclic Normal Load Conditions and Orthotropic Tribological Laws
8. Summary and Conclusions
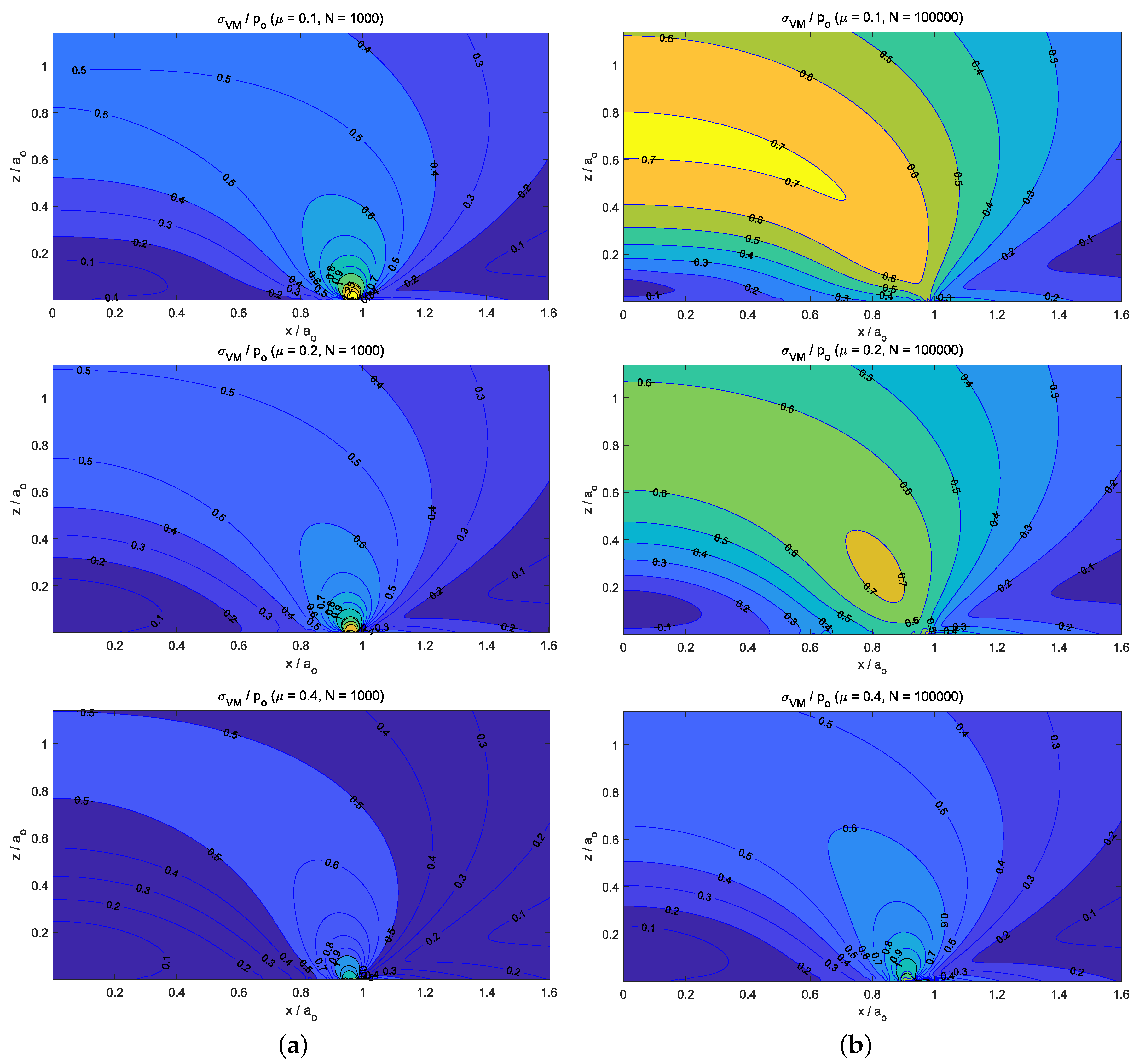
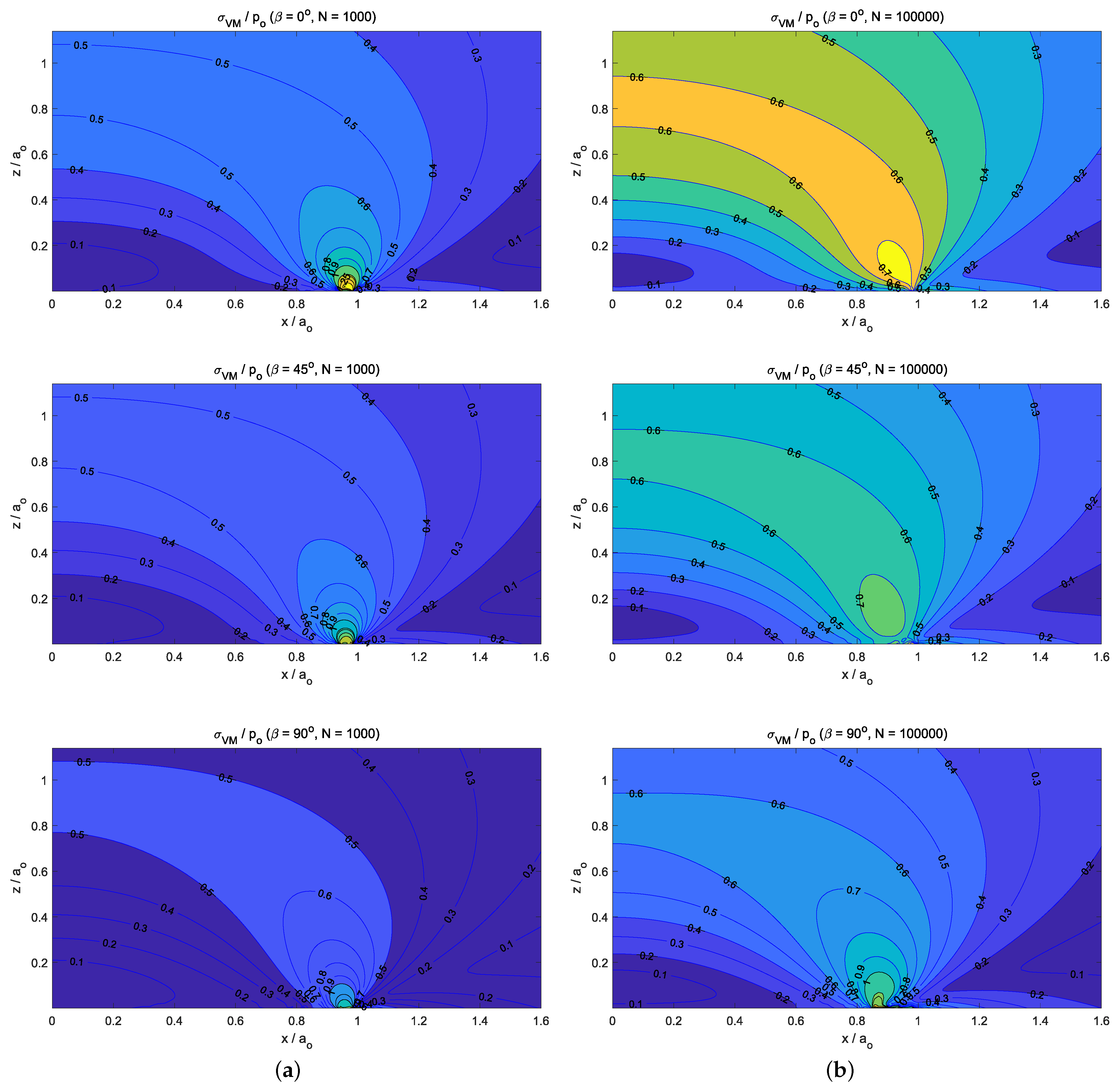
- For the static normally loaded cylindrical flat-punch (see Section 7.1), the stick region in the contact zone increased with the value of the friction coefficient until a threshold value was reached (i.e., in our analysis). Then, all the points of the contact area reached a contact–stick state. Additionally, on the subsurface von Mises stress distributions (see Figure 5b–f), we observed that the size of the region with increased with the friction coefficient value—and new stress gradient around the z-axis appeared—until the threshold value was reached. However, when the friction intensity reached the mentioned threshold value, no more changes were observed in the normalized von Mises stress distribution.
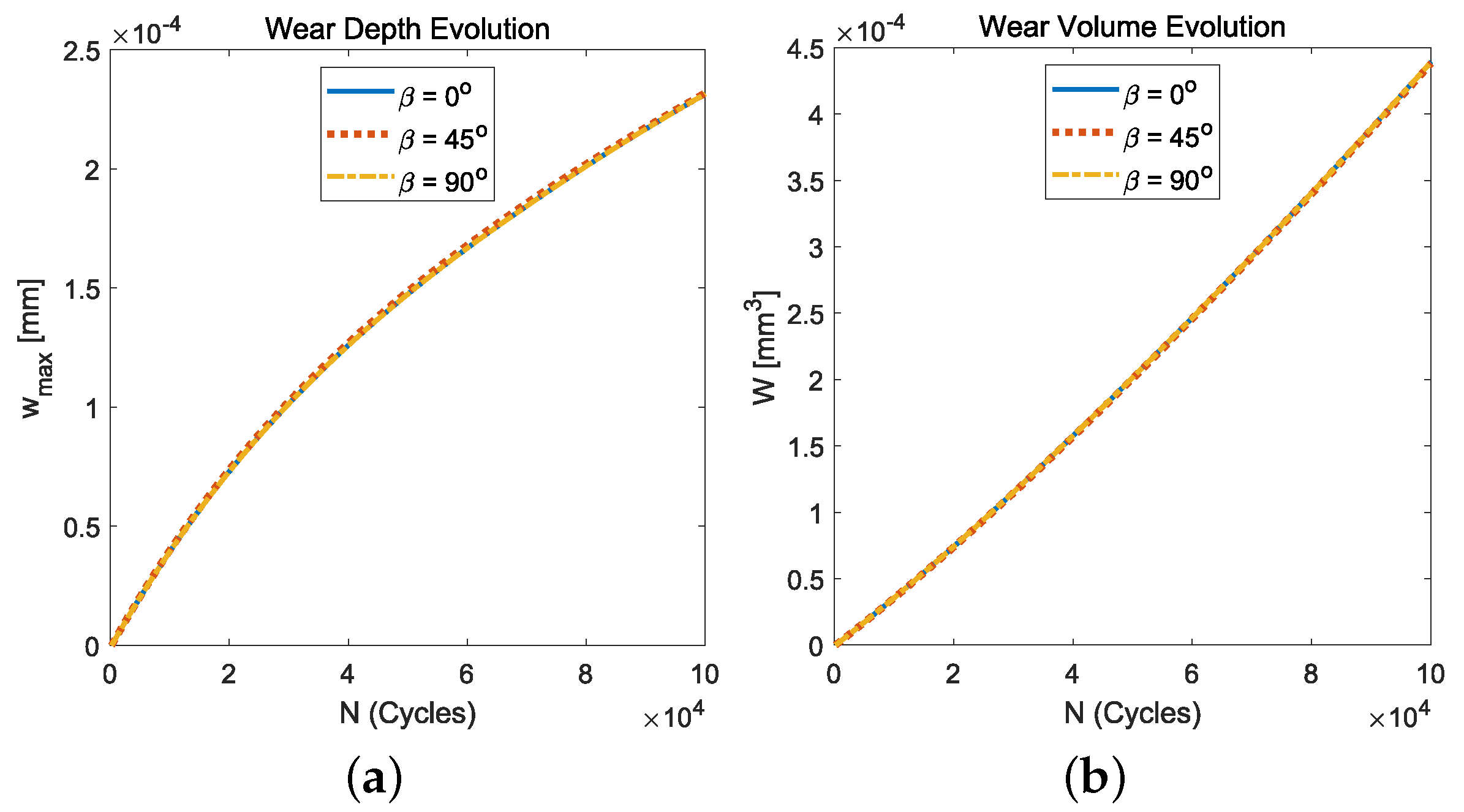
- Regarding the response under isotropic fretting wear conditions caused by the normal cyclic loading conditions (i.e., radial fretting wear), we observed how the smaller the friction coefficient value was, the greater the wear damage (i.e., maximum wear depth or wear volume) obtained. This was due to the fact that the smaller the friction coefficient value was, the bigger the annular sliding contact zone obtained.
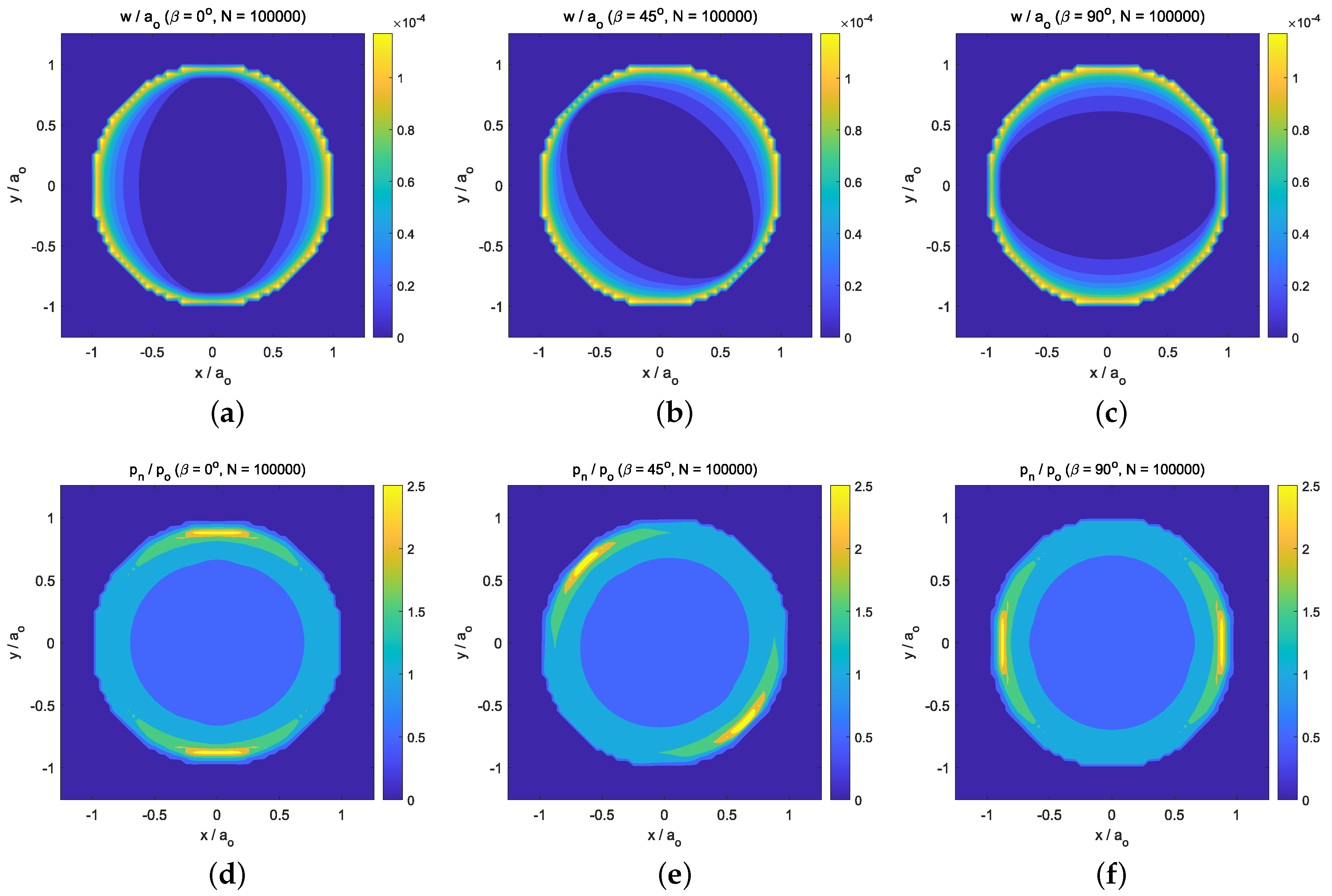
- The influence of friction intensity can be observed—after a big number of load cycles (i.e., )—on the resulting surface wear depth, the normal tractions, and the subsurface von Mises stress values. Due to the fact that isotropic friction and wear laws were considered, their distributions presented a z-axis symmetry. In particular, with regard to the location of the maximum stress value, the low friction values (i.e., ) caused important wear damage on the solid surfaces. Moreover, this also led to a stress distribution where the maximum value of the subsurface von Mises stress was located at and . On the other hand, when high friction values were considered (i.e., ), low wear damage was produced on the solid surfaces, and therefore, the stress distribution presented its maximum value located on the surface and at the edge of the contact circle ().
- Finally, the response under orthotropic fretting wear conditions caused by the normal cyclic loading conditions did not present a z-axis symmetry. The maximum value of the normal contact pressure distributions was located where the wear depth distributions presented the greatest gradient values. This region was located at the intersection of the edge of the contact circle and the direction of the tribological principal axis with the greatest friction coefficient. Moreover, contrary to what was observed for isotropic fretting wear conditions, the location of the maximum values of the subsurface stress after a high number of cycles ( cycles) remained at the edge of the contact circle, which, due to wear, was slightly less than .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Roman symbols: | |
| Cylindrical punch radius | |
| Displacement kernel function to take into account the contribution of the surface | |
| j-component contact traction on the relative i-component displacement on the | |
| solid surface | |
| Displacement kernel function matrix | |
| Tribological axes | |
| E | Young’s modulus |
| Reduced or effective elastic modulus | |
| Elliptic norm based on the friction intensity coefficient | |
| Geometrical gap | |
| Tangential slip velocity (-component) | |
| Tangential slip velocity (-component) | |
| Normal gap | |
| Rigid body normal approach | |
| Rigid body tangential slip | |
| Tangential slip vector | |
| Tangential slip velocity vector | |
| G | Shear modulus |
| Wear coefficient | |
| Principal wear coefficient in the -direction | |
| Principal wear coefficient in the -direction | |
| Contact stiffness | |
| N | Number of load cycles |
| Number of mesh elements | |
| Number of mesh divisions in the x-direction | |
| Number of mesh divisions in the y-direction | |
| P | Static normal load |
| Tangential contact traction (-component) expressed in | |
| Tangential contact traction (-component) expressed in | |
| Average contact pressure | |
| Normal contact pressure | |
| Augmented normal contact traction | |
| Tangential contact traction (x-component) | |
| Tangential contact traction (y-component) | |
| Normal contact traction | |
| Contact traction vector | |
| Tangential contact traction vector | |
| Augmented tangential contact traction vector | |
| Normal projection function | |
| Tangential projection function | |
| r | Radial–cylindrical coordinate |
| Normal penalty parameter | |
| Tangential penalty parameter | |
| Stress kernel function to take into account the contribution of the normal contact traction | |
| on the tress tensor -component in the solid | |
| Stress kernel function to take into account the contribution of the x-component | |
| tangential contact traction on the tress tensor -component in the solid | |
| Stress kernel function to take into account the contribution of the y-component | |
| tangential contact traction on the tress tensor -component in the solid | |
| Stress kernel function matrix | |
| Surface relative normal displacement | |
| Surface relative displacement (x-component) | |
| Surface relative displacement (y-component) | |
| Surface relative displacement (z-component) | |
| Surface relative tangential displacement vector | |
| Cartesian coordinate system | |
| Position vector of a solid interior point | |
| Position vector of a solid surface point | |
| Greek symbols: | |
| Tribological axes’ angle orientation | |
| Contact zone | |
| Tangential slip increment | |
| Element size in the x-direction | |
| Element size in the y-direction | |
| Pseudo-time increment | |
| Wear depth increment | |
| Friction intensity coefficient | |
| Principal friction coefficient in the -direction | |
| Principal friction coefficient in the -direction | |
| Poisson’s ratio | |
| Stress tensor -component | |
| Radial stress | |
| Circumferential stress | |
| von Mises stress | |
| Normal stress | |
| Pseudo-time | |
| Pseudo-time k-instant | |
| Shear stress | |
| Wear depth | |
| Wear rate | |
| Solid domain | |
Appendix A
References
- Johns-Rahnejat, P.M.; Dolatabadi, N.; Rahnejat, H. Analytical Elastostatic Contact Mechanics of Highly-Loaded Contacts of Varying Conformity. Lubricants 2020, 8, 89. [Google Scholar] [CrossRef]
- Jin, X.; Niu, F.; Zhang, X.; Zhou, Q.; Lyu, D.; Keer, L.M.; Hu, Y. Love’s rectangular contact problem revisited: A complete solution. Tribol. Int. 2016, 103, 331–342. [Google Scholar] [CrossRef]
- Fereidouni, H.; Akbarzadeh, S.; Khonsari, M.M. The Relation Between Subsurface Stresses and Useful Wear Life in Sliding Contacts. Tribol. Lett. 2020, 68, 1–3. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts; Almquist and Wiksells Akademiska Handbócker: Stockholm, Sweden, 1946. [Google Scholar]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Galin, L.A. Contact problems of the theory of elasticity in the presence of wear. J. Appl. Math. Mech. 1976, 40, 931–936. [Google Scholar] [CrossRef]
- Galin, L.A.; Goryacheva, I.G. Axisymmetric contact problem of the theory of elasticity oin the presence of wear. J. Appl. Math. Mech. 1977, 41, 826–831. [Google Scholar] [CrossRef]
- Aleksandrov, V.M.; Kovalenko, E.V. Plane conact problems of the theory of elasticity for nonclassical regions in the presence of wear. J. Appl. Mech. Tech. Phys. 1980, 3, 421–4427. [Google Scholar]
- Kovalenko, E.V. Study of the axisymmetric contact problem of the wear of a pair consisting of an annular stamp and a rough half-space. J. Appl. Math. Mech. 1985, 49, 641–647. [Google Scholar] [CrossRef]
- Kragelsky, I.V. Friction and Wear Calculation Methods; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Komogortsev, V.F. Contact between a moving stamp and an elastic half-plane when there is wear. J. Appl. Math. Mech. 1985, 49, 243–246. [Google Scholar] [CrossRef]
- Hills, D.A.; Fellows, L.J. Some observations on contact problems involving fretting in the presence of wear. Wear 1999, 231, 319–324. [Google Scholar] [CrossRef]
- Hills, D.A.; Sackfield, A.; Paynter, R.J.H. Simulation of fretting wear in half-plane geometries. Part 1. The solution for long term wear. J. Tribol. 2009, 131, 031401. [Google Scholar] [CrossRef]
- Goryacheva, I.; Rajeev, P.; Farris, T. Wear in partial slip contact. J. Tribol. 2001, 123, 848–856. [Google Scholar] [CrossRef]
- Olofsson, U.; Andersson, S.; Bjorklund, S. Simulation of mild wear in boundary lubricated spherical roller thrust bearing. Wear 2000, 241, 180–185. [Google Scholar] [CrossRef]
- Enblom, R.; Berg, M. Simulation of railway wheel profile development due to wear-influence of disc braking and contact environment. Wear 2005, 258, 1055–1063. [Google Scholar] [CrossRef]
- Telliskivi, T. Simulation of wear in a rolling-sliding contact by a semi-Winkler model and the Archard’s wear law. Wear 2004, 256, 817–831. [Google Scholar] [CrossRef]
- Hegadekatte, V.; Kurzenhäuser, S.; Kraft, O. Predictive modeling scheme for wear in tribometers. Tribol. Int. 2008, 41, 1020–1031. [Google Scholar] [CrossRef] [Green Version]
- Argatov, I.I. Asymptotic modeling of reciprocating sliding wear with application to local interwire contact. Wear 2011, 271, 1147–1155. [Google Scholar] [CrossRef]
- Argatov, I.I.; Tato, W. Asymptotic modeling of reciprocating sliding wear - Comparison with finite-element simulations. Eur. J. Mech. A Solids 2012, 34, 1–11. [Google Scholar] [CrossRef]
- Argatov, I.I.; Chai, Y.S. Effective wear coefficient and wearing-in period for a functionally graded wear-resisting punch. Acta Mech. 2019, 230, 2295–2307. [Google Scholar] [CrossRef]
- Argatov, I.I.; Chai, Y.S. Wear contact problem with friction: Steady-state regime and wearing-in period. Int. J. Solids Struct. 2020, 193–194, 213–221. [Google Scholar] [CrossRef]
- Di Puccio, F.; Mattei, L. In-silico Analytical Wear Predictions: Application to Joint Prostheses. In Wear in Advanced Engineering Applications and Materials; Rodriguez-Tembleque, L., Aliabadi, M.H., Eds.; World Scientific: Singapore, 2022; pp. 123–148. [Google Scholar]
- Di Puccio, F.; Mattei, L. Simple analytical description of contact pressure and wear evolution in non-conformal contacts. Tribol. Int. 2023, 178, 108084. [Google Scholar] [CrossRef]
- Popov, V.L. Analytic solution for the limiting shape of profiles due to fretting wear. Sci. Rep. 2014, 4, 3749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cubillas, D.; Olave, M.; Llavori, I.; Ulacia, I.; Larrañaga, J.; Zurutuza, A.; Lopez, A. A novel formulation for radial fretting wear: Application to false brinelling in thrust bearings. Wear 2022, 488–489, 204078. [Google Scholar] [CrossRef]
- Johansson, L. Numerical simulation of contact pressure evolution in fretting. J. Tribol. 1994, 116, 247–254. [Google Scholar] [CrossRef]
- Strömberg, N.; Johansson, L.; Klarbring, A. Derivation and analysis of a generalized standard model for contact, friction and wear. Int. J. Solids 1996, 33, 1817–1836. [Google Scholar] [CrossRef]
- Strömberg, N. An augmented lagrangian method for fretting problems. Eur. J. Mech. A Solids 1997, 16, 573–593. [Google Scholar]
- Strömberg, N. Newton method for three-dimensional fretting problems. Int. J. Solids Struct. 1999, 36, 2075–2090. [Google Scholar] [CrossRef]
- Ireman, P.; Klarbring, A.; Stromberg, N. Finite element algorithms for thermoelastic wear problems. J. Mech. A Solids 2002, 21, 423–440. [Google Scholar] [CrossRef] [Green Version]
- Ireman, P.; Klarbring, A.; Strömberg, N. Gradient theory of damage coupled to frictional contact and wear, and its numerical treatment. Comput. Model. Eng. Sci. 2009, 52, 125–158. [Google Scholar]
- McColl, I.; Ding, J.; Leen, S. Finite element simulation and experimental validation of fretting wear. Wear 2004, 256, 1114–1127. [Google Scholar] [CrossRef]
- Chai, Y.S.; Lee, C.Y.; Bae, J.W.; Lee, S.Y.; Hwang, J.K. Finite element analysis of fretting wear problems in consideration of frictional contact. Key Eng. Mater. 2005, 297–300, 1406–1411. [Google Scholar] [CrossRef]
- Mary, C.; Fouvry, S. Numerical prediction of fretting contact durability using energy wear approach: Optimisation of finiteelement model. Wear 2007, 263, 444–450. [Google Scholar] [CrossRef]
- Bae, J.W.; Choon, Y.L.; Chai, Y.S. Three dimensional fretting wear analysis by finite element substructure method. Int. J. Precis. Eng. Manufact. 2009, 10, 63–69. [Google Scholar] [CrossRef]
- Paczelt, I.; Mróz, Z. Optimal shapes of contact interfaces due to sliding wear in the steady relative motion. Int. J. Solids Struct. 2007, 44, 895–925. [Google Scholar] [CrossRef] [Green Version]
- Farah, P.; Wall, W.; Popp, A. An implicit finite wear contact formulation based on dual mortar methods. Int. J. Num. Meth. Engng. 2017, 111, 325–353. [Google Scholar] [CrossRef]
- Doca, T.; Andrade Pires, F. Finite element modeling of wear using the dissipated energy method coupled with a dual mortar contact formulation. Comput. Struct. 2017, 191, 62–79. [Google Scholar] [CrossRef]
- Sfantos, G.K.; Aliabadi, M.H. Application of BEM and optimization technique to wear problems. Int. J. Solids Struct. 2006, 43, 3626–3642. [Google Scholar] [CrossRef] [Green Version]
- Sfantos, G.K.; Aliabadi, M.H. Wear simulation using an incremental sliding boundary element method. Wear 2006, 260, 1119–1128. [Google Scholar] [CrossRef]
- Sfantos, G.K.; Aliabadi, M.H. A boundary element formulation for three dimensional sliding wear simulation. Wear 2007, 262, 672–683. [Google Scholar] [CrossRef]
- Paczelt, I.; Kucharski, S.; Mróz, Z. The experimental and numerical analysis of quasi-steady wear processes for a sliding spherical indenter. Wear 2012, 274–275, 127–148. [Google Scholar] [CrossRef]
- Nowell, D. Simulation of fretting wear in half-plane geometries. Part II. Analysis of the transient wear problem using quadratic programming. J. Tribol. 2010, 132, 021402. [Google Scholar] [CrossRef]
- Gallego, L.; Nelias, D.; Deyber, S. A fast and efficient contact algorithm for fretting problems applied to fretting modes i, ii and iii. Wear 2010, 268, 208–222. [Google Scholar] [CrossRef]
- Kim, T.W.; Moon, S.M.; Cho, Y.J. Prediction of fretting wear using boundary element method. Tribol. Int. 2011, 44, 1571–1576. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, L.; Abascal, R.; Aliabadi, M.H. A boundary element formulation for 3D fretting wear problems. Eng. Anal. Bound. Elem. 2011, 35, 935–943. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, L.; Aliabadi, M.H. Numerical simulation of fretting wear in fiber-reinforced composite materials. Eng. Fract. Mech. 2016, 168, 13–27. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, L.; Abascal, R.; Aliabadi, M.H. A boundary element formulation for wear modeling on 3D contact and rolling-contact problems. Int. J. Solids. Struct. 2010, 47, 2600–2612. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Tembleque, L.; Abascal, R.; Aliabadi, M.H. Anisotropic wear framework for 3D contact and rolling problems. Comput. Methods Appl. Mech. Eng. 2012, 241, 1–19. [Google Scholar] [CrossRef]
- Aghababaei, R.; Warner, D.; Molinari, J.F. Critical length scale controls adhesive wear mechanisms. Nat. Commun. 2016, 7, 11816. [Google Scholar] [CrossRef] [Green Version]
- Aghababaei, R.; Warner, D.; Molinari, J.F. On the debris-level origins of adhesive wear. Proc. Natl. Acad. Sci. USA 2017, 114, 7935–7940. [Google Scholar] [CrossRef] [Green Version]
- Huber, M.T. Zur Theorie der beruhrung fester elastischer korper. Ann. Phys. 1904, 319, 153–163. [Google Scholar] [CrossRef] [Green Version]
- Huber, M.T.; Fuchs, S. Spannungverleitung bei der beruhrung zweier elastischer zylinder. Phys. Zeitschr. 1914, 15, 298–303. [Google Scholar]
- Lyman, J. Reversing normal strains produced by rolling contact load. J. Lubr. Technol. 1967, 89, 76–80. [Google Scholar] [CrossRef]
- Poritsky, H. Stresses and deflections of cylindrical bodies in contact with application to contact of gears and locomotive wheels. J. Appl. Mech. 1950, 18, 191–201. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Mihailidis, A.; Bakolas, V.; Drivakos, N. Subsurface stress field of a dry line contact. Wear 2001, 249, 546–5562. [Google Scholar] [CrossRef]
- Barber, J.R. Contact problems for the thin elastic layer. Int. J. Mech. Sci. 1990, 32, 129–132. [Google Scholar] [CrossRef] [Green Version]
- Teodorescu, M.; Rahnejat, H.; Gohar, R.; Dowson, D. Harmonic decomposition analysis of contact mechanics of bonded layered elastic solids. Appl. Math. Model. 2009, 33, 467–485. [Google Scholar] [CrossRef]
- Chidlow, S.J.; Teodorescu, M.; Vaughan, N.D. A solution method for the sub-surface stresses and local deflection of a semi-infinite inhomogeneous elastic medium. Appl. Math. Model. 2012, 36, 3486–3501. [Google Scholar] [CrossRef]
- Elsharkawy, A.A.; Hamrock, B.J. Subsurface stresses in micro-EHL line contacts. J. Tribol. 1991, 113, 645–655. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, A.; Gao, P. A study of spur gear pitting under EHL conditions: Theoretical analysis and experiments. Tribol. Int. 2016, 94, 146–154. [Google Scholar] [CrossRef]
- Sivayogan, G.; Rahmani, R.; Rahnejat, H. Lubricated loaded tooth contact analysis and non-newtonian thermoelastohydrodynamics of high-performance spur gear transmission systems. Lubricants 2020, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- Sackfield, A.; Hills, D.A. Some useful results in the classical Hertzian contact problem. J. Strain Anal. Eng. Des. 1983, 18, 101–105. [Google Scholar] [CrossRef]
- Sackfield, A.; Hills, D.A. Some useful results in the tangentially loaded Hertzian contact problem. J. Strain Anal. Eng. Des. 1983, 18, 107–110. [Google Scholar] [CrossRef]
- Greenwood, J.A. Subsurface stresses in an elliptical Hertzian contact. J. Strain Anal. Eng. Des. 2022, 57, 677–687. [Google Scholar] [CrossRef]
- Johns-Rahnejat, P.M.; Gohar, R. Point contact elastohydrodynamic pressure distribution and sub-surface stress field. In Proceedings of the Tri-Annual Conference on Multi-Body Dynamics: Monitoring and Simulation Techniques, Bradford, UK, 25–27 March 1997; Mechanical Engineering Publishing: Bradford, UK, 1997; pp. 161–179. [Google Scholar]
- Güler, M.A.; Kucuksucu, A.; Yilmaz, K.B.; Yildrim, B. On the analytical and finite element solution of plane contact problem of a rigid cylindrical punch sliding over a functionally graded orthotropic medium. Int. J. Mech. Sci. 2016, 120, 12–29. [Google Scholar] [CrossRef]
- Meshcheryakova, A.R.; Goryacheva, I.G. Stress State of Elastic Bodies with an Intermediate Layer in Rolling Contact with Slip. Phys. Mesomech. 2021, 23, 91–101. [Google Scholar] [CrossRef]
- Juliá, J.; Rodríguez-Tembleque, L. Subsurface stress evolution under orthotropic wear and frictional contact conditions. Int. J. Mech. Sci. 2022, 234, 107695. [Google Scholar] [CrossRef]
- Sneddon, I.N. Boussinesq’s problem for a flat-ended cylinder. Proc. Camb. Philos. Soc. 1946, 42, 29–39. [Google Scholar] [CrossRef]
- Harding, J.W.; Sneddon, I.N. The elastic stresses produced by the indentation of the plane surface of a semi-infinite elastic solid by a rigid punch. Proc. Camb. Philos. Soc. 1945, 41, 16–26. [Google Scholar] [CrossRef]
- Barquins, M.; Maugis, D. Adhesive contact of axisymmetric punches on an elastic half-space: The modified Hertz-Huber’s stress tensor for contacting spheres. J. Mec. Theor. Appl. 1982, 12, 331–357. [Google Scholar]
- Fischer-Cripps, A.C. Introduction to Contact Mechanics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Popov, V.L.; Heß, M.; Willert, E. Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Kalker, J.J.; Jacobson, B. Rolling Contact Phenomena; Springer: Vienna, Austria, 2000. [Google Scholar]
- Willner, K. Fully Coupled Frictional Contact Using Elastic Halfspace Theory. J. Tribol. 2008, 130, 031405. [Google Scholar] [CrossRef]
- Pohrt, R.; Li, Q. Complete boundary element formulation for normal and tangential contact problems. Phys. Mesomech. 2014, 17, 334–340. [Google Scholar] [CrossRef]
- Kikuchi, N.; Oden, J. Contact Problems in Elasticity: A Study of Variational Inequalities and Finite Element Methods; SIAM: Philadelphia, PA, USA, 1987. [Google Scholar]
- Laursen, T.A. Computational Contact and Impact Mechanics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Wriggers, P. Computational Contact Mechanics; Spriger: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Liu, S.; Wang, Q. Studying Contact Stress Fields Caused by Surface Tractions with a Discrete Convolution and Fast Fourier Transform Algorithm. J. Tribol. 2002, 124, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Kalker, J.J. Three-Dimensional Elastic Bodies in Rolling Contact; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Wayne Chen, W.; Jane Wang, Q. A numerical model for the point contact of dissimilar materials considering tangential tractions. Mech. Mater. 2008, 40, 936–948. [Google Scholar] [CrossRef]
- Bazrafshan, M.; de Rooij, M.B.; Schipper, D.J. On the role of adhesion and roughness in stick-slip transition at the contact of two bodies: A numerical study. Tribol. Int. 2018, 121, 381–388. [Google Scholar] [CrossRef]
- Alart, P.; Curnier, A. A mixed formulation for frictional contact problems prone to Newton like solution methods. Comput. Methods Appl. Mech. Eng. 1991, 92, 353–375. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, L.; Abascal, R. Fast FE-BEM algorithms for orthotropic frictional contact. Int. J. Numer. Methods Eng. 2013, 94, 687–707. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, L.; Abascal, R. A 3D FEM-BEM rolling contact formulation for unstructured meshes. Int. J. Solids Struct. 2010, 47, 330–353. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, L.; Abascal, R. A FEM-BEM fast methodology for 3D frictional contact problems. Comput. Struct. 2010, 88, 924–937. [Google Scholar] [CrossRef]
- Rabinowicz, E. Friction and Wear of Materials; John Wiley & Sons: Hoboken, NJ, USA, 1965. [Google Scholar]
- Paczelt, I.; Mróz, Z. Solution of wear problems for monotonic and periodic sliding with p-version of the finite element method. Comput. Meth. Appl. Mech. Eng. 2012, 249–252, 75–103. [Google Scholar] [CrossRef]
- Stupkiewicz, S. An ALE formulation for implicit time integration of quasi-steady-state wear problems. Comput. Meth. Appl. Mech. Eng. 2013, 260, 130–142. [Google Scholar] [CrossRef]
- Cavalieri, J.F.; Cardona, A. Three-dimensional numerical solution for wear prediction using a mortar contact algorithm. Int. J. Numer. Methods Eng. 2013, 96, 467–486. [Google Scholar] [CrossRef]
- Lengiewicz, J.; Stupkiewicz, S. Efficient model of evolution of wear in quasi-steady-state sliding contacts. Wear 2013, 303, 611–621. [Google Scholar] [CrossRef]
- Mróz, Z.; Stupkiewicz, S. An anisotropic friction and wear model. Int. J. Solids Struct. 1994, 31, 1113–1131. [Google Scholar] [CrossRef]
- Mróz, Z.; Kucharski, S.; Paczelt, I. Anisotropic friction and wear rules with account for contact state evolution. Wear 2018, 396, 1–11. [Google Scholar] [CrossRef]
- Kachanov, M.; Shafiro, B.; Tsukrov, T. Handbook of Elasticity Solutions; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Mossakovskii, V.I. The fundamental mixed problem of the theory of elasticity for ahalf-space with a circular line separating the boundary conditions. Prikl. Matem. Mekhanika 1954, 18, 187–196. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juliá, J.M.; Rodríguez-Tembleque, L. Wear and Subsurface Stress Evolution in a Half-Space under Cyclic Flat-Punch Indentation. Lubricants 2023, 11, 265. https://doi.org/10.3390/lubricants11060265
Juliá JM, Rodríguez-Tembleque L. Wear and Subsurface Stress Evolution in a Half-Space under Cyclic Flat-Punch Indentation. Lubricants. 2023; 11(6):265. https://doi.org/10.3390/lubricants11060265
Chicago/Turabian StyleJuliá, Javier M., and Luis Rodríguez-Tembleque. 2023. "Wear and Subsurface Stress Evolution in a Half-Space under Cyclic Flat-Punch Indentation" Lubricants 11, no. 6: 265. https://doi.org/10.3390/lubricants11060265
APA StyleJuliá, J. M., & Rodríguez-Tembleque, L. (2023). Wear and Subsurface Stress Evolution in a Half-Space under Cyclic Flat-Punch Indentation. Lubricants, 11(6), 265. https://doi.org/10.3390/lubricants11060265





