A New Thermal Elasto-Hydrodynamic Lubrication Solver Implementation in OpenFOAM
Abstract
:1. Introduction
2. Materials and Methods
2.1. Thermo-Elastohydrodynamic Lubrication Model
2.1.1. Reynolds Equation
2.1.2. Film Height
2.1.3. Temperature Equation
2.1.4. Fluid Viscosity
2.1.5. Cavitation
2.1.6. Material Properties
2.2. Solid Region Models
2.3. Boundary Conditions
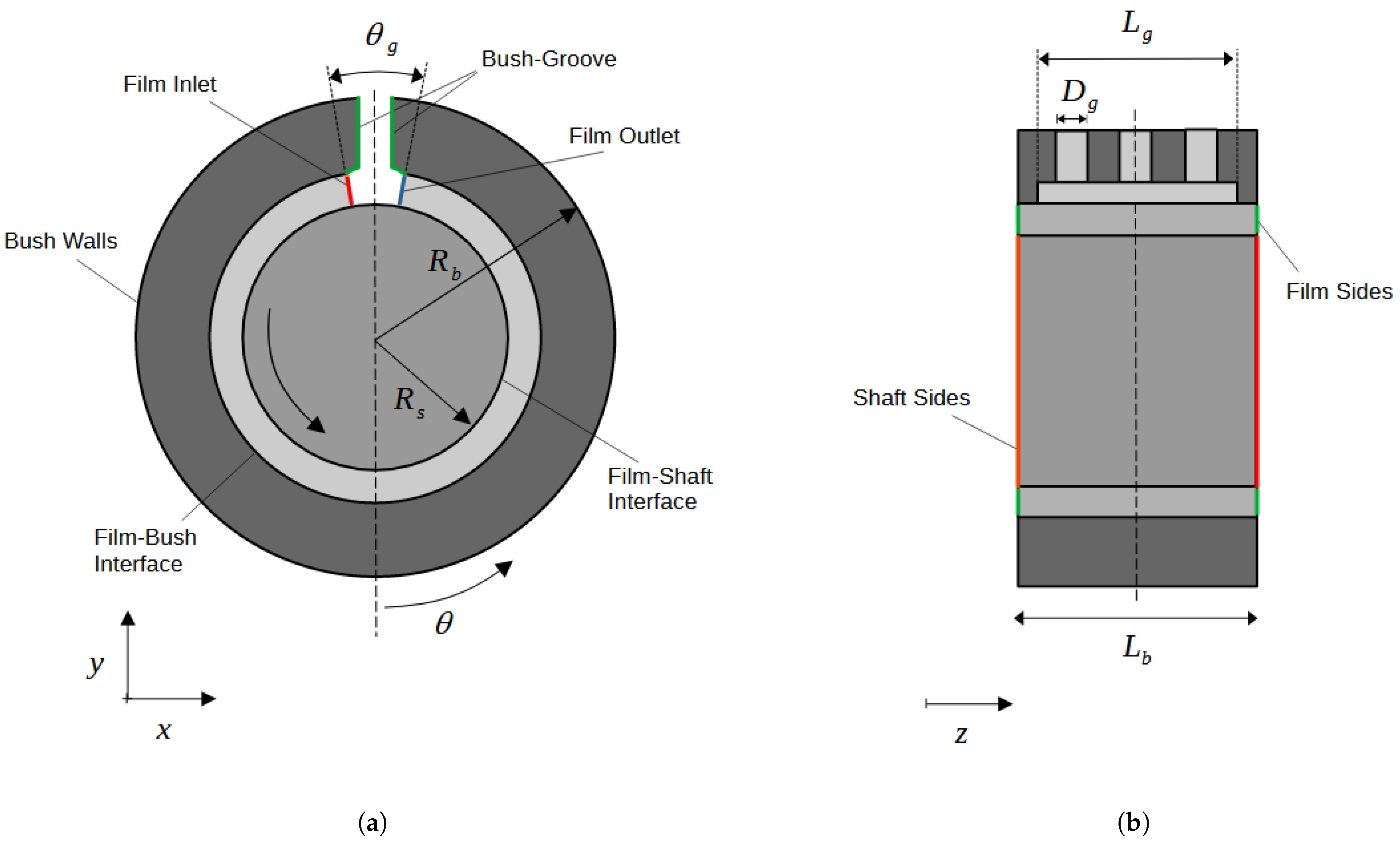
2.4. Numerical Setup
2.4.1. Mesh Setup
2.4.2. Discretisation
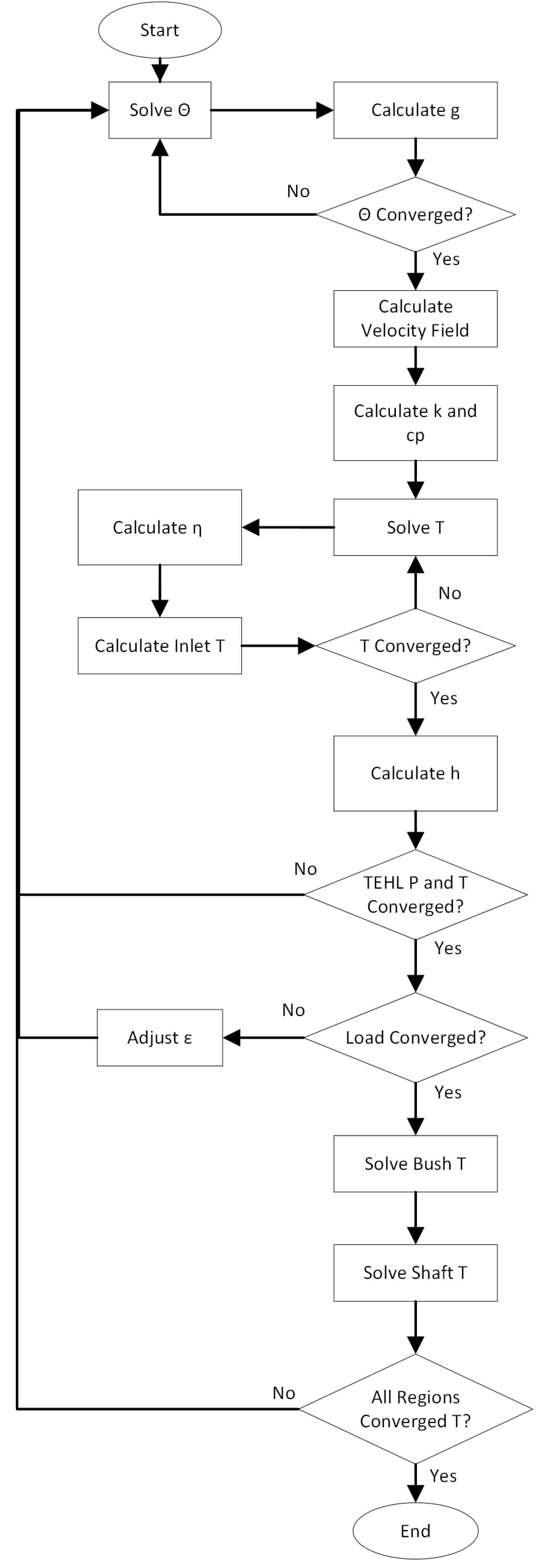
2.4.3. Procedure
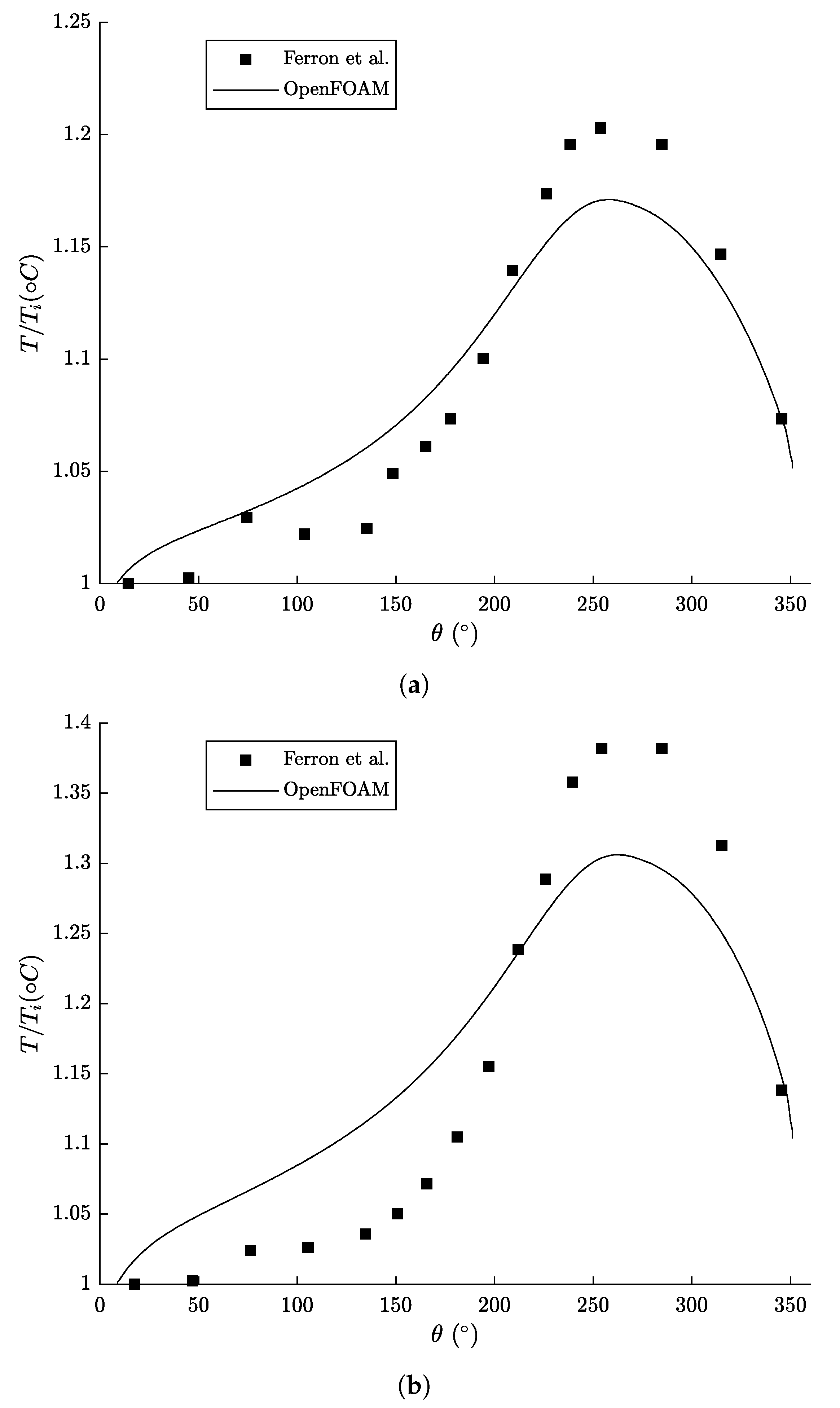
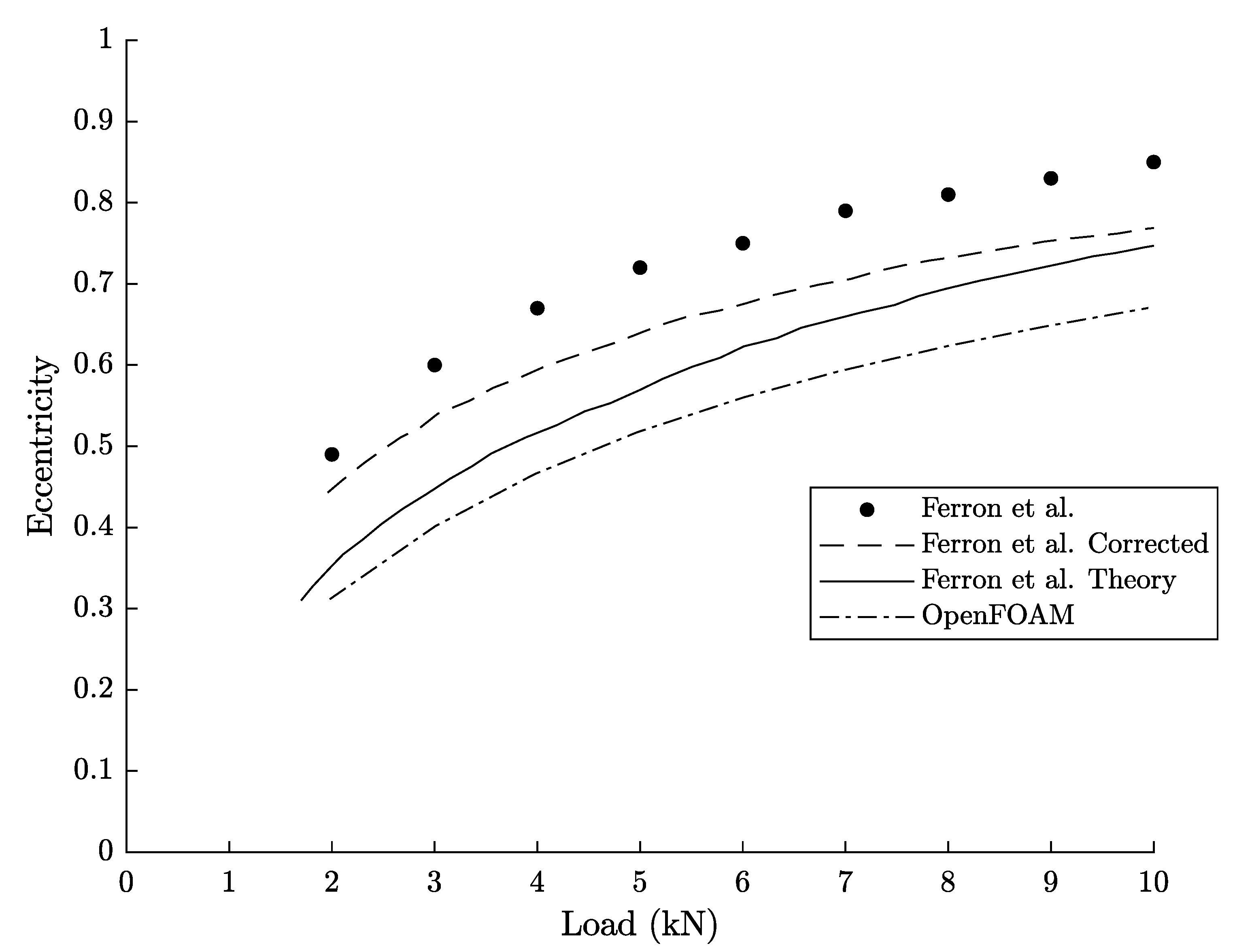
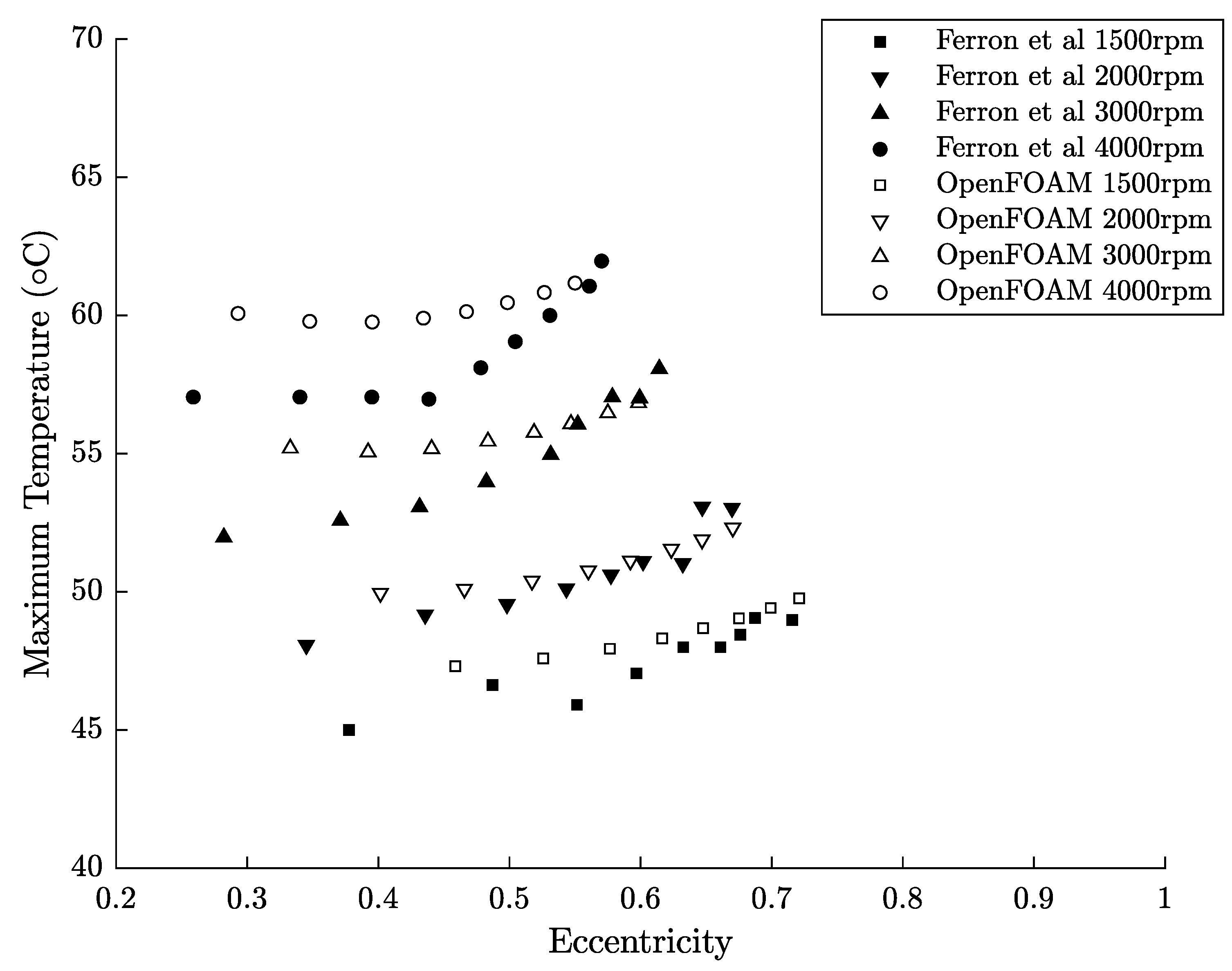
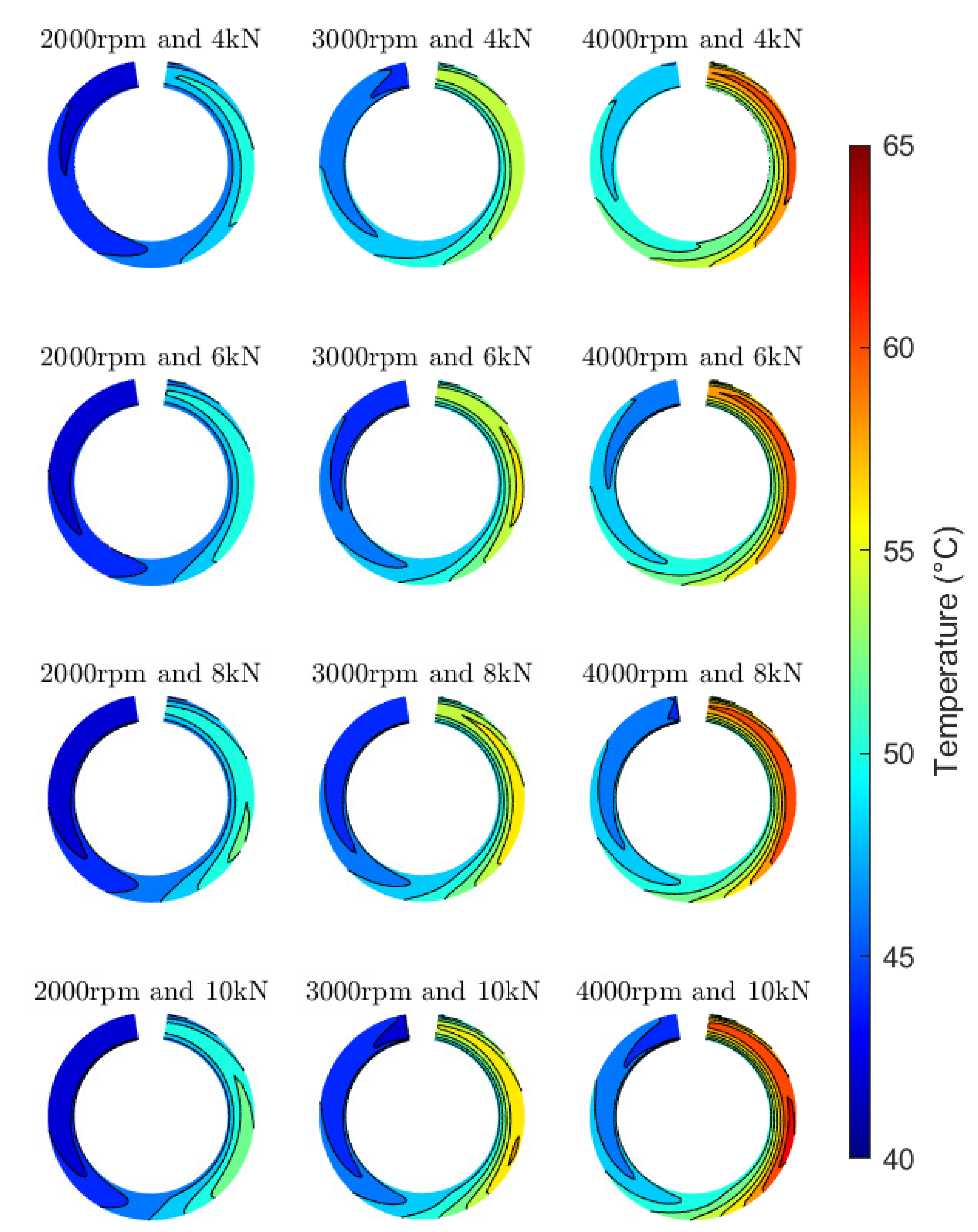
3. Results and Discussion
3.1. Case Description
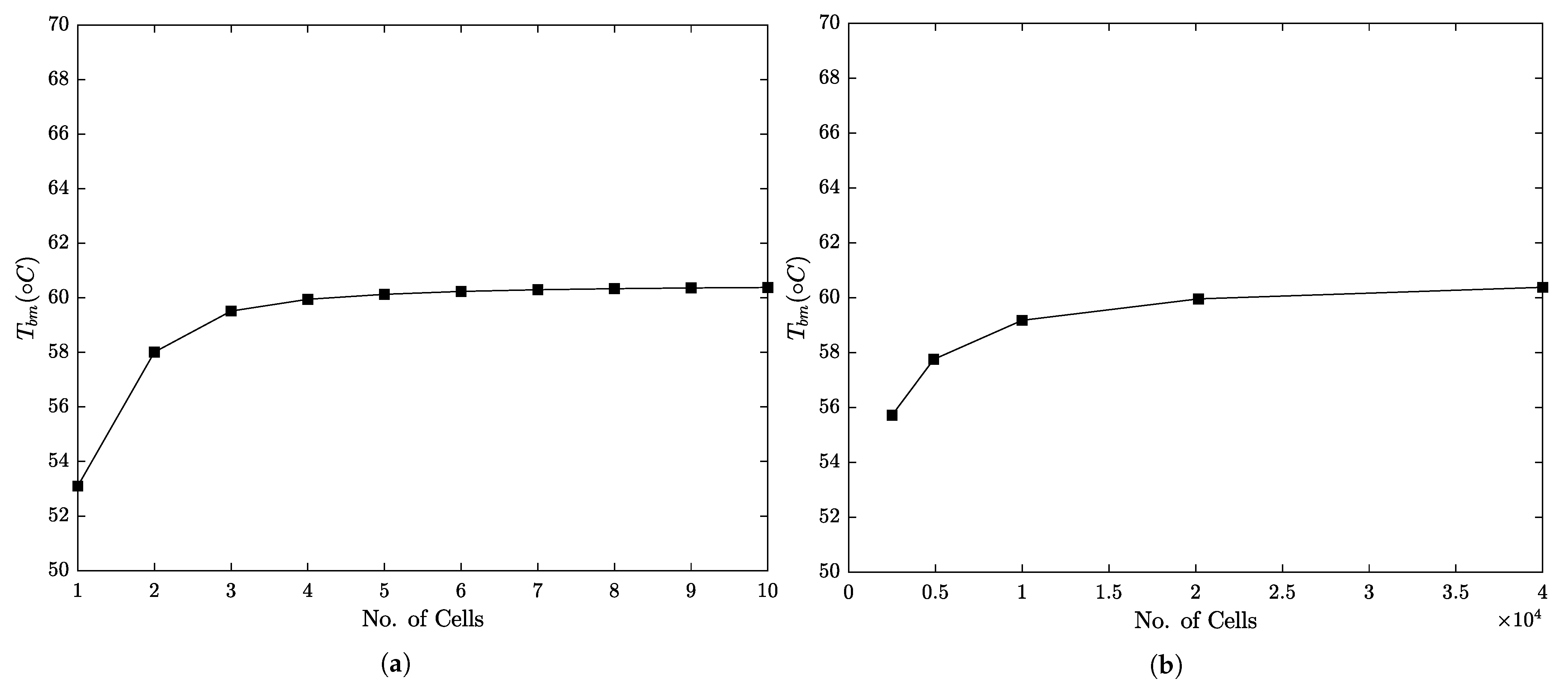
3.2. Mesh Study
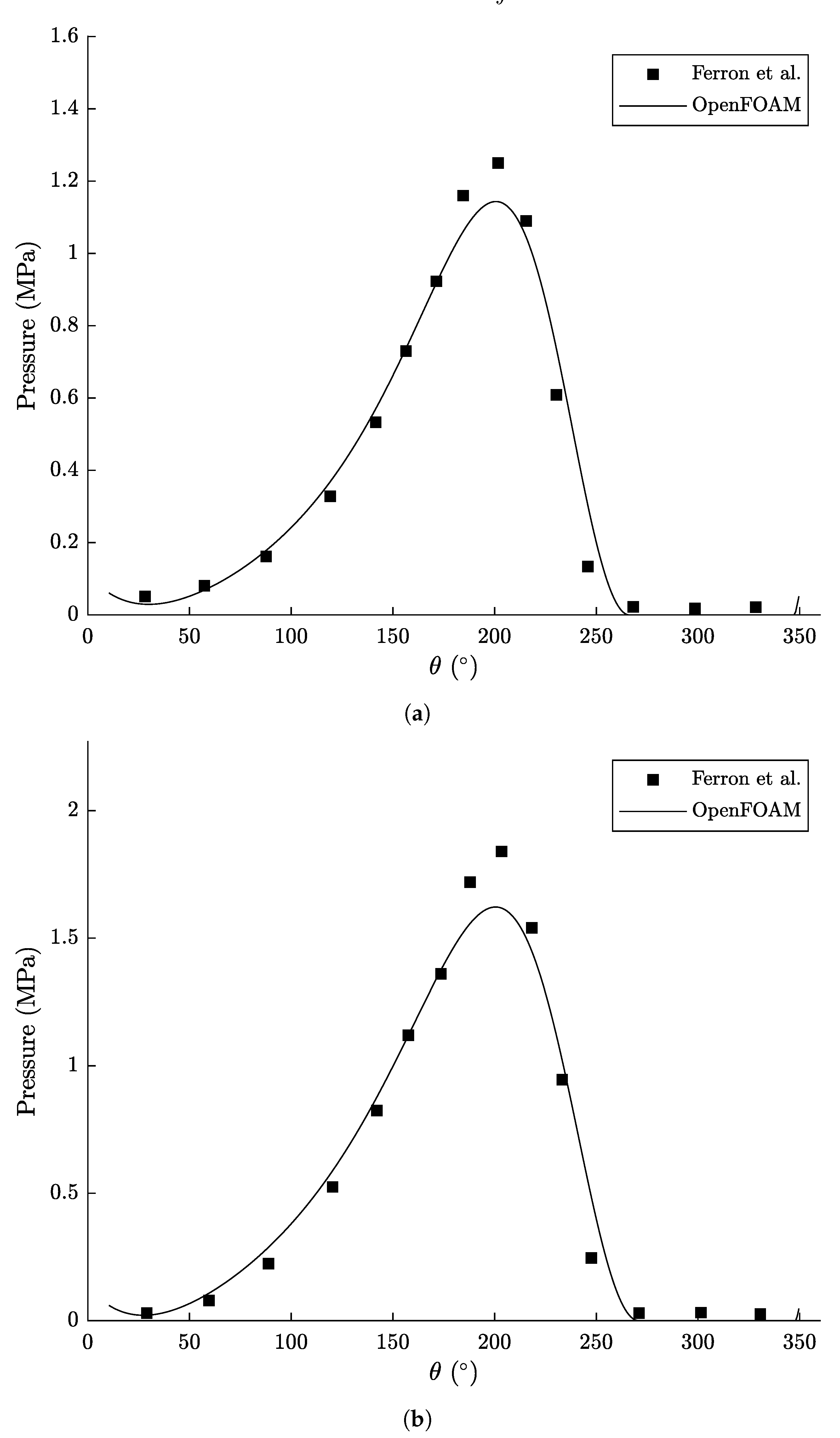
3.3. Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Thermal expansion coefficient | |
| Lubricant properties () | |
| P | Lubricant pressure (Pa) |
| Reference pressure (Pa) | |
| h | Film height (m) |
| Film height generated from the eccentricity of the shaft (m) | |
| Surface deformation (m) | |
| Thermal dilation (m) | |
| Temperature in the lubricant film (C) | |
| Temperature in the bush (C) | |
| Reference temperature (C) | |
| Relative density | |
| g | Switch variable |
| Lubricant density () | |
| Lubricant density at reference pressure (kg/m) | |
| Dynamic viscosity () | |
| Dynamic viscosity at reference temperature (Pas) | |
| Shaft surface velocity () | |
| Couette term of velocity () | |
| Coordinates in the circumferential, radial and axial directions, respectively | |
| c | Clearance (m) |
| Eccentricity | |
| Angular coordinate () | |
| e | Distance between shaft and bush axes (m) |
| E | Young’s modulus (Pa) |
| v | Poisson’s ratio |
| Lubricant specific heat capacity () | |
| Thermal conductivity of the lubricant liquid and gaseous phases, respectively () | |
| Thermal conductivity of the shaft and bush, respectively () | |
| Unit vector parallel to the bush in the direction of the flow | |
| Non-dimensional film height | |
| Heat generation (Km) | |
| E | Young’s modulus Pa |
| v | Poisson’s ratio |
| R | Radius |
References
- European Commission, Directorate-General for Mobility and Transport, Directorate-General for Research and Innovation. Flightpath 2050: Europe’s Vision for Aviation: Maintaining Global Leadership and Serving Society’s Needs; Publications Office of the European Union: Luxembourg, 2011. [Google Scholar] [CrossRef]
- Hartinger, M.; Dumont, M.; Ioannides, S.; Gosman, D.; Spikes, H. CFD modeling of a thermal and shear-thinning elastohydrodynamic line contact. J. Tribol.-Trans. ASME 2008, 130, 041503. [Google Scholar] [CrossRef]
- Hajishafiee, A.; Kadiric, A.; Ioannides, S.; Dini, D. A Coupled Finite-volume CFD Solver for Two-dimensional Elasto-hydrodynamic Lubrication Problems with Particular Application to Rolling Element Bearings. Tribol. Int. 2017, 109, 258–273. [Google Scholar] [CrossRef] [Green Version]
- Dhande, D.Y.; Pande, D.W. Multiphase flow analysis of hydrodynamic journal bearing using CFD coupled Fluid Structure Interaction considering cavitation. J. King Saud-Univ.-Eng. Sci. 2018, 30, 345–354. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Zhang, S.; Wang, Y.; Xu, W.W.; Wang, Z. Investigations of the three-dimensional temperature field of journal bearings considering conjugate heat transfer and cavitation. Ind. Lubr. Tribol. 2019, 71, 109–118. [Google Scholar] [CrossRef]
- Reynolds, O. On the Theory of Lubrication and its Application to Mr Beauchamp Tower’s Experiments, including an Experimental Determination of the Viscosity of Olive Oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Jakobsson, B.; Floberg, L. The Finite Journal Bearing, Considering Vaporization; Gumperts Förlag: Göteborg, Sweden, 1957. [Google Scholar]
- Olsson, K. Cavitation in Dynamically loaded Journal Bearings; Scandinavian University Books: Göteborg, Sweden, 1965. [Google Scholar]
- Elrod, H.G.; Adams, M.L. A Computer Program for Cavitation and Starvation Problems. In Cavitation and Related Phenomena in Lubrication; Mechanical Engineering Publications Ltd.: London, UK, 1974; Volume 1. [Google Scholar]
- Vijayaraghavan, D.; Keith, T. An Efficient, Robust, and Time Accurate Numerical Scheme Applied to a Cavitation Algorithm. J. Tribol.-Trans. ASME 1990, 112, 44–51. [Google Scholar] [CrossRef]
- Fesanghary, M.; Khonsari, M. A Modification of the Switch Function in the Elrod Cavitation Algorithm. J. Tribol.-Trans. ASME 2011, 133, 024501. [Google Scholar] [CrossRef]
- Bayada, G.; Chupin, L. Compressible Fluid Model for Hydrodynamic Lubrication Cavitation. J. Tribol.-Trans. ASME 2013, 135, 041702. [Google Scholar] [CrossRef] [Green Version]
- Ransegnola, T.; Sadeghi, F.; Vacca, A. An Efficient Cavitation Model for Compressible Fluid Film Bearings. Tribol. Trans. 2021, 64, 434–453. [Google Scholar] [CrossRef]
- Alakhramsing, S.; van Ostayen, R.; Eling, R. Thermo-Hydrodynamic Analysis of a Plain Journal Bearing on the Basis of a New Mass Conserving Cavitation Algorithm. Lubricants 2015, 3, 256–280. [Google Scholar] [CrossRef]
- Stefani, F.; Rebora, A. Steadily loaded journal bearings: Quasi-3D mass-energy-conserving analysis. Tribol. Int. 2009, 42, 448–460. [Google Scholar] [CrossRef]
- Banwait, S.S.; Chandrawat, H.N. Study of thermal boundary conditions for a plain journal bearing. Tribol. Int. 1998, 31, 289–296. [Google Scholar] [CrossRef]
- Linjamaa, A.; Lehtovaara, A.; Larsson, R.; Kallio, M.; Sochting, S. Modelling and analysis of elastic and thermal deformations of a hybrid journal bearing. Tribol. Int. 2018, 118, 451–457. [Google Scholar] [CrossRef]
- Hertz. On the Contact of Elastic Solids. Crelle’s J. 1881, 92, 156–171. [Google Scholar]
- Bouyer, J.; Fillon, M. On the Significance of Thermal and Deformation Effects on a Plain Journal Bearing Subjected to Severe Pperating Conditions. J. Tribol.-Trans. ASME 2004, 126, 819–822. [Google Scholar] [CrossRef]
- Zhang, C.; Yi, Z.; Zhang, Z. THD Analysis of High Speed Heavily Loaded Journal Bearings Including Thermal Deformation, Mass Conserving Cavitation, and Turbulent Effects. J. Tribol.-Trans. ASME 2000, 122, 597–602. [Google Scholar] [CrossRef]
- Giacopini, M.; Fowell, M.; Dini, D.; Strozzi, A. A Mass-Conserving Complementarity Formulation to Study Lubricant Films in the Presence of Cavitation. J. Tribol.-Trans. ASME 2010, 132, 041702. [Google Scholar] [CrossRef]
- Profito, F.; Giacopini, M.; Zachariadis, D.; Dini, D. A General Finite Volume Method for the Solution of the Reynolds Lubrication Equation with a Mass-Conserving Cavitation Model. Tribol. Lett. 2015, 60, 18. [Google Scholar] [CrossRef] [Green Version]
- V. Škurić, H.; Jasak, A.A.; Jaegar, P.D. Finite Area Algorithm for Thin Film Cavitation in OpenFOAM. Int. Sci. J. Trans Motauto World 2019, 4, 3–7. [Google Scholar]
- Ardah, S.; Profito, F.J.; Dini, D. An integrated finite volume framework for thermal elasto-hydrodynamic lubrication. Tribol. Int. 2023, 177, 107935. [Google Scholar] [CrossRef]
- Wang, Y.; Jacobs, G.; König, F.; Zhang, S.; Goeldel, S.V. Investigation of Microflow Effects in Textures on Hydrodynamic Performance of Journal Bearings Using CFD Simulations. Lubricants 2023, 11, 20. [Google Scholar] [CrossRef]
- Ferron, J.; Frene, J.; Boncompain, R. A Study of the Therohydrodynamic Performance of a Plain Journal Bearing Comparison Between Theory and Experiments. J. Lubr. Technol.-Trans. ASME 1983, 105, 422–428. [Google Scholar] [CrossRef]
- Dhande, D.Y.; Pande, D.W. A two-way FSI analysis of multiphase flow in hydrodynamic journal bearing with cavitation. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3399–3412. [Google Scholar] [CrossRef]





| Boundary Name | Boundary Type | |
|---|---|---|
| Relative Density, (-) | Temperature, T (C) | |
| Film Inlet | Dirichlet | Dirichlet |
| Film Outlet | Dirichlet | Neumann |
| Film Sides | Dirichlet/Neumann | Neumann |
| Property | Symbol | Value |
|---|---|---|
| Shaft Radius (mm) | 25 | |
| Bush Radius (mm) | 50 | |
| Bush Length (mm) | L | 80 |
| Clearance (m) | c | 145 |
| Groove Angle () | 18 | |
| Groove Length (mm) | 70 | |
| Feed Hole Diameter (mm) | 14 | |
| No. Feed Holes | 3 |
| Symbol | Value | Units |
|---|---|---|
| 0 | Pa | |
| Pa | ||
| 860 | ||
| 1.225 | ||
| 2000 | ||
| 1000 | ||
| 0.0293 | Pas | |
| Pas | ||
| 0.13 | ||
| 0.05 | ||
| −0.04 | ||
| 40 | C | |
| 50 | ||
| 100 | ||
| K | ||
| K | ||
| 200 | GPa | |
| 113 | GPa | |
| 0.28 | ||
| 0.35 | ||
| 50 | ||
| 1500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Layton, J.; Rothwell, B.C.; Ambrose, S.; Eastwick, C.; Medina, H.; Rebelo, N. A New Thermal Elasto-Hydrodynamic Lubrication Solver Implementation in OpenFOAM. Lubricants 2023, 11, 308. https://doi.org/10.3390/lubricants11070308
Layton J, Rothwell BC, Ambrose S, Eastwick C, Medina H, Rebelo N. A New Thermal Elasto-Hydrodynamic Lubrication Solver Implementation in OpenFOAM. Lubricants. 2023; 11(7):308. https://doi.org/10.3390/lubricants11070308
Chicago/Turabian StyleLayton, James, Benjamin C. Rothwell, Stephen Ambrose, Carol Eastwick, Humberto Medina, and Neville Rebelo. 2023. "A New Thermal Elasto-Hydrodynamic Lubrication Solver Implementation in OpenFOAM" Lubricants 11, no. 7: 308. https://doi.org/10.3390/lubricants11070308
APA StyleLayton, J., Rothwell, B. C., Ambrose, S., Eastwick, C., Medina, H., & Rebelo, N. (2023). A New Thermal Elasto-Hydrodynamic Lubrication Solver Implementation in OpenFOAM. Lubricants, 11(7), 308. https://doi.org/10.3390/lubricants11070308





