Dynamics-Based Calculation of the Friction Power Consumption of a Solid Lubricated Bearing in an Ultra-Low Temperature Environment
Abstract
:1. Introduction
2. Calculation of Traction Coefficient of Solid Lubricant
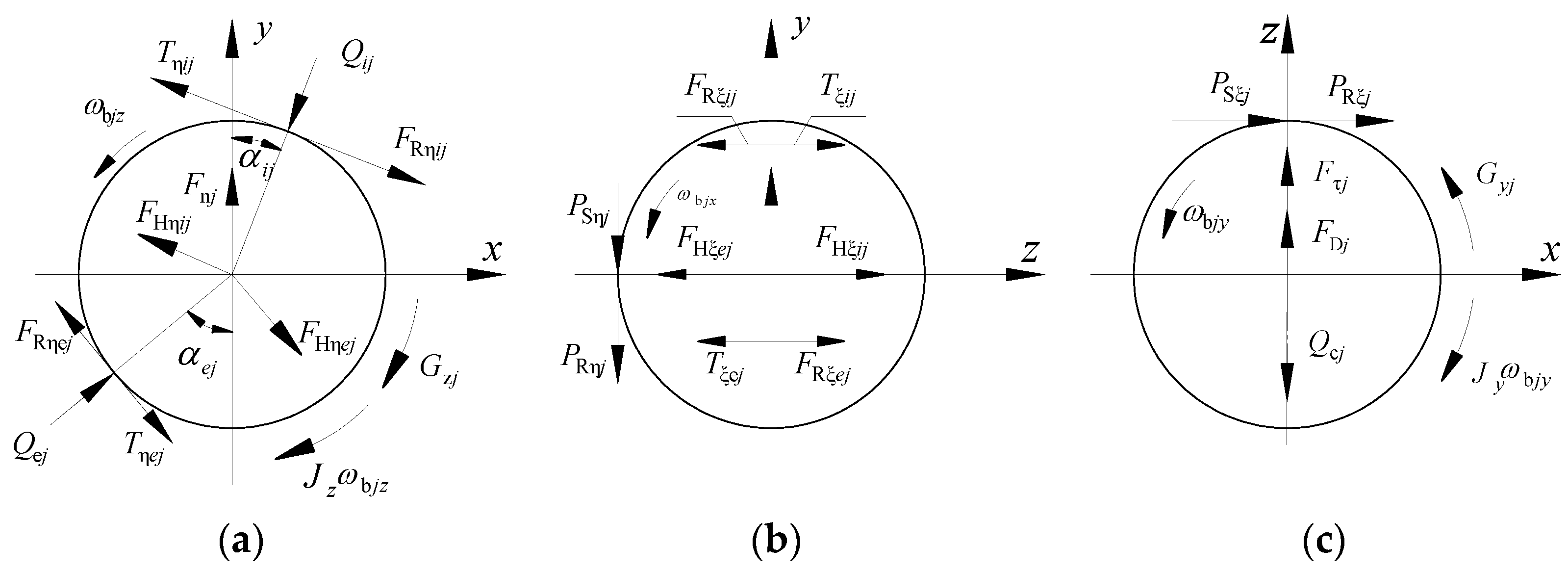
3. Bearing Dynamics Modeling
3.1. Differential Formula of Ball
3.2. Differential Formula of Cage
3.3. Differential Formula of Inner Ring
4. Source and Theoretical Calculation of Friction Power Consumption
4.1. Friction Power Consumption Caused by Elastic Lag between Ball and Raceway
4.2. Friction Power Consumption Caused by Differential Sliding between Ball and Raceway
4.3. Friction Power Consumption Caused by Ball Spin Sliding
4.4. Friction Power Consumption Caused by Sliding between Cage and Guide Surface
4.5. Friction Power Consumption Caused by Contact between Ball and Cage
4.6. Total Friction Power Consumption of Ball Bearings
5. Influencing Factors of Friction Power Consumption
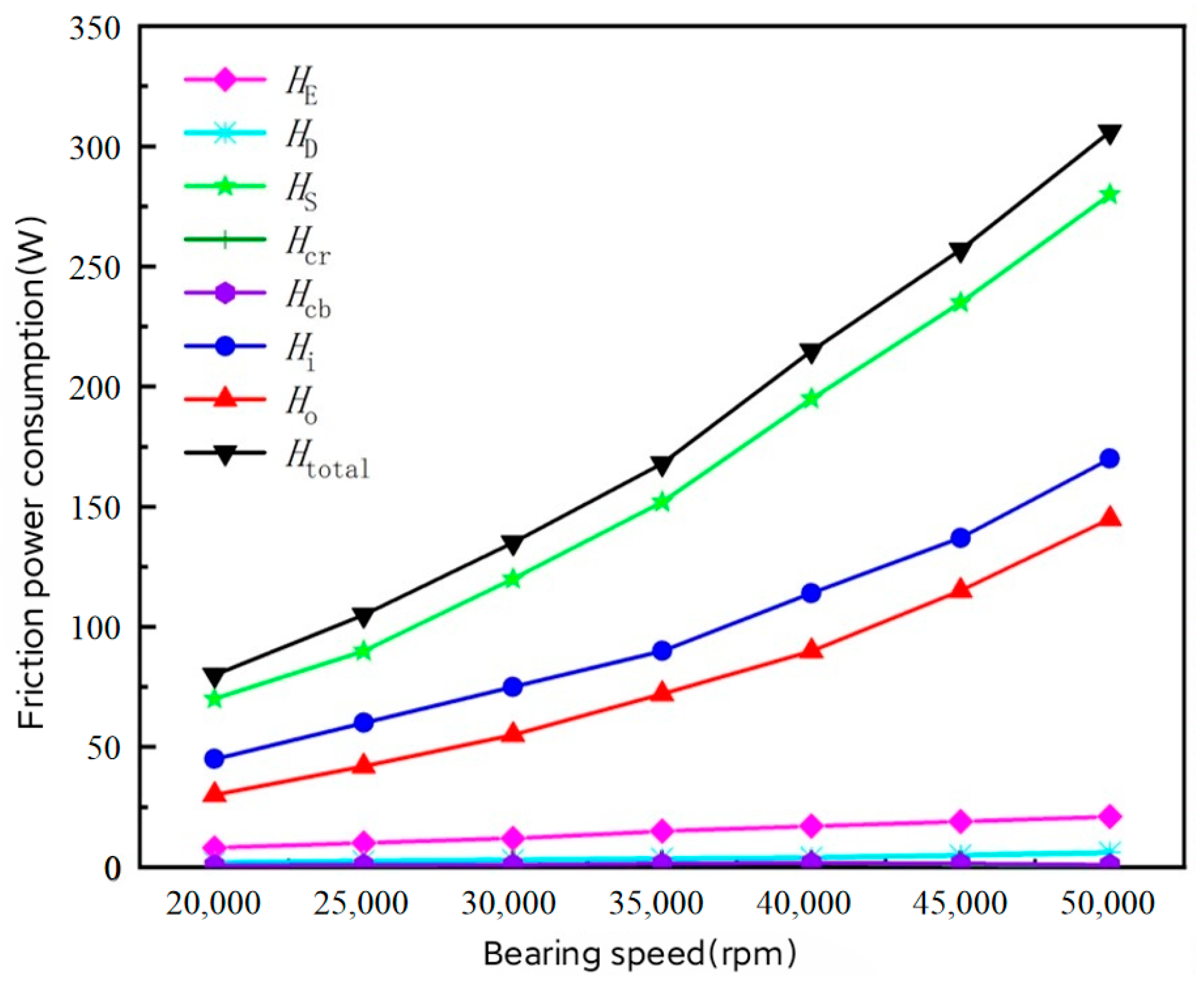
5.1. Influence of the Bearing Speed on Friction Power Consumption
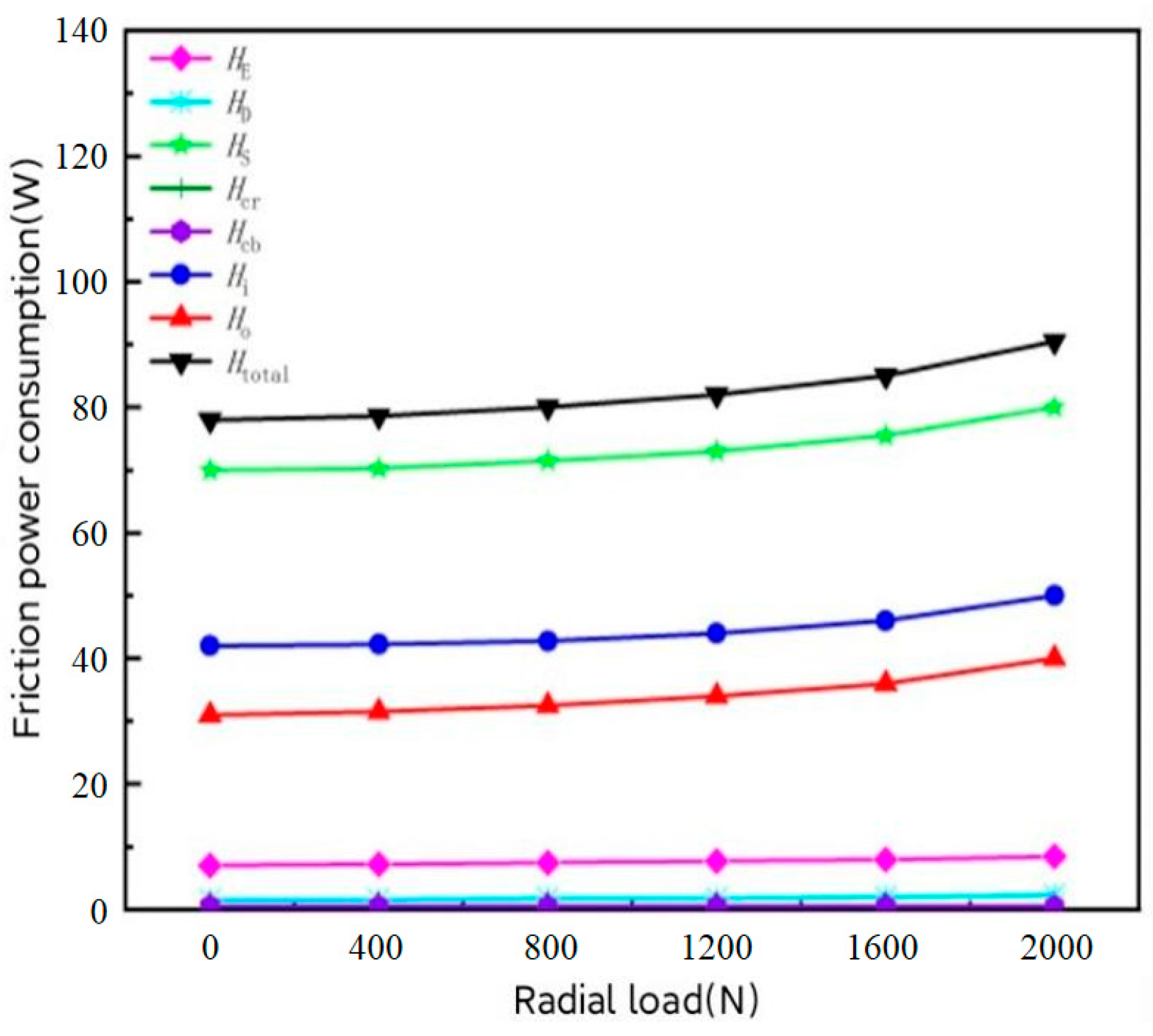
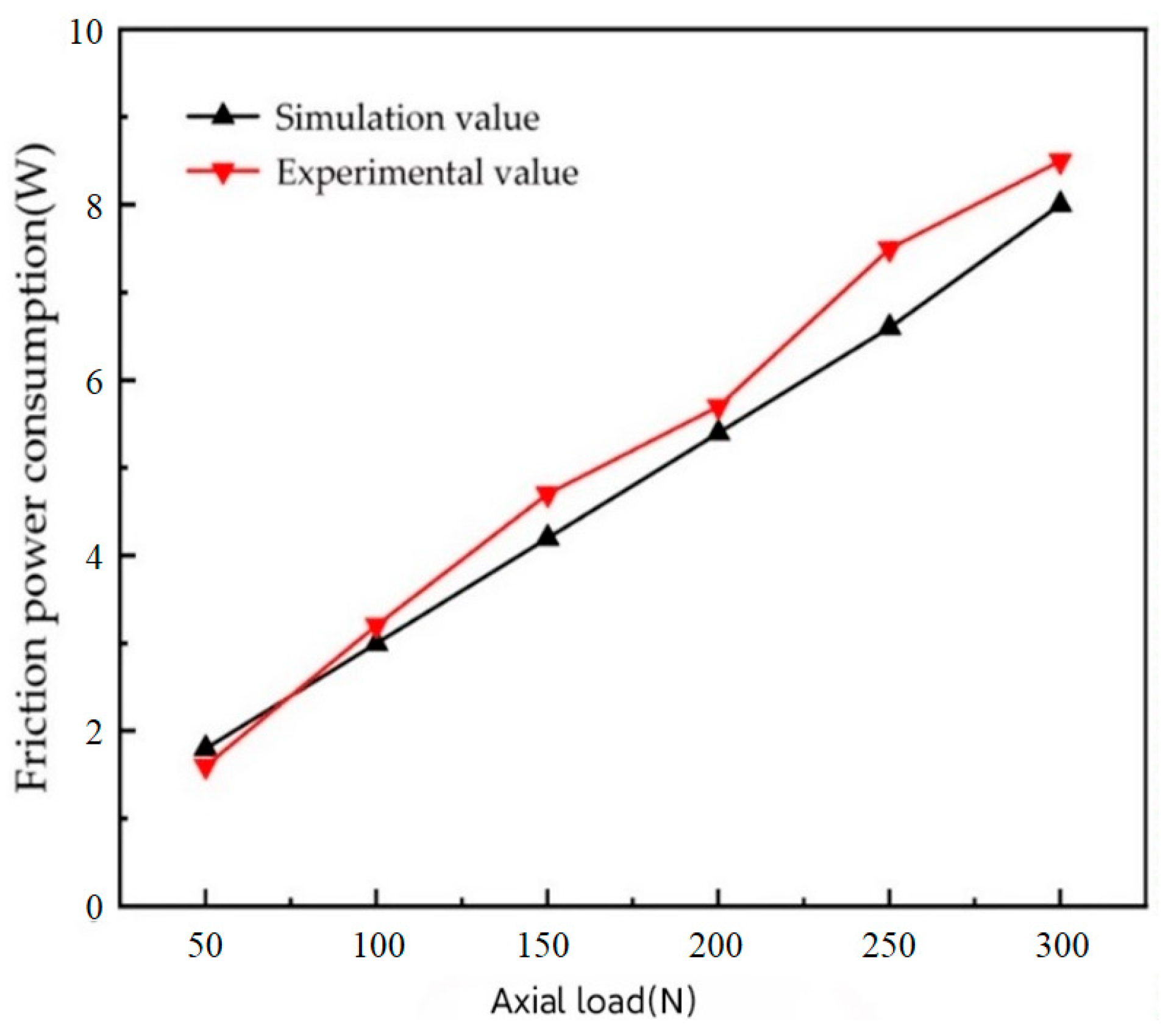
5.2. Influence of Load on Friction Power Consumption
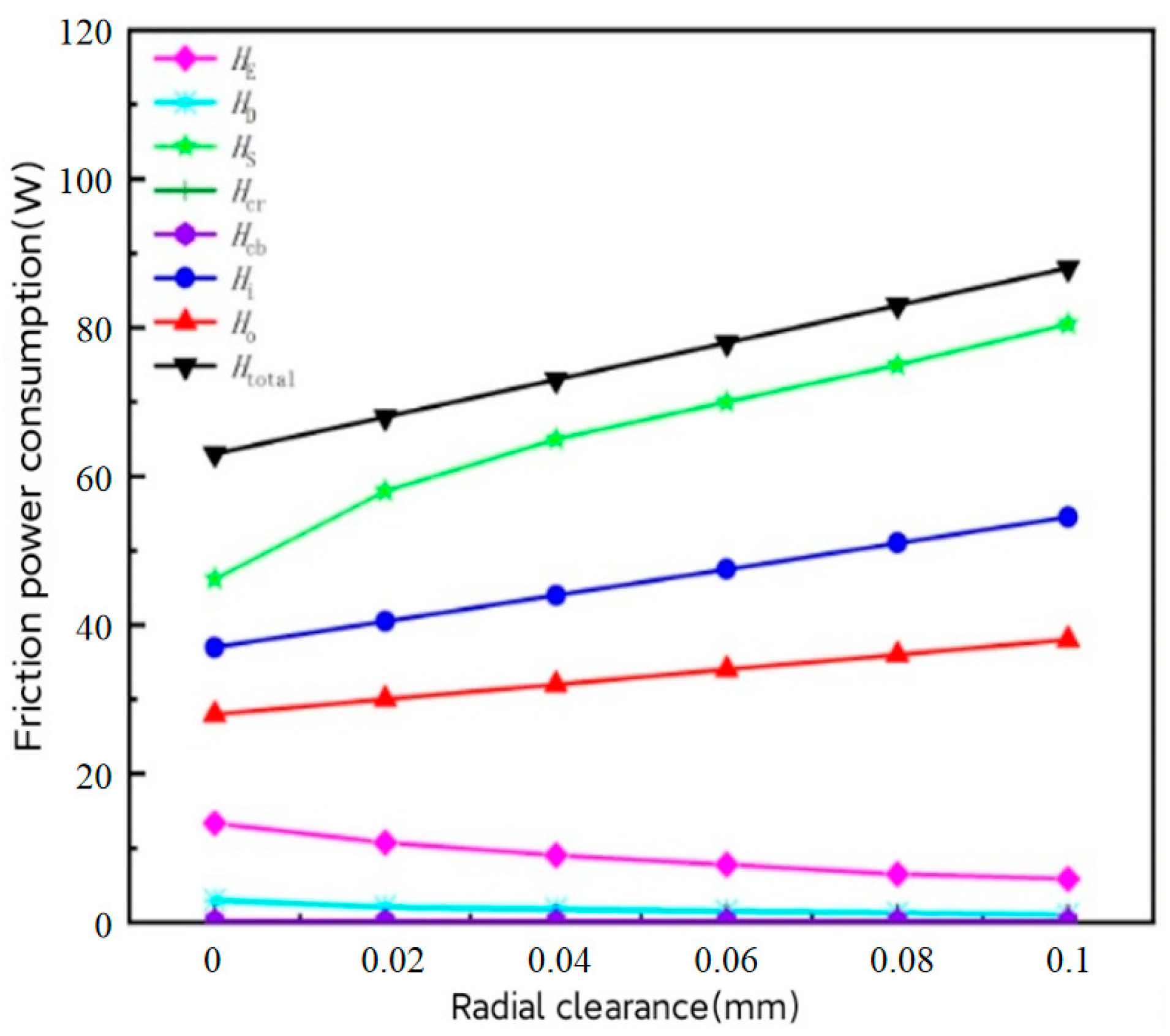
5.3. Influence of Radial Clearance on Friction Power Consumption
6. Experimental Comparison of Friction Power Consumption of Solid Lubricated Ball Bearings
6.1. Main Parameters of Test Bearing
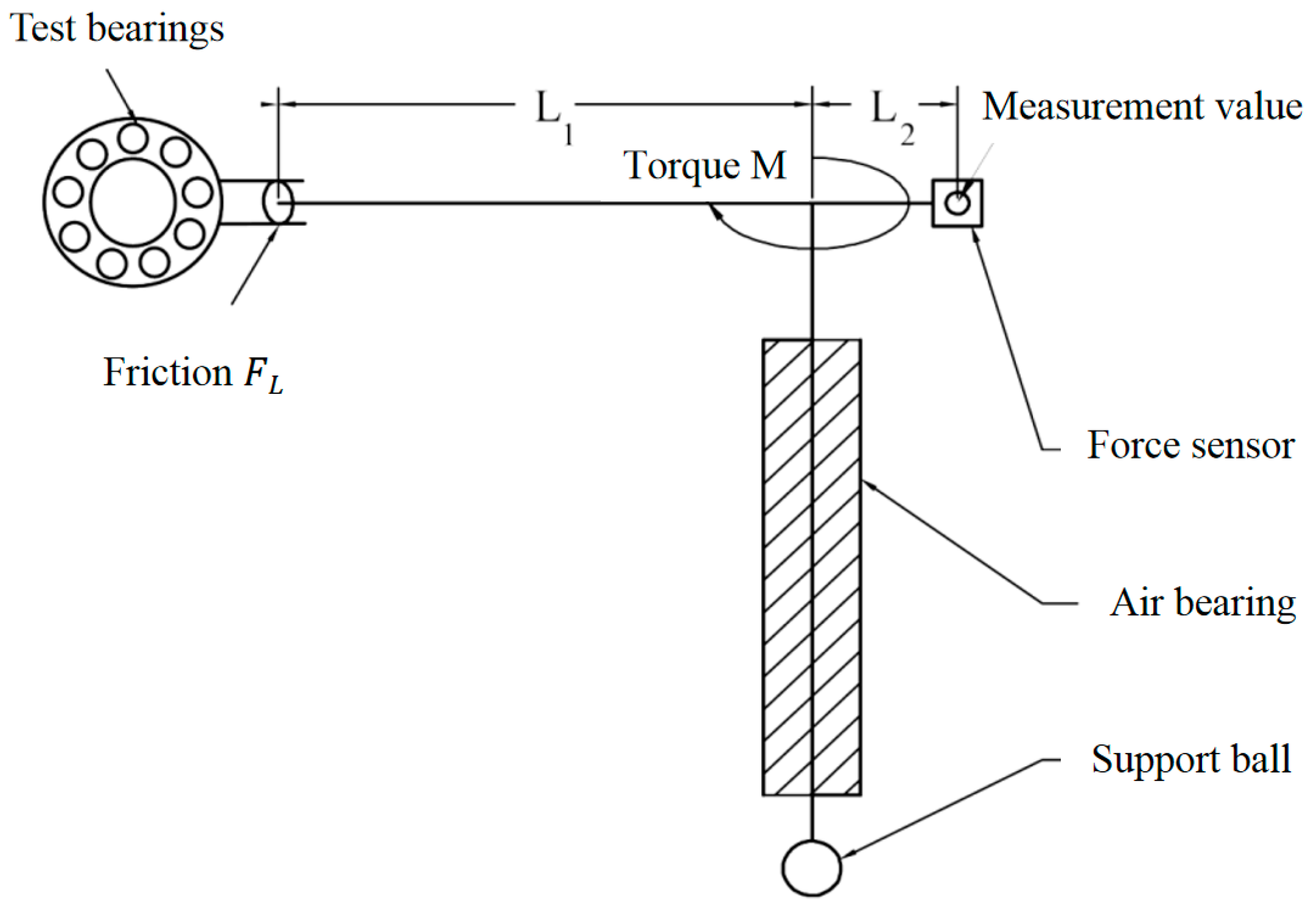
6.2. Test Equipment and Experimental Principle
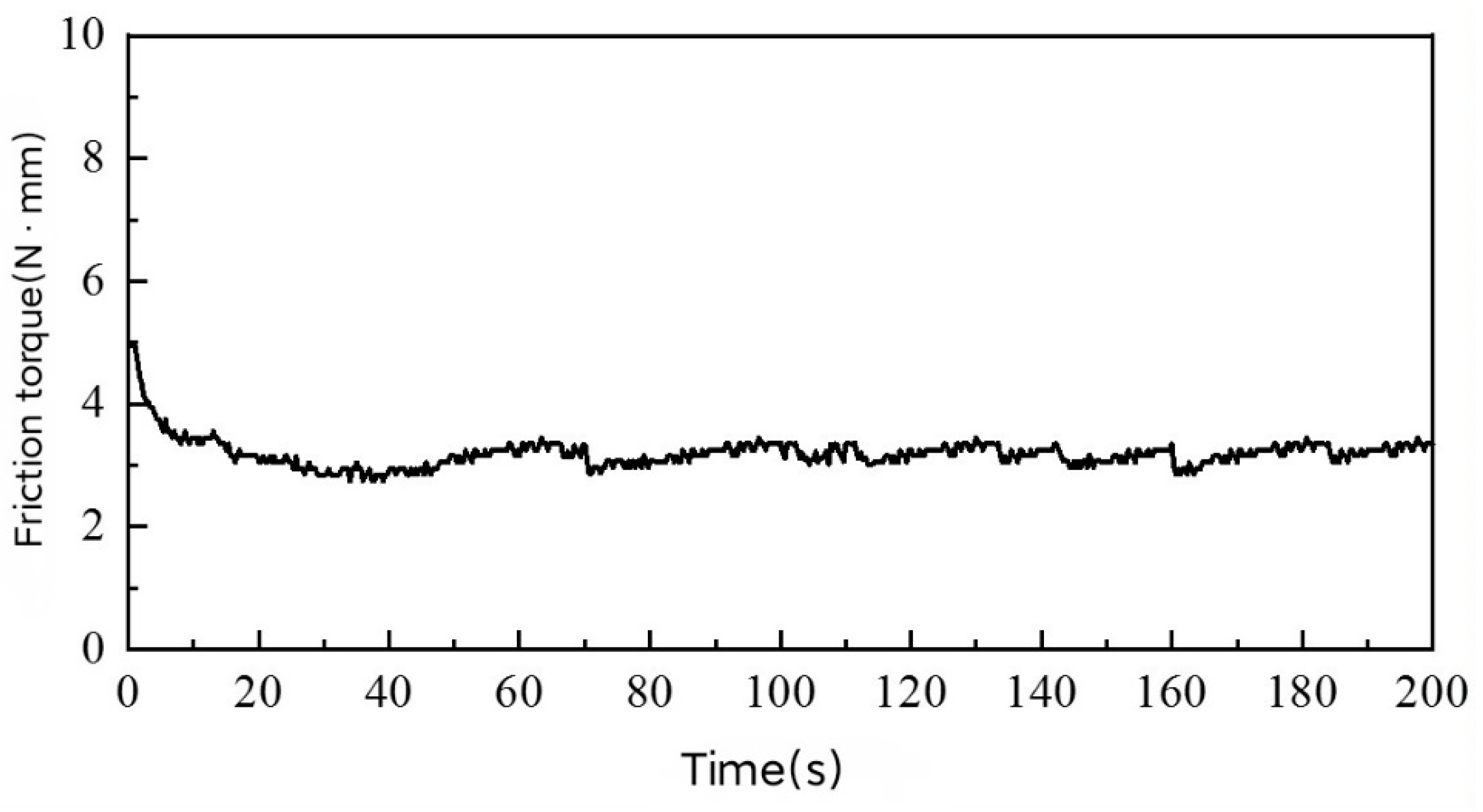
6.3. Analysis of Test Results
7. Conclusions
- The traction coefficient of MoS2 solid lubricating material first increases and then slightly decreases with an increase in sliding speed. The traction coefficient decreases with an increase in load.
- As the bearing speed increases, total friction power consumption also increases. A slight upward trend is observed in total friction power consumption with an increase in radial load and radial clearance, while an increase in axial load results in a more obvious upward trend in total friction power consumption.
- The simulation value of friction torque, based on the bearing dynamic model proposed in this study, shows good consistency with the experimental results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J. Dynamic Analysis on Cage Dynamic Characteristics and Strength of Angular Contact Ball Bearing in Ultra-Low Temperature Environment. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2020. [Google Scholar]
- Yan, H.Y. The Principle and Application of Solid Lubrication Technology. Technol. Mark. 2016, 23, 133. (In Chinese) [Google Scholar]
- Gu, L.; Wang, L.Q.; Li, X.J. Research Status of Cryogenic Solid Lubrication. Tribology 2002, 22, 314–320. (In Chinese) [Google Scholar]
- Kang, J.J.; Li, G.L.; Wang, H.D. Development of Research on the Layered Solid Lubrication Films. Heat. Treat. Met. 2007, 32, 15–18. (In Chinese) [Google Scholar]
- Dunckle, C.G.; Aggleton, M.; Glassman, J. Friction of molybdenum disulfide titanium films under cryogenic vacuum conditions. Tribol. Intern. 2011, 44, 1819–1826. [Google Scholar] [CrossRef]
- Ma, G.Z.; Xu, B.S.; Wang, H.D. State of Research on Space Solid Lubrication Materials. Mater. Rep. 2010, 24, 68–71. (In Chinese) [Google Scholar]
- Wong, K.C.; Lu, X.; Cotter, J. Surface and friction characterization of MoS2 and WS2 third body thin films under simulated wheel/rail rolling–sliding contact. Wear 2007, 264, 526–534. [Google Scholar] [CrossRef]
- Kwak, W.; Lee, J.; Lee, Y. Theoretical and experimental approach to ball bearing frictional characteristics compared with cryogenic friction model and dry friction model. Mech. Syst. Signal Process. 2019, 124, 424–438. [Google Scholar] [CrossRef]
- Burris, D.L. Investigation of the tribological behavior of polytetrafluoroethylene at cryogenic temperatures. Tribol. Trans. 2008, 51, 92–100. [Google Scholar] [CrossRef]
- Hubner, W.; Gradt, T.; Schneider, T. Tribological behaviour of materials at cryogenic temperatures. Wear 1998, 216, 150–159. [Google Scholar] [CrossRef]
- Zhang, W.H.; Deng, S.E.; Chen, G.D. Influence of Lubricant Traction Coefficient on Cage’s Nonlinear Dynamic Behavior in High-Speed Cylindrical Roller Bearing. J. Tribol. 2017, 139, 061502. [Google Scholar] [CrossRef]
- Yukhno, T.P.; Vvedensky, Y.V.; Sentyurikhina, L.N. Low temperature investigations on frictional behavior and wear resistance of solid lubricant coatings. Tribol. Intern. 2001, 34, 293–298. [Google Scholar] [CrossRef]
- Cao, P.; Bai, Y.; Zhang, Y.H. Tribological Characteristics of Deposited Ag Film Bearing under Dry, Oil and Grease Lubricating. Lubr. Eng. 2011, 36, 29–31. (In Chinese) [Google Scholar]
- Duan, X.S.; Chen, R.; Mai, N.N. Research on Solid-lubrication Craft of Joint Bearing. Lubr. Eng. 2015, 40, 116–119. (In Chinese) [Google Scholar]
- Lu, J.H.; Kuang, Y.F. Research on the Lubrication and Friction Reduction Performance of Lead Tin Alloy Coating. Mater. Prot. 2007, 40, 12–13. (In Chinese) [Google Scholar]
- Christian, B.; Alexander, H.; Jens, R. Cage Friction in High-Speed Spindle Bearings. Tribol. Trans. 2014, 57, 77–85. [Google Scholar]
- Popescu, A.; Houpert, L.; Olaru, D.N. Four approaches for calculating power losses in an angular contact ball bearing. Mech. Mach. Theory 2020, 144, 103669. [Google Scholar] [CrossRef]
- Burris, D.L.; Sawyer, W.G. Addressing practical challenges of low friction coefficient measurements. Tribol. Lett. 2009, 35, 17–23. [Google Scholar] [CrossRef]
- Deng, S.E.; Li, X.L.; Wang, J.G. Analysis on the Friction Torque Fluctuation of Angular Contact Ball Bearings. J. Mech. Eng. 2011, 47, 104–112. (In Chinese) [Google Scholar] [CrossRef]
- Deng, S.E.; Li, X.L.; Wang, J.G. Frictional Torque Characteristic of Angular Contact Ball Bearings. J. Mech. Eng. 2011, 47, 114–120. (In Chinese) [Google Scholar] [CrossRef]
- Li, S.S.; Chen, J.; Ling, J. Analytic and Experimental Study on Friction Torque for High-speed Micro Ball Bearing. Lubr. Eng. 2013, 38, 32–35. (In Chinese) [Google Scholar]
- Cui, Y.F.; Deng, S.E.; Deng, K.W. Friction Torque Characteristics of Control Moment Gyros Bearing Unit. Aerosp. Control Appl. 2020, 46, 73–80. (In Chinese) [Google Scholar]
- Liu, Y.Y.; Yang, H.S.; Su, B. Simulation Analysis of the Friction Power Consumption of Double Row Angular Contact Ball Bearings for Aero-engine. J. Mech. Transm. 2021, 45, 129–135. (In Chinese) [Google Scholar]
- Yu, C.G.; Chen, W.H.; Liang, B. Study on the tribological properties of a self-lubricating spherical plain bearing at a cryogenic and wide temperature range. Sci. Sin. 2020, 50, 775–785. (In Chinese) [Google Scholar]
- Qiu, S.D. Experimental Study and Low Temperature Friction Characteristic of Angular Contact Ball Bearing. J. Mech. Transm. 2018, 42, 180–184. (In Chinese) [Google Scholar]
- Zheng, C.T.; Xu, S.R.; Yang, D.Q. State and Development on Research of Friction Torque of Ball Bearing. Bearing 2009, 8, 52–56. (In Chinese) [Google Scholar]
- Gao, F.; Yang, Y.X.; Zhao, Y. Analysis of dynamic friction moment fluctuation of precision shafting at low temperature and its optimization adjustment. Bearing 2023, 1–7. Available online: http://kns.cnki.net/kcms/detail/41.1148.TH.20230821.1545.002.html (accessed on 1 September 2023). (In Chinese).
- Liu, F.B.; Su, B.; Zhang, G.T. Development of a Cryogenic Tester with Air Bearing to Test Sliding-Rolling Contact Friction. Lubricants 2022, 10, 119. [Google Scholar] [CrossRef]
- Gupta, P.K. Traction Coefficients for Some Solid Lubricants for Rolling Bearing Dynamics Modeling. Tribol. Trans. 2000, 43, 647–652. [Google Scholar] [CrossRef]
- Zhang, K.; Li, J.H. Analysis and Calculation of Friction torque of Ball Bearings. Bearing 2001, 8–11. (In Chinese) [Google Scholar] [CrossRef]
- Deng, S.E.; Jia, Q.Y. Design Principle of Rolling Bearings, 2nd ed.; China Standard Press: Beijing, China, 2014; pp. 222–244. [Google Scholar]
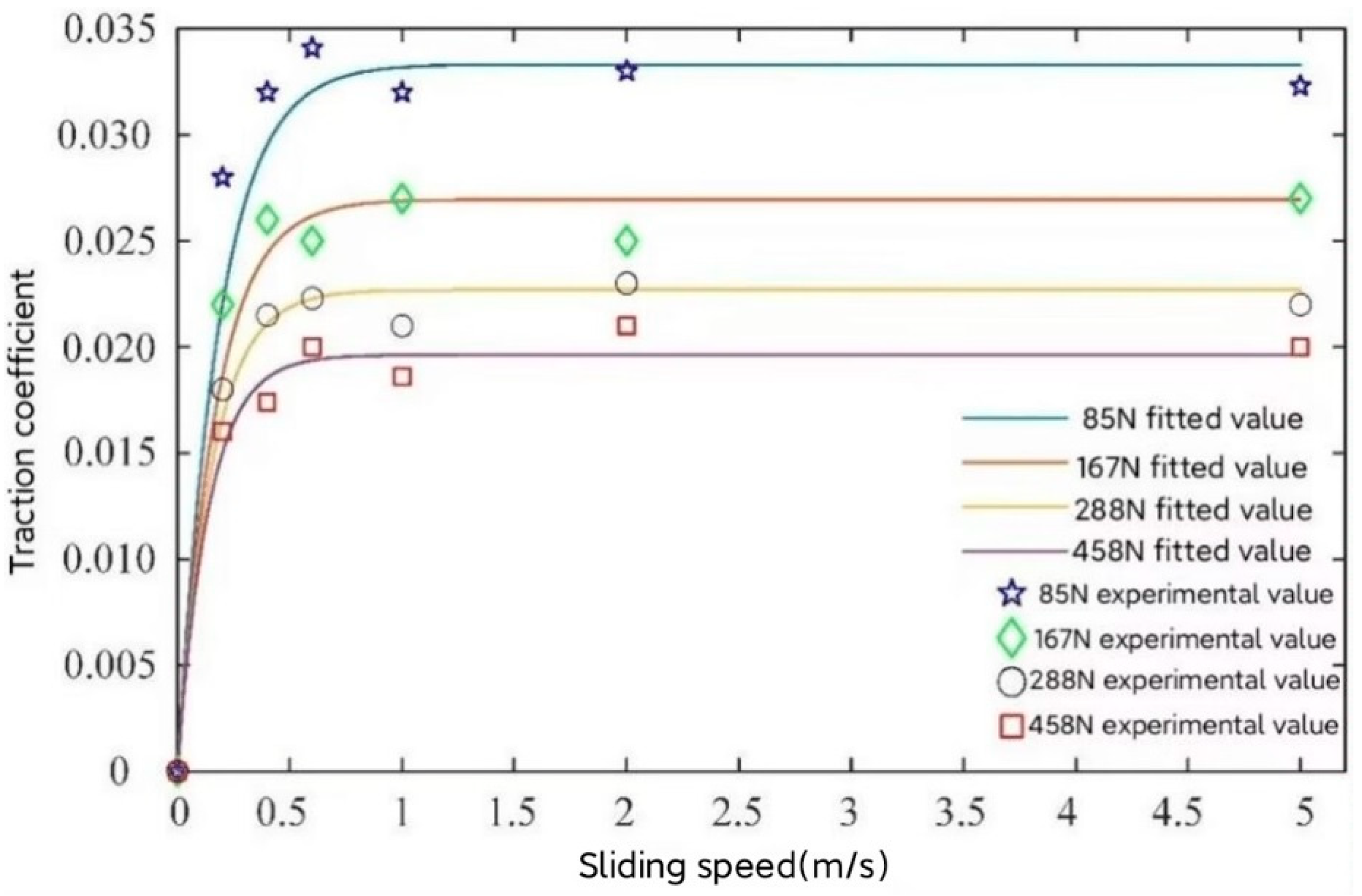


| Rolling Speed (m/s) | Load (N) | A | B | C | D | Residual Error | Correlation Coefficient |
|---|---|---|---|---|---|---|---|
| 10 | 85 | −0.0320 | 0.154 | 4.445 | 0.0320 | 0.0009 | 0.998 |
| 10 | 167 | −0.0270 | 0.158 | 5.280 | 0.0270 | 0.0014 | 0.9933 |
| 10 | 288 | −0.022 | 0.0797 | 5.714 | 0.022 | 0.0008 | 0.9959 |
| 10 | 458 | −0.0199 | 73,932 | 133,607 | 0.0199 | 0.0026 | 0.9532 |
| Ai | Bi | Ci | Di | ||
|---|---|---|---|---|---|
| i | 0 | −1.05 × 10−3 | −4.14 × 10−5 | 42.64 | 1.05 × 10−3 |
| 1 | −0.32 | −0.54 | 0.18 | −0.32 | |
| Correlation coefficient | 0.99 | 0.956 | 0.987 | 0.956 | |
| Parameters | Symbol | Value |
|---|---|---|
| Outside diameter | D | 47 mm |
| Bore diameter | d | 20 mm |
| Width | B | 14 mm |
| Ball diameter | DW | 7.938 mm |
| Initial radial clearance | u0 | 0.091 mm |
| Number of balls | Z | 10 |
| Contact angle | α | 25° |
| Axial loading | Fa | 2000 N |
| Bearing speed | n | 20,000 rpm |
| Material | Modulus of Elasticity (GPa) | Poisson’s Ratio | Density (g/cm3) | Coefficient of Linear Expansion (10−6 °C−1) | Thermal Conductivity (W/(m·°C)) |
|---|---|---|---|---|---|
| G95Cr18 | 200 | 0.28 | 7.8 | 11.5 | 29.3 |
| Nylon 66 | 2.83 | 0.4 | 1.15 | 1.2 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, B.; Mao, S.; Zhang, G.; Li, H.; Cui, Y. Dynamics-Based Calculation of the Friction Power Consumption of a Solid Lubricated Bearing in an Ultra-Low Temperature Environment. Lubricants 2023, 11, 372. https://doi.org/10.3390/lubricants11090372
Su B, Mao S, Zhang G, Li H, Cui Y. Dynamics-Based Calculation of the Friction Power Consumption of a Solid Lubricated Bearing in an Ultra-Low Temperature Environment. Lubricants. 2023; 11(9):372. https://doi.org/10.3390/lubricants11090372
Chicago/Turabian StyleSu, Bing, Shuanglong Mao, Guangtao Zhang, Han Li, and Yongcun Cui. 2023. "Dynamics-Based Calculation of the Friction Power Consumption of a Solid Lubricated Bearing in an Ultra-Low Temperature Environment" Lubricants 11, no. 9: 372. https://doi.org/10.3390/lubricants11090372
APA StyleSu, B., Mao, S., Zhang, G., Li, H., & Cui, Y. (2023). Dynamics-Based Calculation of the Friction Power Consumption of a Solid Lubricated Bearing in an Ultra-Low Temperature Environment. Lubricants, 11(9), 372. https://doi.org/10.3390/lubricants11090372





