In Situ Measurement of Grease Capacitive Film Thickness in Bearings: A Review
Abstract
1. Introduction
- Capacitance measurement methods: Currently, no commercial bearing testing rig is available. Several homemade rigs were recently reported to measure bearing capacitance [17,23,48,49,50,51]. A deeper understanding of the physics behind capacitance measurement methods is important for future capacitance testing rig design and optimization;
- Capacitive film thickness models and electric networks: Current models primarily focus on the film thickness in fully flooded conditions. A more comprehensive model encompassing all three lubrication regimes (fully flooded, starved, and mixed) is necessary to reflect bearing operation in the real world;
- Dielectric constant of lubricants: Accurate film thickness determination relies heavily on the lubricant’s dielectric constant, which is a function of temperature and pressure (among other parameters). A suitable model for grease is needed;
- Grease starvation: It is necessary to develop a grease starvation model based on current capacitive film thickness data.
| Elementary Particle/Fundamental Carriers | Method | High-Spatial Resolution (~nm) | Real-Bearing Test | In Situ Measurement |
|---|---|---|---|---|
| Electron | Capacitance | √ | √ | √ |
| Resistance | √ | √ | ||
| Photon | Optical | √ | √ | |
| X-ray | √ | |||
| Phonon | Ultrasonic | √ | √ |
| Lubricants | Rig Configuration | Capacitance Measurement | Central Film Thickness Range (µm) | Lubrication Regime | Research Area | Reference |
|---|---|---|---|---|---|---|
| Oil and grease | Twin-disk rig and ball bearing test rig | Measure the capacitor voltage change during charging | 0.2~1.2 | Fully flooded and starved | Bearing currents and electrical erosive wear study | [16] |
| Grease | Deep-groove ball bearing and optical rig (WAM5) | Lubcheck + oscilloscope | 0~0.2 | Fully flooded and starved | Difference in the lubrication mechanism between ultra-low speed and medium speeds | [18] |
| Oil and grease | Deep-groove ball bearing | Capacitive voltage divider (Lubcheck) | 0.04~0.2 | Mix to fully flooded | Film thickness and condition monitoring (metallic contact time fraction) | [49] |
| Grease | Deep-groove ball bearing | Lubcheck Mk3 | 0.5~3 | Starved | Grease starvation quantification | [50] |
| Grease | Angular contact ball bearing | Constant–current charge | 0~0.7 | Starved | Influence of lubricating grease composition on grease service life and tribological performance characteristics in high-speed rolling bearings | [48] |
| Oil | FEA simulation on a ball bearing | 10~1000 | Fully flooded | Analyze bearing current discharges and their effect on bearing damage by using simulation | [52] | |
| Gear oil | Pair of gears | RLC bridge and oscilloscope | 5~140 | Fully flooded | Studied the effect of change in speed, oil viscosity, and helix angle on the load-carrying capacity of the oil film | [53] |
| SAE 30, 60 | Engine crankshaft journal and bearing shell | Transformer ratio arm bridge | 0.65~8 | Fully flooded | Measured the relative effects of oil rheology and engine operating condition | [54] |
| Grease | Deep-groove ball bearing | Lubcheck Mk3 | Starved | Grease replenishment study | [55] | |
| Mineral oil | Twin-disk machine | Capacitance bridge | 0.5 | Fully flooded | In general terms, it appears the elasto-hydrodynamic theory may have slightly underestimated the film thicknesses | [56] |
| Oil | Engine connecting–rod bearing | Capacitance bridge | 0~10 | Fully flooded | Thermal effects on oil film thickness of an engine connecting–rod bearing | [57] |
| Sunflower oil | Ball-on-disk tribometer | LCR meter | 0.001~0.01 | Boundary | Measured the thickness of boundary films under a pure sliding contact between metallic surfaces | [58] |
| Air/oil | Online transportation tube | Electrical capacitance tomography sensor | 60~140 | Air/oil transportation | Monitoring of the in-tube air/oil flow | [59] |
| Oil | Single-cylinder diesel engine | Capacitance probe | 0.2~8 | Fully flooded | Oil film thickness between engine cylinder liner and piston ring | [60] |
| Oil | Motored engine | Capacitance probe | 0~4 | Fully flooded | Oil film thickness between engine cylinder liner and piston ring | [61] |
| Oil | Internal combustion engine | Capacitance transducers | 0~80 | Fully flooded and starved | Measured capacitance between the sensor and piston ring | [62] |
| Grease | Angular contact ball bearings | Relative film thickness | Starved | Combined grease life testing with film thickness measurement | [63] | |
| Grease | Radial ball bearings | High-frequency oscilloscope | Starved | Bearing film thickness measurement | [64,65] | |
| Oil | Single-cylinder diesel engine | Capacitance transducer | 6~18 | Cavitation | Film between piston ring and liner | [66] |
| Oil | Diesel engine | Capacitance transducer | 2~8 | Fully flooded | Film between piston ring and cylinder | [67] |
| Oil | Modified MTM test rig | Digital storage oscilloscope with large memory | 0.05~0.9 | Fully flooded | Electric discharge behavior and current damage in EV motor bearings | [68] |
| Oil | Four-disk machine | Capacitance gauge | 4~26 | Fully flooded | Measured film shape, pressure, and temperature profiles | [69] |
| Oil | Diesel engine | Capacitance gauge | 0.4~2.5 | Fully flooded | Piston rings and the cylinder liner | [70] |
| Oil | Diesel engine | Capacitance gauge | 1~11 | Fully flooded | Piston rings and the cylinder liner | [71] |
| Oil | Two-spherical ball contact | LCR meter | 0~2.5 | Fully flooded | Measured the film thickness from pure rolling to pure sliding | [72] |
| Oil | Thrust pad bearing | Capacitance probes | 2.5~25 | Fully flooded | Compared the deflection of a circular pad with theory | [73] |
| Oil | Twin disk | LC oscillator | 0.2~1.8 | Fully flooded | Prediction of lubrication film thickness under conditions of different surface velocity directions | [74] |
| Oil | Bearing in a diesel engine | Transducer | 10~60 | Fully flooded | Measured the hydrodynamic oil film thickness present in slide bearings | [75] |
| Oil | EHD rig | Impedance/gain-phase analyzer | 0.015~0.2 | Fully flooded | Quantitative measurements of film thickness and consideration of cavitation | [76] |
| Oil with different polarity | EHD rig | Impedance analyzer | 0.01 | Fully flooded | Influence of a lubricant’s polarity on capacitance measurements | [77] |
2. Capacitance Measurement Methods
2.1. Oscilloscope
2.2. AC Bridge
2.3. LCR Meter and Impedance Analyzer
2.4. Capacitive Voltage Divider
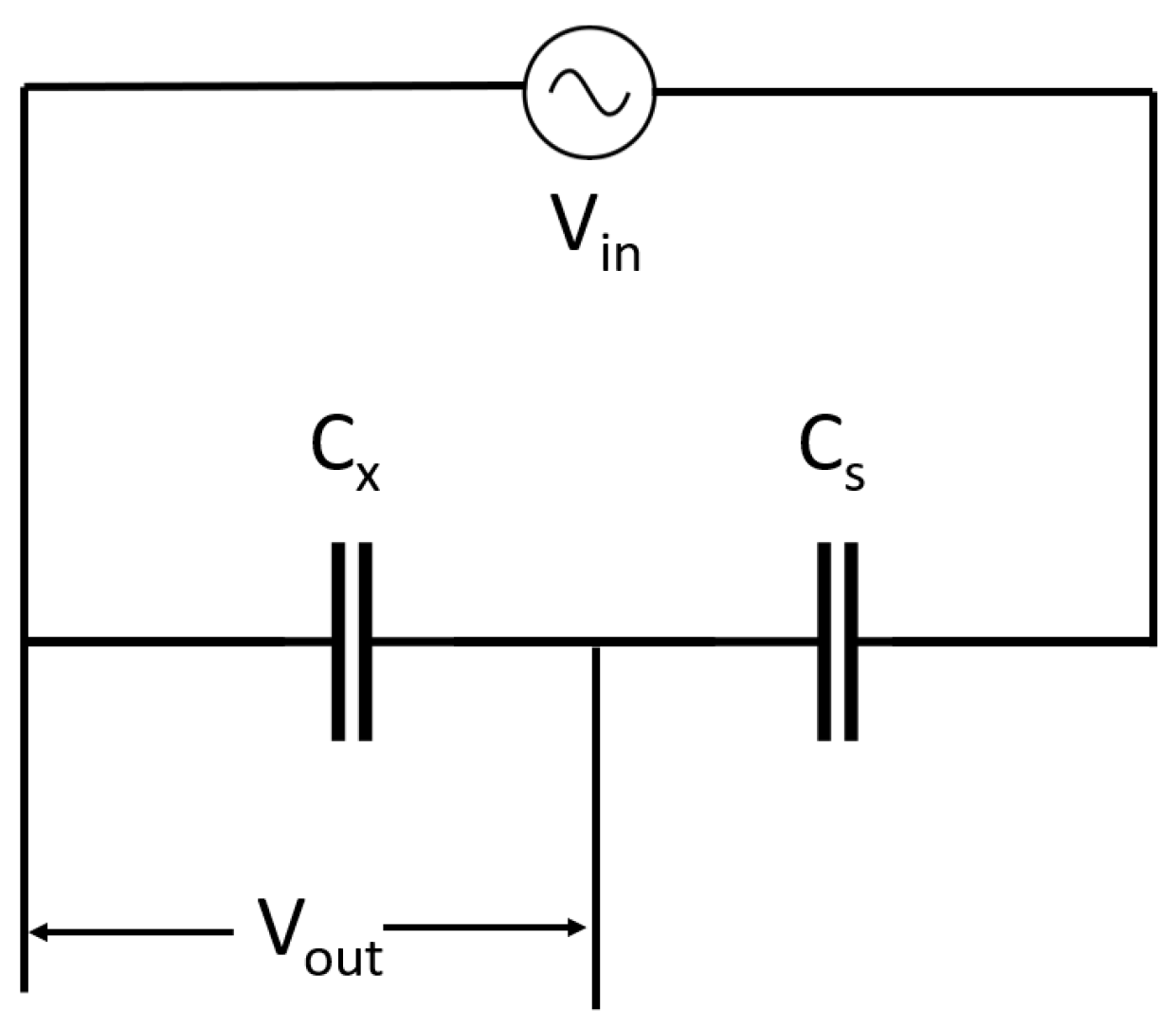
2.5. Capacitance Probe/Transducer
2.6. Summary
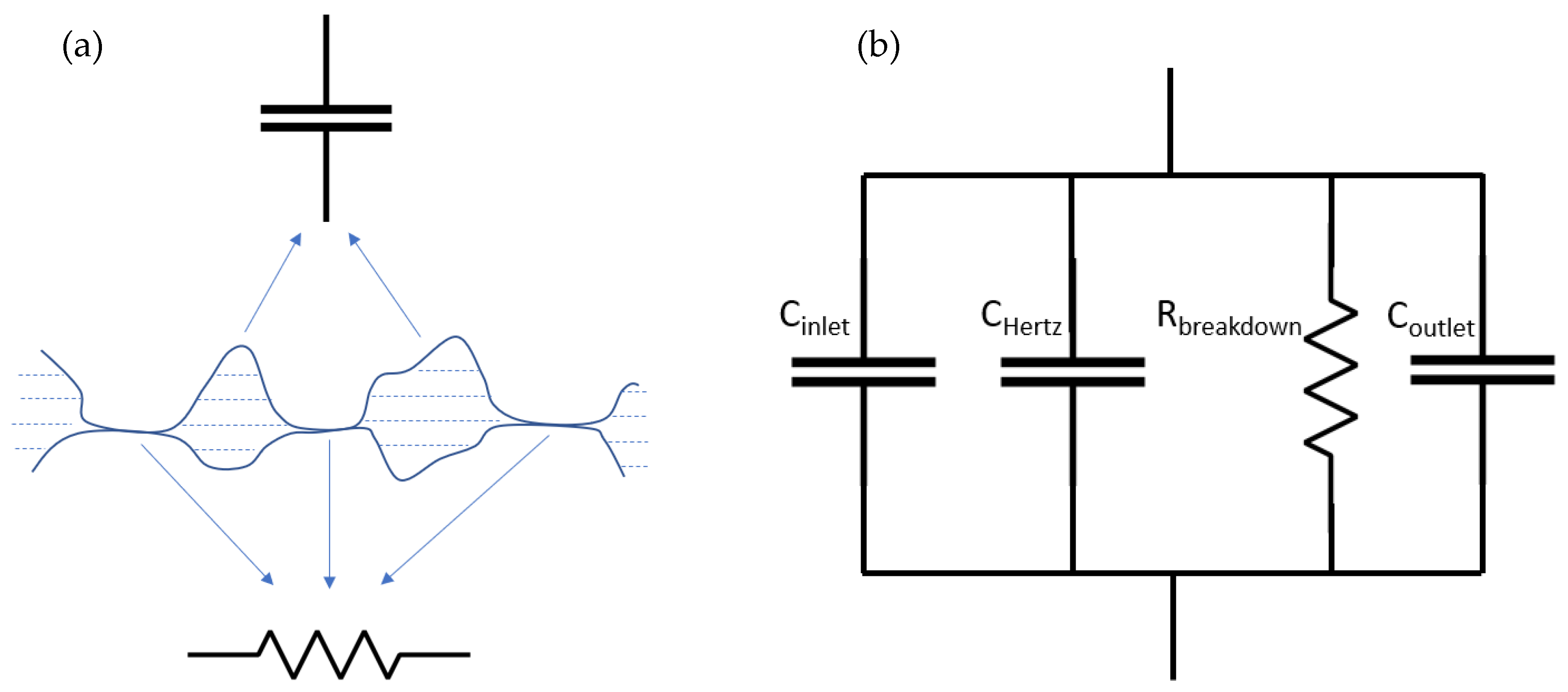
3. Capacitive Film Thickness Models and Electric Networks
- The capacitance of the film thickness can be modeled as a parallel plate capacitor;
- Film in the contact region is composed of oil without any thickener;
- A deep-groove ball bearing under axial load is used so the load on each ball is considered equally distributed;
- A polymer cage is used to simplify the electronic network;
- The effect of surface asperities on resistance measurement is neglected;
- The temperature gradient through the inlet, contact, and outlet regions is neglected.
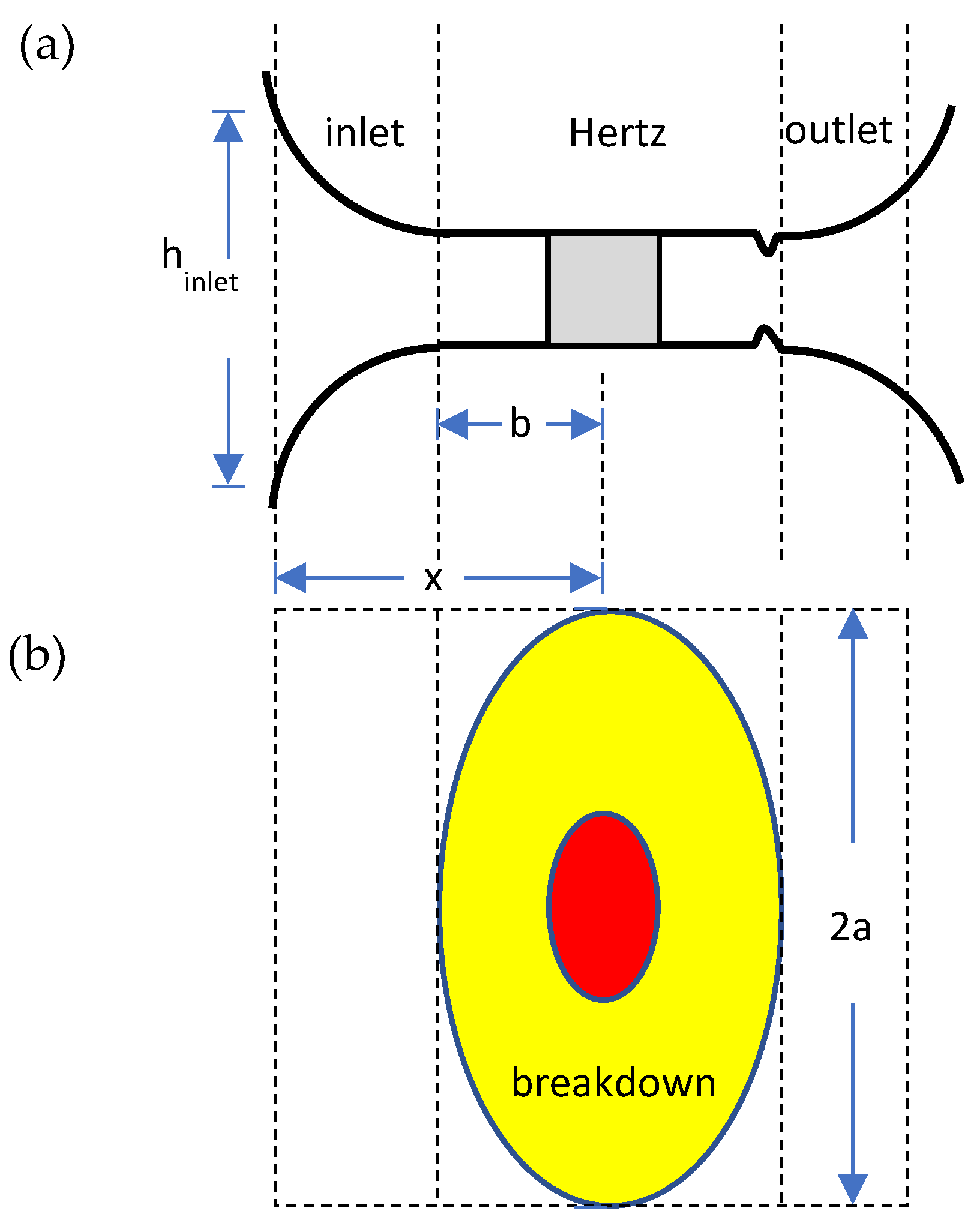
3.1. Fully Flooded
3.2. Starved
3.3. Mixed
- It is assumed there will be sufficient lubricant supply in the mixed regime; otherwise, it may cause premature bearing damage;
- It is assumed that there is no tribofilm formation on the surface. Tribofilms significantly increase contact resistance.
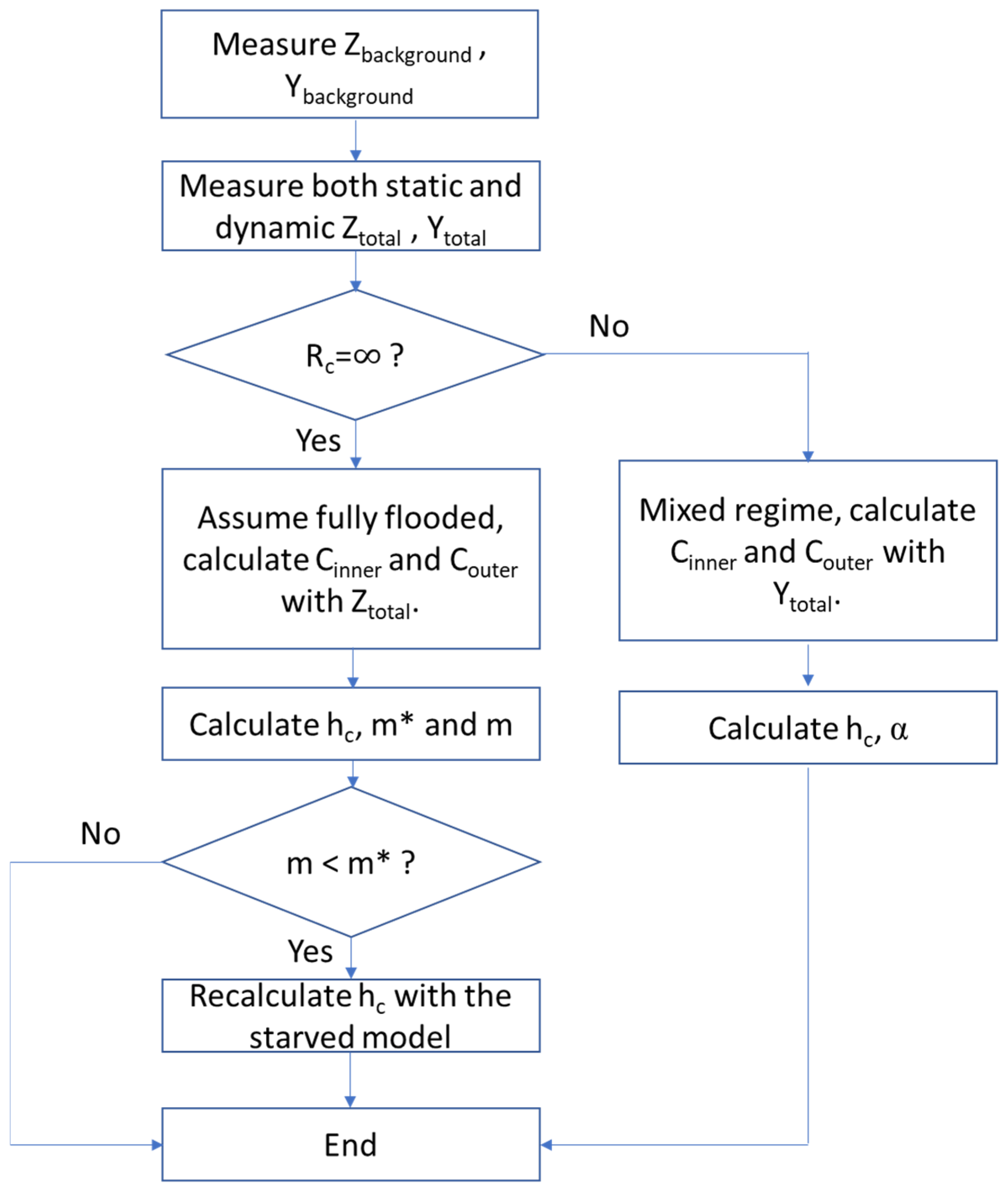
3.4. Program Flow Chart of Film Thickness Measurement
- (1)
- Measure the background impedance and admittance using a hybrid bearing under the same contact pressure;
- (2)
- Measure both the static and dynamic impedance and admittance using the testing bearing;
- (3)
- If the electrical contact resistance is finite, the bearing is in the mixed mode. The and are calculated with admittance. Then, the breakdown ratio and the central film thickness are calculated. The program ends;
- (4)
- If the electrical contact resistance approaches infinity, the bearing is in either fully flooded or starved mode. and are calculated to determine the starvation degree. If < , calculate the film thickness with the starved model. Otherwise, use the fully flooded model.
4. Dielectric Constant of Lubricants
4.1. Revisiting Classic Dielectric Models
4.2. Evaluation of Dielectric Models
4.3. Summary
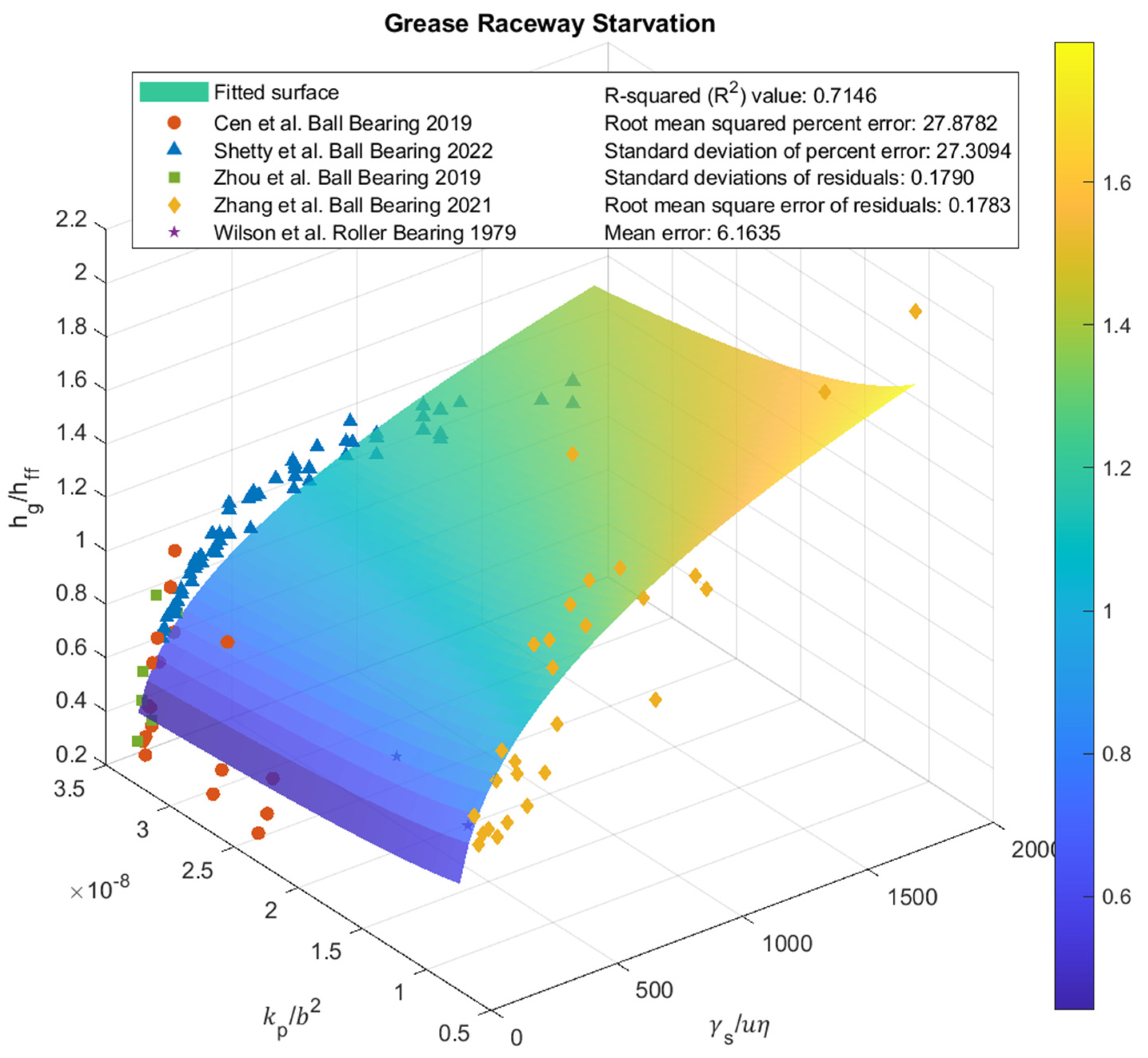
5. Grease Starvation Factor
6. Conclusions
- (1)
- The mechanisms of mainstream electronic components in capacitance measurement were reviewed. For analyzing complex electrical behavior, the LCR meter and impedance analyzer seem to be more suitable. It enables more accurate capacitance measurement;
- (2)
- Current capacitive models and programs can only measure one or two lubrication regimes. A new capacitive model, electric network, and program flow chart to measure lubricant film thickness in fully flooded, starved, and mixed regimes was developed. It is more comprehensive compared to the literature models;
- (3)
- Current dielectric constant models were reviewed, and suitable ones for lubricants were proposed. Modifying the CM and Onsager models with measured data to develop an engineering model is suggested. It facilitates a more precise film thickness measurement;
- (4)
- A new dimensionless grease starvation model was developed based on the 113 literature capacitive film thickness data points from five different authors. It is a function of surface tension, entrainment velocity, contact geometry, dynamic viscosity, and permeability. The R-squared value of 0.71 indicated a strong correlation, considering the variability in bearing types, operating conditions, grease formulations, testing rigs, and capacitive film thickness models.
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Contact ellipse semi-major: m | |
| Contact ellipse semi-minor: m | |
| Capacitance: F | |
| Total bearing capacitance: F | |
| Bearing capacitance: F | |
| Background capacitance: F | |
| Inner race capacitance: F | |
| Outer race capacitance: F | |
| Inlet region capacitance: F | |
| Hertzian contact region capacitance: F | |
| Outlet region capacitance: F | |
| Frequency: Hz | |
| Central film thickness: m | |
| Outer race central film thickness: m | |
| Inner race central film thickness: m | |
| Grease film thickness: m | |
| Fully flooded film thickness: m | |
| Dimensionless fully flooded film thickness | |
| Starved dimensionless central film thickness | |
| Current: Ampere | |
| Imaginary unit | |
| Permeability: m2 | |
| Inductance: H | |
| Dimensionless inlet distance | |
| Dimensionless inlet distance at boundary between fully flooded and starved conditions | |
| Refractive index | |
| Charge: C | |
| Effective radius of roller pair = : m | |
| Radii of cylinders or rollers in contact: m | |
| Effective radius in x direction: m | |
| Contact resistance: ohm | |
| Outer-race radius (rolling): m | |
| Inner-race radius (rolling): m | |
| Ball radius: m | |
| Entrainment velocity: m/s | |
| Voltage: Volt | |
| Reactance: ohm | |
| Admittance: S | |
| Impedance of each electric component: ohm | |
| Number of balls in the bearing | |
| Vacuum permittivity: F/m | |
| Dielectric constant of oil at ambient pressure | |
| Dielectric constant of oil at Hertzian contact pressure | |
| Dielectric constant of oil at outlet pressure | |
| Dielectric constant of air | |
| Breakdown ratio | |
| Density of lubricants: kg/m³ | |
| Surface Tension: N/m | |
| Dynamic viscosity: Pa·s | |
| Lubricant dynamic viscosity at outer race: Pa·s | |
| Lubricant dynamic viscosity at inner race: Pa·s | |
| Angular frequency: rad/s | |
| Phase angle: rad | |
| Starvation factor |
References
- Hamrock, B.; Dowson, D. Ball Bearing Lubrication: The Elastohydrodynamics of Elliptical Contacts; John Wiley & Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Lugt, P. Grease Lubrication in Rolling Bearings; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Poll, G.; Li, X.; Bader, N.; Guo, F. Starved lubrication in rolling contacts—A review. Bear. World J. 2019, 4, 69–81. [Google Scholar]
- Albahrani, S.; Philippon, D.; Vergne, P.; Bluet, J. A review of in situ methodologies for studying elastohydrodynamic lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 86–110. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Zhu, D.; Wang, Q. EHL Experimental Techniques and Experimental-Numerical Result Comparisons. In Proceedings of the STLE/ASME 2006 International Joint Tribology Conference, San Antonio, TX, USA, 23–25 October 2006; ASME: New York, NY, USA, 2006; Volume 2006, pp. 235–251. [Google Scholar] [CrossRef]
- Åström, H.; Isaksson, O.; Höglund, E. Video recordings of an EHD point contact lubricated with grease. Tribol. Int. 1991, 24, 179–184. [Google Scholar] [CrossRef]
- Cameron, A.; Gohar, R. Theoretical and experimental studies of the oil film in lubricated point contact. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1966, 291, 520–536. [Google Scholar]
- Cann, P.; Damiens, B.; Lubrecht, A. The transition between fully flooded and starved regimes in EHL. Tribol. Int. 2004, 37, 859–864. [Google Scholar] [CrossRef]
- Cen, H.; Lugt, P.; Morales-Espejel, G. Film Thickness of Mechanically Worked Lubricating Grease at Very Low Speeds. Tribol. Trans. 2014, 57, 1066–1071. [Google Scholar] [CrossRef]
- Noda, T.; Shibasaki, K.; Miyata, S.; Taniguchi, M. X-ray CT Imaging of Grease Behavior in Ball Bearing and Numerical Validation of Multi-Phase Flows Simulation. Tribol. Online 2020, 15, 36–44. [Google Scholar] [CrossRef]
- Gray, W.; Dwyer-Joyce, R. In-situ measurement of the meniscus at the entry and exit of grease and oil lubricated rolling bearing contacts. Front. Mech. Eng. 2022, 8, 1056950. [Google Scholar] [CrossRef]
- Courtney-Pratt, J.; Tudor, G. An Analysis of the Lubrication between the Piston Rings and Cylinder Wall of a Running Engine. Proc. Inst. Mech. Eng. 1946, 155, 293–299. [Google Scholar] [CrossRef]
- Crook, A. Simulated gear-tooth contacts: Some experiments upon their lubrication and subsurface deformations. Proc. Inst. Mech. Eng. 1957, 171, 187–214. [Google Scholar] [CrossRef]
- Lord, J.; Larsson, R. Film-forming capability in rough surface EHL investigated using contact resistance. Tribol. Int. 2008, 41, 831–838. [Google Scholar] [CrossRef]
- Lane, T.; Hughes, J. A study of the oil-film formation in gears by electrical resistance measurements. Br. J. Appl. Phys. 1952, 3, 315–318. [Google Scholar] [CrossRef]
- Bader, N.; Furtmann, A.; Tischmacher, H.; Poll, G. Capacitances and lubricant film thicknesses of grease and oil lubricated bearings. In Proceedings of the STLE Annual Meeting & Exhibition, Atlanta, GA, USA, 21–25 May 2017. [Google Scholar]
- Zhang, X.; Glovnea, R. Grease film thickness measurement in rolling bearing contacts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 1430–1439. [Google Scholar] [CrossRef]
- Cen, H.; Lugt, P.; Morales-Espejel, G. On the Film Thickness of Grease-Lubricated Contacts at Low Speeds. Tribol. Trans. 2014, 57, 668–678. [Google Scholar] [CrossRef]
- Wittek, E.; Kriese, M.; Tischmacher, H.; Gattermann, S.; Ponick, B.; Poll, G. Capacitances and lubricant film thicknesses of motor bearings under different operating conditions. In Proceedings of the The XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Wilson, A. The Relative Thickness of Grease and Oil Films in Rolling Bearings. Proc. Inst. Mech. Eng. 1979, 193, 185–192. [Google Scholar] [CrossRef]
- Morales-Espejel, G.; Lugt, P.; Pasaribu, H.; Cen, H. Film thickness in grease lubricated slow rotating rolling bearings. Tribol. Int. 2014, 74, 7–19. [Google Scholar] [CrossRef]
- Leenders, P.; Houpert, L. Paper XXI(i) study of the lubricant film in rolling bearings; effects of roughness. In Fluid Film Lubrication–Osborne Reynolds Centenary; Tribology Series; Elsevier: Amsterdam, The Netherlands, 1987; Volume 11, pp. 629–638. [Google Scholar]
- Maruyama, T.; Maeda, M.; Nakano, K. Lubrication Condition Monitoring of Practical Ball Bearings by Electrical Impedance Method. Tribol. Online 2019, 14, 327–338. [Google Scholar] [CrossRef]
- Crook, A. The lubrication of rollers. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1958, 250, 387–409. [Google Scholar]
- Cen, H.; Bai, D.; Chao, Y.; Li, Y.; Li, R. EHL film thickness in rolling element bearings evaluated by electrical capacitance method: A review. Tribol.-Mater. Surf. Interfaces 2021, 15, 55–77. [Google Scholar] [CrossRef]
- Glovnea, R.; Furtuna, M.; Nagata, Y.; Sugimura, J. Electrical Methods for the Evaluation of Lubrication in Elastohydrodynamic Contacts. Tribol. Online 2012, 7, 46–53. [Google Scholar] [CrossRef]
- Appleby, M.; Choy, F.; Du, L.; Zhe, J. Oil debris and viscosity monitoring using ultrasonic and capacitance/inductance measurements. Lubr. Sci. 2013, 25, 507–524. [Google Scholar] [CrossRef]
- Prashad, H.; Rao, K. Analysis of Capacitive Effect and Life Estimation of Hydrodynamic Journal Bearings on Repeated Starts and Stops of a Machine Operating under the Influence of Shaft Voltages. Tribol. Trans. 1994, 37, 641–645. [Google Scholar] [CrossRef]
- Murali, S.; Choy, F.; Zhe, J.; Carletta, J.; Xia, X. Oil Debris Detection Using Static and Dynamic Capacitance Measurements. In Proceedings of the STLE/ASME 2008 International Joint Tribology Conference, Miami, FL, USA, 20–22 October 2008; ASMEDC: Houston, TX, USA, 2008; pp. 241–243. [Google Scholar] [CrossRef]
- Potyrailo, R.; Tokarev, I.; Go, S.; Ottikkutti, P.; Kuzhiyil, N.; Mihok, J.; Anzini, C.; Shartzer, S. Multivariable Electrical Resonant Sensors for Independent Quantitation of Aging and External Contaminants in Lubricating Oils. IEEE Sens. J. 2019, 19, 1542–1553. [Google Scholar] [CrossRef]
- Shi, H.; Yu, S.; Xie, Y.; Li, W.; Zhang, H.; Zheng, Y.; Zhang, S.; Li, G.; Sun, Y.; Chen, H. Comprehensive detection method for multi-contaminants in hydraulic oil based on inductance-resistance-capacitance analysis. Tribol. Int. 2022, 173, 107609. [Google Scholar] [CrossRef]
- Qian, M.; Ren, Y.; Feng, Z. Interference reducing by low-voltage excitation for a debris sensor with triple-coil structure. Meas. Sci. Technol. 2020, 31, 025103. [Google Scholar] [CrossRef]
- Qian, M.; Zhao, G.; Ren, Y.; Diao, W.; Feng, Z.; Li, M. Triple-Coil Inductive Debris Sensor with Special Shielded Coils for Depressing Interference of Dielectric Components. Procedia Manuf. 2019, 39, 1279–1288. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, H. Solid particles, water drops and air bubbles detection in lubricating oil using microfluidic inductance and capacitance measurements. J. Micromechanics Microengineering 2019, 29, 025011. [Google Scholar] [CrossRef]
- Yang, D.; Hu, Z.; Xiao, J. Research on capacitive sensor for online oil monitoring. In Proceedings of the 2011 Prognostics and System Health Managment Conference, Shenzhen, China, 24–25 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Hu, Z.; Yang, Y. Oil Contamination Monitoring Based on Dielectric Constant Measurement. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 249–252. [Google Scholar] [CrossRef]
- Xue, Q.; Ma, M.; Fan, W.; Sun, B.; Cui, Z.; Wang, H. Level set based image segmentation for oil film monitoring using ECT. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Taipei, Taiwan, 23–26 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Murali, S.; Xia, X.; Jagtiani, A.; Carletta, J.; Zhe, J. A Microfluidic Device for Wear Detection in Lubricants. In Proceedings of the ASME 2008 International Mechanical Engineering Congress and Exposition, Boston, MA, USA, 31 October–6 November 2008; ASMEDC: Houston, TX, USA, 2008; pp. 859–863. [Google Scholar] [CrossRef]
- Nihira, T.; Manabe, K.; Tadokoro, C.; Ozaki, S.; Nakano, K. Complex Impedance Measurement Applied to Short-Time Contact Between Colliding Steel Surfaces. Tribol. Lett. 2015, 57, 29. [Google Scholar] [CrossRef]
- Manabe, K.; Nakano, K. Breakdown of oil films and formation of residual films. Tribol. Int. 2008, 41, 1103–1113. [Google Scholar] [CrossRef]
- Maruyama, T.; Nakano, K. In Situ Quantification of Oil Film Formation and Breakdown in EHD Contacts. Tribol. Trans. 2018, 61, 1057–1066. [Google Scholar] [CrossRef]
- Nakano, K.; Akiyama, Y. Simultaneous measurement of film thickness and coverage of loaded boundary films with complex impedance analysis. Tribol. Lett. 2006, 22, 127–134. [Google Scholar] [CrossRef]
- Schirra, T.; Martin, G.; Vogel, S.; Kirchner, E. Ball Bearings as Sensors for Systematical Combination of Load and Failure Monitoring. In Proceedings of the DESIGN 2018 15th International Design Conference, Dubrovnik, Croatia, 21–24 May 2018; The Design Society: Glasgow, UK, 2018; pp. 3011–3022. [Google Scholar] [CrossRef]
- Schnabel, S.; Marklund, P.; Minami, I.; Larsson, R. Monitoring of Running-in of an EHL Contact Using Contact Impedance. Tribol. Lett. 2016, 63, 35. [Google Scholar] [CrossRef]
- Xie, K.; Liu, L.; Li, X.; Zhang, H. Non-contact resistance and capacitance on-line measurement of lubrication oil film in rolling element bearing employing an electric field coupling method. Measurement 2016, 91, 606–612. [Google Scholar] [CrossRef]
- Schritz, B.; Jones Jr, W.; Prahl, J.; Jansen, R. Parched elastohydrodynamic lubrication: Instrumentation and procedure. In Proceedings of the Annual Meeting of the Society of Tribologists and Lubrication Engineers, Ptuqadeiphia, PA, USA, 4–7 May 1991. [Google Scholar]
- Kingsbury, E.; Schritz, B.; Prahl, J. Parched Elasto Hydrodynamic Lubrication Film Thickness Measurement in an Instrument Ball Bearing. Tribol. Trans. 1990, 33, 11–14. [Google Scholar] [CrossRef]
- Franke, E.; Poll, G. Service life and lubrication conditions of different grease types in high-speed rolling bearings. In Lubrication at the Frontier: The Role of the Interface and Surface Layers in the Thin Film and Boundary Regime; Tribology Series; Elsevier: Amsterdam, The Netherlands, 1999; Volume 36, pp. 601–609. [Google Scholar] [CrossRef]
- Heemskerk, R.; Vermeiren, K.; Dolfsma, H. Measurement of Lubrication Condition in Rolling Element Bearings. ASLE Trans. 1982, 25, 519–527. [Google Scholar] [CrossRef]
- Cen, H.; Lugt, P. Film thickness in a grease lubricated ball bearing. Tribol. Int. 2019, 134, 26–35. [Google Scholar] [CrossRef]
- Shetty, P.; Meijer, R.; Osara, J.; Lugt, P. Measuring Film Thickness in Starved Grease-Lubricated Ball Bearings: An Improved Electrical Capacitance Method. Tribol. Trans. 2022, 65, 869–879. [Google Scholar] [CrossRef]
- Adabi, J.; Zare, F.; Ledwich, G.; Ghosh, A.; Lorenz, R. Bearing damage analysis by calculation of capacitive coupling between inner and outer races of a ball bearing. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 903–907. [Google Scholar] [CrossRef]
- Attia, A.; El-Bahloul, A. Lubrication Capacity of Gears of Circular-Arc Tooth-Profile. J. Tribol. 1988, 110, 699–703. [Google Scholar] [CrossRef]
- Bates, T.; Benwell, S. Effect of Oil Rheology on Journal Bearing Performance Part 3—Newtonian Oils in the Connecting-Rod Bearing of an Operating Engine. SAE Trans. 1988, 97, 308–320. [Google Scholar]
- Cen, H.; Lugt, P. Replenishment of the EHL contacts in a grease lubricated ball bearing. Tribol. Int. 2020, 146, 106064. [Google Scholar] [CrossRef]
- Chittenden, R.; Dowson, D.; Taylor, C. Elastohydrodynamic Film Thickness in Concentrated Contacts: Part 1: Experimental Investigation for Lubricant Entrainment Aligned with the Major Axis of the Contact Ellipse. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1986, 200, 207–217. [Google Scholar] [CrossRef]
- Cho, M.-R.; Han, D.-C.; Choi, J.-K. Oil Film Thickness in Engine Connecting-Rod Bearing with Consideration of Thermal Effects: Comparison between Theory and Experiment. J. Tribol. 1999, 121, 901–907. [Google Scholar] [CrossRef]
- Chua, W.; Stachowiak, G. The Study of the Dynamic Thickness of Organic Boundary Films Under Metallic Sliding Contact. Tribol. Lett. 2010, 39, 151–161. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, H.; Yang, C.; Xu, Y. Estimation of in-tube oil film thickness using electrical capacitance tomography. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Dhar, A.; Agarwal, A.; Saxena, V. Measurement of Lubricating Oil Film Thickness between Piston Ring-liner Interface in an Engine Simulator; SAE Technical Paper 2008-28-0071; SAE International: Warrendale, PA, USA, 2008. [Google Scholar] [CrossRef]
- Dhar, A.; Agarwal, A.; Saxena, V. Measurement of dynamic lubricating oil film thickness between piston ring and liner in a motored engine. Sens. Actuators Phys. 2009, 149, 7–15. [Google Scholar] [CrossRef]
- Garcia-Atance Fatjo, G.; Smith, E.; Sherrington, I. Mapping lubricating film thickness, film extent and ring twist for the compression-ring in a firing internal combustion engine. Tribol. Int. 2014, 70, 112–118. [Google Scholar] [CrossRef]
- Gatzen, M.; Pape, F.; Bruening, C.; Gatzen, H.; Arlinghaus, H.; Poll, G. Correlation between performance and boundary layers in high speed bearings lubricated with polymer-enhanced greases. Tribol. Int. 2010, 43, 981–989. [Google Scholar] [CrossRef]
- Gouda, B.; Tandon, N.; Pandey, R.; Babu, C. Design and development of a test rig for performance evaluation of ball bearings. In Proceedings of the Advances in Mechanical Engineering, Industrial Informatics and Management (AMEIIM2022), Raipur, India, 25–26 February 2022; p. 020006. [Google Scholar] [CrossRef]
- Gouda, B.; Tandon, N.; Pandey, R.; Babu, C. Performance improvement of a radial ball bearing using a micro-groove on stationary outer race. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 11521–11536. [Google Scholar] [CrossRef]
- Grice, N.; Sherrington, I. An Experimental Investigation into the Lubrication of Piston Rings in an Internal Combustion Engine-Oil Film Thickness Trends, Film Stability and Cavitation; SAE Technical Paper 930688; SAE International: Warrendale, PA, USA, 1993. [Google Scholar] [CrossRef]
- Gui, C.; Liu, K. Effect of surface roughness on the lubrication properties of the piston ring and cylinder of an engine, and calculation of lubrication and power loss analysis of piston-ring pack of a S195 diesel engine. Lubr. Sci. 1992, 4, 263–275. [Google Scholar] [CrossRef]
- Guo, L.; Mol, H.; Nijdam, T.; de Vries, L.; Bongaerts, J. Study on the electric discharge behaviour of a single contact in EV motor bearings. Tribol. Int. 2023, 187, 108743. [Google Scholar] [CrossRef]
- Hamilton, G.; Moore, S. Deformation and pressure in an elastohydrodynamic contact. Proc. R. Soc. Lond. Math. Phys. Sci. 1971, 322, 313–330. [Google Scholar] [CrossRef]
- Hamilton, G.; Moore, S. First Paper: Measurement of the Oil-Film Thickness between the Piston Rings and Liner of a Small Diesel Engine. Proc. Inst. Mech. Eng. 1974, 188, 253–261. [Google Scholar] [CrossRef]
- Hamilton, G.; Moore, S. Second Paper: Comparison between Measured and Calculated Thicknesses of the Oil-Film Lubricating Piston Rings. Proc. Inst. Mech. Eng. 1974, 188, 262–268. [Google Scholar] [CrossRef]
- Hegedus, P. Evaluation and Prediction of Elastohydrodynamic Lubrication Film Thickness under Conditions of Severe Sliding and Zero Entrainment. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 2018. [Google Scholar]
- Hemingway, E. The Measurement of Film Thickness in Thrust Bearings and the Deflected Shape of ‘Parallel’ Surface Thrust Pads. Proc. Inst. Mech. Eng. 1965, 180, 1025–1034. [Google Scholar] [CrossRef]
- Hoehn, B.; Michaelis, K.; Mayer, J.; Weigl, A. Influence of surface velocity directions on lubricant film formation in EHL point contacts. Tribol. Int. 2012, 47, 9–15. [Google Scholar] [CrossRef]
- Irani, K.; Pekkari, M.; Ångström, H. Oil film thickness measurement in the middle main bearing of a six-cylinder supercharged 9 litre diesel engine using capacitive transducers. Wear 1997, 207, 29–33. [Google Scholar] [CrossRef]
- Jablonka, K.; Glovnea, R.; Bongaerts, J. Evaluation of EHD films by electrical capacitance. J. Phys. D Appl. Phys. 2012, 45, 385301. [Google Scholar] [CrossRef]
- Jablonka, K.; Glovnea, R.; Bongaerts, J.; Morales-Espejel, G. The effect of the polarity of the lubricant upon capacitance measurements of EHD contacts. Tribol. Int. 2013, 61, 95–101. [Google Scholar] [CrossRef]
- Horowitz, P.; Hill, W. The Art of Electronics, 3rd ed.; 19th printing; Cambridge University Press: New York, NY, USA, 2022; ISBN 978-0-521-80926-9. [Google Scholar]
- Moore, S. Piston ring lubrication in a two-stroke diesel engine. Wear 1981, 72, 353–369. [Google Scholar] [CrossRef]
- Dyson, A.; Naylor, H.; Wilson, A. Paper 10: The measurement of oil-film thickness in elastohydrodynamic contacts. Proc. Inst. Mech. Eng. Conf. Proc. 1965, 180, 119–134. [Google Scholar] [CrossRef]
- ten Napel, W.; Bosma, R. The Influence of Surface Roughness on the Capacitive Measurement of Film Thickness in Elastohydrodynamic Contacts. Proc. Inst. Mech. Eng. 1970, 185, 635–639. [Google Scholar] [CrossRef]
- Wen, B.; Ren, H.; Dang, P.; Hao, X.; Han, Q. Measurement and calculation of oil film thickness in a ball bearing. Ind. Lubr. Tribol. 2018, 70, 1500–1508. [Google Scholar] [CrossRef]
- Zhang, P.; Zhu, B.; Liu, S. Study of measuring EHL oil-film thickness with electric capacity method. Lubr. Eng. 1982, 7, 16–22. [Google Scholar]
- Schirra, T.; Martin, G.; Puchtler, S.; Kirchner, E. Electric impedance of rolling bearings—Consideration of unloaded rolling elements. Tribol. Int. 2021, 158, 106927. [Google Scholar] [CrossRef]
- Schneider, V.; Bader, N.; Liu, H.; Poll, G. Method for in situ film thickness measurement of ball bearings under combined loading using capacitance measurements. Tribol. Int. 2022, 171, 107524. [Google Scholar] [CrossRef]
- Schneider, V.; Liu, H.; Bader, N.; Furtmann, A.; Poll, G. Empirical formulae for the influence of real film thickness distribution on the capacitance of an EHL point contact and application to rolling bearings. Tribol. Int. 2021, 154, 106714. [Google Scholar] [CrossRef]
- Magdun, O.; Binder, A. Calculation of roller and ball bearing capacitances and prediction of EDM currents. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1051–1056. [Google Scholar] [CrossRef]
- Hunter, S. Oil Film Thickness Measurement and Analysis for an Angular Contact Ball Bearing Operating in Parched Elastohydrodynamic Lubrication. In Proceedings of the Institution of Mechanical Engineers, International Conference, IMechE 1987-5, Cincinnati, OH, USA, 14–17 June 1987; Case Western Reserve University: Cleveland, OH, USA, 1987. [Google Scholar]
- Bartz, M. Lubricant Film Formation in Grease Lubricated High Speed Spindle Bearings. Ph.D. Thesis, University of Hanover, Hanover, Germany, 1996. [Google Scholar]
- Gemeinder, Y.; Schuster, M.; Radnai, B.; Sauer, B.; Binder, A. Calculation and validation of a bearing impedance model for ball bearings and the influence on EDM-currents. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1804–1810. [Google Scholar] [CrossRef]
- Gonda, A. Determination of Rolling Bearing Electrical Capacitances with Experimental and Numerical Investigation Methods. Ph.D. Thesis, Rheinland-Pfälzische Technische Universität Kaiserslautern-Landau, Kaiserslautern, Germany, 2024. [Google Scholar]
- Crook, A. The lubrication of rollers II. Film thickness with relation to viscosity and speed. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1961, 254, 223–236. [Google Scholar]
- Dowson, D.; Higginson, G. Elasto-Hydrodynamic Lubrication: International Series on Materials Science and Technology; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Hamrock, B.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part IV—Starvation Results. J. Lubr. Technol. 1977, 99, 15–23. [Google Scholar] [CrossRef]
- Nogi, T. An Analysis of Starved EHL Point Contacts with Reflow. Tribol. Online 2015, 10, 64–75. [Google Scholar] [CrossRef]
- Zhang, X.; Jablonka, K.; Glovnea, R. Experimental Rig for Measuring Lubricant Film Thickness in Rolling Bearings. Appl. Mech. Mater. 2014, 658, 381–386. [Google Scholar] [CrossRef]
- Bondi, A. Physical Chemistry of Lubricating Oils; Reinhold Publishing Corporation: Washington, DC, USA, 1951. [Google Scholar]
- Dowson, D. Elastohydrodynamic lubrication. In The Fundamentals of Roller and Gear Lubrication; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Bair, S. High Pressure Rheology for Quantitative Elastohydrodynamics; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Hirschfelder, J.; Curtiss, C.; Bird, R. The Molecular Theory of Gases and Liquids; John Wiley & Sons: Hoboken, NJ, USA, 1964. [Google Scholar]
- Galvin, G.; Naylor, H.; Wilson, A. Paper 14: The Effect of Pressure and Temperature on Some Properties of Fluids of Importance in Elastohydrodynamic Lubrication. Inst. Mech. Eng. Conf. Proc. 1963, 178, 283–290. [Google Scholar] [CrossRef]
- Fuks, I.; Gundyrev, A.; Shekhter, Y.; Perekrestova, V.; Fedorova, T.; Kartinin, B. Chemical composition of dispersion medium and dielectric constant of lithium greases. Chem. Technol. Fuels Oils 1974, 10, 480–483. [Google Scholar] [CrossRef]
- Carey, A. The dielectric constant of lubrication oils. Comput. Syst. Inc. 1998, 835, 675–683. [Google Scholar]
- Khanmamedov, S.; Bardetskii, A. Relation between dielectric and viscosity characteristics of turbine oils. Chem. Technol. Fuels Oils 1988, 24, 209–211. [Google Scholar] [CrossRef]
- Debye, P. Polar Molecules; Dover: New York, NY, USA, 1929. [Google Scholar]
- Fröhlich, H. Theory of Dielectrics: Dielectric Constant and Dielectric Loss; Clarendon Press: Oxford, UK, 1958. [Google Scholar]
- Onsager, L. Electric moments of molecules in liquids. J. Am. Chem. Soc. 1936, 58, 1486–1493. [Google Scholar] [CrossRef]
- Kirkwood, J. The dielectric polarization of polar liquids. J. Chem. Phys. 1939, 7, 911–919. [Google Scholar] [CrossRef]
- Valiskó, M.; Boda, D.; Liszi, J.; Szalai, I. Relative permittivity of dipolar liquids and their mixtures. Comparison of theory and experiment. Phys. Chem. Chem. Phys. 2001, 3, 2995–3000. [Google Scholar] [CrossRef]
- Kiselev, V.; Kornilov, D.; Konovalov, A. Changes in Permittivity and Density of Molecular Liquids under High Pressure. J. Phys. Chem. B 2014, 118, 3702–3709. [Google Scholar] [CrossRef]
- Wedeven, L.; Evans, D.; Cameron, A. Optical analysis of ball bearing starvation. J. Lubr. Technol. 1971, 93, 349–361. [Google Scholar] [CrossRef]
- Damiens, B.; Venner, C.; Cann, P.; Lubrecht, A. Starved Lubrication of Elliptical EHD Contacts. J. Tribol. 2004, 126, 105–111. [Google Scholar] [CrossRef]
- van Zoelen, M.; Venner, C.; Lugt, P. Prediction of film thickness decay in starved elasto-hydrodynamically lubricated contacts using a thin layer flow model. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 541–552. [Google Scholar] [CrossRef]
- Chiu, Y. An Analysis and Prediction of Lubricant Film Starvation in Rolling Contact Systems. ASLE Trans. 1974, 17, 22–35. [Google Scholar] [CrossRef]
- Chevalier, F.; Lubrecht, A.; Cann, P.; Colin, F.; Dalmaz, G. Film thickness in starved EHL point contacts. J. Tribol. 1998, 120, 126–133. [Google Scholar] [CrossRef]
- Wandel, S.; Bader, N.; Schwack, F.; Glodowski, J.; Lehnhardt, B.; Poll, G. Starvation and relubrication mechanisms in grease lubricated oscillating bearings. Tribol. Int. 2022, 165, 107276. [Google Scholar] [CrossRef]
- Wandel, S.; Bader, N.; Glodowski, J.; Lehnhardt, B.; Leckner, J.; Schwack, F.; Poll, G. Starvation and Re-lubrication in Oscillating Bearings: Influence of Grease Parameters. Tribol. Lett. 2022, 70, 114. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M. A study on the effect of starvation in mixed elastohydrodynamic lubrication. Tribol. Int. 2015, 85, 26–36. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Lin, J.; Wang, D. Study on Factors Influencing Film Formation of Grease and Calculation Model for Grease Film Thickness. Lubricants 2022, 10, 123. [Google Scholar] [CrossRef]
- Zhou, Y.; Bosman, R.; Lugt, P. An Experimental Study on Film Thickness in a Rolling Bearing for Fresh and Mechanically Aged Lubricating Greases. Tribol. Trans. 2019, 62, 557–566. [Google Scholar] [CrossRef]
- Akchurin, A.; Ende, D.; Lugt, P. Modeling impact of grease mechanical ageing on bleed and permeability in rolling bearings. Tribol. Int. 2022, 170, 107507. [Google Scholar] [CrossRef]
- Zhang, Q.; Mugele, F.; Van Den Ende, D.; Lugt, P. A Model Configuration For Studying Stationary Grease Bleed In Rolling Bearings. Tribol. Trans. 2021, 64, 1127–1137. [Google Scholar] [CrossRef]
- Ross, S. Variation with Temperature of Surface Tension of Lubricating Oils; NACA: Washington, DC, USA, 1950. [Google Scholar]
- Chen, H.; Wang, W.; Liang, H.; Zhao, Z. Patterns of interfacial flow around a lubricated rolling point contact region. Phys. Fluids 2021, 33, 102118. [Google Scholar] [CrossRef]
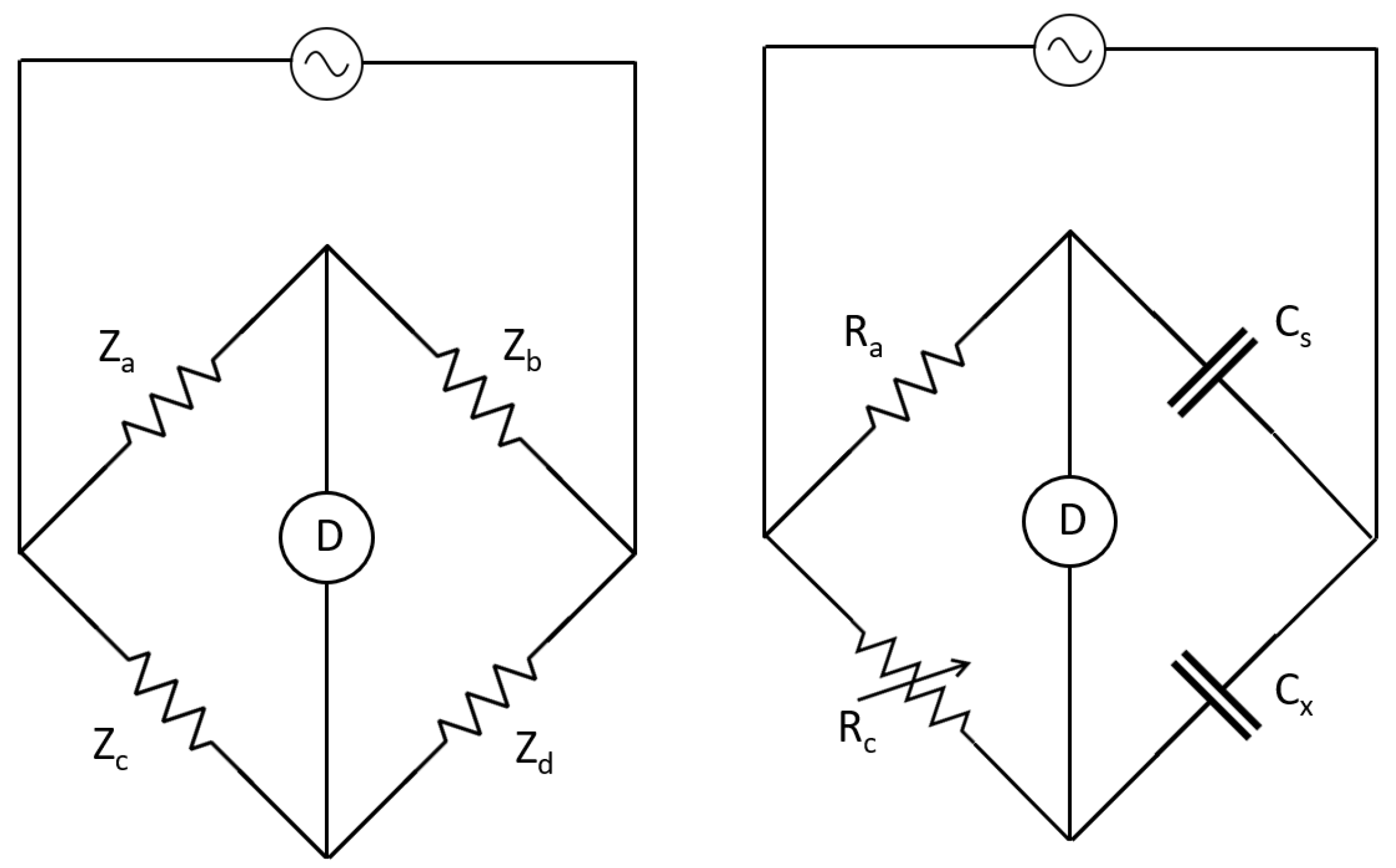
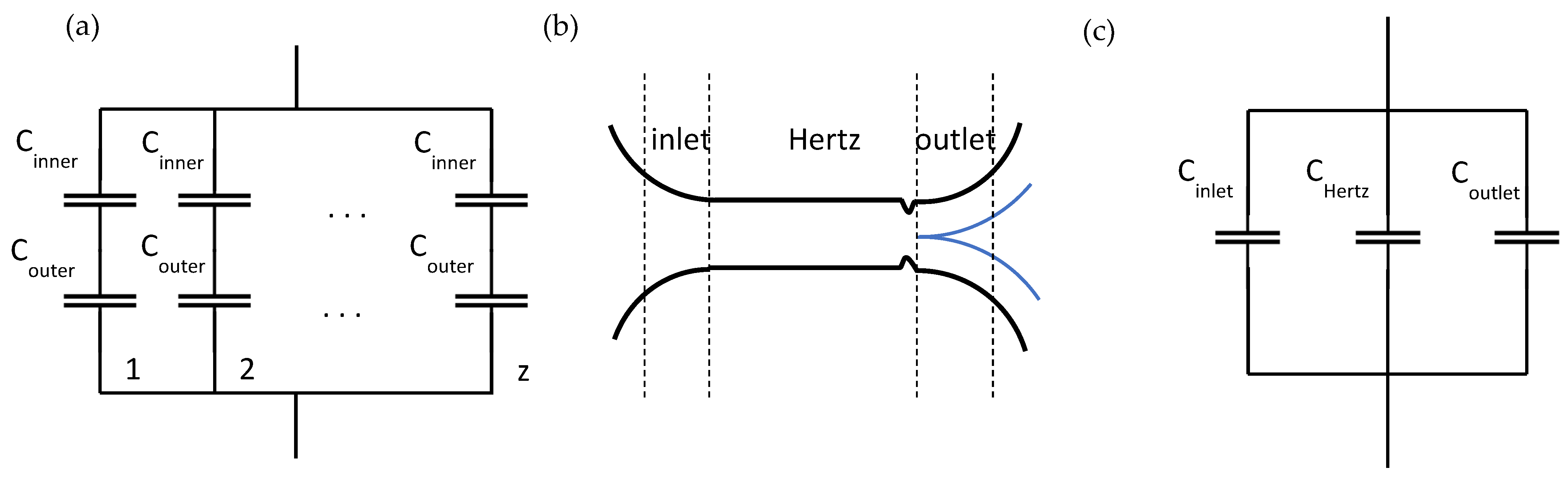
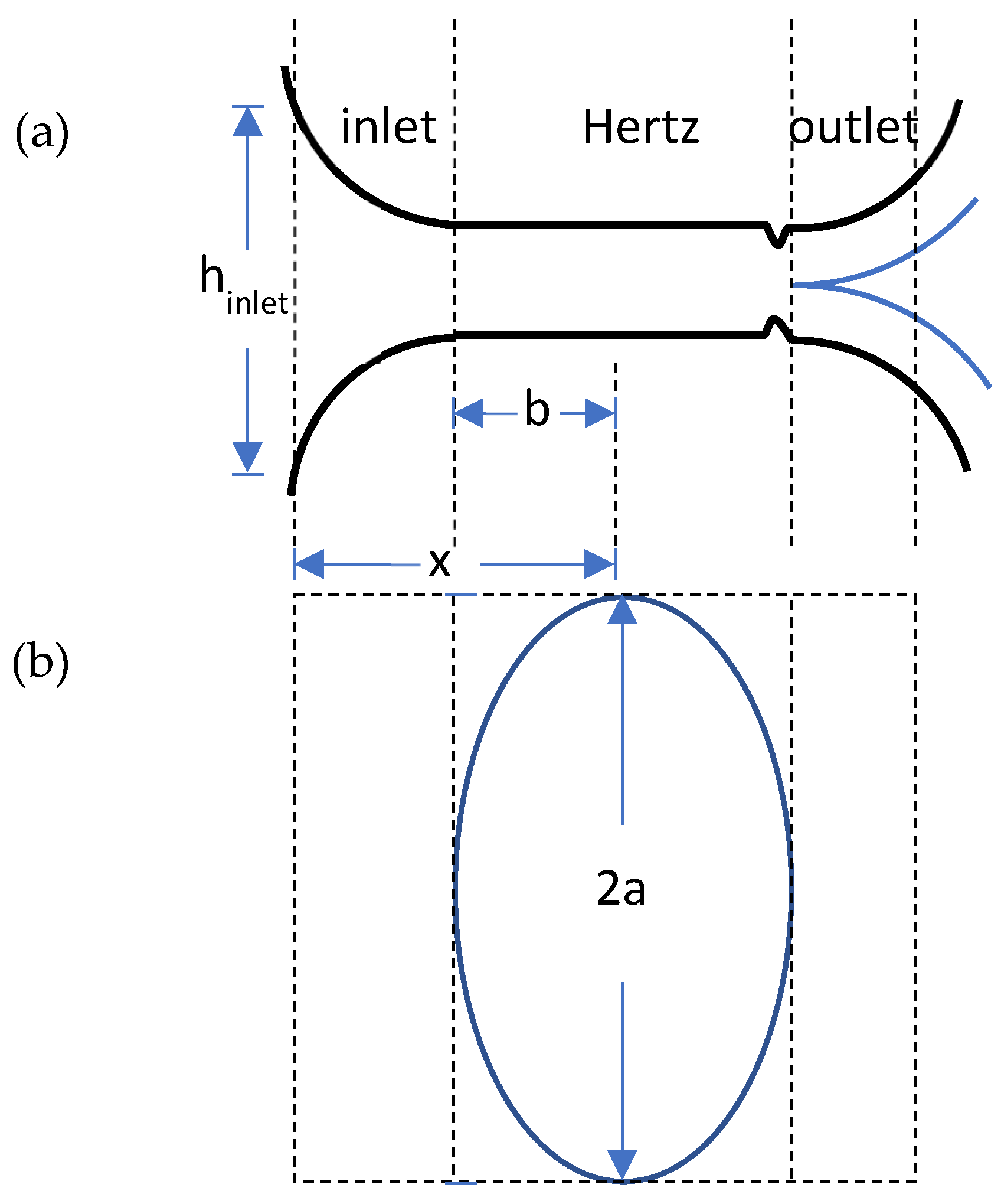
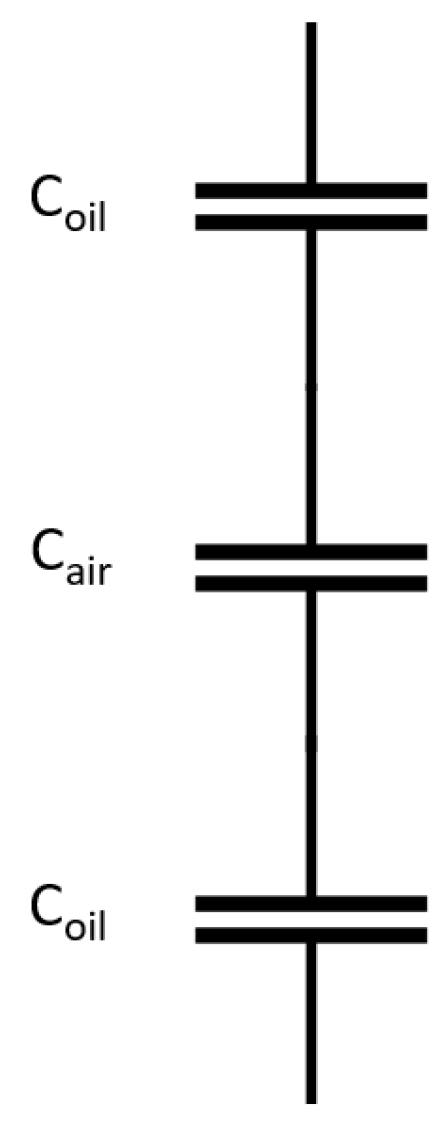

| Testing Rig | Lubrication Regime | Capacitance Calculation and Some Assumptions | Reference |
|---|---|---|---|
| Twin disk and ball bearing | Fully flooded | For single contact, the total capacitance of a contact can be calculated by the following equation, if and are known or if one assumed or calculated a value for : For multipoint contact, all contacts at one ring are in parallel with each other and then in series with the other rings’ capacitances. The full film EHL is considered as a capacitor connected in parallel with a resistor. Bartz approximated the kC factor for ball bearings as 3~4. Gemeinder used 3.5 for calculation. Schneider extended the factor to a wider operating range. | [16,19,63,85,89,90] |
| Ball bearing under radial load | Fully flooded | The total capacitance of a loaded inner ring contact is divided into five zones: the inlet; outlet; Hertzian; and two side zones. The inlet, outlet, and side capacitances were determined using line contact curve-fitted approximations. | [22] |
| Ball bearing | Mixed | It is theoretically shown that the oil film thickness and breakdown ratio can be simultaneously measured from the complex impedance. Contact resistor: Oil film capacitor: | [23] |
| Twin disk | Fully flooded | Assume inlet is full of oil, and outlet has two equally thick oil layers adhering to it. | [24] |
| Steel–oil–mercury system | Mixed | The total impedance can be calculated as | [40] |
| Pin-on-disk | Mixed | h2 is the maximum oil film thickness in the surrounding area (defined as the vertical position of the center of the ball). Studied the relationship between air entrainment ratio and film thickness. | [41] |
| Unloaded ball bearing | Fully flooded |
Using the impedance method: | [43,84] |
| Ball bearing under axial load | Starved and fully flooded |
he starved inlet distance is based on Dowson and Hamrock. | [51] |
| Twin-disk machine | Fully flooded | For the outlet zone, it is assumed the relative composite dielectric constant of the two-phase fluid can be described as where and are the volume percentages of oil and air, respectively. | [56] |
| Four-disk machine | Fully flooded | The outlet region is assumed to be made up of two oil layers, and the remainder of the gap is made up of air. Each oil layer is assumed to be half of the central film thickness. | [69] |
| Pin-on-disk | Fully flooded | Considered the inlet and contact as the flooded region, where is 1; hc is the central film thickness, and hgap is the gap between the solid bodies, given by the Hertzian deformation for dry contacts. In the cavitation region, The cavitation region was estimated to be about 25% of the total area surrounding the contact. | [76] |
| Twin disks | Fully flooded | For the Hertzian region, the dielectric constant is normally estimated at mean surface temperature and mean contact pressure. | [80,81] |
| Ball bearing | Fully flooded | The total measured capacitance includes the capacitance of the Hertzian, inlet, and outlet regions. | [82,83] |
| Ball bearing under combined load | Fully flooded | Inner ring and outer ring connected in series. | [85] |
| Ball bearing | Fully flooded | Accounted for the geometry change in surfaces outside the Hertzian contact zone due to the elastohydrodynamic pressure. The relationship between the Hertzian contact area capacitance and total capacitance was determined using an empirical formula based on numerical simulation. | [86] |
| Roller bearing and ball bearing | Fully flooded | For the roller bearing, the Hertzian contact area is considered a flat rectangular surface, where L is the length of the roller elements. For the cavitation region, assuming a long flat over for the raceway, it can be calculated as | [87] |
| Ball bearing | Fully flooded |
The cavitation domain can be modeled numerically as | [91] |
| Lubricants | Dielectric Constant Models and Measurements | Reference |
|---|---|---|
| Grease and oil | The dielectric constant of the grease (measured at laboratory temperature, atmospheric pressure, and a frequency of 100 kHz) was 3.07 in the unused condition and 2.60 after being sheared between the rollers, while that of the base oil was 2.32. The dielectric constant of the grease decreased on shearing to approach but did not equal that of the base oil. A further investigation, not reported in this paper, showed that the remaining difference was caused by the polar constituents of the grease and by the presence of fragments of disrupted soap fibers. | [20] |
| Shell Turbo 68 oil | The dielectric constant was reported as 2.65, 3, and 1 in the inlet, Hertzian zone, and outlet, respectively. | [22] |
| Grease | The dielectric properties of the greases were determined experimentally in a separate setup consisting of a plate capacitor with exactly known geometry. | [48] |
| Lithium grease | The measured capacitance and Hamrock–Dowson film thickness equation were used to back-calculate the dielectric constant. | [51] |
| SAE 20, SAE 60 | The dielectric constants of both fresh and used oils were measured using a cylindrical brass capacitor and an excitation signal of 100 kHz. The dielectric constant of the oil was determined as the ratio of the capacitance of the cell filled with oil and air. Measurements were made at 100 °C, 125 °C, and 150 °C. | [54] |
| Shell HVI 160 medium viscosity mineral oil |
The relationship between the dielectric constant and the pressure was described by the Clausius–Mossotti (CM) relationship. | [56] |
| Sunflower oil | The dielectric constant of the bulk lubricant at the test temperature was then calculated as follows: Dyson and Galvin found the CM equation to be relatively accurate for non-polar fluids (such as mineral oil). The equation overestimates the dielectric constant at high pressures. Chua mentioned that the discrepancy might be because the polarizability did not change linearly with density. The Onsager formula was considered more suitable. | [58] |
| Naphthenic oil |
Non-polar oil should obey the Clausius–Mossotti equation. Some direct measurements on similar mineral oils by Galvin, Naylor, and Wilson (1963) suggested a better relationship: | [69,101] |
| NYE 182 | The dielectric constant of the lubricant at pressure can be approximated by making use of the Clausius–Mossotti equation. | [72] |
| Paraffinic oil | The resulting variations in dielectric constant with temperature and pressure are substantially in agreement with those found by Galvin, Naylor, and Wilson in 1963. | [73,101] |
| PAO4, PAO40 | For non-polar lubricants, the dielectric constant can be calculated using the Clausius–Mossotti equation. | [76] |
| Glycerol, PEG, and PAO | For polar fluids, the CM equation is not valid. More complex Onsager or Kirkwood relationships must be applied. | [77] |
| Paraffinic oil | From 0 to 350 MPa, the dielectric constant decreases with an increase in temperature and increases with an increase in pressure. | [80] |
| Oil | A modified CM equation can be used based on the work of Bondi and Schrader. | [91,97] |
| PAO4 | The dielectric constant of a non-polar lubricant at the contact pressure is estimated using the Clausius–Mossotti equation. | [96] |
| Lithium grease | The dielectric constant of lithium grease depends primarily on the polarity of the dispersion medium (e.g., additives.) Organic additives (LZ-318, USI, DPA, Khloref 40) have a stronger influence on the dielectric constant than inorganic additives (mica, graphite, and MoS2). When lithium greases are heated to close to their dropping point (180–200 °C), a sharp increase in the dielectric constant is observed. | [102] |
| Mineral oil, synthetic oil, and additives | Hydrocarbon lubrication oils have a dielectric constant from 2.1 to 2.8, which depends on the viscosity of the oil, the paraffinic/naphthenic content, and the additive package. The dielectric constant of hydrocarbon fuels (which contain smaller carbon chains than lubrication oils) correlates with fuel density (kg/m3), within an accuracy of 2% | [103] |
| Lubricants | Testing Rig | Starvation Models | Reference |
|---|---|---|---|
| High-viscosity PAO | Pin-on-disk | Fully flooded and starved transition of oil-lubricated contact: where is base oil dynamic viscosity; is the entrainment speed; is the contact width; is oil height (lubricant volume), and is oil surface tension. | [8] |
| Grease | Deep-groove ball bearing | Grease starvation depends on speed, load, temperature, and grease properties: where is the rotational speed, and is the bearing pitch diameter. | [50] |
| Grease | Deep-groove ball bearing | A power–law relationship is found between the normalized film thickness and speed x viscosity x contact width: where is the entrainment speed; is the dynamic viscosity of the base oil, and is the semi-minor. | [55] |
| Oil | Optical interferometry + numerical simulation | Both the Damiens and Van Zoelen models show the same film thickness decay with time: where is the resistance to side flow, which is a function of Moe’s dimensionless numbers (M, L) and contact ellipticity . | [112,113] |
| Oil | Optical EHD rig | The surface tension gradient is considered the driving force for fluid recovery. The amount of lubricant replenishment can be predicted as follows: where is oil surface tension; is dynamic viscosity, and is the time interval between successive rolling-element passages. | [114] |
| Oil | Numerical simulation | Effects of inlet supply starvation on film thickness in EHL point contact: where indicates dimensionless film thickness reduction; is the dimensionless film thickness on the track, and is the resistance to the side flow. | [115] |
| Grease | Angular contact ball bearings | The starvation number for oscillating grease-lubricated bearings: where is base oil dynamic viscosity; a is the semi-major; b is the semi-minor; is overrolling frequency; is surface tension, and is the oil-separation rate. | [116,117] |
| Parameter | Unit | Dimension (m, L, t) |
|---|---|---|
| Lubricant/air surface tension | N/m or kg/s2 | |
| Entrainment velocity | m/s | |
| Dynamic viscosity | Pa·s or kg/ms | |
| Half contact width | m | |
| Permeability | m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, W. In Situ Measurement of Grease Capacitive Film Thickness in Bearings: A Review. Lubricants 2024, 12, 329. https://doi.org/10.3390/lubricants12100329
Dai W. In Situ Measurement of Grease Capacitive Film Thickness in Bearings: A Review. Lubricants. 2024; 12(10):329. https://doi.org/10.3390/lubricants12100329
Chicago/Turabian StyleDai, Wei. 2024. "In Situ Measurement of Grease Capacitive Film Thickness in Bearings: A Review" Lubricants 12, no. 10: 329. https://doi.org/10.3390/lubricants12100329
APA StyleDai, W. (2024). In Situ Measurement of Grease Capacitive Film Thickness in Bearings: A Review. Lubricants, 12(10), 329. https://doi.org/10.3390/lubricants12100329