Leakage Characteristics and Experimental Research of Staggered Labyrinth Sealing
Abstract
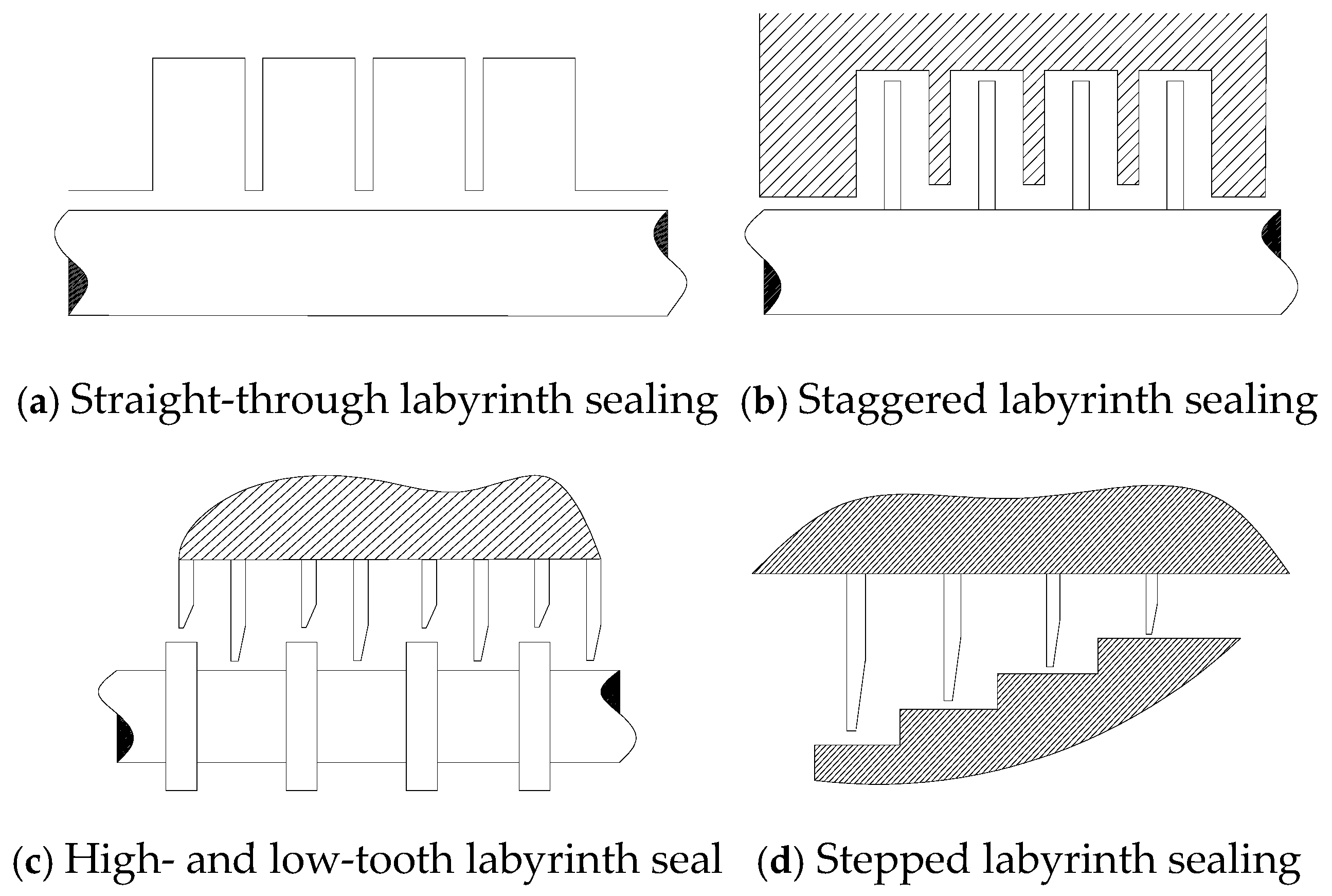
:1. Introduction
2. Theoretical Calculation of the Leakage for Staggered Labyrinth Seals Under Multiple Effects
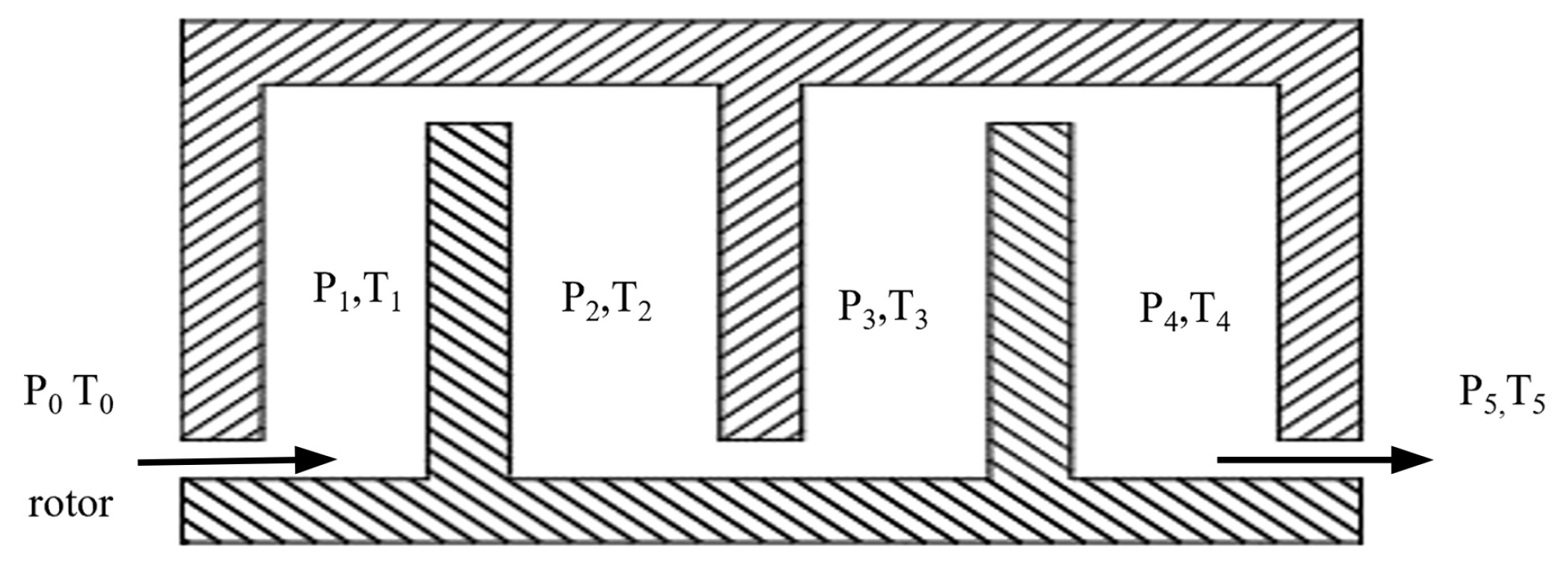
2.1. Thermodynamic Effect in Staggered Labyrinth Seals
2.2. Friction Effect in Staggered Labyrinth Seals
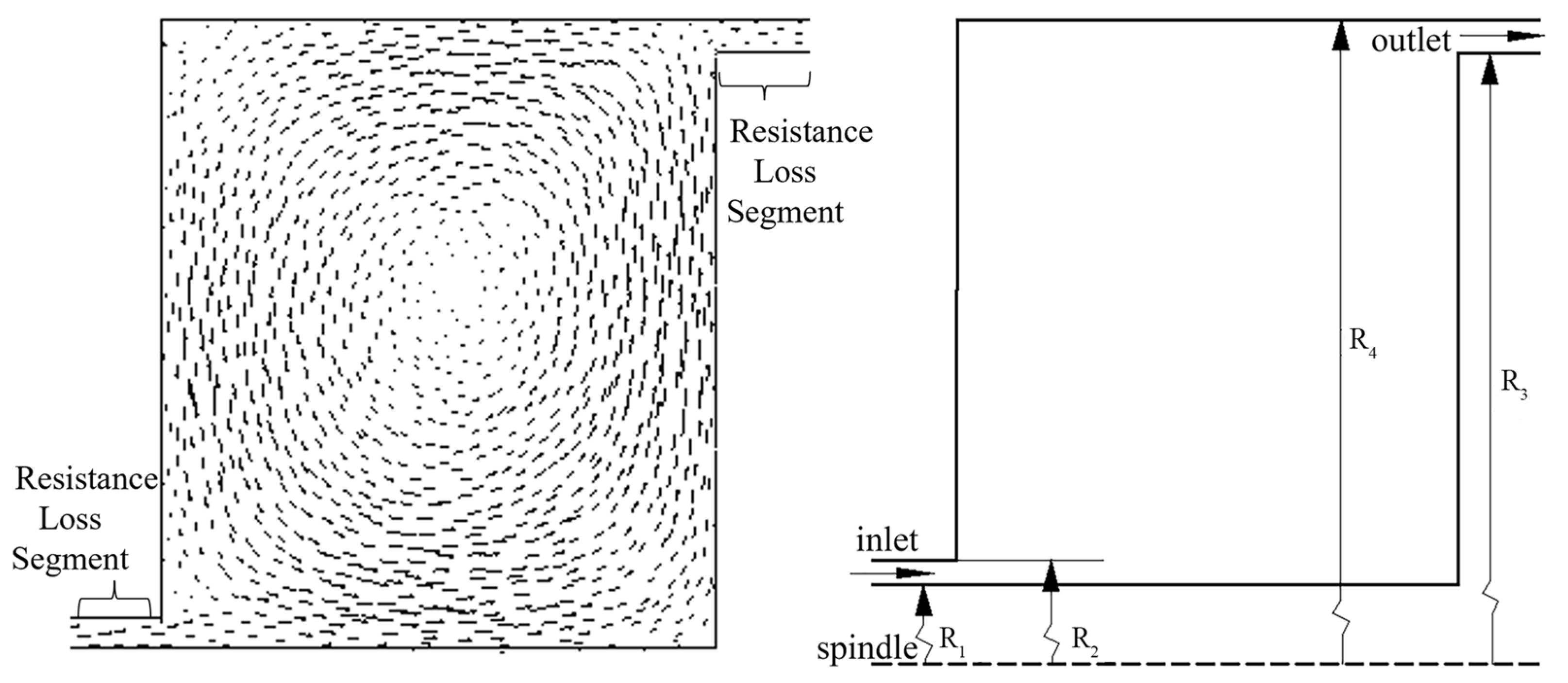
2.2.1. Calculation of Resistance Loss Along the Route for Staggered Labyrinth Seals
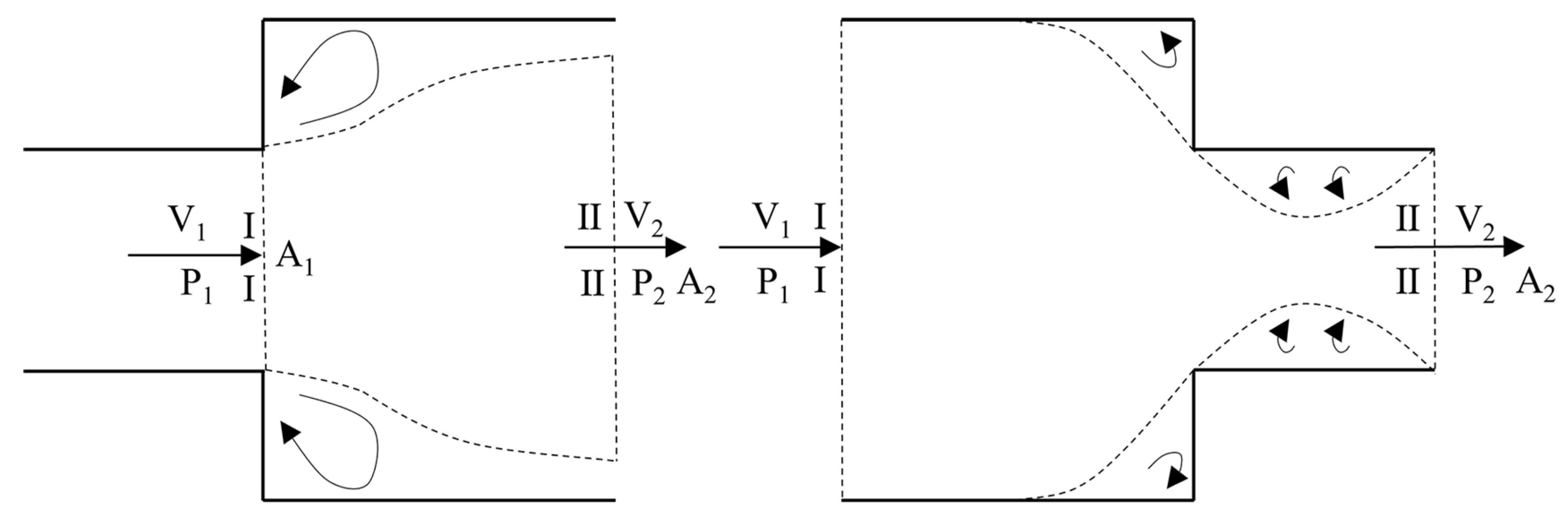
2.2.2. Calculation of Local Resistance Loss for Staggered Labyrinth Seals
3. Parametric Simulation of the Flow Field of a Staggered Labyrinth Seal
3.1. Governing Equations and Turbulence Models
3.2. Parametric Simulation
3.3. Simulation Results of Leakage Characteristics of Staggered Labyrinth Seals Under the Main Influencing Factors
3.3.1. Grid-Independent Verification
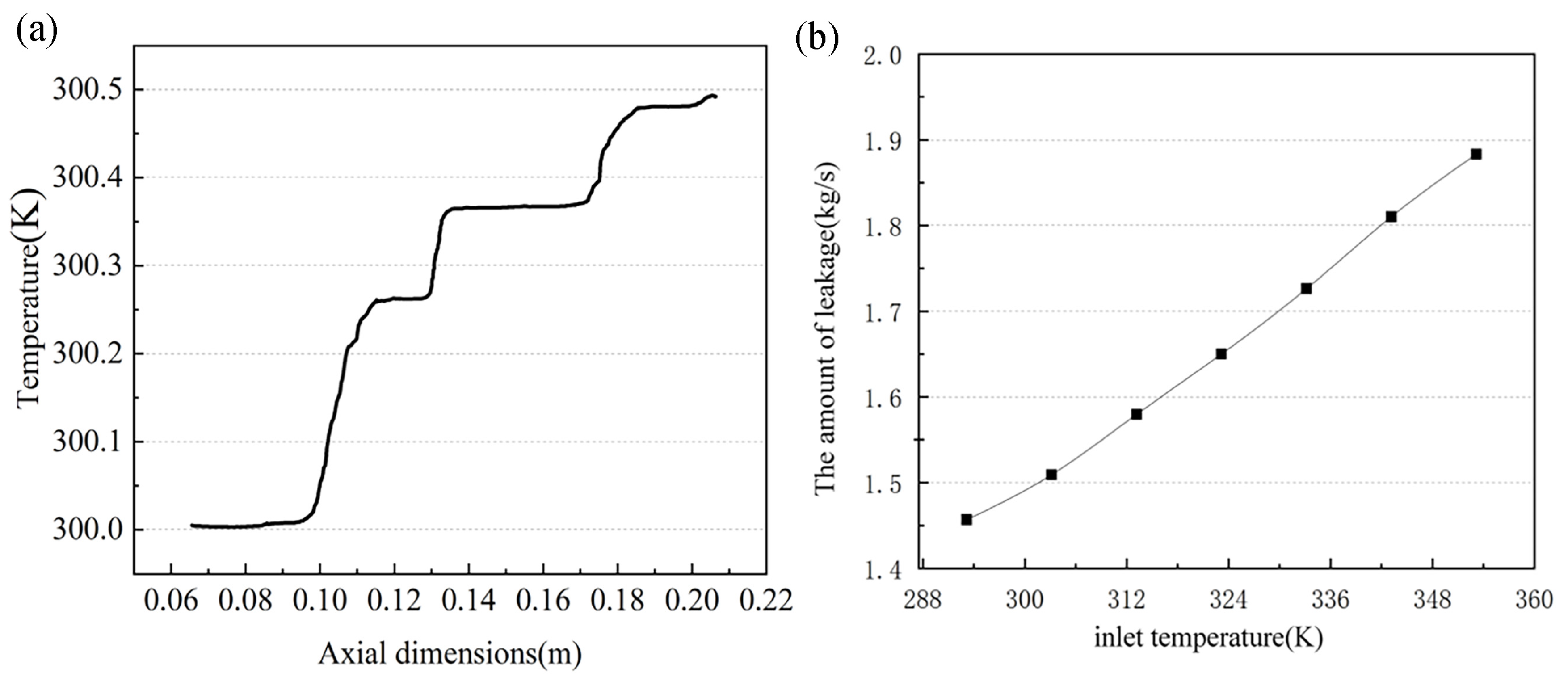
3.3.2. Effect of Total Inlet Temperature on Leakage Characteristics
3.3.3. Effect of Total Inlet Pressure on Leakage Characteristics
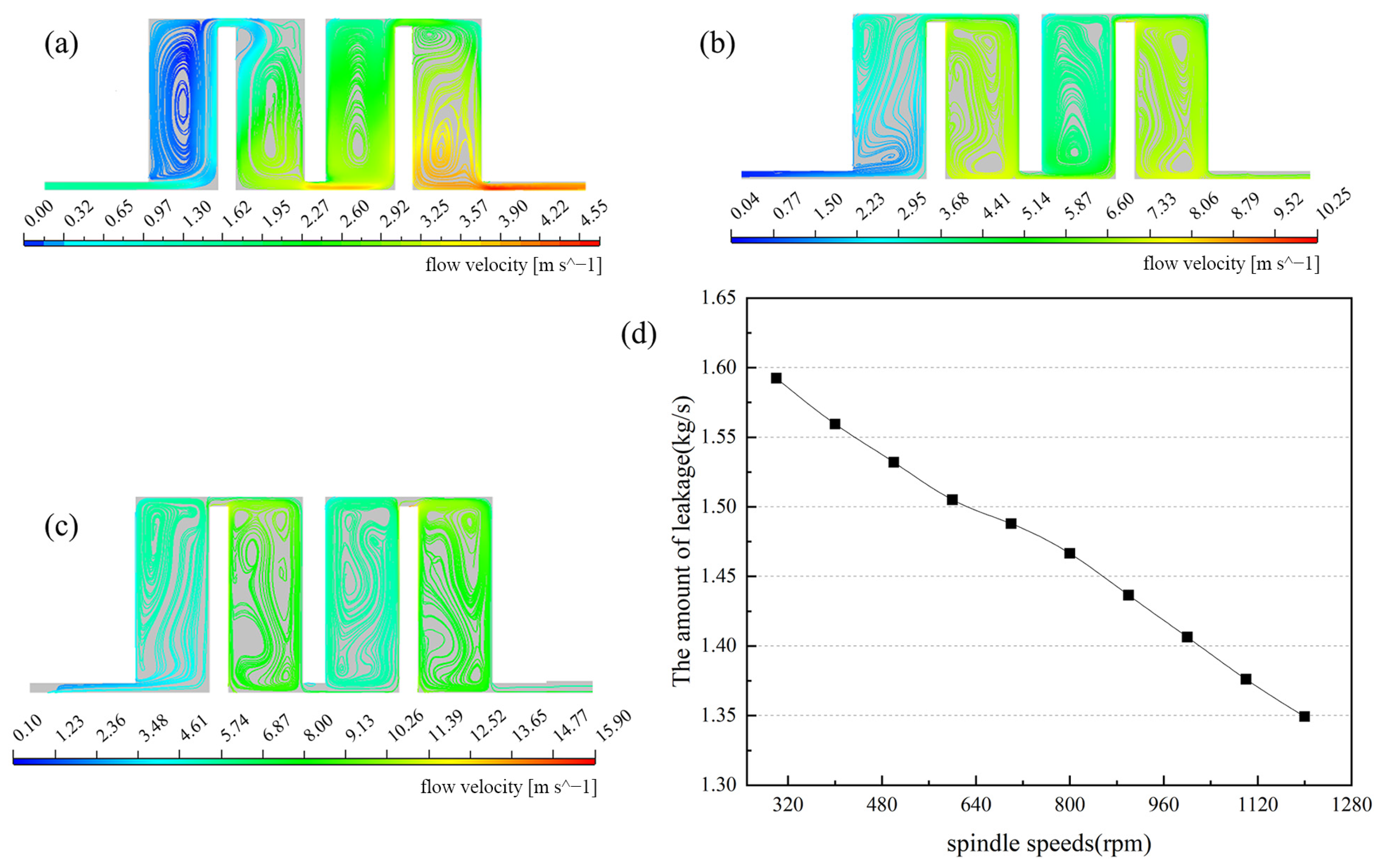
3.3.4. Effect of Spindle Speed on Leakage Characteristics
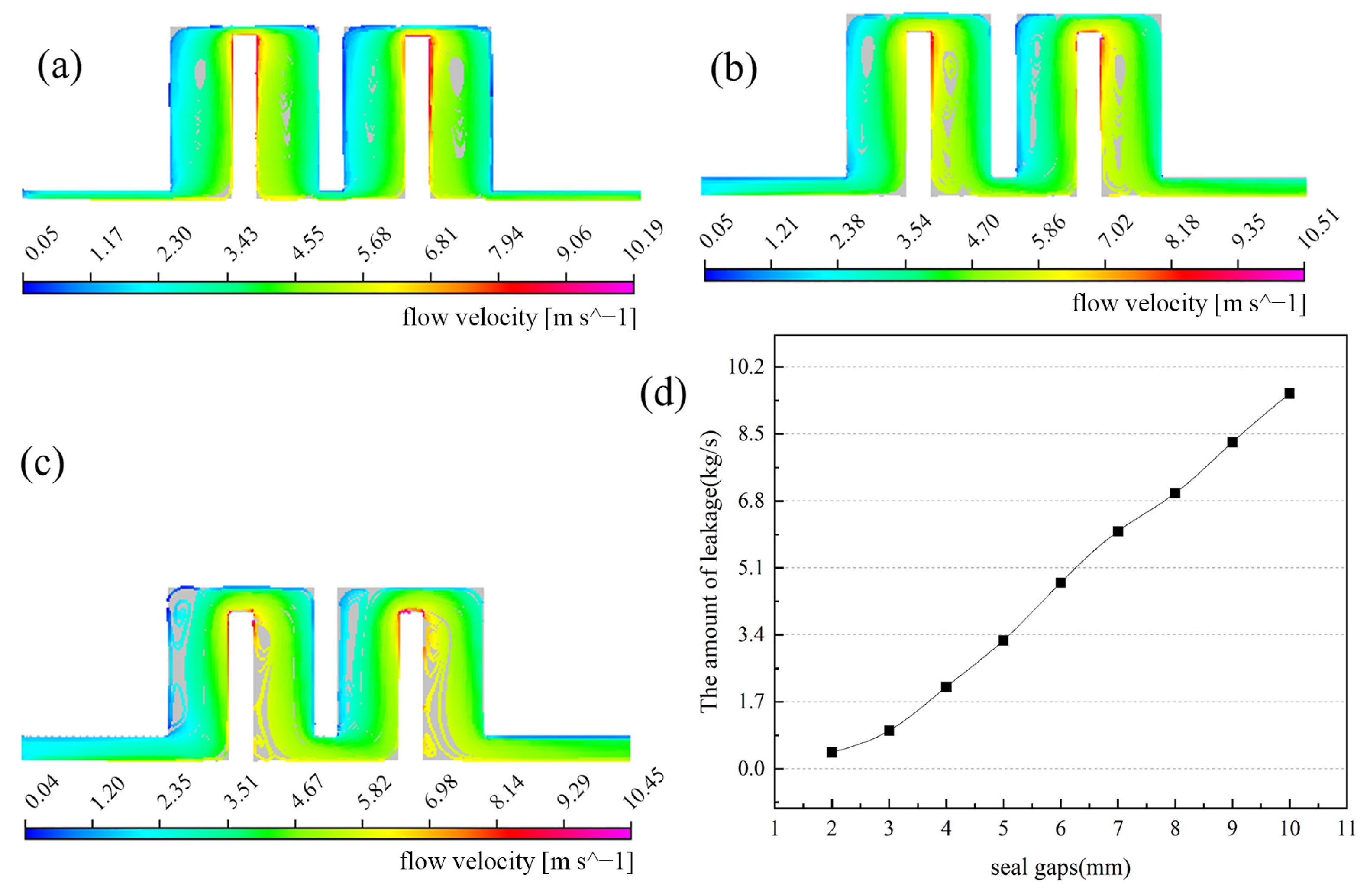
3.3.5. Effect of Seal Clearance on Leak Characteristics
4. Experimental Verification of Staggered Labyrinth Seals
4.1. Staggered Labyrinth Seal Leakage Test Bench
4.2. The Results and Discussion of the Leakage Test of the Staggered Labyrinth Seal
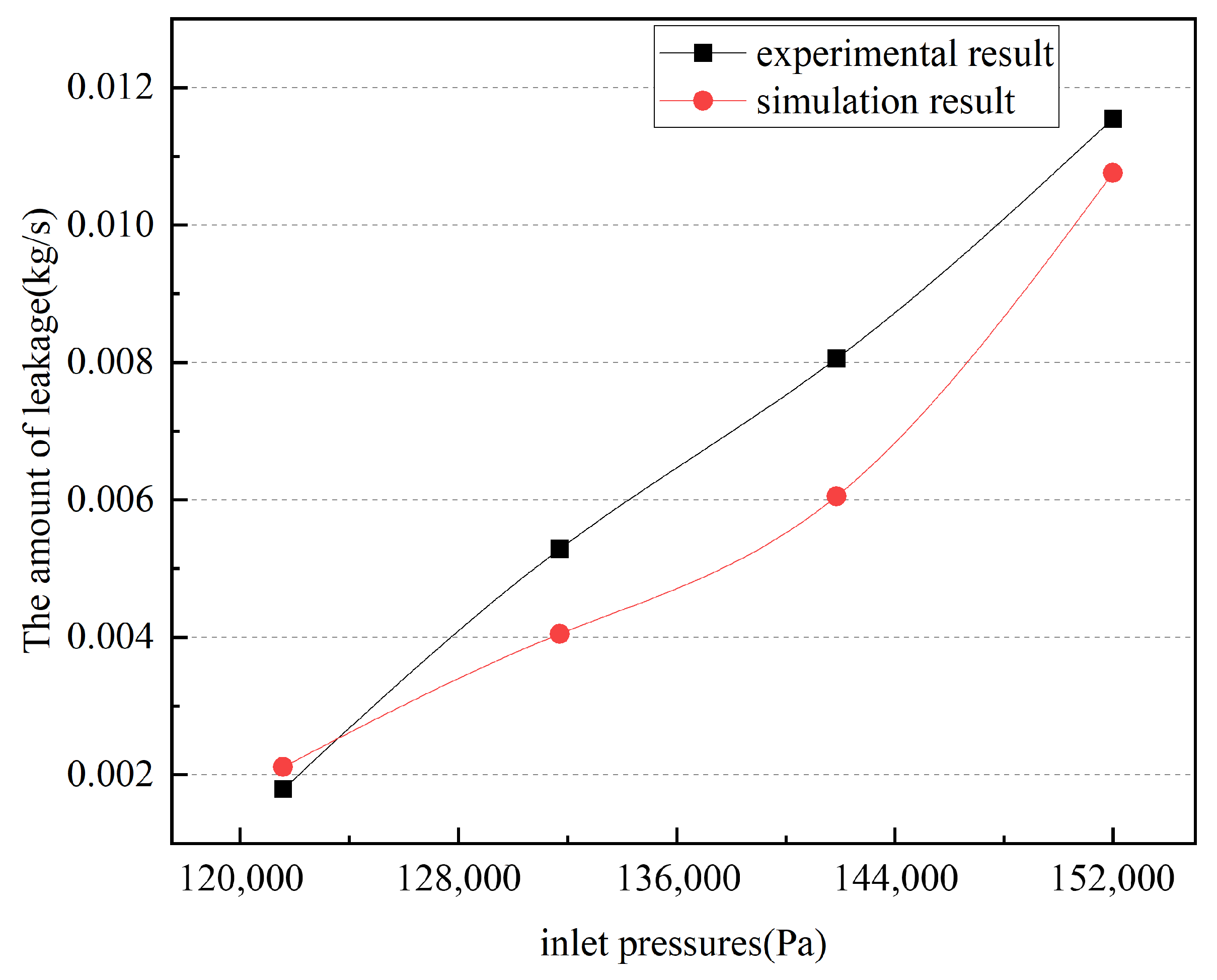
4.2.1. The Influence of the Total Inlet Pressure on the Leakage of the Staggered Labyrinth Seal Was Verified by the Test
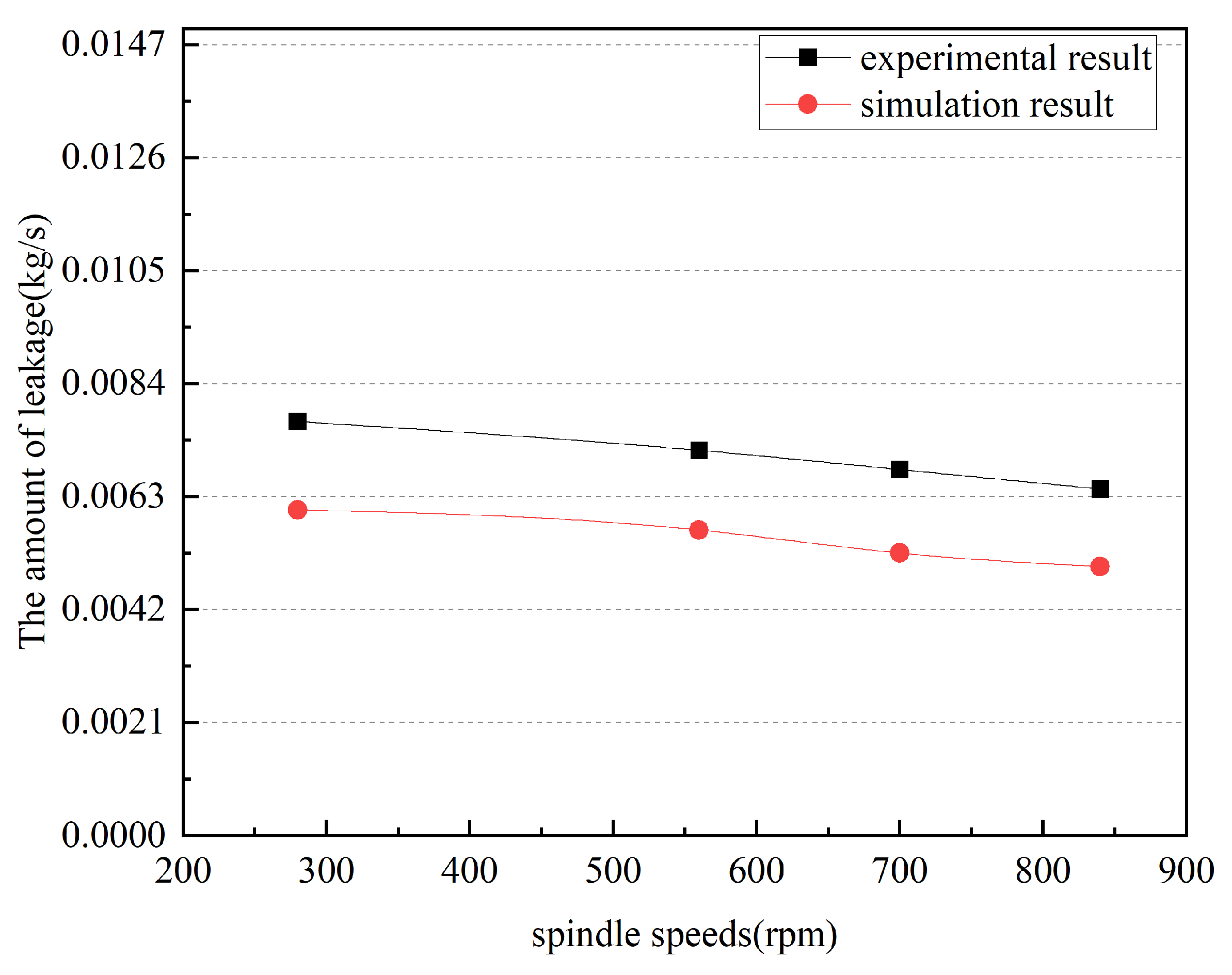
4.2.2. The Influence of Spindle Speed on the Leakage of Staggered Labyrinth Sealing Device Was Verified by the Test
4.2.3. The Influence of Seal Clearance on the Leakage of Staggered Labyrinth Seal Was Verified by Experiment
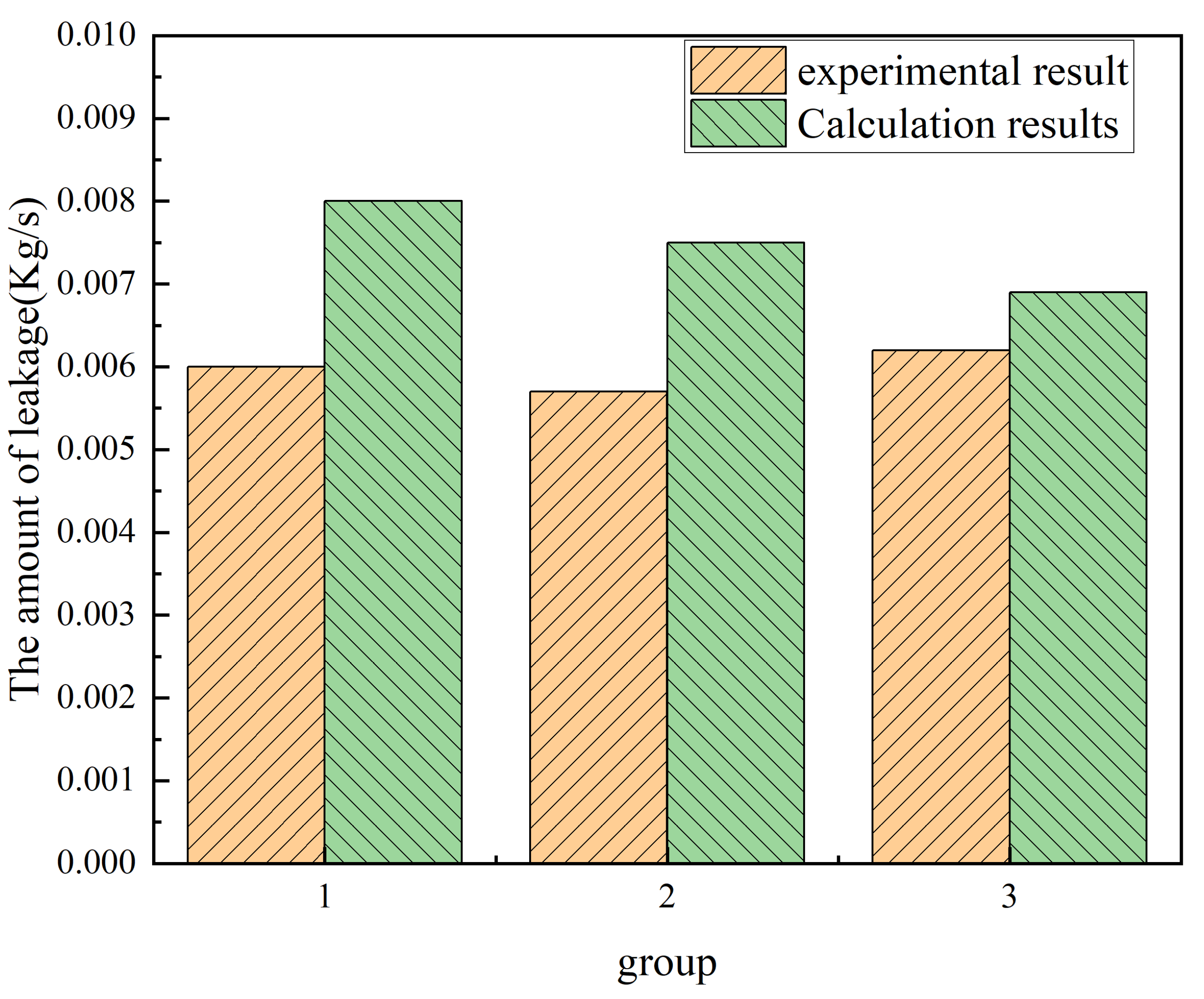
4.3. Experimental Verification of the Leakage Calculation Method of Staggered Labyrinth Seal Under Multiple Effects
5. Conclusions
- (1)
- A method for calculating the leakage of staggered labyrinth seals considering thermodynamic effects and frictional effects under liquid medium was proposed.
- (2)
- The leakage characteristics of labyrinth seals were investigated by comparing experimental and simulation results. Based on the calculation method of leakage under liquid medium, a method of calculating the leakage of staggered labyrinth seals considering the friction effect and thermodynamic effect was proposed, and the traditional calculation method was optimized. At the same time, corresponding simulation analyses were carried out, and the results showed that the leakage volume of the staggered labyrinth seal is different under different influencing factors, and the leakage volume is directly proportional to the total inlet pressure and the sealing gap, and inversely proportional to the spindle speed.
- (3)
- Verification experiments were designed, and the experimental results were compared with the theoretical values and simulation results to verify the accuracy of the theory. The experimental results showed that the leakage calculation method proposed in this paper can calculate the leakage and has reference significance to a certain extent.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.J. Study of Flow Characteristics and Efficiency Improvement Technology for Turbine Seal. Master’s Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Lin, M. 3D Flow Field Analysis and Piston Structure Optimization for Reciprocating Compressor Based on CFD. Master’s Thesis, Shenyang Ligong University, Shenyang, China, 2013. [Google Scholar]
- Wang, Y.F.; Zhang, W.F.; Pan, B.; Li, C. Effect of shaft misalignment on dynamic and static characteristics of interlocking labyrinth seals. Hangkong Xuebao 2020, 41, 212–223. [Google Scholar]
- Yang, Y.L. Flow Fields Study and Rotordynamic Analysis of Labyrinth Seals. Master’s Thesis, Huazhong University of Science & Technology, Wuhan, China, 2006. [Google Scholar]
- Li, Y.H. Research the Characteristics of the Large Motor Sliding Bearing Labyrinth Seal Resisting Negative Pressure. Master’s Thesis, Xiangtan University, Xiangtan, China, 2015. [Google Scholar]
- Zhang, Y.; Zhang, K.L.; Yao, Y.; Wang, X.P. Numerical Analysis of the Rotor Speed Effect on Labyrinth Seal Characteristics. Mach. Des. Manu. 2017, 3, 183–185. [Google Scholar]
- Zhang, Y. Numerical Analysis of Flow Filed and Labyrinth Seal for High-Speed Train Gearbox. Master’s Thesis, Southewest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Yucel, U.; Kazakia, J.Y. Analytical prediction techniques for axisymmetric Flow in Gas Labyrinth Seals. J. Eng. Gas Turbines Power 2001, 123, 255–257. [Google Scholar] [CrossRef]
- Wang, C. The Research of Locomotive Traction Gear Box Sealing Device Internal Flow Field and Structure Optimization Design. Master’s Thesis, Dalian Jiaotong University, Dalian, China, 2015. [Google Scholar]
- Subrnabuab, S.; Sekhar, A.S. Prasad BVSS. Rotordynamic Characterization of Rotating Labyrinth Gas Turbine Seals with Radial Growth: Combined Centrifugal and Thermal Effects. Int. J. Mech. Sci. 2017, 123, 1–19. [Google Scholar]
- Jia, W.C.; Xu, H.H.; Wei, L.H. Orthogonal Simulation Test and Optimization for Leakage of Labyrinth Seal in High Speed Gear Box. Lubr. Eng. 2018, 43, 126–131. [Google Scholar]
- Yuan, J.B.; Shi, X.X.; Hu, T.; Mei, Z.J. Summarize on the Labyrinth Seal Research for High Speed Gear Box. Hydr. Pneu. Seals 2019, 39, 72–77. [Google Scholar]
- Martin, M. Labyrinth Packings. Engineering 1980, 1, 35–36. [Google Scholar]
- Zhu, G.T. Analysis of Leakage Character of a Labyrinth Piston Compressor. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2006. [Google Scholar]
- Egli, A. The Leakage of Steam Through Labyrinth Seals. Trans. ASME 1935, 57, 115–122. [Google Scholar] [CrossRef]
- Kearton, W.J.; Keh, T.H.; Eng, D. Leakage of Air through Labyrinth Glands of Staggered Type. Proc. I Mesh. E 1952, 166, 319–320. [Google Scholar] [CrossRef]
- Zhu, G.T.; Liu, W.H. Analysis of Calculational Methods on Leakage for Labyrinth Seals. Lubr. Eng. 2006, 176, 123–126. [Google Scholar]
- Zhai, L.; Zhu, Z.; Zhang, Z.; Guo, J.; Cui, B. Theoretical Solutions for Dynamic Characteristics of Spiral-Grooved Liquid Seals. Tribol. T 2018, 62, 22–33. [Google Scholar] [CrossRef]
- Zhou, W.J.; Zhao, Z.B.; Wang, Y.F.; Shi, J.L.; Gan, B.; Li, B.; Qiu, N. Research on leakage performance and dynamic characteristics of a novel labyrinth seal with staggered helical teeth structure. Alex. Eng. J. 2021, 60, 3177–3187. [Google Scholar] [CrossRef]
- Han, L.; Wang, Y.; Liu, K.; Ban, Z.; Qin, B.; Liu, H.; Dai, M. Theoretical Leakage Equations Towards Liquid-Phase Flow in the Straight-Through Labyrinth Seal. ASME J. Tribol. 2022, 144, 1448–1462. [Google Scholar] [CrossRef]
- Raparelli, T.; Mazza, L.; Trivella, A. Experimental analysis and preliminary model of non-conventional lip seals. Trib. Int. 2023, 181, 108311. [Google Scholar] [CrossRef]
- Wang, Y.M.; Liu, W.; Liu, Y. Current Research and Developing Trends on Non-contacting Mechanical Seals. Hydr. Pneu. Seals 2011, 31, 29–33. [Google Scholar]
- Lin, L. Theoretical Research on the Principles of Seal in Labyrinth Piston Compressors. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2007. [Google Scholar]
- Li, G.B.; Cui, H. Fundamentals of Fluid Mechanics and Thermal Engineering, 1st ed.; Beijing Institute of Technology Press: Beijing, China, 2016; pp. 58–81. [Google Scholar]
- Wei, W.; Wu, J.Q.; Ma, X.D. The Strong about Thermodynamics First Law. J. Xinjiang Norm. Univ. 2011, 30, 59–62. [Google Scholar]
- McCulloh, R.S. Treatise on the Mechanical Theory of Heat and Its Applications to the Steam-Engine, Etc, 1st ed.; University of Michigan Library: Ann Arbor, MI, USA, 2005; pp. 77–97. [Google Scholar]
- Clausius, R. On the Motive Power of Heat, and on the Laws Which Can Be Deduced from It for the Theory of Heat. Philos. Mag 1865, 40, 1–35. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Sun, D.; Lu, J.; Wang, W.; Ai, Y.T.; Wang, Z. Numerical Investigations for Sealing Mechanism of Labyrinth Seals Based on Thermodynamic Effect. Therm. Turbine 2018, 47, 175–181. [Google Scholar]
- Lu, J. Study of Labyrinth Seals on Sealing Mechanism and New Vibration Suppression Seal Structure. Master’s Thesis, Shenyang Aerospace University, Shenyang, China, 2019. [Google Scholar]
- Xu, W.J.; Wang, L.W. Numerical Study on Leakage and Dynamic Coefficients of Three Types of Labyrinth Seals. Lubr. Eng. 2017, 42, 96–101. [Google Scholar]
- Yu, Y.Q.; Zhang, Y.X.; Kang, Y.J. Research on Wellhead at Offshore Platform Based on Straight-through Labyrinth Seal. Hydr. Pneu. Seals 2009, 23, 2830–2838. [Google Scholar]
- Tong, S.K.; Cha, K.S. ; Cha, K.S. Comparative analysis of the influence of labyrinth seal configuration on leakage behavior. J. Mech. Sci. Technol. 2009, 23, 2830–2838. [Google Scholar]
- Wang, W.Z.; Liu, Y.Z.; Meng, G.; Jiang, P.N. A nonlinear model of flow-structure interaction between steam leakage through labyrinth seal and the whirling rotor. J. Mech. Sci. Technol. 2009, 23, 3302–3315. [Google Scholar] [CrossRef]

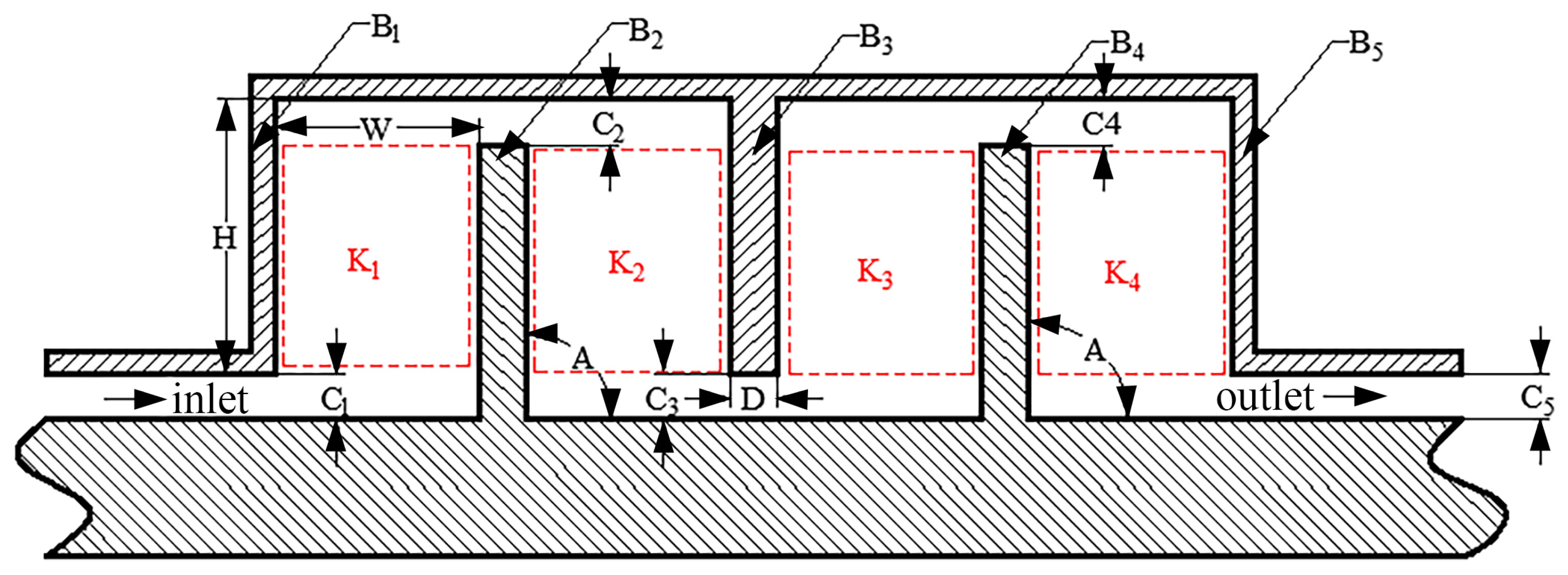




| Parameter | Value |
|---|---|
| The length of the entry extension L1 | 30 mm |
| The length of the outlet extension L2 | 30 mm |
| Seal gap C | 0.5–10 mm |
| Seal cavity depth H | 40–100 mm |
| Width of the sealing chamber W | 35–80 mm |
| Blade thickness D | 10 mm |
| Blade inclination A | 90° |
| Parameter | Value |
|---|---|
| Inlet pressure | 101,325–20,265,030 Pa |
| Outlet pressure | 101,325 Pa |
| Total inlet temperature | 293.15–353.15 K |
| Rotate speed | 300–1200 rpm |
| Number of sealing stages | 4 |
| Media | L-ckc320 |
| Parameter | Value |
|---|---|
| Inlet pressure | 101,325–20,265,030 Pa |
| Rotate speed | 300–1200 rpm |
| Seal gap | 3–10 mm |
| Group | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Total inlet pressure (Pa) | 121,590, 131,722.5, 141,855, 151,987.5 | 141,855 | 131,722.5 | 131,722.5 |
| Seal gap (mm) | 3 | 3 | 3 | 1, 3, 5, 7 |
| Spindle speed (rpm) | 280 | 280,560, 700,840 | 280 | 280 |
| Blade Inclination (°) | Blade Thickness (mm) | Sealing Gap (mm) | Cavity Depth (mm) | Cavity Width (mm) |
|---|---|---|---|---|
| 80 | 9 | 1.5 | 70 | 35 |
| Group | 1 | 2 | 3 |
|---|---|---|---|
| The average temperature of the first seal cavity () | 294.25 | 294.25 | 294.3 |
| The average temperature of the second seal cavity () | 294.55 | 294.5 | 294.5 |
| The average temperature of the third seal cavity () | 294.8 | 294.8 | 294.75 |
| The average temperature of the fourth seal cavity () | 294.87 | 295.17 | 295 |
| The average pressure of the cavity of the first seal () | 138,811.3 | 138,249.3 | 138,049.3 |
| The average pressure of the cavity of the second seal () | 136,214 | 136,056 | 135,743.7 |
| The average pressure of the cavity of the second seal () | 128,204.3 | 127,861 | 127,487 |
| The average pressure of the cavity of the first seal () | 125,760.7 | 125,390 | 125,276.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Cao, Y.; Sun, Z.; Tang, S.; Choi, S.-B. Leakage Characteristics and Experimental Research of Staggered Labyrinth Sealing. Lubricants 2024, 12, 369. https://doi.org/10.3390/lubricants12110369
Wang N, Cao Y, Sun Z, Tang S, Choi S-B. Leakage Characteristics and Experimental Research of Staggered Labyrinth Sealing. Lubricants. 2024; 12(11):369. https://doi.org/10.3390/lubricants12110369
Chicago/Turabian StyleWang, Na, Yongbing Cao, Zhencong Sun, Shixin Tang, and Seung-Bok Choi. 2024. "Leakage Characteristics and Experimental Research of Staggered Labyrinth Sealing" Lubricants 12, no. 11: 369. https://doi.org/10.3390/lubricants12110369
APA StyleWang, N., Cao, Y., Sun, Z., Tang, S., & Choi, S.-B. (2024). Leakage Characteristics and Experimental Research of Staggered Labyrinth Sealing. Lubricants, 12(11), 369. https://doi.org/10.3390/lubricants12110369







