Measurement and Dynamic Analysis of the Centroid Trajectories of Angular-Contact Ball Bearing Cages
Abstract
1. Introduction
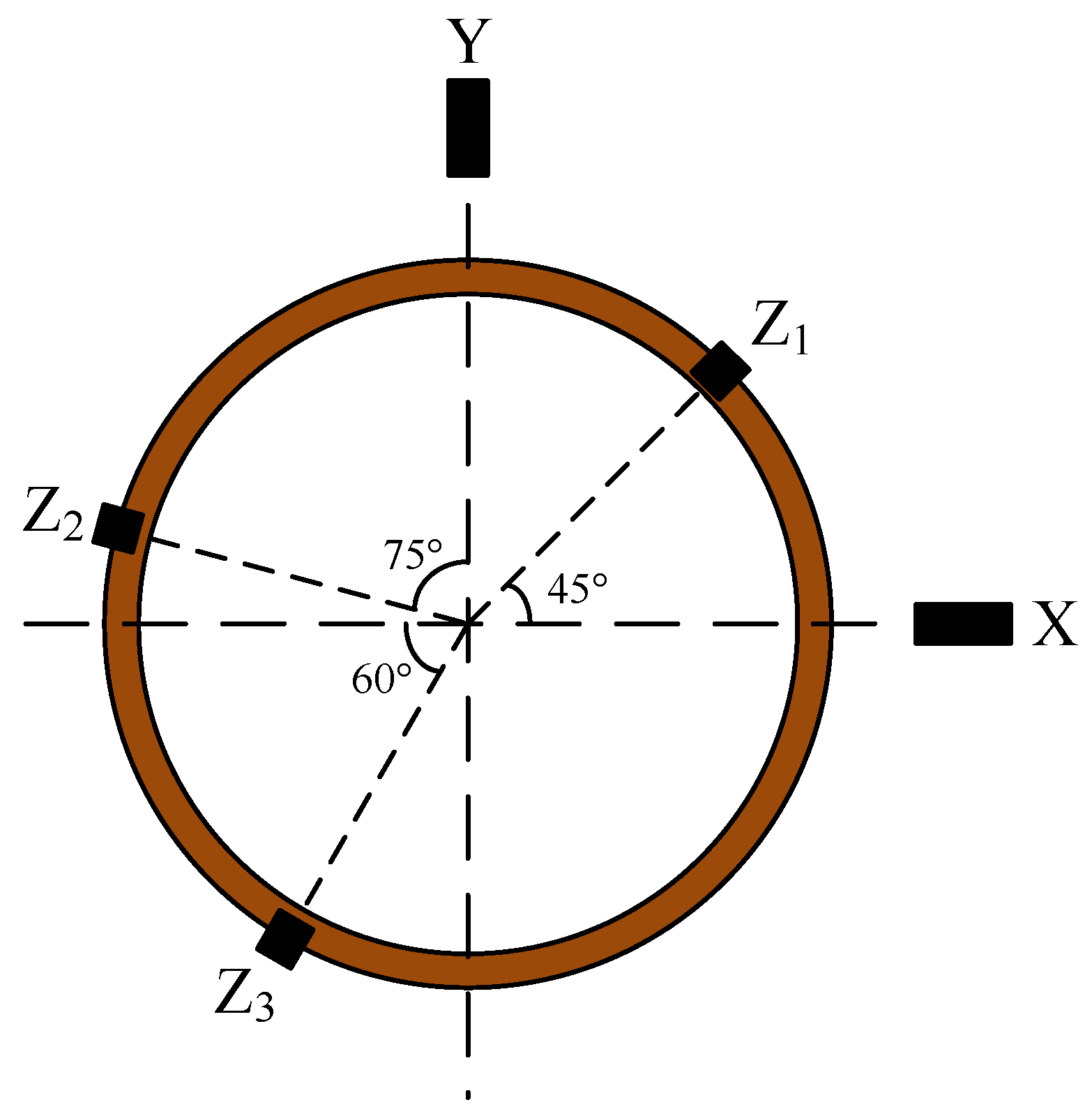
2. Measurement Solution for Cage Centroid Trajectory
2.1. Measurement Solution
2.2. Cage Centroid Trajectory Solution
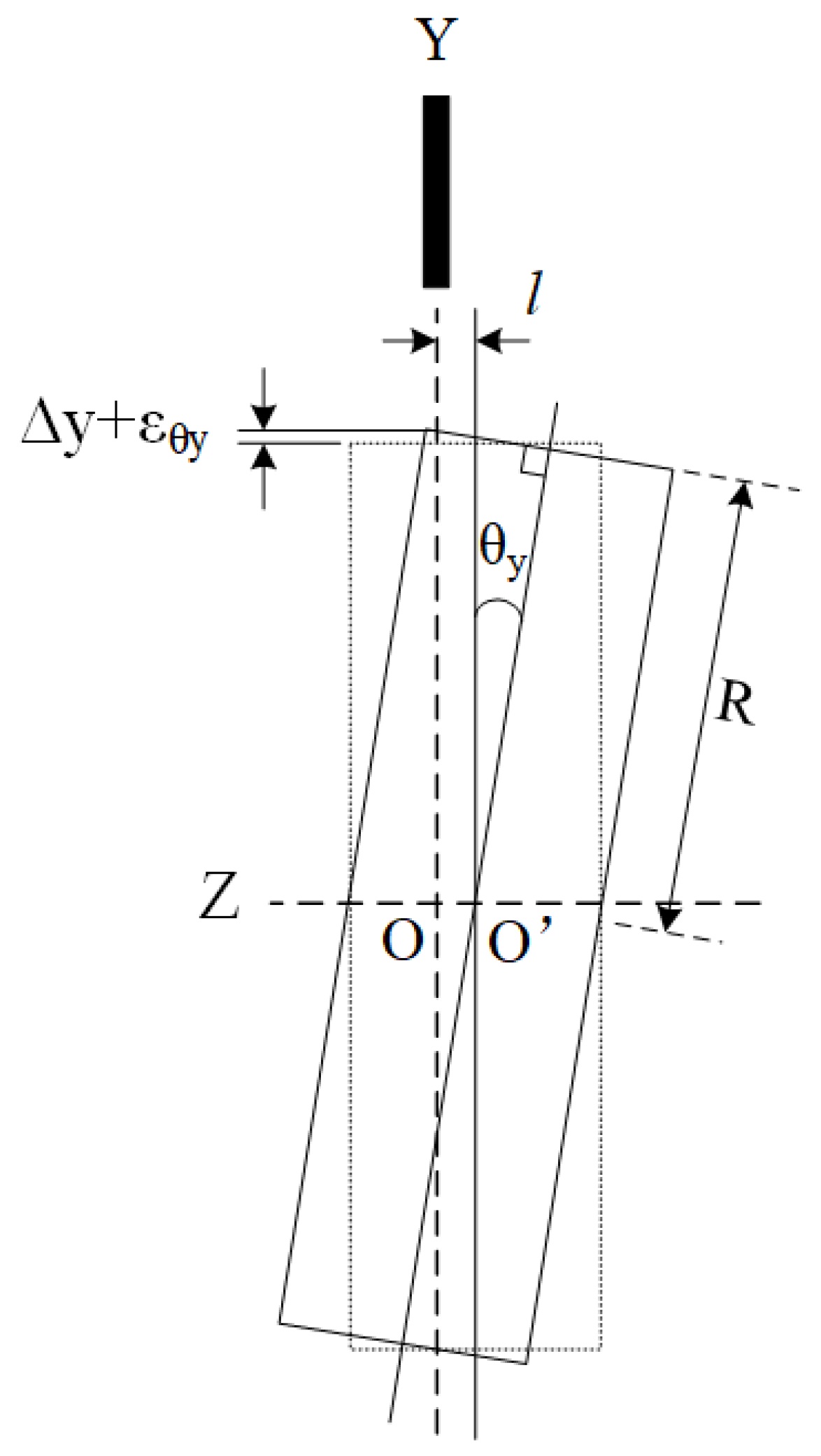
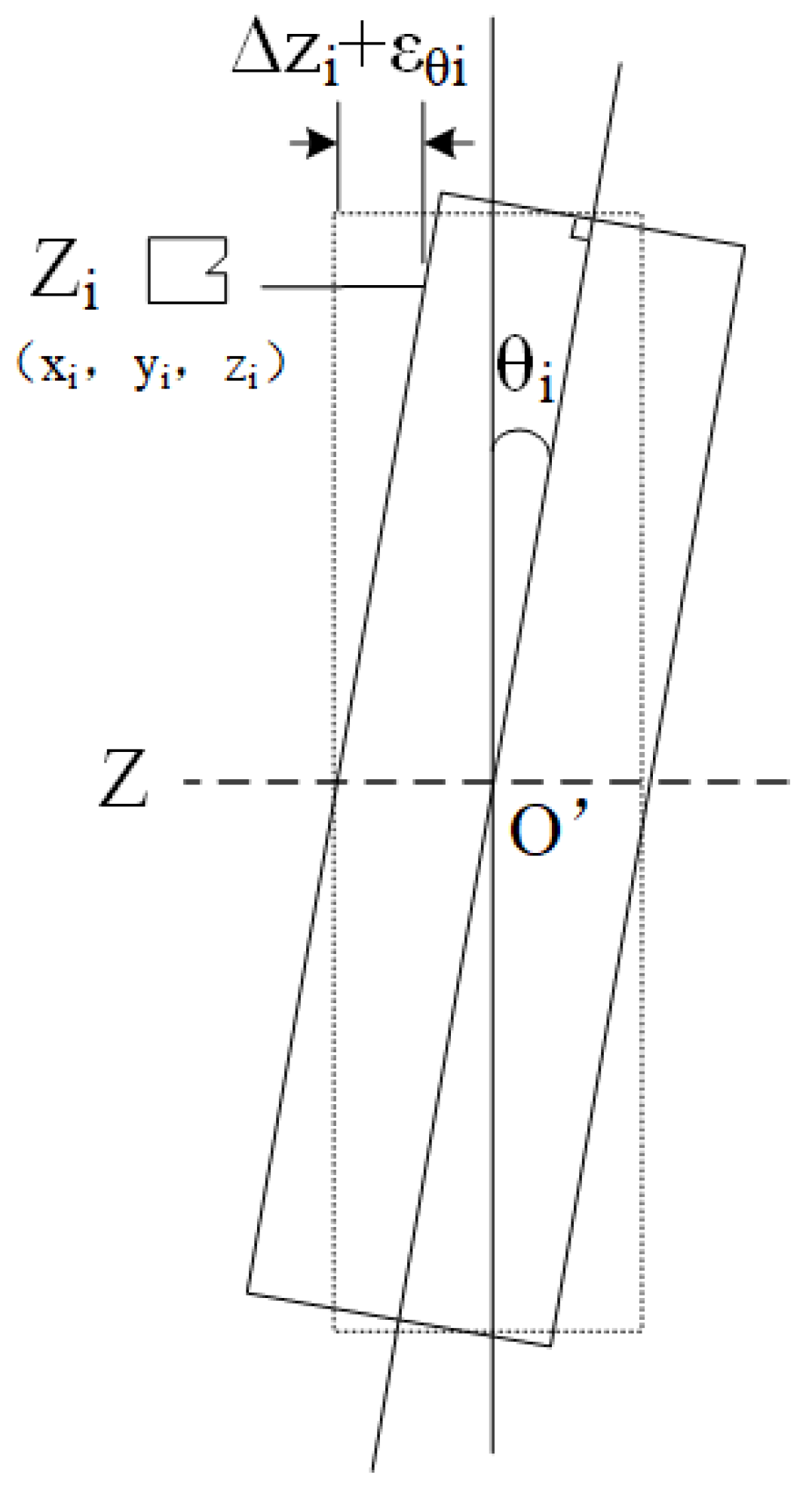
2.2.1. Cage Deflection Angle Solution
2.2.2. Cage Centroid Radial Vibration Solution
2.2.3. Cage Centroid Axial Vibration Solution
3. Angular-Contact Ball Bearing Dynamic Model
3.1. Bearing Dynamic Model
3.2. Boundary Condition Settings
3.3. Model Verification
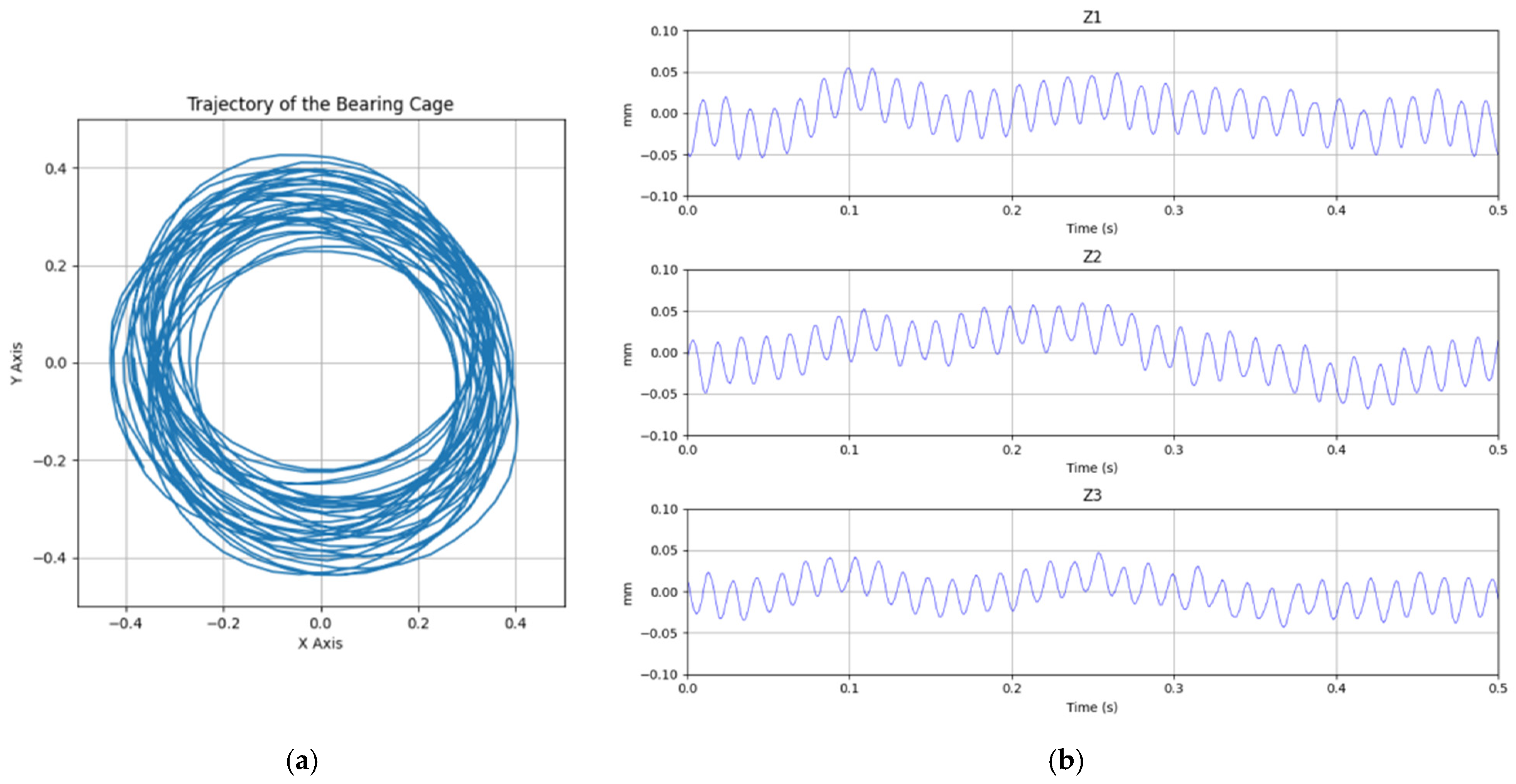
4. Cage Motion Test and Simulation Verification
4.1. Cage Deflection Error Test and Simulation Comparison Verification
4.2. Dynamic Characteristics of Cage with Rotational Speed
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Petuya, K. Angular Contact Ball Bearing Modelling with Flexible Cage. Ph.D. Thesis, INSA de Lyon, Villeurbanne, France, 2022. (In English). [Google Scholar]
- Boesiger, E.A.; Donley, A.D.; Loewenthal, S. An Analytical and Experimental Investigation of Ball Bearing Retainer Instabilities. ASME J. Tribol. 1992, 114, 530–538. [Google Scholar] [CrossRef]
- Xu, F.; Ding, N.; Li, N.; Liu, L.; Hou, N.; Xu, N.; Guo, W.; Tian, L.; Xu, H.; Lawrence Wu, C.; et al. A Review of Bearing Failure Modes, Mechanisms and Causes. Eng. Fail. Anal. 2023, 152, 107518. [Google Scholar] [CrossRef]
- Li, Y.; Tao, C.H.; Zhang, W.; Jiang, T. Fracture analysis on cage rivets of a cylindrical roller bearing. Eng. Fail. Anal. 2008, 15, 796–801. [Google Scholar] [CrossRef]
- Fan, R.; Yao, T.; Liu, X.; Xiong, T. Stability Analysis of Angular Contact Ball Bearing Cage. Mach. Des. Res. 2017, 33, 76–81. [Google Scholar]
- Gupta, P.K.; Dill, J.F.; Bandow, H.E. Dynamics of Rolling Element—Bearings Experimental Validation of the DREB and RAPIDREB Computer Programs. J. Tribol. Trans. ASME 1985, 107, 132–137. [Google Scholar] [CrossRef]
- Schwarz, S.; Grillenberger, H.; Tremmel, S.; Wartzack, S. Prediction of Rolling Bearing Cage Dynamics Using Dynamic Simulations and Machine Learning Algorithms. Tribol. Trans. 2022, 65, 225–241. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Zhu, Y.; He, G.; Ma, S.; Hong, J. Dynamic Performance Analysis of Cage in Four-Point Contact Ball Bearing. Lubricants 2022, 10, 149. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, H.; Yu, T.; Li, B. A high-precision instrument for analyzing nonlinear dynamic behavior of bearing cage. Rev. Sci. Instrum. 2016, 87, 085105. [Google Scholar] [CrossRef] [PubMed]
- Huang, D. Detection and CharacteristicA nalysis for M assCenterO rbitofBearing Cag. China Mech. Eng. 2012, 23, 1779–1784. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, P.; Chao, B.; Yan, K.; Hong, J. A Non-Intrusive Rolling Bearing Cage Traj ectory Extraction Method Using Image Processing Program. J. Xi’an Jiaotong Univ. 2024, 58, 95–105. [Google Scholar] [CrossRef]
- Zhu, M. Mechanical Characteristics of High Speed Speed Precision Ball Bearing and Stability Analysis of Cage. Master’s Thesis, Inner Mongolia University of Science & Technology, Hohhot, China, 2022. [Google Scholar]
- Zhao, Z. Research on Trajectory and Measurement Technology of Rolling Bearing Cage. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2015. [Google Scholar] [CrossRef]
- Sun, Y.; Song, B.; Liu, H.; Wen, B. Analysis on Dynamic Characteristics of Cages in Heavy Axle Load Railway Freight Bearings. Bearing 2019, 12, 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, T.; Liu, Z.; Cheng, X. Stability Study of Thin Walled Four Point Contact Ball Bearing Cage. Light Ind. Mach. 2021, 39, 1–6. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, S. Influence of Rheological Model on Computation of Traction Coefficient of Aviation Lubricating Oils. Acta Aeronaut. Astronaut. Sin. 2009, 30, 220–225. [Google Scholar]
- Tu, W.; He, H.; Liu, L.; Luo, Y. Analysis on Cage Dynamic Characteristic of Angular Contact Ball Bearing During Deceleration. J. Mech. Transm. 2019, 43, 125–129. [Google Scholar] [CrossRef]
- Wen, B.; Ren, H.; Zhang, H.; Han, Q. Experimental investigation of cage motions in an angular contact ball bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 1041–1055. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Y.; Deng, S.; Cao, D. Dynamic stability of cages in high-speed tapered roller bearings with grease lubrication. J. Vib. Shock 2019, 38, 49–57. [Google Scholar]
- Yao, T.; Wang, L.; Liu, X.; Huang, Y. Dynamic stability analysis on the cage of ball bearing under varying working environment. J. Vib. Shock 2016, 35, 172–180. [Google Scholar]
- Sakaguchi, T.; Harada, K. Dynamic Analysis of Cage Behavior in a Tapered Roller Bearing. ASME J. Tribol. 2006, 128, 604–611. [Google Scholar] [CrossRef]
- Niu, L.; Cao, H.; He, Z.; Li, Y. An investigation on the occurrence of stable cage whirl motions in ball bearings based on dynamic simulations. Tribol. Int. 2016, 103, 12–24. [Google Scholar] [CrossRef]
- Rivera, M.P. Bearing-Cage Frictional Instability—A Mechanical Model. Tribol. Trans. 1991, 34, 117–121. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, X.; He, Y. The Effect of Geometric and Working Parameters on Dynamic Performance of Flexible Cages on Bearings. Flight Control Detect. 2021, 4, 73–79. [Google Scholar]



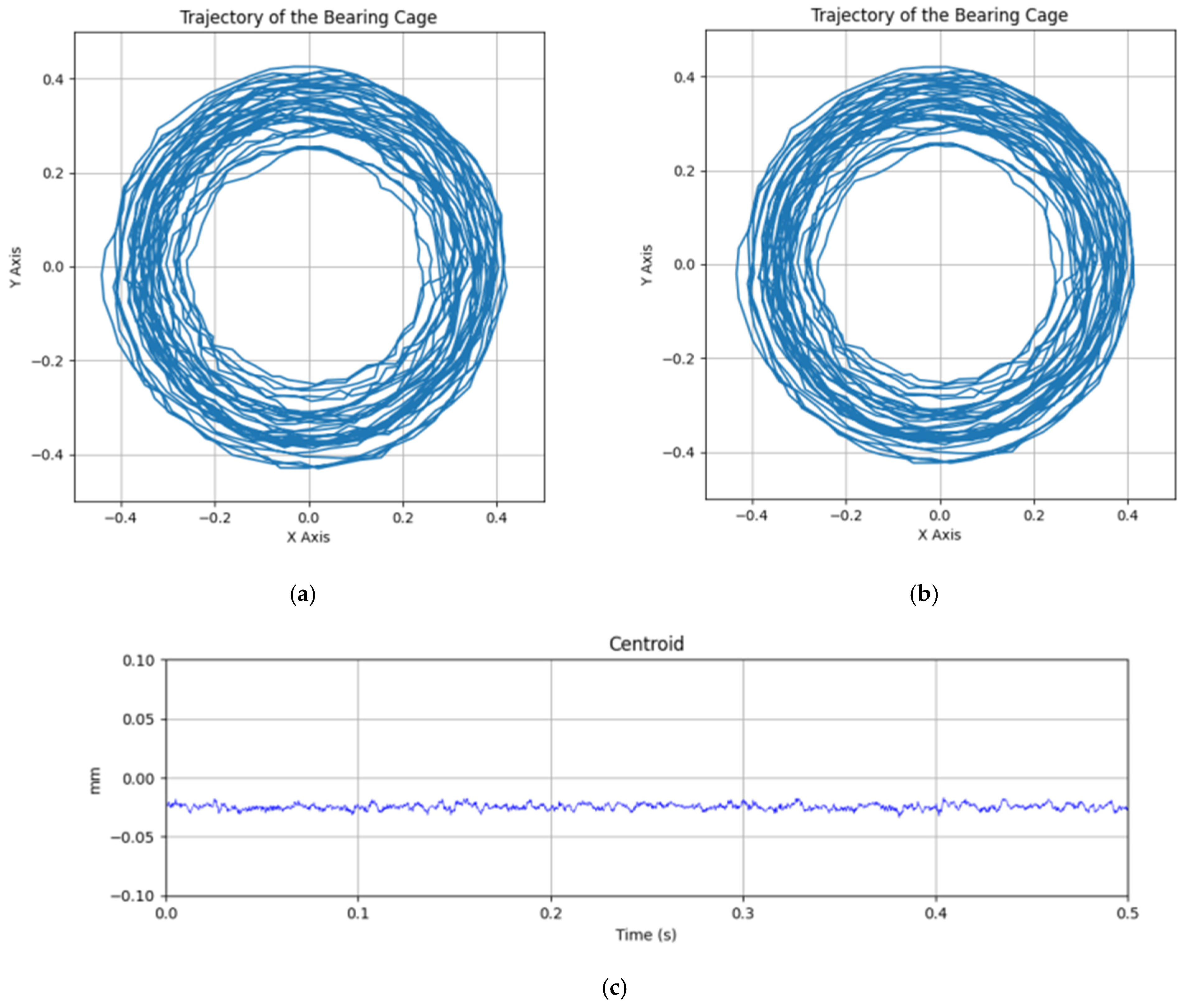
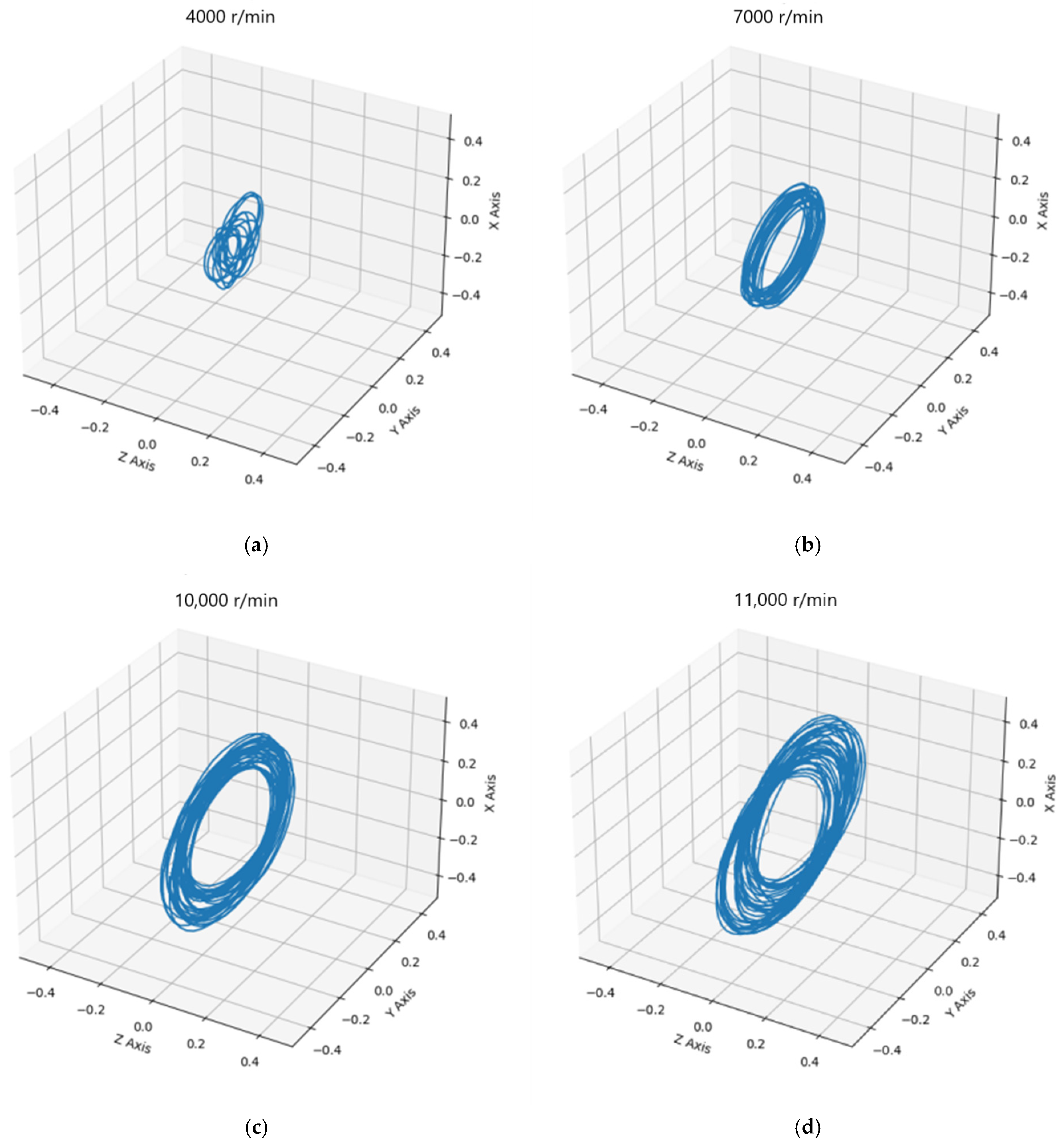
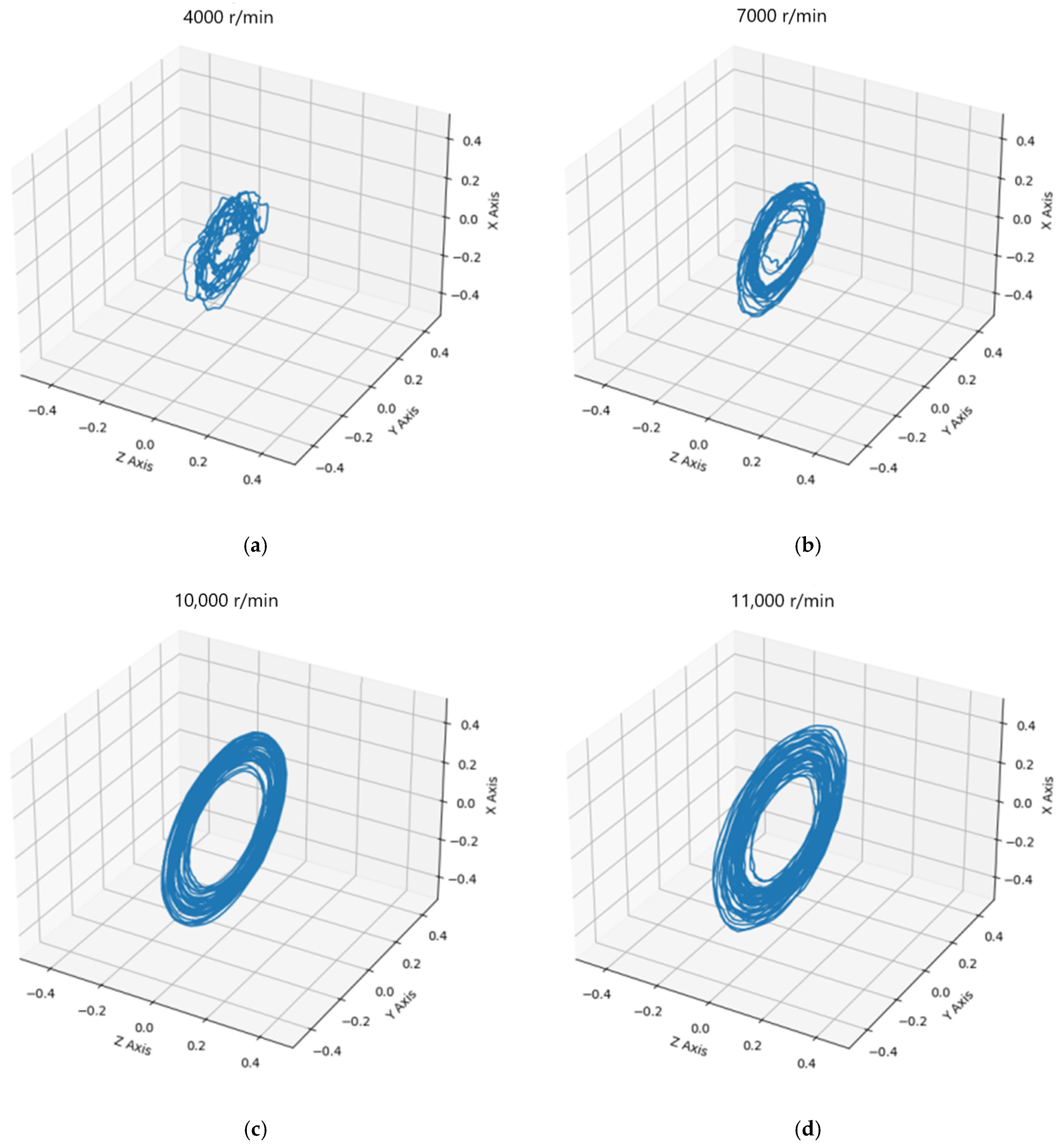

| Parameters | Value |
|---|---|
| Bearing bore diameter/d | 50 mm |
| Bearing outside diameter/D | 80 mm |
| Bearing width/B | 16 mm |
| Roller diameter/Dw | 9.525 mm |
| Number of rollers/Z | 18 |
| Contact angle/α | 15° |
| Material | Density (kg/m3) | Poisson’s Ratio | Elastic Modulus (GPa) |
|---|---|---|---|
| GGr15Z bearing steel | 7800 | 0.30 | 208 |
| Polyimide | 1120 | 0.34 | 2.62 |
| Inner Ring Rotational Speed (r/min) | Cage Theoretical Rotational Speed (r/min) | Cage Simulated Rotational Speed (r/min) | Error |
|---|---|---|---|
| 4000 | 1716.9 | 1712.5 | 0.25% |
| 7000 | 3004.6 | 2986.9 | 0.59% |
| 10,000 | 4292.3 | 4258.3 | 0.79% |
| 11,000 | 4721.5 | 4748.5 | 0.57% |
| Inner Ring Rotational Speed (r/min) | Vortex Radius Difference (mm) | Error | |
|---|---|---|---|
| Measured Results | Solved Results | ||
| 4000 | 0.2436 | 0.2311 | 5.40% |
| 7000 | 0.2239 | 0.2167 | 3.33% |
| 10,000 | 0.2381 | 0.2314 | 2.91% |
| 11,000 | 0.2813 | 0.2709 | 3.86% |
| Inner Ring Rotational Speed (r/min) | Vortex Radius Difference (mm) | Error | |
|---|---|---|---|
| Origin Point | Centroid | ||
| 4000 | 0.2661 | 0.2549 | 4.40% |
| 7000 | 0.2488 | 0.2413 | 3.12% |
| 10,000 | 0.1941 | 0.1886 | 2.95% |
| 11,000 | 0.2594 | 0.2512 | 3.25% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, J.; Ma, X.; Liu, C.; Zuo, M.; Jin, D.; Zhang, H. Measurement and Dynamic Analysis of the Centroid Trajectories of Angular-Contact Ball Bearing Cages. Lubricants 2024, 12, 379. https://doi.org/10.3390/lubricants12110379
You J, Ma X, Liu C, Zuo M, Jin D, Zhang H. Measurement and Dynamic Analysis of the Centroid Trajectories of Angular-Contact Ball Bearing Cages. Lubricants. 2024; 12(11):379. https://doi.org/10.3390/lubricants12110379
Chicago/Turabian StyleYou, Jinyuan, Xiqiang Ma, Chunyang Liu, Mengjie Zuo, Dongliang Jin, and Hao Zhang. 2024. "Measurement and Dynamic Analysis of the Centroid Trajectories of Angular-Contact Ball Bearing Cages" Lubricants 12, no. 11: 379. https://doi.org/10.3390/lubricants12110379
APA StyleYou, J., Ma, X., Liu, C., Zuo, M., Jin, D., & Zhang, H. (2024). Measurement and Dynamic Analysis of the Centroid Trajectories of Angular-Contact Ball Bearing Cages. Lubricants, 12(11), 379. https://doi.org/10.3390/lubricants12110379





