Physics-Informed Neural Network (PINN) for Solving Frictional Contact Temperature and Inversely Evaluating Relevant Input Parameters
Abstract
1. Introduction
2. Theory and Methods
2.1. Heat-Transfer Theory
2.2. Frictional Contact-Temperature Simulation Method
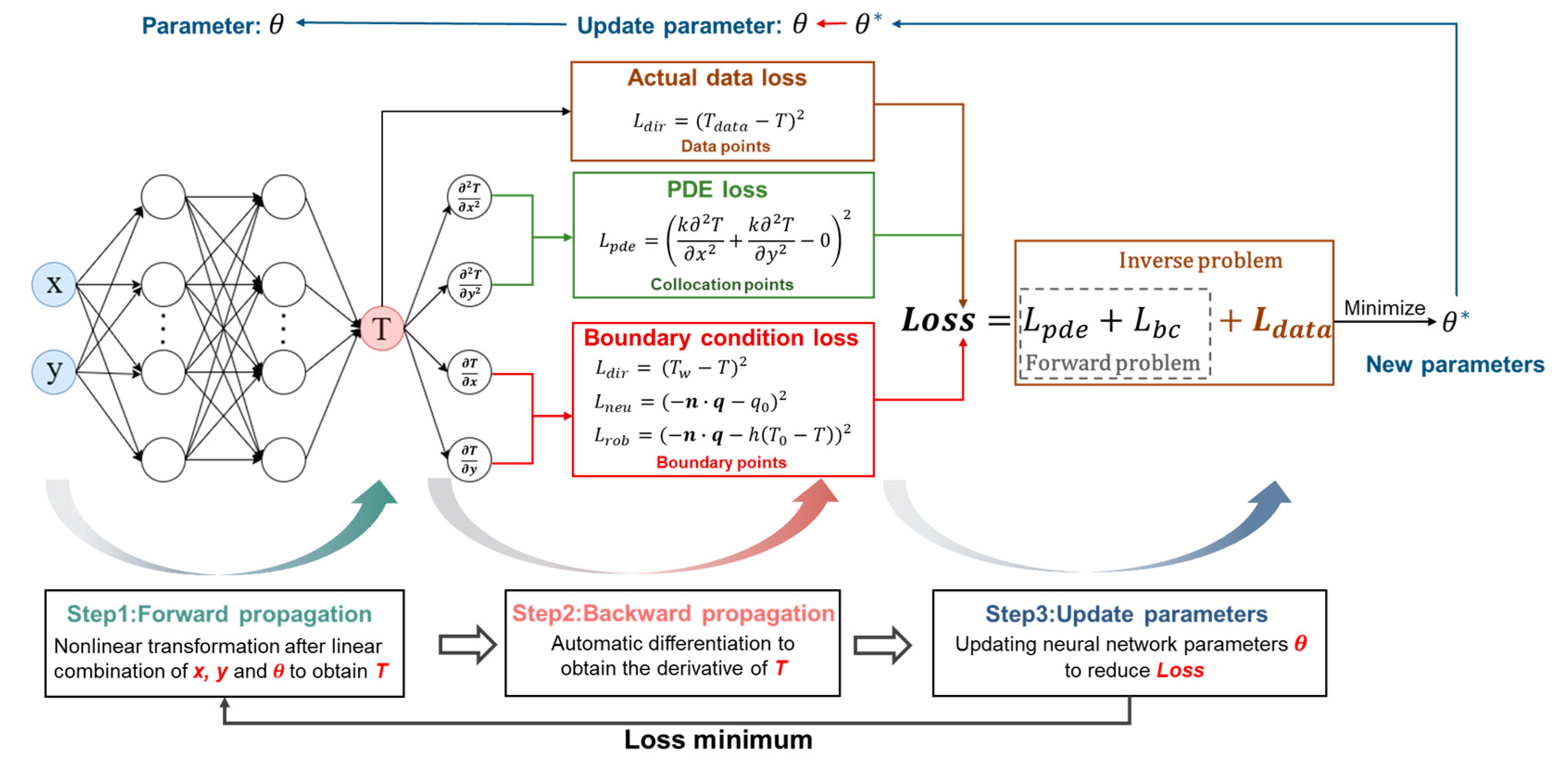
2.3. PINN Theory and Method
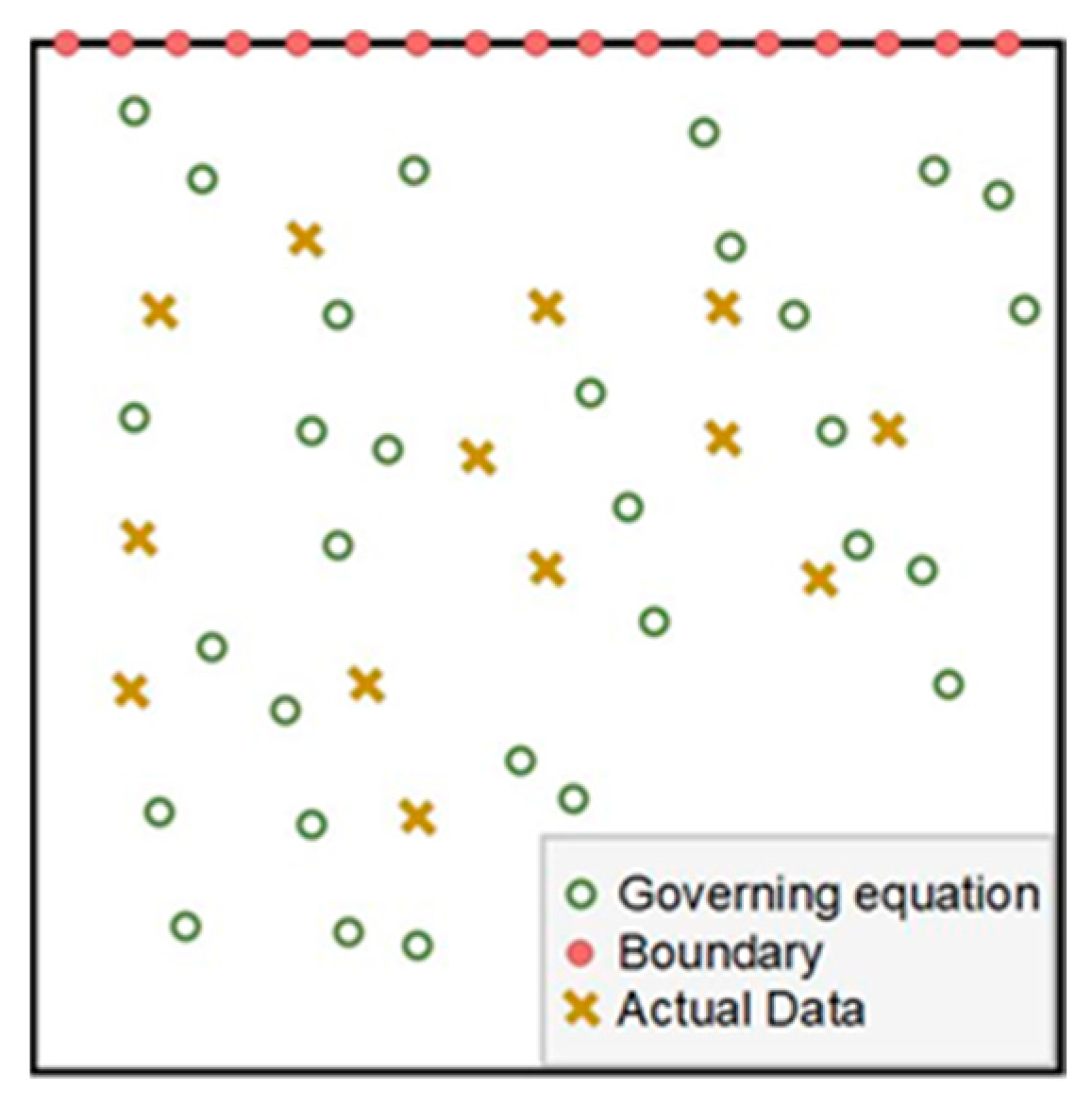
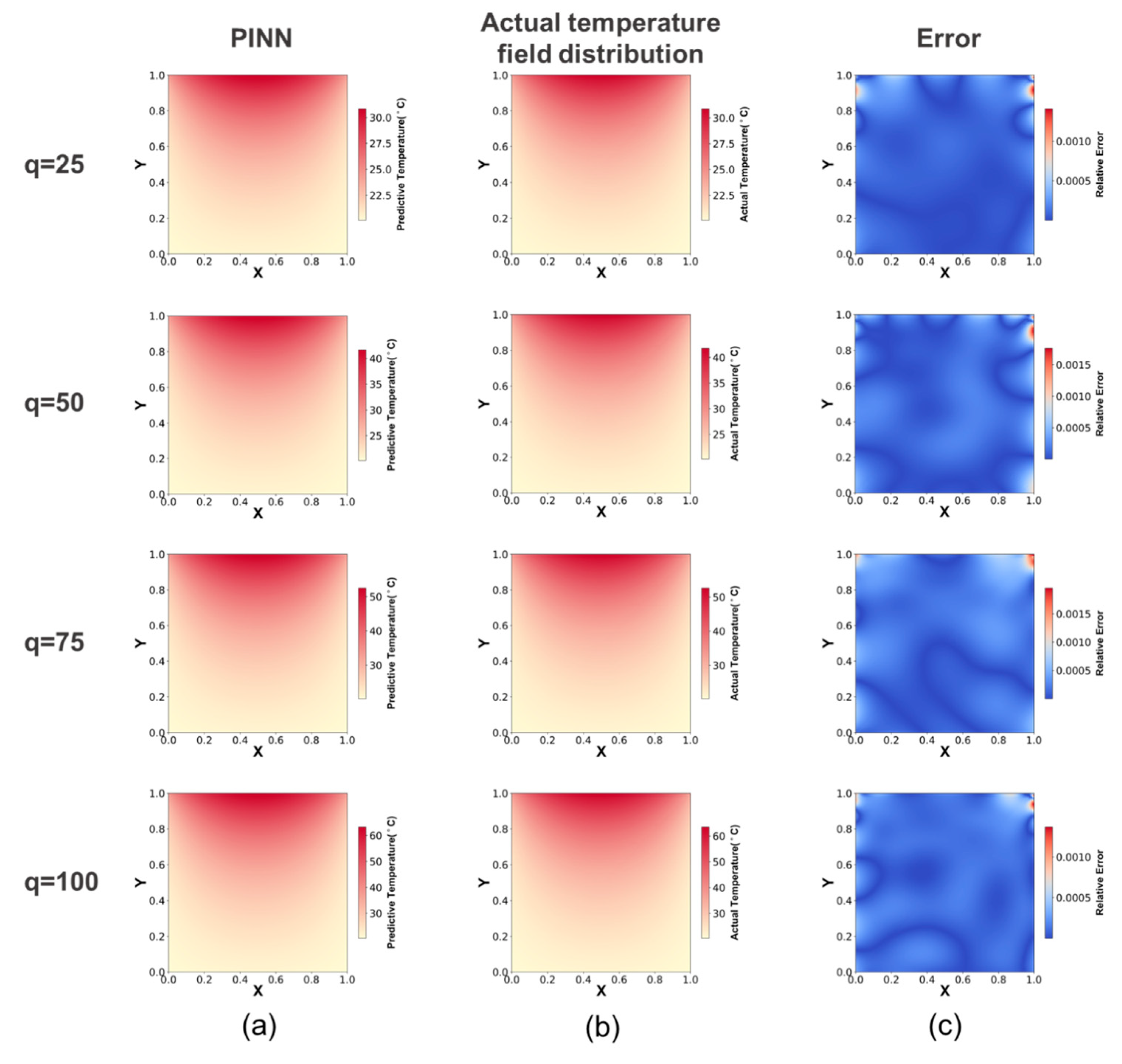
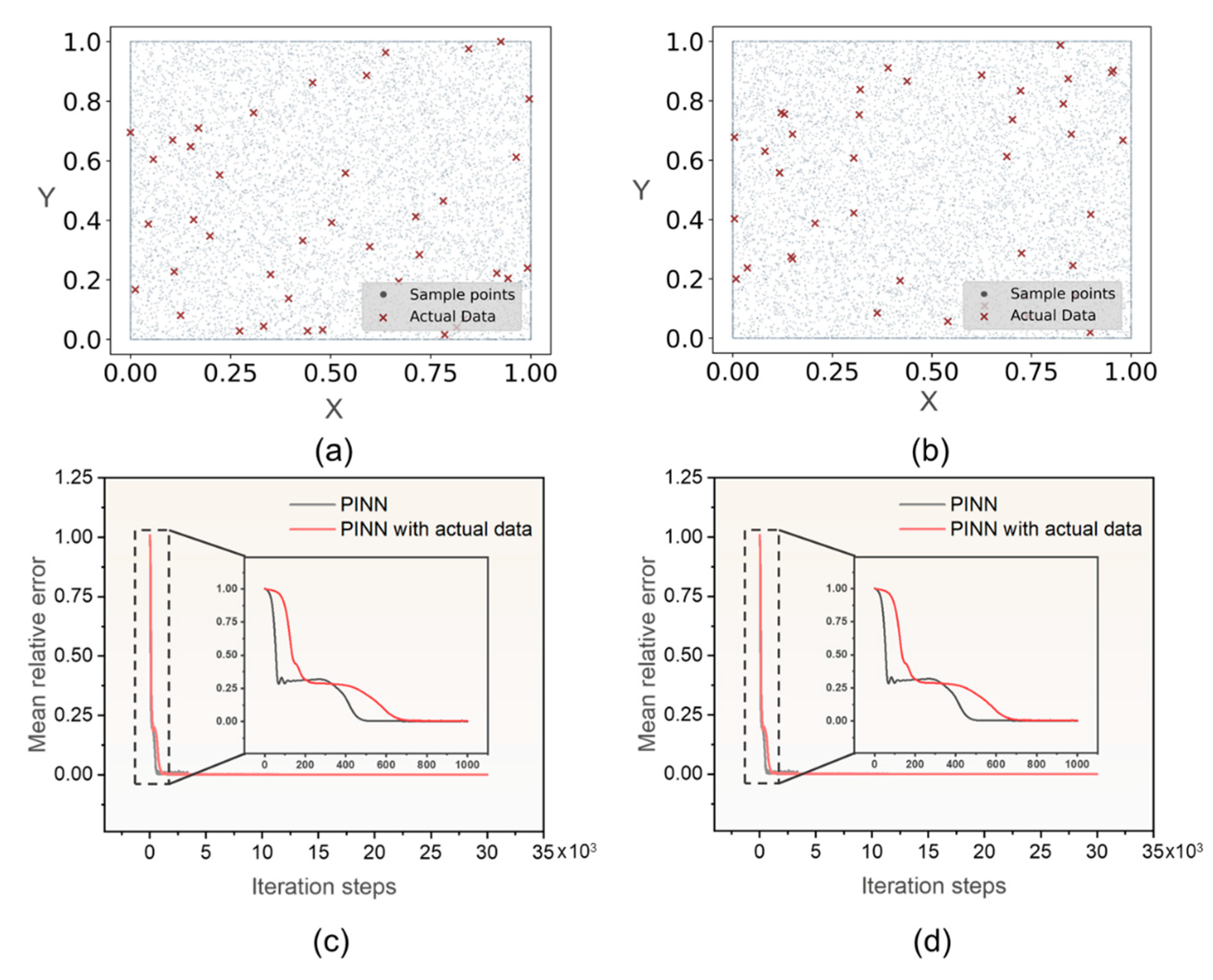
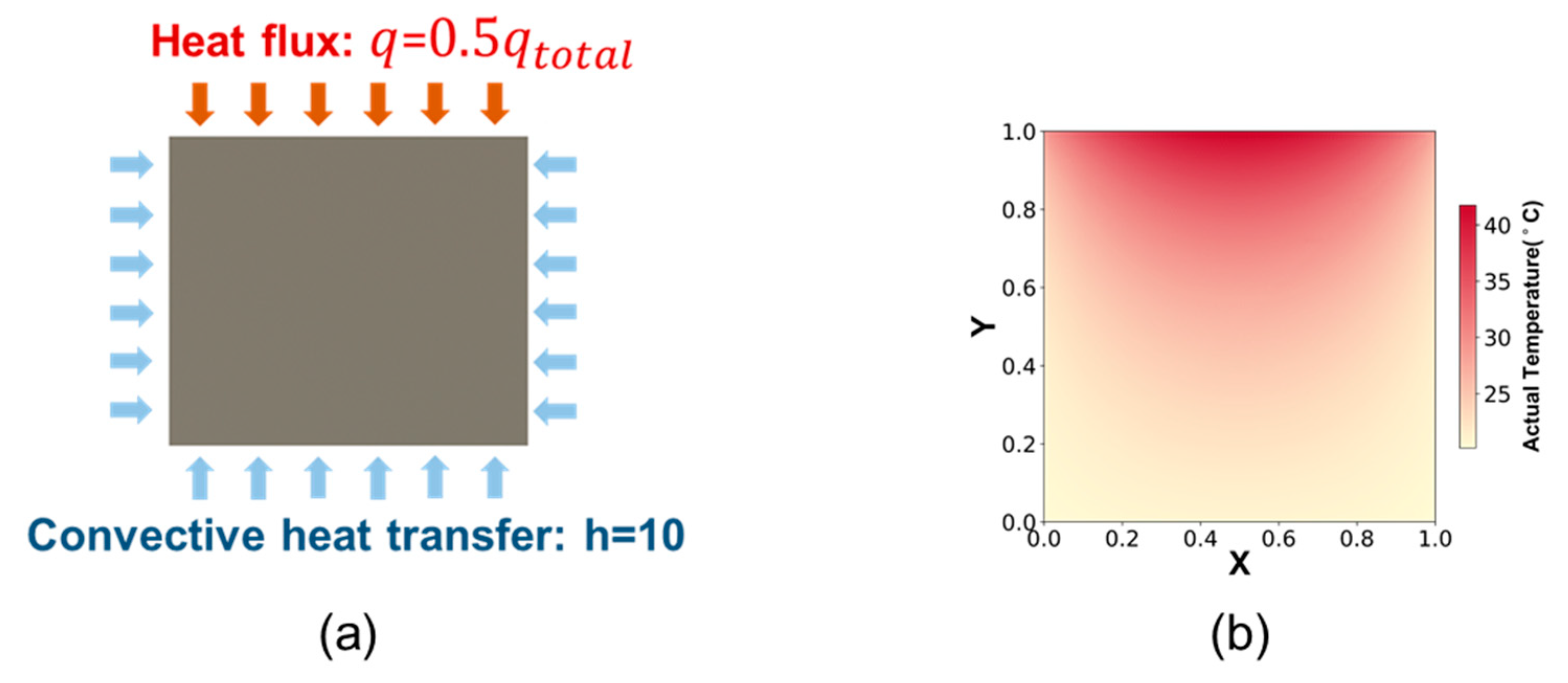
3. Frictional Contact Temperature Forward Calculation by the PINN
4. Frictional Contact Temperature Inverse Calculation by the PINN
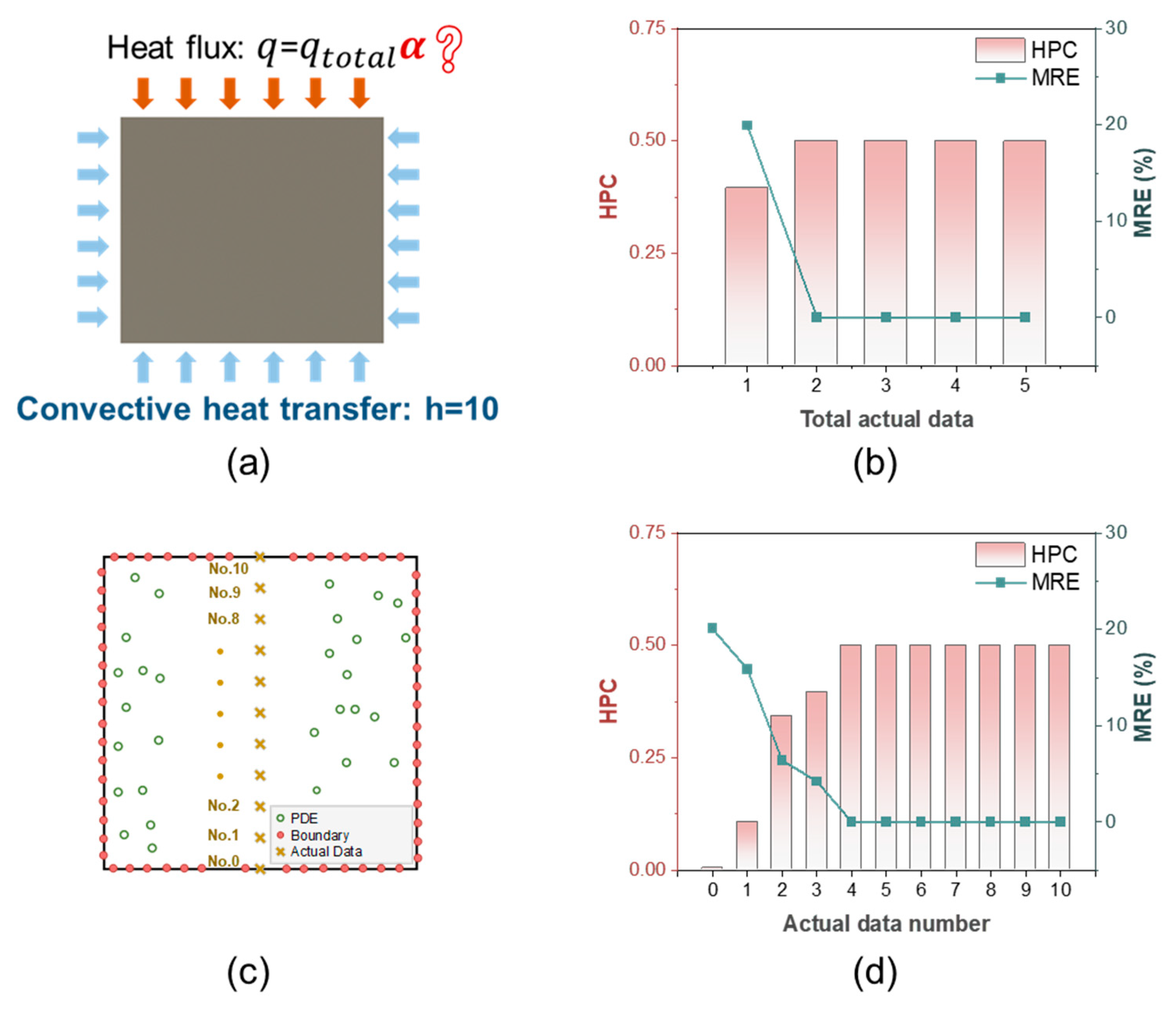
4.1. Inverse Problem for HPC
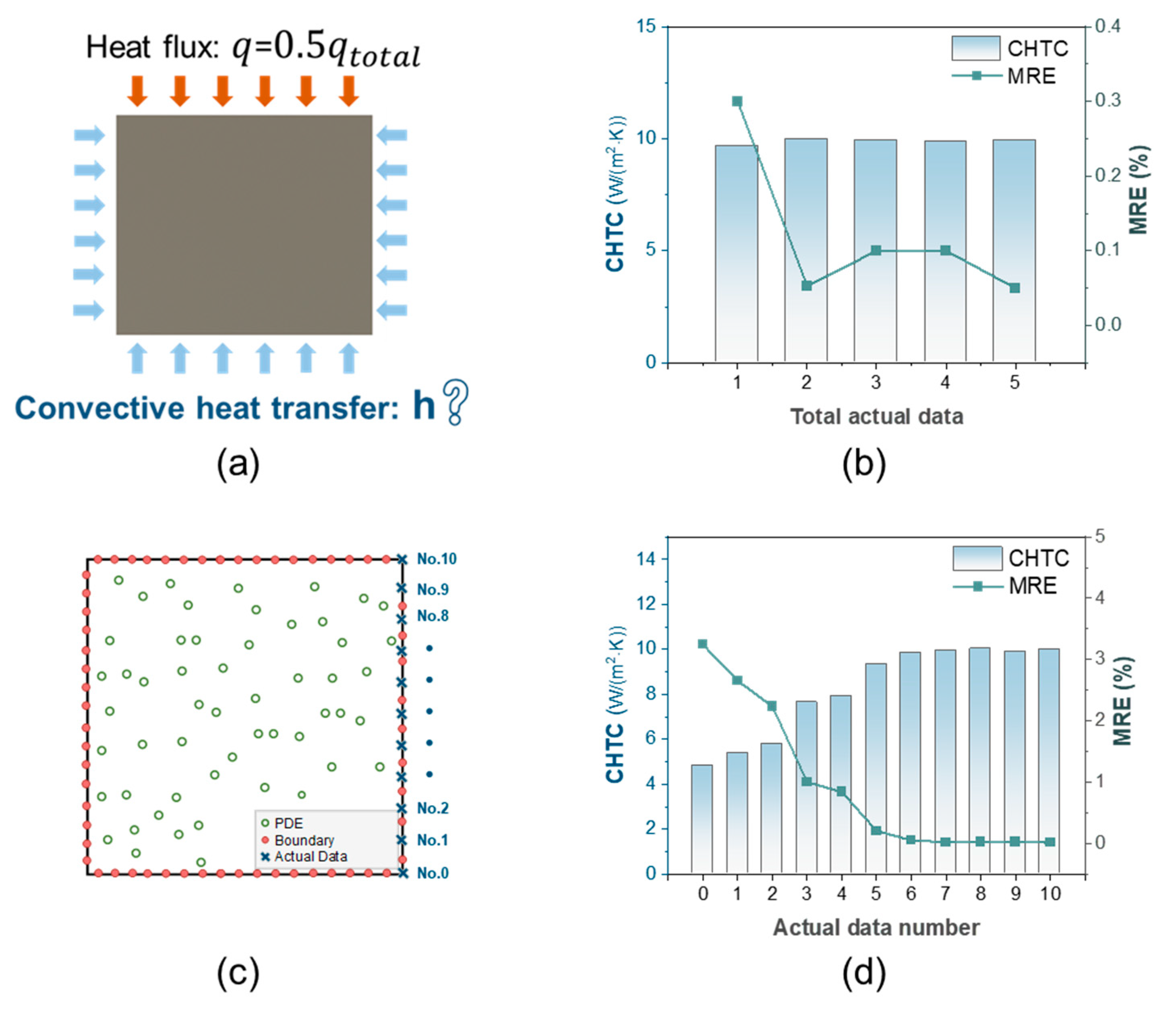
4.2. Inverse Problem for CHTC
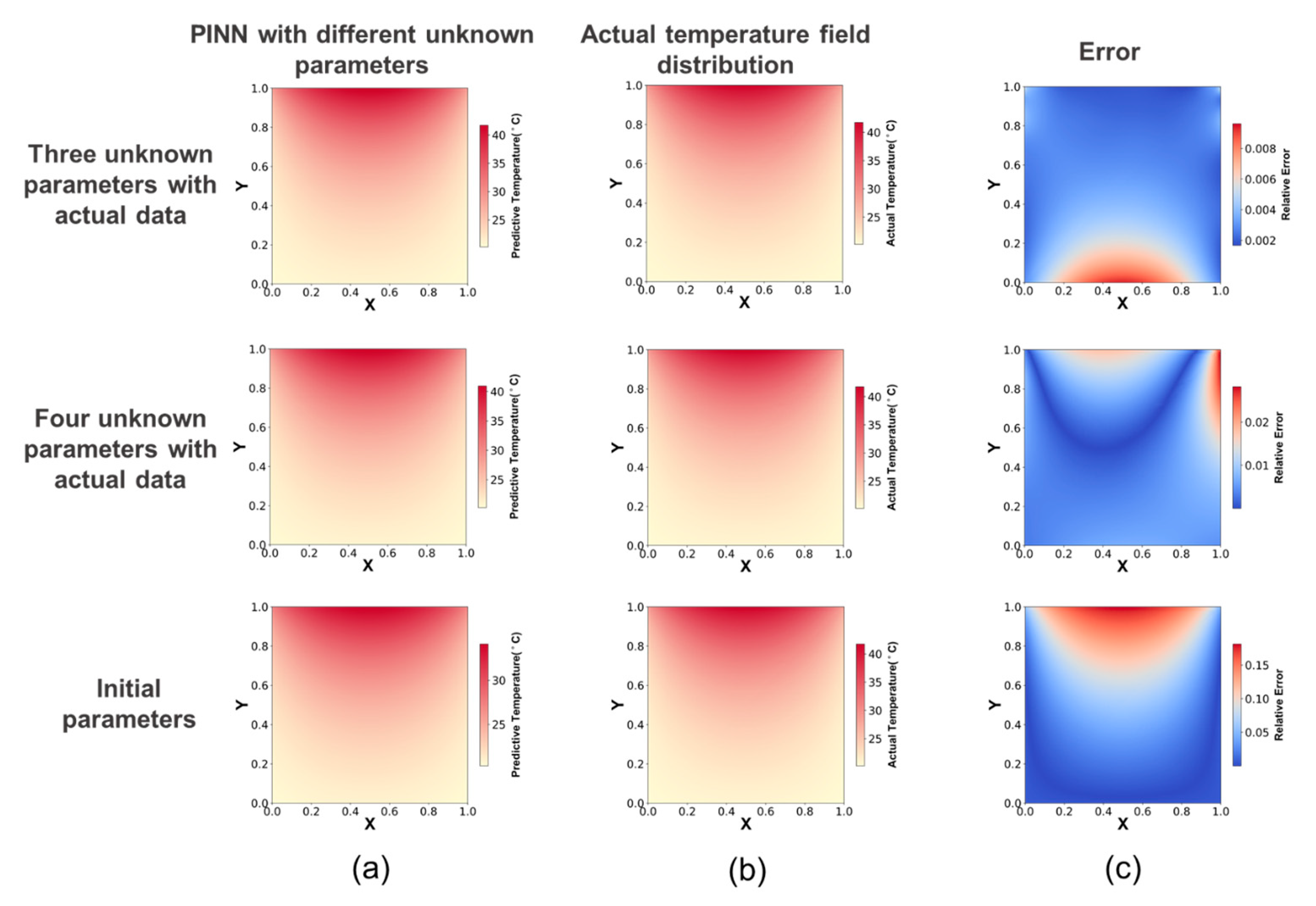
4.3. Inverse Problem for Multiple Unknown Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| T | |
| x, y, z | Spatial coordinates, m |
| k | |
| c | |
| Radiant emissivity | |
| h | |
| Heat partitioning coefficient | |
| L | Total loss function |
| PDE loss function | |
| Boundary condition loss function | |
| Actual data loss function | |
| w | Neural network weight |
| b | Neural network bias |
| p | Unknown parameter |
| Weights of each loss function |
References
- Meng, Y.; Xu, J.; Jin, Z.; Prakash, B.; Hu, Y. A Review of Recent Advances in Tribology. Friction 2020, 8, 221–300. [Google Scholar] [CrossRef]
- Abdullah, O.I.; Schlattmann, J. Thermal Behavior of Friction Clutch Disc Based on Uniform Pressure and Uniform Wear Assumptions. Friction 2016, 4, 228–237. [Google Scholar] [CrossRef]
- Lin, Z.; Qu, T.; Zhang, K.; Zhang, Q.; Wang, S.; Wang, G.; Gao, B.; Fan, G. Modeling of Contact Temperatures and Their Influence on the Tribological Performance of PEEK and PTFE in a Dual-Pin-on-Disk Tribometer. Friction 2023, 11, 546–566. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, G.; Wang, H.; Fu, K. Comparative Study on the Wear Behaviour of Two High-Temperature-Resistant Polymers. Tribol. Lett. 2017, 65, 34. [Google Scholar] [CrossRef]
- Albers, A.; Klotz, T.; Fink, C.; Ott, S. Investigation of the Heat Distribution in Dry Friction Systems during Fade and Recovery Using Fiber-Optic Sensing and Infrared Technology. Friction 2022, 10, 422–435. [Google Scholar] [CrossRef]
- Wang, H.; Liu, D.; Yan, L.; Wang, C.; Yang, S.; Zhu, Y. Tribological Simulation of Porous Self-Lubricating PEEK Composites with Heat-Stress Coupled Field. Tribol. Int. 2014, 77, 43–49. [Google Scholar] [CrossRef]
- Ying, S.; Yupeng, Y. Temperature Field Analysis of Pin-on-Disk Sliding Friction Test. Int. J. Heat Mass Transf. 2017, 107, 339–346. [Google Scholar] [CrossRef]
- Belhocine, A.; Bouchetara, M. Thermal Analysis of a Solid Brake Disc. Appl. Therm. Eng. 2012, 32, 59–67. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Adamowicz, A.; Grzes, P. Three-Dimensional FE Model for the Calculation of Temperature of a Disc Brake at Temperature-Dependent Coefficients of Friction. Int. Commun. Heat Mass Transf. 2013, 42, 18–24. [Google Scholar] [CrossRef]
- Rahaman, M.L.; Zhang, L. Interface Temperature during Contact Sliding of Two Solids: Relationship between Predicted Flash Temperature and the Experimentally Measured. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 3–13. [Google Scholar] [CrossRef]
- Xia, Y.; Yano, A.; Hayashi, N.; Horaguchi, N.; Xie, G.; Guo, D. Analysis of Temperature and Heat Partitioning Coefficient during Friction between Polymer and Steel. Tribol. Int. 2022, 171, 107561. [Google Scholar] [CrossRef]
- Czimmermann, T.; Ciuti, G.; Milazzo, M.; Chiurazzi, M.; Roccella, S.; Oddo, C.M.; Dario, P. Visual-Based Defect Detection and Classification Approaches for Industrial Applications—A survey. Sensors 2020, 20, 1459. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, Y.; Zhao, F.; Zhang, E.; Wu, Z.; Shao, L. Surface Defect Detection Methods for Industrial Products: A Review. Appl. Sci. 2021, 11, 7657. [Google Scholar] [CrossRef]
- Shah, A.; Shah, M.; Pandya, A.; Sushra, R.; Sushra, R.; Mehta, M.; Patel, K.; Patel, K. A Comprehensive Study on Skin Cancer Detection Using Artificial Neural Network (ANN) and Convolutional Neural Network (CNN). Clin. eHealth 2023, 6, 76–84. [Google Scholar] [CrossRef]
- Mazurowski, M.A.; Dong, H.; Gu, H.; Yang, J.; Konz, N.; Zhang, Y. Segment Anything Model for Medical Image Analysis: An Experimental Study. Med. Image Anal. 2023, 89, 102918. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Cao, Y.; Wang, W.; Shen, C.; Huang, T. SegGPT: Towards Segmenting Everything in Context. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 6 October 2023; pp. 1130–1140. [Google Scholar]
- Zhao, W.X.; Zhou, K.; Li, J.; Tang, T.; Wang, X.; Hou, Y.; Min, Y.; Zhang, B.; Zhang, J.; Dong, Z.; et al. A Survey of Large Language Models. arXiv 2023, arXiv:2303.18223. [Google Scholar]
- Peng, J.-Z.; Liu, X.; Aubry, N.; Chen, Z.; Wu, W.-T. Data-Driven Modeling of Geometry-Adaptive Steady Heat Conduction Based on Convolutional Neural Networks. Case Stud. Therm. Eng. 2021, 28, 101651. [Google Scholar] [CrossRef]
- Zhu, S.; He, C.; Zhao, N.; Sha, J. Data-Driven Analysis on Thermal Effects and Temperature Changes of Lithium-Ion Battery. J. Power Sources 2021, 482, 228983. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden Fluid Mechanics: Learning Velocity and Pressure Fields from Flow Visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Mao, Z.; Jagtap, A.D.; Karniadakis, G.E. Physics-Informed Neural Networks for High-Speed Flows. Comput. Methods Appl. Mech. Eng. 2020, 360, 112789. [Google Scholar] [CrossRef]
- Zhang, E.; Dao, M.; Karniadakis, G.E.; Suresh, S. Analyses of Internal Structures and Defects in Materials Using Physics-Informed Neural Networks. Sci. Adv. 2022, 8, eabk0644. [Google Scholar] [CrossRef]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A Physics-Informed Deep Learning Framework for Inversion and Surrogate Modeling in Solid Mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Laubscher, R. Simulation of Multi-Species Flow and Heat Transfer Using Physics-Informed Neural Networks. Phys. Fluids 2021, 33, 087101. [Google Scholar] [CrossRef]
- Xie, J.; Chai, Z.; Xu, L.; Ren, X.; Liu, S.; Chen, X. 3D Temperature Field Prediction in Direct Energy Deposition of Metals Using Physics Informed Neural Network. Int. J. Adv. Manuf. Technol. 2022, 119, 3449–3468. [Google Scholar] [CrossRef]
- Fukushima, R.; Kano, M.; Hirahara, K. Physics-Informed Neural Networks for Fault Slip Monitoring: Simulation, Frictional Parameter Estimation, and Prediction on Slow Slip Events in a Spring-Slider System. J. Geophys. Res. Solid Earth 2023, 128, e2023JB027384. [Google Scholar] [CrossRef]
- Marian, M.; Tremmel, S. Physics-Informed Machine Learning—An Emerging Trend in Tribology. Lubricants 2023, 11, 463. [Google Scholar] [CrossRef]
- Olejnik, P.; Ayankoso, S. Friction Modelling and the Use of a Physics-Informed Neural Network for Estimating Frictional Torque Characteristics. Meccanica 2023, 58, 1885–1908. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, L.; Wong, P.P.L. Application of Physics-Informed Neural Network in the Analysis of Hydrodynamic Lubrication. Friction 2023, 11, 1253–1264. [Google Scholar] [CrossRef]
- Kurt, H.I.; Oduncuoglu, M. Application of a Neural Network Model for Prediction of Wear Properties of Ultrahigh Molecular Weight Polyethylene Composites. Int. J. Polym. Sci. 2015, 2015, e315710. [Google Scholar] [CrossRef]
- Hasan, M.S.; Kordijazi, A.; Rohatgi, P.K.; Nosonovsky, M. Triboinformatic Modeling of Dry Friction and Wear of Aluminum Base Alloys Using Machine Learning Algorithms. Tribol. Int. 2021, 161, 107065. [Google Scholar] [CrossRef]
- Markidis, S. The Old and the New: Can Physics-Informed Deep-Learning Replace Traditional Linear Solvers? Front. Big Data 2021, 4, 669097. [Google Scholar] [CrossRef]
- Weinan, E.; Han, J.; Jentzen, A. Algorithms for Solving High Dimensional PDEs: From Nonlinear Monte Carlo to Machine Learning. Nonlinearity 2022, 35, 278–310. [Google Scholar] [CrossRef]
- Yang, M.; Foster, J.T. Multi-Output Physics-Informed Neural Networks for Forward and Inverse PDE Problems with Uncertainties. Comput. Methods Appl. Mech. Eng. 2022, 402, 115041. [Google Scholar] [CrossRef]
- Miao, Z.; Chen, Y. VC-PINN: Variable Coefficient Physics-Informed Neural Network for Forward and Inverse Problems of PDEs with Variable Coefficient. Phys. D Nonlinear Phenom. 2023, 456, 133945. [Google Scholar] [CrossRef]
- Maddu, S.; Sturm, D.; Müller, C.L.; Sbalzarini, I.F. Inverse Dirichlet Weighting Enables Reliable Training of Physics Informed Neural Networks. Mach. Learn. Sci. Technol. 2022, 3, 015026. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Zhang, H.; Liu, Y.; Li, J.-Y.; Liu, C.-B. Generalized Conditional Symmetry Enhanced Physics-Informed Neural Network and Application to the Forward and Inverse Problems of Nonlinear Diffusion Equations. Chaos Solitons Fractals 2023, 168, 113169. [Google Scholar] [CrossRef]
- Xu, C.; Cao, B.T.; Yuan, Y.; Meschke, G. Transfer Learning Based Physics-Informed Neural Networks for Solving Inverse Problems in Engineering Structures under Different Loading Scenarios. Comput. Methods Appl. Mech. Eng. 2023, 405, 115852. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks for Heat Transfer Problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Go, M.-S.; Lim, J.H.; Lee, S. Physics-Informed Neural Network-Based Surrogate Model for a Virtual Thermal Sensor with Real-Time Simulation. Int. J. Heat Mass Transf. 2023, 214, 124392. [Google Scholar] [CrossRef]
- Liao, S.; Xue, T.; Jeong, J.; Webster, S.; Ehmann, K.; Cao, J. Hybrid Thermal Modeling of Additive Manufacturing Processes Using Physics-Informed Neural Networks for Temperature Prediction and Parameter Identification. Comput. Mech. 2023, 72, 499–512. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, F.; Qiu, L. Multi-Domain Physics-Informed Neural Networks for Solving Transient Heat Conduction Problems in Multilayer Materials. J. Appl. Phys. 2023, 133, 245103. [Google Scholar] [CrossRef]
- Pang, H.; Wu, L.; Liu, J.; Liu, X.; Liu, K. Physics-Informed Neural Network Approach for Heat Generation Rate Estimation of Lithium-Ion Battery under Various Driving Conditions. J. Energy Chem. 2023, 78, 1–12. [Google Scholar] [CrossRef]
- McClenny, L.D.; Braga-Neto, U.M. Self-Adaptive Physics-Informed Neural Networks. J. Comput. Phys. 2023, 474, 111722. [Google Scholar] [CrossRef]
- Shi, S.; Liu, D.; Null, R.J.; Han, Y. An Adaptive Physics-Informed Neural Network with Two-Stage Learning Strategy to Solve Partial Differential Equations. Numer. Math. Theor. Meth. Appl. 2023, 16, 298–322. [Google Scholar] [CrossRef]
- Wang, S.; Yu, X.; Perdikaris, P. When and Why PINNs Fail to Train: A Neural Tangent Kernel Perspective. J. Comput. Phys. 2022, 449, 110768. [Google Scholar] [CrossRef]
- Xiang, Z.; Peng, W.; Liu, X.; Yao, W. Self-Adaptive Loss Balanced Physics-Informed Neural Networks. Neurocomputing 2022, 496, 11–34. [Google Scholar] [CrossRef]
- Cipolla, R.; Gal, Y.; Kendall, A. Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics; IEEE: Piscataway, NJ, USA, 2018; ISBN 978-1-5386-6420-9. [Google Scholar]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and Mitigating Gradient Flow Pathologies in Physics-Informed Neural Networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- Xiong, C.; Chen, M.; Yu, L. Analytical Model and Material Equivalent Methods for Steady State Heat Partition Coefficient between Two Contact Discs in Multi-Disc Clutch. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 857–871. [Google Scholar] [CrossRef]
- Longo, G.A.; Gasparella, A. Refrigerant R134a Vaporisation Heat Transfer and Pressure Drop inside a Small Brazed Plate Heat Exchanger. Int. J. Refrig. 2007, 30, 821–830. [Google Scholar] [CrossRef]
- Vollaro, A.D.L.; Galli, G.; Vallati, A. CFD Analysis of Convective Heat Transfer Coefficient on External Surfaces of Buildings. Sustainability 2015, 7, 9088–9099. [Google Scholar] [CrossRef]
- Kuwahara, F.; Shirota, M.; Nakayama, A. A Numerical Study of Interfacial Convective Heat Transfer Coefficient in Two-Energy Equation Model for Convection in Porous Media. Int. J. Heat Mass Transf. 2001, 44, 1153–1159. [Google Scholar] [CrossRef]

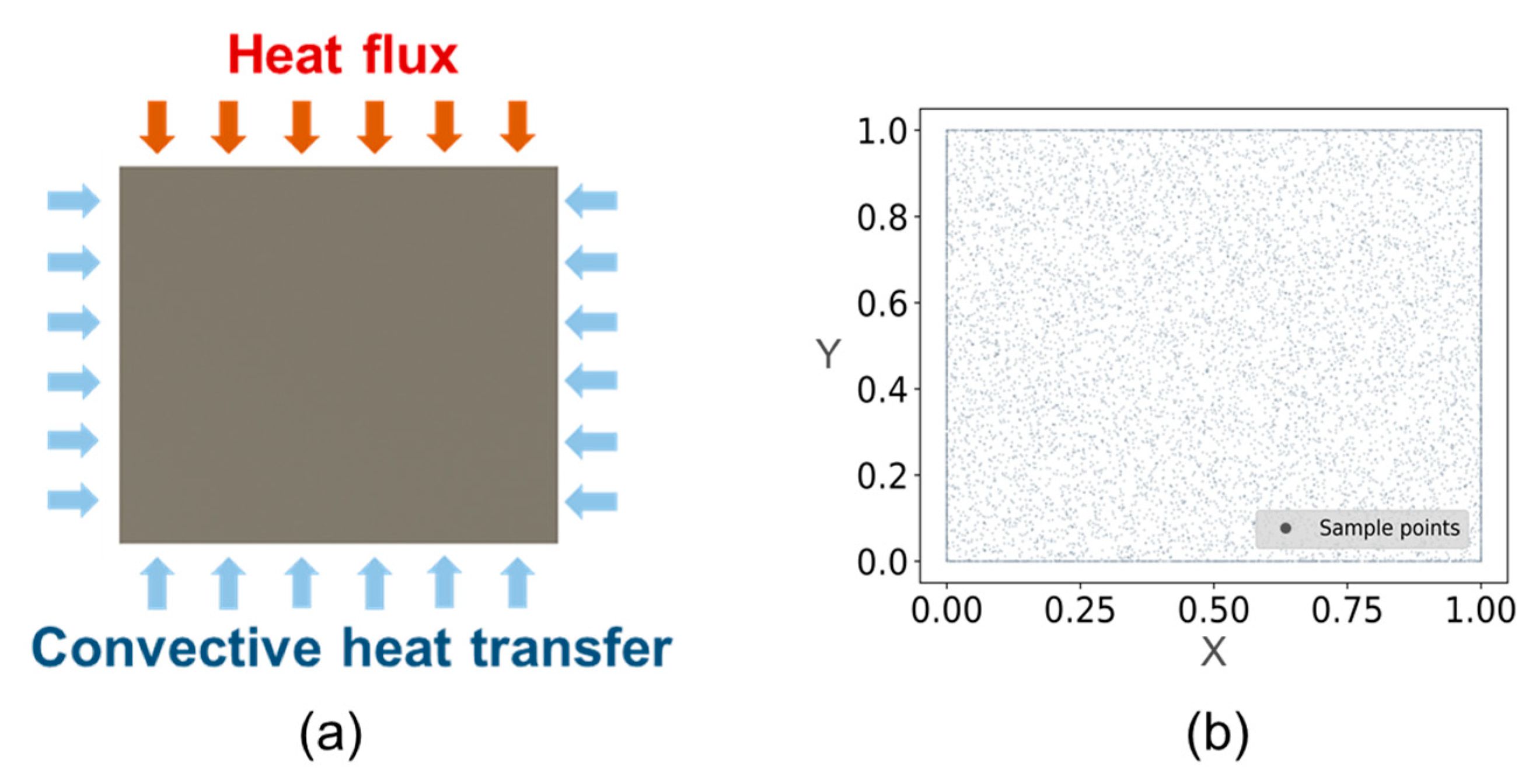
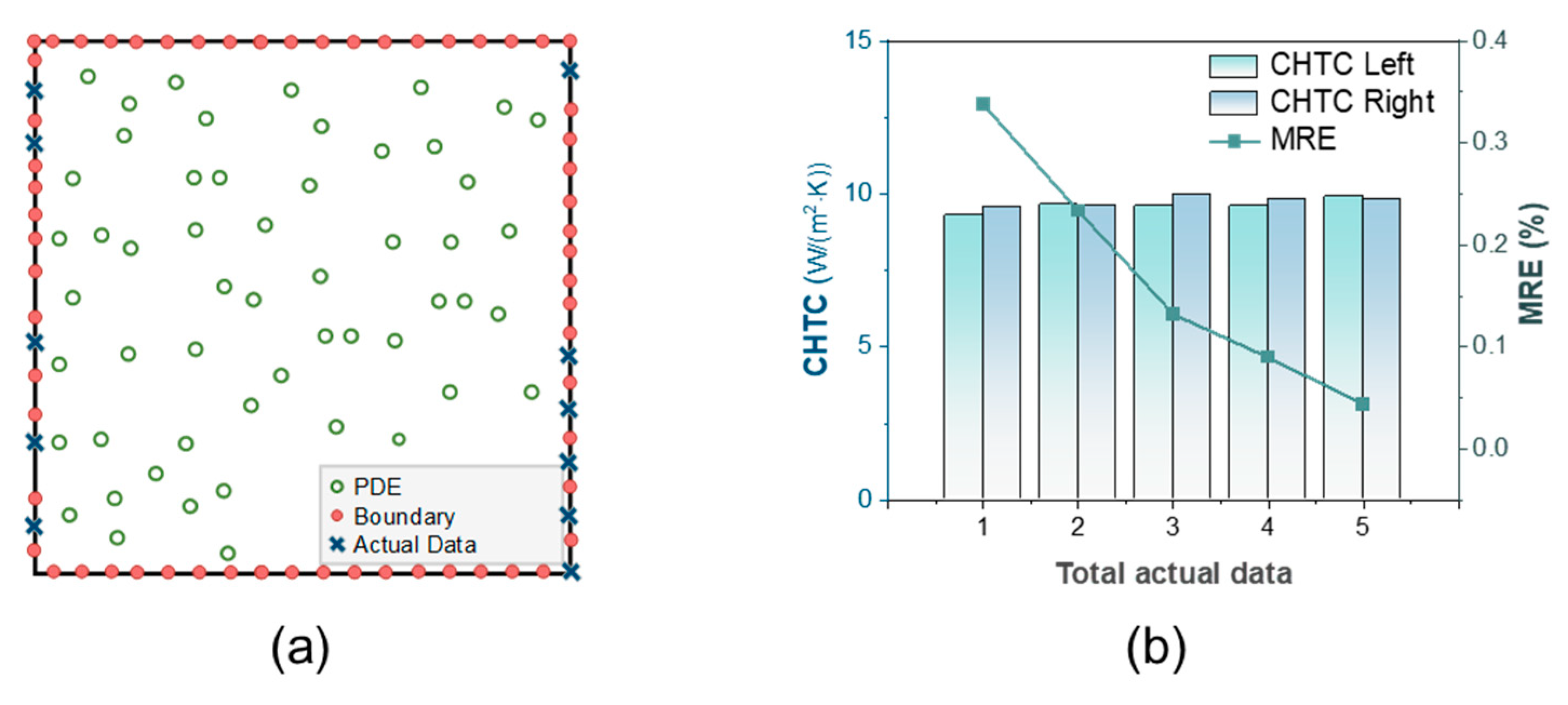
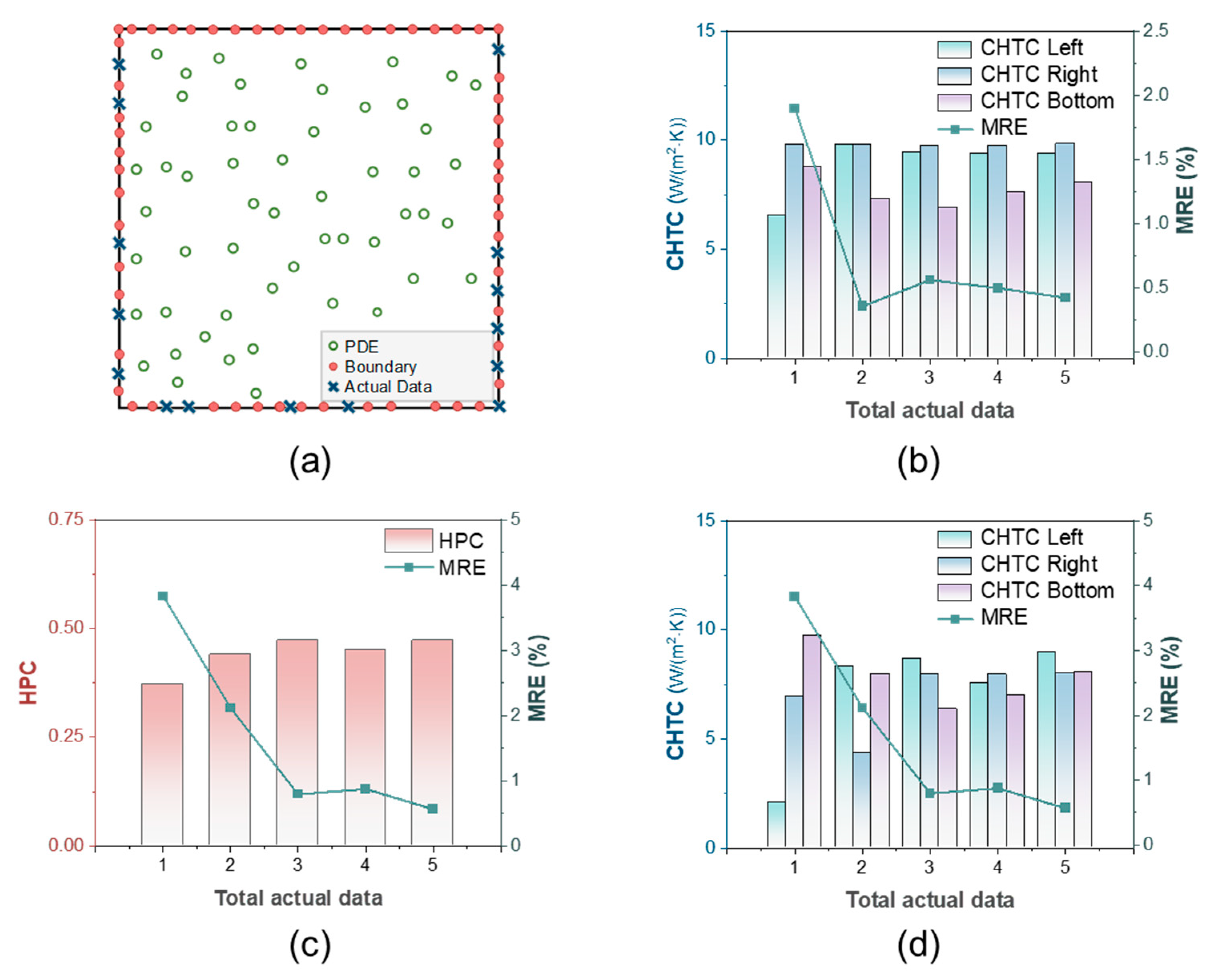
| Heat Flux | CHTC | Ambient Temperature °C | X, Y Length m | Thermal Conductivity |
|---|---|---|---|---|
| (25, 50, 75, 100) | 10 | 20 | 1 | 1 |
| Heat Flux W/m2 | PINN | PINN with Actual Data |
|---|---|---|
| 25 | 0.008% | 0.006% |
| 50 | 0.013% | 0.009% |
| 75 | 0.019% | 0.008% |
| 100 | 0.012% | 0.007% |
| Total Heat Flux W/m2 | HPC (Top) | CHTC (Left, Right, Bottom) | Ambient Temperature °C | X, Y Length m | Thermal Conductivity |
|---|---|---|---|---|---|
| 100 | 0.5 | 10 | 20 | 1 | 1 |
| Actual Data Number | No.0 | No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 | No.9 | No.10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperature (°C) | 20.2 | 20.4 | 20.6 | 20.8 | 21.2 | 21.6 | 22.1 | 22.8 | 23.8 | 25.3 | 28.2 |
| PINN with Different Unknown Parameters | Three Unknown Parameters with Actual Data | Four Unknown Parameters with Actual Data | Initial Parameters without Actual Data |
|---|---|---|---|
| MRE | 0.03% | 0.79% | 5.16% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Meng, Y. Physics-Informed Neural Network (PINN) for Solving Frictional Contact Temperature and Inversely Evaluating Relevant Input Parameters. Lubricants 2024, 12, 62. https://doi.org/10.3390/lubricants12020062
Xia Y, Meng Y. Physics-Informed Neural Network (PINN) for Solving Frictional Contact Temperature and Inversely Evaluating Relevant Input Parameters. Lubricants. 2024; 12(2):62. https://doi.org/10.3390/lubricants12020062
Chicago/Turabian StyleXia, Yichun, and Yonggang Meng. 2024. "Physics-Informed Neural Network (PINN) for Solving Frictional Contact Temperature and Inversely Evaluating Relevant Input Parameters" Lubricants 12, no. 2: 62. https://doi.org/10.3390/lubricants12020062
APA StyleXia, Y., & Meng, Y. (2024). Physics-Informed Neural Network (PINN) for Solving Frictional Contact Temperature and Inversely Evaluating Relevant Input Parameters. Lubricants, 12(2), 62. https://doi.org/10.3390/lubricants12020062





