Simulation Analysis and Experimental Research on Electric Thermal Coupling of Current Bearing
Abstract
:1. Introduction
2. Simulation Model of Heat Generation in Current-Carrying Bearings
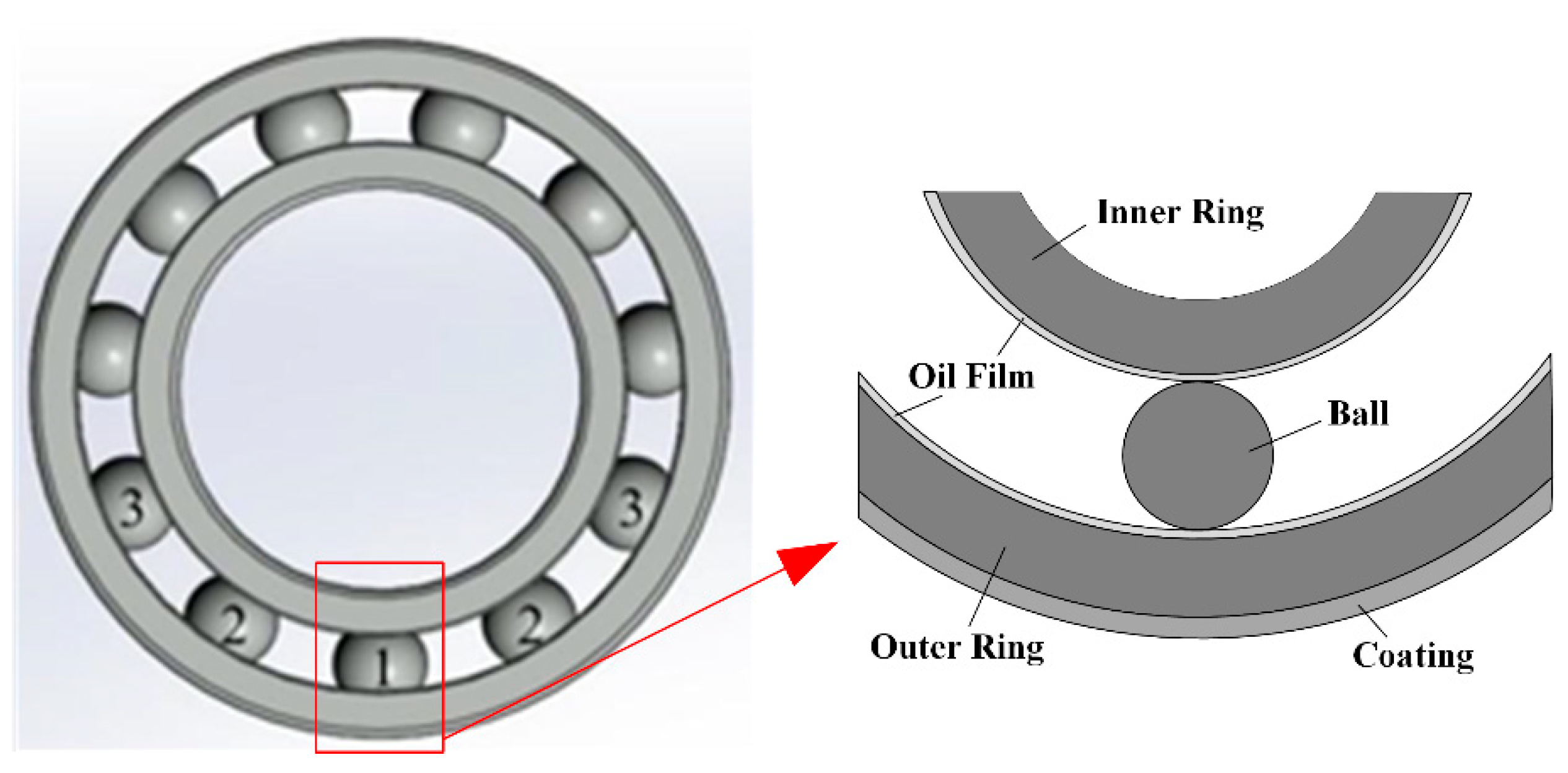
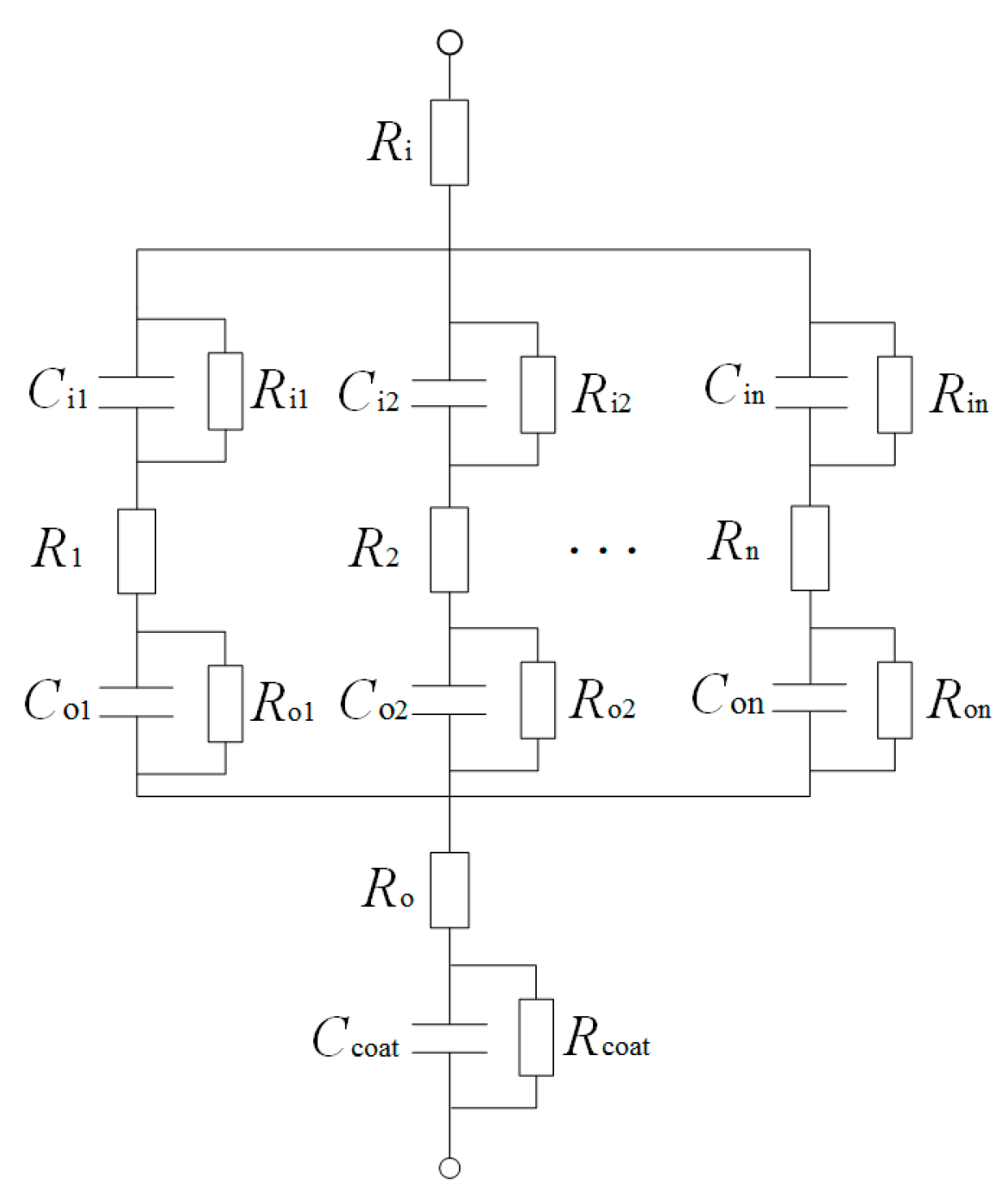
2.1. Equivalent Circuit of Current Bearing
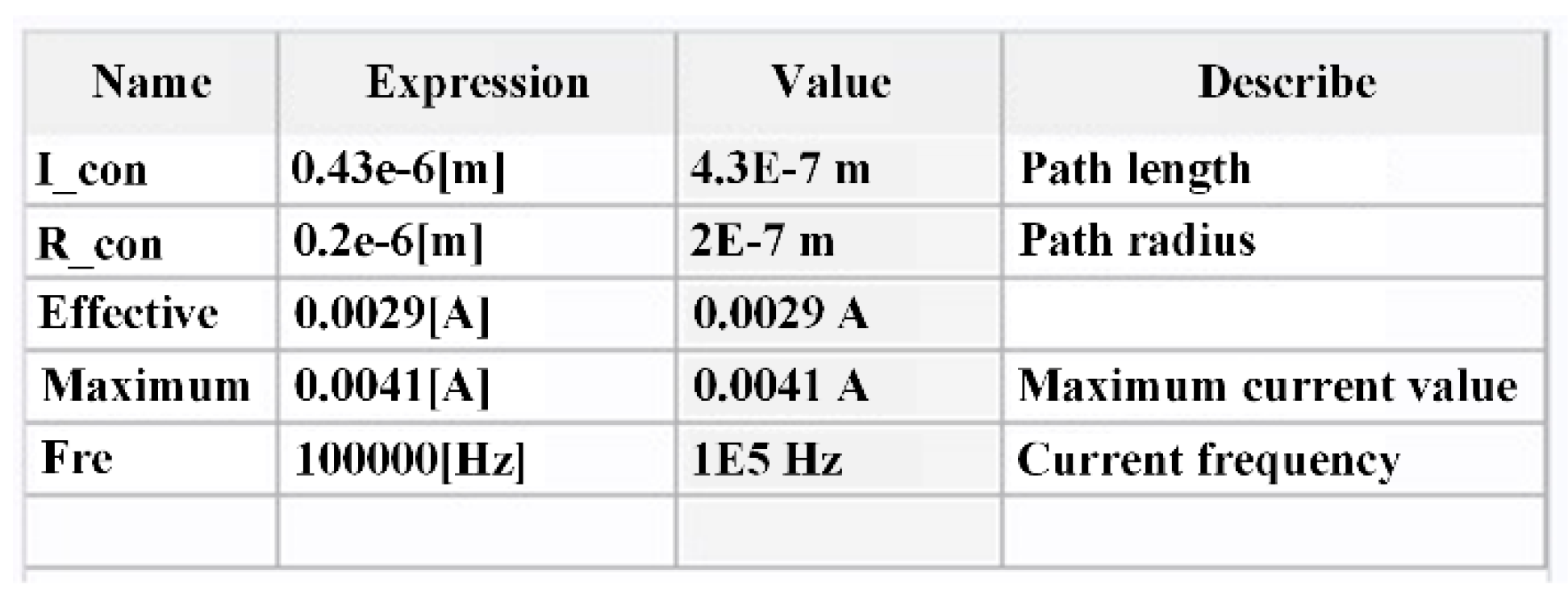
2.2. Calculation of Current-Carrying Bearing Capacitance
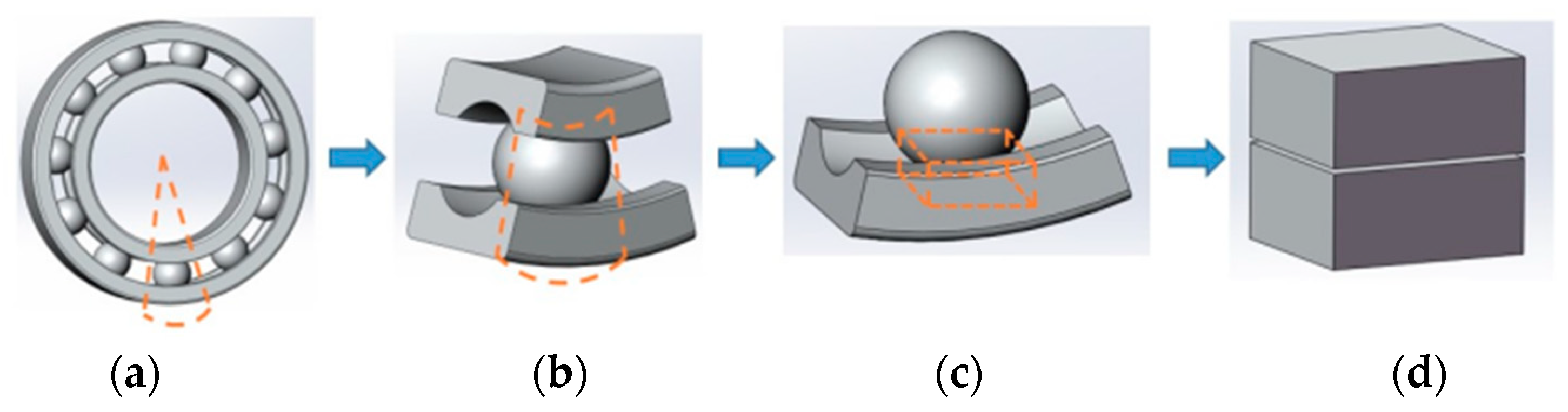
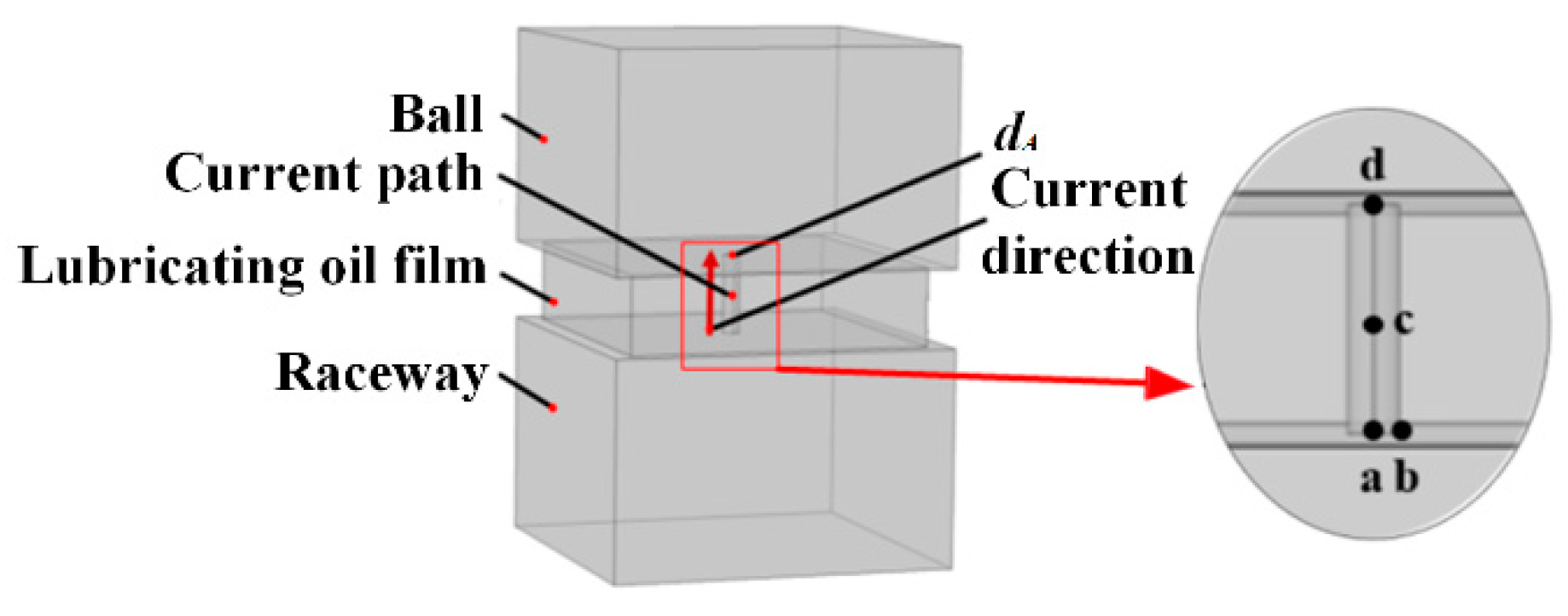
2.3. Calculation Model of Bearing Heat Source
3. Simulation and Analysis of Temperature Field in Current-Carrying Bearings
3.1. Temperature Field Simulation Model
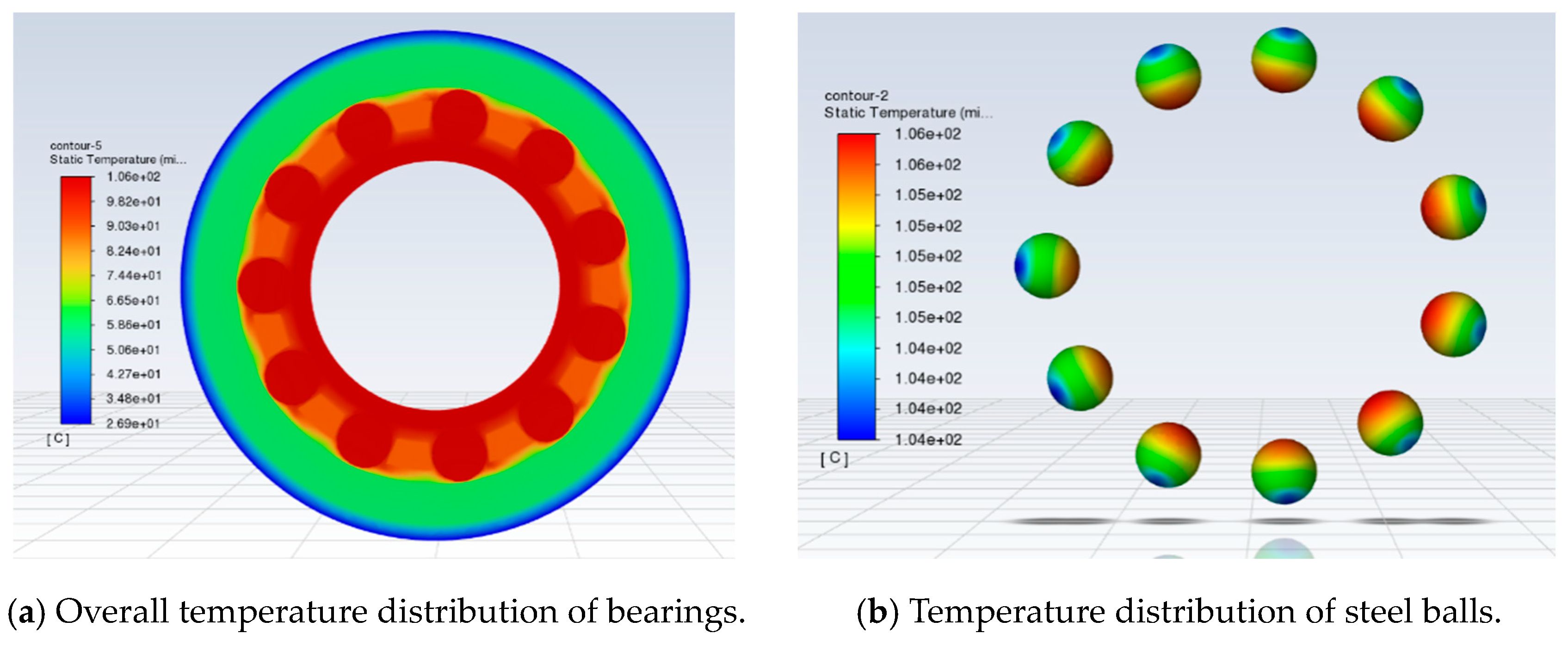
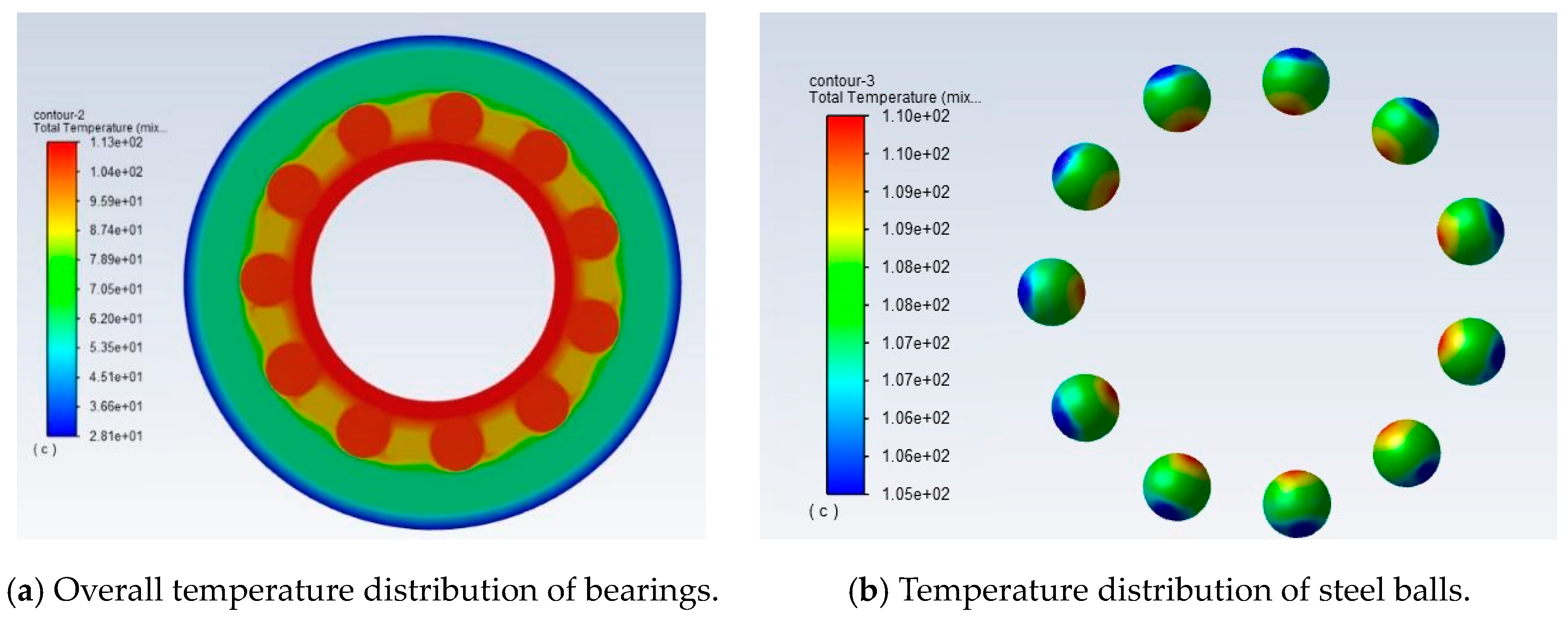
3.2. Simulation Results of Frictional Heat Generation Temperature Field
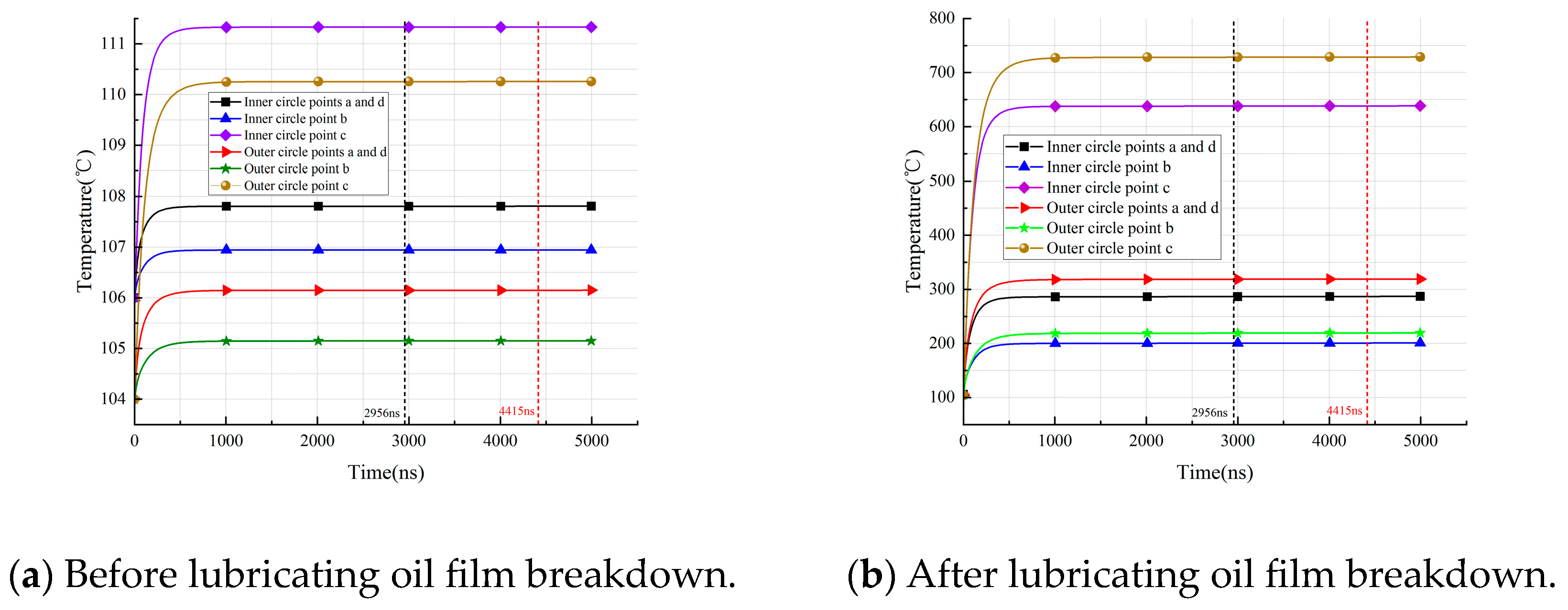
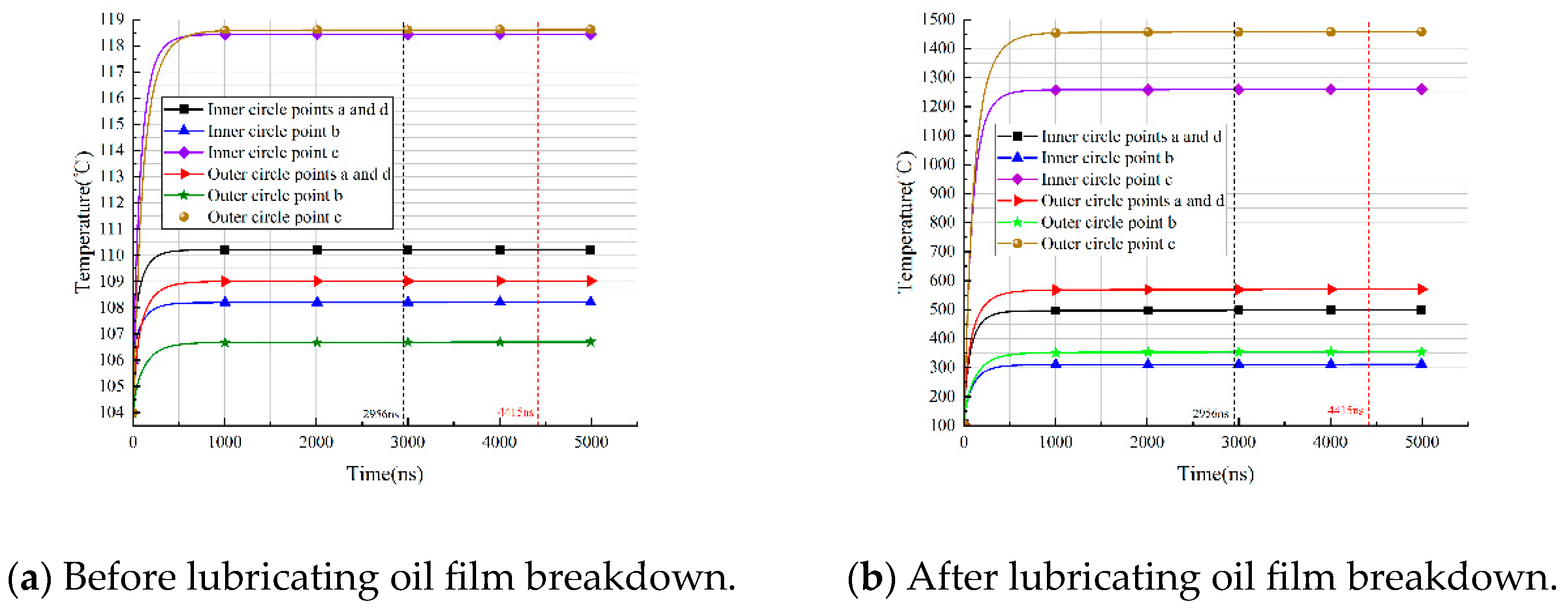
3.3. Simulation Analysis of Local Temperature Rise in the Contact Area of Current Bearing
4. Experimental Verification of Electric Thermal Coupling Temperature Field for Current Bearing
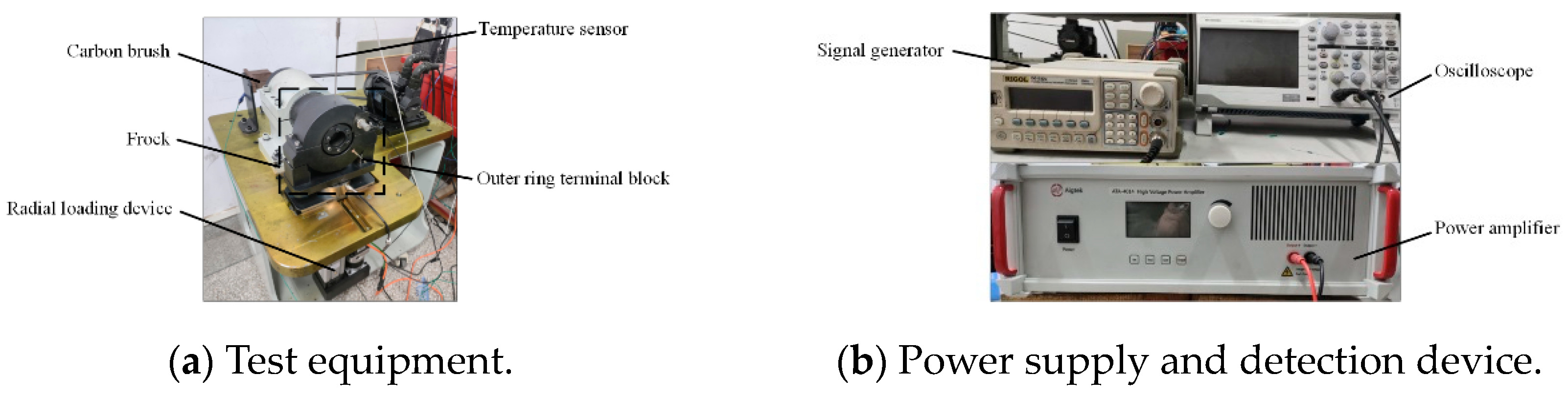
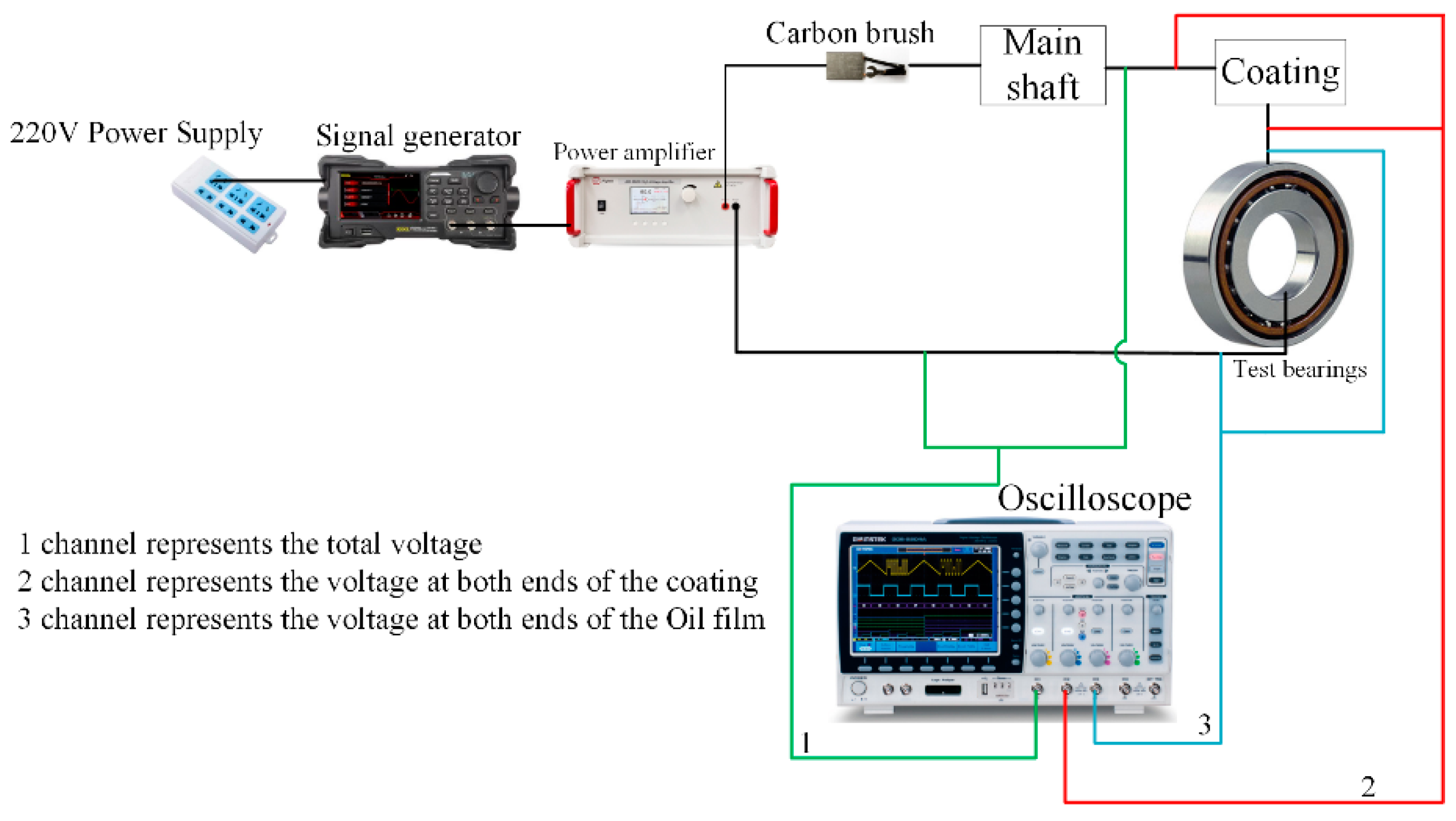
4.1. Test Conditions
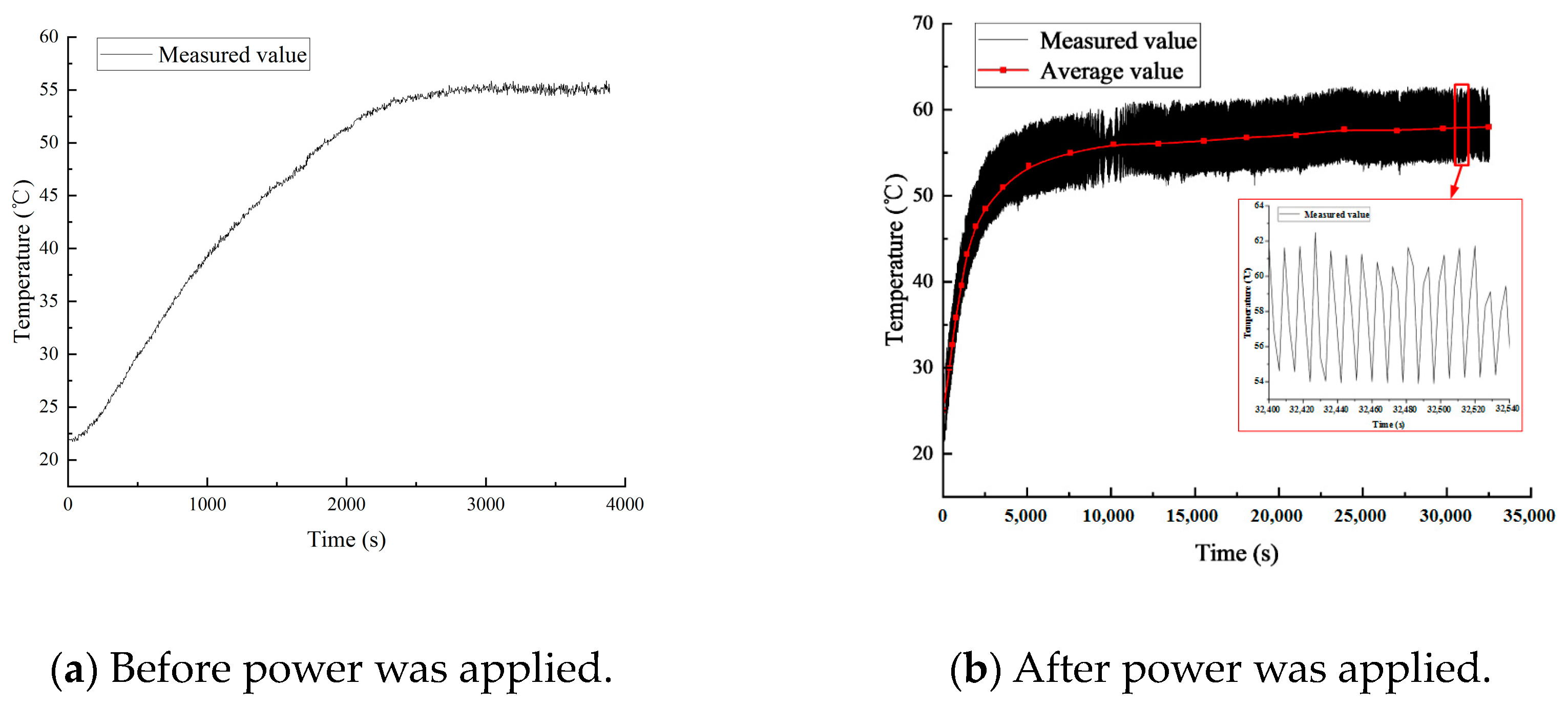
4.2. Results and Discussion of Outer Ring Temperature Rise Test
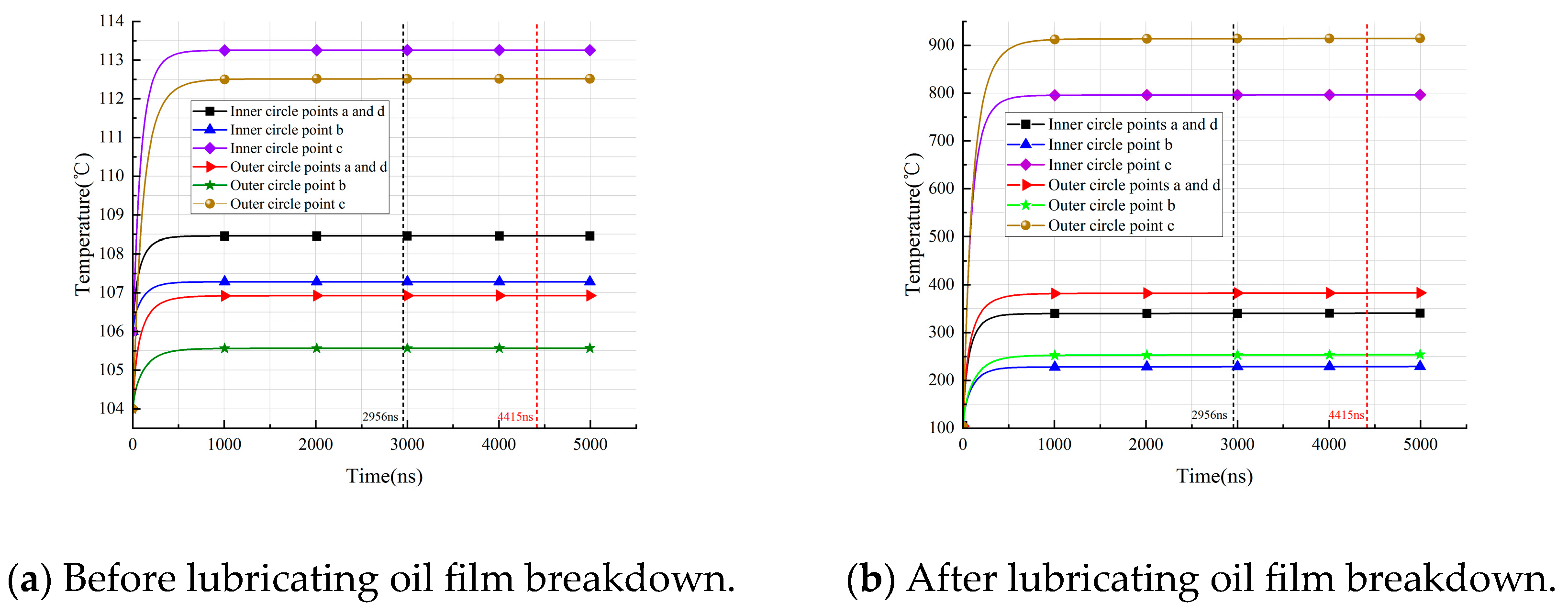
4.3. Verification of Temperature Rise Test in Contact Area
5. Conclusions
- (1)
- Electrical environmental factors can cause an increase in the overall temperature rise in the bearing. Specifically, the temperature of the outer ring of the bearing can increase by approximately 3 °C compared to the temperature before powering on.
- (2)
- In an electrical environment, the contact areas of bearings experience localized high temperatures due to the breakdown and discharge of the lubricating oil film. The temperature rise in the contact area between the rolling element and the outer raceway is particularly significant, increasing the likelihood of electrical corrosion damage.
- (3)
- The consistency between the experimental results and simulation results is good, which verifies the accuracy of the simulation model.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lou, Z.F. The Analysis and Suppression of Bearing Current in Varied Frequency Supply AC Motor. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2015. [Google Scholar]
- Ma, J.J.; Xue, Y.J.; Han, Q.K.; Li, X.J.; Yu, C.X. Motor Bearing Damage Induced by Bearing Current: A Review. Machines 2022, 10, 1167. [Google Scholar] [CrossRef]
- Liu, R.F.; Sang, B.Q.; Cao, J.C. Investigation on the Influence of Motors Grounding States on Bearing Voltage in Inverter Drive System. Proc. CSEE 2015, 35, 177–183. (In Chinese) [Google Scholar]
- He, F.; Xie, G.X.; Luo, J.B. Electrical bearing failures in electric vehicles. Friction 2020, 8, 4–28. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, B.D.; Liu, W.F. Determination of Key Parameters in Distribution Parameters Common Mode Equivalent Circuit and Calculation of the Bearing Currents. Trans. China Electrotech. Soc. 2014, 29, 124–131. (In Chinese) [Google Scholar]
- Ma, S.Y.; Wang, Z.W.; Li, C. Computational Analysis and Experimental Verification of Equivalent Capacitance of Cylindrical Roller Bearings Under Current-Carrying Condition. Bearing 2023, 9, 11–18. (In Chinese) [Google Scholar]
- Busse, D.; Erdman, J.; Kerkman, R.; Schlegel, D.; Skibinski, G. The effects of PWM voltage source inverters on the mechanical performance of rolling bearings. IEEE Trans. 1997, 33, 567–576. [Google Scholar] [CrossRef]
- Wang, Q.Q. Research on Capacitances Calculation and the Bearing Damage Degree in Bearing Currents of AC Motors. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Puchtler, S.; Maier, R.; Kuhn, M.; Burkhardt, Y. The Influence of Load and Speed on the Initial Breakdown of Rolling Bearings Exposed to Electrical Currents. Lubricants 2024, 12, 1. [Google Scholar] [CrossRef]
- Li, Y.; Qiu, L.; Zhi, Y.J.; Gao, Z.F.; Ma, J.E.; Zhang, J.; Fang, Y.T. An overview of bearing voltages and currents in rail transportation traction motors. Appl. Phys. Eng. 2023, 24, 226–242. [Google Scholar] [CrossRef]
- Tischmacher, H.; Gattermann, S. Investigations on Bearing Currents in Converter-Fed Electrical Motors. In Proceedings of the 20th International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1764–1770. [Google Scholar]
- Miliani, E.H. Leakage current and commutation losses reduction in electric drives for Hybrid Electric Vehicle. J. Power Sources 2014, 255, 266–273. [Google Scholar] [CrossRef]
- Romanenko, A.; Ahola, J.; Muetze, A. Influence of electric discharge activity on bearing lubricating grease degradation. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015; SEP: Montreal, QC, Canada, 2015; Volume 18–24, pp. 4851–4856. [Google Scholar]
- Niu, K.; Zeng, Z.X.; Chen, T.H. Research Progress of the Mechanism of Shaft Current Corrosion in Bearing and the Protection Technology. Lubr. Eng. 2023, 48, 179–188. (In Chinese) [Google Scholar]
- Binder, A.; Muetze, A. Scaling Effects of Inverter-Induced Bearing Currents in AC Machines. IEEE Ind. Appl. 2008, 44, 769–776. [Google Scholar] [CrossRef]
- Lu, F.M. Principle of Electrical Erosion and Insulation Protection Indexes of PWM Frequency Modulation Motor Bearing. Bearing 2019, 5, 6–9. (In Chinese) [Google Scholar]
- Liu, R.F.; Sang, B.Q.; Li, W.L. Calculations and Measurements of Bearing Capacitance in AC Motor Bearings. Proc. CSEE 2017, 37, 2986–2993. (In Chinese) [Google Scholar]
- Xiong, F.; Shi, W.; Liao, A.H. Calculation of Equivalent Capacitance of Traction Motor Bearings for Rail Vehicle Considering Radial Clearance Variation of Bearings and Air Gap Eccentricity of Motor. Bearing 2023, 10, 49–56. (In Chinese) [Google Scholar]
- Suo, L.C.; Zhao, W.S.; Liang, L.P. Research on the Mechanism of Dielectric Breakdown in Powder Mixing Electric Discharge Machining. Electromachining Mould. 2001, 5, 10–13. (In Chinese) [Google Scholar]
- Nakao, Y.; Hamano, N.; Naito, T.; Nakagami, Y.; Shimizu, R.; Sakai, Y.; Tagashira, H. Influence of Molecular Structure on Propagation of Positive Streamer Discharge in Dielectric Liquids. Electr. Eng. Jpn. 2004, 149, 15–20. [Google Scholar] [CrossRef]
- Lei, J.T.; Su, B.; Zhang, S.L. Dynamics-Based Thermal Analysis of High-Speed Angular Contact Ball Bearings with Under-Race Lubrication. Machines 2023, 11, 691. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Yang, H.S.; Su, B. Simulation Analysis of the Friction Power Consumption of Double Row Angular Contact Ball Bearings for Aero-engine. J. Mech. Transm. 2021, 45, 129–135. (In Chinese) [Google Scholar]
- Li, J.S.; Yuan, Y.; Hao, D.Q. Analysis and Experimental Study on Bearing Temperature Rise of High Speed Machine Tools. J. Mech. Transm. 2023, 47, 129–136. (In Chinese) [Google Scholar]
- Xie, Y.B.; Zhang, M.Z.; Wang, D.F. Simulation Analysis on Temperature Field of Grease-Lubricated Bearings for Motorized Spindles with Cooling Systems of Different Structures. Bearing 2023, 11, 22–26. (In Chinese) [Google Scholar]
- Wang, Q.Q.; Liu, R.F.; Ren, X.J. The Motor Bearing Discharge Breakdown Based on the Multi-Physics Field Analysis. Trans. China Electrotech. Soc. 2020, 35, 4251–4257. (In Chinese) [Google Scholar]
- Deng, S.E.; Jia, Q.Y.; Xue, J.X. Principles of Rolling Bearing Design, 2nd ed.; China Standard Press: Beijing, China, 2014; pp. 138–139. [Google Scholar]
- Muetze, A.; Binder, A. Practical Rules for Assessment of Inverter-Induced Bearing Currents in Inverter-Fed AC Motors up to 500 kW. IEEE T. Ind. Electron. 2007, 54, 1614–1622. [Google Scholar] [CrossRef]
- Tang, J. Electrotechnics, 2nd ed.; Higher Education Press: Beijing, China, 2005; pp. 64–65. [Google Scholar]




| Parameter | Meaning | Value |
|---|---|---|
| Inside diameter | 75 mm | |
| Width | 25 mm | |
| Coefficient of curvature radius of inner raceway groove | 0.5097 | |
| Steel ball diameter | 17.462 mm | |
| Radial clearance | 46~71 μm | |
| The elastic modulus of steel | ||
| Vacuum dielectric constant | 8.85 × 10−12 F/m | |
| Outside diameter | 130 mm | |
| Bearing pitch diameter | 102.5 mm | |
| Coefficient of curvature radius of outer raceway groove | 0.5268 | |
| Number of steel balls | 11 | |
| Dimensionless geometric parameters | 0.17 | |
| Viscosity–pressure coefficient | ||
| Dielectric constant of lubricating grease | 2.5 |
| Parameter | Value |
|---|---|
| 40 °C base oil viscosity | 220 mm2/s |
| Density | 880 kg/m3 |
| 100 °C base oil viscosity | 19 mm2/s |
| Steel Ball Number | 1 | 2 | 3 |
|---|---|---|---|
| /pF | 93.36 | 79.95 | 45.35 |
| /pF | 79.12 | 67.96 | 38.83 |
| /pF | 42.83 | 36.73 | 20.92 |
| /pF | 158.13 | ||
| /pF | 142.58 | ||
| Voltage Peak to Peak Value (V) | Frequency (kHz) | Unbreakable Shaft Current (mA) | Breakdown Rear Axle Current (mA) |
|---|---|---|---|
| 60 | 100 | 2.69 | 27.33 |
| 90 | 100 | 4.03 | 41.00 |
| 60 | 130 | 3.49 | 35.53 |
| 90 | 130 | 5.24 | 53.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Mao, S.; Tian, H.; Su, B.; Cui, Y. Simulation Analysis and Experimental Research on Electric Thermal Coupling of Current Bearing. Lubricants 2024, 12, 73. https://doi.org/10.3390/lubricants12030073
Wang Z, Mao S, Tian H, Su B, Cui Y. Simulation Analysis and Experimental Research on Electric Thermal Coupling of Current Bearing. Lubricants. 2024; 12(3):73. https://doi.org/10.3390/lubricants12030073
Chicago/Turabian StyleWang, Zhiwei, Shuanglong Mao, Heng Tian, Bing Su, and Yongcun Cui. 2024. "Simulation Analysis and Experimental Research on Electric Thermal Coupling of Current Bearing" Lubricants 12, no. 3: 73. https://doi.org/10.3390/lubricants12030073
APA StyleWang, Z., Mao, S., Tian, H., Su, B., & Cui, Y. (2024). Simulation Analysis and Experimental Research on Electric Thermal Coupling of Current Bearing. Lubricants, 12(3), 73. https://doi.org/10.3390/lubricants12030073





