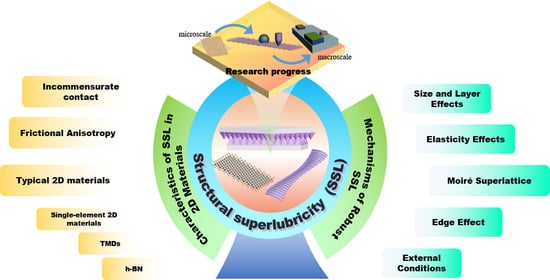
Structural Superlubricity of Two-Dimensional Materials: Mechanisms, Properties, Influencing Factors, and Applications
Abstract
:1. Introduction
2. Structural Superlubricity Characteristics of 2D Materials
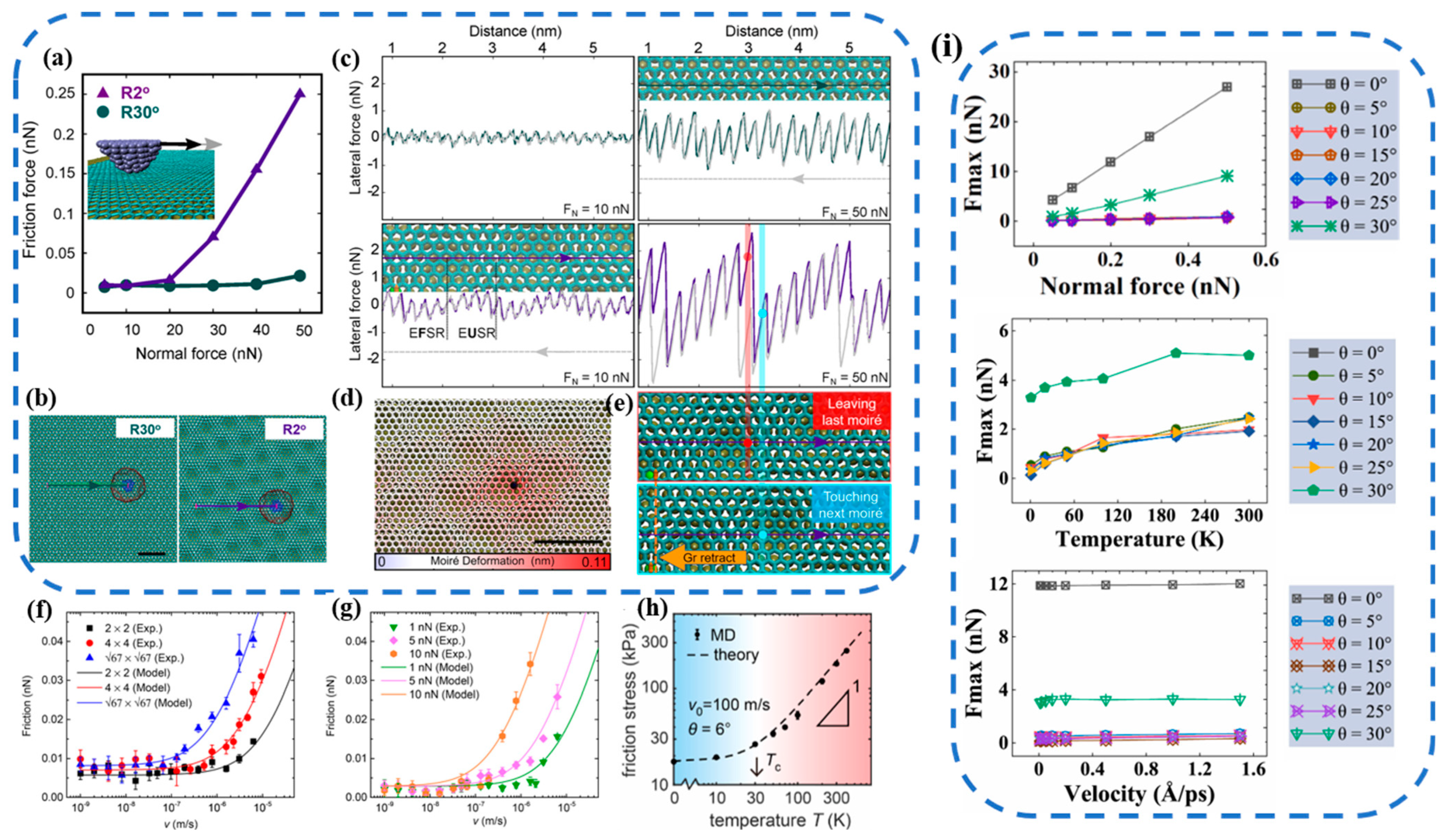
2.1. Incommensurate Contacts and Frictional Anisotropy
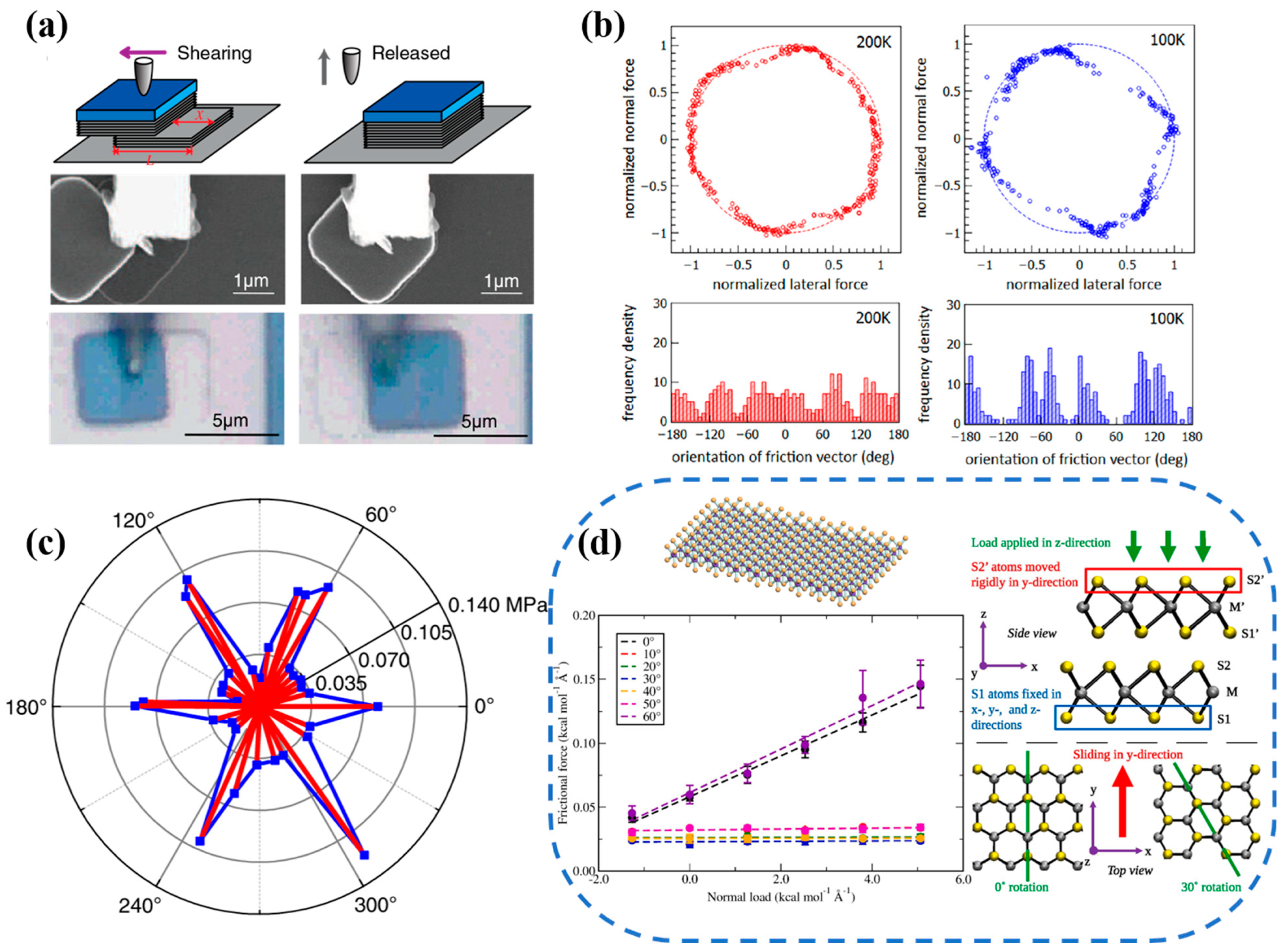
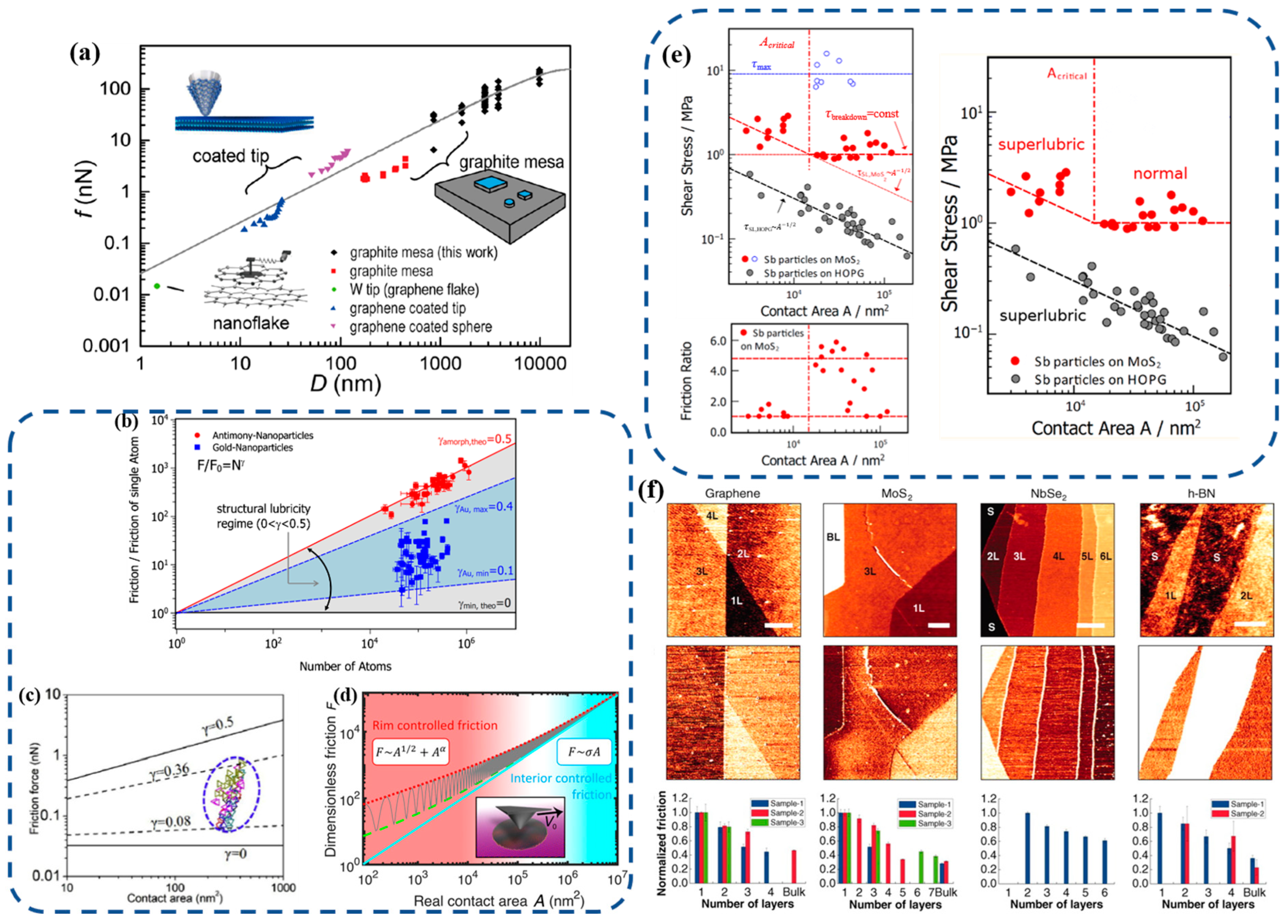
2.2. Single-Element 2D Materials
2.3. TMDs
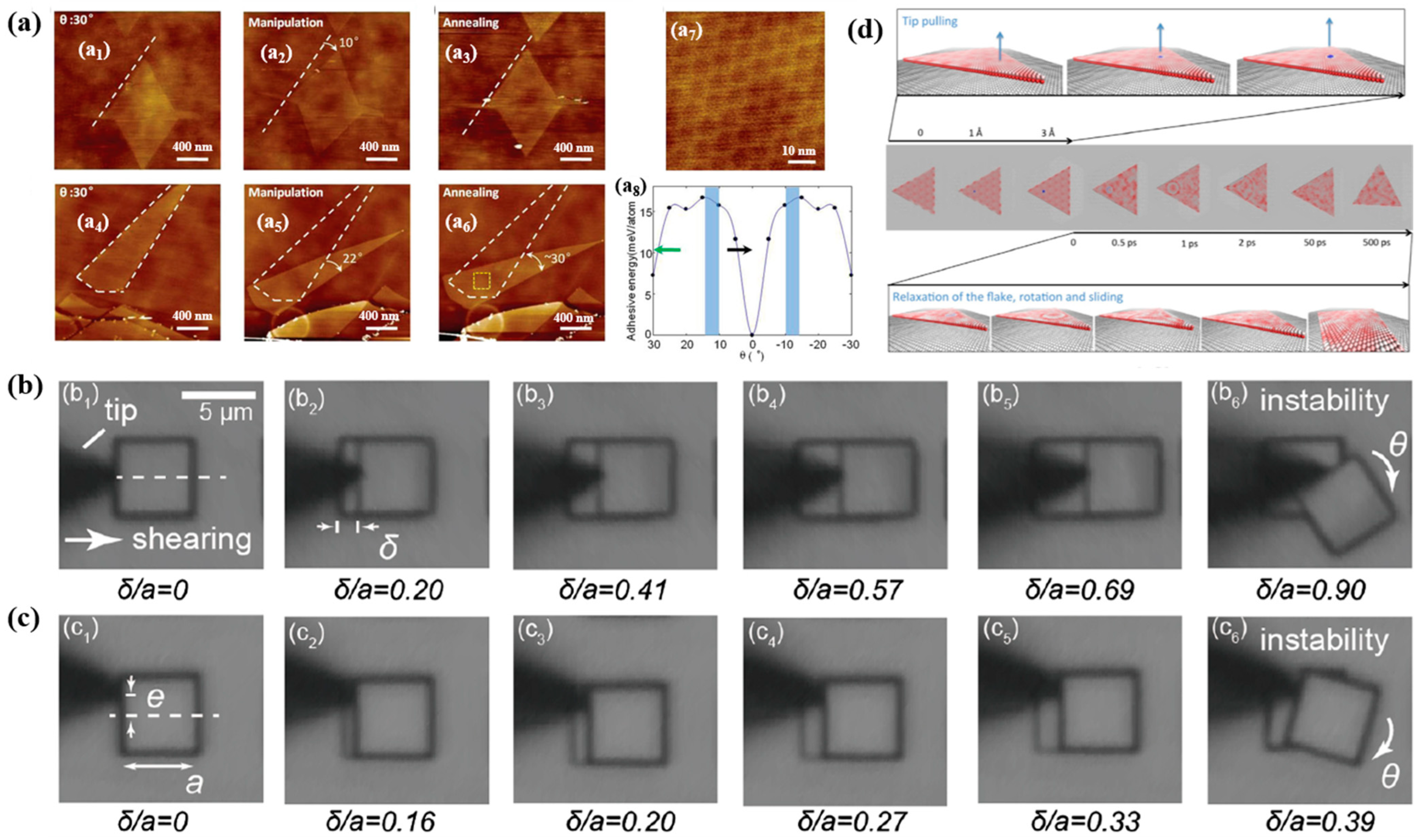
2.4. h-BN-Based 2D Materials
3. Mechanisms Affecting the Robust Structural Superlubricity
3.1. Methods of Microdynamic Simulation
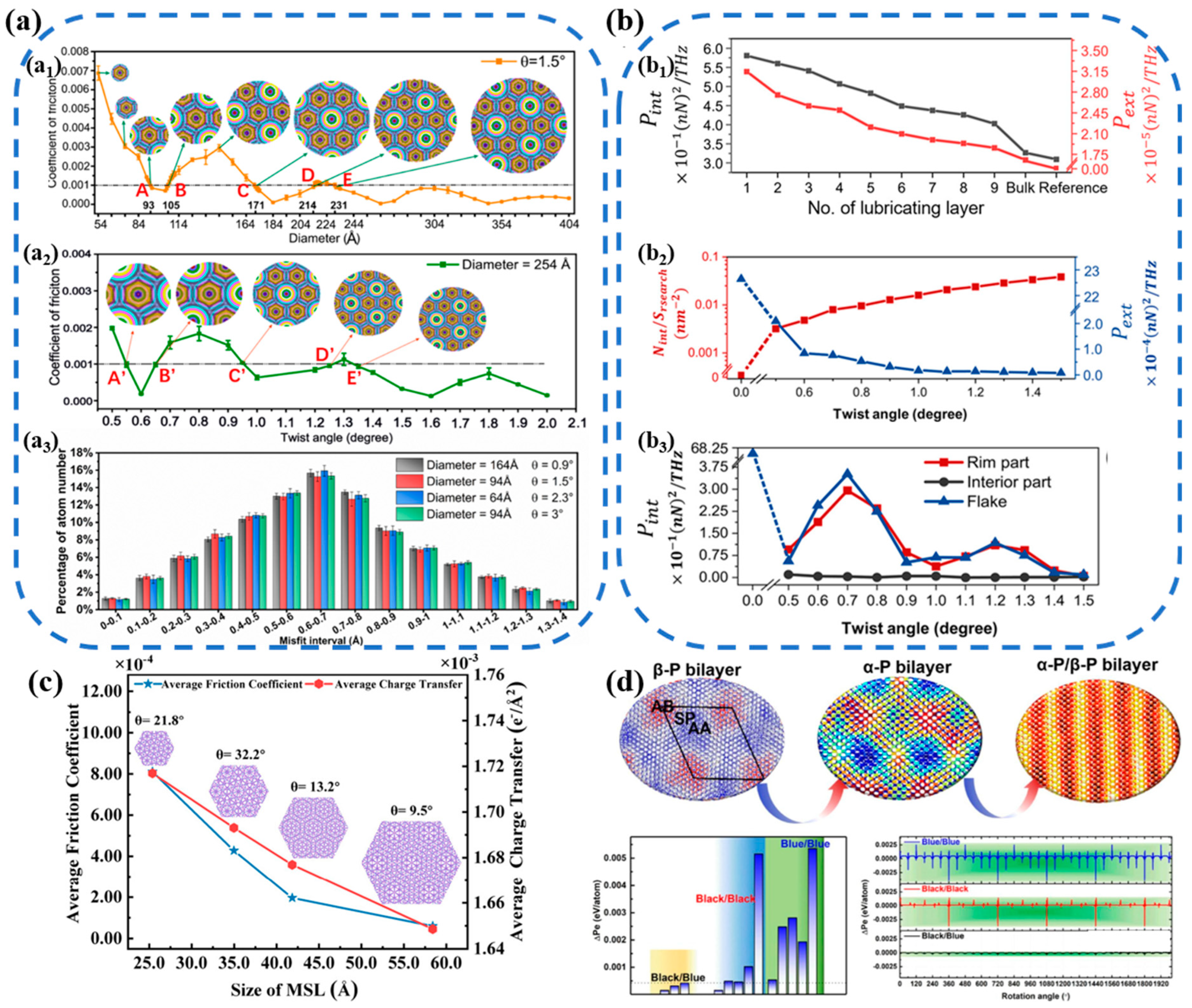
3.2. Size and Layer Effect
3.3. Elasticity Effect

3.4. Moiré Superlattice
3.5. Edge Effect
3.6. External Conditions
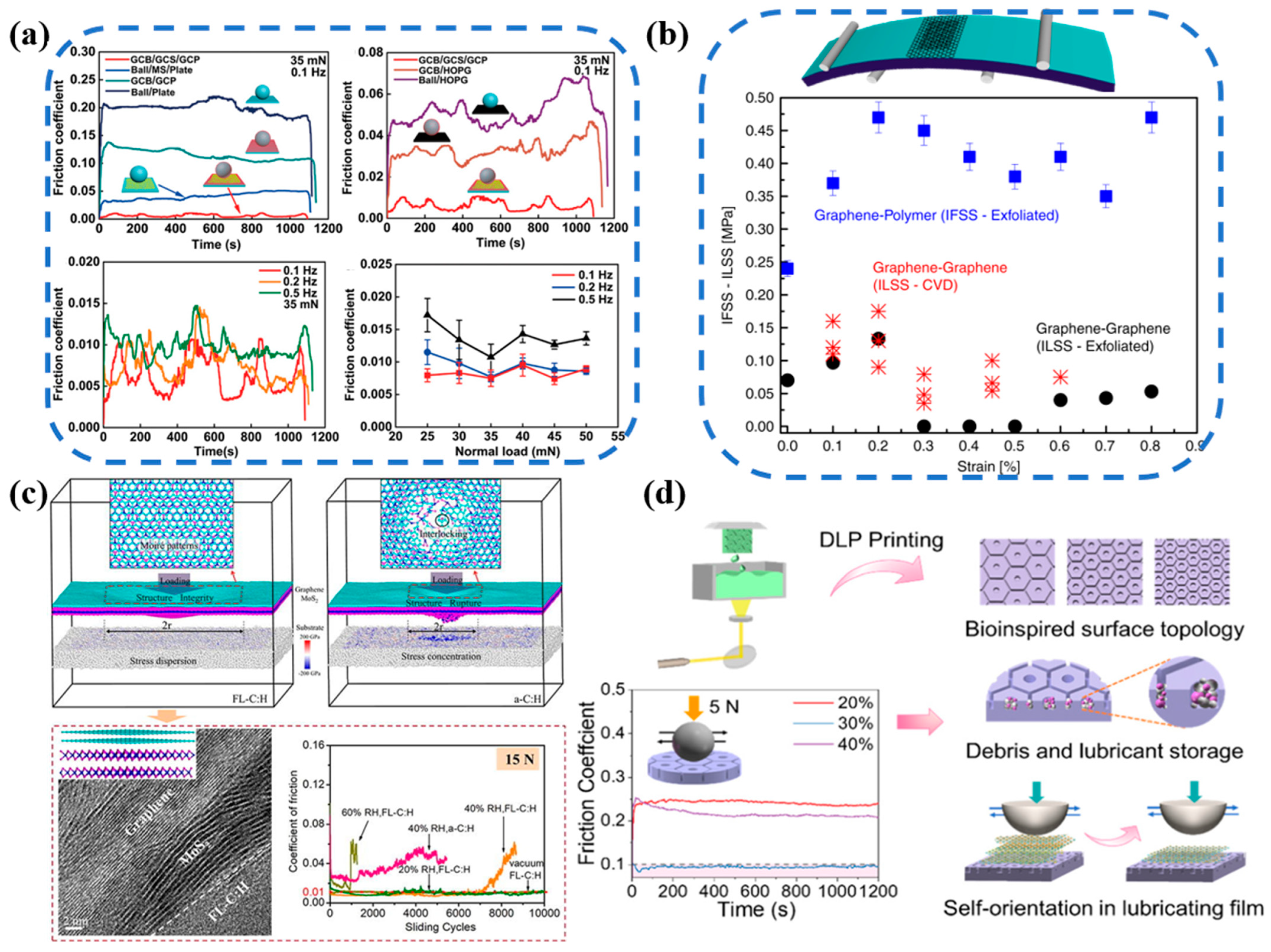
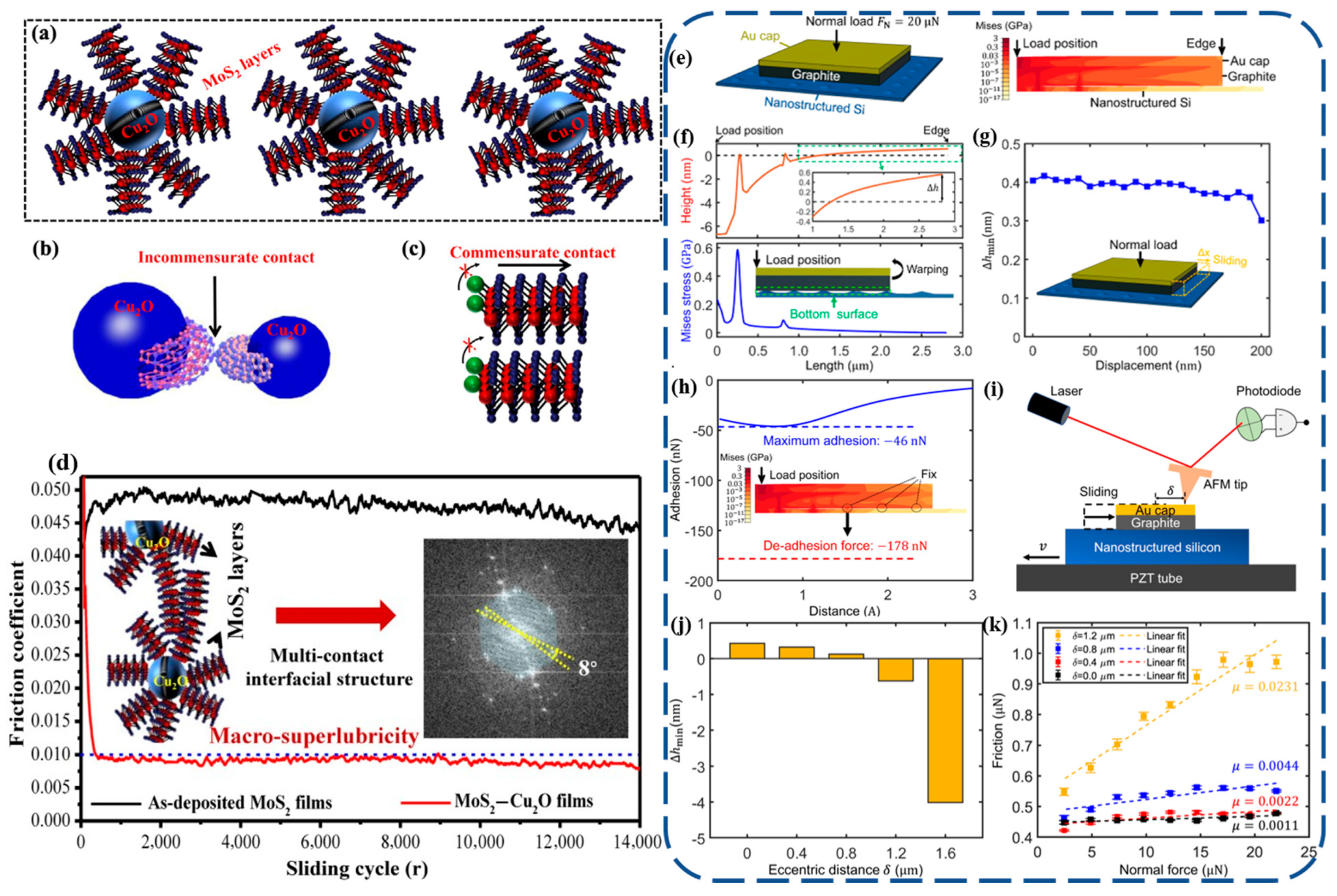
4. Progress in Macroscale Structural Superlubricity
5. Summary and Prospects
- Applying strain to a 2D material enhances its load-bearing capacity, modulates the shape of its moiré superlattice, and improves its environmental stability.
- Designing microsphere-shaped friction test probes coated with a 2D material enables the substrate to be covered with a coating or microspheres made from 2D materials. The objective was to achieve numerous point contacts, dividing the whole into a multitude of microscale contacts, which significantly increases the size of materials used for structural superlubricity, and achieves a span from nanometers to millimeters.
- Combination of various mechanisms and technologies. Preparation of 2D materials with fewer defects and higher stiffness with disproportionate contact conditions. Twisting and applying strain to regulate the moiré superlattice on the surface can minimize surface friction while enhancing environmental stability. Finally, edge friction should be suppressed by methods such as edge modification.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| MEMS | microelectromechanical systems |
| TMDs | transition metal dichalcogenides |
| AFM | atomic force microscopy |
| FFM | friction force microscopy |
| GDY | graphyne |
| MD | molecular dynamics |
| HOPGs | highly oriented pyrolytic graphites |
| COF | coefficient of friction |
| SPM | scanning probe microscopy |
| PES | potential energy surface |
| DFT | density functional theory |
| REBO | reactive empirical bond order |
| EAM | embedded atom method |
| SMD | smoothed molecular dynamics |
| tBLG | twisted bilayer graphene |
| SP | saddle point |
| 1L/BfL/SiC (0001) | epitaxial graphene layer/buffer layer/SiC (0001) |
| RMSDs | root-mean-square displacements |
| GCP | graphene-coated plate |
| GCS | graphene-coated microspheres |
| GCB | graphene-coated balls |
| ILSS | interlaminar shear stress |
| FL-C: H | fullerene-like carbon hydride |
| BSEG | ball-shearing exfoliated graphene |
| RH | relative humidity |
| English and Greek Alphabet | |
| stiffness coefficient | |
| period | |
| amplitude | |
| dimensionless parameter for identifying stick-slip motion | |
| θc | critical angle |
| γ | lattice mismatch angle orientation related to frictional anisotropy |
| friction stress in the moiré tile area | |
| D | contact size |
| Lm | the minimum moiré period |
| δ | the eccentric distance |
| LR2 | moiré period with a 2° twist angle |
| LR30 | moiré period with a 30° twist angle |
| moiré period | |
| m | mass of the top thin layer of graphene |
| ∆z | amplitude of the out-of-plane deformation |
| ∆x | the maximum half-width of the out-of-plane deformation |
| η | dissipation coefficient |
| v | sliding velocity |
References
- Han, T.; Zhang, S.; Zhang, C. Unlocking the Secrets behind Liquid Superlubricity: A State-of-the-Art Review on Phenomena and Mechanisms. Friction 2022, 10, 1137–1165. [Google Scholar] [CrossRef]
- Holmberg, K.; Erdemir, A. Influence of Tribology on Global Energy Consumption, Costs and Emissions. Friction 2017, 5, 263–284. [Google Scholar] [CrossRef]
- Zheng, Z.; Guo, Z.; Liu, W.; Luo, J. Low Friction of Superslippery and Superlubricity: A Review. Friction 2023, 11, 1121–1137. [Google Scholar] [CrossRef]
- Liu, H.; Yang, B.; Wang, C.; Han, Y.; Liu, D. The Mechanisms and Applications of Friction Energy Dissipation. Friction 2023, 11, 839–864. [Google Scholar] [CrossRef]
- Shinjo, K. Dynamics of Friction: Superlubric State. Surf. Sci. 1993, 283, 473–478. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, C.; Liao, N.; Zhang, M. A DFT Analysis on the Superlubricity Performance of Structural Superlubricity Micro/Nano-Component on Silicon-Based Surface. Tribol. Int. 2023, 189, 109005. [Google Scholar] [CrossRef]
- Luo, J.; Liu, M.; Ma, L. Origin of Friction and the New Frictionless Technology—Superlubricity: Advancements and Future Outlook. Nano Energy 2021, 86, 106092. [Google Scholar] [CrossRef]
- Khan, Z.H.; Kermany, A.R.; Öchsner, A.; Iacopi, F. Mechanical and Electromechanical Properties of Graphene and Their Potential Application in MEMS. J. Phys. Appl. Phys. 2017, 50, 053003. [Google Scholar] [CrossRef]
- Yu, Q.; Chen, X.; Zhang, C.; Luo, J. Influence Factors on Mechanisms of Superlubricity in DLC Films: A Review. Front. Mech. Eng. 2020, 6, 65. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, W.; Chen, X.; Qi, W.; Zhang, C.; Zhang, C.; Luo, J. The Effect of Roughness Level of α-C: H Films on Its Tribological Behaviors Rubbing against Steel and Self-Mated Materials. Tribol. Int. 2023, 187, 108754. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Y.; Zhang, J. Scaling up to Macroscale Superlubricity of Sp2-Dominated Structural Carbon Films: Graphene and Carbon Onion. Appl. Surf. Sci. 2023, 636, 157784. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, W. A Systematic Review of the Recent Advances in Superlubricity Research. Coatings 2023, 13, 1989. [Google Scholar] [CrossRef]
- Luo, J.; Zhou, X. Superlubricitive Engineering—Future Industry Nearly Getting Rid of Wear and Frictional Energy Consumption. Friction 2020, 8, 643–665. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y. Superlubricity Achieved with Two-Dimensional Nano-Additives to Liquid Lubricants. Friction 2020, 8, 1007–1024. [Google Scholar] [CrossRef]
- Peyrard, M.; Aubry, S. Critical Behaviour at the Transition by Breaking of Analyticity in the Discrete Frenkel-Kontorova Model. J. Phys. C Solid State Phys. 1983, 16, 1593. [Google Scholar] [CrossRef]
- Müser, M.H. Structural Lubricity: Role of Dimension and Symmetry. Europhys. Lett. 2004, 66, 97. [Google Scholar] [CrossRef]
- Dietzel, D.; Schwarz, U.D.; Schirmeisen, A. Nanotribological Studies Using Nanoparticle Manipulation: Principles and Application to Structural Lubricity. Friction 2014, 2, 114–139. [Google Scholar] [CrossRef]
- Zheng, Q.; Liu, Z. Experimental Advances in Superlubricity. Friction 2014, 2, 182–192. [Google Scholar] [CrossRef]
- Baykara, M.Z.; Vazirisereshk, M.R.; Martini, A. Emerging Superlubricity: A Review of the State of the Art and Perspectives on Future Research. Appl. Phys. Rev. 2018, 5, 041102. [Google Scholar] [CrossRef]
- Berman, D.; Erdemir, A.; Sumant, A.V. Approaches for Achieving Superlubricity in Two-Dimensional Materials. ACS Nano 2018, 12, 2122–2137. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, T.; Li, Z. Recent Advances of Two-Dimensional Lubricating Materials: From Tunable Tribological Properties to Applications. J. Mater. Chem. A 2023, 11, 9239–9269. [Google Scholar] [CrossRef]
- Wang, J.; Ma, M.; Tosatti, E. Kinetic Friction of Structurally Superlubric 2D Material Interfaces. J. Mech. Phys. Solids 2023, 180, 105396. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, F.; Yang, K.; Xiong, Y.; Tang, J.; Chen, H.; Duan, M.; Li, Z.; Zhang, H.; Xiong, B. Review of Two-Dimensional Nanomaterials in Tribology: Recent Developments, Challenges and Prospects. Adv. Colloid Interface Sci. 2023, 321, 103004. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Li, Z.; Klausen, L.H.; Li, Q.; Dong, M. Friction Behaviors of Two-Dimensional Materials at the Nanoscale. Mater. Today Phys. 2022, 27, 100771. [Google Scholar] [CrossRef]
- Hod, O.; Meyer, E.; Zheng, Q.; Urbakh, M. Structural Superlubricity and Ultralow Friction across the Length Scales. Nature 2018, 563, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Yang, R.; Zhang, G. Structural Superlubricity in 2D van Der Waals Heterojunctions. Nanotechnology 2022, 33, 102002. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Qin, H.; Zhang, S.; Li, Q.; Ouyang, W.; Liu, Y. The Origin of Moiré-Level Stick-Slip Behavior on Graphene/h-BN Heterostructures. Adv. Funct. Mater. 2022, 32, 2204209. [Google Scholar] [CrossRef]
- Mate, C.M.; McClelland, G.M.; Erlandsson, R.; Chiang, S. Atomic-Scale Friction of a Tungsten Tip on a Graphite Surface. Phys. Rev. Lett. 1987, 59, 1942–1945. [Google Scholar] [CrossRef] [PubMed]
- Belim, S.V.; Tikhomirov, I.V.; Bychkov, I.V. Simulation of Epitaxial Film–Substrate Interaction Potential. Coatings 2022, 12, 853. [Google Scholar] [CrossRef]
- Hirano, M.; Shinjo, K. Superlubricity and Frictional Anisotropy. Wear 1993, 168, 121–125. [Google Scholar] [CrossRef]
- Claerbout, V.E.P.; Polcar, T.; Nicolini, P. Superlubricity Achieved for Commensurate Sliding: MoS2 Frictional Anisotropy in Silico. Comput. Mater. Sci. 2019, 163, 17–23. [Google Scholar] [CrossRef]
- Levita, G.; Cavaleiro, A.; Molinari, E.; Polcar, T.; Righi, M.C. Sliding Properties of MoS2 Layers: Load and Interlayer Orientation Effects. J. Phys. Chem. C 2014, 118, 13809–13816. [Google Scholar] [CrossRef]
- Dienwiebel, M.; Verhoeven, G.S.; Pradeep, N.; Frenken, J.W.M.; Heimberg, J.A.; Zandbergen, H.W. Superlubricity of Graphite. Phys. Rev. Lett. 2004, 92, 126101. [Google Scholar] [CrossRef]
- Song, Y.; Qu, C.; Ma, M.; Zheng, Q. Structural Superlubricity Based on Crystalline Materials. Small 2020, 16, 1903018. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yang, J.; Grey, F.; Liu, J.Z.; Liu, Y.; Wang, Y.; Yang, Y.; Cheng, Y.; Zheng, Q. Observation of Microscale Superlubricity in Graphite. Phys. Rev. Lett. 2012, 108, 205503. [Google Scholar] [CrossRef]
- Konrad, J.; Gnecco, E.; Dietzel, D.; Schirmeisen, A. Anisotropy of Nanoscale Friction: Influence of Lattice Structure, Temperature, and Wear. Phys. Rev. B 2023, 107, 195438. [Google Scholar] [CrossRef]
- Wang, D.; Chen, G.; Li, C.; Cheng, M.; Yang, W.; Wu, S.; Xie, G.; Zhang, J.; Zhao, J.; Lu, X.; et al. Thermally Induced Graphene Rotation on Hexagonal Boron Nitride. Phys. Rev. Lett. 2016, 116, 126101. [Google Scholar] [CrossRef]
- Filippov, A.E.; Dienwiebel, M.; Frenken, J.W.M.; Klafter, J.; Urbakh, M. Torque and Twist against Superlubricity. Phys. Rev. Lett. 2008, 100, 046102. [Google Scholar] [CrossRef]
- Song, Y.; Mandelli, D.; Hod, O.; Urbakh, M.; Ma, M.; Zheng, Q. Robust Microscale Superlubricity in Graphite/Hexagonal Boron Nitride Layered Heterojunctions. Nat. Mater. 2018, 17, 894–899. [Google Scholar] [CrossRef]
- Kabengele, T.; Johnson, E.R. Theoretical Modeling of Structural Superlubricity in Rotated Bilayer Graphene, Hexagonal Boron Nitride, Molybdenum Disulfide, and Blue Phosphorene. Nanoscale 2021, 13, 14399–14407. [Google Scholar] [CrossRef]
- Ru, G.; Qi, W.; Wei, Y.; Tang, K.; Xue, T. Superlubricity in Bilayer Isomeric Tellurene and Graphene/Tellurene van Der Waals Heterostructures. Tribol. Int. 2021, 159, 106974. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, M.; Jin, L.; Li, L.; Mo, Y.; Su, G.; Li, X.; Zhu, H.; Tian, Y. Recent Advances in Friction and Lubrication of Graphene and Other 2D Materials: Mechanisms and Applications. Friction 2019, 7, 199–216. [Google Scholar] [CrossRef]
- Ruan, X.; Shi, J.; Wang, X.; Wang, W.Y.; Fan, X.; Zhou, F. Robust Superlubricity and Moiré Lattice’s Size Dependence on Friction between Graphdiyne Layers. ACS Appl. Mater. Interfaces 2021, 13, 40901–40908. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Miao, Y.; Li, Y.; Bai, H.; Ma, F. Unveiling the Moiré Pattern Evolution and Superlubricity in Twisted Bilayer 2D Phosphorene at Atomistic Scale. Appl. Surf. Sci. 2022, 606, 154796. [Google Scholar] [CrossRef]
- Ouyang, J.-H.; Li, Y.-F.; Zhang, Y.-Z.; Wang, Y.-M.; Wang, Y.-J. High-Temperature Solid Lubricants and Self-Lubricating Composites: A Critical Review. Lubricants 2022, 10, 177. [Google Scholar] [CrossRef]
- Chen, X.; Li, J. Superlubricity of Carbon Nanostructures. Carbon 2020, 158, 1–23. [Google Scholar] [CrossRef]
- Qu, C.; Shi, S.; Ma, M.; Zheng, Q. Rotational Instability in Superlubric Joints. Phys. Rev. Lett. 2019, 122, 246101. [Google Scholar] [CrossRef] [PubMed]
- Oyarzún-Aravena, A.M.; Gottschalk-Ojeda, C.; Moya-Barría, I.; Vallejos-Burgos, F. Edge Type Effect in the Gasification Mechanism of Graphene Clusters with H2O and/or CO2: Armchair vs. Zigzag. Carbon 2022, 193, 412–427. [Google Scholar] [CrossRef]
- Qu, C.; Wang, K.; Wang, J.; Gongyang, Y.; Carpick, R.W.; Urbakh, M.; Zheng, Q. Origin of Friction in Superlubric Graphite Contacts. Phys. Rev. Lett. 2020, 125, 126102. [Google Scholar] [CrossRef]
- Yan, W.; Bhuiyan, F.H.; Tang, C.; Wei, L.; Jiang, Y.; Jang, S.; Liu, Y.; Wu, J.; Wang, W.; Wang, Y.; et al. Understanding and Preventing Lubrication Failure at the Carbon Atomic Steps. Small 2023, 19, 2301515. [Google Scholar] [CrossRef]
- Gong, P.; Li, J.; Wang, J.; Wu, W.; Li, C.; Wang, D.; Shi, J.; Liu, J.; Zhou, F.; Liu, W. Controlled Growing of Graphdiyne Film for Friction Reduction and Antiwear. ACS Nano 2023, 17, 8252–8261. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Li, Y.; Liu, H.; Guo, Y.; Li, Y.; Zhu, D. Architecture of Graphdiyne Nanoscale Films. Chem. Commun. 2010, 46, 3256. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Cai, X.; Yi, S.; Chen, J.; Dai, Y.; Niu, C.; Guo, Z.; Xie, M.; Liu, F.; Cho, J.-H.; et al. Multivalency-Driven Formation of Te-Based Monolayer Materials: A Combined First-Principles and Experimental Study. Phys. Rev. Lett. 2017, 119, 106101. [Google Scholar] [CrossRef] [PubMed]
- Özoğul, A.; İpek, S.; Durgun, E.; Baykara, M.Z. Structural Superlubricity of Platinum on Graphite under Ambient Conditions: The Effects of Chemistry and Geometry. Appl. Phys. Lett. 2017, 111, 211602. [Google Scholar] [CrossRef]
- Dietzel, D.; Feldmann, M.; Schwarz, U.D.; Fuchs, H.; Schirmeisen, A. Scaling Laws of Structural Lubricity. Phys. Rev. Lett. 2013, 111, 235502. [Google Scholar] [CrossRef] [PubMed]
- Cihan, E.; İpek, S.; Durgun, E.; Baykara, M.Z. Structural Lubricity under Ambient Conditions. Nat. Commun. 2016, 7, 12055. [Google Scholar] [CrossRef] [PubMed]
- Kaul, A.B. Two-Dimensional Layered Materials: Structure, Properties, and Prospects for Device Applications. J. Mater. Res. 2014, 29, 348–361. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Gao, S.; Chen, Q.; Peng, L.; Liu, K.; Wei, X. Superlubricity between MoS2 Monolayers. Adv. Mater. 2017, 29, 1701474. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Ju, S.; Ji, L.; Liu, X.; Zhou, H.; Chen, J.; Zhao, X. Superlubricity of Molybdenum Disulfide Film. Surf. Sci. Technol. 2023, 1, 27. [Google Scholar] [CrossRef]
- Martin, J.M.; Pascal, H.; Donnet, C.; Le Mogne, T.; Loubet, J.L.; Epicier, T. Superlubricity of MoS2: Crystal Orientation Mechanisms. Surf. Coat. Technol. 1994, 68–69, 427–432. [Google Scholar] [CrossRef]
- Martin, J.M.; Donnet, C.; Le Mogne, T.; Epicier, T. Superlubricity of Molybdenum Disulphide. Phys. Rev. B 1993, 48, 10583–10586. [Google Scholar] [CrossRef] [PubMed]
- Dietzel, D.; Brndiar, J.; Štich, I.; Schirmeisen, A. Limitations of Structural Superlubricity: Chemical Bonds versus Contact Size. ACS Nano 2017, 11, 7642–7647. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Shi, J.; Liu, L.; Yu, P.; Xi, N.; Wang, Y. Experimental Study and Modeling of Atomic-Scale Friction in Zigzag and Armchair Lattice Orientations of MoS2. Sci. Technol. Adv. Mater. 2016, 17, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Meng, Z.; Tao, X.; Wang, Z. Superlubricity of Molybdenum Disulfide Subjected to Large Compressive Strains. Friction 2022, 10, 209–216. [Google Scholar] [CrossRef]
- Büch, H.; Rossi, A.; Forti, S.; Convertino, D.; Tozzini, V.; Coletti, C. Superlubricity of Epitaxial Monolayer WS2 on Graphene. Nano Res. 2018, 11, 5946–5956. [Google Scholar] [CrossRef]
- Li, P.; Yi Wang, W.; Zou, C.; Gao, X.; Wang, J.; Fan, X.; Song, H.; Li, J. Lattice Distortion Optimized Hybridization and Superlubricity of MoS2/MoSe2 Heterointerfaces via Moiré Patterns. Appl. Surf. Sci. 2023, 613, 155760. [Google Scholar] [CrossRef]
- Roy, S.; Zhang, X.; Puthirath, A.B.; Meiyazhagan, A.; Bhattacharyya, S.; Rahman, M.M.; Babu, G.; Susarla, S.; Saju, S.K.; Tran, M.K.; et al. Structure, Properties and Applications of Two-Dimensional Hexagonal Boron Nitride. Adv. Mater. 2021, 33, 2101589. [Google Scholar] [CrossRef]
- Leven, I.; Krepel, D.; Shemesh, O.; Hod, O. Robust Superlubricity in Graphene/h -BN Heterojunctions. J. Phys. Chem. Lett. 2013, 4, 115–120. [Google Scholar] [CrossRef]
- Liao, M.; Silva, A.; Du, L.; Nicolini, P.; Claerbout, V.E.P.; Kramer, D.; Yang, R.; Shi, D.; Polcar, T.; Zhang, G. Twisting Dynamics of Large Lattice-Mismatch van Der Waals Heterostructures. ACS Appl. Mater. Interfaces 2023, 15, 19616–19623. [Google Scholar] [CrossRef]
- Wang, K.; Qu, C.; Wang, J.; Quan, B.; Zheng, Q. Characterization of a Microscale Superlubric Graphite Interface. Phys. Rev. Lett. 2020, 125, 026101. [Google Scholar] [CrossRef]
- Koren, E.; Duerig, U. Moiré Scaling of the Sliding Force in Twisted Bilayer Graphene. Phys. Rev. B 2016, 94, 045401. [Google Scholar] [CrossRef]
- Minkin, A.S.; Lebedeva, I.V.; Popov, A.M.; Knizhnik, A.A. Atomic-Scale Defects Restricting Structural Superlubricity: Ab Initio Study Study on the Example of the Twisted Graphene Bilayer. Phys. Rev. B 2021, 104, 075444. [Google Scholar] [CrossRef]
- Liu, J.; Yang, X.; Fang, H.; Yan, W.; Ouyang, W.; Liu, Z. In Situ Twistronics: A New Platform Based on Superlubricity. Adv. Mater. 2023, 2305072. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Ma, M.; Song, Y.; He, Q.; Zheng, Q. Structural Superlubricity in Graphite Flakes Assembled under Ambient Conditions. Nanoscale 2018, 10, 14314–14320. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Li, T.; Wang, J.; Xia, K.; Tan, Z.; Peng, D.; Xiang, X.; Liu, B.; Ma, M.; Zheng, Q. Robust Microscale Structural Superlubricity between Graphite and Nanostructured Surface. Nat. Commun. 2023, 14, 2931. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Wang, J.; Jiang, H.; Zhao, S.; Wu, Z.; Tian, K.; Ma, M.; Zheng, Q. 100 Km Wear-Free Sliding Achieved by Microscale Superlubric Graphite/DLC Heterojunctions under Ambient Conditions. Natl. Sci. Rev. 2022, 9, nwab109. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Dong, Y.; Perez, D.; Martini, A.; Carpick, R.W. Speed Dependence of Atomic Stick-Slip Friction in Optimally Matched Experiments and Molecular Dynamics Simulations. Phys. Rev. Lett. 2011, 106, 126101. [Google Scholar] [CrossRef] [PubMed]
- Braun, O.M. Bridging the Gap Between the Atomic-Scale and Macroscopic Modeling of Friction. Tribol. Lett. 2010, 39, 283–293. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A Second-Generation Reactive Empirical Bond Order (REBO) Potential Energy Expression for Hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783–802. [Google Scholar] [CrossRef]
- Yan, S.; He, L. Adhesive Force between a Spherical Rigid Particle and an Incompressible Elastic Substrate. Mech. Mater. 2012, 49, 66–71. [Google Scholar] [CrossRef]
- Feng, S.; Xu, Z. Robustness of Structural Superlubricity beyond Rigid Models. Friction 2022, 10, 1382–1392. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Crespi, V.H. Registry-Dependent Interlayer Potential for Graphitic Systems. Phys. Rev. B 2005, 71, 235415. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Embedded-Atom Method: Derivation and Application to Impurities, Surfaces, and Other Defects in Metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef]
- Liao, M.; Nicolini, P.; Du, L.; Yuan, J.; Wang, S.; Yu, H.; Tang, J.; Cheng, P.; Watanabe, K.; Taniguchi, T.; et al. UItra-Low Friction and Edge-Pinning Effect in Large-Lattice-Mismatch van Der Waals Heterostructures. Nat. Mater. 2022, 21, 47–53. [Google Scholar] [CrossRef]
- Jiang, J.-W.; Park, H.S. A Gaussian Treatment for the Friction Issue of Lennard-Jones Potential in Layered Materials: Application to Friction between Graphene, MoS2, and Black Phosphorus. J. Appl. Phys. 2015, 117, 124304. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, L.; Liu, Y. Large-Scale Simulation of Graphene and Structural Superlubricity with Improved Smoothed Molecular Dynamics Method. Comput. Methods Appl. Mech. Eng. 2022, 392, 114644. [Google Scholar] [CrossRef]
- Gao, E.; Wu, B.; Wang, Y.; Jia, X.; Ouyang, W.; Liu, Z. Computational Prediction of Superlubric Layered Heterojunctions. ACS Appl. Mater. Interfaces 2021, 13, 33600–33608. [Google Scholar] [CrossRef]
- Losi, G.; Restuccia, P.; Righi, M.C. Superlubricity in Phosphorene Identified by Means of Ab Initio Calculations. 2D Mater. 2020, 7, 025033. [Google Scholar] [CrossRef]
- Cheng, Z.; Feng, H.; Sun, J.; Lu, Z.; He, Q.-C. Strain-Driven Superlubricity of Graphene/Graphene in Commensurate Contact. Adv. Mater. Interfaces 2023, 10, 2202062. [Google Scholar] [CrossRef]
- Liu, S.-W.; Wang, H.-P.; Xu, Q.; Ma, T.-B.; Yu, G.; Zhang, C.; Geng, D.; Yu, Z.; Zhang, S.; Wang, W.; et al. Robust Microscale Superlubricity under High Contact Pressure Enabled by Graphene-Coated Microsphere. Nat. Commun. 2017, 8, 14029. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Luo, J. Superlubricity of Graphite Sliding against Graphene Nanoflake under Ultrahigh Contact Pressure. Adv. Sci. 2018, 5, 1800810. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Chen, X.; Liu, Y.; Luo, J. Microscale Superlubricity at Multiple Gold–Graphite Heterointerfaces under Ambient Conditions. Carbon 2020, 161, 827–833. [Google Scholar] [CrossRef]
- Yan, W.; Ouyang, W.; Liu, Z. Origin of Frictional Scaling Law in Circular Twist Layered Interfaces: Simulations and Theory. J. Mech. Phys. Solids 2023, 170, 105114. [Google Scholar] [CrossRef]
- de Wijn, A.S. (In)Commensurability, Scaling, and Multiplicity of Friction in Nanocrystals and Application to Gold Nanocrystals on Graphite. Phys. Rev. B 2012, 86, 085429. [Google Scholar] [CrossRef]
- Wang, J.; Cao, W.; Song, Y.; Qu, C.; Zheng, Q.; Ma, M. Generalized Scaling Law of Structural Superlubricity. Nano Lett. 2019, 19, 7735–7741. [Google Scholar] [CrossRef] [PubMed]
- Bai, H.; Bao, H.; Li, Y.; Xu, H.; Li, S.; Ma, F. Moiré Pattern Based Universal Rules Governing Interfacial Superlubricity: A Case of Graphene. Carbon 2022, 191, 28–35. [Google Scholar] [CrossRef]
- Lee, C.; Li, Q.; Kalb, W.; Liu, X.-Z.; Berger, H.; Carpick, R.W.; Hone, J. Frictional Characteristics of Atomically Thin Sheets. Science 2010, 328, 76–80. [Google Scholar] [CrossRef]
- Chen, Y.; Guan, Z.; Liu, J.; Yang, W.; Wang, H. Anomalous Layer-Dependent Lubrication on Graphene-Covered Substrate: Competition between Adhesion and Plasticity. Appl. Surf. Sci. 2022, 598, 153762. [Google Scholar] [CrossRef]
- Morovati, V.; Xue, Z.; Liechti, K.M.; Huang, R. Interlayer Coupling and Strain Localization in Small-Twist-Angle Graphene Flakes. Extreme Mech. Lett. 2022, 55, 101829. [Google Scholar] [CrossRef]
- Bai, H.; Bao, H.; Li, Y.; Xu, H.; Li, S.; Ma, F. One-Dimensional Strain Solitons Manipulated Superlubricity on Graphene Interface. J. Phys. Chem. Lett. 2022, 13, 7261–7268. [Google Scholar] [CrossRef]
- Sharp, T.A.; Pastewka, L.; Robbins, M.O. Elasticity Limits Structural Superlubricity in Large Contacts. Phys. Rev. B 2016, 93, 121402. [Google Scholar] [CrossRef]
- Rejhon, M.; Lavini, F.; Khosravi, A.; Shestopalov, M.; Kunc, J.; Tosatti, E.; Riedo, E. Relation between Interfacial Shear and Friction Force in 2D Materials. Nat. Nanotechnol. 2022, 17, 1280–1287. [Google Scholar] [CrossRef] [PubMed]
- Monti, J.M.; Robbins, M.O. Sliding Friction of Amorphous Asperities on Crystalline Substrates: Scaling with Contact Radius and Substrate Thickness. ACS Nano 2020, 14, 16997–17003. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Kim, S.; Zhou, S.; Chiu, H.-C.; Nélias, D.; Berger, C.; de Heer, W.; Polloni, L.; Sordan, R.; Bongiorno, A.; et al. Elastic Coupling between Layers in Two-Dimensional Materials. Nat. Mater. 2015, 14, 714–720. [Google Scholar] [CrossRef]
- Yankowitz, M. Unravelling the Magic of Twisted Trilayer Graphene. Nat. Mater. 2023, 22, 286–287. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Shui, L.; Ouyang, W.; Liu, Z. Thermodynamic Model of Twisted Bilayer Graphene: Entropy Matters. J. Mech. Phys. Solids 2022, 167, 104972. [Google Scholar] [CrossRef]
- Liu, Z.; Vilhena, J.G.; Hinaut, A.; Scherb, S.; Luo, F.; Zhang, J.; Glatzel, T.; Gnecco, E.; Meyer, E. Moiré-Tile Manipulation-Induced Friction Switch of Graphene on a Platinum Surface. Nano Lett. 2023, 23, 4693–4697. [Google Scholar] [CrossRef]
- Bai, H.; Zou, G.; Bao, H.; Li, S.; Ma, F.; Gao, H. Deformation Coupled Moiré Mapping of Superlubricity in Graphene. ACS Nano 2023, 17, 12594–12602. [Google Scholar] [CrossRef]
- Song, Y.; Hinaut, A.; Scherb, S.; Pellmont, Y.; Pawlak, R.; Huang, S.; Liu, Z.; Glatzel, T.; Meyer, E. Observation of Robust Superlubricity of MoS2 on Au (111) in Ultrahigh Vacuum. Appl. Surf. Sci. 2022, 601, 154230. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, J.; Kong, D.; Shan, G.; Dou, K. Edge-Pinning Effect of Graphene Nanoflakes Sliding atop Graphene. Mater. Today Phys. 2023, 38, 101266. [Google Scholar] [CrossRef]
- Sun, S.; Ru, G.; Qi, W.; Liu, W. Molecular Dynamics Study of the Robust Superlubricity in Penta-Graphene van Der Waals Layered Structures. Tribol. Int. 2023, 177, 107988. [Google Scholar] [CrossRef]
- Kim, J.S.; Warner, J.H.; Robertson, A.W.; Kirkland, A.I. Formation of Klein Edge Doublets from Graphene Monolayers. ACS Nano 2015, 9, 8916–8922. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Kim, S.H. Measuring Nanoscale Friction at Graphene Step Edges. Friction 2020, 8, 802–811. [Google Scholar] [CrossRef]
- Levita, G.; Restuccia, P.; Righi, M. Graphene and MoS2 Interacting with Water: A Comparison by Ab Initio Calculations. Carbon 2016, 107, 878–884. [Google Scholar] [CrossRef]
- Dong, C.; Jiang, D.; Fu, Y.; Wang, D.; Wang, Q.; Weng, L.; Hu, M.; Gao, X.; Sun, J. Macro-Superlubricity in Sputtered MoS2-Based Films by Decreasing Edge Pinning Effect. Friction 2024, 12, 52–63. [Google Scholar] [CrossRef]
- Song, Y.; Gao, X.; Hinaut, A.; Scherb, S.; Huang, S.; Hod, O.; Urbakh, M.; Meyer, E. Velocity Dependence of Moiré Friction. Nano Lett. 2022, 22, 9529–9536. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.; Lu, Z.; Li, Q.; Xue, Q.; Du, S.; Pu, J.; Wang, L. Superlubricity Enabled by Pressure-Induced Friction Collapse. J. Phys. Chem. Lett. 2018, 9, 2554–2559. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; She, D.; Liu, Z.; Wang, X.; Zhong, L.; Wang, C.; Wang, G.; Mao, S.X. Atomistic Observation on Diffusion-Mediated Friction between Single-Asperity Contacts. Nat. Mater. 2022, 21, 173–180. [Google Scholar] [CrossRef]
- Wang, K. Structural Superlubricity with a Contaminant-Rich Interface. J. Mech. Phys. Solids 2022, 169, 105063. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, Y.; Huang, S.; Meng, F.; Chen, L.; Xie, W.; Chang, K.; Zhang, C.; Lu, Y.; Lin, C.; et al. Macroscale Superlubricity Enabled by Graphene-Coated Surfaces. Adv. Sci. 2020, 7, 1903239. [Google Scholar] [CrossRef]
- Li, P.; Ju, P.; Ji, L.; Li, H.; Liu, X.; Chen, L.; Zhou, H.; Chen, J. Toward Robust Macroscale Superlubricity on Engineering Steel Substrate. Adv. Mater. 2020, 32, 2002039. [Google Scholar] [CrossRef] [PubMed]
- Androulidakis, C.; Koukaras, E.N.; Paterakis, G.; Trakakis, G.; Galiotis, C. Tunable Macroscale Structural Superlubricity in Two-Layer Graphene via Strain Engineering. Nat. Commun. 2020, 11, 1595. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Ouyang, W.; Cao, W.; Ma, M.; Zheng, Q. Robust Superlubricity by Strain Engineering. Nanoscale 2019, 11, 2186–2193. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Sun, C.; Yang, X.; Wang, Y.; Gao, K.; Zhang, J.; Li, J. Toward High Load-Bearing, Ambient Robust and Macroscale Structural Superlubricity through Contact Stress Dispersion. Chem. Eng. J. 2022, 431, 133548. [Google Scholar] [CrossRef]
- Yang, X.; Li, R.; Wang, Y.; Zhang, J. Tunable, Wide-Temperature, and Macroscale Superlubricity Enabled by Nanoscale Van Der Waals Heterojunction-to-Homojunction Transformation. Adv. Mater. 2023, 35, 2303580. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.; Chai, Z.; Shi, Q.; Liu, Y.; Wang, W. Graphene Superlubricity: A Review. Friction 2023, 11, 1953–1973. [Google Scholar] [CrossRef]
- Yuan, W.; Yao, Y.; Keer, L.; Jiao, Y.; Yu, J.; Li, Q.; Feng, X.-Q. 3D-Printed Biomimetic Surface Structures with Abnormal Friction Properties. Extreme Mech. Lett. 2019, 26, 46–52. [Google Scholar]
- Zhao, Y.; Mei, H.; Chang, P.; Chen, C.; Cheng, L.; Dassios, K.G. Infinite Approaching Superlubricity by Three-Dimensional Printed Structures. ACS Nano 2021, 15, 240–257. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Mei, H.; Chang, P.; Yang, Y.; Huang, W.; Liu, Y.; Cheng, L.; Zhang, L. 3D-Printed Topological MoS2/MoSe2 Heterostructures for Macroscale Superlubricity. ACS Appl. Mater. Interfaces 2021, 13, 34984–34995. [Google Scholar] [CrossRef]
- Zhai, W.; Zhou, K. Nanomaterials in Superlubricity. Adv. Funct. Mater. 2019, 29, 1806395. [Google Scholar] [CrossRef]
- Yuan, S.; Chen, X.; Zhang, C. Reducing Friction by Control of Isoelectric Point: A Potential Method to Design Artificial Cartilage. Adv. Mater. Interfaces 2020, 7, 2000485. [Google Scholar] [CrossRef]



| Factors | Mechanisms | Methods to Sustain Robust Superlubricity |
|---|---|---|
| Size Effects | scaling law/generalized scaling law [55,95] | the scaling law should remain sublinear (0 < < 0.5) [55] |
| Elasticity Effects | localized strain soliton [81,99,100] | select 2D materials with high stiffness [102] |
| Stiffness affecting superlubricity [102] | ||
| Moiré Superlattice | different sizes and shapes control friction [96] | control the shape by twisting and applying strain [44,96,106,107] |
| Edge Effect (contact size D < 10 μm) | interactions among edge atoms [84,113,114] | edge modification, or modulation by external conditions [114,115] |
| Normal Load | superlubric state (The formation of sublayers) [118] nonsuperlubric state (critical load Fc without sublayers) [107] | control variables to obtain the most stable parameters for superlubricity [106,107,116]. |
| Sliding Velocity | friction increases as speed and load increase (up to Vc) [116] | |
| Temperature | moiré fluctuations (<Tc) and thermal bending fluctuations (>Tc) [22] |
| Methods | Examples | Relevant Performance |
|---|---|---|
| strain engineering in surface materials | epitaxial bilayered graphene [122] | ILSS: 0.13 MPa [122] |
| combination of multiple microcontact points | GCP/GCS/GCB composite system [120] | COF: 0.006 [120] |
| strain + multiple contact points + heterostructure | graphene/MoS2/fullerene-like carbon hydride (FL-C: H) ternary composite systems [124] | COF: 0.007 [124] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.-B.; Zhou, S.-J.; Ouyang, J.-H.; Wang, S.-Q.; Chen, L. Structural Superlubricity of Two-Dimensional Materials: Mechanisms, Properties, Influencing Factors, and Applications. Lubricants 2024, 12, 138. https://doi.org/10.3390/lubricants12040138
Wu F-B, Zhou S-J, Ouyang J-H, Wang S-Q, Chen L. Structural Superlubricity of Two-Dimensional Materials: Mechanisms, Properties, Influencing Factors, and Applications. Lubricants. 2024; 12(4):138. https://doi.org/10.3390/lubricants12040138
Chicago/Turabian StyleWu, Fan-Bin, Sheng-Jian Zhou, Jia-Hu Ouyang, Shu-Qi Wang, and Lei Chen. 2024. "Structural Superlubricity of Two-Dimensional Materials: Mechanisms, Properties, Influencing Factors, and Applications" Lubricants 12, no. 4: 138. https://doi.org/10.3390/lubricants12040138
APA StyleWu, F.-B., Zhou, S.-J., Ouyang, J.-H., Wang, S.-Q., & Chen, L. (2024). Structural Superlubricity of Two-Dimensional Materials: Mechanisms, Properties, Influencing Factors, and Applications. Lubricants, 12(4), 138. https://doi.org/10.3390/lubricants12040138