Driving Water through Sub-2-Nanometer Carbon Nanotubes
Abstract
1. Introduction
2. Simulation Methods
3. Results and Discussions
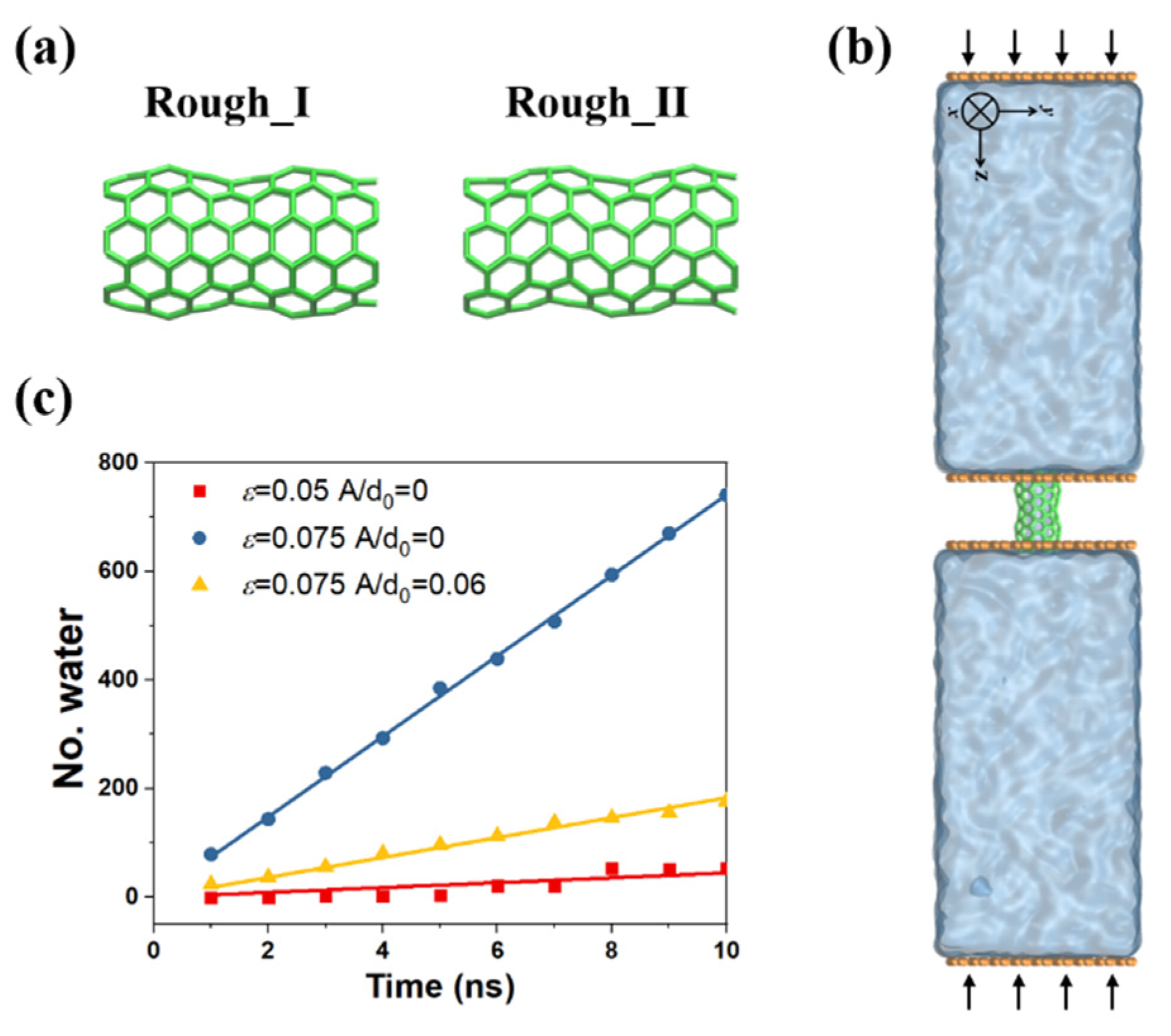
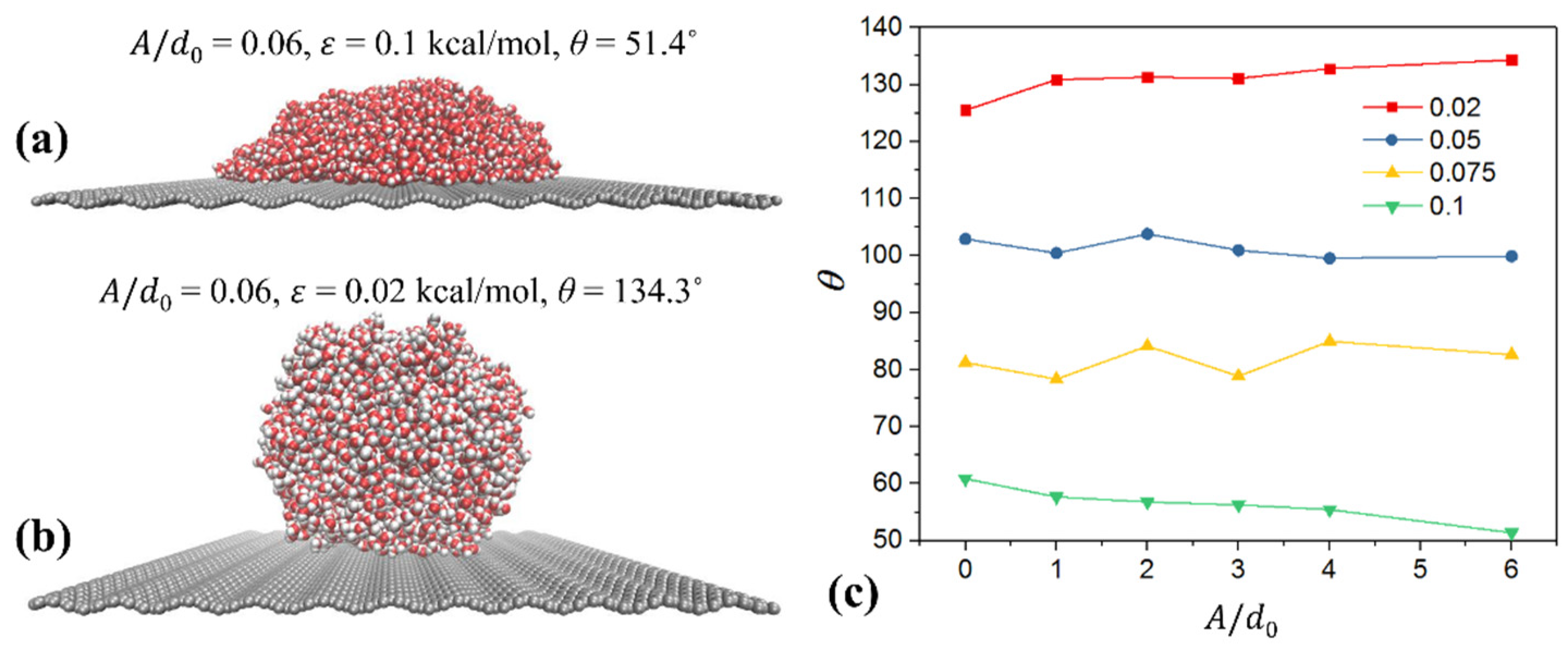
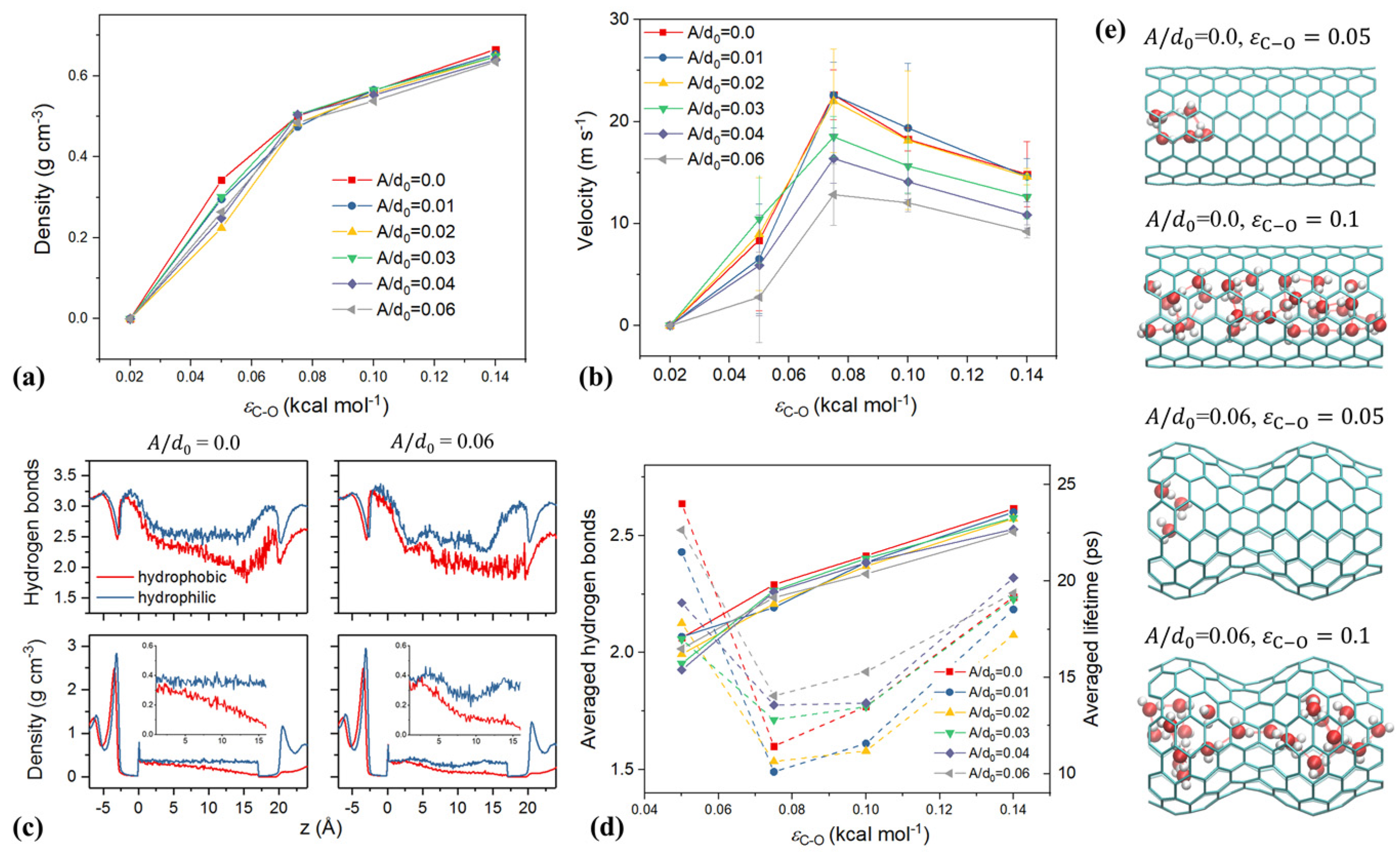
Coupling Effect of Tube Roughness and Wettability
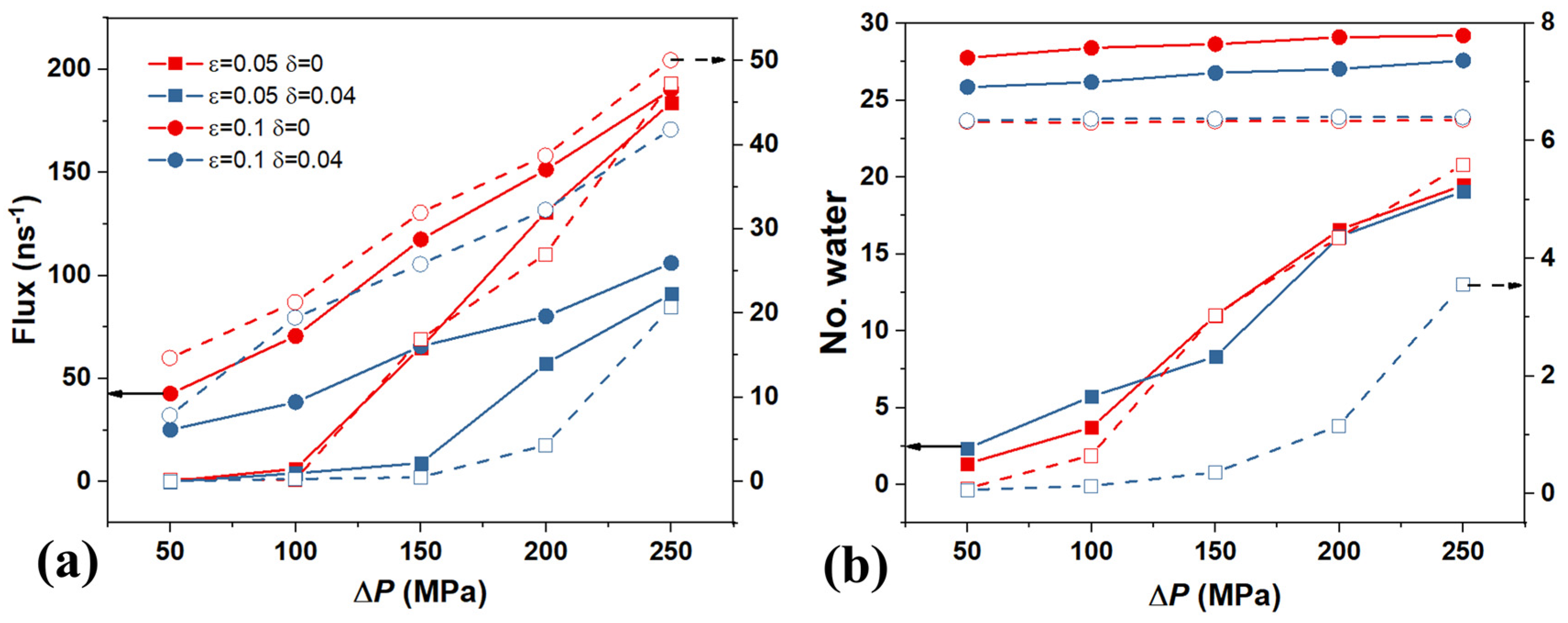
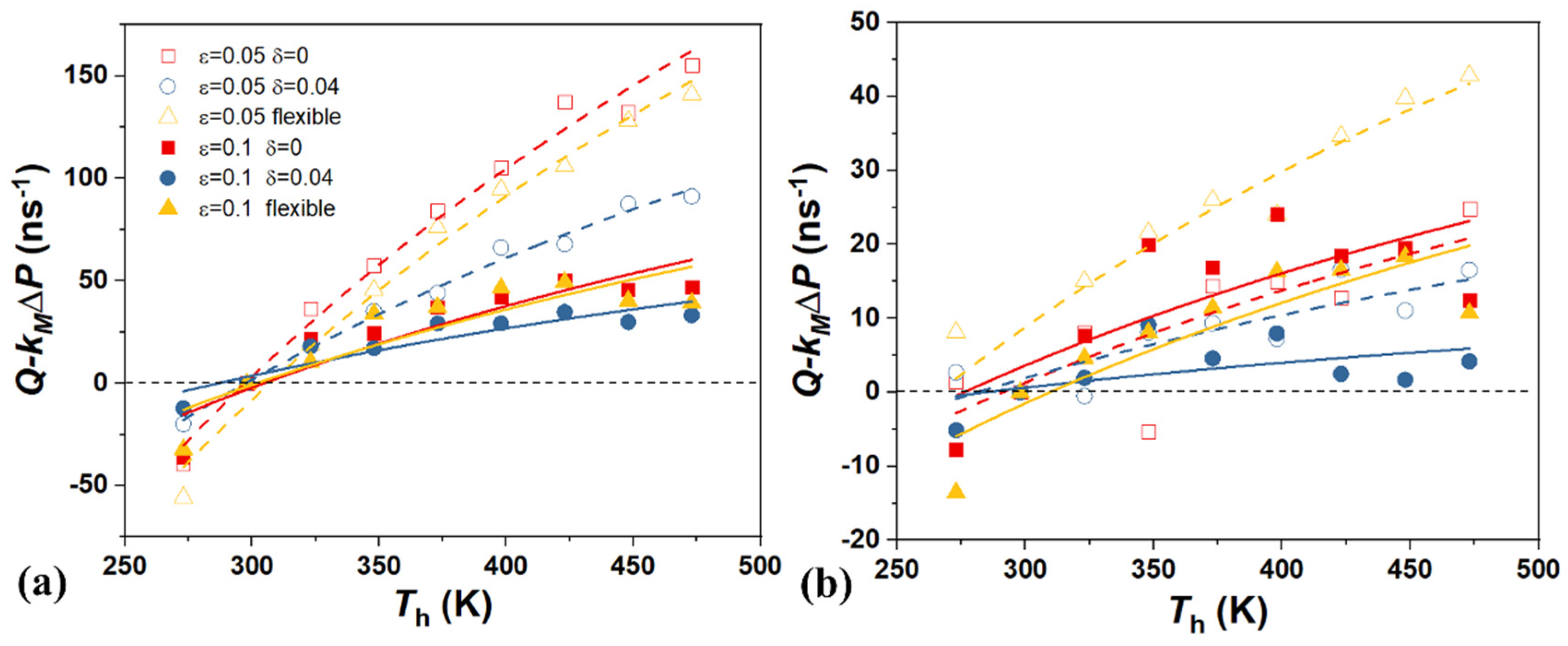
4. The Effect of Driving Force
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, J.B.; Lu, X.C.; Wen, S.Z. Developments and unsolved problems in nano-lubrication. Prog. Nat. Sci. 2001, 11, 173. [Google Scholar]
- Raviv, U.; Klein, J. Fluidity of bound hydration layers. Science 2002, 297, 1540. [Google Scholar] [CrossRef] [PubMed]
- Klein, J. Hydration lubrication. Friction 2013, 1, 1. [Google Scholar] [CrossRef]
- Li, J.; Cao, W.; Li, J.; Ma, M.; Luo, J. Molecular Origin of superlubricity between graphene and a highly hydrophobic surface in water. J. Phys. Chem. Lett. 2019, 10, 2978. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Cao, W.; Wang, Z.; Ma, M.; Luo, J. Origin of hydration lubrication of zwitterions on graphene. Nanoscale 2018, 10, 16887. [Google Scholar] [CrossRef] [PubMed]
- Algara-Siller, G.; Lehtinen, O.; Wang, F.C.; Nair, R.R.; Kaiser, U.; Wu, H.A.; Geim, A.K.; Grigorieva, I.V. Square ice in graphene nanocapillaries. Nature 2015, 519, 443. [Google Scholar] [CrossRef] [PubMed]
- Fumagalli, L.; Esfandiar, A.; Fabregas, R.; Hu, S.; Ares, P.; Janardanan, A.; Yang, Q.; Radha, B.; Taniguchi, T.; Watanabe, K.; et al. Anomalously low dielectric constant of confined water. Science 2018, 360, 1339. [Google Scholar] [CrossRef] [PubMed]
- Hummer, G.; Rasaiah, J.C.; Noworyta, J.P. Water conduction through the hydrophobic channel of a carbon nanotube. Nature 2001, 414, 188. [Google Scholar] [CrossRef] [PubMed]
- Hinds, B.J.; Chopra, N.; Rantell, T.; Andrews, R.; Gavalas, V.; Bachas, L.G. Aligned multiwalled carbon nanotube membranes. Science 2004, 303, 62. [Google Scholar] [CrossRef]
- Naguib, N.; Ye, H.; Gogotsi, Y.; Yazicioglu, A.G.; Megaridis, C.M.; Yoshimura, M. Observation of water confined in nanometer channels of closed carbon nanotubes. Nano Lett. 2004, 4, 2237. [Google Scholar] [CrossRef]
- Holt, J.K.; Park, H.G.; Wang, Y.M.; Stadermann, M.; Artyukhin, A.B.; Grigoropoulos, C.P.; Noy, A.; Bakajin, O. Fast mass transport through sub-2-nanometer carbon nanotubes. Science 2006, 312, 1034. [Google Scholar] [CrossRef] [PubMed]
- Whitby, M.; Quirke, N. Fluid flow in carbon nanotubes and nanopipes. Nat. Nanotechnol. 2007, 2, 87. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Yuan, Q.; Zhao, Y.; Xie, S.; Liu, Z. Measurement of the rate of water translocation through carbon nanotubes. Nano Lett. 2011, 11, 2173. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Grey, F.; Shen, L.; Urbakh, M.; Wu, S.; Liu, J.Z.; Liu, Y.; Zheng, Q. Water transport inside carbon nanotubes mediated by phonon-induced oscillating friction. Nat. Nanotechnol. 2015, 10, 692. [Google Scholar] [CrossRef] [PubMed]
- Secchi, E.; Marbach, S.; Nigues, A.; Stein, D.; Siria, A.; Bocquet, L. Massive radius-dependent flow slippage in carbon nanotubes. Nature 2016, 537, 210. [Google Scholar] [CrossRef] [PubMed]
- Tunuguntla, R.H.; Henley, R.Y.; Yao, Y.-C.; Anh, P.T.; Wanunu, M.; Noy, A. Enhanced water permeability and tunable ion selectivity in subnanometer carbon nanotube porins. Science 2017, 357, 792. [Google Scholar] [CrossRef] [PubMed]
- Min, H.; Kim, Y.-T.; Lee, C.Y. Experimental measurements in single-nanotube fluidic channels. MRS Bull. 2017, 42, 300. [Google Scholar] [CrossRef]
- Faucher, S.; Aluru, N.; Bazant, M.Z.; Blankschtein, D.; Brozena, A.H.; Cumings, J.; Pedro de Souza, J.; Elimelech, M.; Epsztein, R.; Fourkas, J.T.; et al. Critical knowledge gaps in mass transport through single-digit nanopores: A review and perspective. J. Phys. Chem. C 2019, 123, 21309. [Google Scholar] [CrossRef]
- Aluru, N.R.; Aydin, F.; Bazant, M.Z.; Blankschtein, D.; Brozena, A.H.; de Souza, J.P.; Elimelech, M.; Faucher, S.; Fourkas, J.T.; Koman, V.B.; et al. Fluids and electrolytes under confinement in single-digit nanopores. Chem. Rev. 2023, 123, 2737. [Google Scholar] [CrossRef] [PubMed]
- Emmerich, T.; Vasu, K.S.; Nigues, A.; Keerthi, A.; Radha, B.; Siria, A.; Bocquet, L. Enhanced nanofluidic transport in activated carbon nanoconduits. Nat. Mater. 2022, 21, 696. [Google Scholar] [CrossRef]
- Falk, K.; Sedlmeier, F.; Joly, L.; Netz, R.R.; Bocquet, L. Molecular origin of fast water transport in carbon nanotube membranes: Superlubricity versus curvature dependent friction. Nano Lett. 2010, 10, 4067. [Google Scholar] [CrossRef]
- Xiong, W.; Liu, J.Z.; Ma, M.; Xu, Z.; Sheridan, J.; Zheng, Q. Strain engineering water transport in graphene nanochannels. Phys. Rev. E 2011, 84, 056329. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.D.; Shen, L.; Sheridan, J.; Liu, J.Z.; Chen, C.; Zheng, Q. Friction of water slipping in carbon nanotubes. Phys. Rev. E 2011, 83, 036316. [Google Scholar] [CrossRef] [PubMed]
- Thiemann, F.L.; Schran, C.; Rowe, P.; Muller, E.A.; Michaelides, A. Water flow in single-wall nanotubes: Oxygen makes it slip, hydrogen makes it stick. ACS Nano 2022, 16, 10775. [Google Scholar] [CrossRef]
- Kannam, S.K.; Daivis, P.J.; Todd, B.D. Modeling slip and flow enhancement of water in carbon nanotubes. MRS Bull. 2017, 42, 283. [Google Scholar] [CrossRef]
- Sam, A.; Hartkamp, R.; Kumar Kannam, S.; Babu, J.S.; Sathian, S.P.; Daivis, P.J.; Todd, B.D. Fast transport of water in carbon nanotubes: A review of current accomplishments and challenges. Mol. Simulat. 2020, 47, 905. [Google Scholar] [CrossRef]
- Kavokine, N.; Bocquet, M.L.; Bocquet, L. Fluctuation-induced quantum friction in nanoscale water flows. Nature 2022, 602, 84. [Google Scholar] [CrossRef] [PubMed]
- Sendner, C.; Horinek, D.; Bocquet, L.; Netz, R.R. Interfacial water at hydrophobic and hydrophilic surfaces: Slip, viscosity, and diffusion. Langmuir 2009, 25, 10768. [Google Scholar] [CrossRef]
- Calabro, F. Modeling the effects of material chemistry on water flow enhancement in nanotube membranes. MRS Bull. 2017, 42, 289. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability effect on nanoconfined water flow. Proc. Natl. Acad. Sci. USA 2017, 114, 3358. [Google Scholar] [CrossRef]
- Tao, J.; Song, X.; Zhao, T.; Zhao, S.; Liu, H. Confinement effect on water transport in CNT membranes. Chem. Eng. Sci. 2018, 192, 1252. [Google Scholar] [CrossRef]
- Melillo, M.; Zhu, F.; Snyder, M.A.; Mittal, J. Water transport through nanotubes with varying interaction strength between tube wall and water. J. Phys. Chem. Lett. 2011, 2, 2978. [Google Scholar] [CrossRef] [PubMed]
- Gravelle, S.; Joly, L.; Detcheverry, F.; Ybert, C.; Cottin-Bizonne, C.; Bocquet, L. Optimizing water permeability through the hourglass shape of aquaporins. Proc. Natl. Acad. Sci. USA 2013, 110, 16367. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Li, Y.; Park, T.; Chen, X. Effect of wall roughness on fluid transport resistance in nanopores. J. Chem. Phys. 2011, 135, 144703. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Huang, L.L.; Ma, M.; Lu, L.H.; Lu, X.H. Water in narrow carbon nanotubes: Roughness promoted diffusion transition. J. Phys. Chem. C 2018, 122, 19124. [Google Scholar] [CrossRef]
- Thomas, J.A.; McGaughey, A.J.H. Water flow in carbon nanotubes: Transition to subcontinuum transport. Phys. Rev. Lett. 2009, 102, 184502. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1. [Google Scholar] [CrossRef]
- Park, S.; Srivastava, D.; Cho, K. Generalized chemical reactivity of curved surfaces: Carbon nanotubes. Nano Lett. 2003, 3, 1273. [Google Scholar] [CrossRef]
- Song, X.; Liu, S.; Yan, H.; Gan, Z. First-principles study on effects of mechanical deformation on outer surface reactivity of carbon nanotubes. Phys. E Low-Dimens. Syst. Nanostruct. 2009, 41, 626. [Google Scholar] [CrossRef]
- Celebi, A.T.; Nguyen, C.T.; Hartkamp, R.; Beskok, A. The role of water models on the prediction of slip length of water in graphene nanochannels. J. Chem. Phys. 2019, 151, 174705. [Google Scholar] [CrossRef]
- Sam, A.; Kannam, S.K.; Hartkamp, R.; Sathian, S.P. Water flow in carbon nanotubes: The effect of tube flexibility and thermostat. J. Chem. Phys. 2017, 146, 234701. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.Y.; Gao, Y.R.; Chen, X.Y.; Zeng, X.C.; Francisco, J.S.; Zhu, C.Q. Anomalous water transport in narrow-diameter carbon nanotubes. Proc. Natl. Acad. Sci. USA 2022, 119, e2211348119. [Google Scholar] [CrossRef] [PubMed]
- Qu, C.Y.; Cao, W.; Liu, B.T.; Wang, A.L.; Xie, F.K.; Ma, M.; Shan, W.Z.; Urbakh, M.; Zheng, Q.S. Direct Measurement of Adhesions of Liquids on Graphite. J. Phys. Chem. C 2019, 123, 11671. [Google Scholar] [CrossRef]
- Detcheverry, F.; Bocquet, L. Thermal fluctuations in nanofluidic transport. Phys. Rev. Lett. 2012, 109, 024501. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.M.; Sendner, C.; Horinek, D.; Netz, R.R.; Bocquet, L. Water slippage versus contact angle: A quasiuniversal relationship. Phys. Rev. Lett. 2008, 101, 226101. [Google Scholar] [CrossRef]
- Fu, L.; Merabia, S.; Joly, L. What controls thermo-osmosis? Molecular simulations show the critical role of interfacial hydrodynamics. Phys. Rev. Lett. 2017, 119, 214501. [Google Scholar] [CrossRef] [PubMed]
- Barragan, V.M.; Kjelstrup, S. Thermo-osmosis in membrane systems: A review. J. Non-Equilib. Thermodyn. 2017, 42, 217. [Google Scholar] [CrossRef]
- Xu, S.; Hutchinson, A.J.; Taheri, M.; Corry, B.; Torres, J.F. Thermodiffusive desalination. Nat. Commun. 2024, 15, 2996. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Merabia, S.; Joly, L. Understanding fast and robust thermo-osmotic flows through carbon nanotube membranes: Thermodynamics meets hydrodynamics. J. Phys. Chem. Lett. 2018, 9, 2086. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897. [Google Scholar] [CrossRef]
- Zhao, K.; Wu, H. Fast Water Thermo-pumping Flow Across Nanotube Membranes for Desalination. Nano Lett. 2015, 15, 3664. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Cao, W. Driving Water through Sub-2-Nanometer Carbon Nanotubes. Lubricants 2024, 12, 220. https://doi.org/10.3390/lubricants12060220
Liu J, Cao W. Driving Water through Sub-2-Nanometer Carbon Nanotubes. Lubricants. 2024; 12(6):220. https://doi.org/10.3390/lubricants12060220
Chicago/Turabian StyleLiu, Jian, and Wei Cao. 2024. "Driving Water through Sub-2-Nanometer Carbon Nanotubes" Lubricants 12, no. 6: 220. https://doi.org/10.3390/lubricants12060220
APA StyleLiu, J., & Cao, W. (2024). Driving Water through Sub-2-Nanometer Carbon Nanotubes. Lubricants, 12(6), 220. https://doi.org/10.3390/lubricants12060220





