Research on Design and Optimization of Micro-Hole Aerostatic Bearing in Vacuum Environment
Abstract
1. Introduction
2. Theory and Methods
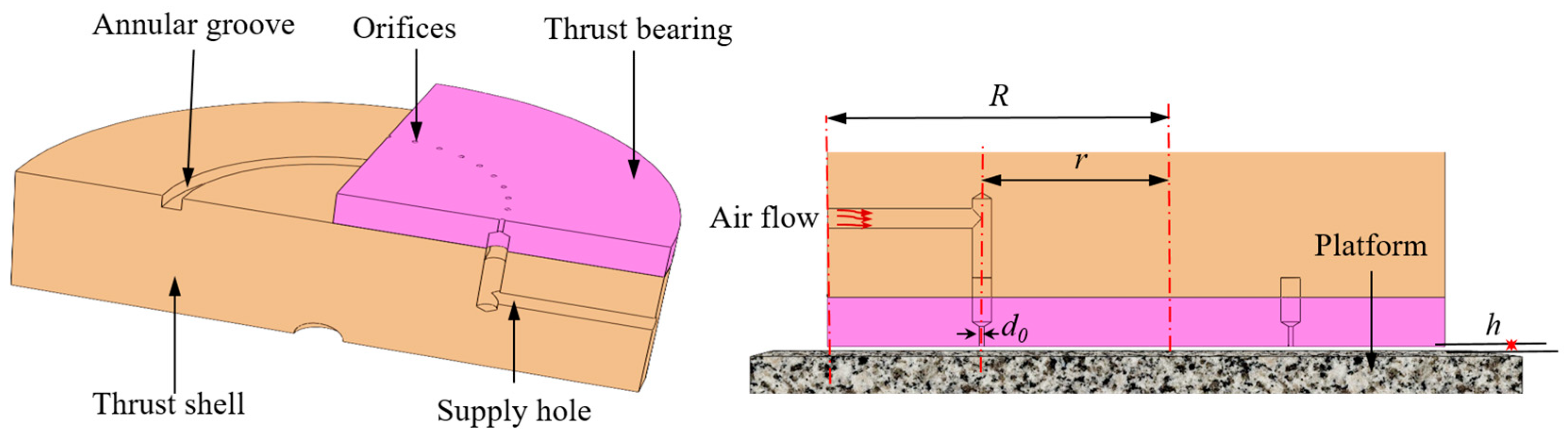
2.1. Structure of Air Bearing
2.2. Theory Model
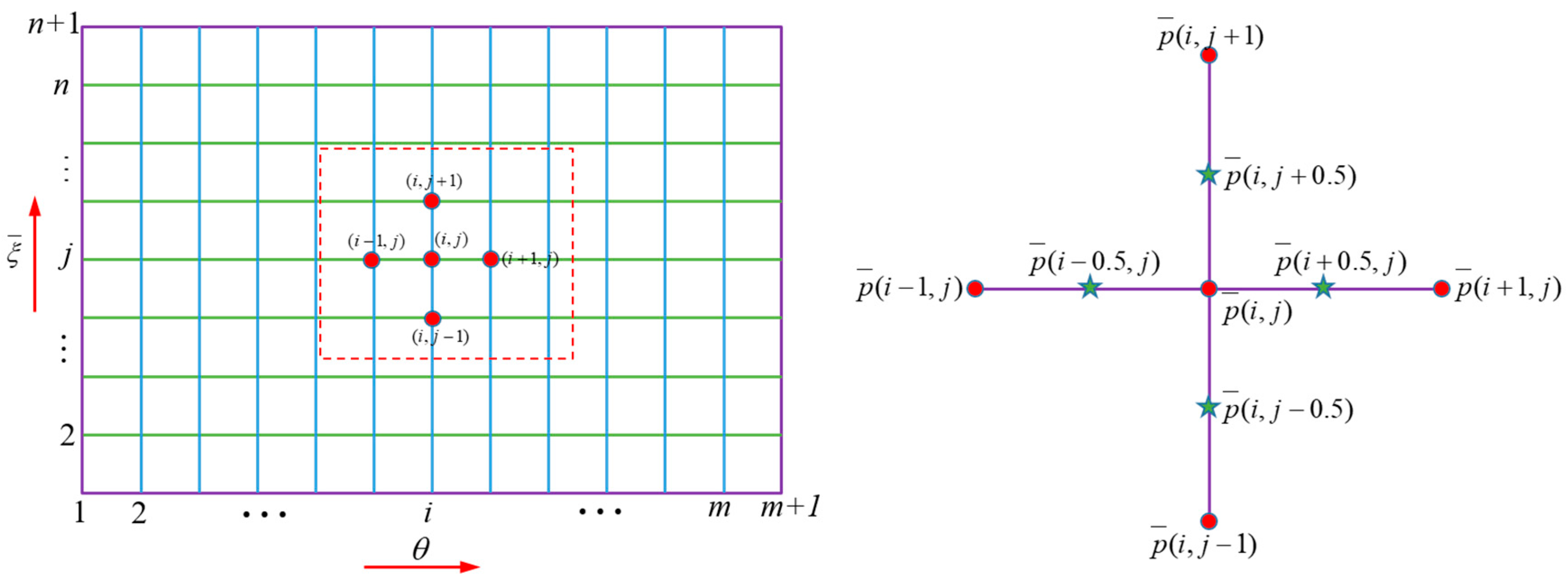
2.3. Solution Algorithm
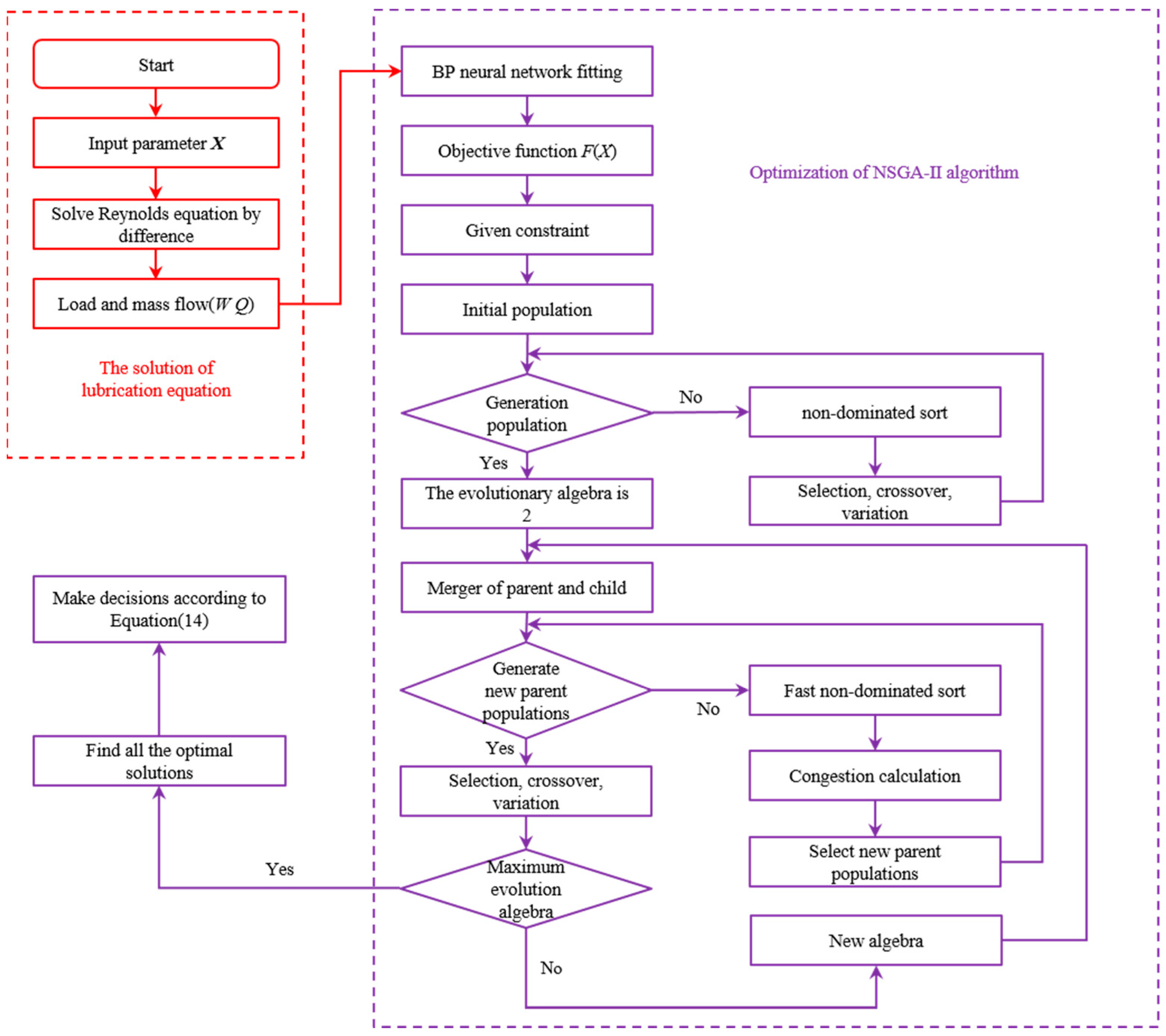
2.4. Optimization Method
- 1.
- Input bearing parameters (distribution diameter of orifice, number of orifices, aperture, etc.) and solve Reynolds equation according to Equations (1)–(9) to obtain pressure distribution;
- 2.
- According to the pressure distribution, the bearing capacity W and mass flow Q are solved according to Equation (10);
- 3.
- The objective function F(X) is obtained by using the BP neural network and Equation (11);
- 4.
- Constraints of the independent variables are given, and the population is initialized;
- 5.
- Select, cross, and mutate the population, then perform non-sequential sorting to obtain the next generation of the population;
- 6.
- Merge the offspring and parent populations to form a new population, then conduct a fast, non-dominated sorting, calculate crowding distance, and rank the population based on non-inferior levels;
- 7.
- Repeat the process of selecting, crossing, and mutating the population, then evaluate if the evolutionary generation criteria are met; if so, output the results; if not, continue the process until the criteria are met;
- 8.
- Make decisions on multiple solutions to obtain the optimal bearing parameters.
3. Experiment
3.1. Experimental Apparatus
3.2. Experimental Methods
3.2.1. Experimental Conditions
3.2.2. Variables of Experimental Measurement
4. Results and Discussion
4.1. Influence of Geometric Parameters on Bearing Performance
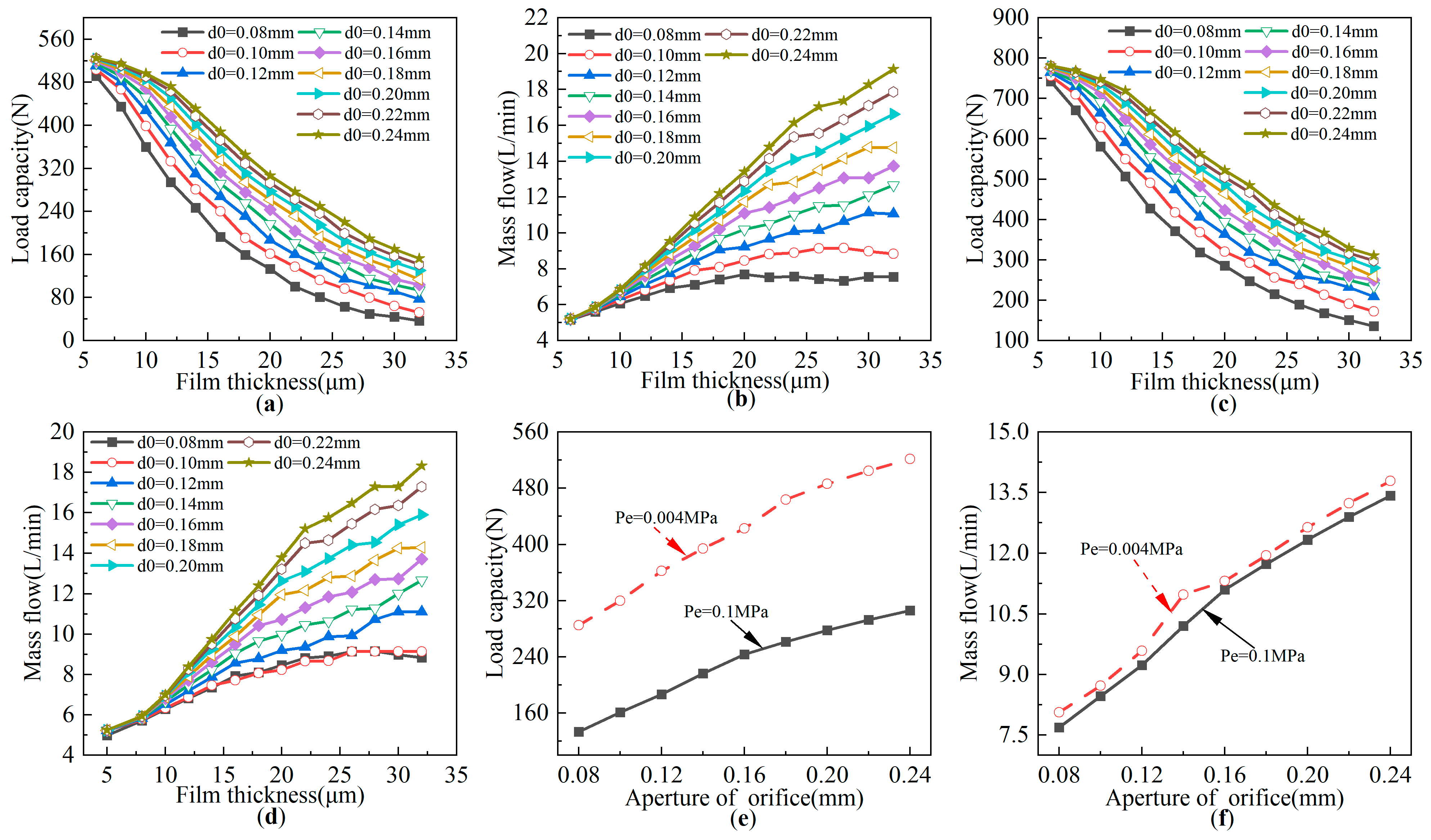
4.1.1. Influence of Number of Orifices on Bearing Performance
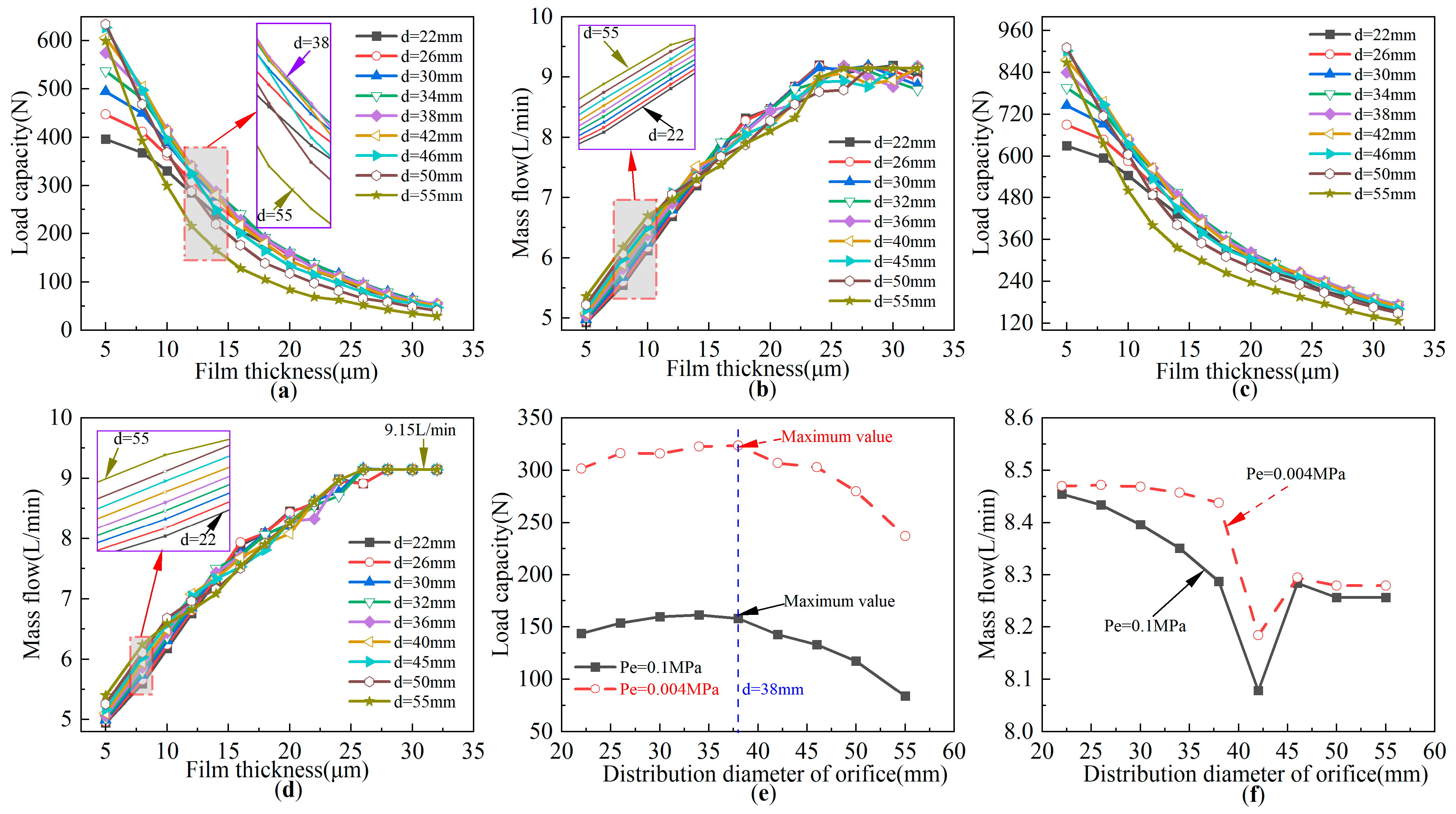
4.1.2. Influence of Distribution Diameter of Orifice on Bearing Performance
4.1.3. Influence of Orifice Aperture on Bearing Performance
4.2. Influence of Environmental Conditions on Bearing Performance
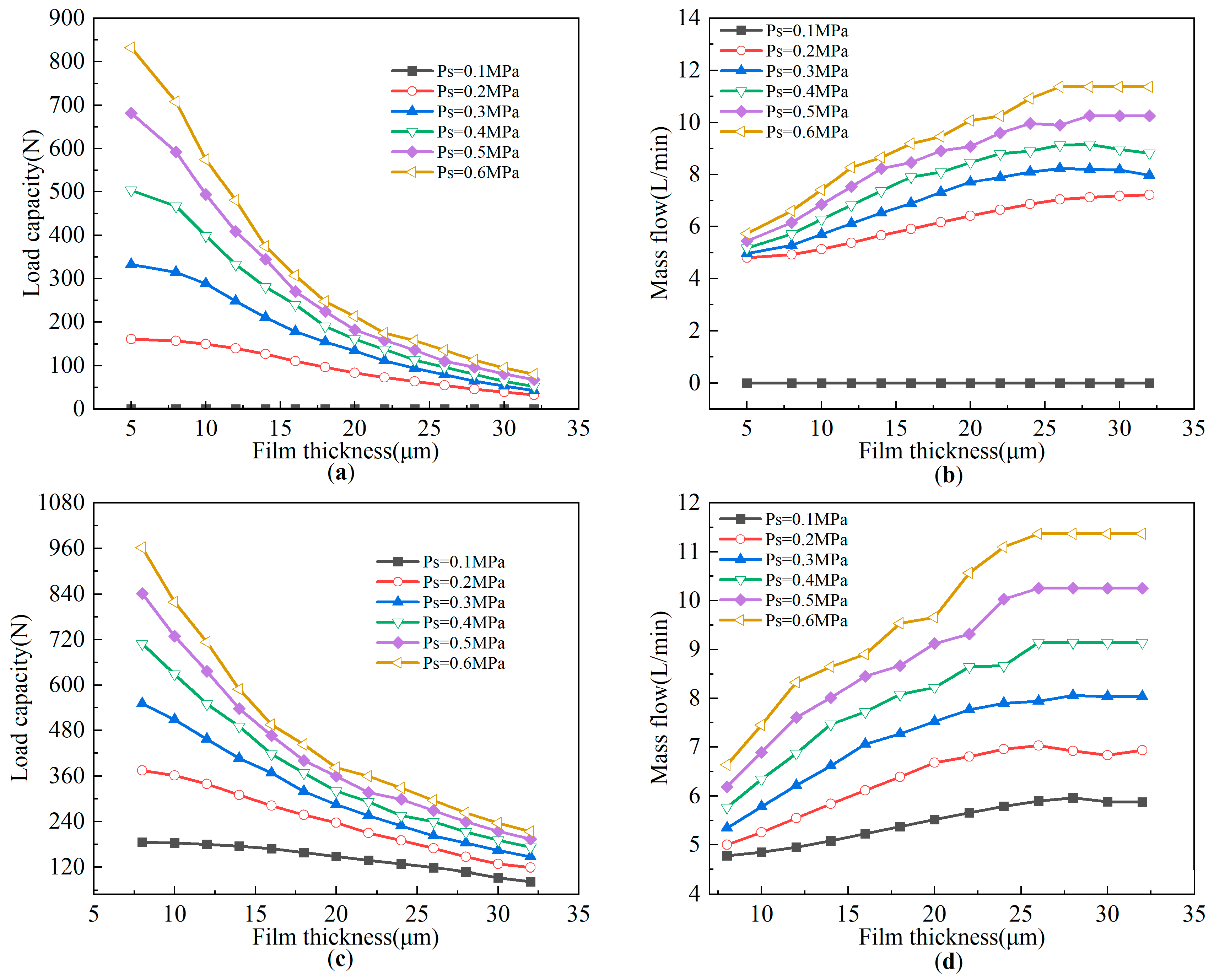
4.2.1. Influence of Air Supply Pressure on Bearing Performance
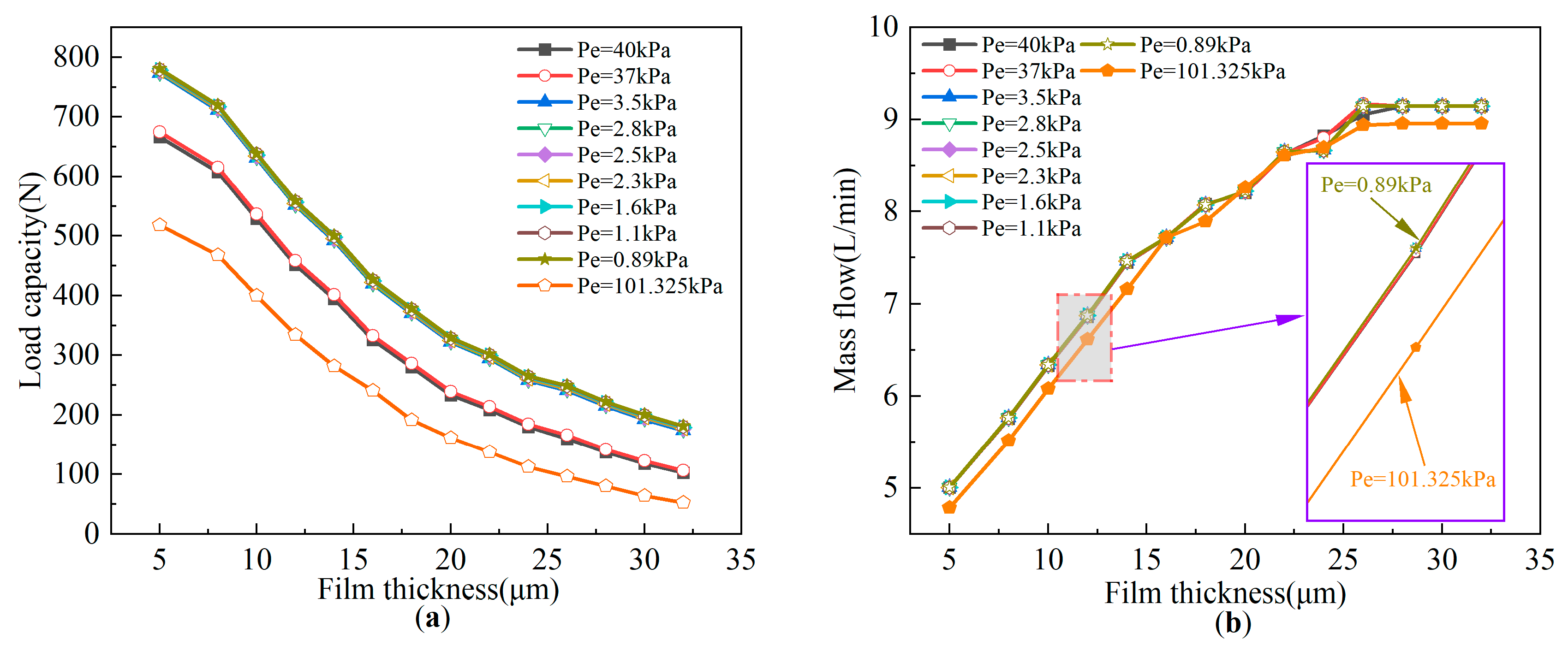
4.2.2. Influence of Environmental Pressure on Bearing Performance
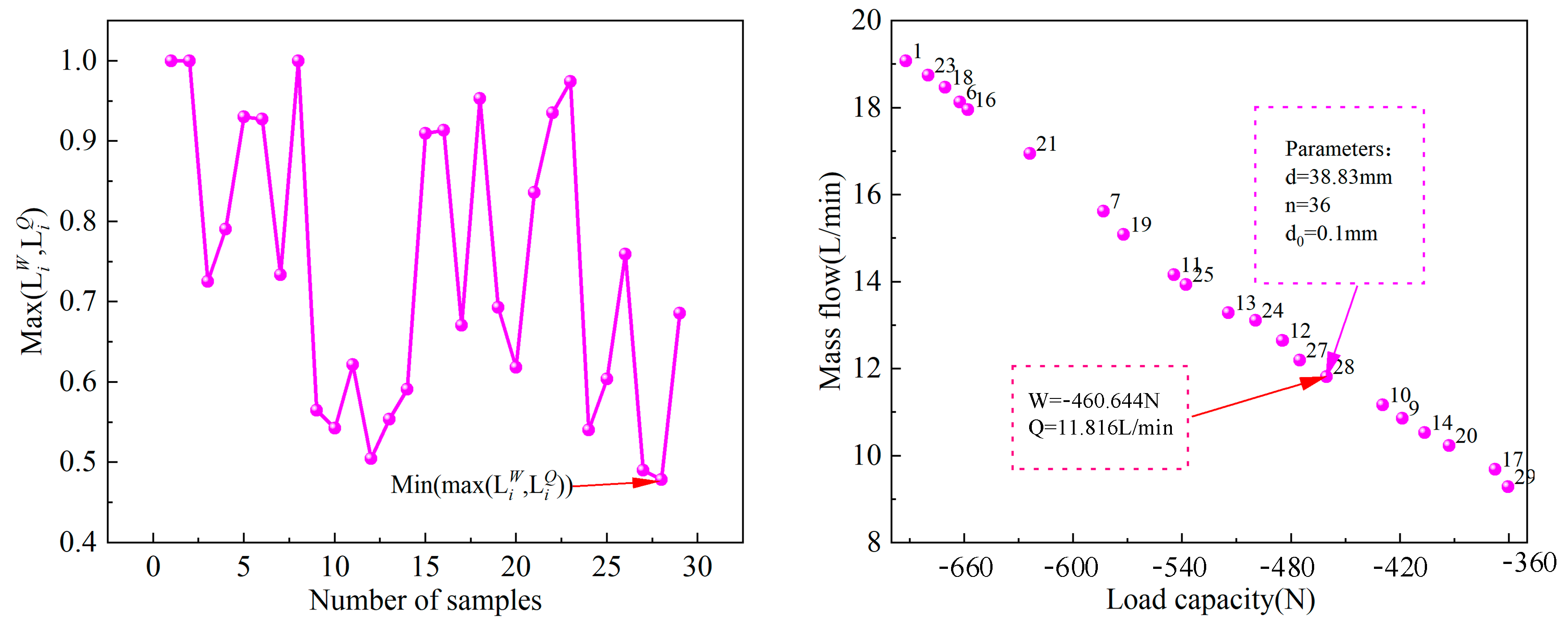
4.3. Pareto Frontier Optimal Solution
4.4. Comparison between Simulation and Experiment
5. Conclusions
- 1.
- In the vacuum environment, because the outlet pressure of the bearing is lower than that of the atmospheric pressure, the pressure difference between the inside and outside of the bearing increases, and the outlet flow rate increases, resulting in the bearing capacity and flow rate being increased compared with the atmospheric pressure environment and gradually increasing with the decrease in vacuum degree;
- 2.
- With the optimization goals of maximum load capacity and minimum mass flow of bearings in the vacuum, the objective function was fitted using a BP neural network and combined with the NSGA-II multi-objective optimization algorithm to optimize the bearing parameters. When the bearing’s aperture of the orifice is 0.1 mm, the number of orifices is 36, and the distribution diameter of the orifice is 38.83 mm, the bearing has a maximum load capacity of 460.644 N and a minimum mass flow rate of 11.816 L/min;
- 3.
- Experiments are carried out on the optimized bearing parameters in atmospheric pressure and vacuum environments. The maximum error between the experimental and theoretical values is 10%, which verified the correctness and feasibility of the simulation and provided a theoretical and experimental method for the design of the aerostatic thrust bearing in a vacuum;
- 4.
- When designing bearings for application in a vacuum environment, the optimization and experimental methods proposed in this paper can quickly design ideal parameters, greatly improving the efficiency of design. This is of great significance for the design, manufacturing, and maintenance of bearings;
- 5.
- Although the optimization method of bearing parameters presented in this paper is carried out under specific fields, materials, and experimental conditions, the analysis and calculation methods presented in this paper are still of popularization significance for other fields, materials, and experimental conditions. In future studies, we will try to obtain the output values for how to use numerical methods in other experimental conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wapman, J.D.; Sternberg, D.C.; Lo, K.; Wang, M.; Jones-Wilson, L.; Mohan, S. Jet Propulsion Laboratory Small Satellite Dynamics Testbed Planar Air-Bearing Propulsion System Characterization. J. Spacecr. Rockets 2021, 58, 954–971. [Google Scholar] [CrossRef]
- Miyatake, M.; Yoshimoto, S. Numerical investigation of static and dynamic characteristics of aerostatic thrust bearings with small feed holes. Tribol. Int. 2010, 43, 1353–1359. [Google Scholar] [CrossRef]
- Gao, S.; Cheng, K.; Chen, S.; Ding, H.; Fu, H. Computational design and analysis of aerostatic journal bearings with application to ultra-high speed spindles. Proc. Inst. Mech. Eng. Part C 2017, 231, 1205–1220. [Google Scholar] [CrossRef]
- Chakraborty, B.; Bhattacharjee, B.; Chakraborti, P.; Biswas, N. Evaluation of the performance characteristics of aerostatic bearing with porous alumina (Al2O3) membrane using theoretical and experimental methods. Proc. Inst. Mech. Eng. Part J 2024, 13506501241245760. [Google Scholar] [CrossRef]
- Khim, G.; Park, C.H.; Lee, H.; Kim, S.W. Analysis of additional leakage resulting from the feeding motion of a vacuum-compatible air bearing stage. Vacuum 2006, 81, 466–474. [Google Scholar] [CrossRef]
- Fukui, S.; Kaneko, R. Experimental Investigation of Externally Pressurized Bearings Under High Knudsen Number Conditions. J. Tribol. 1988, 110, 144–147. [Google Scholar] [CrossRef]
- Trost, D. Design and analysis of hydrostatic gas bearings for vacuum applications. In Proceedings of the ASPE Spring Topical Meeting on Challenges at the Intersection of Precision Engineering and Vacuum Technology, Orlando, FL, USA, 2 April 2006. [Google Scholar]
- Schenk, C.; Buschmann, S.; Risse, S.; Eberhardt, R.; Tünnermann, A. Comparison between flat aerostatic gas-bearing pads with orifice and porous feedings at high-vacuum conditions. Precis. Eng. 2008, 32, 319–328. [Google Scholar] [CrossRef]
- Gans, R. Lubrication theory at arbitrary Knudsen number. J. Tribol. 1985, 107, 431–433. [Google Scholar] [CrossRef]
- Chan, C.-W. Modified Particle Swarm Optimization Algorithm for Multi-Objective Optimization Design of Hybrid Journal Bearings. J. Tribol. 2015, 137, 021101. [Google Scholar] [CrossRef]
- Wang, N.; Chang, Y.Z. Application of the Genetic Algorithm to the Multi-Objective Optimization of Air Bearings. Tribol. Lett. 2004, 17, 119–128. [Google Scholar] [CrossRef]
- Wang, N.; Cha, K.-C. Multi-objective optimization of air bearings using hypercube-dividing method. Tribol. Int. 2010, 43, 1631–1638. [Google Scholar] [CrossRef]
- Yifei, L.; Yihui, Y.; Hong, Y.; Xinen, L.; Jun, M.; Hailong, C. Modeling for optimization of circular flat pad aerostatic bearing with a single central orifice-type restrictor based on CFD simulation. Tribol. Int. 2017, 109, 206–216. [Google Scholar] [CrossRef]
- Wang, N.; Chen, H.-Y. A two-stage multiobjective optimization algorithm for porous air bearing design. Tribol. Int. 2016, 93, 355–363. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, L.; Wang, J. Multi-objective optimization of elliptical tube fin heat exchangers based on neural networks and genetic algorithm. Energy 2023, 269, 126729. [Google Scholar] [CrossRef]
- Wang, G.; Li, W.; Liu, G.; Feng, K. A novel optimization design method for obtaining high-performance micro-hole aerostatic bearings with experimental validation. Tribol. Int. 2023, 185, 108542. [Google Scholar] [CrossRef]
- Chang, L.; Tenghui, J.; Xing, H.; Xiansheng, J. Study on parameter optimization of laser cladding Fe60 based on GA-BP neural network. J. Adhes. Sci. Technol. 2023, 37, 2556–2586. [Google Scholar]
- Gao, F.; Zheng, Y.; Li, Y.; Li, W. A back propagation neural network-based adaptive sampling strategy for uncertainty surfaces. Trans. Inst. Meas. Control. 2024, 46, 1012–1023. [Google Scholar] [CrossRef]
- Ding, C.; Ding, Y.; Yuan, Z.; Li, J. Structural Optimization Design of Electromagnetic Repulsion Mechanism Based on BP Neural Network and NSGA–II. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 1914–1922. [Google Scholar]
- Guofang, L.; Xing, L.; Meng, L.; Tong, N.; Shaopei, W.; Wangcai, D. Multi-objective optimisation of high-speed rail profile with small radius curve based on NSGA-II Algorithm. Veh. Syst. Dyn. 2023, 61, 3111–3135. [Google Scholar]
- Kim, I.Y.; de Weck, O.L. Adaptive weighted-sum method for bi-objective optimization: Pareto front generation. Struct. Multidiscip. Optim. 2005, 29, 149–158. [Google Scholar] [CrossRef]
- Xu, X.F.; Xu, S.; Zhou, T. An Improved Spectral Clustering Algorithm Using Minimum Maximum Principle. Appl. Mech. Mater. 2012, 1810, 1881–1884. [Google Scholar] [CrossRef]







| Environmental pressure (Pa) | 40,000 | 37,000 | 3500 | 2800 | 2500 | 2300 | 1600 | 1100 | 890 |
| Air supply pressure (MPa) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| Parameters | Value |
|---|---|
| Bearing diameter D (mm) | 64 |
| Distribution diameter of orifice d (mm) | 32 |
| Number of orifices n | 36 |
| Aperture of orifice d0 (mm) | 0.1 |
| Air film thickness h (μm) | 15 |
| Air supply pressure Ps (MPa) | 0.5 |
| Ambient pressure Pe (MPa) | 0.1 |
| Viscosity of air η (N·s·m−2) | 1.82 × 10−5 |
| Ambient temperature Ta (k) | 293.15 |
| Adiabatic coefficient k | 1.4 |
| Critical pressure ratio βk | 0.528 |
| Throttle coefficient Ψ | 0.8 |
| Algorithms | NSGA-II Algorithm | Particle Swarm Optimization | Simulated Annealing Algorithm | Tabu Search Algorithm |
|---|---|---|---|---|
| Bearing capacity W (N) | 460.644 | 480.598 | 500.987 | 470.325 |
| Mass flow Q (L/min) | 11.816 | 12.658 | 14.658 | 12.126 |
| Ratio | 38.98 | 37.97 | 34.18 | 38.79 |
| Parameters | Value |
|---|---|
| Bearing diameter D (mm) | 64 |
| Distribution diameter of orifice d (mm) | 38.8 |
| Number of orifices n | 36 |
| Aperture of orifice d0 (mm) | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, G.; Li, Y.; Li, Y.; Zang, L.; Zhao, M.; Li, Z.; Yu, H.; Xu, J.; Liang, H.; Zhang, G.; et al. Research on Design and Optimization of Micro-Hole Aerostatic Bearing in Vacuum Environment. Lubricants 2024, 12, 224. https://doi.org/10.3390/lubricants12060224
Fan G, Li Y, Li Y, Zang L, Zhao M, Li Z, Yu H, Xu J, Liang H, Zhang G, et al. Research on Design and Optimization of Micro-Hole Aerostatic Bearing in Vacuum Environment. Lubricants. 2024; 12(6):224. https://doi.org/10.3390/lubricants12060224
Chicago/Turabian StyleFan, Guozhen, Youhua Li, Yuehua Li, Libin Zang, Ming Zhao, Zhanxin Li, Hechun Yu, Jialiang Xu, Hongfei Liang, Guoqing Zhang, and et al. 2024. "Research on Design and Optimization of Micro-Hole Aerostatic Bearing in Vacuum Environment" Lubricants 12, no. 6: 224. https://doi.org/10.3390/lubricants12060224
APA StyleFan, G., Li, Y., Li, Y., Zang, L., Zhao, M., Li, Z., Yu, H., Xu, J., Liang, H., Zhang, G., & Hou, W. (2024). Research on Design and Optimization of Micro-Hole Aerostatic Bearing in Vacuum Environment. Lubricants, 12(6), 224. https://doi.org/10.3390/lubricants12060224





