CFD-Based Investigation of Static and Dynamic Pressure Effect in Aerostatic Bearings with Annular Grooves at High Speed
Abstract
1. Introduction
2. Methods
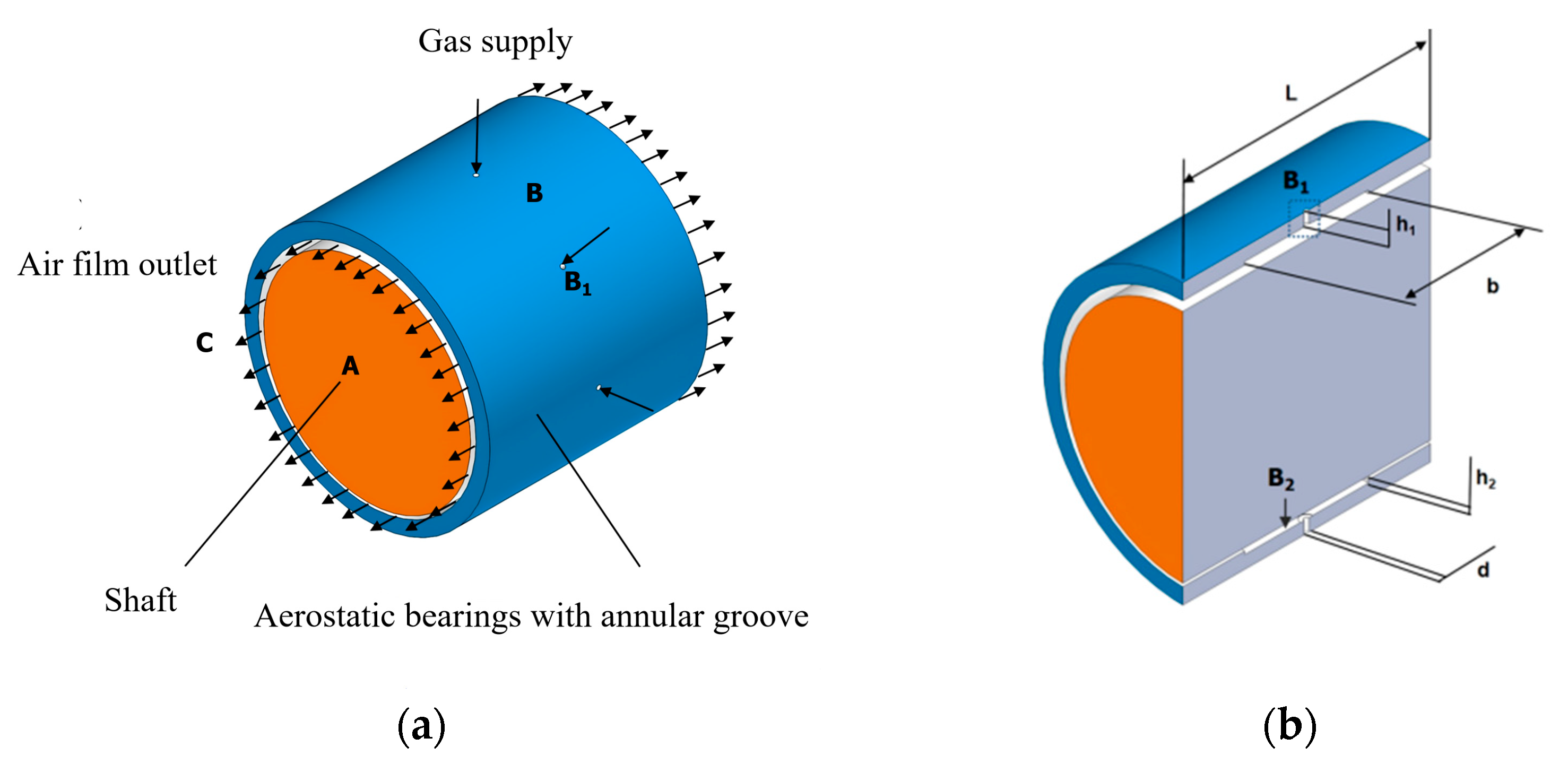
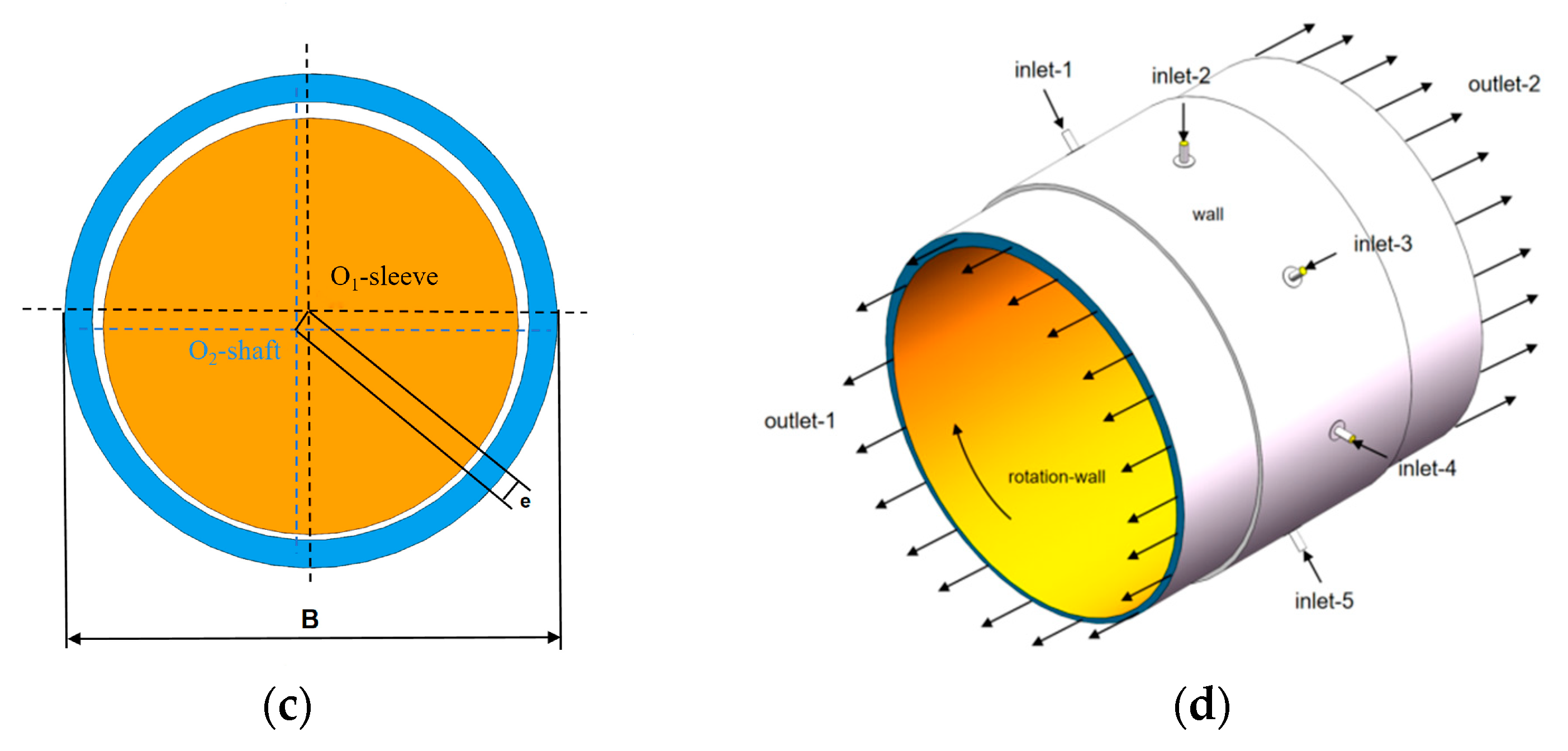
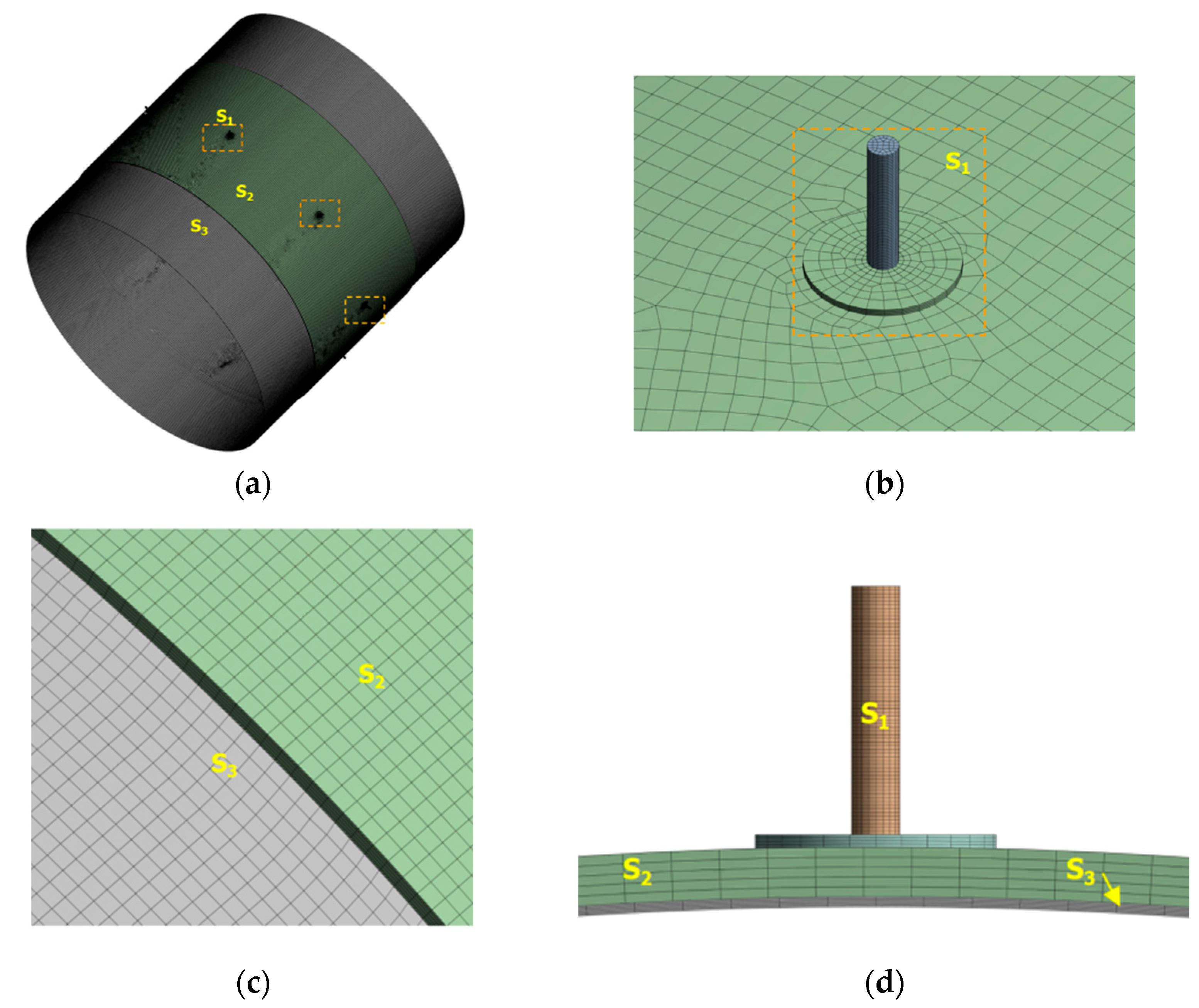
2.1. Flow Field and Mesh Model of Annular Groove Gas Journal Bearing
2.2. Shear Stress Transport k-ω Model
3. Results and Discussion
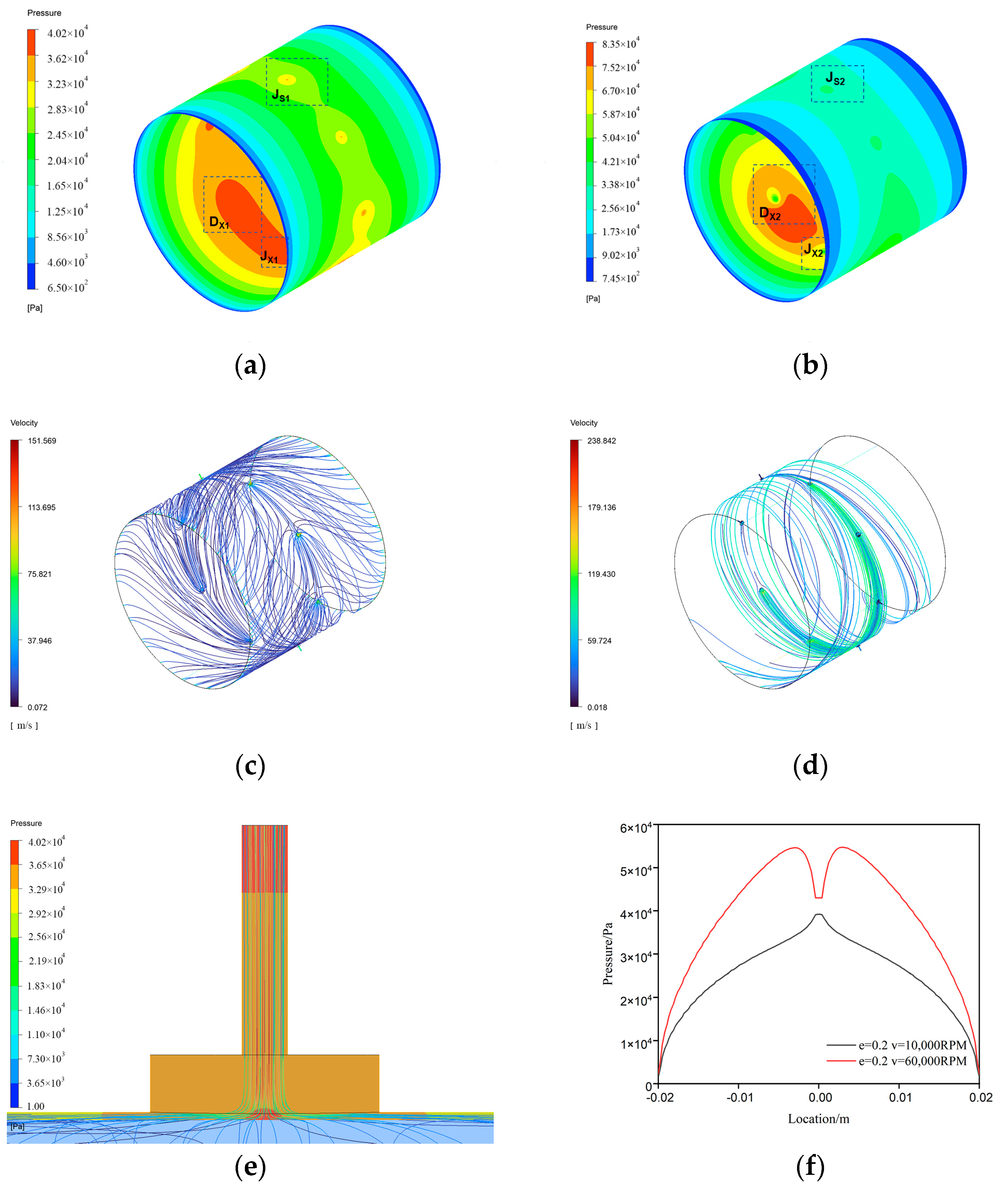
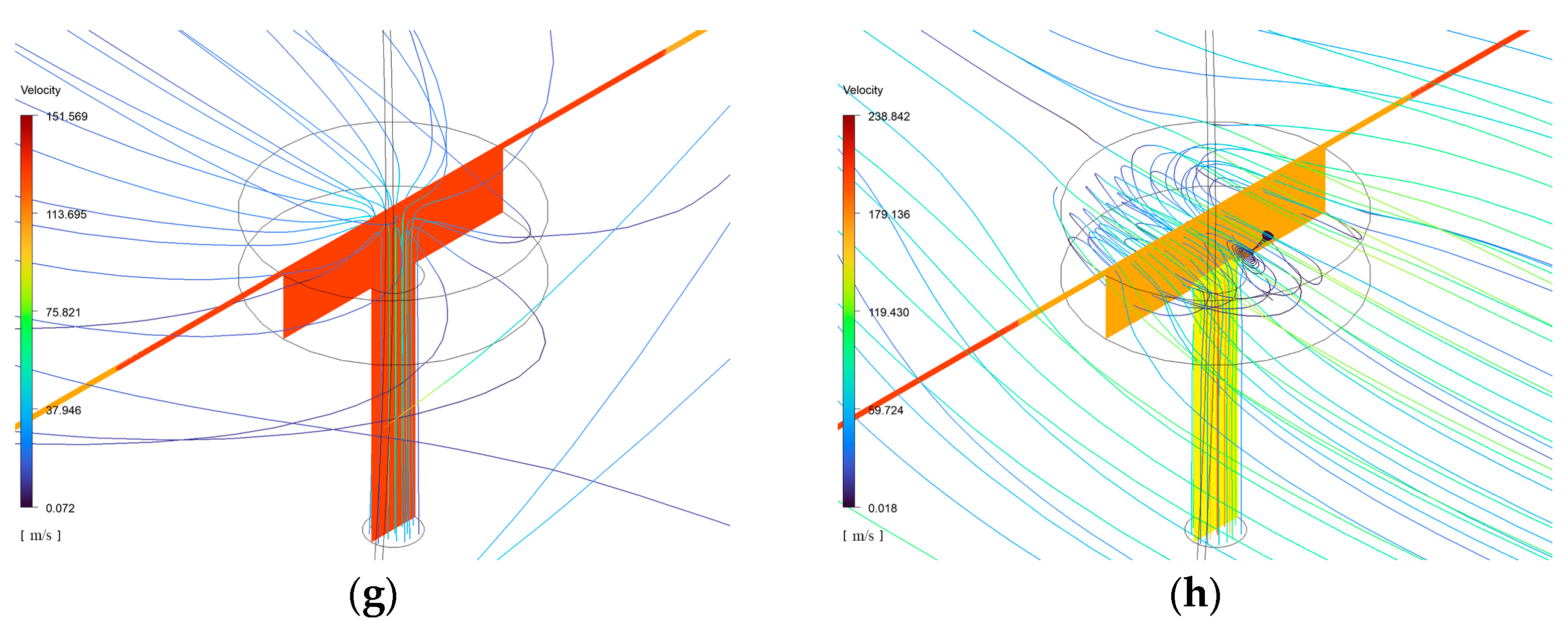
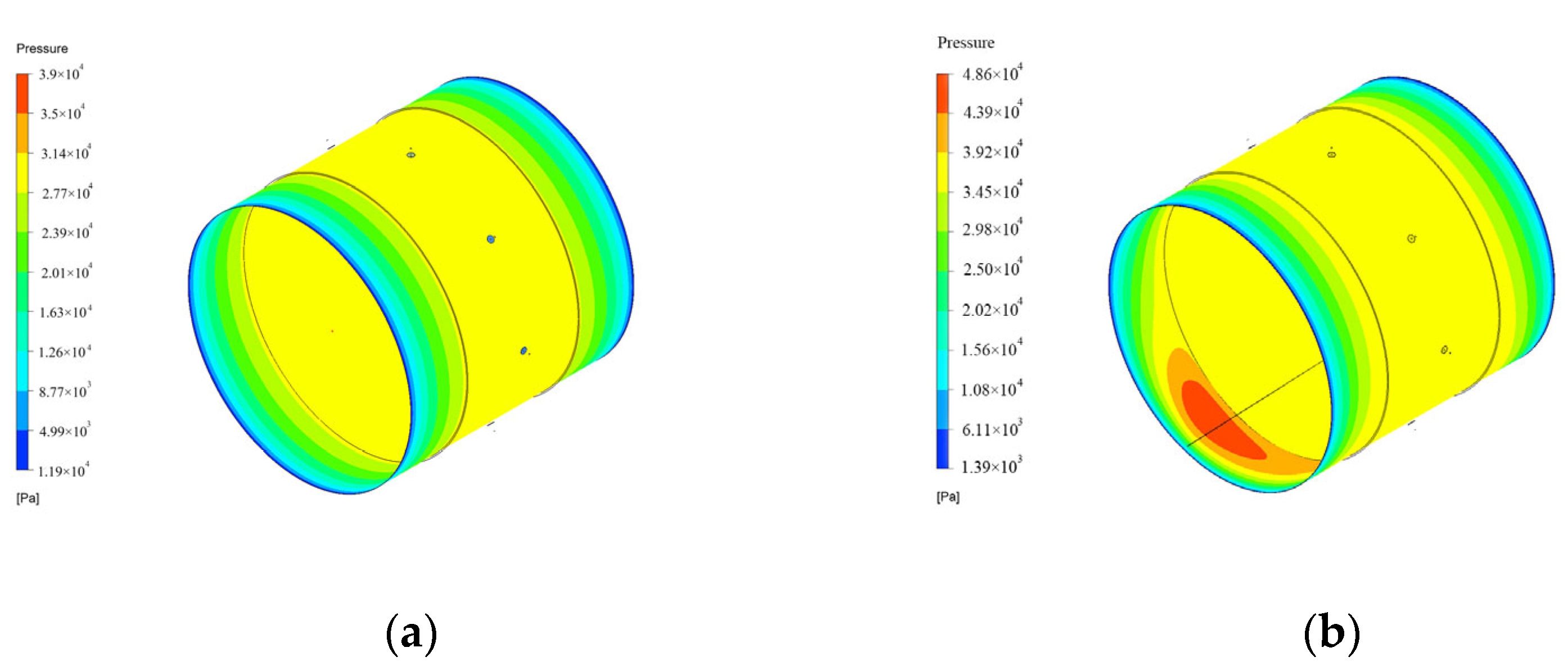
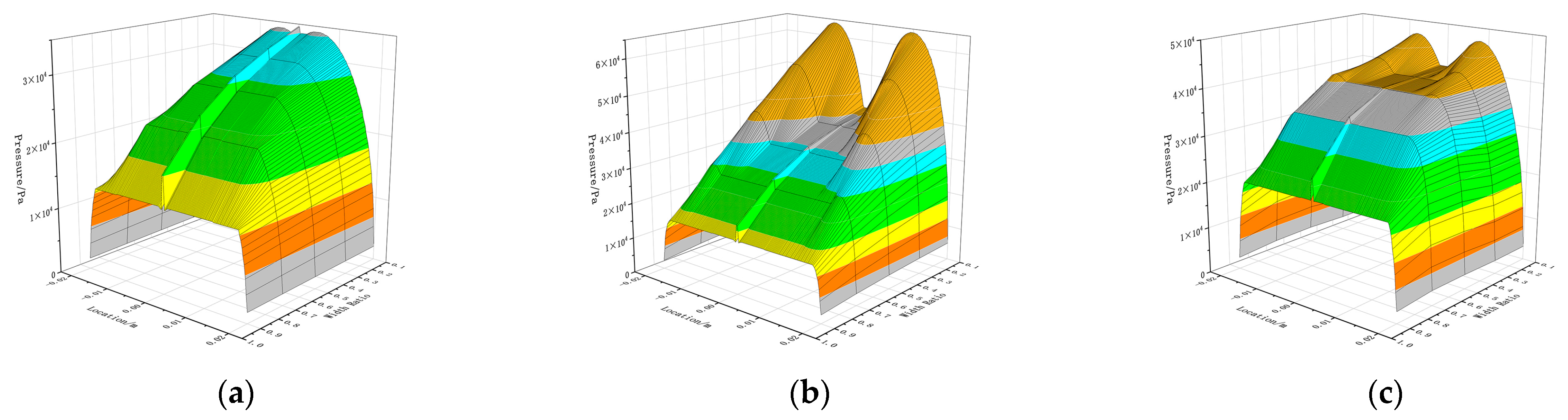
3.1. Analysis of the Mechanism of Dynamic-Static Pressure Effects
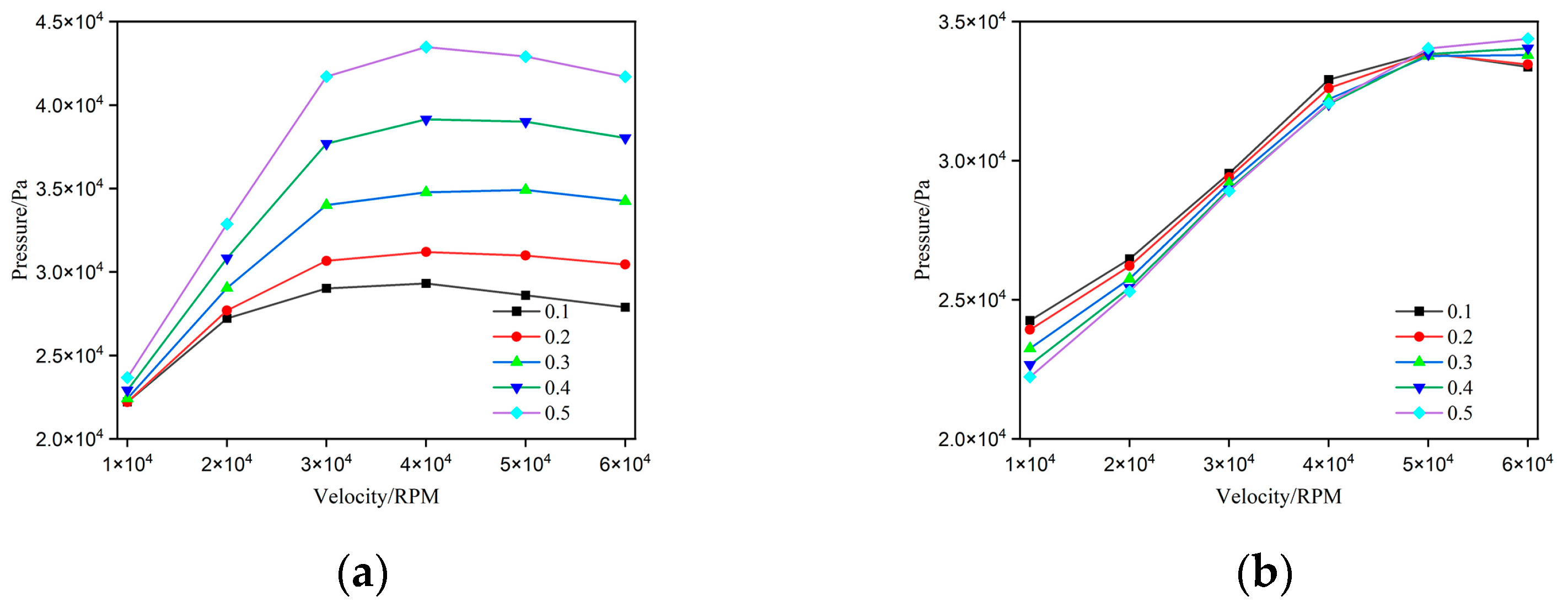
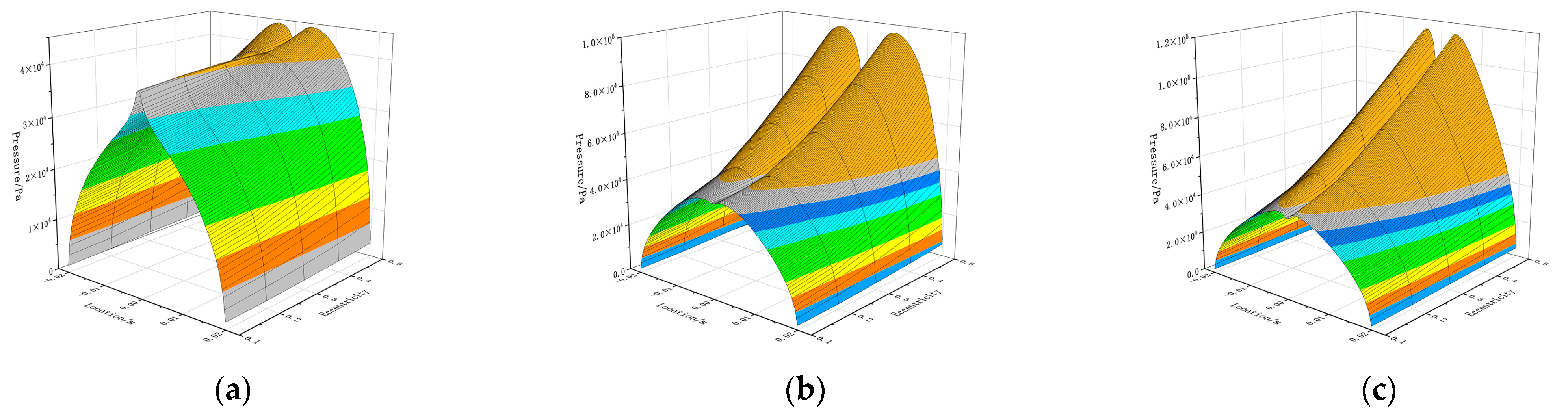
3.2. Eccentricity
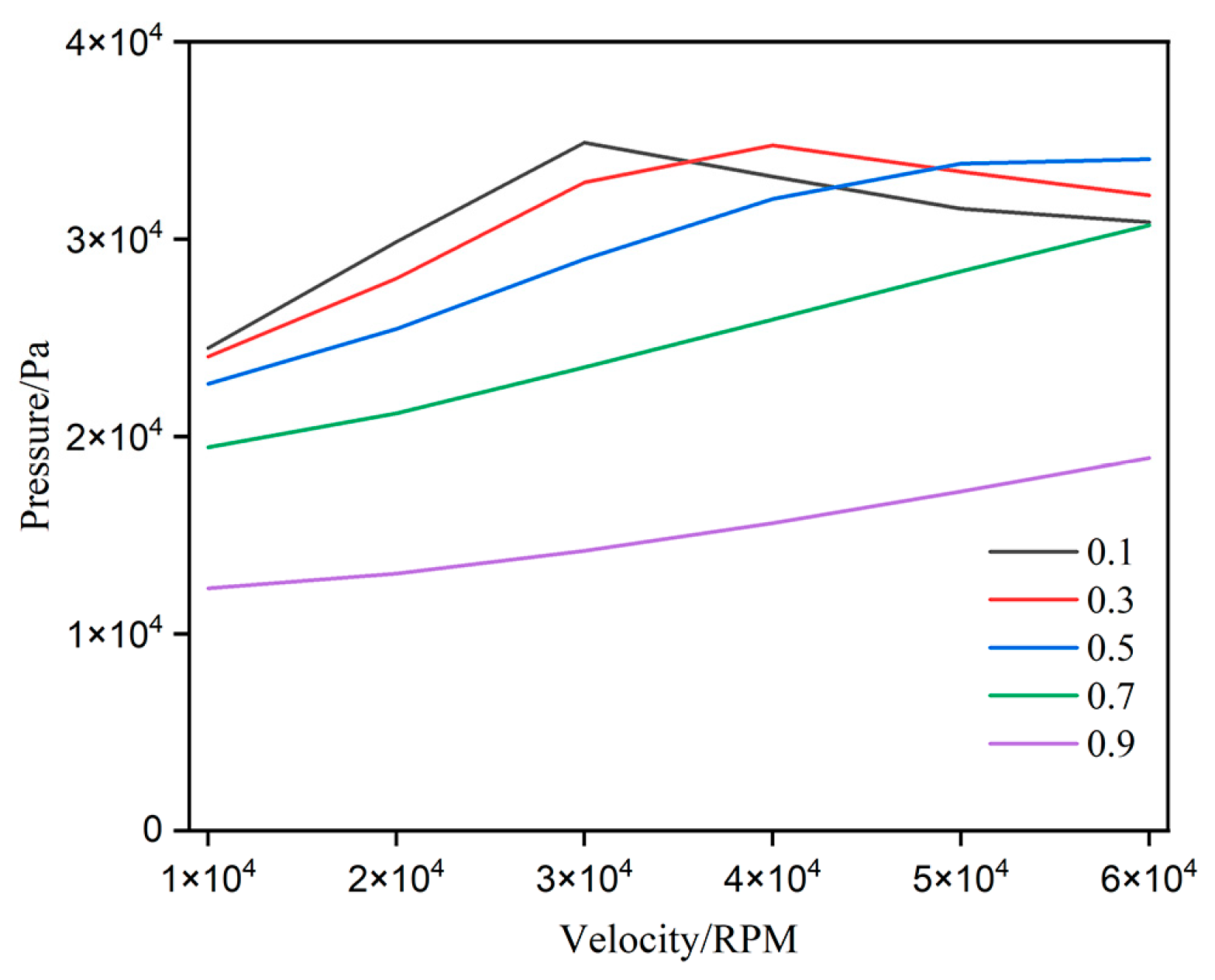
3.3. Width Ratio
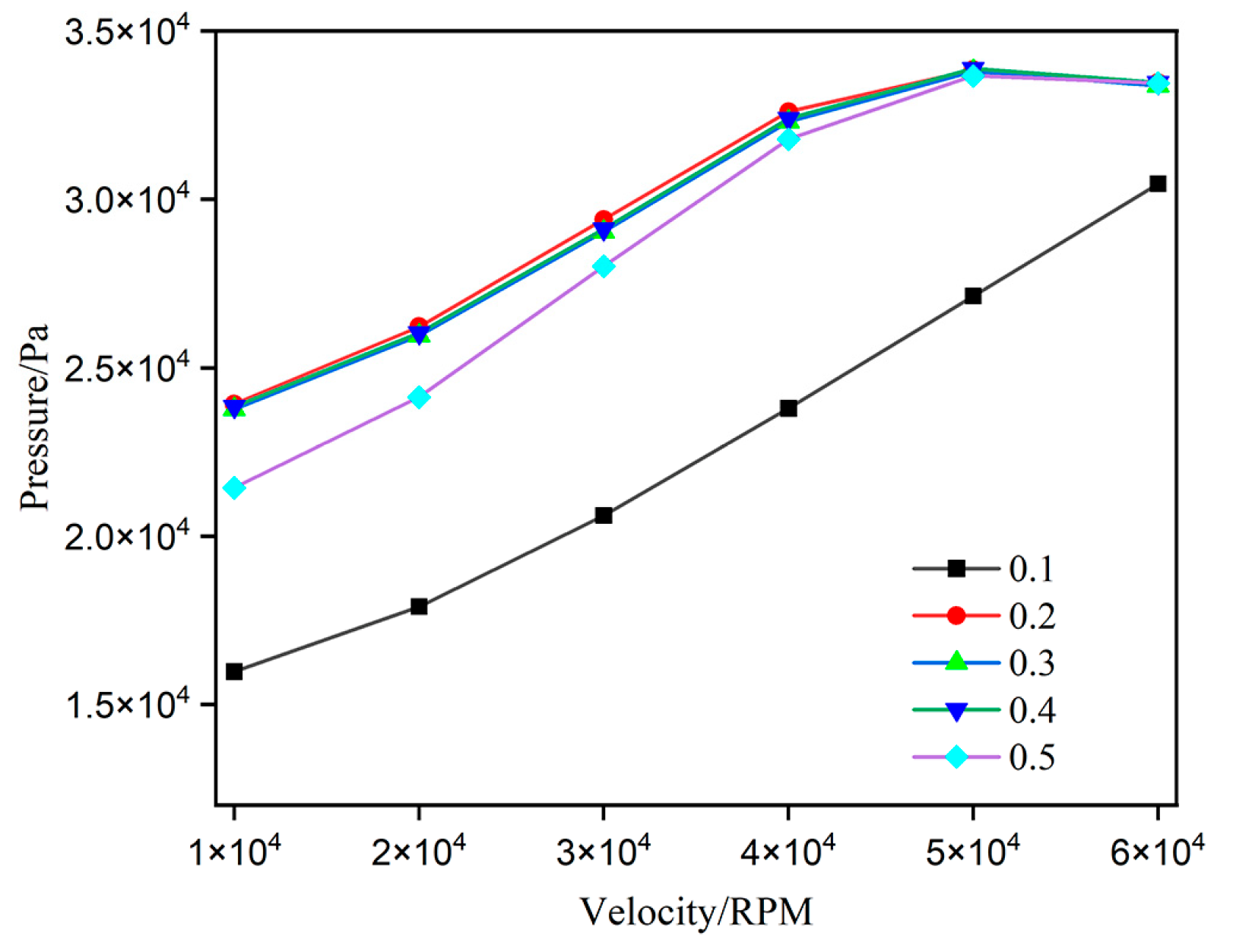
3.4. Depth Ratio
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rowe, W.B. Hydrostatic and hybrid bearing design. Tribol. Int. 1983, 17, 353. [Google Scholar] [CrossRef]
- Colombo, F.; Lentini, L.; Raparelli, T.; Trivella, A. Special Issue “Gas Bearings: Modelling, Design and Applications”. Appl. Sci. 2022, 12, 9048. [Google Scholar] [CrossRef]
- Belforte, G.; Colombo, F.; Raparelli, T.; Trivella, A.; Viktorov, V. Comparison between grooved and plane aerostatic thrust bearings: Static performance. Meccanica 2011, 46, 547–555. [Google Scholar] [CrossRef]
- Chen, X.; Mills, J.K.; Shi, K.; Bao, G. Numerical investigation on the static performance of aerostatic journal bearings with different pocket shapes by the finite-element method. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 1897–1911. [Google Scholar] [CrossRef]
- Li, P.; Li, J.; Shi, Z.; Zhang, H.; Xiao, S.; Li, X.; Gu, F. Effects of manufacturing errors and micro-groove surfaces on the static and dynamic characteristics of water-lubricated bearings. Phys. Scr. 2023, 98, 95903. [Google Scholar] [CrossRef]
- Stanev, P.T.; Wardle, F.; Corbett, J. Investigation of grooved hybrid air bearing performance. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2004, 218, 95–106. [Google Scholar] [CrossRef]
- Su, C.T.; Lie, K.N. Rotation effects on hybrid hydrostatic/hydrodynamic journal bearings. Ind. Lubr. Tribol. 2001, 53, 261–269. [Google Scholar] [CrossRef]
- Powell, J.W. Design of Aerostatic Bearings; The Machinery Publishing CO: Brighton, UK, 1970. [Google Scholar]
- Yao, S. Gas Thrust Bearing Technology Based on the Principle of Hybrid Lubrication; Harbin Institute of Technology: Harbin, China, 2006. [Google Scholar]
- Yu, X.; Shi, G.; Jiang, H.; Dai, R.; Jia, W.; Yang, X.; Gao, W. Effect of texture parameters on the lubrication performance of static and dynamic pressure thrust bearings and multi-objective optimization. Ind. Lubr. Tribol. 2024, 76, 526–536. [Google Scholar] [CrossRef]
- Gao, S.; Shi, Y.; Xu, L.; Chen, H.; Cheng, K. Investigation on influences of herringbone grooves for the aerostatic journal bearings applied to ultra-high-speed spindles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5795–5812. [Google Scholar] [CrossRef]
- Schlums, H.; Hühne, C.; Sinapius, M. Design of a Herringbone-Grooved Bearing for Application in an Electrically Driven Air Compressor. Machines 2022, 10, 662. [Google Scholar] [CrossRef]
- Cui, W.; Li, S.; Zhu, B.; Yang, F.; Chen, B. Research on the influence of a micro-groove-orifice structure and its layout form on the static characteristics of aerostatic journal bearings under a high gas supply pressure. Adv. Mech. Eng. 2023, 15, 1–18. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; Jiang, H.; Gao, W.; Shi, G.; Dai, R.; Jia, W.; Wang, J.; Jiao, J. Investigation on the Dynamic Pressure Effect of Clearance Oil Film at a Stepped Hydrostatic Thrust Bearing Working in Heavy Loading Duty. Tribol. Trans. 2024, 67, 173–184. [Google Scholar] [CrossRef]
- Ke, C.; Qiu, S.; Li, K.; Xiong, L.; Peng, N.; Zhang, X.; Dong, B.; Liu, L. Numerical Computation and Experimental Research for Dynamic Properties of Ultra-High-Speed Rotor System Supported by Helium Hydrostatic Gas Bearings. Lubricants 2024, 12, 302. [Google Scholar] [CrossRef]
- Guo, M.; Tian, Z.; Rong, Z.Y. CFD-based method for hydrostatic bearings performance: Static characteristics with various recess shapes. Int. J. Hydromechatronics 2024, 7, 176–192. [Google Scholar] [CrossRef]
- Hariharan, G.; Kumar, S.; Kumar, N. Enhancing performance in water lubricated bearings with groove structures: A CFD analysis. Cogent Eng. 2024, 11, 2399762. [Google Scholar] [CrossRef]
- Wang, Y.; Jacobs, G.; Zhang, S.; Klinghart, B.; König, F. Lubrication mechanism analysis of textures in journal bearings using CFD simulations. Ind. Lubr. Tribol. 2024. [Google Scholar] [CrossRef]
- Sun, C.; Zhao, J. Hydrodynamic Performance Analysis of Contra-Rotating Propellers Based on CFD. Ship Sci. Technol. 2019, 41, 36–40. [Google Scholar]
- Liu, A.; Wang, Y.; Hao, C. Reliability of the SST k-ω Model in Impinging Jet Cooling. J. Nanchang Hangkong Univ. Nat. Sci. Ed. 2009, 23, 5. [Google Scholar]



| Parameter | Value |
|---|---|
| Bearing outer diameter B (mm) | 40 |
| Bearing length L (mm) | 40 |
| Number of throttling Holes N | 8 |
| Throttling hole length h1 (mm) | 1 |
| Throttling hole diameter d (mm) | 0.2 |
| Pressure-equalizing groove depth h2 (mm) | 0.1/0.2/0.3/0.4/0.5 |
| Pressure-equalizing groove width b (mm) | 4/12/20/28/36 |
| Average gas film clearance Ha (um) | 20 |
| Minimum gas film thickness Hmin (um) | 18/16/14/12/10 |
| Parameter | Value |
|---|---|
| Depth ratio (h2/h1) | 0.1, 0.2, 0.3, 0.4, 0.5 |
| Width ratio (b/B) | 0.1, 0.3, 0.5, 0.7, 0.9 |
| Eccentricity (e/Ha) | 0.1, 0.2, 0.3, 0.4, 0.5 |
| Rotational speed (v, rpm) | 10,000, 20,000, 30,000, 40,000, 50,000, 60,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Li, M.; Cheng, P.; Wang, D.; Shao, C.; Zhou, J. CFD-Based Investigation of Static and Dynamic Pressure Effect in Aerostatic Bearings with Annular Grooves at High Speed. Lubricants 2025, 13, 46. https://doi.org/10.3390/lubricants13020046
Song W, Li M, Cheng P, Wang D, Shao C, Zhou J. CFD-Based Investigation of Static and Dynamic Pressure Effect in Aerostatic Bearings with Annular Grooves at High Speed. Lubricants. 2025; 13(2):46. https://doi.org/10.3390/lubricants13020046
Chicago/Turabian StyleSong, Wentao, Minggui Li, Peng Cheng, Decheng Wang, Chenxi Shao, and Junying Zhou. 2025. "CFD-Based Investigation of Static and Dynamic Pressure Effect in Aerostatic Bearings with Annular Grooves at High Speed" Lubricants 13, no. 2: 46. https://doi.org/10.3390/lubricants13020046
APA StyleSong, W., Li, M., Cheng, P., Wang, D., Shao, C., & Zhou, J. (2025). CFD-Based Investigation of Static and Dynamic Pressure Effect in Aerostatic Bearings with Annular Grooves at High Speed. Lubricants, 13(2), 46. https://doi.org/10.3390/lubricants13020046




