Effects of Driving Conditions on Tire Hydroplaning Performance
Abstract
1. Introduction
2. Tire Hydroplaning Modeling Methods
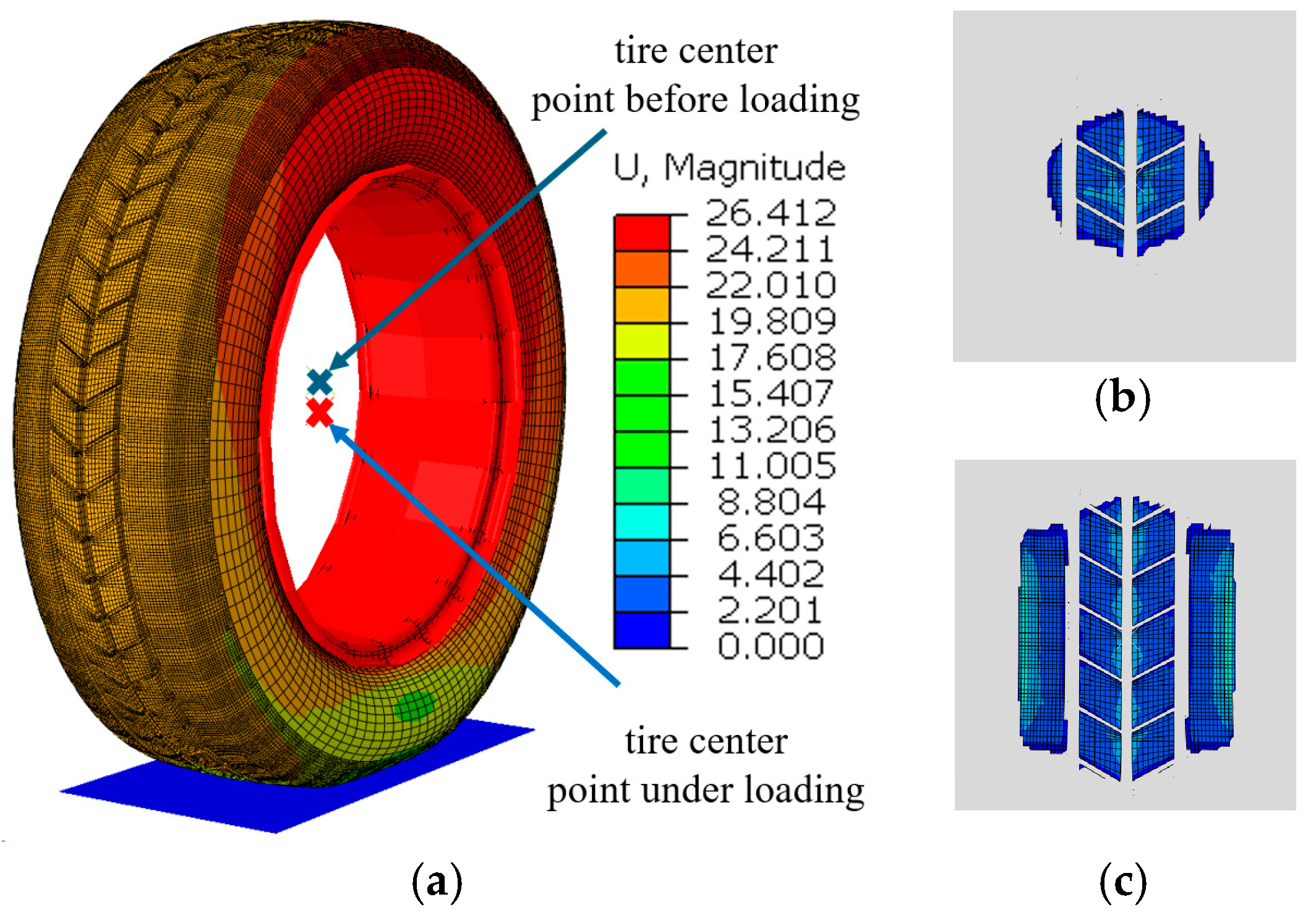
2.1. Geometric Model of the Tire
2.2. Setting Up the Hydroplaning Model
3. Simulation and Validation of the Tire Hydroplaning Model
3.1. Tire Hydroplaning
3.2. Validation of the Fluid–Structure Coupling Model
4. Effects of Various Environmental Conditions on Tire Hydroplaning
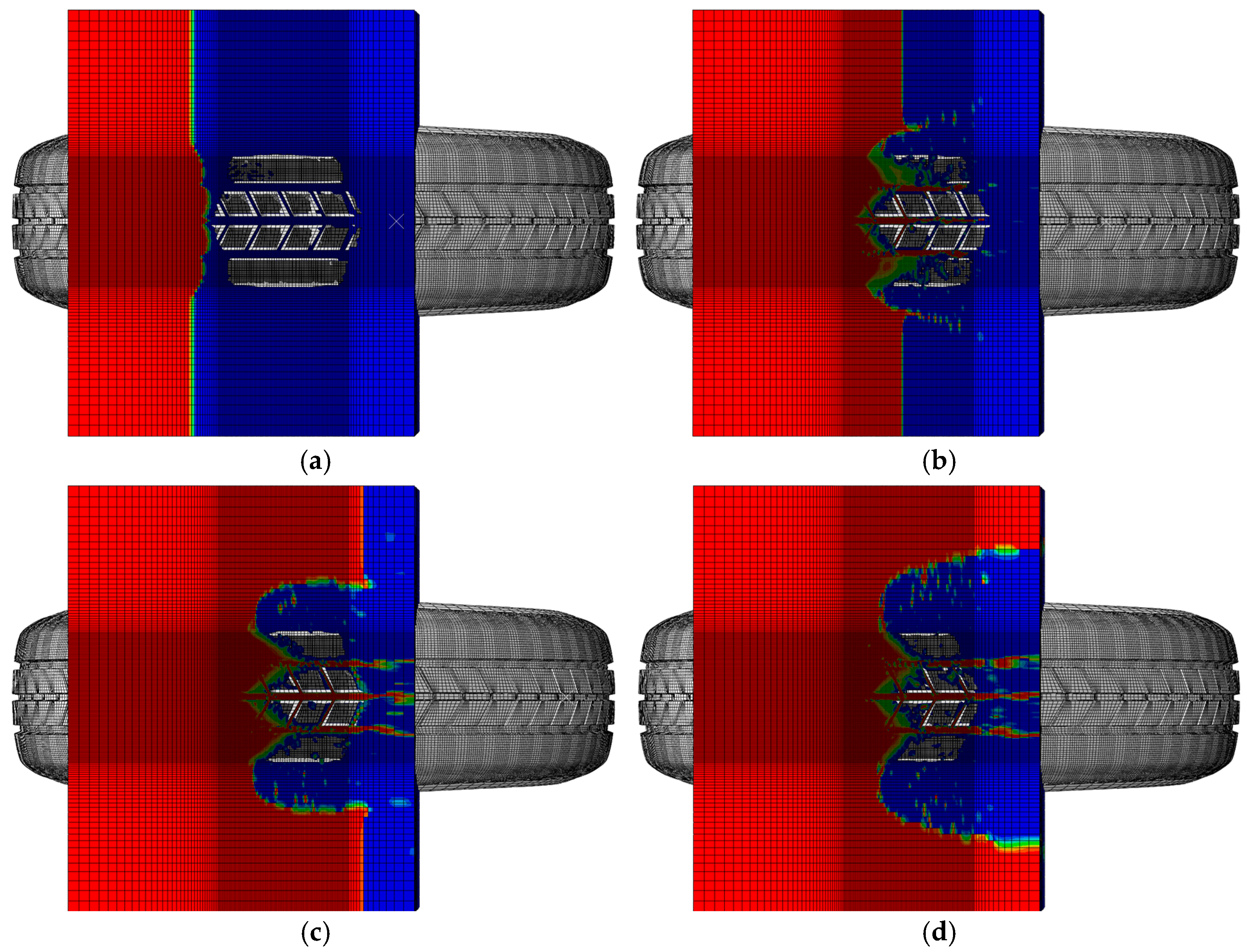
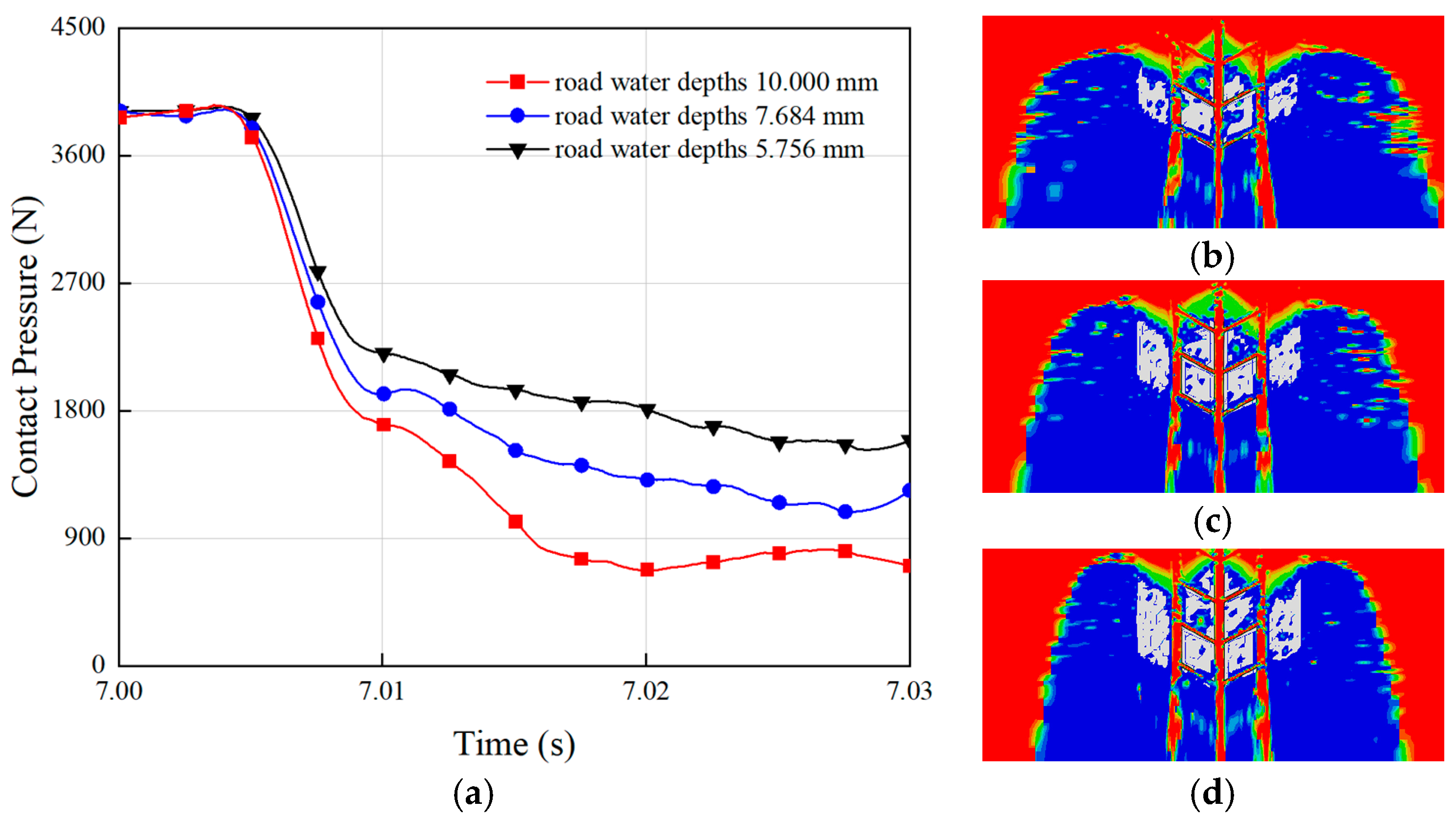
4.1. Under the Conditions of Different Road Water Depths
4.2. Under the Conditions of Different Driving Speeds
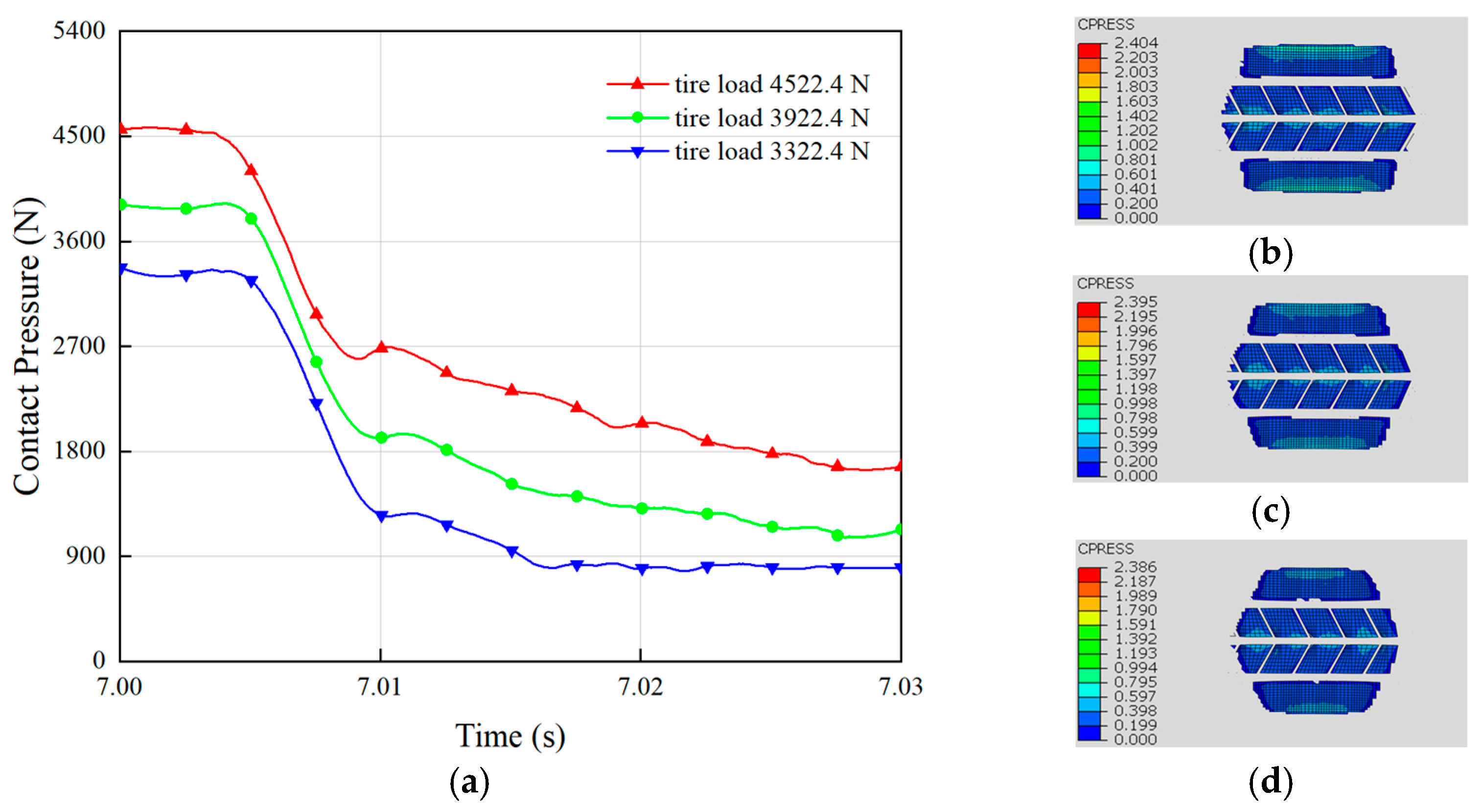
4.3. Under the Conditions of Different Tire Loads
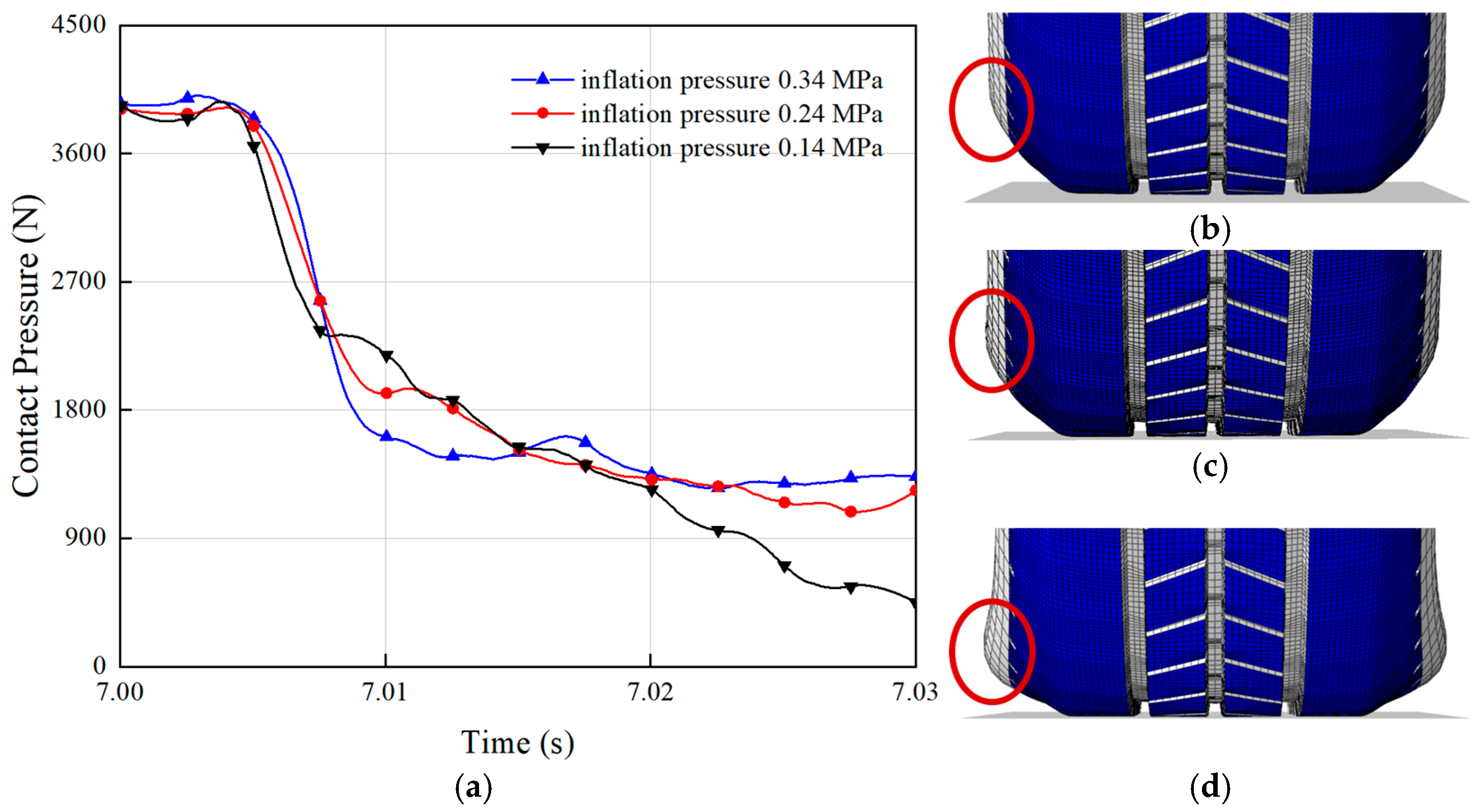
4.4. Under the Conditions of Different Inflation Pressures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murad, M.M.; Abaza, K.A. Pavement Friction in a Program to Reduce Wet Weather Traffic Accidents at the Network Level. Transp. Res. Record 2006, 1949, 126–136. [Google Scholar] [CrossRef]
- Schmid, F.; Lohner, T.; Stahl, K. Friction in Oil-Lubricated Rolling–Sliding Contacts with Technical and High-Performance Thermoplastics. Lubricants 2024, 12, 372. [Google Scholar] [CrossRef]
- Liang, X.; Han, M.; He, T.; Cui, L.; Yang, Z.; Ouyang, W. A Mixed Lubrication Deterministic Model of an Elastic Support Water-Lubricated Tilting Pad Thrust Bearing. Lubricants 2023, 11, 262. [Google Scholar] [CrossRef]
- Ding, Y.M.; Wang, H. Computational investigation of hydroplaning risk of wide-base truck tyres on roadway. Int. J. Pavement Eng. 2020, 21, 122–133. [Google Scholar] [CrossRef]
- Hermange, C.; Oger, G.; Le Chenadec, Y.; Le Touzé, D. A 3D SPH–FE coupling for FSI problems and its application to tire hydroplaning simulations on rough ground. Comput. Meth. Appl. Mech. Eng. 2019, 355, 558–590. [Google Scholar] [CrossRef]
- Hermange, C.; Oger, G.; Le Chenadec, Y.; de Leffe, M.; Le Touzé, D. In-depth analysis of hydroplaning phenomenon accounting for tire wear on smooth ground. J. Fluids Struct. 2022, 111, 103555. [Google Scholar] [CrossRef]
- Spitzhuttl, F.; Goizet, F.; Unger, T.; Biesse, F. The real impact of full hydroplaning on driving safety. Accid. Anal. Prev. 2020, 138, 105458. [Google Scholar] [CrossRef]
- Hermange, C.; Todoroff, V.; Biesse, F.; Le-Chenadec, Y. Experimental investigation of the leading parameters influencing the hydroplaning phenomenon. Veh. Syst. Dyn. 2021, 60, 2375–2392. [Google Scholar] [CrossRef]
- Dreher, R.C.; Horne, W.B. Phenomena of Pneumatic Tire Hydroplaning. 1963. Available online: https://ntrs.nasa.gov/citations/19640000612 (accessed on 20 October 2024).
- Dehnad, M.H.; Khodaii, A. Evaluating the effect of different asphalt mixtures on hydroplaning using a new lab-scale apparatus. Pet. Sci. Technol. 2016, 34, 1726–1733. [Google Scholar] [CrossRef]
- Srirangam, S.K.; Anupam, K.; Scarpas, A.; Kasbergen, C.; Kane, M. Safety Aspects of Wet Asphalt Pavement Surfaces through Field and Numerical Modeling Investigations. Transp. Res. Record 2014, 2446, 37–51. [Google Scholar] [CrossRef]
- Zheng, B.; Huang, X.; Zhang, W.; Zhao, R.; Zhu, S. Adhesion characteristics of tire-asphalt pavement interface based on a proposed tire hydroplaning model. Adv. Mater. Sci. Eng. 2018, 2018, 5916180. [Google Scholar] [CrossRef]
- Suzuki, T.; Fujikawa, T. Improvement of Hydroplaning Performance Based on Water Flow around Tires. SAE Trans. 2001, 110, 830–835. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, Z.; Jiang, B.; Wang, H.; Wang, G.; Qian, H. Optimization of tire tread pattern based on flow characteristics to improve hydroplaning resistance. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2020, 234, 2961–2974. [Google Scholar] [CrossRef]
- Löwer, J.; Wagner, P.; Unrau, H.J.; Bederna, C.; Gauterin, F. Dynamic measurement of the fluid pressure in the tire contact area on wet roads. Automot. Engine Technol. 2020, 5, 29–36. [Google Scholar] [CrossRef]
- Allbert, B.J. Tires and Hydroplaning. SAE Trans. 1968, 77, 593–603. Available online: https://www.jstor.org/stable/44565087 (accessed on 20 October 2024).
- Ong, G.P.; Fwa, T.F. Wet-Pavement Hydroplaning Risk and Skid Resistance: Modeling. J. Transp. Eng. 2007, 133, 590–598. [Google Scholar] [CrossRef]
- Ong, G.P.; Fwa, T.F. Mechanistic Interpretation of Braking Distance Specifications and Pavement Friction Requirements. Transp. Res. Record 2010, 2155, 145–157. [Google Scholar] [CrossRef]
- Cho, J.; Lee, H.; Sohn, J.; Kim, G.; Woo, J. Numerical investigation of hydroplaning characteristics of three-dimensional patterned tire. Eur. J. Mech. A Solids 2006, 25, 914–926. [Google Scholar] [CrossRef]
- Wies, B.; Roeger, B.; Mundl, R. Influence of Pattern Void on Hydroplaning and Related Target Conflicts. Tire Sci. Technol. 2009, 37, 187–206. [Google Scholar] [CrossRef]
- El-Sayegh, Z.; El-Gindy, M.; Johansson, I.; Oijer, F. Modeling of Tire-Wet Surface Interaction Using Finite Element Analysis and Smoothed-Particle Hydrodynamics Techniques; SAE Technical Paper 2018-01-1118; SAE: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Kumar, S.S.; Anupam, K.; Scarpas, T.; Kasbergen, C. Study of Hydroplaning Risk on Rolling and Sliding Passenger Car. Procedia Soc. Behav. Sci. 2012, 53, 1019–1027. [Google Scholar] [CrossRef]
- Baranowski, P.; Małachowski, J.; Mazurkiewicz, Ł. Local blast wave interaction with tire structure. Def. Technol. 2020, 16, 520–529. [Google Scholar] [CrossRef]
- Liang, C.; Gao, Z.; Hong, S.; Wang, G.; Kwaku Asafo-Duho, B.M.; Ren, J.; Palumbo, D. A Fatigue Evaluation Method for Radial Tire Based on Strain Energy Density Gradient. Adv. Mater. Sci. Eng. 2021, 2021, 85349542. [Google Scholar] [CrossRef]
- Ge, Y.; Yan, Y.; Yan, X.; Meng, Z. Study on Static Stiffness Characteristics and Influencing Factors of Radial Pneumatic Tire with Complex Tread Patterns by Computer Simulation Method. In Proceedings of the 2022 2nd International Conference on Computational Modeling, Simulation and Data Analysis (CMSDA), Zhuhai, China, 2–4 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Q.; Pei, J.; Wang, Z.; Hu, D.; Huang, G.; Meng, Y.; Lyu, L.; Zheng, F. Analysis of tire-pavement interaction modeling and rolling energy consumption based on finite element simulation. Constr. Build Mater. 2024, 425, 136101. [Google Scholar] [CrossRef]
- Benevides, R.O.; Nunes, L.C.S. Mechanical behavior of the alumina-filled silicone rubber under pure shear at finite strain. Mech. Mater. 2015, 85, 57–65. [Google Scholar] [CrossRef]
- Goodchild, I.R.; Muhr, A.H.; Thomas, A.G. The lateral stiffness and damping of a stretched rubber beam. Plast. Rubber Compos. 2018, 47, 176–186. [Google Scholar] [CrossRef]
- Zhang, L.; Fwa, T.F.; Ong, G.P.; Chu, L. Analysing effect of roadway width on skid resistance of porous pavement. Road Mater. Pavement Des. 2015, 17, 1–14. [Google Scholar] [CrossRef]
- Pasindu, H.R.; Fwa, T.F.; Ong, G.P. Analytical evaluation of aircraft operational risks from runway rutting. Int. J. Pavement Eng. 2015, 17, 810–817. [Google Scholar] [CrossRef]
- Georgescu, A.; Nicolescu, B.; Popa, N.; Boloşteanu, M. On special solutions of the Reynolds equation from lubrication. J. Comput. Appl. Math. 2001, 133, 367–372. [Google Scholar] [CrossRef]
- Goyon, O. High-Reynolds number solutions of Navier-Stokes equations using incremental unknowns. Comput. Meth. Appl. Mech. Eng. 1996, 130, 319–335. [Google Scholar] [CrossRef]
- Dowson, D. A generalized Reynolds equation for fluid-film lubrication. Int. J. Mech. Sci. 1962, 4, 159–170. [Google Scholar] [CrossRef]
- Cho, J.R.; Lee, S.Y. Dynamic analysis of baffled fuel-storage tanks using the ALE finite element method. Int. J. Numer. Methods Fluids 2003, 41, 185–208. [Google Scholar] [CrossRef]
- Wang, N.; Chu, L.; Fwa, T.F. Improved method for evaluation of effect of pavement microtexture on vehicle hydroplaning speed. Constr. Build. Mater. 2024, 451, 138727. [Google Scholar] [CrossRef]
- Dehnad, M.H.; Yazdi, A. A review of numerical and experimental studies on hydroplaning of vehicles in motion on road surfaces. Results Eng. 2024, 23, 102438. [Google Scholar] [CrossRef]
- Fwa, T.F. Pavement skid resistance properties for safe aircraft operations. J. Road. Eng. 2024, 4, 361–385. [Google Scholar] [CrossRef]
- Cerezo, V.; Gothié, M.; Menissier, M.; Gibrat, T. Hydroplaning speed and infrastructure characteristics. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 891–898. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H. Analysis and mitigation of hydroplaning risk considering spatial-temporal water condition on the pavement surface. Int. J. Pavement Eng. 2023, 24, 2036988. [Google Scholar] [CrossRef]
- Meethum, P.; Suvanjumrat, C. Hydroplaning Effects of Tread Patterns of Motorcycle Tires. J. Transp. Eng. Part B Pavements 2025, 151, 04024052. [Google Scholar] [CrossRef]
- Chaiworapuek, W.; Suvanjumrat, C.; Worajinda, N.; Rugsaj, R. Development of contact area model for motorcycle tire hydroplaning through experimental investigation. Int. J. GEOMATE 2024, 26, 66–73. [Google Scholar] [CrossRef]



| Material | ||||
|---|---|---|---|---|
| Inner liner | 0 | 0.479368 | −0.17243 | 0.089642 |
| Rim cushion | 0 | 0.451268 | 0.15744 | 0.080273 |
| Bead filler | 0 | 0.467536 | −0.1742 | 0.081746 |
| Tread rubber | 0 | 1.198421 | −1.16347 | 0.924625 |
| Apex strip | 0 | 0.415456 | −0.17545 | 0.086256 |
| Sidewall | 0 | 0.521692 | 0.18646 | 0.092656 |
| Material | Tensile Modulus (MPa) | Poisson Ratio |
|---|---|---|
| Nylon overlay | 3000 | 0.38 |
| Belt | 20,000 | 0.45 |
| Carcass ply | 4000 | 0.38 |
| Bead wire | 70,000 | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, T.; Wang, S.; Cheng, D.; Zheng, L.; Ren, L. Effects of Driving Conditions on Tire Hydroplaning Performance. Lubricants 2025, 13, 76. https://doi.org/10.3390/lubricants13020076
Deng T, Wang S, Cheng D, Zheng L, Ren L. Effects of Driving Conditions on Tire Hydroplaning Performance. Lubricants. 2025; 13(2):76. https://doi.org/10.3390/lubricants13020076
Chicago/Turabian StyleDeng, Tuo, Shukun Wang, Dichuan Cheng, Long Zheng, and Luquan Ren. 2025. "Effects of Driving Conditions on Tire Hydroplaning Performance" Lubricants 13, no. 2: 76. https://doi.org/10.3390/lubricants13020076
APA StyleDeng, T., Wang, S., Cheng, D., Zheng, L., & Ren, L. (2025). Effects of Driving Conditions on Tire Hydroplaning Performance. Lubricants, 13(2), 76. https://doi.org/10.3390/lubricants13020076




