Parametric Structure Optimization Design of High-Pressure Abrasive Water Jet Nozzle Based on Computational Fluid Dynamics-Discrete Element Method (CFD-DEM)
Abstract
1. Introduction
2. Models and Methods
2.1. The Parametric Design Method of the HP-AWJ Nozzle
- (1)
- Converging tube angle α
- (2)
- Abrasive incidence angle θ
- (3)
- Abrasive feed height LDa
2.2. Multi-Parameter Optimization Method Based on Response Surface Methodology (RSM)
3. Results and Discussion
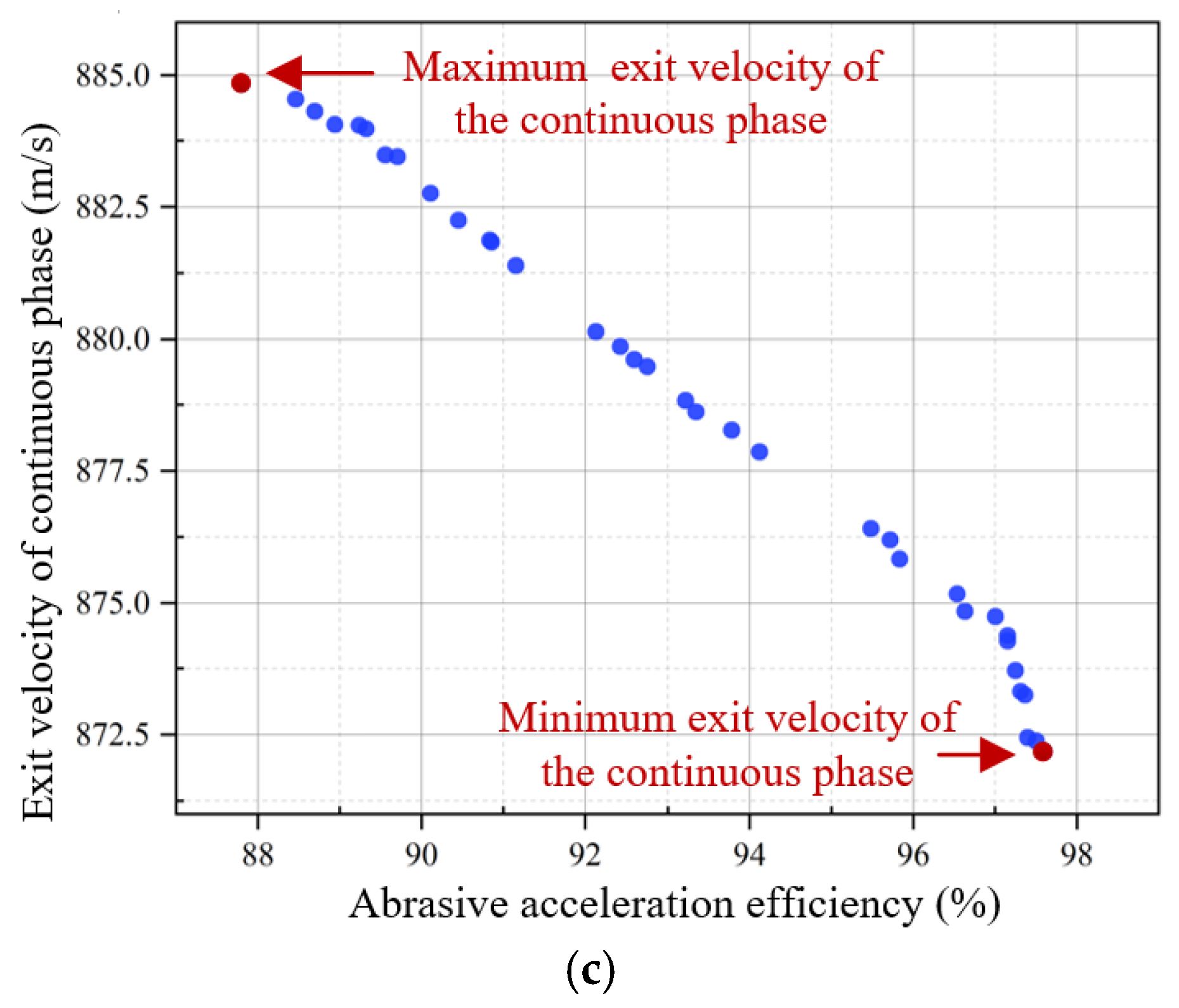
3.1. Analysis on the Exit Velocity of the Flow Field
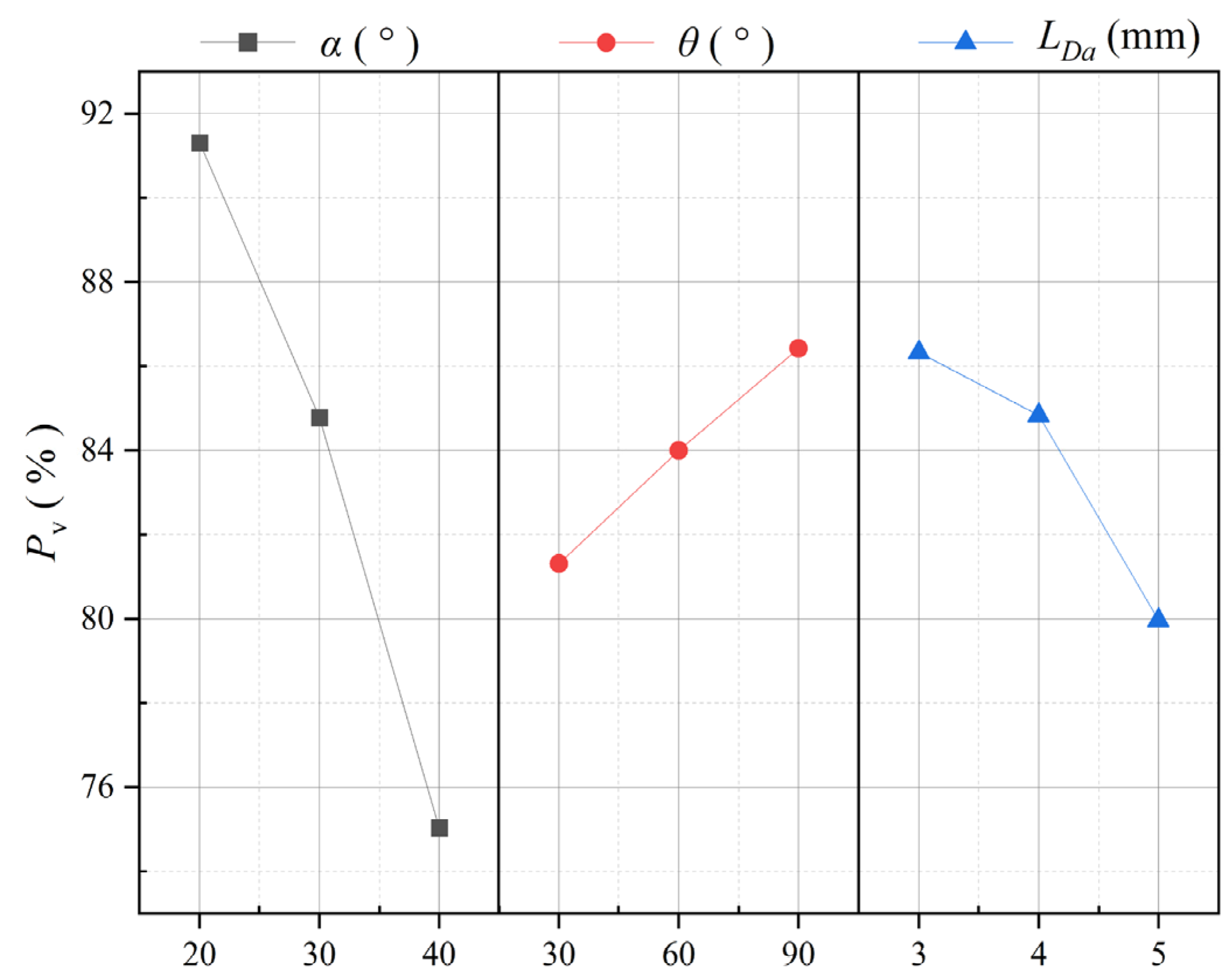
3.2. Analysis of Particle Acceleration Efficiency
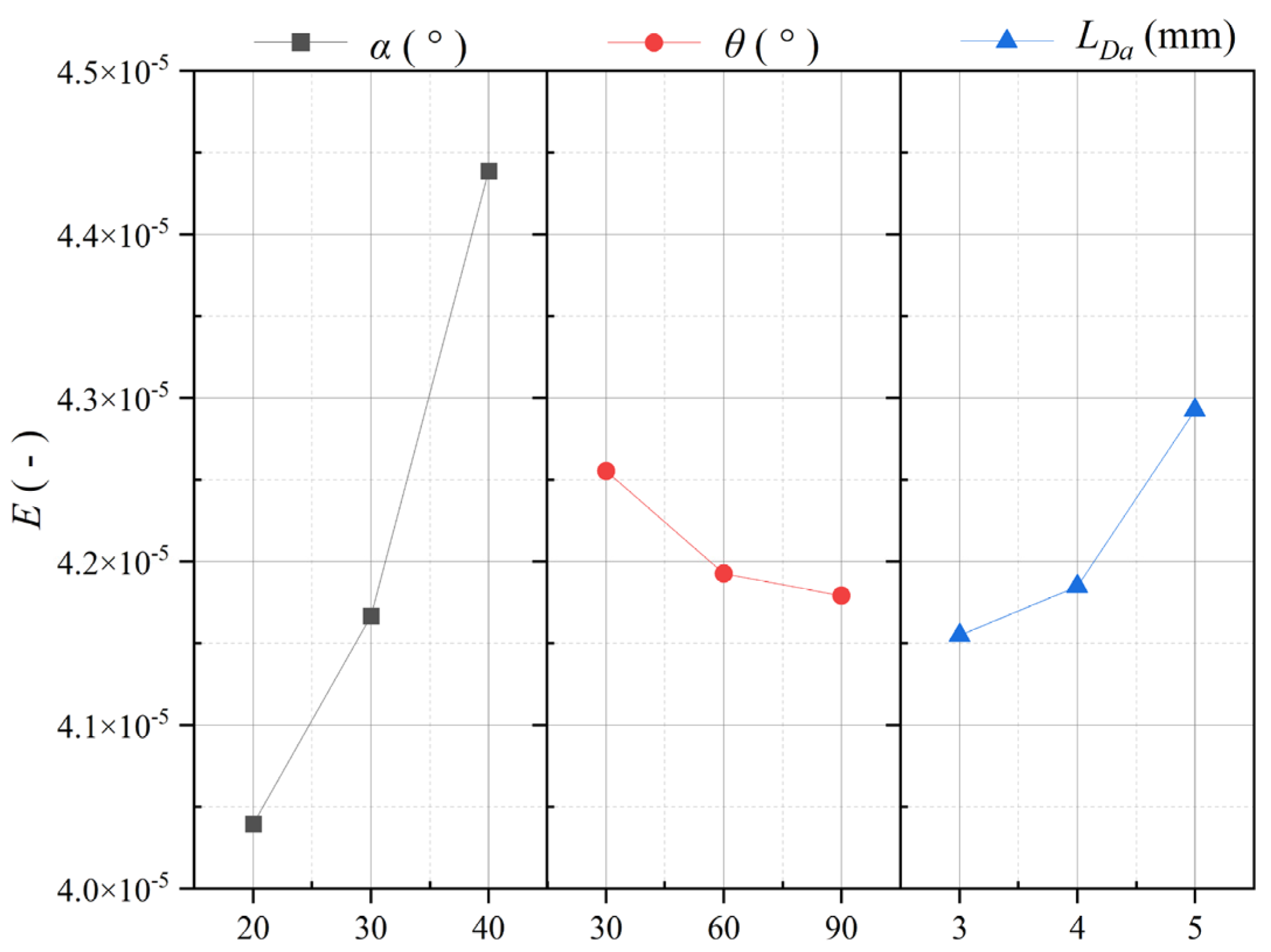
3.3. Analysis of Wear Rate of Nozzle Wall E
3.4. Nozzle Structure Optimization Based on HTS Algorithm
3.4.1. Heat Conduction Stage
3.4.2. Convection Stage
3.4.3. Radiation Stage
3.5. Multi-Objective and Multi-Response Optimization of Nozzle Structure Based on MOHTS Algorithm
4. Conclusions
- (1)
- A mathematical regression model was generated using the RSM technique, and the results of the ANOVA method showed the applicability of the developed model.
- (2)
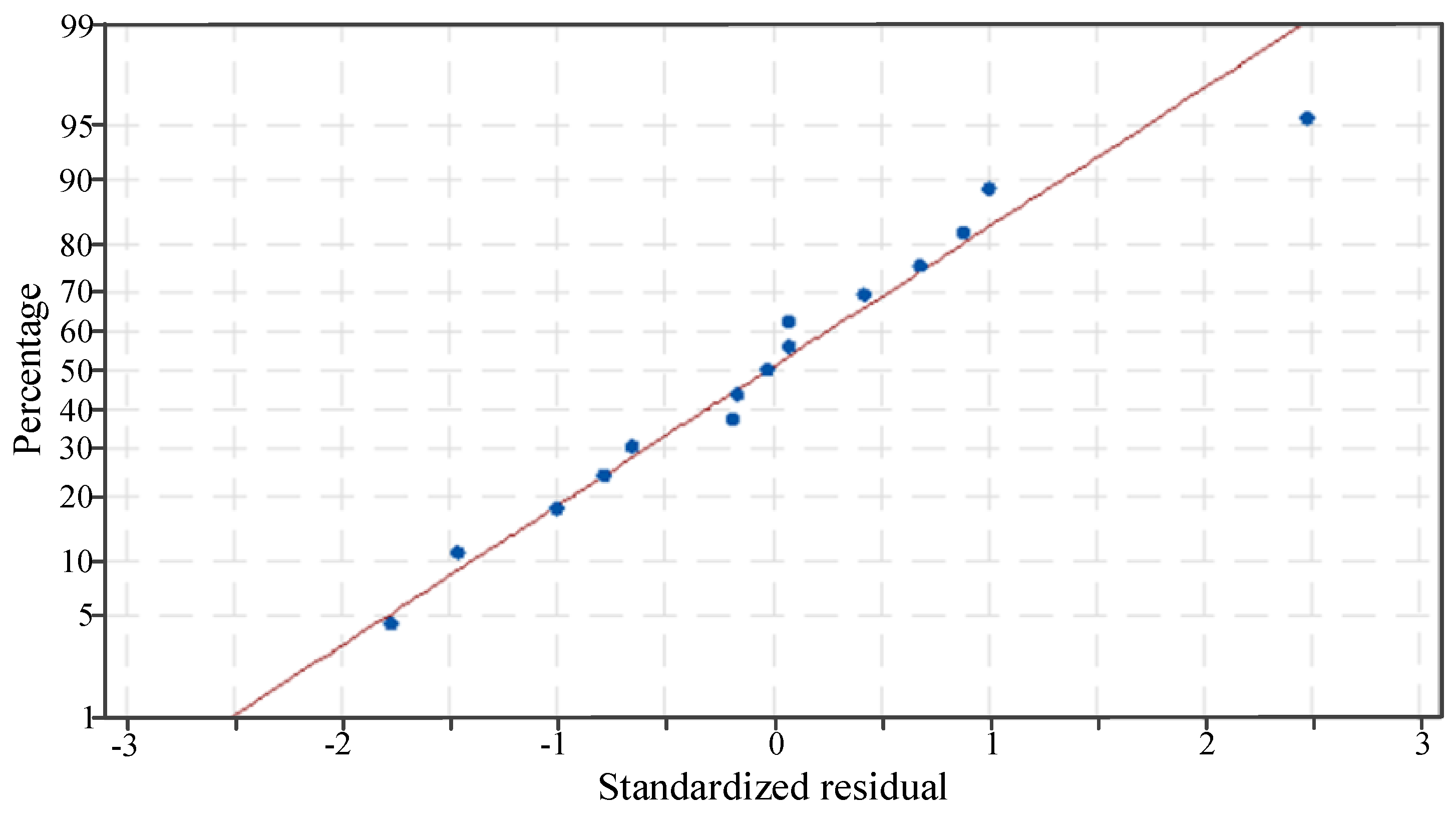
- The probability of normality, the importance of the model terms and the missing fitting insignificance of all responses highlighted the good prediction ability of the developed model in predicting the exit velocity of the flow field, the particle acceleration efficiency and the wear rate of the focusing tube.
- (3)
- The optimization results of the HTS algorithm based on a single objective showed that the maximum exit velocity of the flow field was 876.98 m/s under the conditions α = 20°, θ = 90° and LDa = 5 mm. The maximum particle acceleration efficiency was 95.132% and the minimum wear rate of the focusing tube was 4.1026 × 10−5 under the conditions α = 20°, θ = 90° and LDa = 3 mm.
- (4)
- Considering the optimal results of the response values, a weight ratio of 0.33 was assigned to all response surfaces to obtain two optimal results of the exit velocity of the flow field , the particle acceleration efficiency Pv and the wear rate of the focusing tube E. The optimal results were as follows: = 883.1263 m/s, Pv = 89.6432% and E = 4.0461 × 10−5 (when α = 20°, θ = 30° and LDa = 4.2 mm) and = 883.5880 m/s, Pv = 89.6239% and E = 4.0435 × 10−5 (when α = 20°, θ = 31° and LDa = 3.7 mm).
- (5)
- The 3D Pareto diagram and its 2D projection diagrams in the XY, ZY and XZ planes were drawn according to the best advantages of the Pareto values. Non-dominated feasible solutions are highlighted in the figures. Each Pareto point provided a unique solution with corresponding design parameter values for the HP-AWJ nozzle. The appropriate result point could be selected by observing the results of the desired exit velocity of the flow field, the particle acceleration efficiency and the wear rate of the focusing tube.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oh, T.-M.; Cho, G.-C. Rock cutting depth model based on kinetic energy of abrasive waterjet. Rock Mech. Rock Eng. 2016, 49, 1059–1072. [Google Scholar] [CrossRef]
- Fowler, G.; Pashby, I.R.; Shipway, P.H. The effect of particle hardness and shape when abrasive water jet milling titanium alloy Ti6Al4V. Wear 2009, 266, 613–620. [Google Scholar] [CrossRef]
- Yuvaraj, N.; Kumar, M.P. Cutting of aluminium alloy with abrasive water jet and cryogenic assisted abrasive water jet: A comparative study of the surface integrity approach. Wear 2016, 362, 18–32. [Google Scholar] [CrossRef]
- Nanduri, M.; Taggart, D.G.; Kim, T.J. A study of nozzle wear in abrasive entrained water jetting environment. J. Trib. 2000, 122, 465–471. [Google Scholar] [CrossRef]
- Paola, B.A.; Barreto, C.T. A microscopic study on kerfs in rocks subjected to abrasive waterjet cutting. Wear 2020, 448, 203210. [Google Scholar]
- Gupta, A. Performance optimization of abrasive fluid jet for completion and stimulation of oil and gas wells. J. Energy Resour. Technol. 2012, 134, 021001. [Google Scholar] [CrossRef]
- Zou, X.; Fu, L.; Wu, L.; Zuo, W. Research on Multiphase Flow and Nozzle Wear in a High-Pressure Abrasive Water Jet Cutting Head. Machines 2023, 11, 614. [Google Scholar] [CrossRef]
- Wang, X.; Ge, Z.; Deng, Q.; Yao, Z.; Cui, Y.; Ge, B. Effects of nozzle inner surface wear ontherock-breakingability of premixed abrasive water jets. OceanEngineering 2025, 322, 120548. [Google Scholar]
- Shao, C.; Ge, Z.; Zhou, Z.; Liu, W.; Li, Z.; Tian, C.; Chang, W. Experimental and numerical investigation of abrasive water jet nozzle erosion. Powder Technol. 2023, 430, 119031. [Google Scholar] [CrossRef]
- Li, Z.; Yao, S.; Yun, F.; Wang, X.; Wang, L.; Wu, Y. Simulation and Optimization of the Nozzle Section Geometry for a Suspension Abrasive Water Jet. Machines 2021, 10, 3. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Zhang, J.; Feng, L.; Liu, H.; Hao, C. Structural optimization design of ice abrasive water jet nozzle based on multi-objective algorithm. Flow Meas. Instrum. 2024, 97, 102586. [Google Scholar] [CrossRef]
- Schwartzentruber, J.; Narayanan, C.; Papini, M.; Liu, H. Optimized abrasive waterjet nozzle design using genetic algorithms. In Proceedings of the 23rd International Conference on Water Jetting, Seattle, WA, USA, 16–18 November 2016. [Google Scholar]
- Qiang, Z.; Miao, X.; Wu, M.; Sawhney, R. Optimization of abrasive waterjet machining using multi-objective cuckoo search algorithm. Int. J. Adv. Manuf. Technol. 2018, 99, 1257–1266. [Google Scholar] [CrossRef]
- Perec, A.; Radomaka-Zalas, A.; Fajdek-Bieda, A.; Pude, F. Process Optimization by Applying the Response Surface Methodology (RSM) to the Abrasive Suspension Water Jet Cutting of Phenolic Composites. FU Mech Eng. 2023, 21, 575. [Google Scholar] [CrossRef]
- Kawecka, E. The Whale Optimization Algorithm in Abrasive Water Jet Machining of Tool Steel. Procedia Comput. Sci. 2023, 225, 1037–1044. [Google Scholar] [CrossRef]
- Kawecka, E. The use of metaheuristic optimization algorithm in abrasive water jet machining of white marble. AIP Conf. Proc. 2024, 3130, 020015. [Google Scholar]
- Perec, A. Desirability Function Analysis (DFA) in Multiple Responses Optimization of Abrasive Water Jet Cutting Process. Rep. Mech. Eng. 2022, 3, 11–19. [Google Scholar] [CrossRef]
- Perec, A.; Kawecka, E.; Radomaka-Zalas, A.; Pude, F. Optimization of Abrasive Waterjet Cutting by Using the CODAS Method with Regard to Interdependent Processing Parameters. Stroj. Vestn. J. Mech. Eng. 2023, 69, 367–375. [Google Scholar] [CrossRef]
- Perec, A.; Kawecka, E. Modeling of the Abrasive Water Jet machining by ANN in uncertainty conditions. Procedia Comput. Sci. 2024, 246, 2176–2184. [Google Scholar] [CrossRef]
- Rao, R.V.; Rai, D.P.; Balic, J. Multi-objective optimization of abrasive waterjet machining process using Jaya algorithm and PROMETHEE Method. J. Intell. Manuf. 2019, 30, 2101–2127. [Google Scholar] [CrossRef]
- Shukla, R.; Singh, D. Experimentation investigation of abrasive water jet machining parameters using Taguchi and Evolutionary optimization techniques. Swarm Evol. Comput. 2017, 32, 167–183. [Google Scholar] [CrossRef]
- Santhanakumar, M.; Adalarasan, R.; Rajmohan, M. Experimental modelling and analysis in abrasive waterjet cutting of ceramic tiles using grey-based response surface methodology. Arab. J. Sci. Eng. 2015, 40, 3299–3311. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mitra, A. Parametric optimization of abrasive water-jet machining processes using grey wolf optimizer. Mater. Manuf. Process. 2018, 33, 1471–1482. [Google Scholar] [CrossRef]
- Pawar, P.J.; Vidhate, U.S.; Khalkar, M.Y. Improving the quality characteristics of abrasive water jet machining of marble material using multi-objective artificial bee colony, algorithm. J. Comput. Des. Eng. 2018, 5, 319–328. [Google Scholar] [CrossRef]
- Qiang, Z.; Wu, M.; Miao, X.; Sawhney, R. CFD research on particle movement and nozzle wear in the abrasive water jet cutting head. Int. J. Adv. Manuf. Technol. 2018, 95, 4091–4100. [Google Scholar] [CrossRef]
- Tamilarasan, A.; Renugambal, A.; Manikanta, D.; Reddy, G.S.; Sravankumar, K.; Sreekar, B.; Prasadreddy, G.V. Application of crow search algorithm for the optimization of abrasive water jet cutting process parameters. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Tamilnadu, India, 8–9 March 2018. [Google Scholar]
- Arumugam, S.; Chengareddy, P.; Tamilarasan, A.; Santhanam, V. RSM and crow search algorithm-based optimization of ultrasonicated transesterification process parameters on synthesis of polyol ester-based biolubricant. Arab. J. Sci. Eng. 2019, 44, 5535–5548. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.J.; Mani Prabu, S.S.; Palani, I.A.; Patel, V.K.; Parikh, D.M.; de Lacalle, L.N.L. Multi-response optimization of WEDM process parameters for machining of superelastic nitinol shape-memory alloy using a heat-transfer search algorithm. Materials 2019, 12, 1277. [Google Scholar] [CrossRef] [PubMed]
- Chaudhari, R.; Vora, J.J.; Prabu, S.M.; Palani, I.A.; Patel, V.K.; Parikh, D.M. Pareto optimization of WEDM process parameters for machining a NiTi shape memory alloy using a combined approach of RSM and heat transfer search algorithm. Adv. Manuf. 2021, 9, 64–80. [Google Scholar] [CrossRef]
- Wankhede, V.; Jagetiya, D.; Joshi, A.; Chaudhari, R. Experimental investigation of FDM process parameters using Taguchi analysis. Mater. Today Proc. 2020, 27, 2117–2120. [Google Scholar] [CrossRef]
- Chaurasia, A.; Wankhede, V.; Chaudhari, R. Experimental investigation of high-speed turning of INCONEL 718 using PVD-coated carbide tool under wet condition. In Proceedings of the Innovations in Infrastructure: Proceedings of ICIIF, Singapore, 29 September 2018. [Google Scholar]
- Sheth, M.; Gajjar, K.; Jain, A.; Shah, V.; Patel, H.; Chaudhari, R.; Vora, J. Multi-objective optimization of inconel 718 using Combined approach of taguchi—Grey relational analysis. In Proceedings of the Advances in Mechanical Engineering: Select Proceedings of ICAME 2020, Singapore, 30 June 2020. [Google Scholar]
- Chaudhari, R.; Vora, J.; López de Lacalle, L.N.; Khanna, S.; Patel, V.K.; Ayesta, I. Parametric optimization and effect of nano-graphene mixed dielectric fluid on performance of wire electrical discharge machining process of Ni55. 8Ti shape memory alloy. Materials 2021, 14, 2533. [Google Scholar] [CrossRef]
- Kumar, S.; Tejani, G.G.; Pholdee, N.; Bureerat, S. Multi-objective modified heat transfer search for truss optimization. Eng. Comput. 2021, 37, 3439–3454. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.J.; Patel, V.; Lacalle, L.L.D.; Parikh, D.M. Effect of WEDM process parameters on surface morphology of nitinol shape memory alloy. Materials 2020, 13, 4943. [Google Scholar] [CrossRef] [PubMed]
- Tejani, G.G.; Kumar, S.; Gandomi, A.H. Multi-objective heat transfer search algorithm for truss optimization. Eng. Comput. 2021, 37, 641–662. [Google Scholar] [CrossRef]
- Kumar, S.; Tejani, G.G.; Pholdee, N.; Bureerat, S. Multi-objective passing vehicle search algorithm for structure optimization. Expert Syst. Appl. 2021, 169, 114511. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.J.; Patel, V.; López de Lacalle, L.N.; Parikh, D.M. Surface analysis of wire-electrical-discharge-machining-processed shape-memory alloys. Materials 2020, 13, 530. [Google Scholar] [CrossRef]

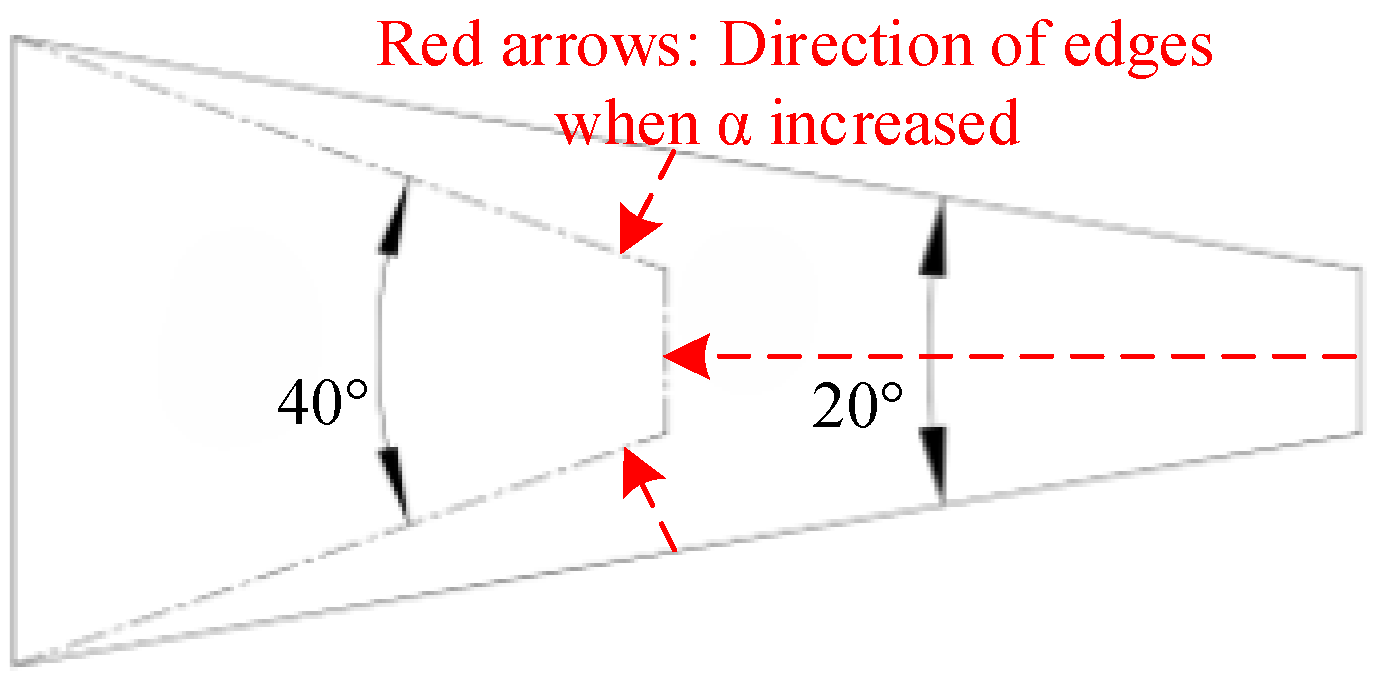
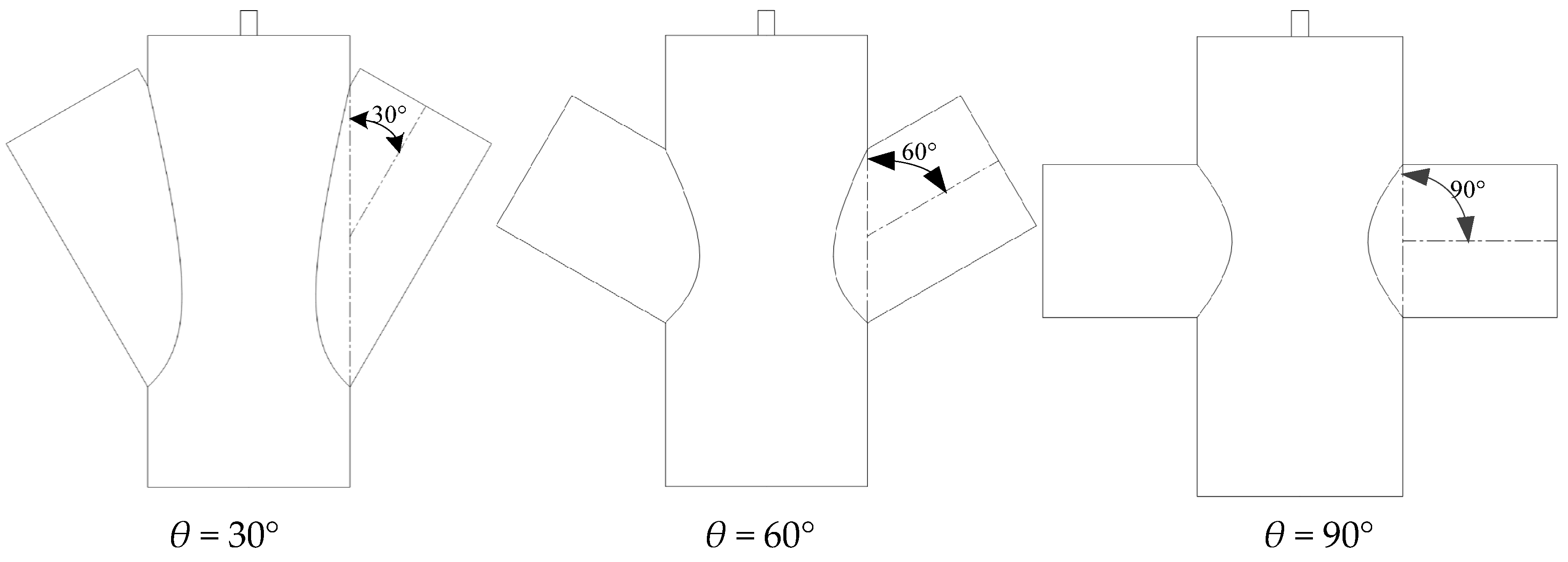

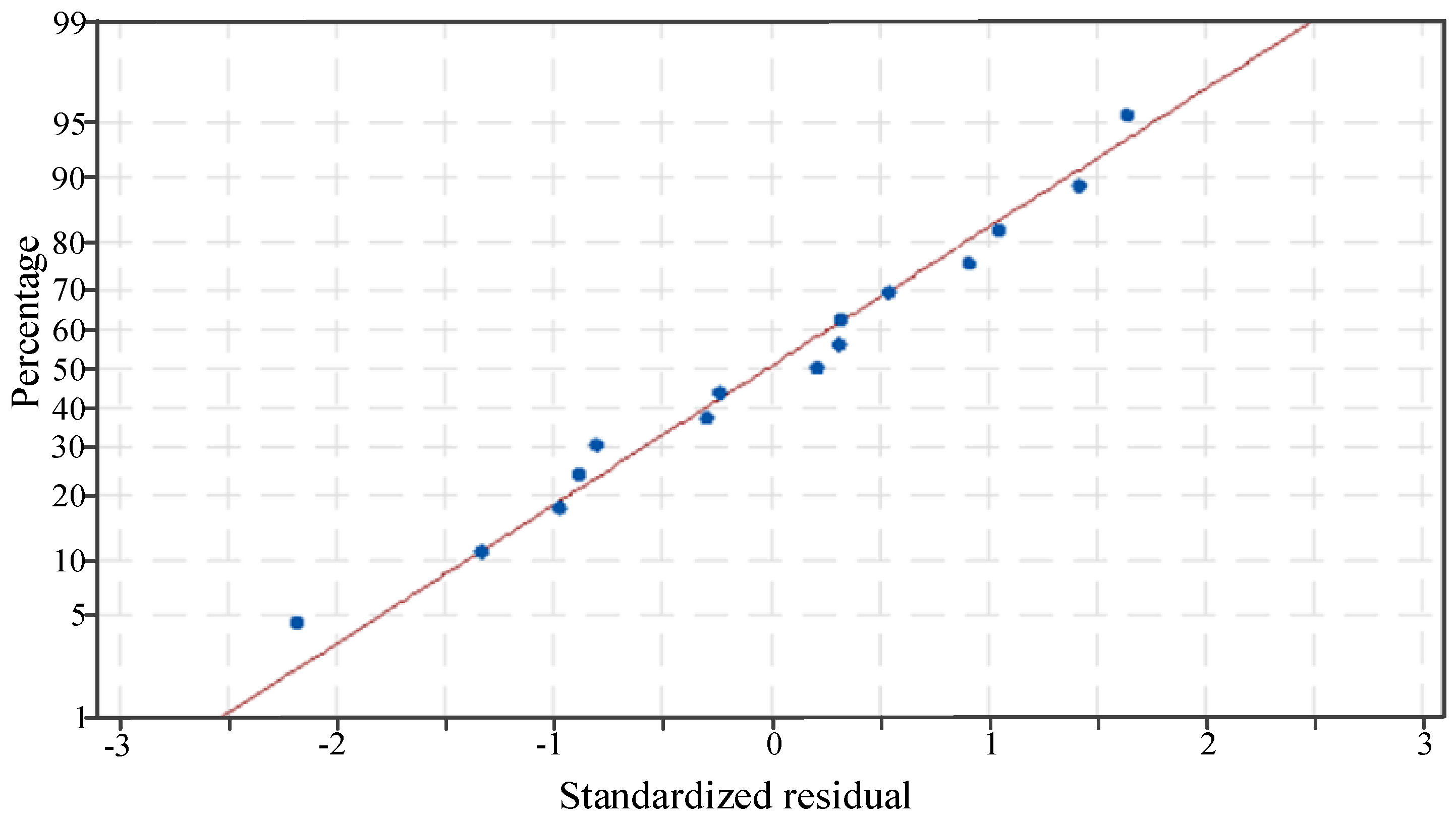
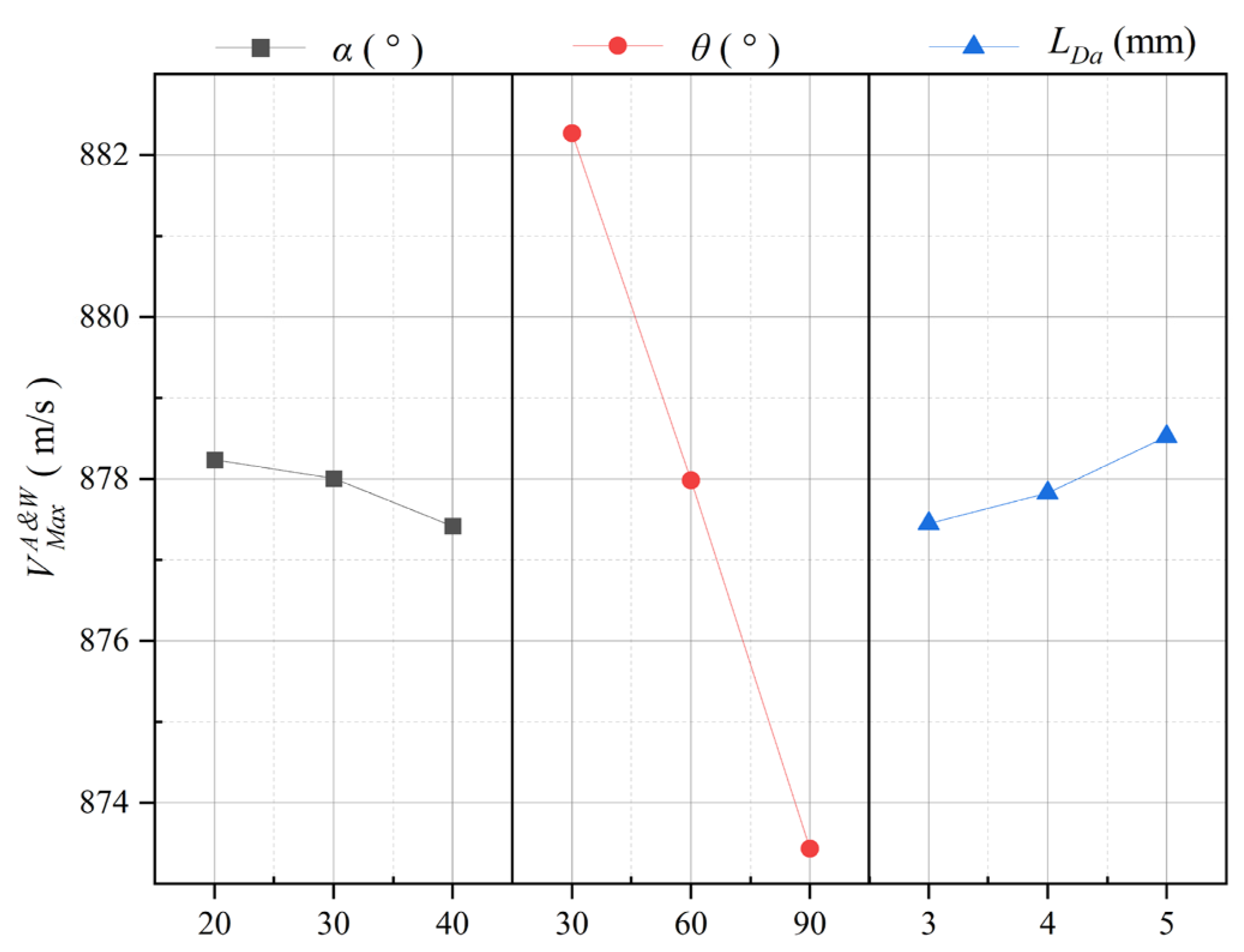



| Condition | α (°) | θ (°) | LDa (mm) | (m/s) | Pv (%) | E (-) |
|---|---|---|---|---|---|---|
| 1 | 40 | 60 | 5.0 | 878.6886 | 73.0298 | 4.4978 × 10−5 |
| 2 | 20 | 30 | 4.0 | 882.6022 | 89.5365 | 4.0365 × 10−5 |
| 3 | 30 | 60 | 4.0 | 877.5058 | 86.4968 | 4.1115 × 10−5 |
| 4 | 40 | 30 | 4.0 | 881.2112 | 73.4514 | 4.4875 × 10−5 |
| 5 | 20 | 60 | 3.0 | 878.6987 | 93.4329 | 3.9843 × 10−5 |
| 6 | 20 | 90 | 4.0 | 872.9613 | 95.6093 | 4.0318 × 10−5 |
| 7 | 30 | 90 | 3.0 | 871.7260 | 93.5406 | 4.0087 × 10−5 |
| 8 | 30 | 60 | 4.0 | 878.0717 | 85.9014 | 4.1257 × 10−5 |
| 9 | 30 | 30 | 5.0 | 881.6780 | 80.6306 | 4.2658 × 10−5 |
| 10 | 20 | 60 | 5.0 | 878.6987 | 86.6962 | 4.1068 × 10−5 |
| 11 | 40 | 90 | 4.0 | 874.0072 | 77.0016 | 4.3752 × 10−5 |
| 12 | 30 | 60 | 4.0 | 878.4459 | 85.8025 | 4.1257 × 10−5 |
| 13 | 40 | 60 | 3.0 | 875.7800 | 76.6479 | 4.3954 × 10−5 |
| 14 | 30 | 90 | 5.0 | 875.0341 | 79.5243 | 4.3003 × 10−5 |
| 15 | 30 | 30 | 3.0 | 883.5884 | 81.6582 | 4.2316 × 10−5 |
| Parameters | Values |
|---|---|
| Water pressure (MPa) | 400 |
| Inlet pressure of abrasive particles and air (Pa) | 101,325 |
| Outlet pressure of the nozzle (Pa) | 101,325 |
| Size of abrasive particles (mm) | 0.125 |
| Source of Variance | Degrees of Freedom | Sum of Squares | Mean Square Error | Value of F | Value of p | Significance |
|---|---|---|---|---|---|---|
| Model | 6 | 170.279 | 28.380 | 104.36 | <0.001 | Significant |
| Linear primary | 3 | 159.871 | 53.290 | 195.96 | <0.001 | Significant |
| α | 1 | 1.340 | 1.340 | 4.93 | 0.057 | Significant |
| θ | 1 | 156.213 | 156.213 | 574.42 | <0.001 | Significant |
| LDa | 1 | 2.318 | 2.318 | 8.52 | 0.019 | Significant |
| Two-factor interaction | 3 | 10.408 | 3.469 | 12.76 | 0.002 | Significant |
| α × θ | 1 | 1.485 | 1.485 | 5.46 | 0.048 | Significant |
| α × LDa | 1 | 2.115 | 2.115 | 7.78 | 0.024 | Significant |
| θ × LDa | 1 | 6.808 | 6.808 | 25.04 | 0.001 | Significant |
| Error | 8 | 2.176 | 0.272 | |||
| Lack of fit | 6 | 1.728 | 0.288 | 1.29 | 0.499 | Insignificant |
| Pure error | 2 | 0.448 | 0.224 | |||
| Total | 14 | 172.454 |
| Source of Variance | Degrees of Freedom | Sum of Squares | Mean Square Error | Value of F | Value of p | Significance |
|---|---|---|---|---|---|---|
| Model | 6 | 727.214 | 121.202 | 96.67 | <0.001 | Significant |
| Linear primary | 3 | 663.123 | 221.041 | 176.31 | <0.001 | Significant |
| α | 1 | 530.471 | 530.471 | 423.12 | <0.001 | Significant |
| θ | 1 | 52.015 | 52.015 | 41.49 | <0.001 | Significant |
| LDa | 1 | 80.637 | 80.637 | 64.32 | <0.001 | Significant |
| Two-factor interaction | 1 | 42.176 | 42.176 | 33.64 | <0.001 | Significant |
| θ × LDa | 1 | 42.176 | 42.176 | 33.64 | <0.001 | Significant |
| Linear square | 2 | 21.915 | 10.958 | 8.74 | 0.010 | Significant |
| α × α | 1 | 11.335 | 11.335 | 9.04 | 0.017 | Significant |
| LDa × LDa | 1 | 12.144 | 12.144 | 9.69 | 0.014 | Significant |
| Error | 8 | 10.030 | 1.254 | |||
| Lack of fit | 6 | 9.748 | 1.625 | 11.52 | 0.082 | Insignificant |
| Pure error | 2 | 0.282 | 0.141 | |||
| Total | 14 |
| Source of Variance | Degrees of Freedom | Sum of Squares | Mean Square Error | Value of F | Value of p | Significance |
|---|---|---|---|---|---|---|
| Model | 8 | 4.187 × 10−11 | 5.234 × 10−12 | 145.52 | <0.001 | Significant |
| Linear primary | 3 | 3.681 × 10−11 | 1.227 × 10−11 | 341.25 | <0.001 | Significant |
| α | 1 | 3.186 × 10−11 | 3.186 × 10−11 | 885.94 | <0.001 | Significant |
| θ | 1 | 1.165 × 10−12 | 1.165 × 10−12 | 32.38 | 0.001 | Significant |
| LDa | 1 | 3.792 × 10−12 | 3.792 × 10−12 | 105.42 | <0.001 | Significant |
| Two-factor interaction | 2 | 1.946 × 10−12 | 9.730 × 10−13 | 27.05 | 0.001 | Significant |
| α × θ | 1 | 2.894 × 10−13 | 2.894 × 10−13 | 8.05 | 0.030 | Significant |
| θ × LDa | 1 | 1.656 × 10−12 | 1.656 × 10−12 | 46.06 | 0.001 | Significant |
| Linear square | 3 | 3.105 × 10−12 | 1.035 × 10−12 | 28.77 | 0.001 | Significant |
| α × α | 1 | 2.253 × 10−12 | 2.253 × 10−12 | 62.65 | <0.001 | Significant |
| θ × θ | 1 | 4.177 × 10−13 | 4.177 × 10−13 | 11.61 | 0.014 | Significant |
| LDa × LDa | 1 | 8.145 × 10−13 | 8.145 × 10−13 | 22.65 | 0.003 | Significant |
| Error | 6 | 2.158 × 10−13 | 3.597 × 10−14 | |||
| Lack of fit | 4 | 2.023 × 10−13 | 5.058 × 10−14 | 7.50 | 0.121 | Insignificant |
| Pure error | 2 | 1.349 × 10−14 | 6.745 × 10−15 | |||
| Total | 14 | 4.209 × 10−11 |
| Optimized Result | α (°) | θ (°) | LDa (mm) | (m/s) | Pv (%) | E (-) |
|---|---|---|---|---|---|---|
| Maximum | 20 | 30 | 5 | 876.98 | 92.33 | 4.3856 × 10−5 |
| Maximum Pv | 20 | 90 | 3 | 870.44 | 95.13 | 4.1026 × 10−5 |
| Minimum E | 20 | 90 | 3 | 870.44 | 95.13 | 4.1026 × 10−5 |
| Condition | α (°) | θ (°) | LDa (mm) | (m/s) | Pv (%) | E (-) |
|---|---|---|---|---|---|---|
| 1 | 20 | 30 | 4.2 | 883.1263 | 89.6432 | 4.0461 × 10−5 |
| 2 | 20 | 31 | 3.7 | 883.5880 | 89.6239 | 4.0435 × 10−5 |
| Number | α (°) | θ (°) | LDa (mm) | (m/s) | Pv (%) | E (-) |
|---|---|---|---|---|---|---|
| 1 | 20 | 30 | 3 | 884.84 | 87.792 | 4.1212 × 10−5 |
| 2 | 20 | 90 | 3 | 872.18 | 97.597 | 3.9700 × 10−5 |
| 3 | 20 | 89 | 3.1 | 872.46 | 97.397 | 3.9731 × 10−5 |
| 4 | 20 | 80 | 3.2 | 874.39 | 97.149 | 3.9803 × 10−5 |
| 5 | 20 | 30 | 3.5 | 884.06 | 89.236 | 4.0871 × 10−5 |
| 6 | 20 | 32 | 3.3 | 884.07 | 88.935 | 4.0934 × 10−5 |
| 7 | 20 | 89 | 3 | 872.39 | 97.497 | 3.9703 × 10−5 |
| 8 | 20 | 34 | 3.4 | 883.49 | 89.548 | 4.0786 × 10−5 |
| 9 | 20 | 51 | 3.4 | 880.15 | 92.122 | 4.0272 × 10−5 |
| 10 | 20 | 80 | 3 | 874.29 | 97.154 | 3.9765 × 10−5 |
| 11 | 20 | 31 | 3.2 | 884.31 | 88.693 | 4.0994 × 10−5 |
| 12 | 20 | 59 | 3.4 | 878.63 | 93.342 | 4.0110 × 10−5 |
| 13 | 20 | 85 | 3 | 873.26 | 97.367 | 3.9730 × 10−5 |
| 14 | 20 | 61 | 3.2 | 878.27 | 93.777 | 4.0068 × 10−5 |
| 15 | 20 | 38 | 3.3 | 882.76 | 90.099 | 4.0661 × 10−5 |
| 16 | 20 | 42 | 3.5 | 881.87 | 90.826 | 4.0501 × 10−5 |
| 17 | 20 | 63 | 3.2 | 877.87 | 94.119 | 4.0029 × 10−5 |
| 18 | 20 | 71 | 3 | 876.19 | 95.715 | 3.9888 × 10−5 |
| 19 | 20 | 78 | 3.2 | 874.85 | 96.625 | 3.9843 × 10−5 |
| 20 | 20 | 44 | 3.6 | 881.39 | 91.148 | 4.0433 × 10−5 |
| 21 | 20 | 42 | 3.5 | 881.84 | 90.844 | 4.0496 × 10−5 |
| 22 | 20 | 73 | 3.2 | 875.84 | 95.836 | 3.9879 × 10−5 |
| 23 | 20 | 31 | 3.8 | 883.46 | 89.698 | 4.0766 × 10−5 |
| 24 | 20 | 53 | 3.3 | 879.86 | 92.425 | 4.0242 × 10−5 |
| 25 | 20 | 76 | 3.1 | 875.18 | 96.536 | 3.9826 × 10−5 |
| 26 | 20 | 83 | 3.1 | 873.73 | 97.247 | 3.9761 × 10−5 |
| 27 | 20 | 70 | 3.1 | 876.41 | 95.485 | 3.9904 × 10−5 |
| 28 | 20 | 58 | 3.3 | 878.84 | 93.217 | 4.0126 × 10−5 |
| 29 | 20 | 30 | 3.6 | 883.98 | 89.322 | 4.0852 × 10−5 |
| 30 | 20 | 38 | 3.8 | 882.25 | 90.439 | 4.0577 × 10−5 |
| 31 | 20 | 78 | 3 | 874.74 | 97.005 | 3.9793 × 10−5 |
| 32 | 20 | 54 | 3.4 | 879.61 | 92.586 | 4.0208 × 10−5 |
| 33 | 20 | 55 | 3.2 | 879.49 | 92.747 | 4.0202 × 10−5 |
| 34 | 20 | 30 | 3.2 | 884.55 | 88.458 | 4.1052 × 10−5 |
| 35 | 20 | 85 | 3.1 | 873.32 | 97.306 | 3.9756 × 10−5 |
| α (°) | θ (°) | LDa (mm) | Predicted Value of MOHTS Algorithm | Simulation Verification Data | Error (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(m/s) | Pv (%) | E (-) | (m/s) | Pv (%) | E (-) | ||||||
| 20 | 30 | 3 | 884.84 | 87.792 | 4.1212 × 10−5 | 880.95 | 90.48 | 4.2683 × 10−5 | 0.44 | 3.06 | 3.57 |
| 20 | 38 | 3.8 | 882.25 | 90.439 | 4.0577 × 10−5 | 878.46 | 93.66 | 4.2022 × 10−5 | 0.43 | 3.56 | 3.37 |
| 20 | 58 | 3.3 | 878.84 | 93.217 | 4.0126 × 10−5 | 871.99 | 96.14 | 4.1683 × 10−5 | 0.78 | 3.14 | 3.88 |
| 20 | 90 | 3 | 872.18 | 97.597 | 3.9700 × 10−5 | 870.44 | 95.13 | 4.1026 × 10−5 | 0.20 | 2.53 | 3.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zou, X.; Guo, Y.; Fu, L. Parametric Structure Optimization Design of High-Pressure Abrasive Water Jet Nozzle Based on Computational Fluid Dynamics-Discrete Element Method (CFD-DEM). Lubricants 2025, 13, 91. https://doi.org/10.3390/lubricants13020091
Wu L, Zou X, Guo Y, Fu L. Parametric Structure Optimization Design of High-Pressure Abrasive Water Jet Nozzle Based on Computational Fluid Dynamics-Discrete Element Method (CFD-DEM). Lubricants. 2025; 13(2):91. https://doi.org/10.3390/lubricants13020091
Chicago/Turabian StyleWu, Lin, Xiang Zou, Yuan Guo, and Liandong Fu. 2025. "Parametric Structure Optimization Design of High-Pressure Abrasive Water Jet Nozzle Based on Computational Fluid Dynamics-Discrete Element Method (CFD-DEM)" Lubricants 13, no. 2: 91. https://doi.org/10.3390/lubricants13020091
APA StyleWu, L., Zou, X., Guo, Y., & Fu, L. (2025). Parametric Structure Optimization Design of High-Pressure Abrasive Water Jet Nozzle Based on Computational Fluid Dynamics-Discrete Element Method (CFD-DEM). Lubricants, 13(2), 91. https://doi.org/10.3390/lubricants13020091




