Research on Feature Extraction Method and Process Optimization of Rolling Bearing Faults Based on Electrostatic Monitoring
Abstract
1. Introduction
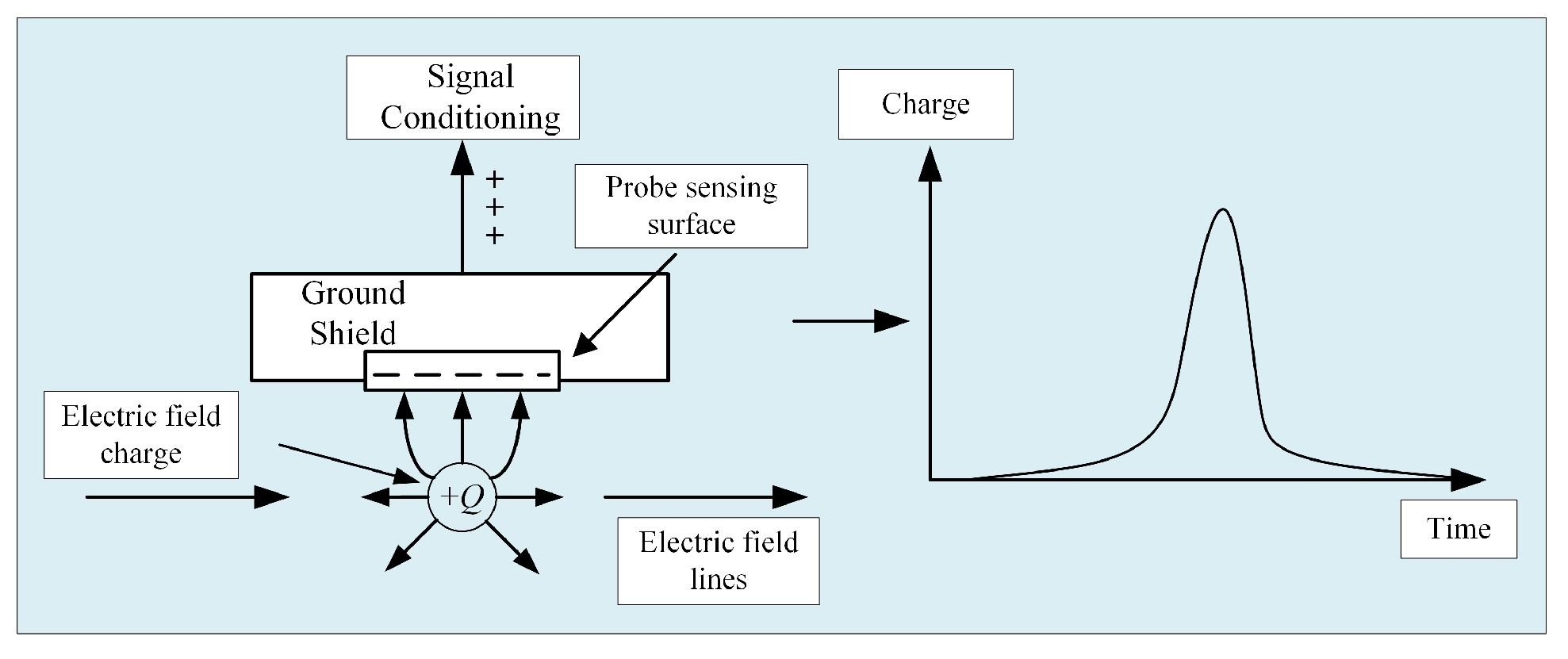
2. Principle of Electrostatic Monitoring
3. Sparse Representation Theory
3.1. Sparse Representation Model
3.2. Parse Dictionary Construction
3.3. Sparse Recovery Algorithm
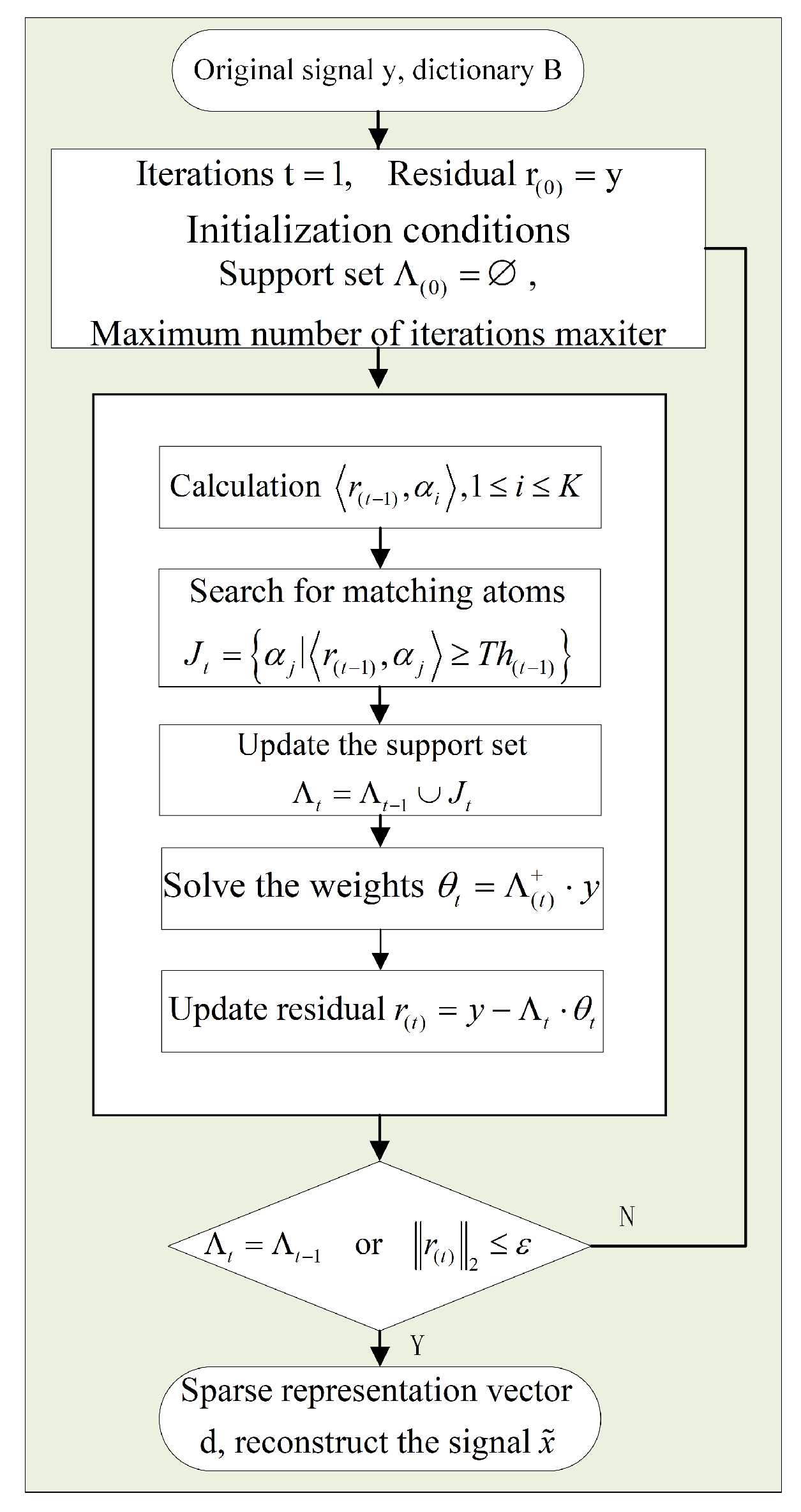
3.3.1. StOMP Algorithm
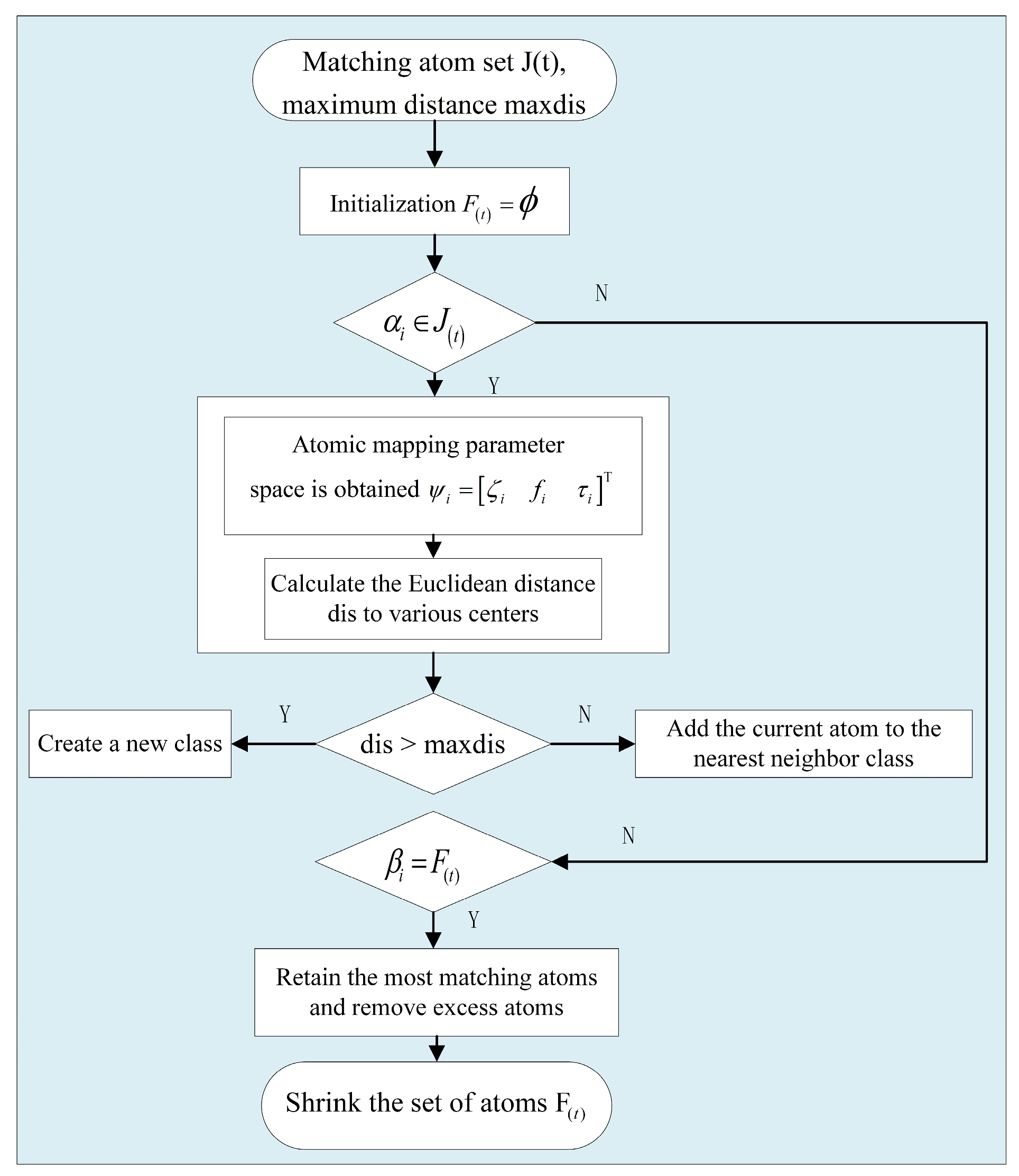
3.3.2. CcStOMP Algorithm
4. Experiments and Analysis of Results
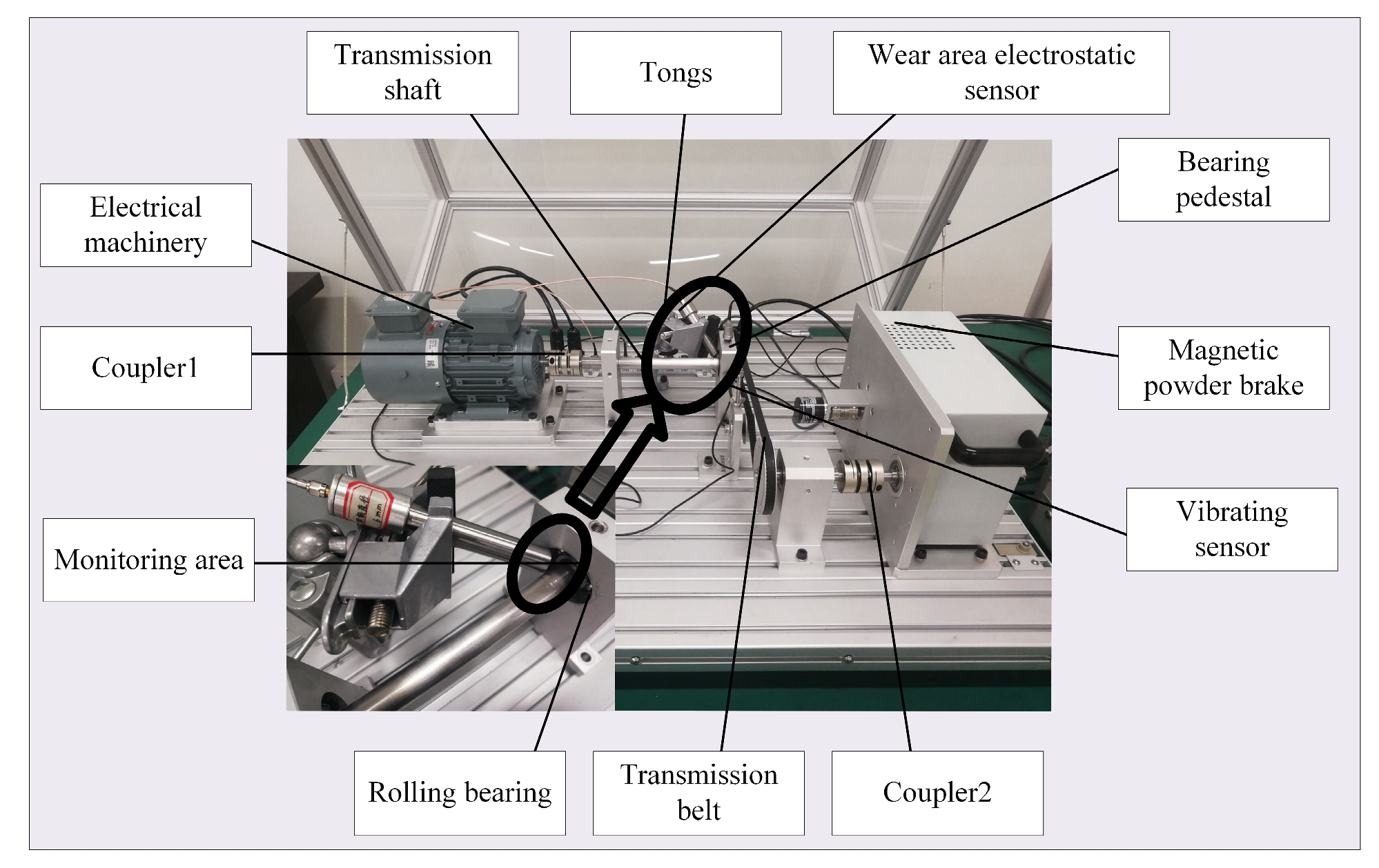
4.1. Experimental Setup
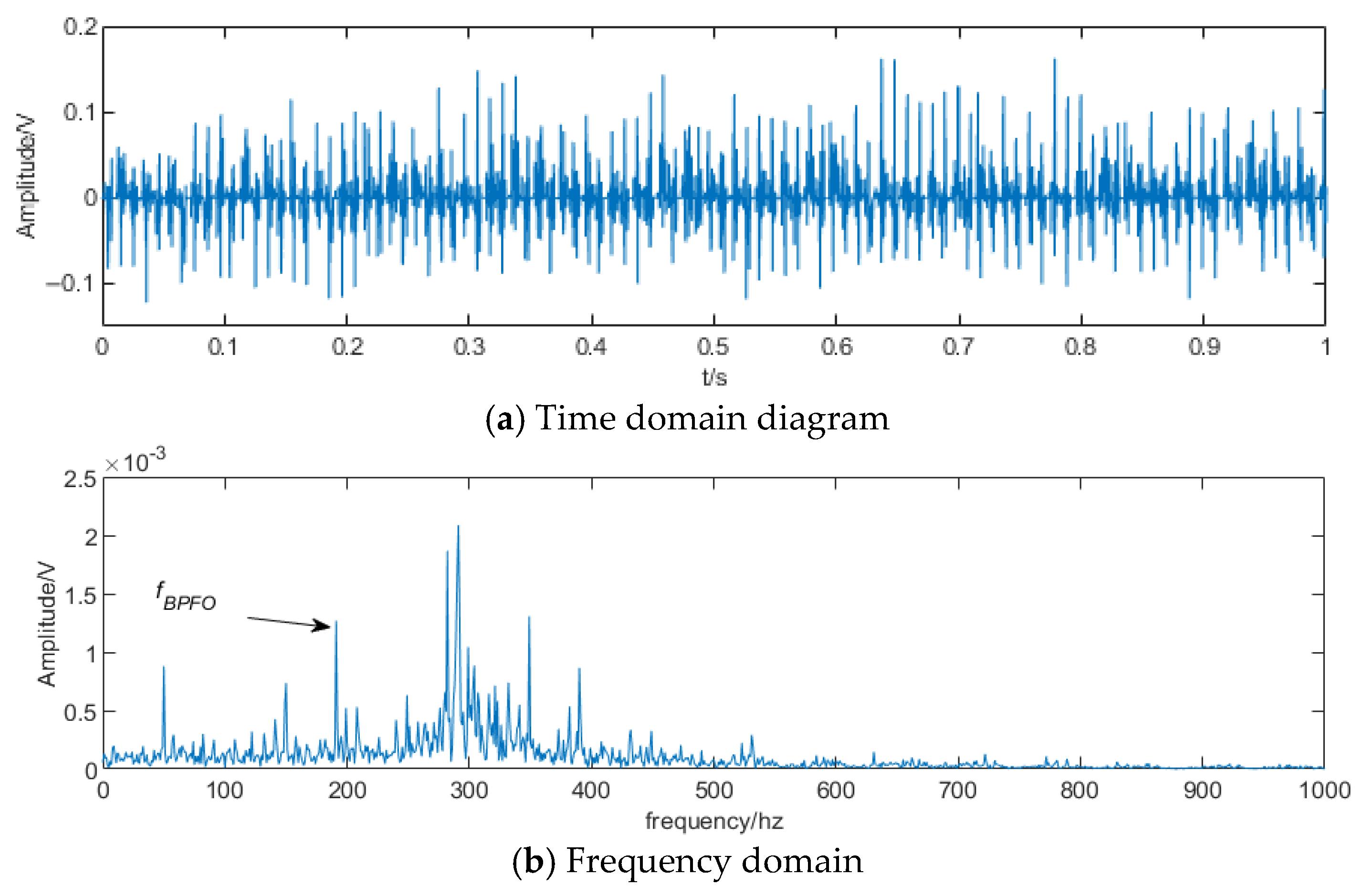
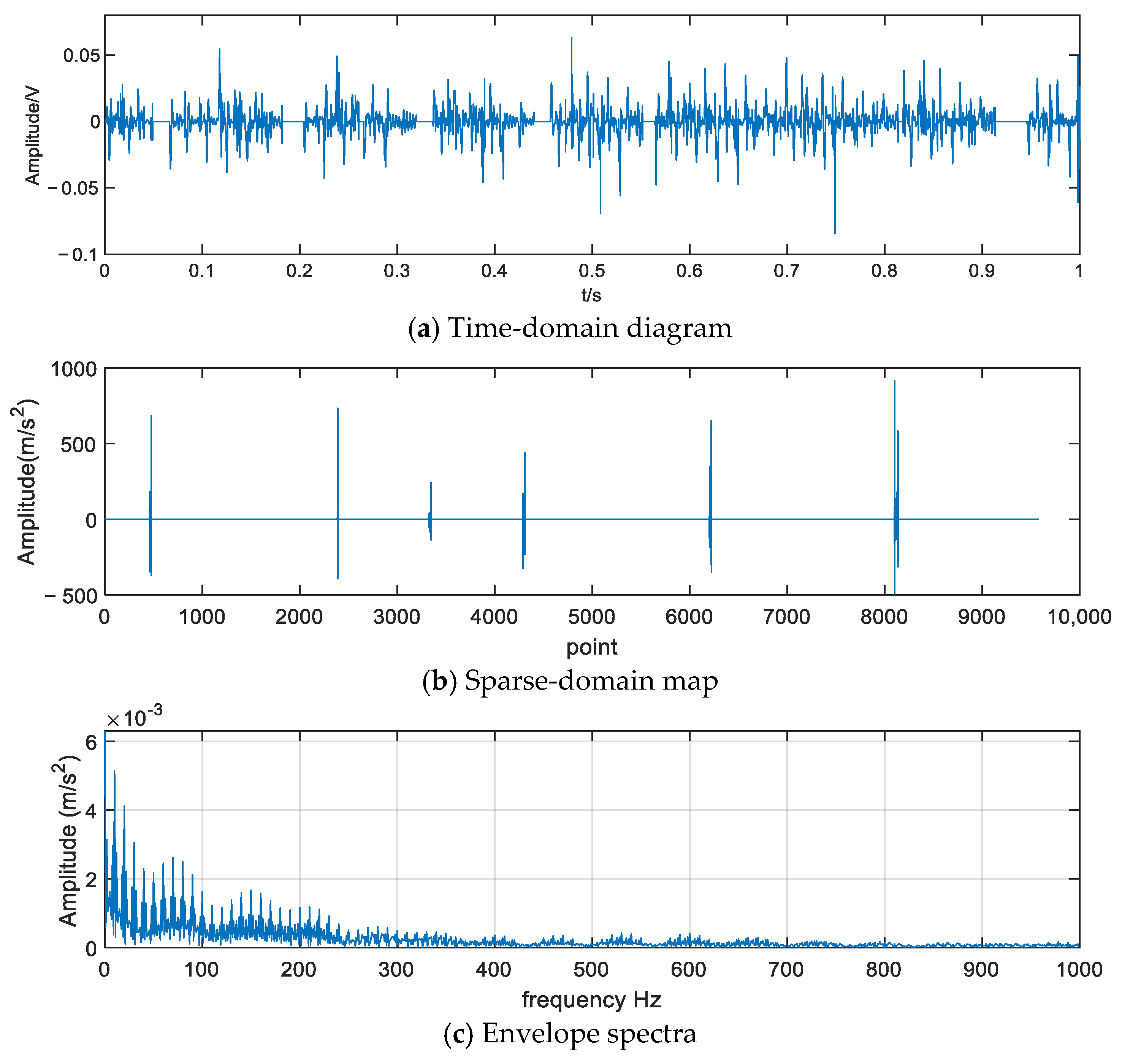
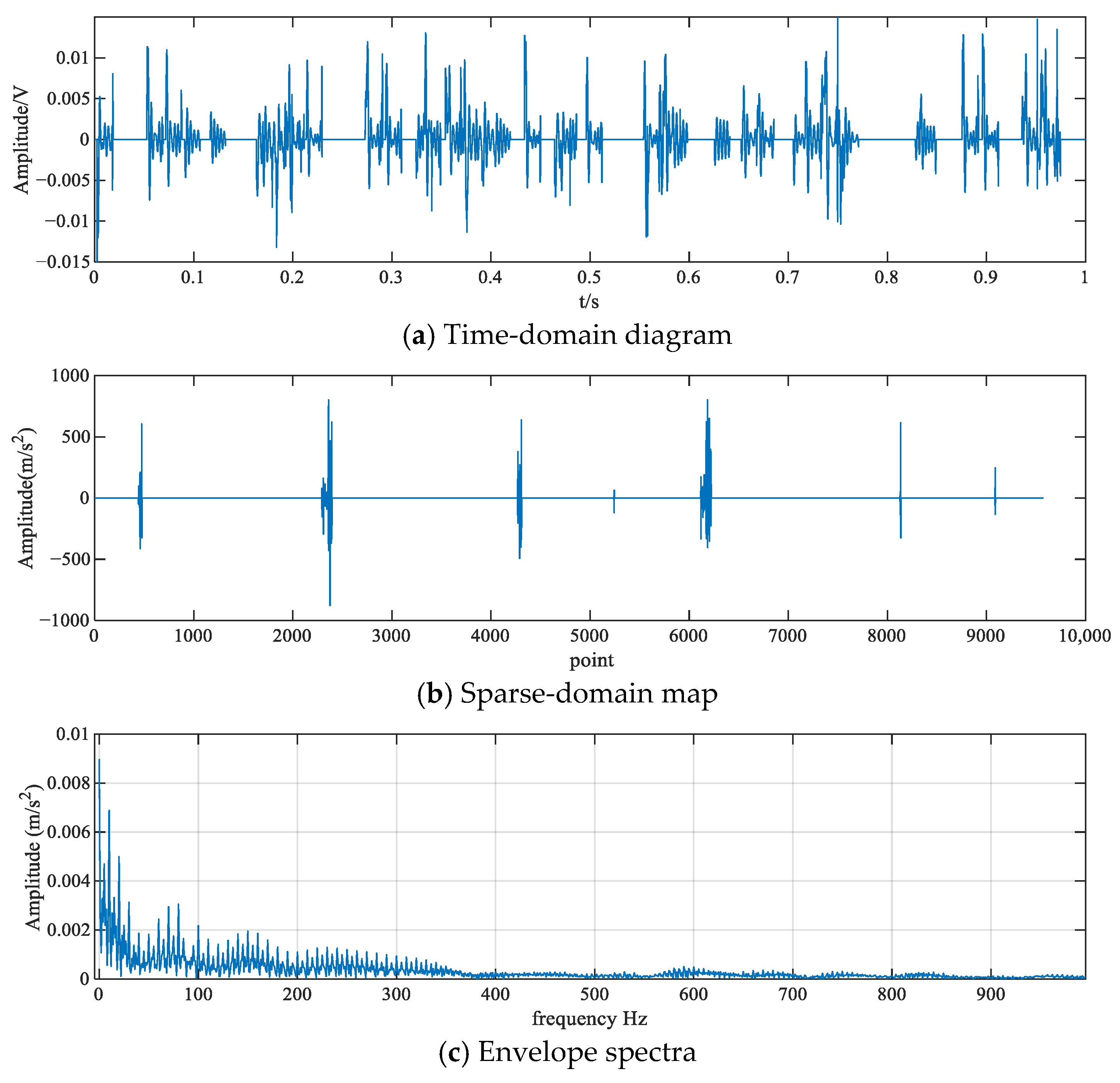
4.2. Analysis of Outer Race Fault Test Results
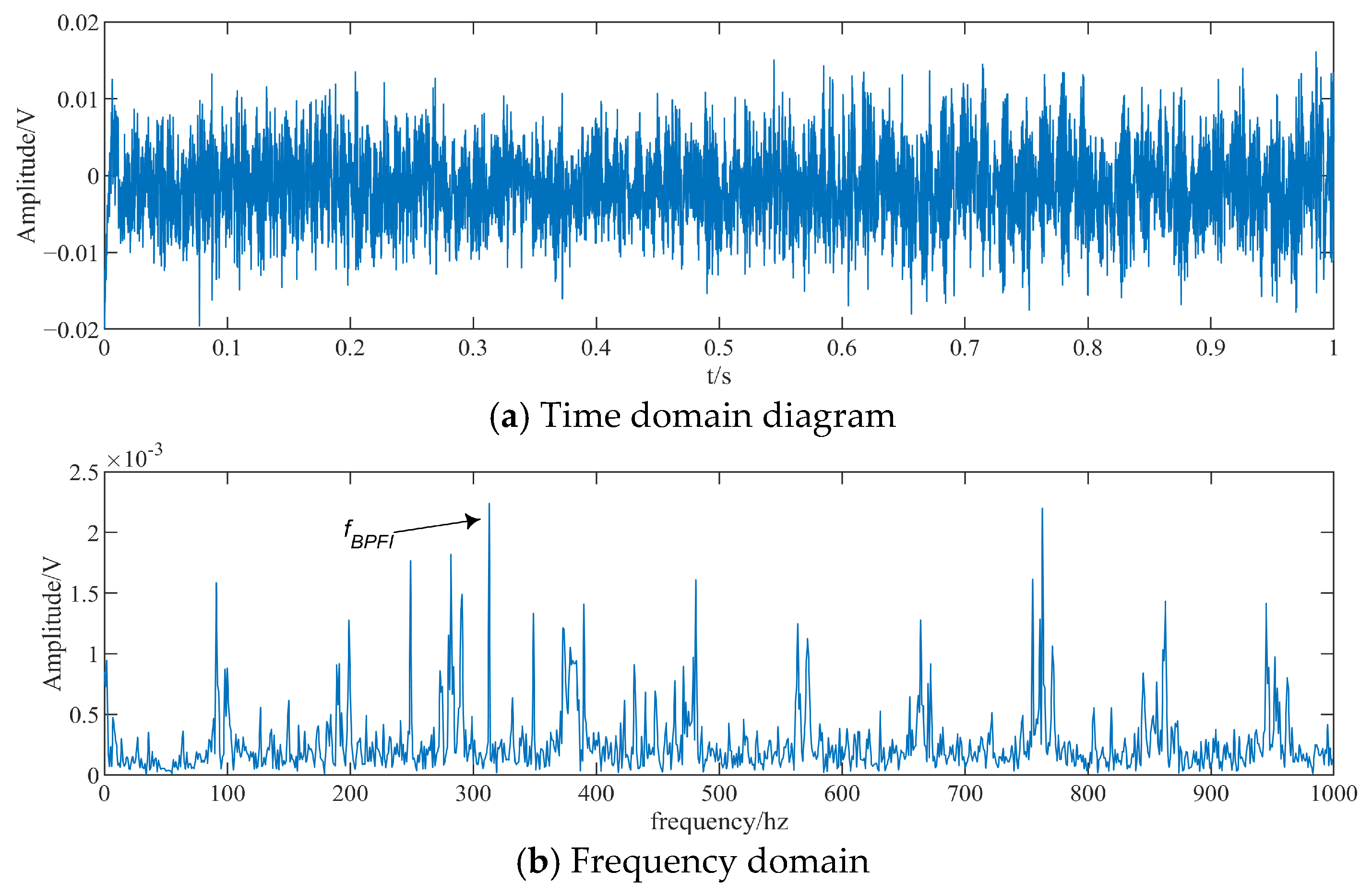
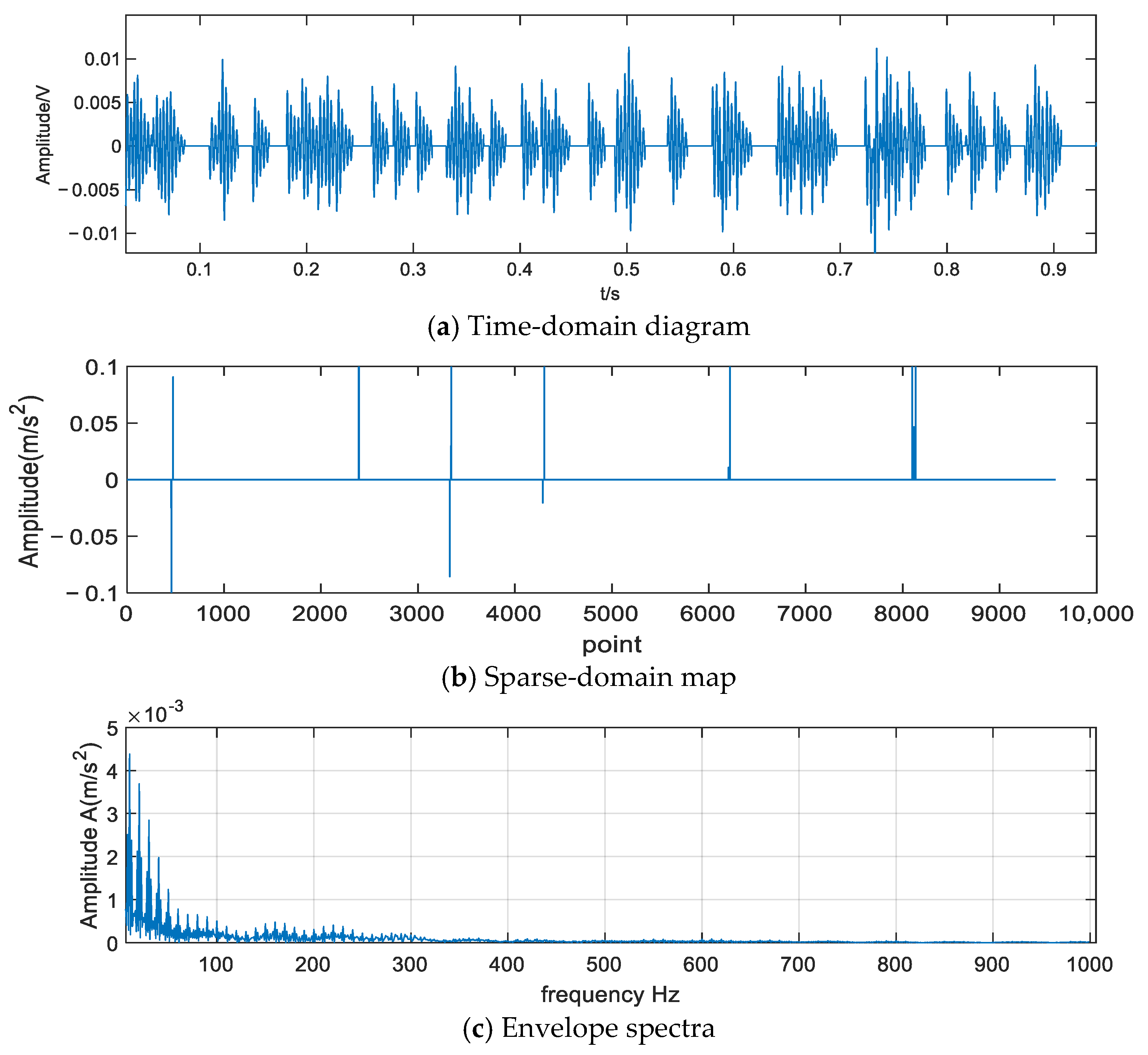
4.3. Analysis of Roller Failure Test Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, L.F.; Zhu, W.; Zhang, G. Research and application of coupled two-dimensional asymmetric bistable stochastic resonance system. Chin. J. Phys. 2021, 73, 420–432. [Google Scholar] [CrossRef]
- Gbashi, S.M.; Olatunji, O.O.; Adedeji, P.A.; Madushele, N. From academic to industrial research: A comparative review of advances in rolling element bearings for wind turbine main shaft. Eng. Fail. Anal. 2024, 163, 108510. [Google Scholar] [CrossRef]
- Rejith, R.; Kesavan, D.; Chakravarthy, P.; Murty, S.N. Bearings for aerospace applications. Tribol. Int. 2023, 181, 108312. [Google Scholar] [CrossRef]
- de la Presilla, R.; Wandel, S.; Stammler, M.; Grebe, M.; Poll, G.; Glavatskih, S. Oscillating rolling element bearings: A review of tribotesting and analysis approaches. Tribol. Int. 2023, 188, 108805. [Google Scholar] [CrossRef]
- El Laithy, M.; Wang, L.; Harvey, T.J.; Vierneusel, B.; Correns, M.; Blass, T. Further understanding of rolling contact fatigue in rolling element bearings—A review. Tribol. Int. 2019, 140, 105849. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, D.; Xu, Y.; Zhen, D.; Gu, F.; Ball, A.D. Early rolling bearing fault diagnosis in induction motors based on on-rotor sensing vibrations. Measurement 2023, 222, 113614. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Wu, X.; Liu, T. Phase-based video vibration measurement and fault feature extraction method for compound faults of rolling bearings. Adv. Eng. Inform. 2024, 62, 102897. [Google Scholar] [CrossRef]
- Ruochen, L.; Hongfu, Z. Mathematical model, simulation, and experimental calibration of electrostatic wear-Site sensor. IEEE Sens. J. 2017, 17, 2428–2438. [Google Scholar] [CrossRef]
- Tian, Z.; Lu, P.; Grundy, J.; Harvey, T.; Powrie, H.; Wood, R. Charge pattern detection through electrostatic array sensing. Sens. Actuators A Phys. 2024, 371, 115295. [Google Scholar] [CrossRef]
- Harvey, T.J.; Wood, R.J.K.; Powrie, H.E.G. Electrostatic wear monitoring of rolling element bearings. Wear 2007, 263, 1492–1501. [Google Scholar] [CrossRef]
- Harvey, T.J.; Wood, R.J.K.; Denuault, G.; Powrie, H.E.G. Investigation of electrostatic charging mechanisms in oil lubricated tribo-contacts. Tribol. Int. 2002, 35, 605–614. [Google Scholar] [CrossRef]
- Harvey, T.J.; Morris, S.; Wang, L.; Wood, R.J.K.; Powrie, H.E.G. Real-time monitoring of wear debris using electrostatic sensing techniques. Proc. Inst. Mech. Eng. Part J. J. Eng. Tribol. 2007, 221, 27–40. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, A.; Zuo, H. Roller Bearing Performance Degradation Assessment Based on Fusion of Multiple Features of Electrostatic Sensors. Sensors 2019, 19, 824. [Google Scholar] [CrossRef] [PubMed]
- Bai, R.; Li, J.; Liu, J.; Shi, Y.; He, S.; Wei, W. Day-ahead photovoltaic power generation forecasting with the HWGC-WPD-LSTM hybrid model assisted by wavelet packet decomposition and improved similar day method. Eng. Sci. Technol. Int. J. 2025, 61, 101889. [Google Scholar] [CrossRef]
- Chen, C.; Luo, Y.; Liu, J.; Yi, Y.; Zeng, W.; Wang, S.; Yao, G. Joint sound denoising with EEMD and improved wavelet threshold for real-time drilling lithology identification. Measurement 2024, 238, 115363. [Google Scholar] [CrossRef]
- Salunkhe, V.G.; Desavale, R.G.; Khot, S.M.; Yelve, N.P. A Novel Incipient Fault Detection Technique for Roller Bearing Using Deep Independent Component Analysis and Variational Modal Decomposition. J. Tribol. 2023, 145, 7. [Google Scholar] [CrossRef]
- Salunkhe, V.G.; Khot, S.M.; Jadhav, P.S.; Yelve, N.P.; Kumbhar, M.B. Experimental Investigation Using Robust Deep VMD-ICA and 1D-CNN for Condition Monitoring of Roller Element Bearing. J. Comput. Inf. Sci. Eng. 2024, 24, 12. [Google Scholar] [CrossRef]
- Song, L.; Yan, R. Bearing fault diagnosis based on Cluster-contraction Stage-wise Orthogonal-Matching-Pursuit. Measurement 2019, 140, 240–253. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, T.; Liu, C. Composite fault diagnosis method of rolling bearings based on sparse representation of cascaded over-complete dictionary. Vib. Shock. 2021, 40, 174–179. [Google Scholar]
- Sun, R.; Yang, Z.; Chen, X.; Tian, S.; Xie, Y. Gear fault diagnosis based on the structured sparsity time-frequency analysis. Mech. Syst. Signal Process. 2018, 102, 346–363. [Google Scholar] [CrossRef]
- Deng, F.; Qiang, Y.; Yang, S.; Hao, R.; Liu, Y. Sparse representation of parametric dictionary based on fault impact matching for wheelset bearing fault diagnosis. ISA Trans. 2021, 110, 368–378. [Google Scholar] [CrossRef]
- He, G.; Ding, K.; Lin, H. Fault feature extraction of rolling element bearings using sparse representation. J. Sound Vib. 2016, 366, 514–527. [Google Scholar] [CrossRef]
- Wang, L.; Cai, G.; You, W. Transients Extraction Based on Averaged Random Orthogonal Matching Pursuit Algorithm for Machinery Fault Diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 3237–3248. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.L. Sparse Solution of Underdetermined Systems of Linear Equations by Stagewise Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Chen, X.; Du, Z.; Li, J.; Li, X.; Zhang, H. Compressed sensing based on dictionary learning for extracting impulse components. Signal Process. 2014, 96, 94–109. [Google Scholar] [CrossRef]




| Type | Parameter | Type | Parameter |
|---|---|---|---|
| Bearing designation | SKF-6204-2Z | Pitch diameter/mm | 33.5 |
| Roller diameter/mm | 7.94 | Number of rollers/n | 8 |
| Contact angle/° | 0 | Defect width/mm | 2.5 |
| Type | Fault Character Frequency/Hz | Fault Characteristics Are Disturbed by Noise | Twice the Fault Characteristic Frequency/Hz |
|---|---|---|---|
| Theoretical fault | 193.17 | / | 386.34 |
| StOMP | 191.07 | severe | Disturbed by noise, unrecognizable |
| CcStOMP | 191.75 | clear | 384.54 |
| Type | Fault Character Frequency/Hz | Fault Characteristics Are Disturbed by Noise | Twice the Fault Characteristic Frequency/Hz |
|---|---|---|---|
| Theoretical fault | 126.03 | / | 252.06 |
| StOMP | 126 | severe | Disturbed by noise, unrecognizable |
| CcStOMP | 126 | clear | 252 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Yin, H.; Sun, J.; Zhang, L. Research on Feature Extraction Method and Process Optimization of Rolling Bearing Faults Based on Electrostatic Monitoring. Lubricants 2025, 13, 178. https://doi.org/10.3390/lubricants13040178
Liu R, Yin H, Sun J, Zhang L. Research on Feature Extraction Method and Process Optimization of Rolling Bearing Faults Based on Electrostatic Monitoring. Lubricants. 2025; 13(4):178. https://doi.org/10.3390/lubricants13040178
Chicago/Turabian StyleLiu, Ruochen, Han Yin, Jianzhong Sun, and Lanchun Zhang. 2025. "Research on Feature Extraction Method and Process Optimization of Rolling Bearing Faults Based on Electrostatic Monitoring" Lubricants 13, no. 4: 178. https://doi.org/10.3390/lubricants13040178
APA StyleLiu, R., Yin, H., Sun, J., & Zhang, L. (2025). Research on Feature Extraction Method and Process Optimization of Rolling Bearing Faults Based on Electrostatic Monitoring. Lubricants, 13(4), 178. https://doi.org/10.3390/lubricants13040178





