An Enhanced Stochastic Two-Scale Model for Metal-to-Metal Seals
Abstract
1. Introduction
2. Theoretical Background
2.1. The Deterministic Model
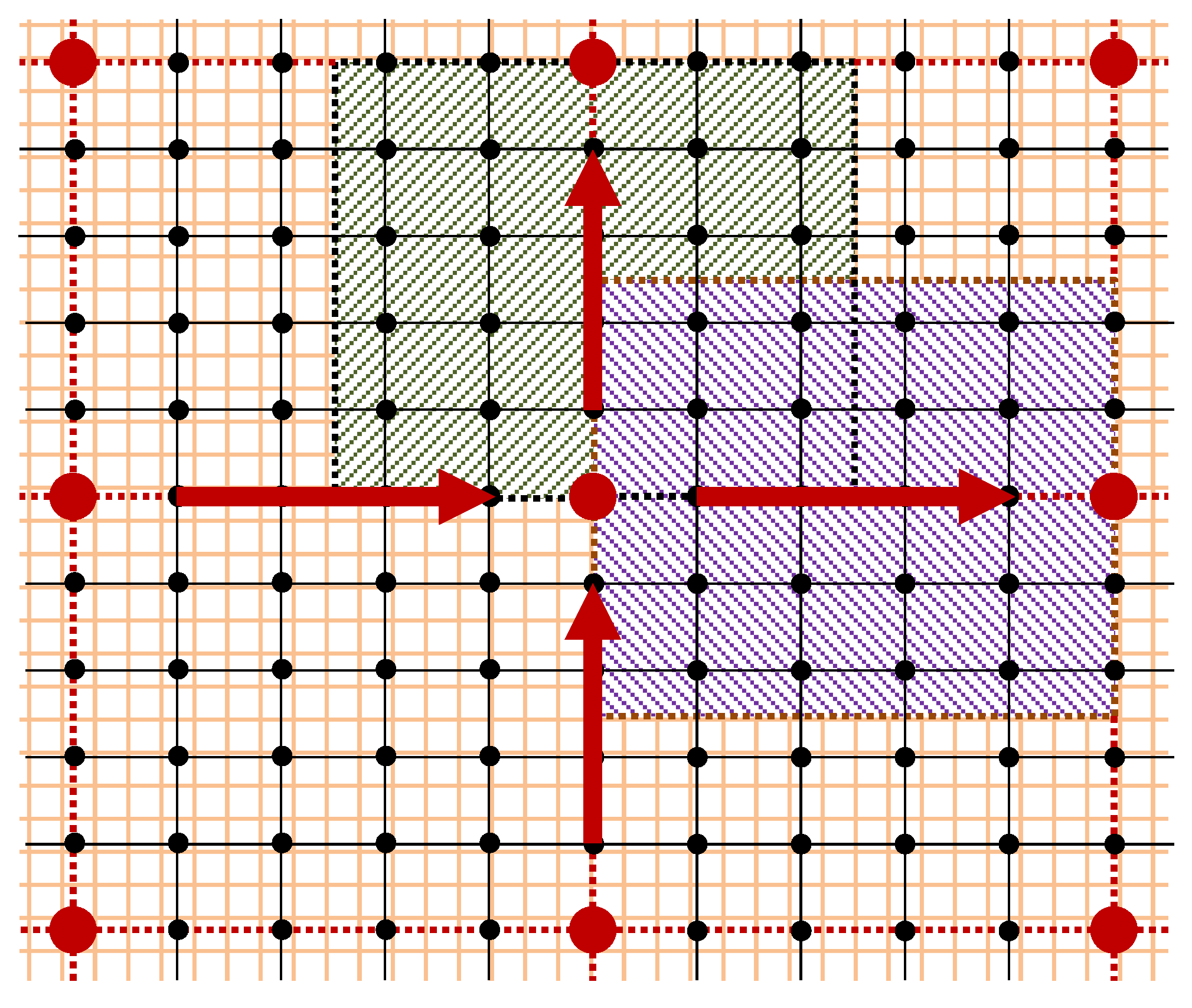
2.2. The Two-Scale Model
2.3. The Two-Scale Stochastic Model
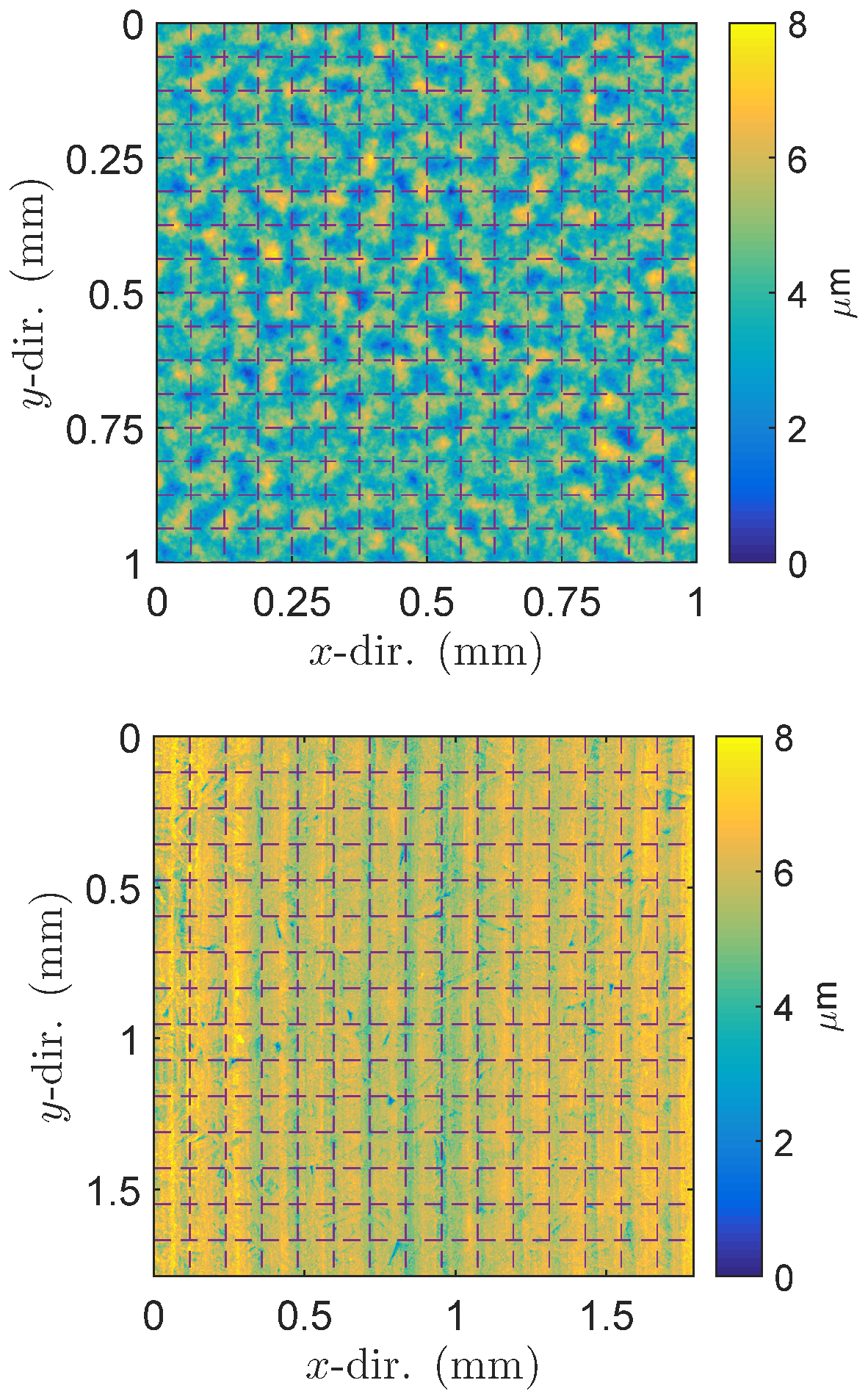
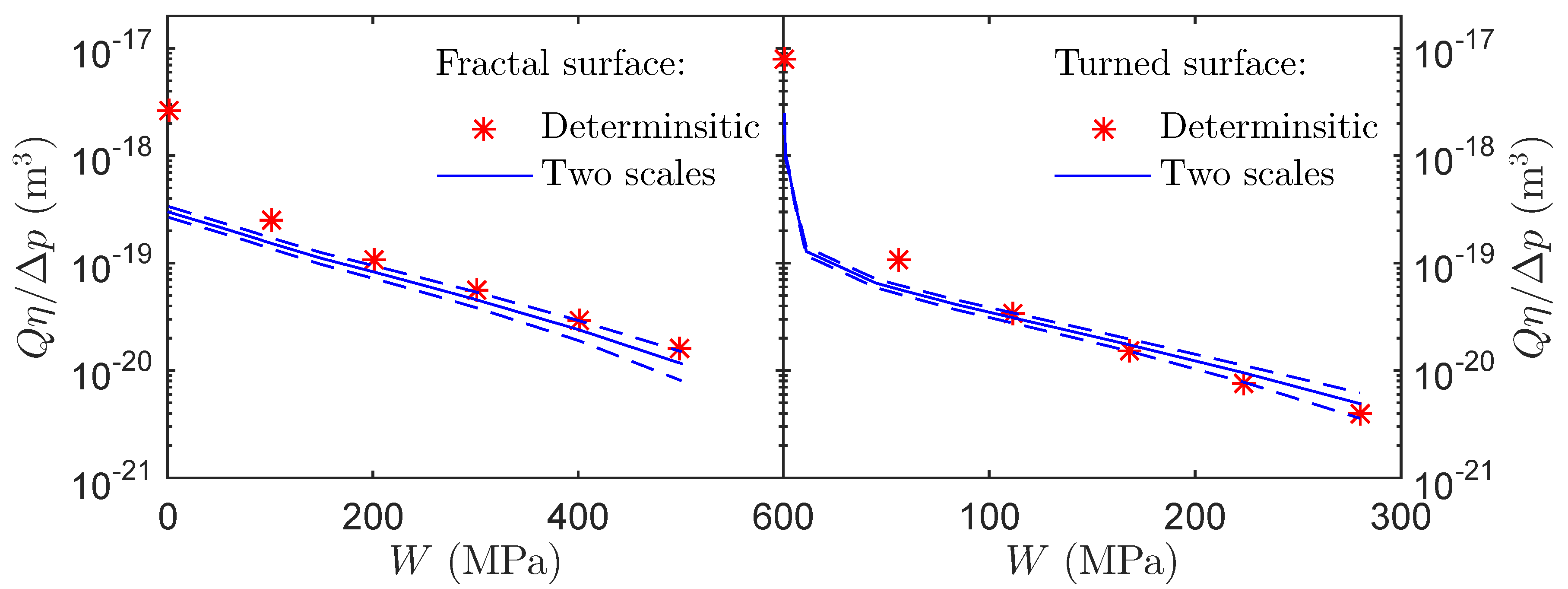
3. Two Case Examples
4. The Permeability of Individual Local-Scale Domains
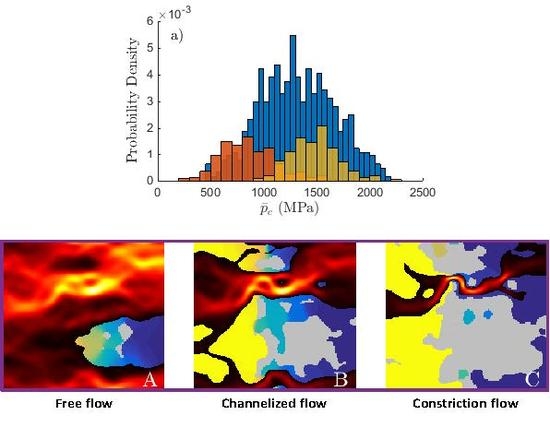
4.1. Qualitative Description
4.2. Quantitative Description
- Find the average pressure, , at which the percolation threshold occurs: This is done by solving (only) the contact mechanics problem at increasing average contact pressures until a pressure at which there is no percolation is reached. Then, the value of is refined by means of a bisecting method.
- Compute the permeability at three average pressures: These can be chosen freely, but we have observed that choosing them around leads to a good performance.
- Find the starting point of the channelized flow regime: Since the free flow regime is neglected, the starting point of the channelized flow regime is not a required parameter. However, it is imperative to ensure that all the points used to fit the parameters in Equation (3) do belong to the channelized flow regime. This is done in the following manner:
- 3.1.
- Compute .
- 3.2.
- Form the groups , , {} and set the index
- 3.3.
- Compute and add the point to the list.
- 3.4.
- Classify the computed points in the groups, using the following steps:
- For every point, obtain , by fitting Equation (3) through the points , and
- Find such that is the smallest one.
- For all points in the list, compute .
- Define as the index of the point with minimum load such that . If , assign instead.
- Define as the index of the point with maximum load such that . If , assign instead.
- Form the groups , ,
- 3.5.
- If , stop.
- Populate the constriction flow regime, until it contains at least four points. For this, compute a point with a pressure between the maximum computed at the given step and . Then, update the group classification following 3.4.
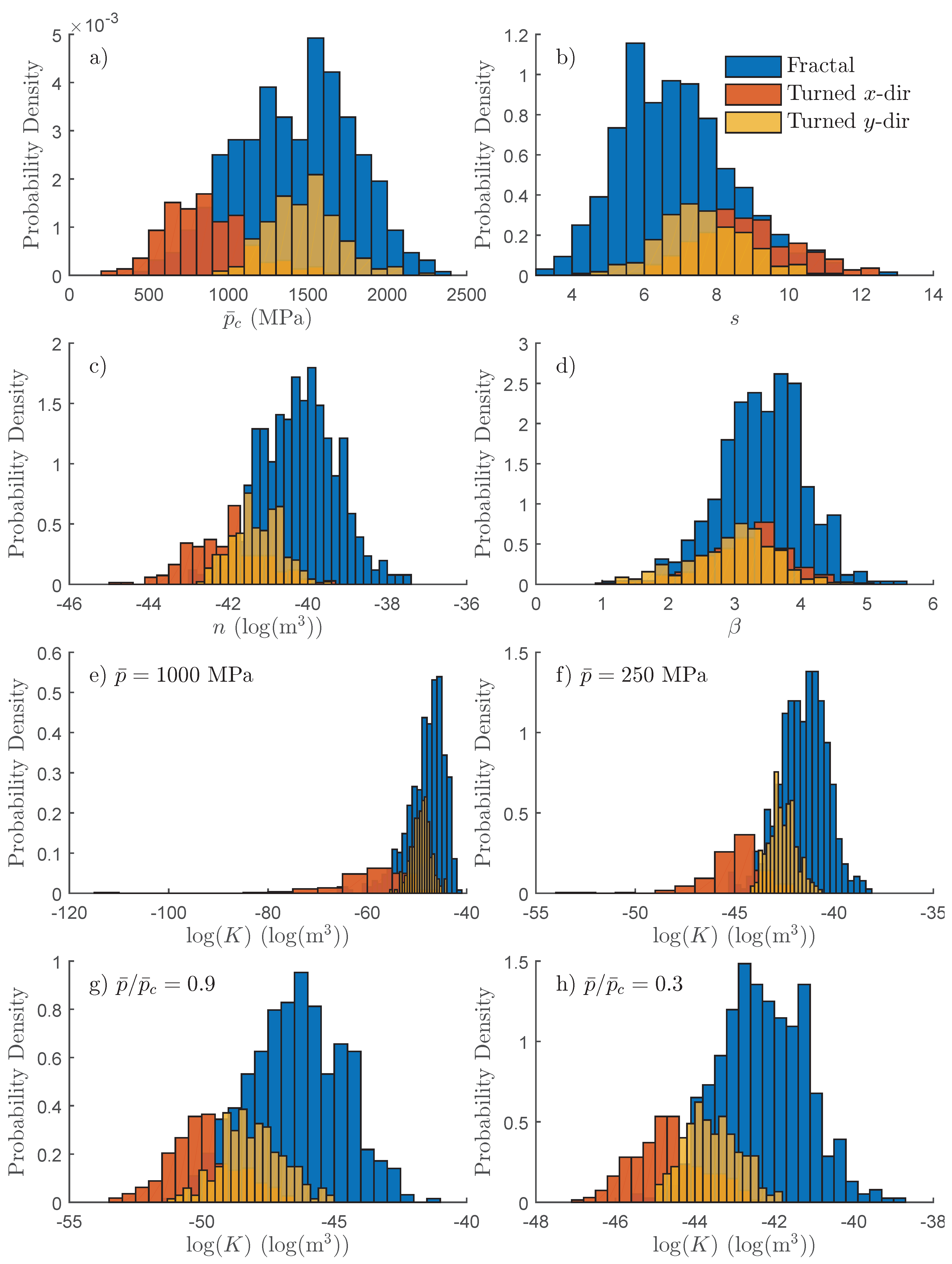
5. A Stochastic Description of the Permeability at the Local Scale
6. Global-Scale Leakage
7. Advantages of the Present Approach
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Flow Chart of the Model Presented in This Work

Appendix B. Flow Chart of the Model Presented the previous work

References
- Marie, C.; Lasseux, D. Experimental leak-rate measurement through a static metal seal. J. Fluids Eng. 2006, 129, 799–805. [Google Scholar] [CrossRef]
- Geoffroy, S.; Prat, M. On the leak through a spiral-groove metallic static ring gasket. J. Fluids Eng. 2004, 126, 48–54. [Google Scholar] [CrossRef]
- Bollfrass, C.A. Sealing tubular connections. J. Pet. Technol. 1985, 37, 955–965. [Google Scholar] [CrossRef]
- Murtagian, G.R.; Fanelli, V.; Villasante, J.A.; Johnson, D.H.; Ernst, H.A. Sealability of stationary metal-to-metal seals. J. Tribol. 2004, 126, 591–596. [Google Scholar] [CrossRef]
- Hamilton, K.; Wagg, B.; Roth, T. Using ultrasonic techniques to accurately examine seal-surface-contact stress in premium connections. SPE Dril. Complet. 2009, 24, 696–704. [Google Scholar] [CrossRef]
- Inose, K.; Sugino, M.; Goto, K. Influence of grease on high-pressure gas tightness by metal-to-metal seals of premium threaded connections. Tribol. Online 2016, 11, 227–234. [Google Scholar] [CrossRef]
- Ernens, D.; de Rooij, M.B.; Pasaribu, H.R.; van Riet, E.J.; van Haaften, W.M.; Schipper, D.J. Mechanical characterization and single asperity scratch behaviour of dry zinc and manganese phosphate coatings. Tribol. Int. 2017, 118, 474–483. [Google Scholar] [CrossRef]
- Ernens, D.; van Riet, E.J.; de Rooij, M.B.; Pasaribu, H.R.; van Haaften, W.M.; Schipper, D.J. The role of phosphate conversion coatings in make-up and seal ability of casing connections. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, The Hague, The Netherlands, 14–16 March 2018. [Google Scholar]
- Anwar, A.A.; Gorash, Y.; Dempster, W.; Hamilton, R. Literature research in relevant fields to understand pressure relief valve leak tightness in a static closed state. Procedia Eng. 2015, 130, 95–103. [Google Scholar] [CrossRef]
- Anwar, A.A.; Gorash, Y.; Dempster, W. Application of multi-scale approaches to the investigation of sealing surface deformation for the improvement of leak tightness in pressure relief valves. In Advanced Methods of Continuum Mechanics for Materials and Structures; Springer: Singapore, 2016; pp. 493–522. [Google Scholar]
- Zhang, B.; Hong, H.; Yu, M.; Yang, H. Leakage analysis and ground tests of knife edge indium seal to lunar sample return devices. Proc. Inst. Mech. Eng. Part G 2018. [Google Scholar] [CrossRef]
- Yan, Y.; Zhai, J.; Gao, P.; Han, Q. A multi-scale finite element contact model for seal and assembly of twin ferrule pipeline fittings. Tribol. Int. 2018, 125, 100–109. [Google Scholar] [CrossRef]
- Brunet, J.-C.; Poncet, A.; Trilhe, P. Leak-tightness assessment of demountable joints for the super fluid helium system of the cern large hadron collider (LHC). In Advances in Cryogenic Engineering; Springer US: Boston, MA, USA, 1994; pp. 657–662. [Google Scholar]
- Roman, A.; Ahmadi, G.; Issen, K.A.; Smith, D.H. Permeability of fractured media under confining pressure: A simplified model. Open Pet. Eng. J. 2012, 5, 36–41. [Google Scholar] [CrossRef]
- Pérrez-Ràfols, F.; Larsson, R.; van Riet, E.; Almqvist, A. On the loading and unloading of metal-to-metal seals: A two-scale stochastic approach. Proc. Inst. Mech. Eng. Part J 2018. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Yang, C. Theory of the leak-rate of seals. J. Phys. Condens. Matter 2008, 20, 315011. [Google Scholar] [CrossRef]
- Lukkassen, D.; Nguetseng, G.; Wall, P. Two-scale convergence. Int. J. Pure Appl. Math. 2002, 2, 33–81. [Google Scholar]
- Sahlin, F.; Larsson, R.; Almqvist, A.; Lugt, P.M.; Marklund, P. A mixed lubrication model incorporating measured surface topography. part 1: Theory of flow factors. Proc. Inst. Mech. Eng. Part J 2010, 224, 335–351. [Google Scholar] [CrossRef]
- Scaraggi, M.; Carbone, G. A two-scale approach for lubricated soft-contact modeling: An application to lip-seal geometry. Adv. Tribol. 2012, 2012, 412190. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Larsson, R.; Lundström, S.; Wall, P.; Almqvist, A. A stochastic two-scale model for pressure-driven flow between rough surfaces. Proc. R. Soc. A 2016, 472, 20160069. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Ràfols, F.; Larsson, R.; Almqvist, A. Modelling of leakage on metal-to-metal seals. Tribol. Int. 2016, 94, 421–427. [Google Scholar] [CrossRef]
- Reynolds, O. On the theory of lubrication and its application of Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. Ser. A 1886, 177, 157–234. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Wall, P.; Almqvist, A. On compressible and piezo-viscous flow in thin porous media. Proc. R. Soc. A 2018, 474, 2209. [Google Scholar] [CrossRef] [PubMed]
- Putignano, C.; Afferrante, L.; Carbone, G.; Demelio, G. A new efficient numerical method for contact mechanics of rough surfaces. Int. J. Solids Struct. 2012, 49, 338–343. [Google Scholar] [CrossRef]
- Nakamura, T.; Funabashi, K. Effects of directional properties of roughness and tangential force on pressure flow between contacting surfaces. Lubr. Sci. 1991, 4, 13–23. [Google Scholar] [CrossRef]
- Robbe-Valloire, F.; Prat, M. A model for face-turned surface microgeometry. application to the analysis of metallic static seals. Wear 2008, 264, 980–989. [Google Scholar] [CrossRef]
- Nitta, I.; Matsuzaki, Y.; Tsukiyama, Y.; Horita, M.; Sakamoto, S. Thorough observation of real contact area of copper gaskets using a laser microscope with a wide field of view. J. Tribol. 2013, 135, 041103. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B.N.J.L. Leak rate of seals: Comparison of theory with experiment. EPL 2009, 86, 44006. [Google Scholar] [CrossRef]
- Dapp, W.B.; Lüke, A.; Persson, B.N.J.; Müser, M.H. Self-affine elastic contacts: Percolation and leakage. Phys. Rev. Lett. 2012, 108, 244301. [Google Scholar] [CrossRef] [PubMed]
- Dapp, W.B.; Müser, M.H. Fluid leakage near the percolation threshold. Sci. Rep. 2016, 6, 19513. [Google Scholar] [CrossRef] [PubMed]
- Persson, B.N.J. Leakage of metallic seals: Role of plastic deformations. Tribol. Lett. 2016, 63, 42. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, J.; Ding, X.; Yang, Z. An approach to calculate leak channels and leak rates between metallic sealing surfaces. J. Tribol. 2017, 139, 011708. [Google Scholar] [CrossRef]
- Tripp, J.H. Surface roughness effects in hydrodynamic lubrication: The flow factor method. J. Lubr. Technol. 1983, 105, 458–463. [Google Scholar] [CrossRef]
- Dapp, W.B.; Müser, M.H. Contact mechanics of and reynolds flow through saddle points: On the coalescence of contact patches and the leakage rate through near-critical constrictions. EPL 2015, 109, 44001. [Google Scholar] [CrossRef]
- Waseem, A.; Guilleminot, J.; Temizer, I. Stochastic multiscale analysis in hydrodynamic lubrication. Int. J. Numer. Methods Eng. 2017, 112, 1070–1093. [Google Scholar] [CrossRef]
- Vakis, A.I.; Yastrebov, V.A.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Hamrock, B.J. Fundamentals of Fluid Film Lubrication; McGraw-Hill, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Sahlin, F.; Larsson, R.; Marklund, P.; Almqvist, A.; Lugt, P.M. A mixed lubrication model incorporating measured surface topography. part 2: Roughness treatment, model validation, and simulation. Proc. Inst. Mech. Eng. Part J 2010, 224, 353–365. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B.N.J. Leak rate of seals: Effective-medium theory and comparison with experiment. Eur. Phys. J. E 2010, 31, 159–167. [Google Scholar] [CrossRef] [PubMed]



| LS Permeability (Average Time Per Domain) | MS Contact Mechanics | GS Flow | Total | |
|---|---|---|---|---|
| Algorithm in [15] | 7986 s | 3301 s | 4406 s | 162 h |
| New algorithm | 4904 s | 3301 s | 11 s | 99 h |
| Difference | 0 % |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Ràfols, F.; Almqvist, A. An Enhanced Stochastic Two-Scale Model for Metal-to-Metal Seals. Lubricants 2018, 6, 87. https://doi.org/10.3390/lubricants6040087
Pérez-Ràfols F, Almqvist A. An Enhanced Stochastic Two-Scale Model for Metal-to-Metal Seals. Lubricants. 2018; 6(4):87. https://doi.org/10.3390/lubricants6040087
Chicago/Turabian StylePérez-Ràfols, Francesc, and Andreas Almqvist. 2018. "An Enhanced Stochastic Two-Scale Model for Metal-to-Metal Seals" Lubricants 6, no. 4: 87. https://doi.org/10.3390/lubricants6040087
APA StylePérez-Ràfols, F., & Almqvist, A. (2018). An Enhanced Stochastic Two-Scale Model for Metal-to-Metal Seals. Lubricants, 6(4), 87. https://doi.org/10.3390/lubricants6040087