Modelling Transitions in Regimes of Lubrication for Rough Surface Contact
Abstract
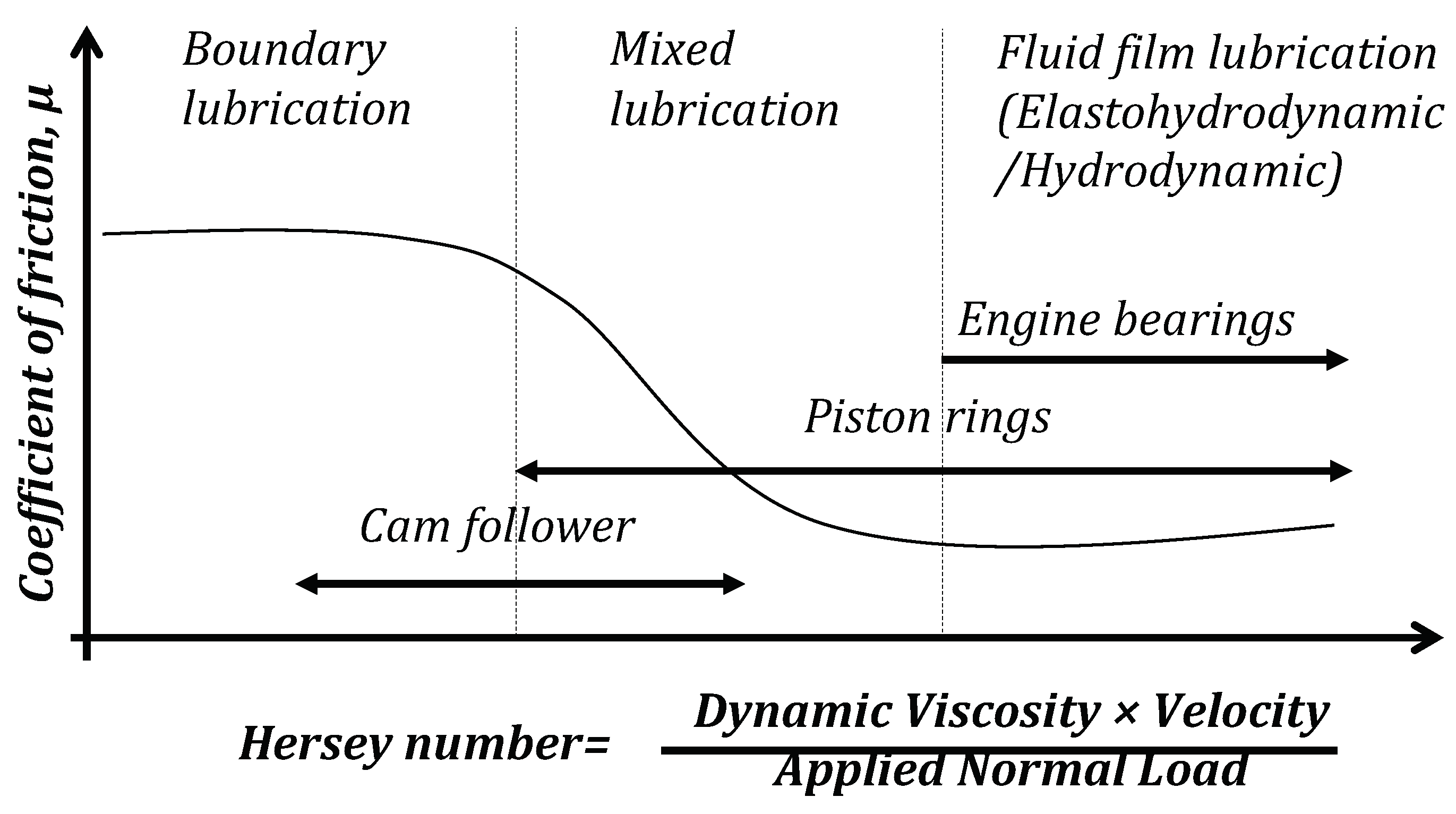
:1. Introduction
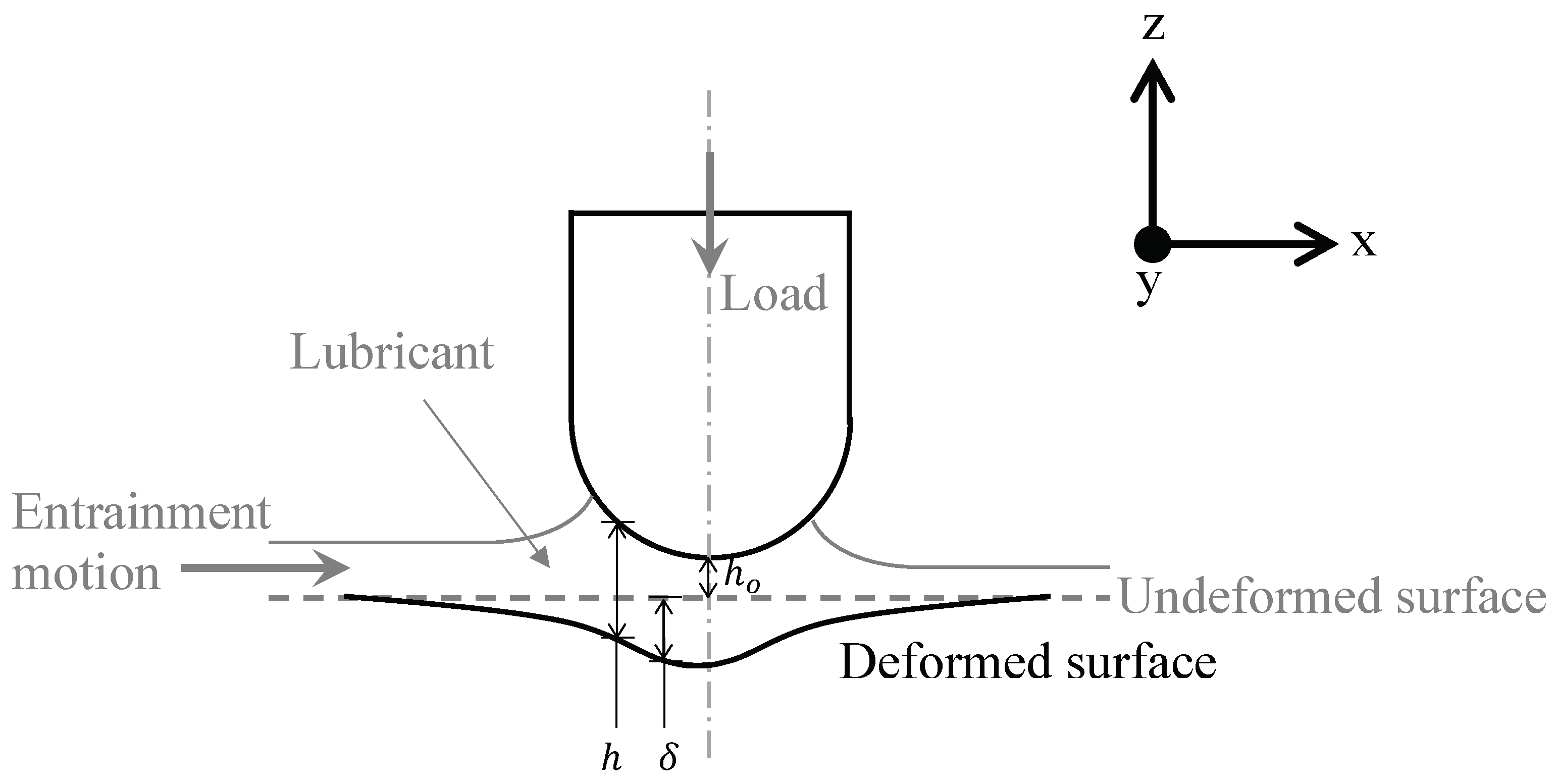
2. Mathematical Approach
2.1. Hydrodynamic Pressure
2.2. Interacting Asperity Pressure
2.3. Frictional Conjunction
2.4. Numerical Method
3. Experimental Approach
3.1. Friction Testing
3.2. Lubricant Viscosity-Pressure Correlation
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A | Apparent contact area (m2) |
| a | Hertzian contact radius in the x-direction (m) |
| b | Hertzian contact radius in the y-direction (m) |
| D | Influence coefficient (m) |
| E | Modulus of elasticity (m) |
| Effective modulus of elasticity (m) | |
| Boundary friction force (N) | |
| Rough surface model statistical function, and (−) | |
| Viscous friction force (N) | |
| Total friction force (N) | |
| Non-dimensional material parameter (−) | |
| Non-dimensional elasticity parameter (−) | |
| Non-dimensional viscosity parameter (−) | |
| H | Non-dimensional elastic lubricant film profile (−) |
| h | Elastic lubricant film profile (m) |
| Minimum clearance (m) | |
| Local gap along conjunction (m) | |
| m | Pressure coefficient of boundary shear strength (−) |
| Slope of the logarithmic linear relationship between the lubricant (−) | |
| Dynamic viscosity and temperature (−) | |
| Interception of the logarithmic linear relationship between | |
| The lubricant dynamic viscosity and temperature (−) | |
| P | Non-dimensional hydrodynamic pressure (−) |
| Asperity interacting pressure (Pa) | |
| Hydrodynamic pressure (Pa) | |
| Maximum Hertzian pressure (Pa) | |
| R | Pin curvature radius (m) |
| T | Temperature (°C) |
| t | Time (s) |
| U | Non-dimensional average contact surface sliding speed in the x-direction (m/s) |
| Non-dimensional sliding speed parameter (−) | |
| u | Contact surface sliding speed in the x-direction (m/s) |
| Average contact surface sliding speed in the x-direction (m/s) | |
| V | Non-dimensional average contact surface sliding speed in the y-direction (m/s) |
| v | Contact surface sliding speed in the y-direction (m/s) |
| Average contact surface sliding speed in the y-direction (m/s) | |
| W | Contact load (N) |
| Reference contact load (N) | |
| Non-dimensional load parameter (−) | |
| X | Non-dimensional coordinate along the x-direction (−) |
| Coordinate along the x-direction (m) | |
| Y | Non-dimensional coordinate along the y-direction (−) |
| Coordinate along the y-direction (m) | |
| Lubricant viscosity-pressure coefficient (Pa−1) | |
| Curvature radius at the asperity peak (m) | |
| Slope of the limiting shear stress-pressure relation (−) | |
| Contact elastic deformation (m) | |
| Surface density of asperity peaks (−) | |
| Lubricant dynamic viscosity (Pa.s) | |
| Bulk lubricant dynamic viscosity at (Pa.s) | |
| Non-dimensional lubricant dynamic viscosity (−) | |
| Separation parameter (−) | |
| Poisson’s ratio (−) | |
| Lubricant density (kg/m3) | |
| Bulk lubricant density at (kg/m3) | |
| Non-dimensional lubricant density (−) | |
| Composite surface roughness (m) | |
| Boundary shear (Pa) | |
| Eyring shear stress (Pa) | |
| Viscous shear (Pa) | |
| Relaxation factor for pressure convergence loop (−) | |
| Relaxation factor for load balance loop (−) |
Appendix A
| Parameters | Non-Dimensional | Relation |
|---|---|---|
| x | X | |
| y | Y | |
| h | H | |
| p | P | |
| U | ||
| V |
Appendix B. Finite Difference Scheme
Appendix C
| Parameter | Value | Unit |
|---|---|---|
| Pin curvature radius, R | 5 | mm |
| Wear track radius | 20 | mm |
| Young’s modulus (disk) | 210.0 | GPa |
| Young’s modulus (pin) | 110.0 | GPa |
| Poisson’s ratio (disk) | 0.27 | - |
| Poisson’s ratio (pin) | 0.21 | - |
| Eyring shear stress | 2 | MPa |
Appendix D
| Lubricant Type | Tsupply (°C) | (-) | m (-) |
|---|---|---|---|
| SAE5W40 | 35 | 0.048 | 0.107 |
| SAE10W40 | 30 | 0.043 | 0.106 |
| SAE15W40 | 23 | 0.051 | 0.115 |
References
- U.S. Energy Information Administration. International Energy Outlook 2017. 2017. Available online: https://www.eia.gov/outlooks (accessed on 19 June 2018).
- Chong, W.W.F.; Ng, J.-H.; Rajoo, S.; Chong, C.T. Passenger transportation sector gasoline consumption due to friction in Southeast Asian countries. Energy Convers. Manag. 2018, 158, 346–358. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Stribeck, R. Die wesentlichen eigenschaften der gleit-und rollenlager. Z. Ver. Deutsch. Ing. 1902, 46, 1341–1348. [Google Scholar]
- Hersey, M.D. The laws of lubrication of horizontal journal bearings. J. Wash. Acad. Sci. 1914, 4, 542–552. [Google Scholar]
- LaFountain, A.R.; Johnston, G.J.; Spikes, H.A. The elastohydrodynamic traction of synthetic base oil blends. Tribol. Trans. 2001, 44, 648–656. [Google Scholar] [CrossRef]
- Wang, W.-Z.; Wang, S.; Shi, F.; Wang, Y.-C.; Chen, H.-B.; Wang, H.; Hu, Y.-Z. Simulations and measurements of sliding friction between rough surfaces in point contacts: From ehl to boundary lubrication. J. Tribol. 2007, 129, 495–501. [Google Scholar] [CrossRef]
- Kovalchenko, A.M.; Erdemir, A.; Ajayi, O.O.; Etsion, I. Tribological behavior of oil-lubricated laser textured steel surfaces in conformal flat and non-conformal contacts. Mater. Perform. Charact. 2017, 6, 1–23. [Google Scholar] [CrossRef]
- He, T.; Zhu, D.; Wang, J.; Wang, Q.J. Experimental and numerical investigations of the stribeck curves for lubricated counterformal contacts. J. Tribol. 2017, 139, 021505. [Google Scholar] [CrossRef]
- Maru, M.M.; Trommer, R.M.; Cavalcanti, K.F.; Figueiredo, E.S.; Silva, R.F.; Achete, C.A. The stribeck curve as a suitable characterization method of the lubricity of biodiesel and diesel blends. Energy 2014, 69, 673–681. [Google Scholar] [CrossRef]
- Hamdan, S.H.; Chong, W.W.F.; Ng, J.-H.; Ghazali, M.J.G.; Wood, R.J.K. Influence of fatty acid methyl ester composition on tribological properties of vegetable oils and duck fat derived biodiesel. Tribol. Int. 2017, 113, 76–82. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Zhu, D.; Cheng, H.S.; Hamrock, B.J. Effect of surface roughness on pressure spike and film constriction in elastohydrodynamically lubricated line contacts. Tribol. Trans. 1990, 33, 267–273. [Google Scholar] [CrossRef]
- Salant, R.F. An average flow model of rough surface lubrication with inter-asperity cavitation. J. Tribol. 2001, 123, 134–143. [Google Scholar]
- Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.D.; Fitzsimons, B. Tribology of piston compression ring conjunction under transient thermal mixed regime of lubrication. Tribol. Int. 2013, 59, 248–258. [Google Scholar] [CrossRef] [Green Version]
- De Kraker, A.; van Ostayen, R.A.J.; Rixen, D.J. Development of a texture averaged reynolds equation. Tribol. Int. 2010, 43, 2100–2109. [Google Scholar] [CrossRef]
- Zhang, H.; Hua, M.; Dong, G.; Zhang, D.; Chin, K. A mixed lubrication model for studying tribological behaviors of surface texturing. Tribol. Int. 2016, 93, 583–592. [Google Scholar] [CrossRef]
- Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.D.; Howell-Smith, S. A numerical model to study the role of surface textures at top dead center reversal in the piston ring to cylinder liner contact. J. Tribol. 2016, 138, 021703. [Google Scholar] [CrossRef]
- Venner, C.H.; Napel, W.E.T. Surface roughness effects in an ehl line contact. J. Tribol. 1992, 114, 616–622. [Google Scholar] [CrossRef]
- Hu, Y.-Z.; Zhu, D. A full numerical solution to the mixed lubrication in point contacts. J. Tribol. 2000, 122, 1–9. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, J.; Wang, Q.J. On the stribeck curves for lubricated counterformal contacts of rough surfaces. J. Tribol. 2015, 137, 021501. [Google Scholar] [CrossRef]
- Majumdar, A.; Tien, C.L. Fractal characterization and simulation of rough surfaces. Wear 1990, 136, 313–327. [Google Scholar] [CrossRef]
- Johnson, K.L.; Greenwood, J.A.; Poon, S.Y. A simple theory of asperity contact in elastohydro-dynamic lubrication. Wear 1972, 19, 91–108. [Google Scholar] [CrossRef]
- Gelinck, E.R.M.; Schipper, D.J. Calculation of stribeck curves for line contacts. Tribol. Int. 2000, 33, 175–181. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. A Math. Phy. 1966, 295, 300–319. [Google Scholar]
- Popovici, R.I.; Schipper, D.J. Stribeck and traction curves for elliptical contacts: Isothermal friction model. Int. J. Sust Constr. Des. 2014, 4. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Wang, J. Friction prediction of rolling-sliding contact in mixed ehl. Measurement 2017, 100, 262–269. [Google Scholar] [CrossRef]
- Lijesh, K.P.; Khonsari, M.M. On the degradation of tribo-components in boundary and mixed lubrication regimes. Tribol. Lett. 2019, 67, 12. [Google Scholar] [CrossRef]
- Teodorescu, M.; Kushwaha, M.; Rahnejat, H.; Rothberg, S.J. Multi-physics analysis of valve train systems: From system level to microscale interactions. Proc. Inst. Mech. Eng. Part K 2007, 221, 349–361. [Google Scholar] [CrossRef] [Green Version]
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Chong, W.W.F.; Teodorescu, M.; Vaughan, N.D. Cavitation induced starvation for piston-ring/liner tribological conjunction. Tribol. Int. 2011, 44, 483–497. [Google Scholar] [CrossRef] [Green Version]
- Zavos, A.; Nikolakopoulos, P.G. Tribology of new thin compression ring of fired engine under controlled conditions-a combined experimental and numerical study. Tribol. Int. 2018, 128, 214–230. [Google Scholar] [CrossRef]
- De la Cruz, M.; Chong, W.W.F.; Teodorescu, M.; Theodossiades, S.; Rahnejat, H. Transient mixed thermo-elastohydrodynamic lubrication in multi-speed transmissions. Tribol. Int. 2012, 49, 17–29. [Google Scholar] [CrossRef]
- Chong, W.W.F.; de la Cruz, M. Elastoplastic contact of rough surfaces: A line contact model for boundary regime of lubrication. Meccanica 2014, 49, 1177–1191. [Google Scholar] [CrossRef]
- Taylor, R.I. Lubrication, Tribology & Motorsport; Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 2002. [Google Scholar]
- Barus, C. Art. x.-isothermals, isopiestics and isometrics relative to viscosity. Am. J. Sci. 1893, 45, 87. [Google Scholar] [CrossRef]
- Roelands, C.J.A.; Vlugter, J.C.; Waterman, H.I. The viscosity-temperature-pressure relationship of lubricating oils and its correlation with chemical constitution. J. Basic Eng. 1963, 85, 601–607. [Google Scholar] [CrossRef]
- Appeldoorn, J.K. A Simplified Viscosity-Pressure-Temperature Equation; Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 1963. [Google Scholar]
- Yasutomi, S.; Bair, S.; Winer, W.O. An application of a free volume model to lubricant rheology i—Dependence of viscosity on temperature and pressure. J. Tribol. 1984, 106, 291–302. [Google Scholar] [CrossRef]
- Wu, C.S.; Klaus, E.E.; Duda, J.L. Development of a method for the prediction of pressure-viscosity coefficients of lubricating oils based on free-volume theory. J. Tribol. 1989, 111, 121–128. [Google Scholar] [CrossRef]
- Bair, S.; Kottke, P. Pressure-viscosity relationships for elastohydrodynamics. Tribol. Trans. 2003, 46, 289–295. [Google Scholar] [CrossRef]
- Bair, S.; Yamaguchi, T. The equation of state and the temperature, pressure, and shear dependence of viscosity for a highly viscous reference liquid, dipentaerythritol hexaisononanoate. J. Tribol. 2017, 139, 011801. [Google Scholar] [CrossRef]
- Bair, S. A critical evaluation of film thickness-derived pressure–viscosity coefficients. Lubr. Sci. 2015, 27, 337–346. [Google Scholar] [CrossRef]
- Khonsari, M.M.; Hua, D.Y. Generalized non-newtonian elastohydrodynamic lubrication. Tribol. Int. 1993, 26, 405–411. [Google Scholar] [CrossRef]
- Bair, S.; Winer, W.O. A rheological model for elastohydrodynamic contacts based on primary laboratory data. J. Lubr. Technol. 1979, 101, 258–264. [Google Scholar] [CrossRef]
- Khonsari, M.M.; Hua, D.Y. Thermal elastohydrodynamic analysis using a generalized non-newtonian formulation with application to bair-winer constitutive equation. J. Tribol. 1994, 116, 37–46. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. Theoretical and experimental investigation of traction coefficient in line-contact ehl of rough surfaces. Tribol. Int. 2014, 70, 179–189. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Gohar, R.; Rahnejat, H. Fundamentals of Tribology; World Scientific Publishing Company: Singapore, 2012. [Google Scholar]
- Reynolds, O. IV. On the theory of lubrication and its application to mr. beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Swift, H.W. The stability of lubricating films in journal bearings. (includes appendix). In Minutes of the Proceedings of the Institution of Civil Engineers; Thomas Telford-ICE Virtual Library: London, UK, 1932; Volume 233, pp. 267–288. [Google Scholar]
- Stieber, W. Hydrodynamische Theorie des Gleitlagers das Schwimmlager; VDI: Berlin, Germany, 1933. [Google Scholar]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: The Fundamentals of Roller And Gear Lubrication; Pergamon Press: Oxford, UK, 1966; Volume 23. [Google Scholar]
- Teodorescu, M.; Taraza, D.; Henein, N.A.; Bryzik, W. Simplified Elasto-Hydrodynamic Friction Model of the Cam-Tappet Contact; Technical report, SAE Technical Paper; SAE: Warrendale, PA, USA, 2003. [Google Scholar]
- Jalali-Vahid, D.; Rahnejat, H.; Jin, Z.M. Elastohydrodynamic solution for concentrated elliptical point contact of machine elements under combined entraining and squeeze-film motion. Proc. Inst. Mech. Eng. J. 1998, 212, 401–411. [Google Scholar] [CrossRef] [Green Version]
- Grimble, D.W.; Theodossiades, S.; Rahnejat, H.; Wilby, M. Thin film tribology of pharmaceutical elastomeric seals. Appl. Math. Model 2013, 37, 406–419. [Google Scholar] [CrossRef]
- Höglund, E. Influence of lubricant properties on elastohydrodynamic lubrication. Wear 1999, 232, 176–184. [Google Scholar] [CrossRef]
- Morgado, P.L.; Otero, J.E.; Lejarraga, J.B.S.; Sanz, J.L.M.; Lantada, A.D.; Munoz-Guijosa, J.M.; Yustos, H.L.; Wiña, L.; García, J.M. Models for predicting friction coefficient and parameters with influence in elastohydrodynamic lubrication. Proc. Inst. Mech. Eng. J. 2009, 223, 949–958. [Google Scholar] [CrossRef] [Green Version]
- Zhao, E.-H.; Ma, B.; Li, H.-Y. Numerical and experimental studies on tribological behaviors of cu-based friction pairs from hydrodynamic to boundary lubrication. Tribol. Trans. 2018, 61, 347–356. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. On the modeling of elastic contact between rough surfaces. Tribol. Trans. 2011, 54, 300–314. [Google Scholar] [CrossRef]
- Esfahanian, M.; Hamrock, B.J. Fluid-film lubrication regimes revisited. Tribol. Trans. 1991, 34, 628–632. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Ståhl, J.; Jacobson, B.O. A non-newtonian model based on limiting shear stress and slip planes—Parametric studies. Tribol. Int. 2003, 36, 801–806. [Google Scholar] [CrossRef]




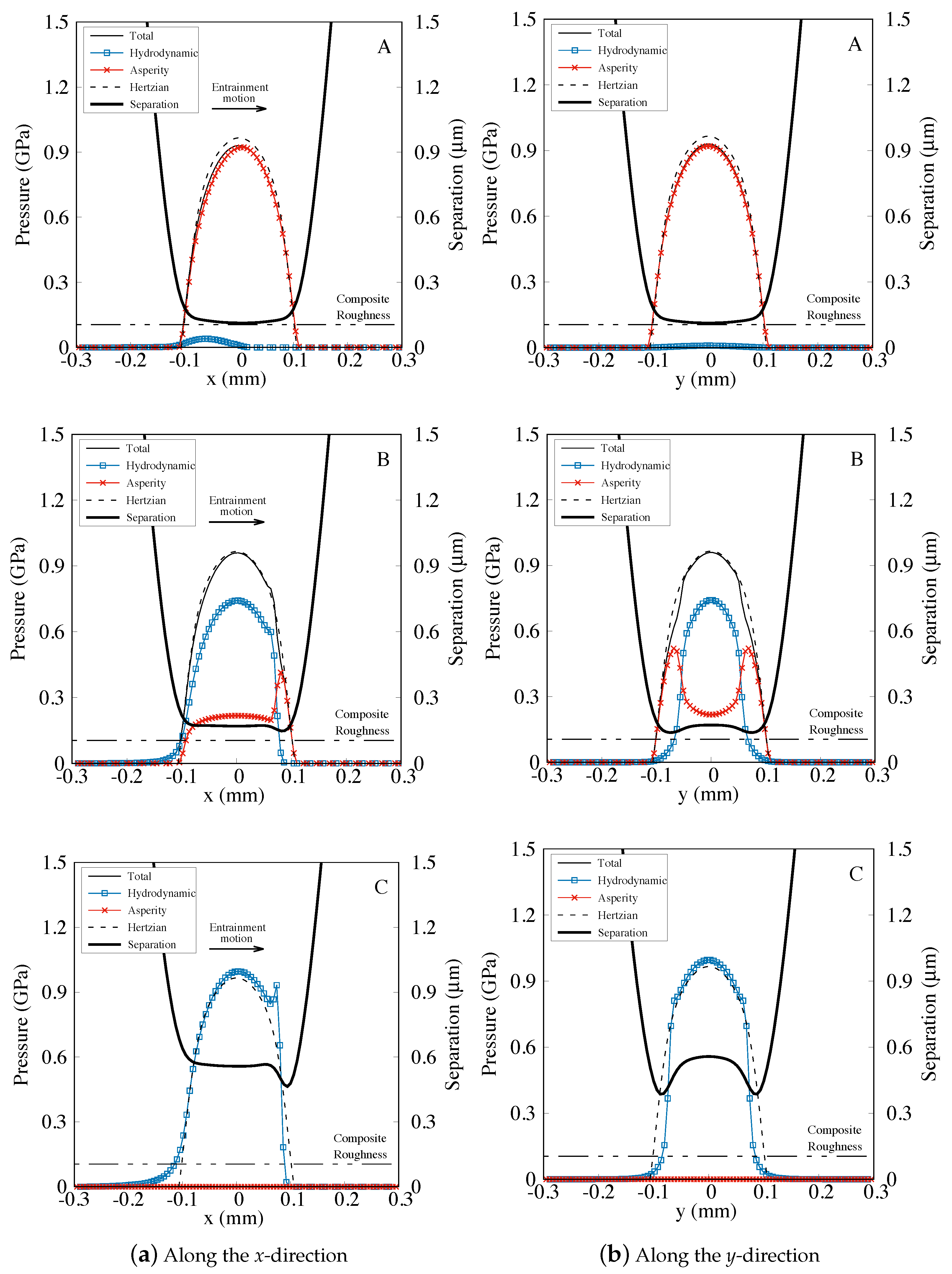



| Parameter | Value | Unit |
|---|---|---|
| Composite surface roughness, | 0.105 | μm |
| 0.4 | - | |
| 0.055 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chong, W.W.F.; Hamdan, S.H.; Wong, K.J.; Yusup, S. Modelling Transitions in Regimes of Lubrication for Rough Surface Contact. Lubricants 2019, 7, 77. https://doi.org/10.3390/lubricants7090077
Chong WWF, Hamdan SH, Wong KJ, Yusup S. Modelling Transitions in Regimes of Lubrication for Rough Surface Contact. Lubricants. 2019; 7(9):77. https://doi.org/10.3390/lubricants7090077
Chicago/Turabian StyleChong, William Woei Fong, Siti Hartini Hamdan, King Jye Wong, and Suzana Yusup. 2019. "Modelling Transitions in Regimes of Lubrication for Rough Surface Contact" Lubricants 7, no. 9: 77. https://doi.org/10.3390/lubricants7090077
APA StyleChong, W. W. F., Hamdan, S. H., Wong, K. J., & Yusup, S. (2019). Modelling Transitions in Regimes of Lubrication for Rough Surface Contact. Lubricants, 7(9), 77. https://doi.org/10.3390/lubricants7090077






