Studies on the Pressure Buildup and Shear Flow Factors in the Cavitation Regime
Abstract
:1. Introduction
1.1. Motivation
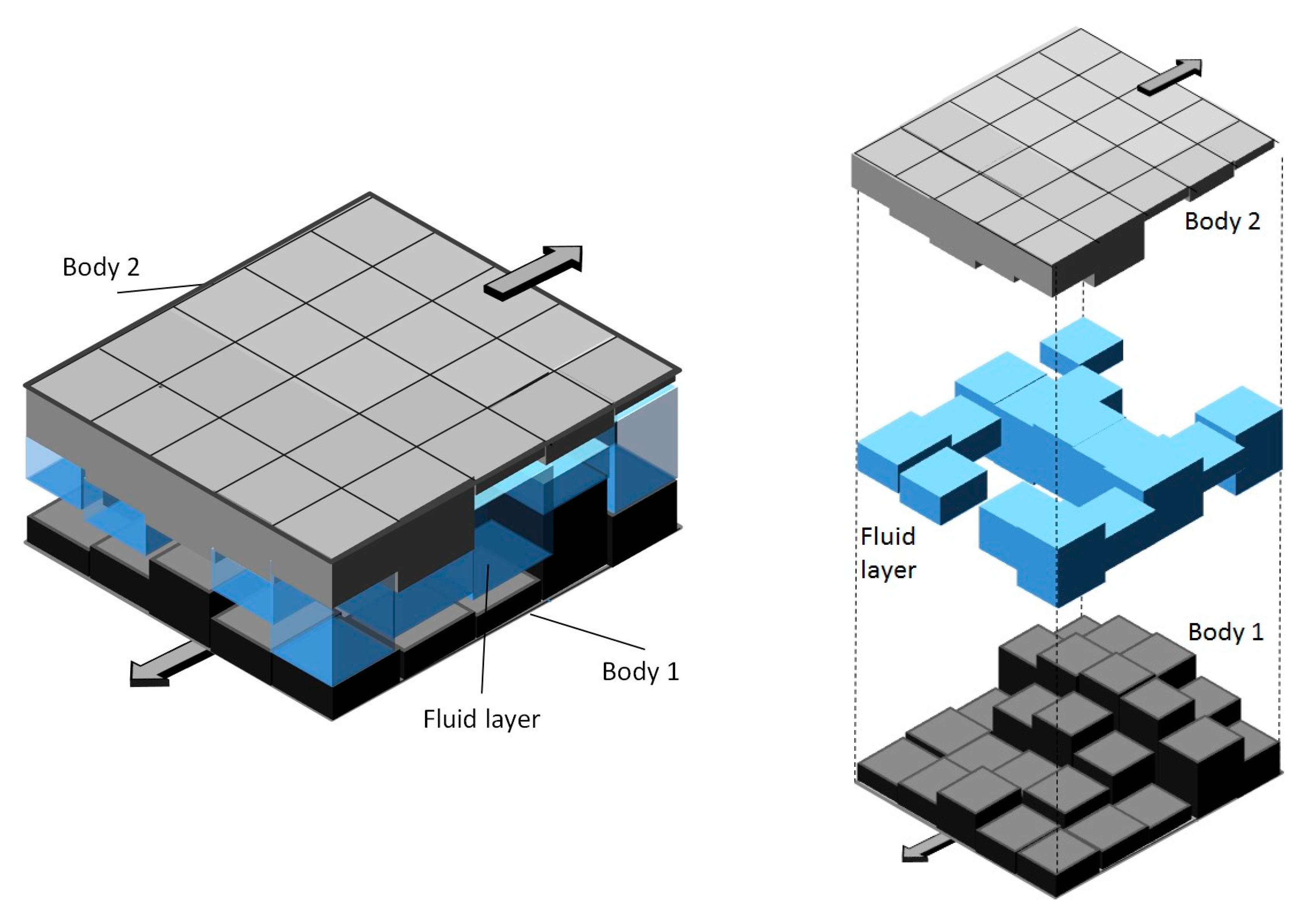
1.2. Common Assumptions and Realization of the micro-EHD Problem
- (1)
- In macroscopically not fully filled areas the pressure corresponds to the cavitation pressure (in most cases assumed to be zero), independent of the microscopic roughness;
- (2)
- In macroscopically not fully filled areas, a shear flow factor is applied, which was determined in advance on a microscopic scale with a fully filled gap.
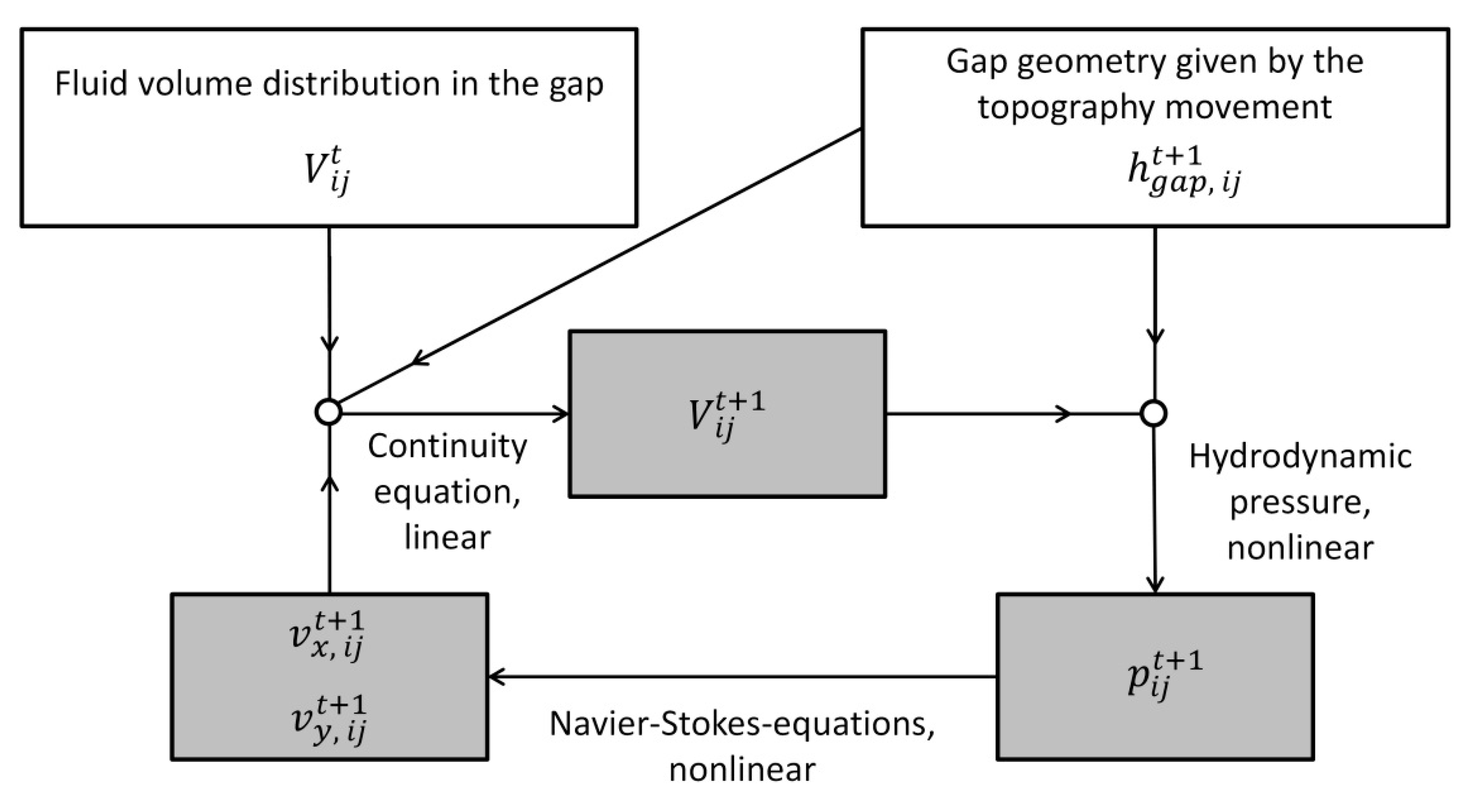
1.3. PFG Model and Its Application to the Calculation of Pressures and Shear Flow Factors
2. Studies with a Partially Filled Gap
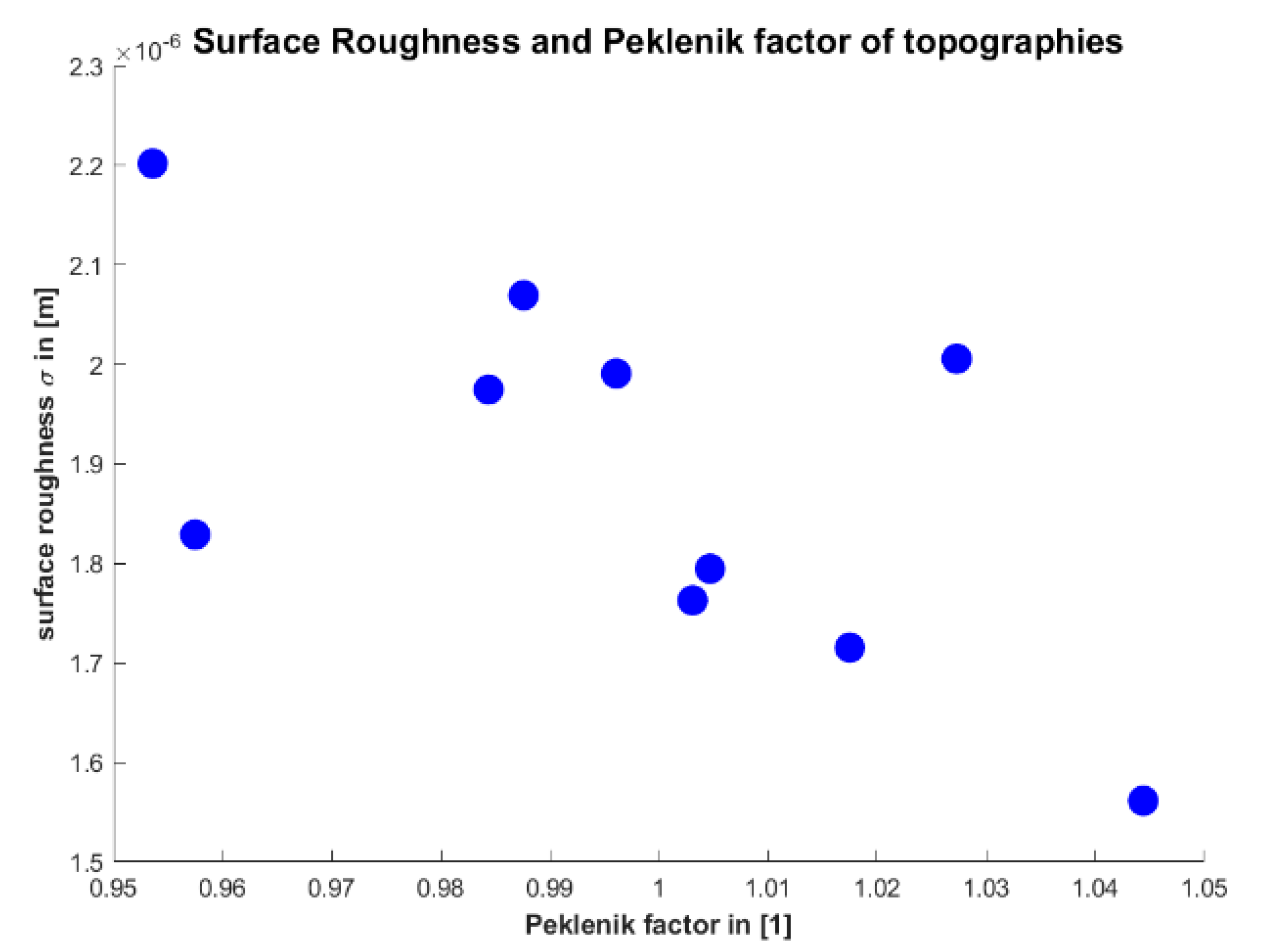
2.1. Varying the Topography
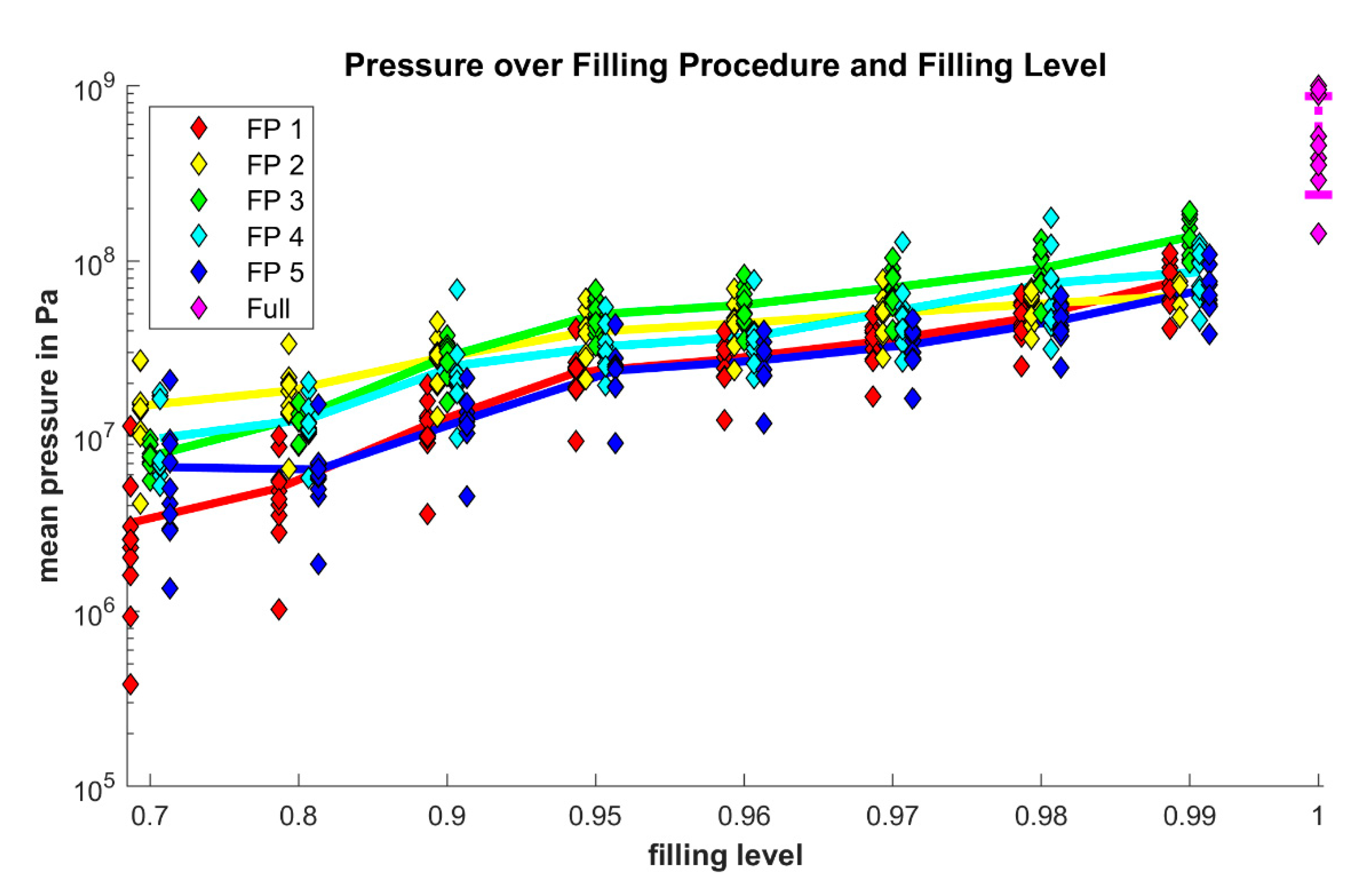
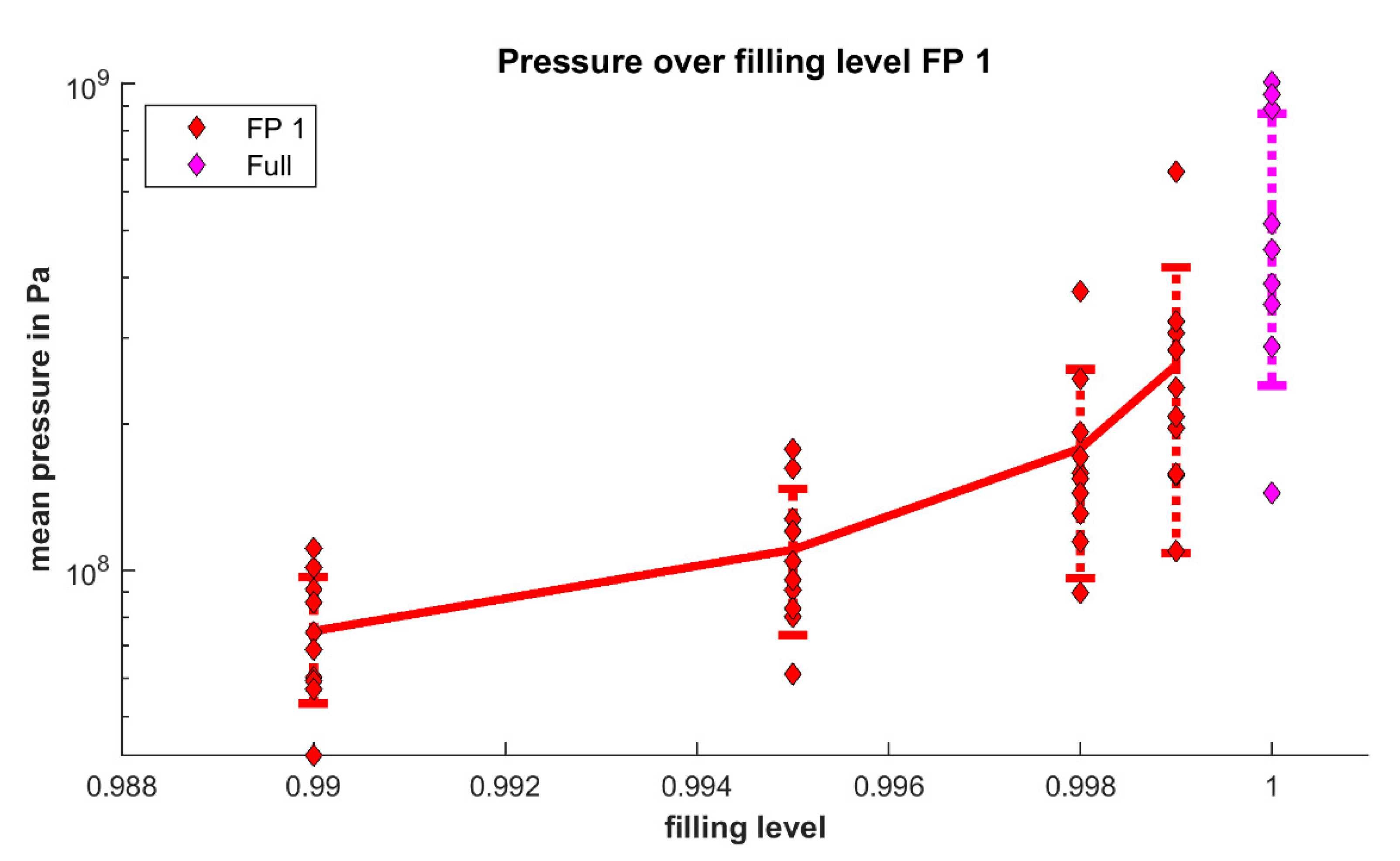
2.2. Varying the Filling Level
2.3. Varying the Initial Fluid Distribution
3. Results
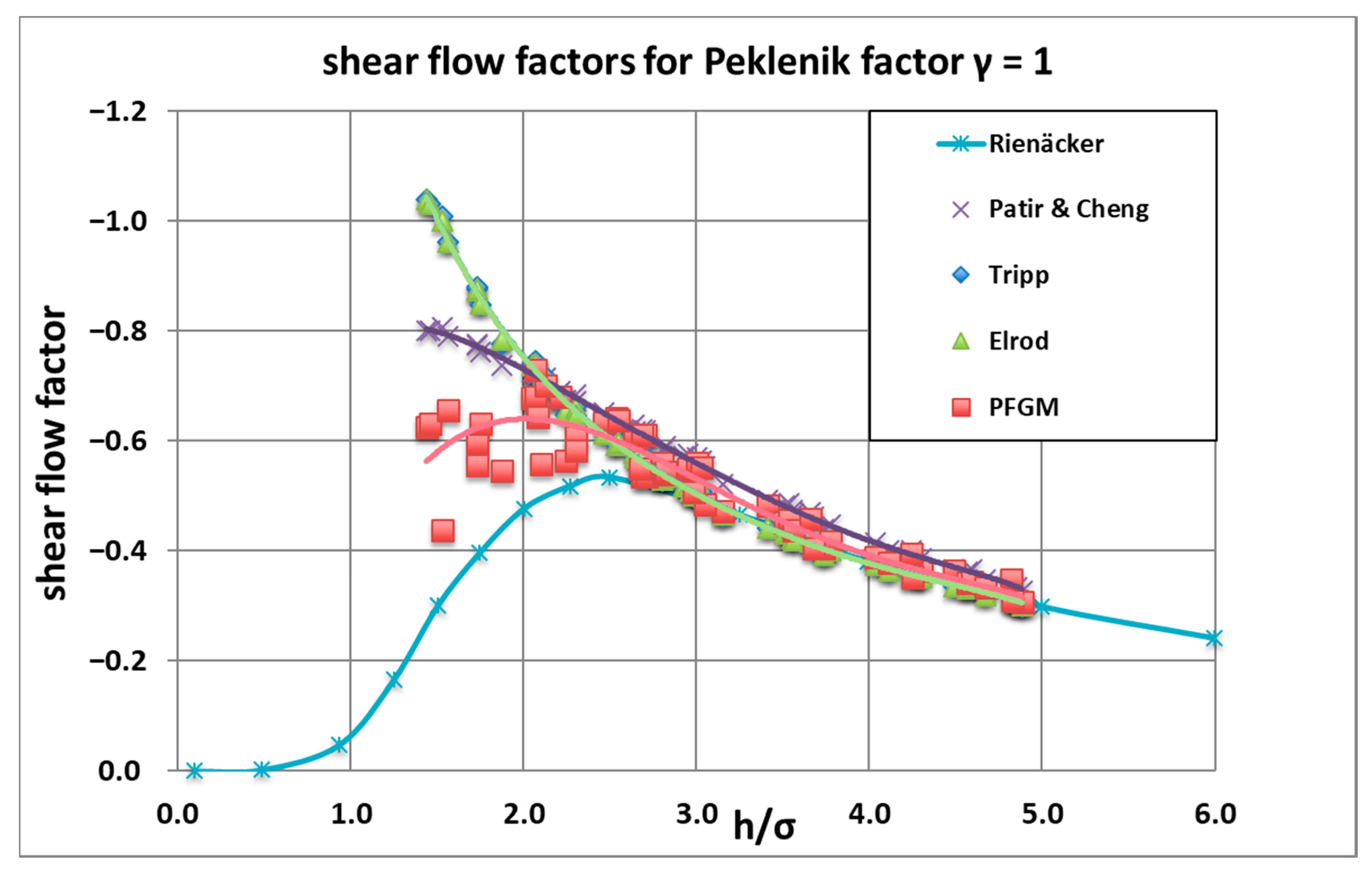
3.1. Shear Flow Factor
3.2. Mean Hydrodynamic Pressure
4. Summary, Discussion and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. A Numerical Solution to the Elasto-Hydrodynamic Problem. J. Mech. Eng. Sci. 1959, 1, 6–15. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.J.; Bair, S.; Vergne, P. A Quantitative Solution for the Full Shear-Thinning EHL Point Contact Problem Including Traction. Tribol. Lett. 2007, 28, 171–181. [Google Scholar] [CrossRef]
- Elrod, H.G.; Adams, M.L. A Computer Program for Cavitation and Starvation Problems. In Proceedings of the 1st Leeds-Lyon Symposium on Tribology, Leeds, UK, 6–9 September 1974; pp. 37–41. [Google Scholar]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lub. Tech. 1978, 100, 12. [Google Scholar] [CrossRef]
- Müller, M.; Ostermeyer, G.-P.; Bubser, F. A contribution to the modeling of tribological processes under starved lubrication. Tribol. Int. 2013, 64, 135–147. [Google Scholar] [CrossRef]
- Müller, M.; Stahl, L.; Ostermeyer, G.-P. Experimental Studies of Lubricant Flow and Friction in Partially Filled Gaps. Lubricants 2018, 6, 110. [Google Scholar] [CrossRef] [Green Version]
- Etsion, I.; Pinkus, O. Solutions of Finite Journal Bearings With Incomplete Films. J. Lub. Tech. 1975, 97, 89. [Google Scholar] [CrossRef]
- Etsion, I.; Barkon, I. Analysis of a Hydrodynamic Thrust Bearing With Incomplete Film. J. Lub. Tech. 1981, 103, 355. [Google Scholar] [CrossRef]
- Tanaka, M. Journal bearing performance under starved lubrication. Tribol. Int. 2000, 33, 259–264. [Google Scholar] [CrossRef]
- Wang, W.-Z.; Li, S.; Shen, D.; Zhang, S.; Hu, Y.-Z. A mixed lubrication model with consideration of starvation and interasperity cavitations. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 1023–1038. [Google Scholar] [CrossRef]
- Dowson, D.; Taylor, C.M. Cavitation in bearings. Annu. Rev. Fluid Mech. 1979, 11, 35–65. [Google Scholar] [CrossRef]
- Ausas, R.; Ragot, P.; Leiva, J.; Jai, M.; Bayada, G.; Buscaglia, G.C. The Impact of the Cavitation Model in the Analysis of Microtextured Lubricated Journal Bearings. J. Tribol. 2007, 129, 868–875. [Google Scholar] [CrossRef]
- Bayada, G.; Martin, S.; Vázquez, C. An Average Flow Model of the Reynolds Roughness Including a Mass-Flow Preserving Cavitation Model. J. Tribol. 2005, 127, 793–802. [Google Scholar] [CrossRef] [Green Version]
- Sahlin, F.; Almqvist, A.; Larsson, R.; Glavatskih, S. A cavitation algorithm for arbitrary lubricant compressibility. Tribol. Int. 2007, 40, 1294–1300. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lub. Tech. 1979, 101, 220. [Google Scholar] [CrossRef]
- Müller, M.; Jäschke, H.; Bubser, F.; Ostermeyer, G.-P. Simulative studies of tribological interfaces with partially filled gaps. Tribol. Int. 2014, 78, 195–209. [Google Scholar] [CrossRef]
- Müller, M.; Völpel, A.; Ostermeyer, G.-P. On the influence of fluid dynamics and elastic deformations on pressure buildup in partially filled gaps. Tribol. Int. 2017, 105, 345–359. [Google Scholar] [CrossRef]
- Tripp, J.H. Surface roughness effects in hydrodynamic lubrication: the flow factor method. J. Lub. Tech. 1983, 105, 458–463. [Google Scholar] [CrossRef] [Green Version]
- Rienäcker, A. Instationäre Elastohydrodynamik von Gleitlagern mit Rauhen Oberflächen und Inverse Bestimmung der Warmkonturen; Universität Kassel: Kassel, Germany, 1995. [Google Scholar]
- Bartel, D. Simulation von Tribosystemen. Grundlagen und Anwendungen; Vieweg+Teubner: Wiesbaden, Germany, 2010; ISBN 978-3-8348-9656-8. [Google Scholar]
- Shen, C.; Khonsari, M.M. On the Magnitude of Cavitation Pressure of Steady-State Lubrication. Tribol. Lett. 2013, 51, 153–160. [Google Scholar] [CrossRef]
- Shen, C.; Khonsari, M.M. Effect of Dimple’s Internal Structure on Hydrodynamic Lubrication. Tribol. Lett. 2013, 52, 415–430. [Google Scholar] [CrossRef]

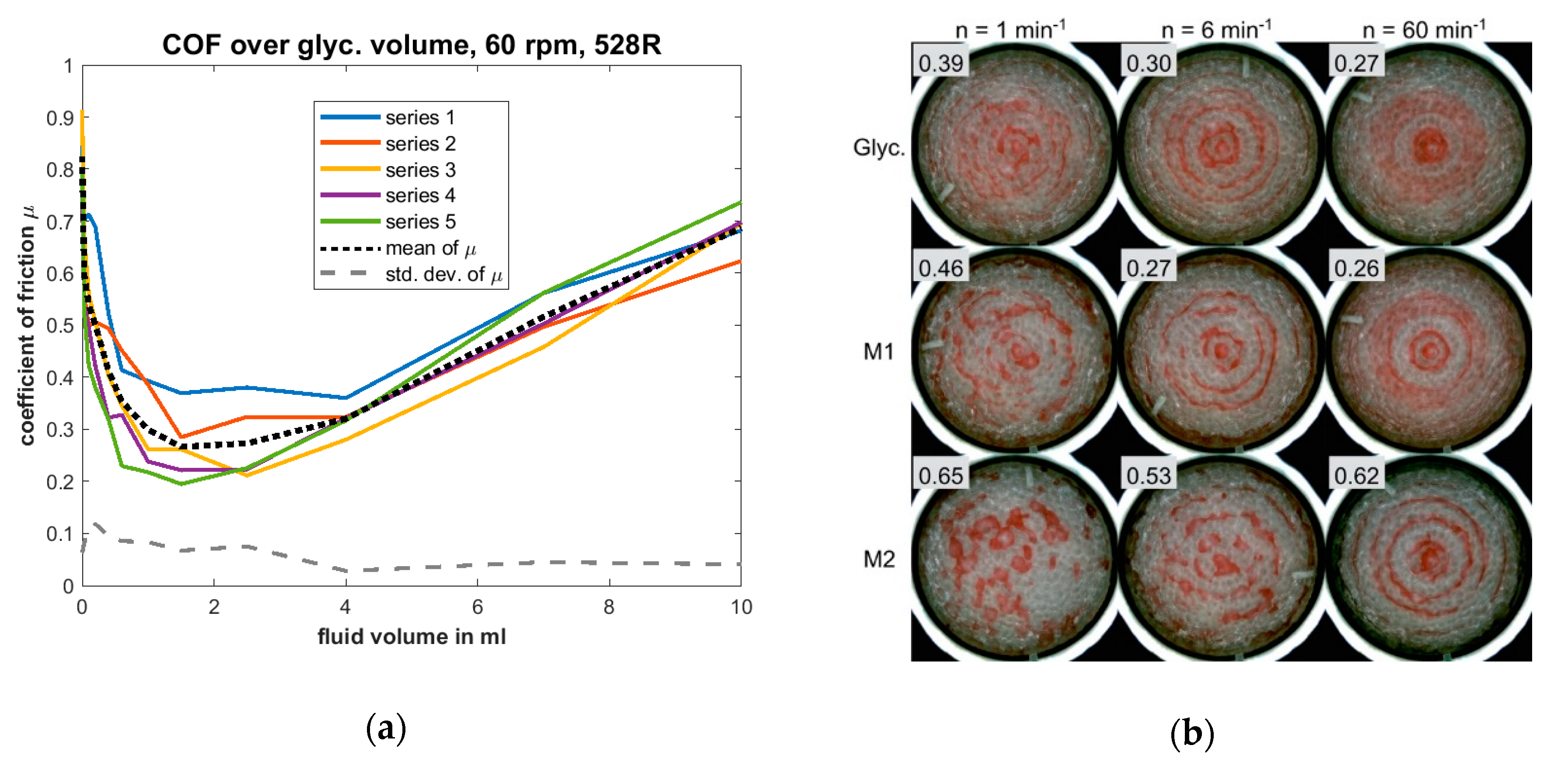



FP1: “filling level”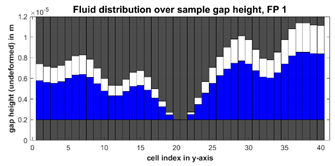 | This procedure applies the filling level to each individual cell. Thus, no cell is initially fully filled, but each cell is partially filled with the same filling level. This procedure corresponds to a state in which initially no cell is fully filled, and no fluid pressure is present. With the movement of the topographies the fluid flows and full cells appear. |
FP 2: “bottom up”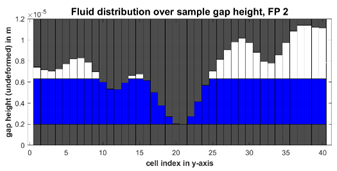 | This procedure fills the gap metaphorically from the bottom up. The fluid is distributed so that the absolute fluid volume in each cell is the same. If a cell is smaller than that volume, the cell is fully filled with its respective fluid volume. This leads to homogenous distribution of fluid in the gap and the number of initially fully filled cells is small. |
FP 3: “big to small” | This procedure fills the gap starting with the cell of greatest gap height. Subsequently, the second greatest cell is filled. This procedure continues until the available fluid volume (according to the filling level) is distributed. The cell that is filled last may only be partially filled (here cell 4). This leads to an inhomogeneous distribution with a relatively large number of fully filled cells. |
FP 4: “random cells”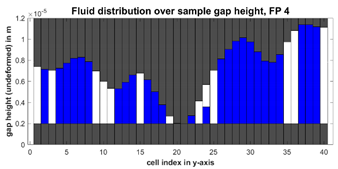 | This procedure fully fills random cells. A random cell is selected and fully filled until the available fluid volume is distributed (according to global filling level). The cell that is filled last may only be partially filled (here cell 24). This procedure leads to a distribution with a large number of fully filled cells. |
FP 5: “random”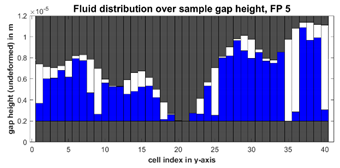 | This procedure chooses a random cell and attempts to fill it with a random amount of fluid. If the chosen amount fits into the cell (cell empty or only partially filled), the procedure fills it and proceeds. If the chosen amount does not fit into the remaining volume in the chosen cell, the procedure continues with a new random cell and a new random amount of fluid. The procedure continues until the complete fluid volume is distributed. Each cell can be chosen multiple times. This leads to a situation where most cells has a high filling level, but none is completely filled. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller, M.; Stahl, L.; Ostermeyer, G.-P. Studies on the Pressure Buildup and Shear Flow Factors in the Cavitation Regime. Lubricants 2020, 8, 82. https://doi.org/10.3390/lubricants8080082
Müller M, Stahl L, Ostermeyer G-P. Studies on the Pressure Buildup and Shear Flow Factors in the Cavitation Regime. Lubricants. 2020; 8(8):82. https://doi.org/10.3390/lubricants8080082
Chicago/Turabian StyleMüller, Michael, Lukas Stahl, and Georg-Peter Ostermeyer. 2020. "Studies on the Pressure Buildup and Shear Flow Factors in the Cavitation Regime" Lubricants 8, no. 8: 82. https://doi.org/10.3390/lubricants8080082






