Analysis of the Effect of the Slip-Pocket in Single and Double Parallel Bearing Considering Cavitation: A Theoretical Approach
Abstract
:1. Introduction
2. Mathematical Model
3. Methodology
- Single pocket. For all computations, the cavitation phenomenon is assumed to occur in the pocket. Here, the cavitation equations (Equations (A1)–(A11) of Appendix A) are used to obtain Xb (non-cavitated region in the pocket as seen in Figure 1) Xb is then used as an indicator of whether cavitation occurs or not. Cavitation in a pocket occurs if 0 < Xb < b, where b is the pocket length.
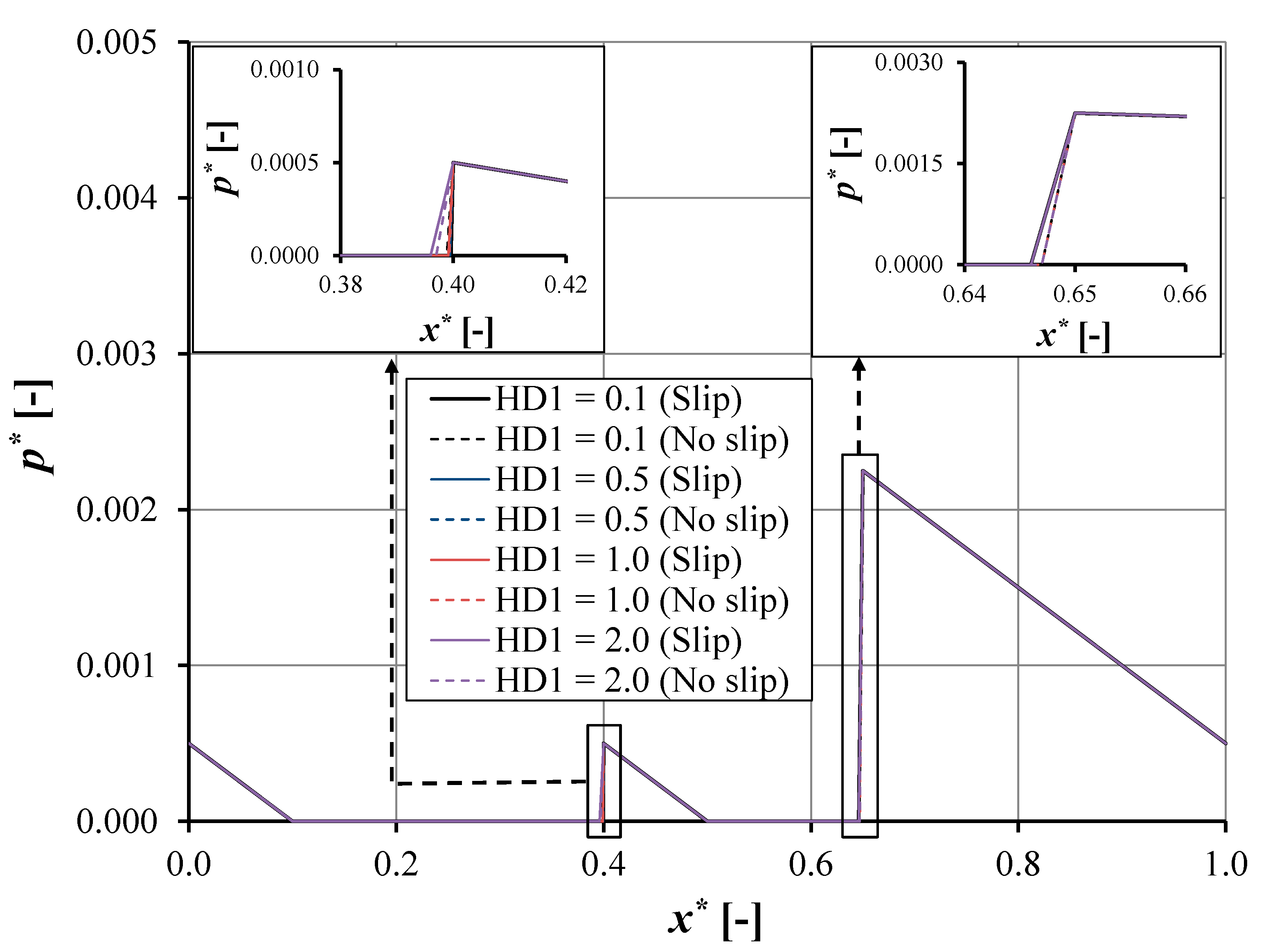
- Double pocket. For all computations, the cavitation phenomenon is assumed to occur in the first and second pockets of the bearing. The cavitation equations (Equations (A12)–(A24), see Appendix A) to obtain Xb and Xd (a non-cavitated region in the first and second pockets as indicated in Figure 2) are used. Xb and Xd will then be used as an indicator of whether cavitation occurs or not. It should be noted that cavitation in the first pocket occurs if 0 < Xb < b, where b is the first pocket length and cavitation in second pocket occurs if 0 < Xd < d, where d is the second pocket length.
4. Results and Discussion
4.1. Case of Single-Pocketed Bearing
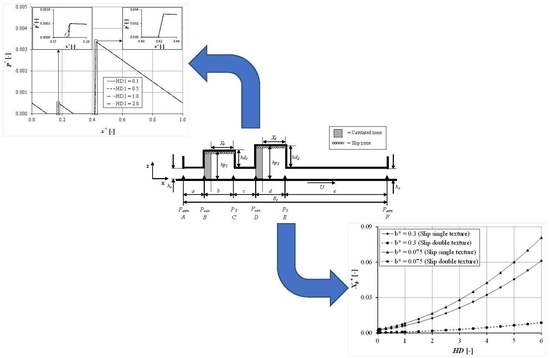
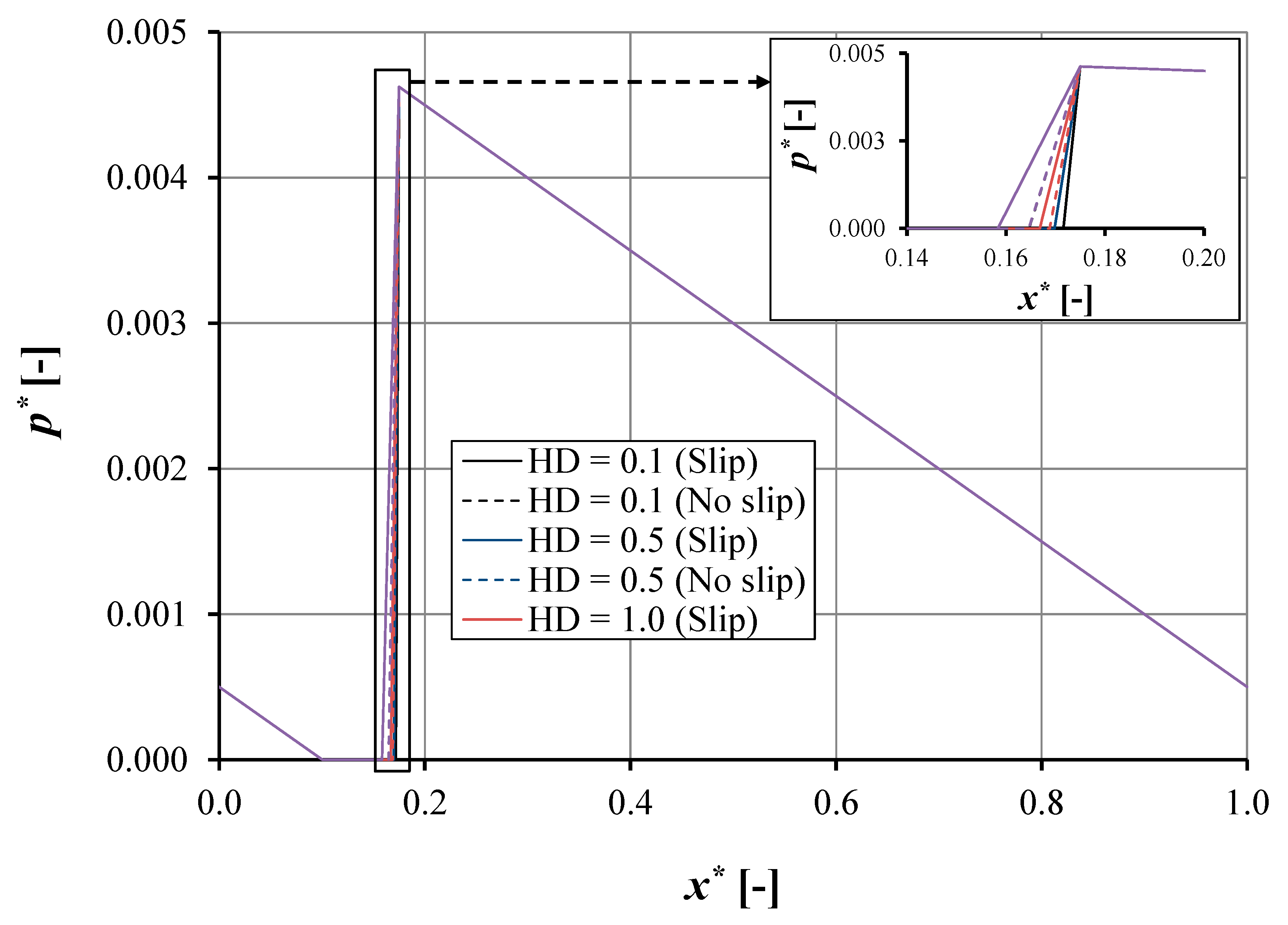
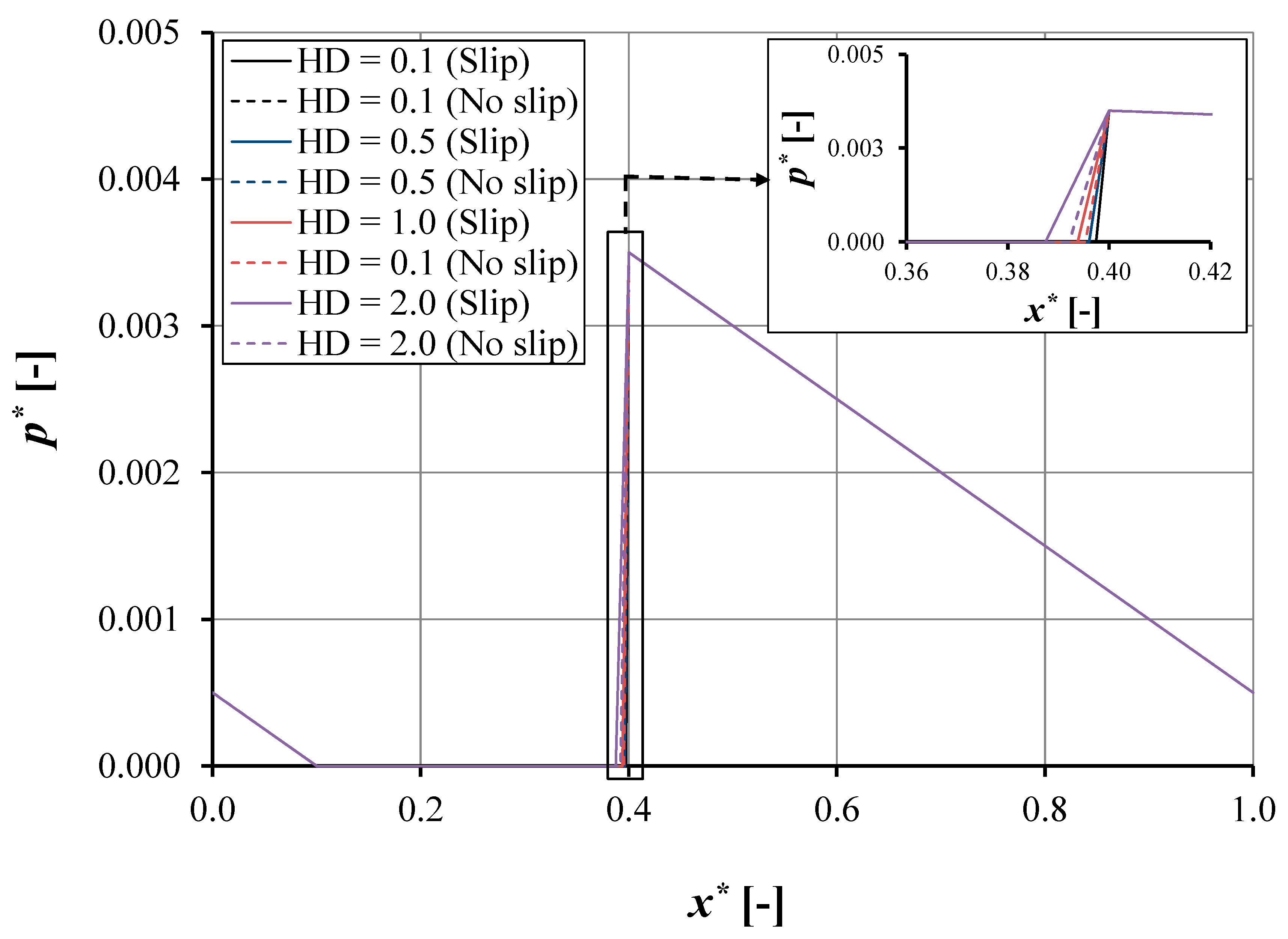
4.1.1. Effect of Pocket Depth with Low Pocket Length
4.1.2. Effect of Pocket Depth with High Pocket Length
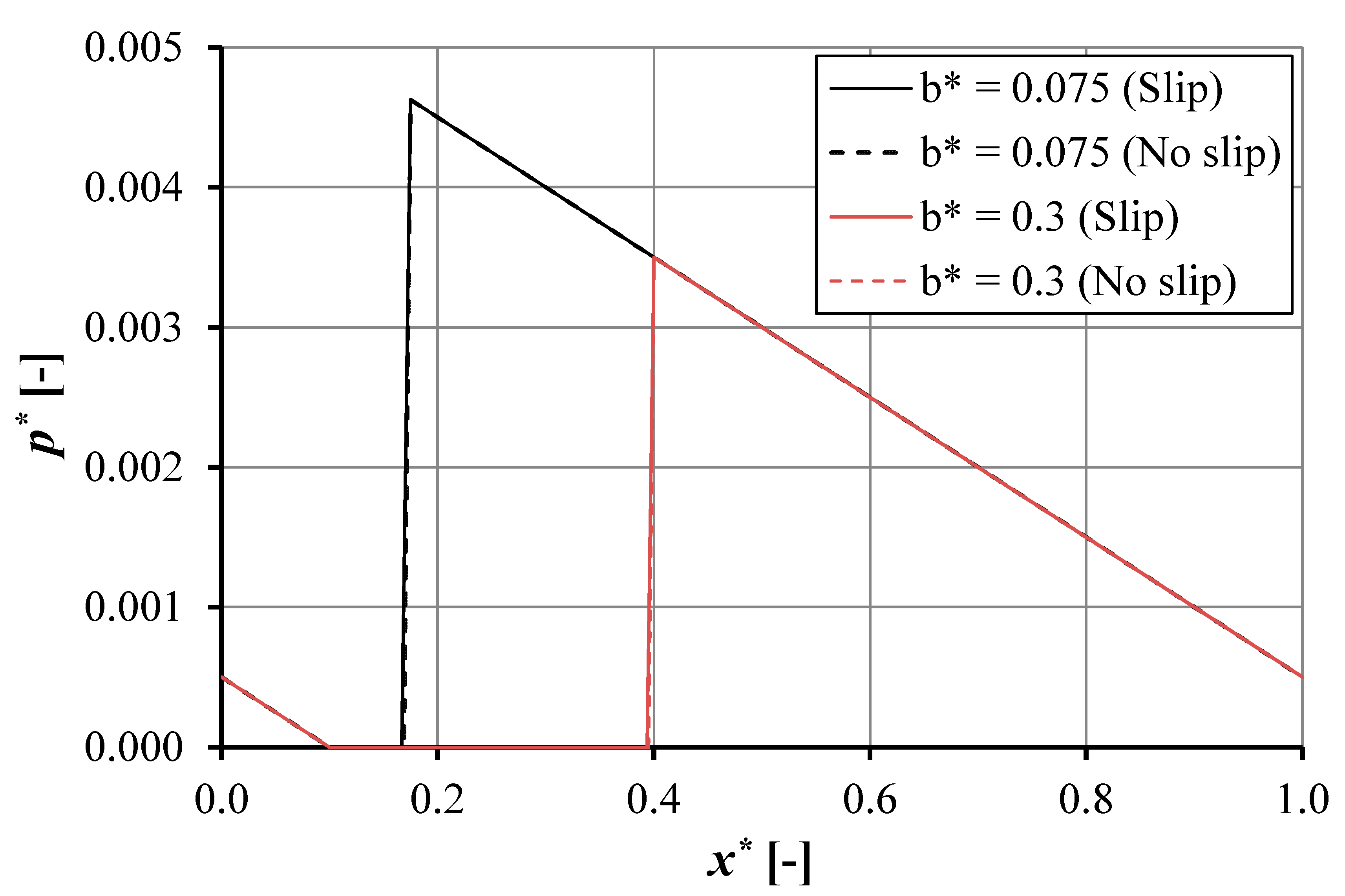
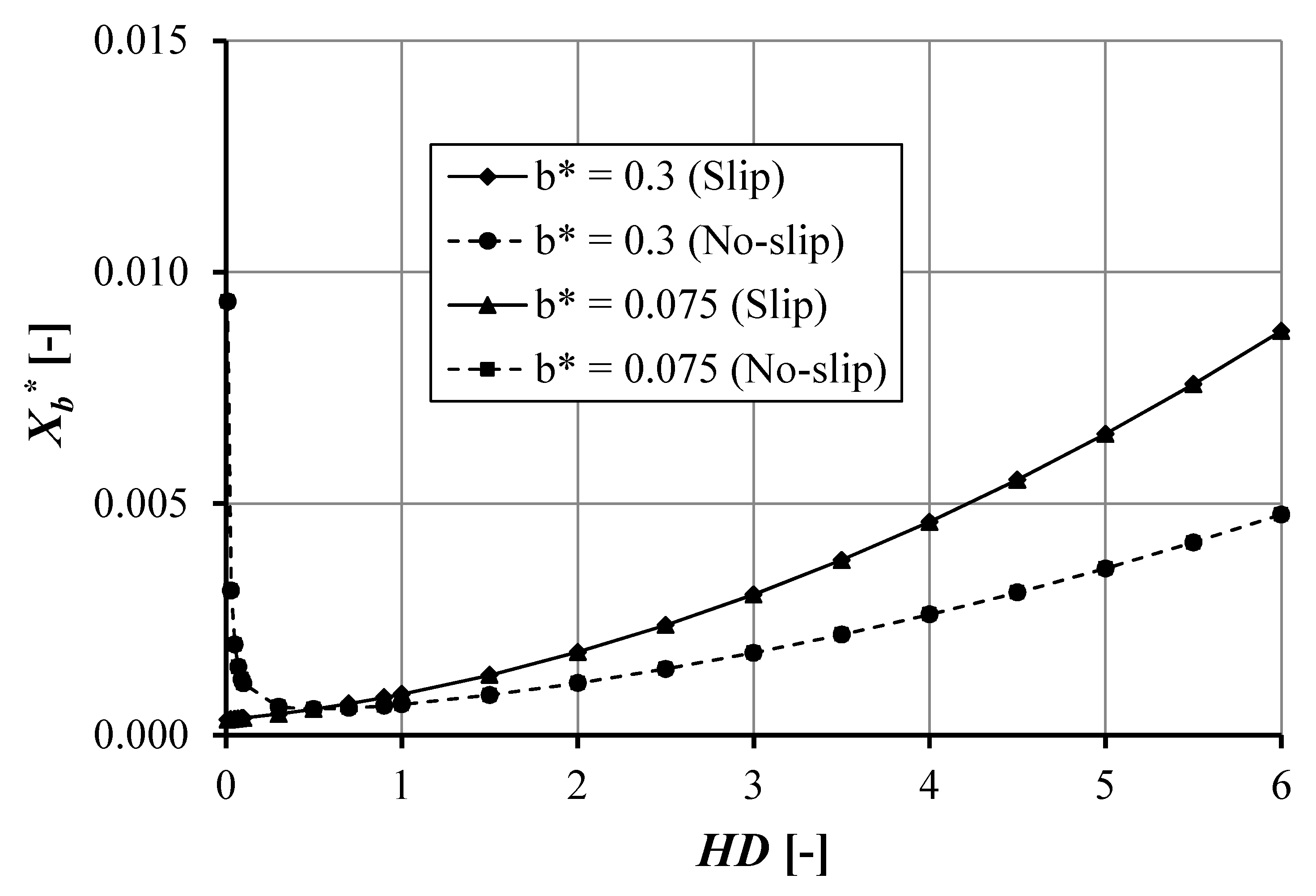
4.1.3. Effect of Pocket Length, b
4.2. Case of Double-Pocketed Bearing
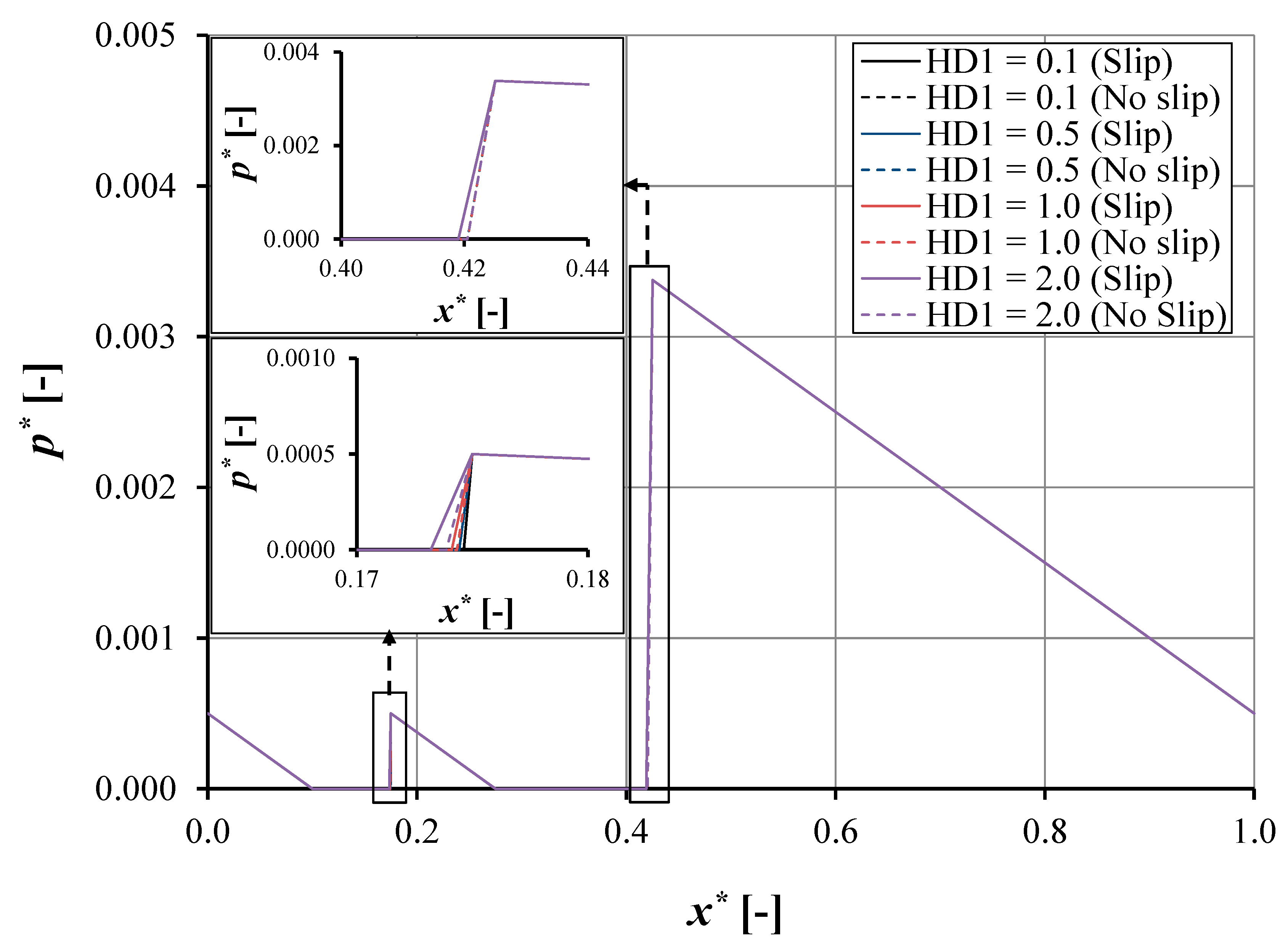
4.2.1. Effect of First Pocket Depth
4.2.2. Effect of First Pocket Length
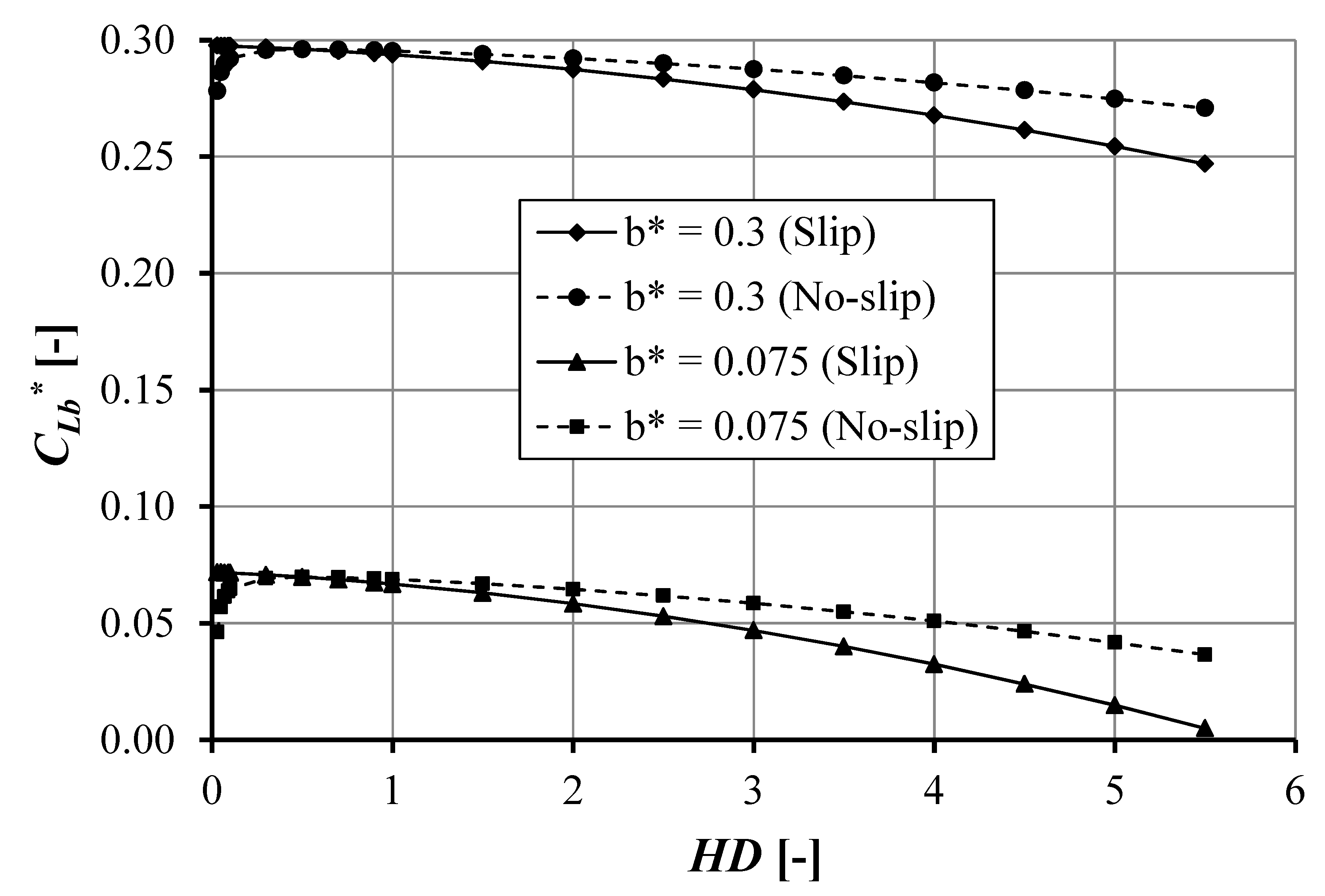
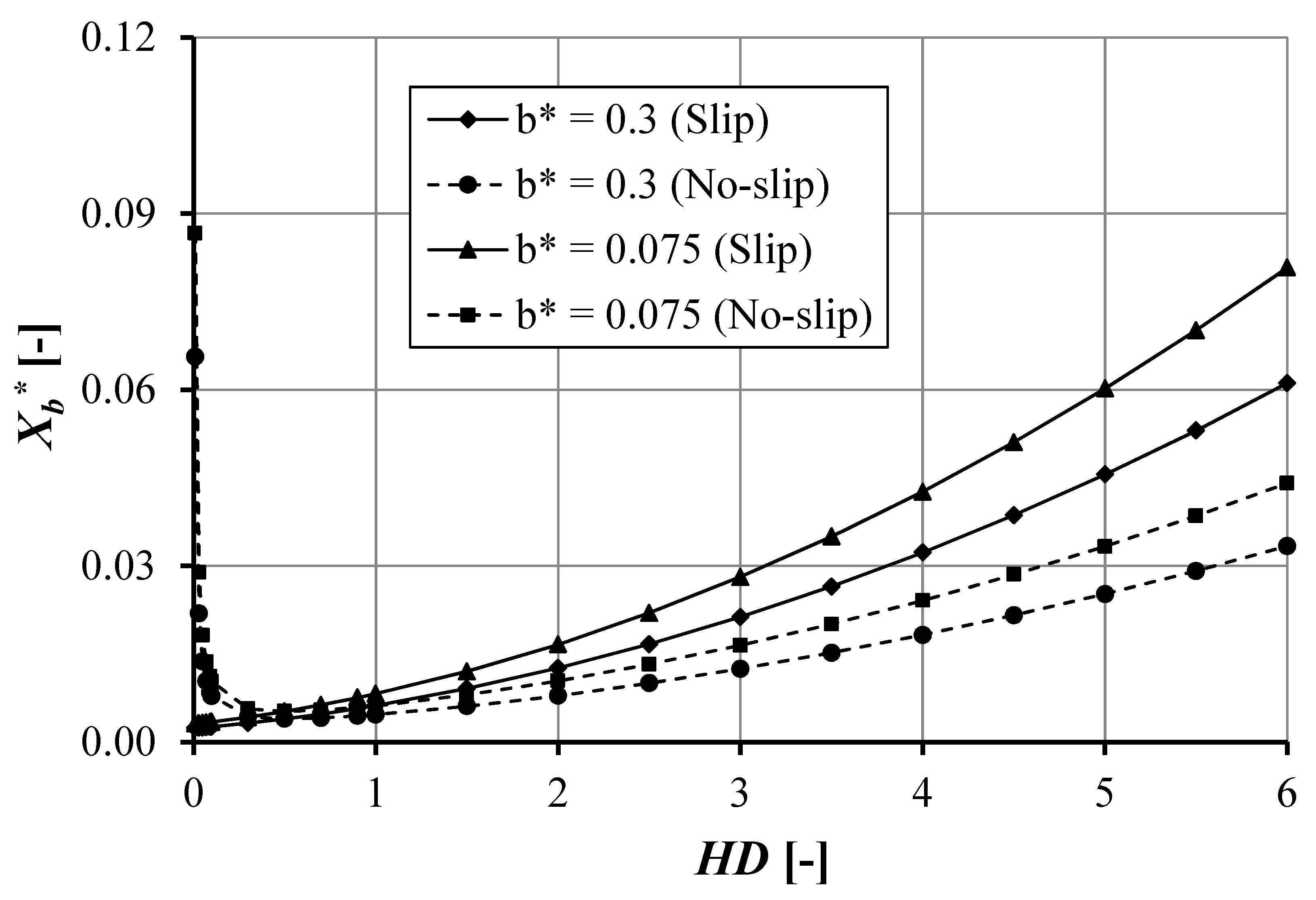
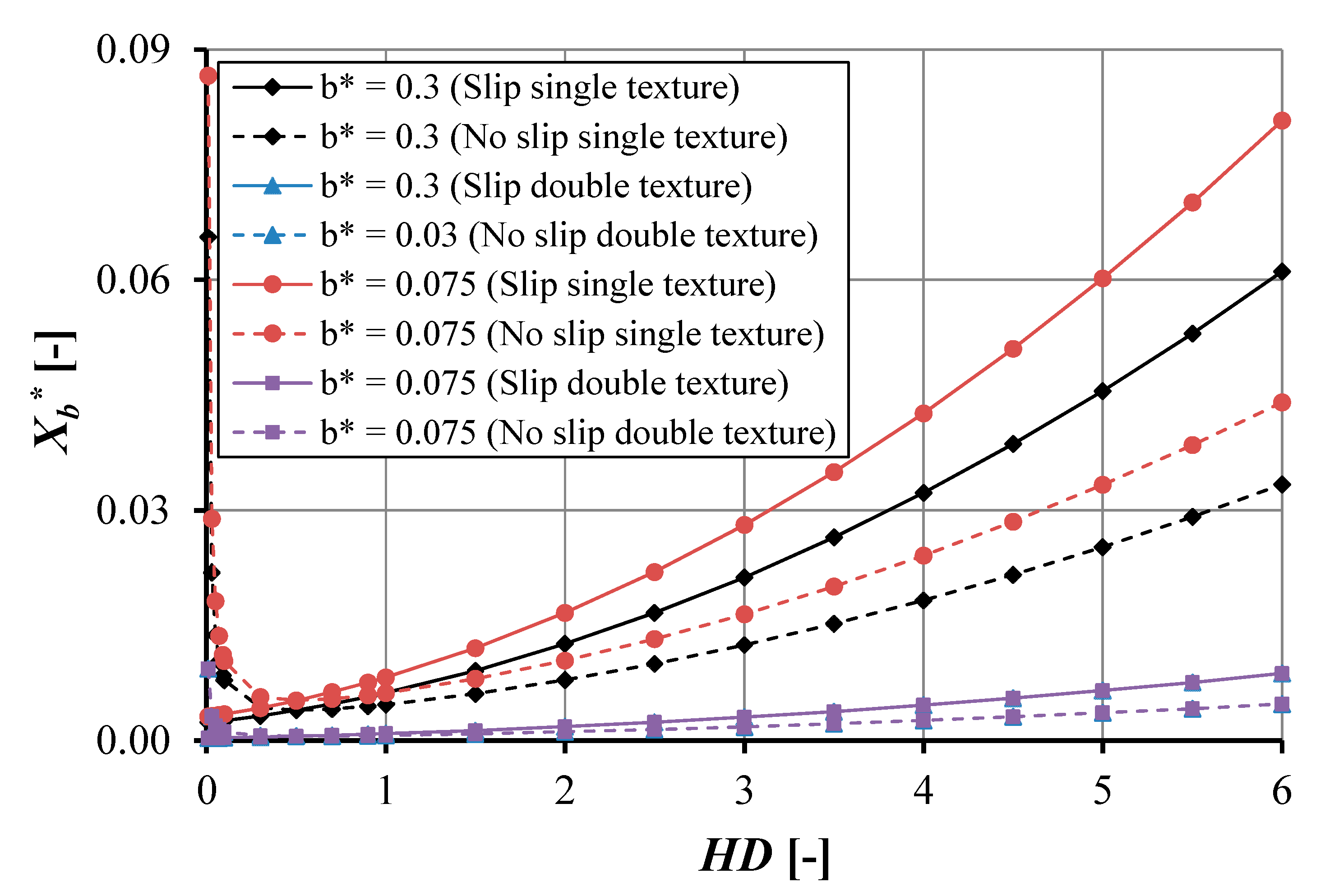
4.2.3. Comparison of Pocket Length in Double Texture
5. Conclusions
- The pocket depth has a strong effect on pressure and load support. For the slip condition, increasing the pocket depth increases the load support. However, for the no-slip condition, the optimal pocket depth is observed; when this value is exceeded, the reduced load support is found.
- When the slip condition is applied on the top edge of the pocket, the slip effect is not as significant as in the no-slip condition. The load support improvement is no more than 3% both for single-pocket and double-pocket, irrespective of the pocket length.
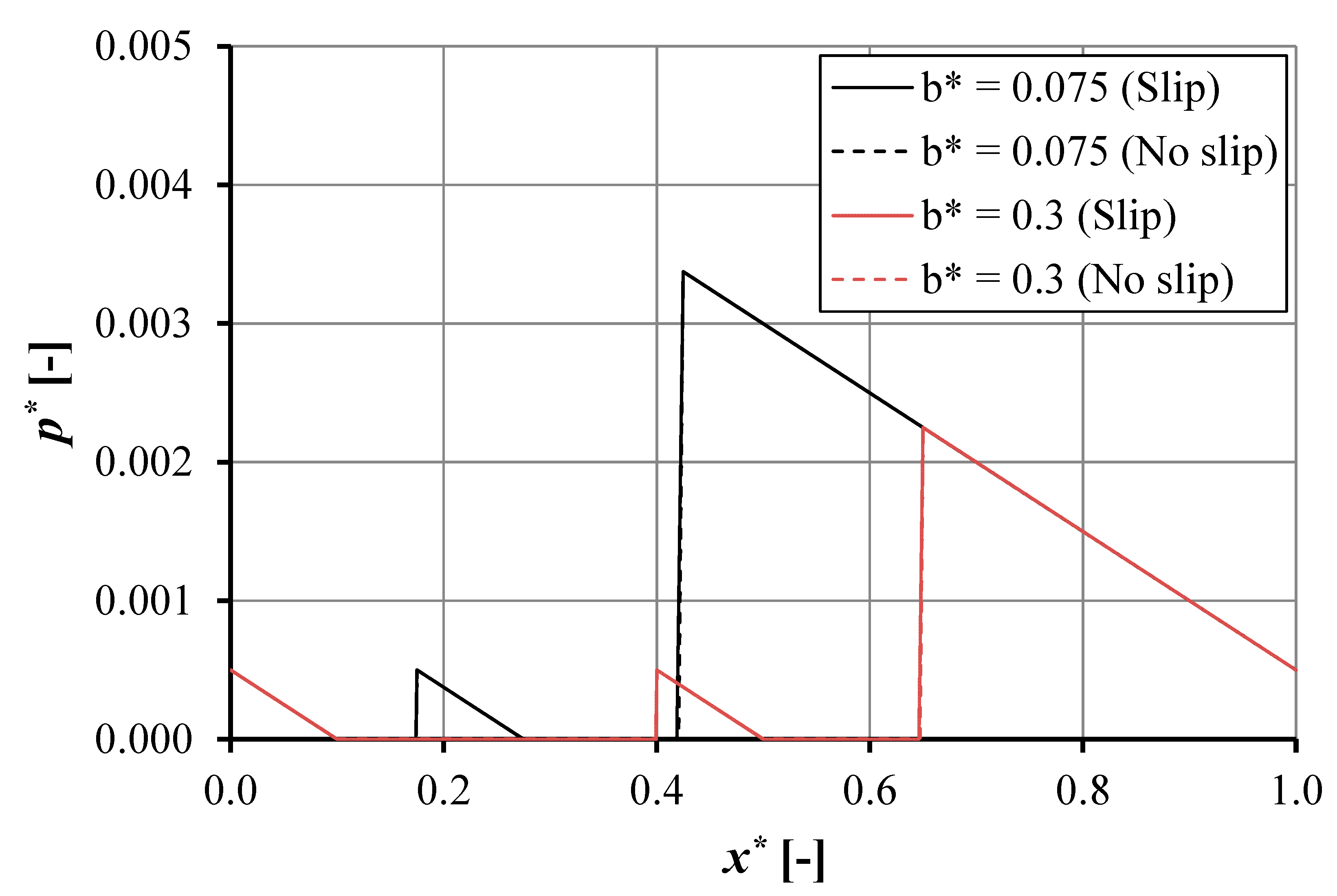
- The maximum pressure and load support increase with reducing pocket length.
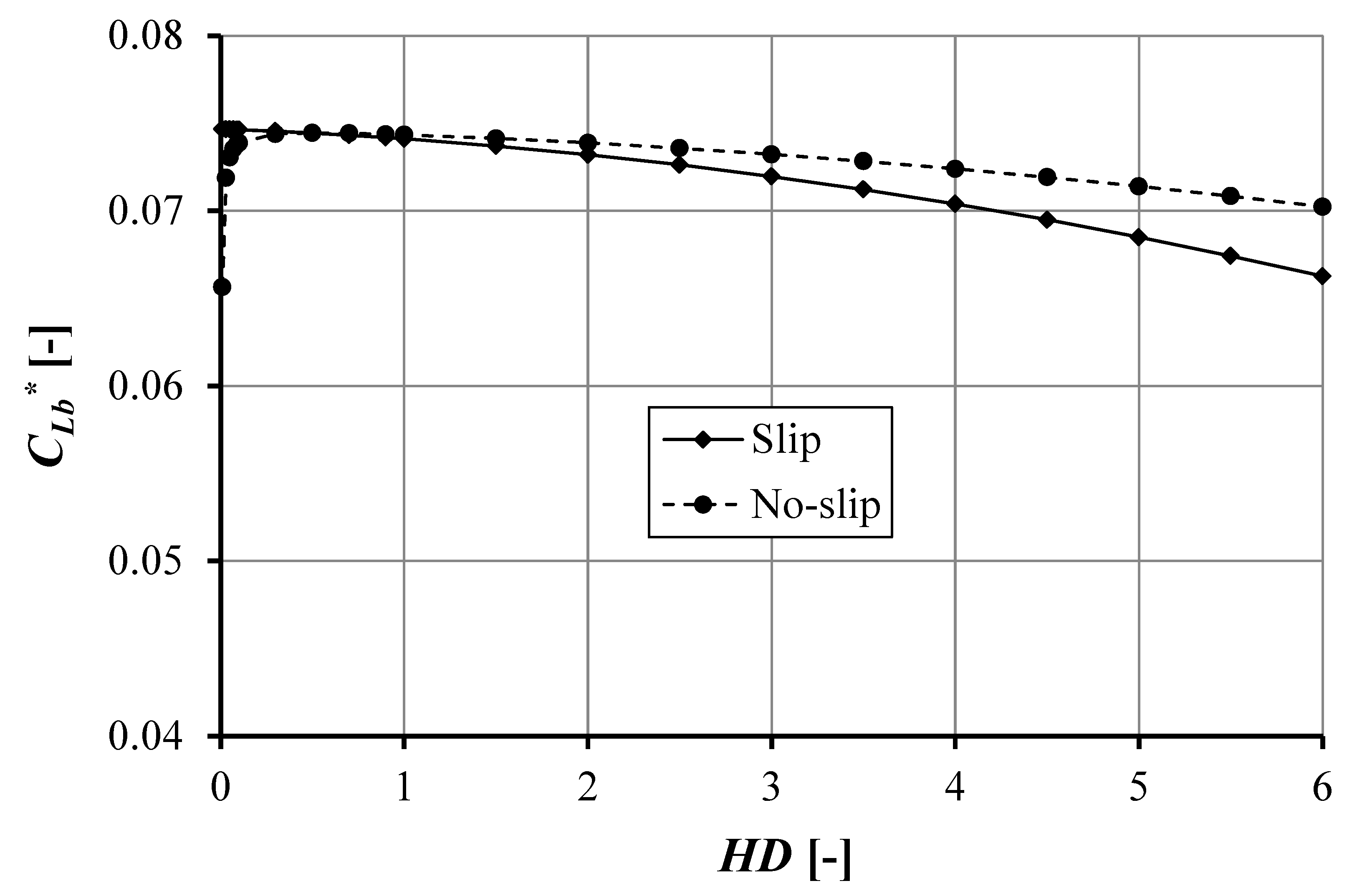
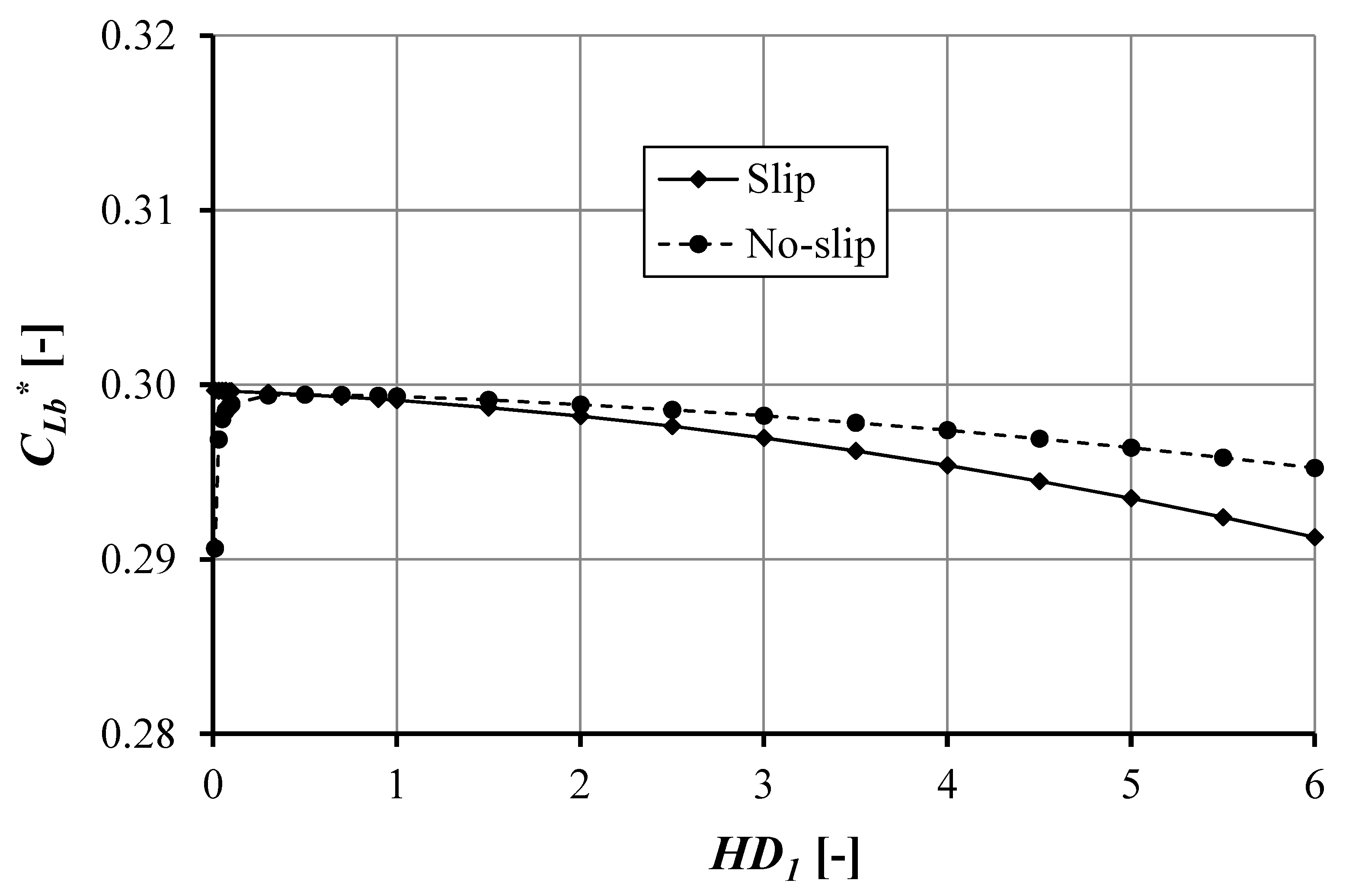
- The slip condition in the pocket reduces the cavitation area both for the single- and double-pocket bearing. This slip effect is more pronounced when a high pocket depth is used.
- The decrease in pocket length enhances the load support and reduces the cavitation area both for the slip and no-slip conditions irrespective of the pocket depth.
- The main interesting finding is that the pocket depth reduces the cavitation area for both the single- and double-pocket bearing. However, the pocket depth has a more important influence in reducing the effect of cavitation in the case of the single pocket than in the case of the double pocket bearing.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | inlet length |
| b | first pocket width |
| Bo | slider length |
| c | length between pockets |
| CL | length of cavitation area |
| CLb | length of cavitation area first pocket |
| CLd | length of cavitation area second pocket |
| d | second pocket width |
| e | outlet land length |
| hd | height of microtexture pocket (excluding film thickness) |
| hd1 | height of microtexture first pocket (excluding film thickness) |
| hd2 | height of microtexture second pocket (excluding film thickness) |
| hp | film thickness in pocket |
| hp1 | film thickness in first pocket |
| hp2 | film thickness in second pocket |
| ho | minimum film thickness |
| P3 | pressure at C |
| P5 | pressure at E |
| patm | atmospheric pressure |
| pcav | cavitation pressure |
| U | sliding velocity |
| w | load support |
| q | flow rate |
| x | coordinate in sliding direction |
| Xb | non-cavitated fraction of first pocket |
| Xd | non-cavitated fraction of second pocket |
| z | coordinate through film thickness |
| μ | lubricant dynamic viscosity |
| αs, αh | slip coefficient at surface s (moving) and h (stationary) |
| Non-dimensional parameters | |
Appendix A
Appendix A.1. Slip in Single Pocket
Cavitation in Single Pocket
Pressure Distribution
Appendix A.2. Slip in Double Pockets
Cavitation in Double Pockets
Pressure Distribution
Appendix B
References
- Kalin, M.; Polajnar, M. The Effect of Wetting and Surface Energy on the Friction and Slip in Oil-Lubricated Contacts. Tribol. Lett. 2013, 52, 185–194. [Google Scholar] [CrossRef]
- Neto, C.; Evans, D.R.; Bonaccurso, E.; Butt, H.J.; Craig, V.S.J. Boundary Slip in Newtonian Liquids: A Review of Experimental Studies. Rep. Prog. Phys. 2005, 68, 2859–2897. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.; Dealy, J. Wall Slip of Molten High Density Polyethylene. I. Sliding Plate Rheometer Studies. J. Rheol. 1991, 35, 497–523. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G.; Brizmer, V.; Kligerman, Y. Experimental Investigation of Laser Surface Textured Parallel Thrust Bearing. Tribol. Lett. 2004, 17, 295–300. [Google Scholar] [CrossRef]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G.; Etsion, I. The Effect of Laser Surface Texturing on Transitions in Lubrication Regimes During Unidirectional Sliding Contact. Tribol. Int. 2005, 38, 219–225. [Google Scholar] [CrossRef]
- Ryk, G.; Kligerman, Y.; Etsion, I. Experimental Investigation of Laser Surface Texturing for Reciprocating Automotive Components. STLE Tribol. Trans. 2002, 45, 444–449. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G. A Laser Surface Textured Hydrostatic Mechanical Seal. STLE Tribol. Trans. 2002, 45, 430–434. [Google Scholar] [CrossRef]
- Wu, C.W.; Ma, G.J.; Zhou, P. Low Friction and High Load Support Capacity of Slider Bearing with a Mixed Slip Surface. ASME J. Tribol. 2006, 128, 904–907. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Ismail, R.; Jamari, J.; Schipper, D.J. Computational Analysis of The Lubricated Sliding Contact with Artificial Slip Boundary. Int. J. Appl. Math. Stat. 2013, 5, 67–68. [Google Scholar]
- Choo, J.H.; Spikes, H.A.; Ratoi, M.; Glovnea, R.P.; Forrest, A. Friction Reduction in Low-Load Hydrodynamic Lubrication with a Hydrophobic Surface. Tribol. Int. 2007, 40, 154–159. [Google Scholar] [CrossRef]
- Choo, J.H.; Glovnea, R.P.; Forrest, A.K.; Spikes, H.A. A Low Friction Bearing Based on Liquid Slip at the Wall. ASME J. Tribol. 2007, 129, 611–620. [Google Scholar] [CrossRef]
- Bayada, G.; Meurisse, M.H. Impact of the Cavitation Model on the Theoretical Performance of Heterogeneous Slip/No-Slip Engineered Contacts in Hydrodynamic Conditions. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 371–381. [Google Scholar] [CrossRef]
- Xie, Z.-L.; Ta, N.; Rao, Z.-S. The Lubrication Performance of Water Lubricated Bearing Consideration of Wall Slip and Inertial Force. J. Hydrol. 2017, 29, 52–60. [Google Scholar] [CrossRef]
- Wu, C.W. Performance of Hydrodynamic Lubrication Journal Bearing with a Slippage Surface. Ind. Lubr. Tribol. 2008, 60, 293–298. [Google Scholar] [CrossRef]
- Wang, L.-L.; Lu, C.-H.; Wang, M. The Numerical Analysis of the Radial Sleeve Bearing with Combined Surface Slip. Tribol. Int. 2012, 47, 100–104. [Google Scholar] [CrossRef]
- Salant, R.F.; Fortier, A.E. Numerical Analysis of a Slider Bearing with a Heterogeneous Slip/No-Slip Surface. Tribol. Trans. 2004, 47, 328–334. [Google Scholar] [CrossRef]
- Guo, F.; Wong, P.L. Theoretical Prediction of Hydrodynamic Effect by Tailored Boundary Slippage. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2006, 220, 43–48. [Google Scholar] [CrossRef]
- Rao, T.V. Analysis of Single-Grooved Slider and Journal Bearing with Partial Slip Surface. ASME J. Tribol. 2010, 132, 014501–1–014501–7. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Ismail, R.; Jamari, J.; Schipper, D.J. Combined Effect of Texturing and Boundary Slippage in Lubricated Sliding Contacts. Tribol. Int. 2013, 66, 274–281. [Google Scholar] [CrossRef] [Green Version]
- Tauviqirrahman, M.; Ismail, R.; Jamari, J.; Schipper, D.J. A Study of Surface Texturing and Boundary Slip on Improving the Load Support of Lubricated Parallel Sliding Contacts. Acta Mech. 2013, 224, 365–381. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Muchammad, M.; Jamari, J.; Schipper, D.J. Numerical Study of the Load Carrying Capacity of Lubricated Parallel Sliding Textured Surfaces including Wall Slip. Tribol. Trans. 2013, 57, 134–145. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Jamari, J.; Wibowo, B.S.; Fauzan, H.M.; Muchammad, M. Multiphase Computational Fluid Dynamics Analysis of Hydrodynamic Journal Bearing Under the Combined Influence of Texture and Slip. Lubricants 2019, 7, 97. [Google Scholar] [CrossRef] [Green Version]
- Kligerman, Y.; Etsion, I.; Shinkarenko, A. Improving Tribological Performance of Piston Rings by Partial Surface Texturing. ASME J. Tribol. 2005, 127, 632–638. [Google Scholar] [CrossRef]
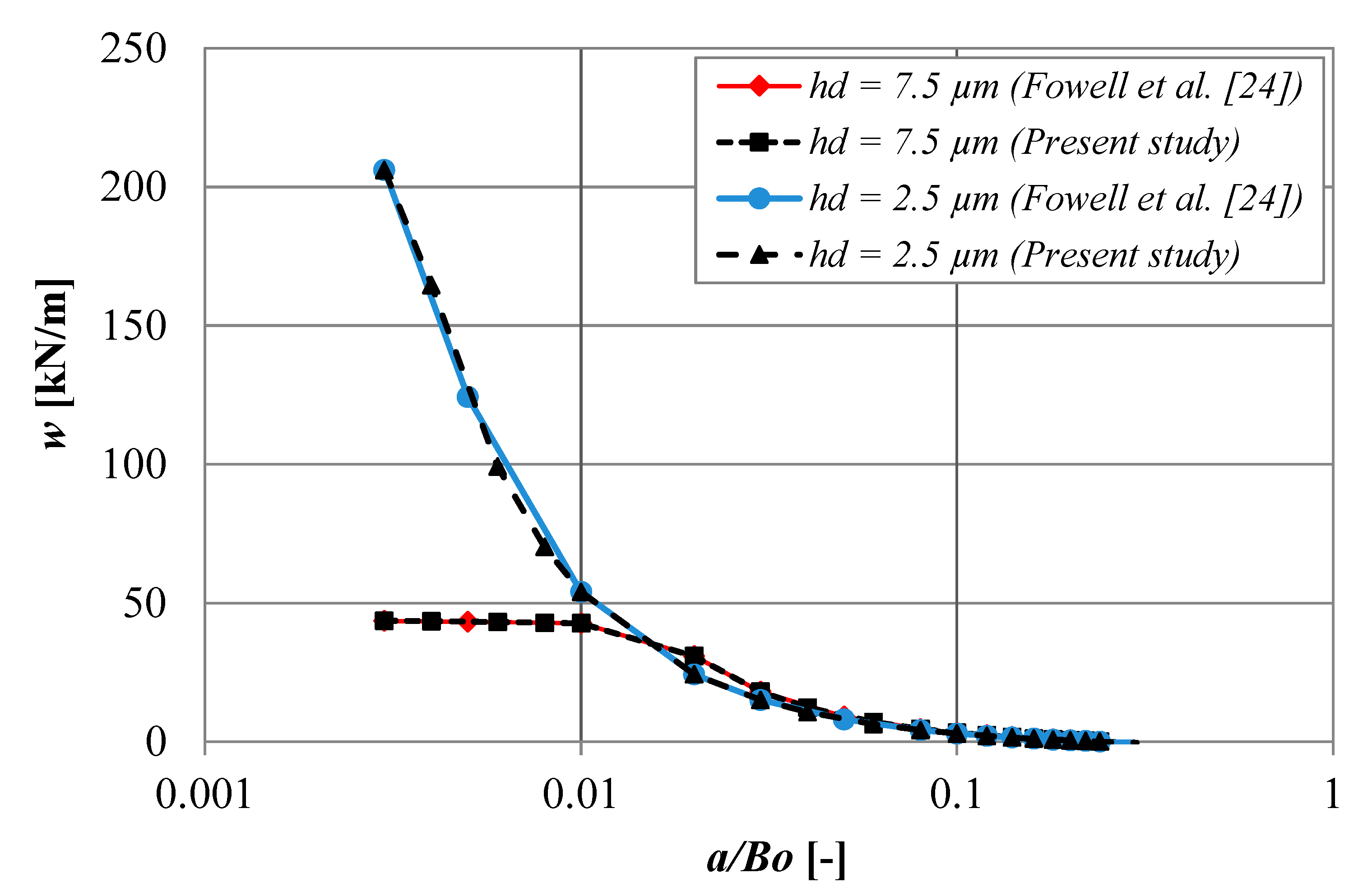
- Fowell, M.; Olver, A.V.; Gosman, A.D.; Spikes, H.A.; Pegg, I. Entrainment and Inlet Suction: Two Mechanisms of Hydrodynamic Lubrication in Textured Bearings. ASME J. Tribol. 2007, 129, 337–347. [Google Scholar] [CrossRef]
- Pascovici, M.D.; Cicone, T.; Fillon, M.; Dobrica, M.B. Analytical Investigation of a Partially Textured Parallel Slider. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 151–158. [Google Scholar] [CrossRef]
- Rahmani, R.; Mirzaee, I.; Shirvani, A.; Shirvani, H. An Analytical Approach for Analysis and Optimization of Slider Bearings with Infinite Width Parallel Thrush. Tribol. Int. 2010, 43, 1551–1565. [Google Scholar] [CrossRef] [Green Version]
- Arghir, M.; Roucou, N.; Helene, M.; Frene, J. Theoretical Analysis of the Incompressible Laminar Flow in a Macro-Roughness Cell. ASME J. Tribol. 2003, 125, 309–318. [Google Scholar] [CrossRef]
- Caramia, G.; Carbone, G.; Palma, P.D. Hydrodynamic Lubrication of Micro-Textured Surfaces: Two Dimensional CFD-Analysis. Tribol. Int. 2015, 88, 62–169. [Google Scholar] [CrossRef]
- Sahlin, F.; Glavatskih, S.B.; Almqvist, T.; Larsson, R. Two-Dimensional CFD-Analysis of Micro-Patterned Surfaces in Hydrodynamic Lubrication. ASME J. Tribol. 2005, 127, 96–102. [Google Scholar] [CrossRef]
- Brajdic-Mitidieri, P.; Gosman, A.D.; Loannides, E.; Spikes, H.A. CFD Analysis of a Low Friction Pocketed Pad Bearing. ASME J. Tribol. 2005, 127, 803–812. [Google Scholar] [CrossRef]
- Dobrica, M.B.; Fillon, M. About the Validity of Reynolds Equation and Inertia Effects in Textured Sliders of Infinite Width. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 69–78. [Google Scholar] [CrossRef]
- Han, J.; Fang, L.; Sun, J.; Ge, S. Hydrodynamic Lubrication of Microdimple Textured Surface Using Three-Dimensional CFD. Tribol. Trans. 2010, 53, 860–870. [Google Scholar] [CrossRef]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic Lubrication of Textured Surfaces: A Review of Modeling Techniques and Key Findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef] [Green Version]
- Sudeep, U.; Tandon, N.; Pandey, R.K. Performance of Lubricated Rolling/ Sliding Concentrated Contact with Surface Textures: A Review. ASME J. Tribol. 2015, 137, 031501–1. [Google Scholar] [CrossRef]
- Brito, F.P.; Miranda, A.S.; Fillon, M. Analysis of the Effect of Grooves in Single and Twin Axial Groove Journal Bearings Under Varying Load Direction. Tribol. Int. 2016, 103, 609–619. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Ni, T. Effect of Groove Textures on Fully Lubricated Sliding with Cavitation. Tribol. Int. 2011, 44, 2022–2028. [Google Scholar] [CrossRef]
- Gherca, A.; Fatu, A.; Hajjam, M.; Maspeyrot, P. Influence of Surface Texturing on the Hydrodynamic Performance of a Thrust Bearing Operating in Steady-State and Transient Lubrication Regime. Tribol. Int. 2016, 102, 305–318. [Google Scholar] [CrossRef]
- Mao, Y.; Zeng, L.; Lu, Y. Modeling and Optimization of Cavitation on A Textured Cylinder Surface Coupled with the Wedge Effect. Tribol. Int. 2016, 104, 212–224. [Google Scholar] [CrossRef]
- Galda, L.; Sep, J.; Prucnal, S. The Effect of Dimple Geometri in Sliding Surface on the Tribological Properties Under Starved Lubrication. Tribol. Int. 2016, 99, 77–84. [Google Scholar] [CrossRef]
- Kasem, H.; Stav, O.; Grützmacher, P.; Gachot, C. Effect of Low Depth Surface Texturing on Friction Reduction in Lubricated Sliding Contact. Lubricants 2018, 6, 62. [Google Scholar] [CrossRef] [Green Version]
- Fortier, A.E.; Salant, R.F. Numerical Analysis of a Journal Bearing with a Heterogeneous Slip/ No-Slip Surface. ASME J. Tribol. 2005, 127, 820–825. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Lu, C. Numerical Analysis of Spiral Oil Wedge Sleeve Bearing Including Cavitation and Wall Slip Effect. Lubr. Sci. 2015, 27, 193–207. [Google Scholar] [CrossRef]
- Ma, G.J.; Wu, C.W.; Zhou, P. Hydrodynamic of Slip Wedge and Optimization of Surface Slip Property. Sci. China Phys. Mech. 2007, 50, 321–330. [Google Scholar] [CrossRef]
- Ma, G.J.; Wu, C.W.; Zhou, P. Influence of Wall Slip on the Hydrodynamic Behavior of a Two-Dimensional Slider Bearing. Acta Mech. Sin. 2007, 23, 655–666. [Google Scholar] [CrossRef]
- Aurelian, F.; Patrick, M.; Mohamed, H. Wall Slip Effects in (Elasto) Hydrodynamic Journal Bearing. Tribol. Int. 2011, 44, 868–877. [Google Scholar] [CrossRef]
- Ma, G.J.; Wu, C.W.; Zhou, P. Wall Slip and Hydrodynamics of Two-Dimensional Journal Bearing. Tribol. Int. 2007, 40, 1056–1066. [Google Scholar] [CrossRef]
- Ma, X.; Meng, X.; Wang, Y.; Peng, X. Suction Effect of Cavitation in the Reverse-Spiral-Grooved Mechanical Face Seals. Tribol. Int. 2019, 132, 142–153. [Google Scholar] [CrossRef]
- Biancofiorea, L.; Giacopinib, M.; Dinic, D. Interplay Between Wall Slip and Cavitation: A Complementary Variable Approach. Tribol. Int. 2019, 137, 324–339. [Google Scholar] [CrossRef]
- Muchammad, M.; Tauviqirrahman, M.; Pratomo, A.W.; Jamari, J.; Schipper, D.J. Theoretical Investigation of Boundary Slip on the Hydrodynamic Lubrication Performance in Pocketed Bearings Including Cavitation. Int. J. Surf. Sci. Eng. 2017, 11, 100–117. [Google Scholar] [CrossRef]




| Parameter | Data Setting | Unit |
|---|---|---|
| Pocket depth, hd | 0.1; 0.5; 1.0; and 2.0 | µm |
| Land film thickness, ho | 1 × 10−6 | m |
| Total length, Bo | 0.02 | m |
| Inlet length, a | 0.002 | m |
| Pocket length, b | 0.0015; 0.006 | m |
| Exit land length, e | 0.0165; 0.012 | m |
| Atmospheric pressure, Patm | 100 | kPa |
| Cavitation pressure, Pcav | 0 | kPa |
| Sliding velocity, U | 1 | m/s |
| Slip coefficient, α | 0.02 | m2s/kg |
| Lubricant viscosity, µ | 0.01 | Pa·s |
| HD | Dimensionless Load Support W* (10−3) | Change in Load Support (%) | |
|---|---|---|---|
| Slip | No-Slip | ||
| 0.1 | 1.647 | 1.663 | −0.97 |
| 0.5 | 1.651 | 1.651 | 0 |
| 1.0 | 1.658 | 1.653 | 0.30 |
| 2.0 | 1.677 | 1.663 | 0.84 |
| HD | Dimensionless Load Support W* (10−3) | Change in Load Support (%) | |
|---|---|---|---|
| Slip | No-Slip | ||
| 0.1 | 0.730 | 0.739 | −1.23 |
| 0.5 | 0.732 | 0.732 | 0 |
| 1.0 | 0.736 | 0.733 | 0.41 |
| 2.0 | 0.747 | 0.739 | 1.07 |
| Parameter | Data Setting | Unit |
|---|---|---|
| First pocket depth, hd1 | 0.1; 0.5; 1.0; and 2.0 | µm |
| Land film thickness, ho | 1 × 10−6 | m |
| Total length, Bo | 0.02 | m |
| Inlet length, a | 0.002 | m |
| First pocket length, b | 0.0015; 0.006 | m |
| Length between pocket, c | 0.002 | m |
| Second pocket length, d | 0.003 | m |
| Exit land length, e | 0.0115; 0.007 | m |
| Atmospheric pressure, Patm | 100 | kPa |
| Cavitation pressure, Pcav | 0 | kPa |
| Sliding velocity, U | 1 | m/s |
| Slip coefficient, α | 0.02 | m2s/kg |
| Lubricant viscosity, µ | 0.01 | Pa·s |
| HD1 | Dimensionless Load Support W* (10−3) | Change in Load Support (%) | |
|---|---|---|---|
| Slip | No-Slip | ||
| 0.1 | 0.6742 | 0.6719 | 0.35 |
| 0.5 | 0.6743 | 0.6718 | 0.37 |
| 1.0 | 0.6744 | 0.6718 | 0.39 |
| 2.0 | 0.6746 | 0.6719 | 0.40 |
| HD1 | Dimensionless Load Support W* (10−3) | Change in Load Support (%) | |
|---|---|---|---|
| Slip | No-Slip | ||
| 0.1 | 0.0358 | 0.0349 | 2.60 |
| 0.5 | 0.0359 | 0.0348 | 3.12 |
| 1.0 | 0.0360 | 0.0348 | 3.27 |
| 2.0 | 0.0362 | 0.0349 | 3.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muchammad, M.; Tauviqirrahman, M.; Jamari, J.; Schipper, D.J. Analysis of the Effect of the Slip-Pocket in Single and Double Parallel Bearing Considering Cavitation: A Theoretical Approach. Lubricants 2021, 9, 3. https://doi.org/10.3390/lubricants9010003
Muchammad M, Tauviqirrahman M, Jamari J, Schipper DJ. Analysis of the Effect of the Slip-Pocket in Single and Double Parallel Bearing Considering Cavitation: A Theoretical Approach. Lubricants. 2021; 9(1):3. https://doi.org/10.3390/lubricants9010003
Chicago/Turabian StyleMuchammad, M., Mohammad Tauviqirrahman, J. Jamari, and D. J. Schipper. 2021. "Analysis of the Effect of the Slip-Pocket in Single and Double Parallel Bearing Considering Cavitation: A Theoretical Approach" Lubricants 9, no. 1: 3. https://doi.org/10.3390/lubricants9010003
APA StyleMuchammad, M., Tauviqirrahman, M., Jamari, J., & Schipper, D. J. (2021). Analysis of the Effect of the Slip-Pocket in Single and Double Parallel Bearing Considering Cavitation: A Theoretical Approach. Lubricants, 9(1), 3. https://doi.org/10.3390/lubricants9010003