Hot Compression Deformation and Activation Energy of Nanohybrid-Reinforced AZ80 Magnesium Matrix Composite

Abstract

The hot deformation test of the nano silicon carbide (nano-SiC) and carbon nano tubes (CNT) hybrid-reinforced AZ80 matrix composite was performed at compression temperatures of 300–450 °C and strain rates of 0.0001–1 s⁻¹. It could be observed that the flow stress of the nanocomposite rose with the reduction of deformation temperature and the increase of strain rate. The hot deformation behaviors of the composite could be described by the sine-hyperbolic Arrhenius equation, and deformation activation energy (Q) was calculated to be 157.8 kJ/mol. The Q values of the extruded nanohybrid/AZ80 composite in this study and other similar studies on extruded AZ80 alloys were compared in order to analyze the effect of the addition of reinforcement, and the effects of deformation conditions on activation energy were analyzed. Finally, the compression microstructure in an unstable condition was carefully analyzed, and results indicated that the phenomenon of local instability was easy to occur at the compression specimen of the nanohybrid/AZ80 composite under deformation conditions of low temperature with high strain rate (300 °C, 0.1–0.01 s⁻¹), and high temperature with low strain rate (450 °C, 0.0001 s⁻¹).

1. Introduction

Compared with traditional iron and steel materials, magnesium alloys have the advantage of lower density, higher specific strength, and stronger damping capacity. As a promising metal-structure material, it has been widely used in automobiles and the aerospace industry [1,2]. The AZ80 alloy has attractive combination properties among magnesium alloys, such as high strength, good plasticity, and excellent deformation ability, but their high temperature strength is relatively poor, which limits their development and application [3]. Therefore, various types of micro or nano reinforcement, such as SiC [4], CNT [5], and Al₂O₃ [6], were introduced into the AZ80 magnesium alloy to combat this limitation. It is greatly important to study the relationship between deformation behavior and deformation conditions (temperature, strain rate, and deformation degree), which could optimize the hot workability and forming processes of composites [7]. The flow behaviors of materials during deformation processes are usually described by the constitution relationship. Meanwhile, the deformation mechanism is generally analyzed by deformation activation energy (Q), which directly reflects workability to some extent [8].

A large number of studies on the hot deformation behavior of metal matrix composites (MMCs) have been carried out over the past few years [9,10,11,12]. Wang et al. [9] found that adding B₄C particles (23 μm) to the AA6061 alloy promoted the occurrence of dynamic recrystallization (DRX), and the flow stress and the Q value of the composite were higher than those of the alloy. Zhou et al. [10] found that the addition of SiC particles could increase the upper limit of the processing strain rate so that the high temperature workability of the AZ91 alloy could be improved. Deng et al. [7] calculated the Q value of the bimodal size (about 0.2 μm 1 vol% + 10 μm 9 vol%) of SiCp/AZ91 composite under different compression temperatures (270–420 °C) and strain rate (0.001–1 s⁻¹) in order to clarify the relationship between deformation mechanisms and deformation conditions. Results showed that the deformation mechanism of the composite was dislocation climb-controlled by the grain boundary at 0.001 s⁻¹, but when the strain rate was decreased to 0.1–1 s⁻¹, the deformation mechanism was changed to a dislocation climb. Zhang et al. [11] compared the workability domains of the AZ91 alloy, micro-SiCp/AZ91 composite, and nano-SiCp/AZ91 composite, and found that the addition of nano-SiCp allowed a relatively higher processing strain rate (0.02–0.1 s⁻¹), so the nano-SiCp effect was better than that of the microsized one. Until now, investigations on the hot deformation behavior of hybrid reinforced composites are very few [12,13,14]. Moreover, there is no report about the hot deformation behavior of nano-SiC and CNT hybrid-reinforced AZ80 composites in the existing literature.

Therefore, this work investigates the flow behavior of the nanohybrid-reinforced AZ80 magnesium matrix composite, followed by modeling the constitutive equation of the composite. In addition, the compression microstructure under different deformation conditions was analyzed. Finally, the nanohybrid-reinforced composite materials were compared with the activation energy of the AZ80 alloy, and the effects of deformation conditions (temperature, strain rate, strain) on activation energy were analyzed.

2. Experiment Procedure

2.1. Materials and Preparation

In this study, a commercial AZ80 magnesium alloy was chosen as the matrix alloy; 0.5 wt% nano-SiC particles (about 40 nm) and 0.5 wt% CNT (10–20 µm in length and 50–60 nm in outer diameter) were mixed by ball-milling with a rotation speed of 350 r/min for 4 h using a PBM-4A planetary mill (ZOOKIN, Changsha, China). Then, about 1 kg of AZ80 alloy ingot was heated to 720 °C under a CO₂/SF₆ gas mixture atmosphere, and temperature was adjusted to 660 °C after the base alloy had melted. The reinforced powder wrapped in aluminum foil was pressed into the surface of the alloy melt with a bell jar. In the process, mechanical agitation was carried out to fully disperse the nano reinforced particles in the molten matrix. After stirring for 15 min, the melt was rapidly reheated to 710 °C and maintained for 15 min. Lastly, casting was carried out to obtain a cylindrical ingot with a specification of Φ90 mm. The as-cast composite was homogenized at 400 °C × 8 h and then extruded at 350 °C; extrusion ratio and extrusion speed were 32 and 0.2 mm/s, respectively.

2.2. Hot Compression Test

The as-extruded rods along the extrusion direction were machined into cylindrical specimens of Φ15 × 10 mm for hot compression tests. The hot compression experiment was conducted on an MTS-CMT5105 universal testing machine (SANS, Shenzhen, China) equipped with an GW900 electrical furnace (SANS, Shenzhen, China) at strain rates from 0.0001 to 0.1 s⁻¹ and temperatures ranging from 300 to 450 °C. Specimens were lubricated with graphite to reduce friction resistance between press indenters and specimens. Samples were heated to the target deformation temperature at a heating rate of 10 °C/s and held for 5 min before compression. Subsequently, the heated specimens were compressed to 70% reduction, immediately followed by water quenching to preserve the deformed microstructure.

2.3. Microstructure Characterization

In order to study the composite microstructure after deformation under different compression conditions, the specimen was sectioned parallel to the compression axis, and the center microstructure of the sample section was observed by using a ZEISS (Oberkochen, Germany) Axio Lab. A1 optical microscope (OM) and a JEOL (Tokyo, Japan) JSM 7800F field emission scanning electron microscope (SEM). The OM specimens were polished and etched with the Picric acid solution (2.75 g picric acid, 2.5 mL acetic acid, 45 mL ethyl alcohol, and 5 mL distilled water). The composition of the material was analyzed using an Oxford (Oxford shire, England) X-Max 80 energy dispersive spectrometer (EDS). The phase compositions were identified by a Panalytical (Almero, The Netherlands) X’Pert Pro X-ray diffraction (XRD), and the XRD analysis was carried out using a Cu Kα1 radiation (λ = 0.154 nm) at the operating parameters of 30 kV, 50 mA at 293 K with 2θ ranging between 20 and 90 deg, and the scanning speed was 4°/s and the scanning step was 0.0334°.

3. Results and Discussion

3.1. Extruded Microstructure Analysis

Figure 1a,c displays the OM and SEM images of the as-extruded nanohybrid/AZ80 composite, respectively, which was vertical to the extrusion direction. Figure 1b,d shows enlarged views of the partial regions (yellow boxes) in Figure 1a,c, respectively. The composite exhibited a bimodal microstructure with an average size of about 5.7 ± 0.3 μm. Moreover, there are some white phases (marked by yellow arrow) and black phases (marked by yellow arrow) distributed along the grain boundary in Figure 1b. Figure 1d shows the XRD pattern of the extruded nanohybrid/AZ80 composite, which demonstrates that the alloy is mainly composed of α-Mg and β-Mg₁₇Al₁₂. There is just a very small volume fraction of other phase, SiC and CNTs in the alloy, leading to the absence of the diffraction peaks in the XRD pattern. According to relevant literature reports [15], white phases are β-Mg₁₇Al₁₂ and black phases are Mn-rich in AZ80 alloy. Due to the poor conductivity of SiC, it is charged and bright in the electron microscope. In addition, combined with the size of the charged particles corresponded to the nominal size of the added reinforcement, those particles (marked by red arrows in Figure 1c) were thought to be nano-SiC particles. The CNT is shown in the following Section 3.5.3.

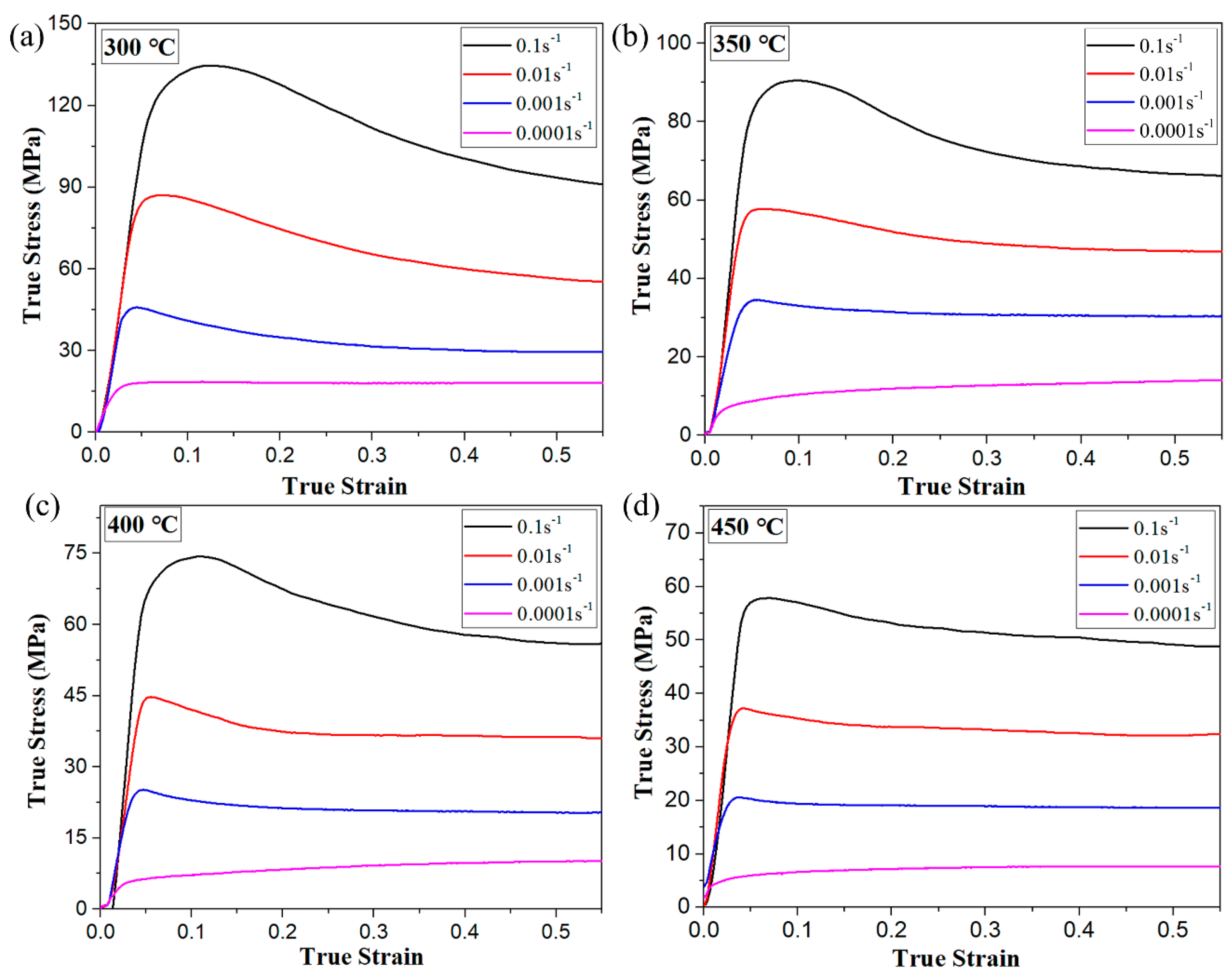
3.2. Flow Stress–Strain Curve Analysis

The compressive flow stress–strain curves of the nanohybrid/AZ80 composite at different compression temperatures and strain rates are shown in Figure 2. Obviously, various compression conditions such as deformation temperature, strain rate, and strain all have remarkable influence on flow stress. The compressive flow stress curves of nanohybrid/AZ80 composites showed classical features, in that the true stress of the AZ80/0.5 wt% SiC-0.5 wt% CNT composite rapidly improved with the rise of true strain in the initial deformation stage; once true stress reached peak stress, it presented a trend of slow decline before gradually stabilizing at strain rates of 0.001–1 s⁻¹. Especially when the composite was hot compressed at strain rates of 0.0001 s⁻¹, true stress first increased and then directly presented a stable state due to no peak stress existing. This phenomenon is mainly related to competition between work-hardening and dynamic-softening effects [16,17].

A great amount of pinning dislocations exists at the beginning of high-temperature compression, which causes work hardening to play a leading role, and flow stress to rapidly increase. As strain continues to increase, dislocation density continuously increases, which promotes the softening mechanism of dynamic recrystallization (DRX) or dynamic recovery (DRV); then, the softening effect is gradually strengthened while work-hardening effects weaken. When the work-hardening and softening effects achieve equilibrium, true stress reaches a peak value. Subsequently, the softening effect plays a leading role when true strain is greater than the true strain corresponding to the peak, so the appearance of stress begins to slowly decline. Finally, when the rate of hardening and softening (DRV or DRX) reaches a dynamic balance, the flow stress curve enters a steady state.

It could also be found that the true stress of composites is reduced with the rise of deformation temperatures at a given strain rate, and it improves with the rise of strain rates at a given temperature. Results can still be explained by the competition between work-hardening and dynamic-softening effects [16,17]. As strain rate increased, the deformation time of the composite was shortened, as was the effective time of dislocation slip and climb, and the softening effect of dynamic recrystallization was suppressed to a certain extent, thereby increasing peak stress and strain, which balanced dynamic recrystallization softening and work hardening. With the elevation of deformation temperature, the critical shear stress of the slip system decreased, resulting in a decrease in the deformation resistance of the composite. In addition, the increased temperature made the cross-slip and climb of the dislocations and the formation and merger of subcrystals become easier, which accelerated the occurrence of dynamic recrystallization, thereby making the strain of dynamic recrystallization softening and strain hardening to equilibrium.

3.3. Deformation Microstructure Analysis

The optical microstructures of composites compressed at different temperatures of 300–450 °C and strain rates of 0.0001–1 s⁻¹ are shown in Figure 3. It displays that the compressed microstructure of the composite kept bimodal distribution at a temperature of 350 °C and strain rate of 0.1 s⁻¹, which was mainly due to insufficient recrystallization as a result of short deformation time. When deformation temperature was kept constant and strain rate reduced to 0.01 s⁻¹, the degree of recrystallization increased due to the prolonged deformation time. The microstructure was mainly composed of equiaxed grains after dynamic recrystallization. When strain rate was further reduced from 0.001 to 0.0001 s⁻¹, the growth phenomenon of dynamically recrystallized grains was more obvious. In addition, there were some irregular second-phase particles distributed along the extruded strip in the hot compressed microstructure, as indicated in Figure 4a,b. For further careful observation of the second-phase particles, the local area (yellow-box area) in Figure 4b was further enlarged, which is shown in Figure 4c,d. According to EDS results, these irregular particles mainly contained Al and Mn elements, and the atomic ratio of Al and Mn was about 1.63:1, so the irregular phases could be identified as the Al₈Mn₅ phase [18]. Moreover, the Al₈Mn₅ phase was broken during hot compression and crushed into smaller particles, as indicated by the red arrow in Figure 4c,d.

3.4. Constitutive Modeling

Constitutive modeling is an important mathematical method that establishes the relationship between flow stress $\left(\sigma \right)$ and hot deformation parameters of materials during the hot deformation process, which can be expressed by a hyperbolic sine function raised by Sellars and Tegart [19,20,21], as represented in Equation (1):

$$\dot{\epsilon }=A{\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]}^n\exp \left(-Q/RT\right),$$

(1)

where $\dot{\epsilon }$ is the strain rate (s⁻¹), σ is the flow stress (MPa), A and α are material constants, n is the stress exponent, Q is the activation energy for hot deformation (kJ/mol), R is the universal gas constant (8.314 J·K⁻¹mol⁻¹), and T is the absolute deformation temperature (K).

The Zener–Hollomon parameter (Z) can describe well the effects of the processing strain rate and deformation temperature on flow stress, as expressed by the following equation [22]:

$$Z=\dot{\epsilon }\exp \left(\frac{Q}{RT}\right)=A{\left[\sin \mathrm{h}\left(\alpha {\sigma }_p\right)\right]}^n$$

(2)

where Z is the temperature compensated strain rate and ${\sigma }_p$ is peak stress.

For a high stress level ($\alpha \sigma >1.2)$ and low stress level ($\alpha \sigma <0.8)$, the relationship between flow stress (σ) and strain rate ($\dot{\epsilon }$) could be expressed by Equations (3) and (4):

$$ln\dot{\epsilon }=ln{A}_1+\beta \sigma -\frac{Q}{RT}$$

(3)

$$ln\dot{\epsilon }=ln{A}_2+n_{1}ln\sigma -\frac{Q}{RT}$$

(4)

where A₁, A₂ (s⁻¹), and $\beta ,\alpha$(= $\beta /n_1)$ are material constants independent of temperature.

By calculating the slope of the linear relationship of ln$\dot{\epsilon }$ − lnσ and ln$\dot{\epsilon }$ − σ, the n₁ and β values of the alloy could be obtained. Figure 5a,b shows the linear relationship of the ln$\dot{\epsilon }$ − σ and ln$\dot{\epsilon }$ − lnσ of the nanohybrid/AZ80 composite, where it could be concluded that α = β/n’ = 0.0025 by the nature of the hyperbolic sine function.

After determining parameter α, Equations (5) and (6) could be obtained by taking the partial derivative of temperature and strain for Equation (1), respectively:

$$1/n=m={\left\{\partial \left[ln\sin \mathrm{h}\left(\alpha \sigma \right)\right]/\partial ln\dot{\epsilon }\right\}}_T$$

(5)

$$Q=n\mathrm{R}{\left\{\partial \left[ln\sin \mathrm{h}\left(\alpha \sigma \right)\right]/\partial \left(1/T\right)\right\}}_{\dot{\epsilon }}.$$

(6)

By substituting Equation (5) into Equation (6), Q could be calculated as shown in the following equation:

$$Q=R{\left\{\frac{\partial ln\dot{\epsilon }}{\partial \left[ln\sin \mathrm{h}\left(\alpha \sigma \right)\right]}\right\}}_T{\left\{\frac{\partial \left[ln\sin \mathrm{h}\left(\alpha \sigma \right)\right]}{\partial \left(1/T\right)}\right\}}_{\dot{\epsilon }}$$

(7)

The relationships of $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]-ln\dot{\epsilon }$ and $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]-1/T$ for the composite were linearly fitted and are plotted in Figure 5c,d, respectively. The value of n for the composite could be obtained by the averaging linear slopes of $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]-ln\dot{\epsilon }$ at various temperatures (Figure 5c), which was obtained as 2.597. Substituting the average slope of the two groups’ straight lines fitted to data ($ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]-ln\dot{\epsilon }$ and $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]-1/T)$ in Figure 5c,d into Equation (7) resulted in a nanohybrid-reinforced AZ80 composite Q value of 157.8 kJ/mol. By linear fit of the relation of $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]-lnZ$, the value of lnA was determined to be 23.13. The important parameters of the composite in the constitutive equation are listed in

Table 1. Material constants and deformation activation energy (Q) of nanohybrid/AZ80 composites in the constitutive equation.

Parameter	Q/KJmol−1	α/Mpa−1	n	A/s−1
Value	157.8	0.025	2.597	1.110 × 1010

.

By generating the values of A, α, n, and Q into Equation (1), we could obtain the constitutive equation of the nanohybrid/AZ80 composite, shown as Equation (8):

$$\epsilon =1.11\times {10}^{10}{\left[\sin \mathrm{h}\left(0.025\sigma \right)\right]}^{2.597}\exp (-1.578\times \frac{{10}^5}{RT})$$

(8)

3.5. Hot Deformation Activation Energy

3.5.1. Effect of Adding Reinforcement on Activation Energy

Q is an important physical parameter that can reflect the difficulty of hot deformation and even the energy barrier that qualitatively impedes the dislocation motion of alloys in the process of plastic deformation. The higher the hot deformation activation energy is, the greater the obstruction forces to the dislocation movement during hot deformation [9]. Many studies on the hot working behavior of AZ80 alloys without reinforcement were done [23,24,25]. Chen et al. [23] compared the workability of an AZ80 alloy casted with and without a variable-frequency ultrasonic field (VUF) by uniaxial hot compression tests at a temperature range of 250–400 °C and strain-rate range of 0.001–1 s⁻¹. They found that the Q of casting AZ80 without VUF (192.38 kJ/mol) was fairly higher than that of casting AZ80 with VUF (165.30 kJ/mol). This is mainly because of the smaller grains and more grain boundaries after ultrasonic vibration, which promotes atom diffusion, leading to low activation energy. Su et al. [24] studied the hot compression behavior of an extruded AZ80 alloy at 275–400 °C and 0.001–1 s⁻¹, and obtained Q = 135 KJ/mol. Lou et al. [25] calculated the activation energy of an extruded AZ80 alloy at a strain of 0.01–50 s⁻¹, and obtained Q = 92 kJ/mol at a lower temperature of 250–300 °C and Q = 135 kJ/mol⁻¹ at higher temperatures of 350–450 °C.

In this study, the activation energy of the nanohybrid/AZ80 composite was estimated as 157.8 KJ/mol, which is higher than that of self-diffusion in pure Mg (Q_L = 135 kJ/mol) [26]. This indicates that the deformation mechanism of the composite is not mainly controlled by the general diffusion mechanism [10]. In general, the deformation mechanism of material under different deformation conditions can be judged based on the values of n and Q. It is reported [27] that when n = 2, it is the dislocation grain boundary sliding mechanism; when n = 3, it is the dislocation sliding mechanism; when n = 5, it is the dislocation climbing mechanism; when n = 8, it is micro structure-invariant model mechanism. The value of extruded nanohybrid/AZ80 composites is 2.597 close to 3. Moreover, since the prismatic slip can be activated in magnesium at high-temperature, the activation energy must be large enough to overcome the cross-slip of screw dislocations from basal to prismatic planes (160 kJ/mol) [27]. Therefore, the deformation mechanism of extruded nanohybrid/AZ80 composites may be cross-slip of dislocations.

In addition, the Q value of the nanohybrid/AZ80 composite was higher than that for unreinforced extruded AZ80 alloys [24,25]. The addition of nano-reinforcement increased the Q value in the present alloy (as shown in Figure 1e) because nano-reinforcement effectively restricts dislocation movement. This result is consistent with other studies reporting the influence of nano-reinforcement on the activation energy of matrix materials [28,29].

Zheng et al. [28] investigated the effects of the addition of nano-β-tricalcium phosphate (β-TCP) on the hot deformation mechanism of an Mg–Zn–Zr alloy. According to the established constitutive equation, the Q value of the composite for hot deformation was almost 60 kJ/mol higher than that of the alloy. On the one hand, the existence of β-TCP nanoparticles can restrict the movement of dislocations in the process of deformation. On the other hand, nanocomposite grains are more refined and uniform than those of the unreinforced alloy, so high grain-boundary density can also impede dislocation movement and increase deformation resistance. Mokdad et al. [29] studied the effects of the addition of CNT on the hot deformation and activation energy of a 2024 aluminum alloy and obtained similar results.

3.5.2. Influence of Hot Deformation Conditions on Activation Energy

According to Equation (7), the theoretical value of deformation activation energy could be obtained (see

Table 2. Deformation activation energy of nanohybrid/AZ80 composite at different strain rates and deformation temperatures.

Strain Rate/s−1	Q/(kJ·mol−1)
	300 °C	350 °C	400 °C	450 °C
0.0001	145.143 ± 1.659	154.674 ± 3.484	158.873 ± 4.212	163.740 ± 3.517
0.001	147.389 ± 2.611	155.224 ± 1.605	159.724 ± 3.373	167.789 ± 0.890
0.01	150.347 ± 2.761	152.971 ± 3.229	162.278 ± 1.691	170.850 ± 3.740
0.1	154.193 ± 2.688	152.678 ± 1.007	161.299 ± 1.702	168.702 ± 1.379

). Q variation with deformation temperature (T) at different strain rates is shown in Figure 6. Q can be used to measure the difficulty of deformation, and its change reflects the change of the deformation mechanism, so the rise or fall of the activation-energy curve indicates that a new dislocation mechanism participates in the deformation process [9]. Obviously, it can be observed from Figure 6 that the deformation mechanism of the composite material was significantly different at different deformation temperatures and the same strain rate. For a strain rate of 0.01 s⁻¹, the Q value of the composite slowly improved with increasing temperature (300–350 °C), and then quickly increased when deformation temperature was higher than 350 °C. When the strain rate was 0.001–0.0001 s⁻¹, the Q value increased rapidly with increasing temperature (300–350 °C), but slowly increased when the temperature was higher than 350 °C. The phenomenon of the Q value increasing with the elevation of deformation temperature may be related to the consumption of much dislocation due to the promotion of DRX. The formation and growth of DRX require a large number of dislocations, and DRX is more intense as deformation temperature is enhanced, the tendency for dislocation consumption is increased, and stress concentration is relaxed. Therefore, the number of potential dislocation sources is reduced, and startup is more difficult, which leads to an increase in Q [10]. However, for the higher strain rate of 0.1 s⁻¹, the deformation activation energy of the composite decreased with the rise of temperature from 300 to 350 °C, and then improved with the rise of temperature from 350 to 450 °C. This abnormal phenomenon may imply the appearance of a transition of the rate-controlling mechanism [30].

3.5.3. Microstructural Analysis of Instability

Figure 7 presents an OM micrograph showing the microstructure of the hybrid-reinforced composite deformed under different hot compression conditions. Figure 7a shows the occurrence of flow localization and the presence of microcracks at 300 °C with a strain rate of 0.1 s⁻¹, which was due to stress concentration that was not relieved at a low temperature and fast deformation rate [31]. Figure 7b shows some microcracks that were observed at the DRX region at 300 °C with a strain rate of 0.01 s⁻¹. This was mainly because fine recrystallized grains were easily deformed, while the original coarse non-DRX grains were poorly plasticized, so microcracks existed at the interface between coarse and small grains [32]. Many second-phase particles were observed near microcracks from Figure 7c. The formation of microcrack and microvoid was analyzed, the main reasons are as follows:

(1) As mentioned in Section 3.3 in the manuscript, the Mn-rich phases were broken during hot compression (as shown in Figure 4c,d), which resulted in microcrack forming. In addition, it can be seen by further observation (Figure 8a) that broken particles debonded from the matrix (marked by red circle) and microvoids exist at the interface between particles and matrix (marked by blue circle). This is because the adhesive strength of interfaces diminished with the increasing temperature due to matrix strength decreases, so the load transfer effect from matrix to particle is decreased [10]. So microcracks and microvoids were generated near hard-brittle particles due to particles broken or debonding, which is consistent with Patel’s [33] and Yang’s [34] researches.

(2) The dislocations may be generated due to the mismatch of elastic modulus and thermal expansion coefficient between the matrix and the nano-reinforcement [35]. During hot deformation process, the dislocations may concentrate around SiCp and CNT, which lead the generation of stress centration at the interface between reinforcements and matrix [11,35]. As the stress become larger than interface bonding strength, microcracks might occur at the interface between SiCp-Mg or CNT-Mg, which can be illustrated in Figure 8b. During the isometric compression test, there is tensile stress at the edge of the specimen, and the microcracks (Figure 8) formed by the above reasons (1 and 2) develop into microvoids under tensile stress.

(3) At a high temperature of 450 °C and a low strain rate of 0.0001 s⁻¹, as the deformation temperature is higher than eutectic temperature of 437 °C [32], β-Mg₁₇Al₁₂ phase distributed near the grain boundary may melt and lead to the formation of liquid. This may also lead to pore formation. According to Bolouri’s research [36], the formation of liquid phase at grain boundary might reduce interface cohesion between the solid grain, intergranular cracks, and micropores will occur in the subsequent deformation process.

4. Conclusions

The hot deformation behavior of a nano-SiCp and CNT hybrid-reinforced AZ80 composite was investigated by establishing a constitutive equation, calculation, and analysis of activation energy. Our conclusions are as follows:

(1)

Deformation temperature and strain rate had significant influence on the flow stress of the nanocomposite. The true stress of the composite rapidly improved with the rise of the true strain in the initial period of deformation; once true stress reached peak stress, it presented a trend of slow decline before gradually stabilizing at strain rates of 0.001–1 s⁻¹. When the composite was hot compressed at strain rates of 0.0001 s⁻¹, true stress first increased and then directly presented a stable state due to no peak stress existing. In addition, the flow stress of the nanocomposite improved with the reduction of deformation temperature and the increase of strain rate.

(2)

The constitutive equation of the nanocomposite could be described by a sine-hyperbolic Arrhenius equation, which can be expressed as:

$$\epsilon =1.11\times {10}^{10}{\left[\sin \mathrm{h}\left(0.025\sigma \right)\right]}^{2.597}\exp (-1.578\times \frac{{10}^5}{RT})$$

(3)

The activation energy of the nanohybrid/AZ80 composite was estimated in this study as 157.8 KJ/mol, which is higher than that for unreinforced extruded AZ80 alloys. The high Q value of the composite was mainly attributed to the addition of nano-reinforcements, which acted as barriers to effectively restrict dislocation motion.

(4)

Under the deformation conditions of low temperature with high strain rate (300 °C, 0.1–0.01 s⁻¹) and high temperature with low strain rate (450 °C, 0.0001 s⁻¹), it was easy for the phenomenon of local instability to occur at the compression specimen of the nanohybrid/AZ80 composite.