New Insights into the Microstructural Changes During the Processing of Dual-Phase Steels from Multiresolution Spherical Indentation Stress–Strain Protocols
Abstract
:1. Introduction
2. Materials and Method
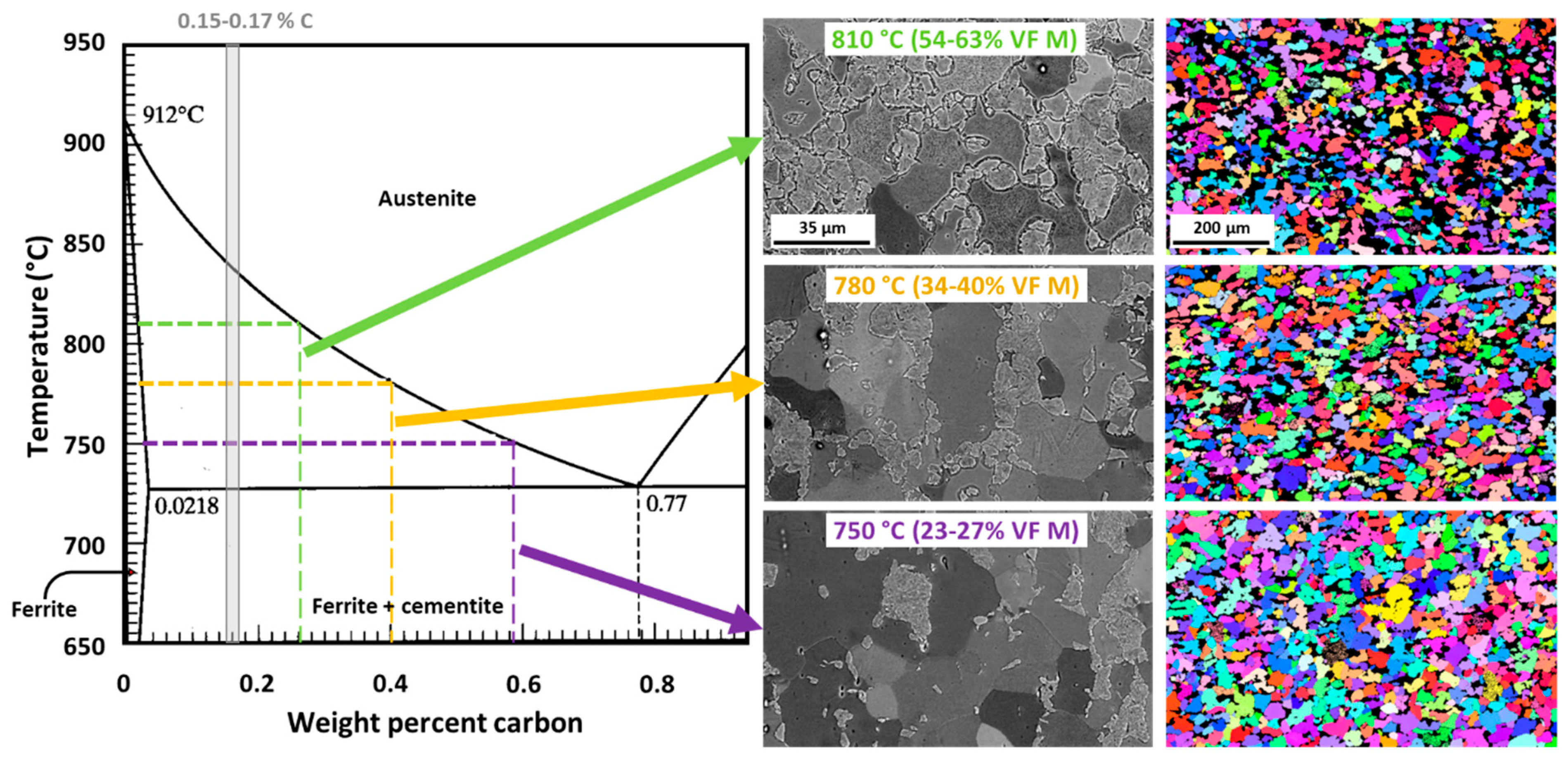
2.1. Sample Preparation
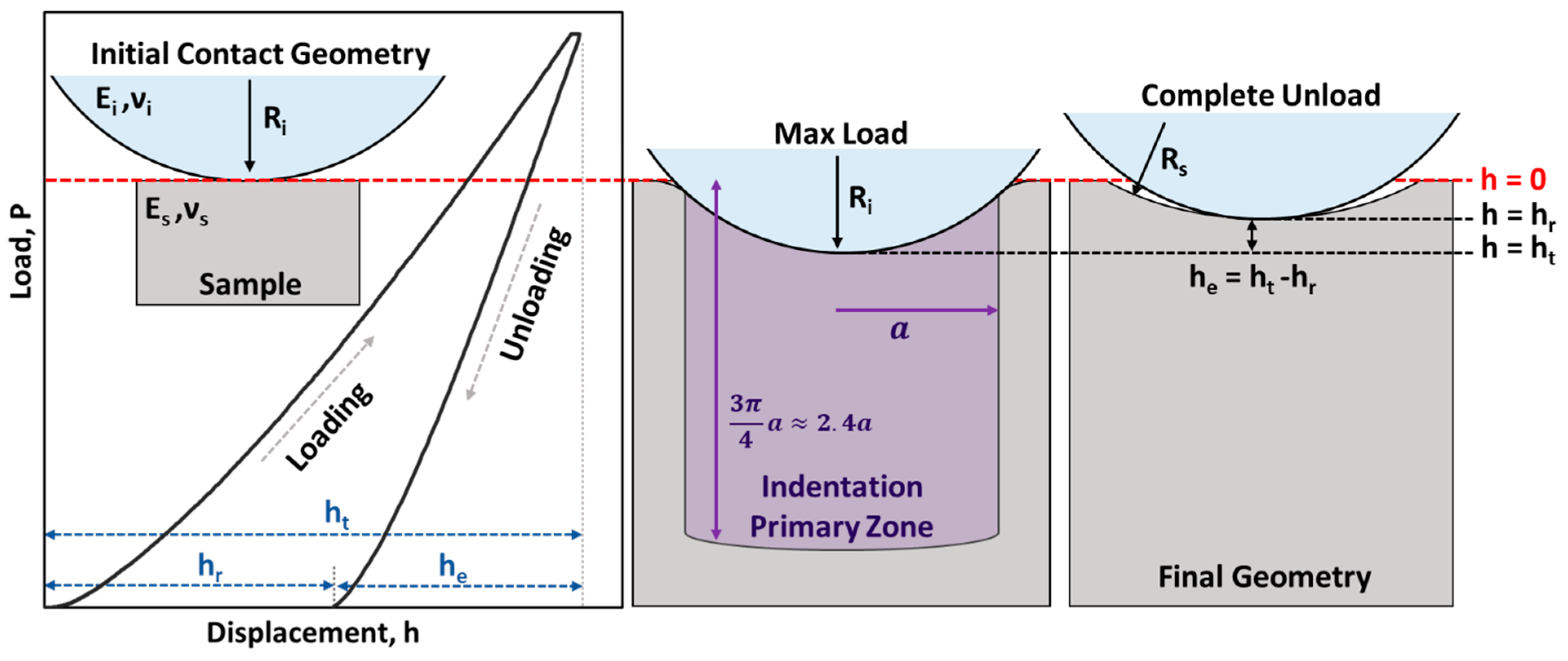
2.2. Spherical Nano-Indentation Stress–Strain Protocols
2.3. Spherical Micro-Indentation Stress–Strain Protocols
3. Results and Discussion
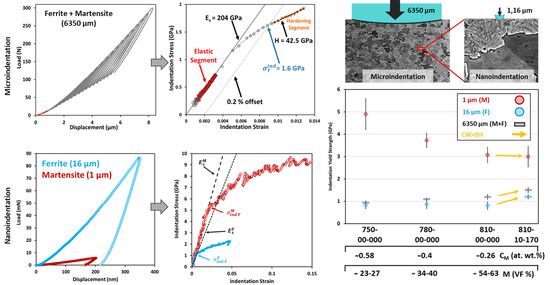
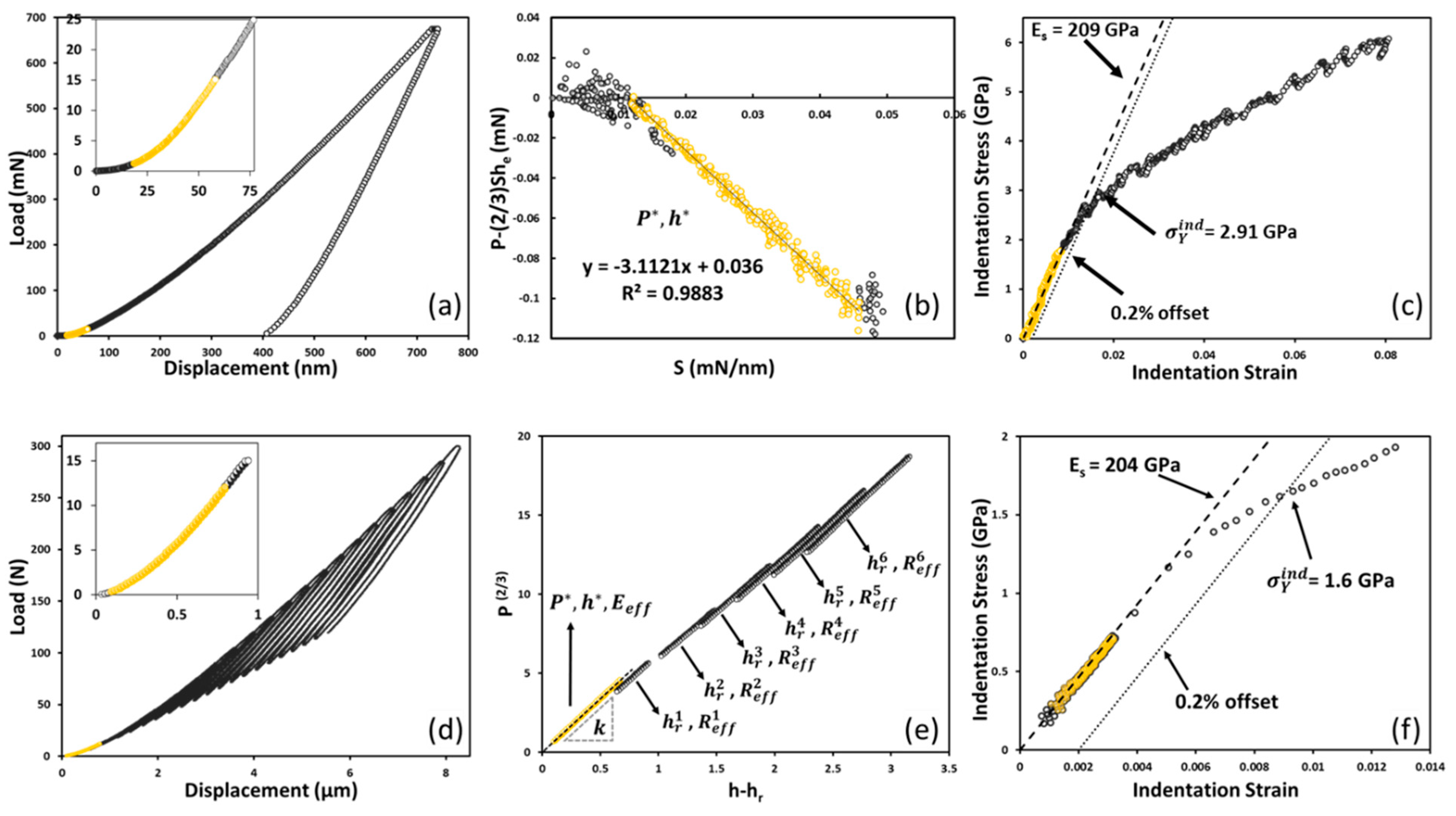
3.1. Microindentation and Results
3.2. Nanoindentation and Results
4. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Tasan, C.C.; Diehl, M.; Yan, D.; Bechtold, M.; Roters, F.; Schemmann, L.; Zheng, C.; Peranio, N.; Ponge, D.; Koyama, M.; et al. An Overview of Dual-Phase Steels: Advances in Microstructure-Oriented Processing and Micromechanically Guided Design. Annu. Rev. Mater. Res. 2015, 45, 391–431. [Google Scholar] [CrossRef]
- Bian, J.; Mohrbacher, H.; Zhang, J.-S.; Zhao, Y.-T.; Lu, H.-Z.; Dong, H. Application potential of high performance steels for weight reduction and efficiency increase in commercial vehicles. Adv. Manuf. 2015, 3, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Fonstein, N. Dual-phase steels. In Automotive Steels: Design, Metallurgy, Processing and Applications; Rana, R., Brat Singh, S., Eds.; Woodhead Publishing: Cambridge, UK, 2017; pp. 169–216. [Google Scholar]
- Horvath, C.D. Advanced steels for lightweight automotive structures. In Materials, Design and Manufacturing for Lightweight Vehicles; Mallick, P.K., Ed.; Woodhead Publishing: Cambridge, UK, 2010; pp. 35–78. [Google Scholar]
- Rashid, M.S. Dual phase steels. Annu. Rev. Mater. Sci. 1981, 11, 245–266. [Google Scholar] [CrossRef]
- Robertson, L.T.; Hilditch, T.B.; Hodgson, P.D. The effect of prestrain and bake hardening on the low-cycle fatigue properties of TRIP steel. Int. J. Fatigue 2008, 30, 587–594. [Google Scholar] [CrossRef]
- Ramazani, A.; Bruehl, S.; Gerber, T.; Bleck, W.; Prahl, U. Quantification of bake hardening effect in DP600 and TRIP700 steels. Mater. Des. 2014, 57, 479–486. [Google Scholar] [CrossRef]
- Kuang, C.-F.; Zhang, S.-G.; Li, J.; Wang, J.; Li, P. Effect of temper rolling on the bake-hardening behavior of low carbon steel. Int. J. Miner. Metall. Mater. 2015, 22, 32–36. [Google Scholar] [CrossRef]
- Waterschoot, T.; Verbeken, K.; de Cooman, B.C. Tempering Kinetics of the Martensitic Phase in DP Steel. ISIJ Int. 2006, 46, 138–146. [Google Scholar] [CrossRef] [Green Version]
- Berbenni, S.; Favier, V.; Lemoine, X.; Berveiller, M. A micromechanical approach to model the bake hardening effect for low carbon steels. Scr. Mater. 2004, 51, 303–308. [Google Scholar] [CrossRef]
- Timokhina, I.B.; Hodgson, P.D.; Pereloma, E.V. Transmission Electron Microscopy Characterization of the Bake-Hardening Behavior of Transformation-Induced Plasticity and Dual-Phase Steels. Metall. Mater. Trans. 2007, 38, 2442–2454. [Google Scholar] [CrossRef] [Green Version]
- Lindqvist, K. Bake Hardening Effect in Advanced High-Strength Steels. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2013. [Google Scholar]
- Kuang, C.-F.; Wang, J.; Li, J.; Zhang, S.-G.; Liu, H.-F.; Yang, H.-L. Effect of Continuous Annealing on Microstructure and Bake Hardening Behavior of Low Carbon Steel. J. Iron Steel Res. Int. 2015, 22, 163–170. [Google Scholar] [CrossRef]
- Wang, H.; Shi, W.; He, Y.-L.; Lu, X.-G.; Li, L. Effect of Overaging on Solute Distributions and Bake Hardening Phenomenon in Bake Hardening Steels. J. Iron Steel Res. Int. 2012, 19, 53–59. [Google Scholar] [CrossRef]
- Durrenberger, L.; Lemoine, X.; Molinari, A. Effects of pre-strain and bake-hardening on the crash properties of a top-hat section. J. Mater. Process. Technol. 2011, 211, 1937–1947. [Google Scholar] [CrossRef]
- Kilic, S.; Ozturk, F.; Sigirtmac, T.; Tekin, G. Effects of Pre-strain and Temperature on Bake Hardening of TWIP900CR Steel. J. Iron Steel Res. Int. 2015, 22, 361–365. [Google Scholar] [CrossRef]
- Šebek, M.; Horňak, P.; Zimovčák, P. Effect of Annealing on the Microstructure Evolution and Mechanical Properties of Dual Phase Steel. Mater. Sci. Forum 2014, 782, 111–116. [Google Scholar] [CrossRef]
- Asadi, M.; de Cooman, B.C.; Palkowski, H. Influence of martensite volume fraction and cooling rate on the properties of thermomechanically processed dual phase steel. Mater. Sci. Eng. 2012, 538, 42–52. [Google Scholar] [CrossRef]
- Vasilyev, A.A.; Lee, H.-C.; Kuzmin, N.L. Nature of strain aging stages in bake hardening steel for automotive application. Mater. Sci. Eng. 2008, 485, 282–289. [Google Scholar] [CrossRef]
- Jeong, W.C. Relationship between mechanical properties and microstructure in a 1.5% Mn–0.3% Mo ultra-low carbon steel with bake hardening. Mater. Lett. 2007, 61, 2579–2583. [Google Scholar] [CrossRef]
- Cao, Y.; Ahlström, J.; Karlsson, B. The influence of temperatures and strain rates on the mechanical behavior of dual phase steel in different conditions. J. Mater. Res. Technol. 2015, 4, 68–74. [Google Scholar] [CrossRef] [Green Version]
- Kuang, C.F.; Li, J.; Zhang, S.G.; Wang, J.; Liu, H.F.; Volinsky, A.A. Effects of quenching and tempering on the microstructure and bake hardening behavior of ferrite and dual phase steels. Mater. Sci. Eng. 2014, 613, 178–183. [Google Scholar] [CrossRef]
- Li, C.-S.; Li, Z.-X.; Cen, Y.-M.; Ma, B.; Huo, G. Microstructure and mechanical properties of dual phase strip steel in the overaging process of continuous annealing. Mater. Sci. Eng. 2015, 627, 281–289. [Google Scholar] [CrossRef]
- Hüseyin, A.; Havva, K.Z.; Ceylan, K. Effect of Intercritical Annealing Parameters on Dual Phase Behavior of Commercial Low-Alloyed Steels. J. Iron Steel Res. Int. 2010, 17, 73–78. [Google Scholar] [CrossRef]
- Zeytin, H.K.; Kubilay, C.; Aydin, H. Investigation of dual phase transformation of commercial low alloy steels: Effect of holding time at low inter-critical annealing temperatures. Mater. Lett. 2008, 62, 2651–2653. [Google Scholar] [CrossRef]
- Demir, B.; Erdoğan, M. The hardenability of austenite with different alloy content and dispersion in dual-phase steels. J. Mater. Process. Technol. 2008, 208, 75–84. [Google Scholar] [CrossRef]
- Sudersanan, N.K.P.D.; Aprameyan, S.; Kempaiah, D.U.N. The Effect of Carbon Content in Martensite on the Strength of Dual Phase Steel. Bonfring Int. J. Ind. Eng. Manag. Sci. 2012, 2, 1–4. [Google Scholar]
- Seyedrezai, H. Thermo-Mechanical Processing of Dual-Phase Steels and its Effects on the Work Hardening Behaviour. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2014. [Google Scholar]
- Schemmann, L.; Zaefferer, S.; Raabe, D.; Friedel, F.; Mattissen, D. Alloying effects on microstructure formation of dual phase steels. Acta Mater. 2015, 95, 386–398. [Google Scholar] [CrossRef]
- Timokhina, I.B.; Pereloma, E.V.; Ringer, S.P.; Zheng, R.K.; Hodgson, P.D. Characterization of the Bake-hardening Behavior of Transformation Induced Plasticity and Dual-phase Steels Using Advanced Analytical Techniques. ISIJ Int. 2010, 50, 574–582. [Google Scholar] [CrossRef] [Green Version]
- Allain, S.Y.P.; Bouaziz, O.; Pushkareva, I.; Scott, C.P. Towards the microstructure design of DP steels: A generic size-sensitive mean-field mechanical model. Mater. Sci. Eng. 2015, 637, 222–234. [Google Scholar] [CrossRef]
- Korzekwa, D.A.; Matlock, D.K.; Krauss, G. Dislocation substructure as a function of strain in a dual-phase steel. Metall. Trans. 1984, 15, 1221–1228. [Google Scholar] [CrossRef]
- Calcagnotto, M.; Ponge, D.; Demir, E.; Raabe, D. Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD. Mater. Sci. Eng. 2010, 527, 2738–2746. [Google Scholar] [CrossRef]
- Cottrell, A.H.; Bilby, B.A. Dislocation theory of yielding and strain ageing of iron. Proc. Phys. Soc. 1949, 62, 49. [Google Scholar] [CrossRef]
- Pan, Z.; Gao, B.; Lai, Q.; Chen, X.; Cao, Y.; Liu, M.; Zhou, H. Microstructure and Mechanical Properties of a Cold-Rolled Ultrafine-Grained Dual-Phase Steel. Materials 2018, 11, 1399. [Google Scholar] [CrossRef] [Green Version]
- Gerbig, D.; Srivastava, A.; Osovski, S.; Hector, L.G.; Bower, A. Analysis and design of dual-phase steel microstructure for enhanced ductile fracture resistance. Int. J. Fract. 2018, 209, 3–26. [Google Scholar] [CrossRef]
- Kundu, J.; Ray, T.; Kundu, A.; Shome, M. Effect of the laser power on the mechanical performance of the laser spot welds in dual phase steels. J. Mater. Process. Technol. 2019, 267, 114–123. [Google Scholar] [CrossRef]
- Samei, J.; Zhou, L.; Kang, J.; Wilkinson, D.S. Microstructural analysis of ductility and fracture in fine-grained and ultrafine-grained vanadium-added DP1300 steels. Int. J. Plast. 2019, 117, 58–70. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, M.; Feng, Z.; Zhang, L.; Cao, W.; Wu, G. Nanoindentation characterization of strengthening mechanism in a high strength ferrite/martensite steel. Mater. Sci. Eng. 2019, 745, 144–148. [Google Scholar] [CrossRef]
- Ghassemi-Armaki, H.; Maaß, R.; Bhat, S.P.; Sriram, S.; Greer, J.R.; Kumar, K.S. Deformation response of ferrite and martensite in a dual-phase steel. Acta Mater. 2014, 62, 197–211. [Google Scholar] [CrossRef]
- Seok, M.-Y.; Kim, Y.-J.; Choi, I.-C.; Zhao, Y.; Jang, J.-I. Predicting flow curves of two-phase steels from spherical nanoindentation data of constituent phases: Isostrain method vs. non-isostrain method. Int. J. Plast. 2014, 59, 108–118. [Google Scholar] [CrossRef]
- Taylor, M.D.; Choi, K.S.; Sun, X.; Matlock, D.K.; Packard, C.E.; Xu, L.; Barlat, F. Correlations between nanoindentation hardness and macroscopic mechanical properties in DP980 steels. Mater. Sci. Eng. 2014, 597, 431–439. [Google Scholar] [CrossRef]
- Choi, B.-W.; Seo, D.-H.; Yoo, J.-Y.; Jang, J.-I. Predicting macroscopic plastic flow of high-performance, dual-phase steel through spherical nanoindentation on each microphase. J. Mater. Res. 2009, 24, 816–822. [Google Scholar] [CrossRef]
- Hayashi, K.; Miyata, K.; Katsuki, F.; Ishimoto, T.; Nakano, T. Individual mechanical properties of ferrite and martensite in Fe-0.16mass% C-1.0mass% Si-1.5mass% Mn steel. J. Alloy. Compd. 2013, 577, S593–S596. [Google Scholar] [CrossRef]
- Scott, C.P.; Amirkhiz, B.S.; Pushkareva, I.; Fazeli, F.; Allain, S.Y.P.; Azizi, H. New insights into martensite strength and the damage behaviour of dual phase steels. Acta Mater. 2018, 159, 112–122. [Google Scholar] [CrossRef]
- Farivar, H.; Richter, S.; Hans, M.; Schwedt, A.; Prahl, U.; Bleck, W. Experimental quantification of carbon gradients in martensite and its multi-scale effects in a DP steel. Mater. Sci. Eng. 2018, 718, 250–259. [Google Scholar] [CrossRef]
- Banadkouki, S.S.G.; Fereiduni, E. Effect of prior austenite carbon partitioning on martensite hardening variation in a low alloy ferrite—Martensite dual phase steel. Mater. Sci. Eng. 2014, 619, 129–136. [Google Scholar] [CrossRef]
- Cheng, G.; Zhang, F.; Ruimi, A.; Field, D.P.; Sun, X. Quantifying the effects of tempering on individual phase properties of DP980 steel with nanoindentation. Mater. Sci. Eng. 2016, 667, 240–249. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Ruimi, A.; Field, D.P. Phase Identification of Dual-Phase (DP980) Steels by Electron Backscatter Diffraction and Nanoindentation Techniques. Microsc. Microanal. 2016, 22, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Gao, S.; Tian, Y.; Terada, D.; Shibata, A.; Tsuji, N. Influence of Tempering on Mechanical Properties of Ferrite and Martensite Dual Phase Steel. Mater. Today Proc. 2015, 2, S667–S671. [Google Scholar] [CrossRef]
- Hernandez, V.H.B.; Panda, S.K.; Kuntz, M.L.; Zhou, Y. Nanoindentation and microstructure analysis of resistance spot welded dual phase steel. Mater. Lett. 2010, 64, 207–210. [Google Scholar] [CrossRef]
- Azuma, M.; Goutianos, S.; Hansen, N.; Winther, G.; Huang, X. Effect of hardness of martensite and ferrite on void formation in dual phase steel. Mater. Sci. Technol. 2012, 28, 1092–1100. [Google Scholar] [CrossRef]
- Weaver, J.S.; Pathak, S.; Reichardt, A.; Vo, H.T.; Maloy, S.A.; Hosemann, P.; Mara, N.A. Spherical nanoindentation of proton irradiated 304 stainless steel: A comparison of small scale mechanical test techniques for measuring irradiation hardening. J. Nucl. Mater. 2017, 493, 368–379. [Google Scholar] [CrossRef]
- Pathak, S.; Michler, J.; Wasmer, K.; Kalidindi, S.R. Studying grain boundary regions in polycrystalline materials using spherical nano-indentation and orientation imaging microscopy. J. Mater. Sci. 2012, 47, 815–823. [Google Scholar] [CrossRef]
- Pathak, S.; Stojakovic, D.; Kalidindi, S.R. Measurement of the local mechanical properties in polycrystalline samples using spherical nanoindentation and orientation imaging microscopy. Acta Mater. 2009, 57, 3020–3028. [Google Scholar] [CrossRef]
- Vachhani, S.J.; Doherty, R.D.; Kalidindi, S.R. Studies of grain boundary regions in deformed polycrystalline aluminum using spherical nanoindentation. Int. J. Plast. 2016, 81, 87–101. [Google Scholar] [CrossRef] [Green Version]
- Khosravani, A.; Morsdorf, L.; Tasan, C.C.; Kalidindi, S.R. Multiresolution mechanical characterization of hierarchical materials: Spherical nanoindentation on martensitic Fe-Ni-C steels. Acta Mater. 2018, 153, 257–269. [Google Scholar] [CrossRef]
- Weaver, J.S.; Priddy, M.W.; McDowell, D.L.; Kalidindi, S.R. On capturing the grain-scale elastic and plastic anisotropy of alpha-Ti with spherical nanoindentation and electron back-scattered diffraction. Acta Mater. 2016, 117, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Weaver, J.S.; Kalidindi, S.R. Mechanical characterization of Ti-6Al-4V titanium alloy at multiple length scales using spherical indentation stress-strain measurements. Mater. Des. 2016, 111, 463–472. [Google Scholar] [CrossRef] [Green Version]
- Pathak, S.; Kalidindi, S.R.; Mara, N.A. Investigations of orientation and length scale effects on micromechanical responses in polycrystalline zirconium using spherical nanoindentation. Scr. Mater. 2016, 113, 241–245. [Google Scholar] [CrossRef] [Green Version]
- Vachhani, S.J.; Kalidindi, S.R. Grain-scale measurement of slip resistances in aluminum polycrystals using spherical nanoindentation. Acta Mater. 2015, 90, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Kalidindi, S.R.; Pathak, S. Determination of the effective zero-point and the extraction of spherical nanoindentation stress-strain curves. Acta Mater. 2008, 56, 3523–3532. [Google Scholar] [CrossRef]
- Pathak, S.; Shaffer, J.; Kalidindi, S.R. Determination of an effective zero-point and extraction of indentation stress-strain curves without the continuous stiffness measurement signal. Scr. Mater. 2009, 60, 439–442. [Google Scholar] [CrossRef]
- Hertz, H. Miscellaneous Papers; MacMillan and Co. Ltd.: New York, NY, USA, 1896. [Google Scholar]
- Fischer-Cripps, A.C. Critical review of analysis and interpretation of nanoindentation test data. Surf. Coat. Technol. 2006, 200, 4153–4165. [Google Scholar] [CrossRef]
- Chudoba, T.; Griepentrog, M.; Dück, A.; Schneider, D.; Richter, F. Young’s modulus measurements on ultra-thin coatings. J. Mater. Res. 2004, 19, 301–314. [Google Scholar] [CrossRef]
- Chudoba, T.; Schwarzer, N.; Richter, F. Determination of elastic properties of thin films by indentation measurements with a spherical indenter. Surf. Coat. Technol. 2000, 127, 9–17. [Google Scholar] [CrossRef]
- Richter, F.; Herrmann, M.; Molnar, F.; Chudoba, T.; Schwarzer, N.; Keunecke, M.; Bewilogua, K.; Zhang, X.W.; Boyen, H.G.; Ziemann, P. Substrate influence in Young’s modulus determination of thin films by indentation methods: Cubic boron nitride as an example. Surf. Coat. Technol. 2006, 201, 3577–3587. [Google Scholar] [CrossRef]
- Grau, P.; Berg, G.; Fränzel, W.; Meinhard, H. Recording hardness testing. Problems of measurement at small indentation depths. Phys. Status Solidi 1994, 146, 537–548. [Google Scholar] [CrossRef]
- Ullner, C. Requirement of a robust method for the precise determination of the contact point in the depth sensing hardness test. Measurement 2000, 27, 43–51. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Chaudhri, M.M. Indentation of elastic solids with a rigid Vickers pyramidal indenter. Mech. Mater. 2006, 38, 1213–1228. [Google Scholar] [CrossRef]
- Fernandez-Zelaia, P.; Nguyen, V.; Zhang, H.; Kumar, A.; Melkote, S.N. The effects of material anisotropy on secondary processing of additively manufactured CoCrMo. Addit. Manuf. 2019, 29, 100764. [Google Scholar] [CrossRef]
- Weaver, J.S.; Jones, D.R.; Li, N.; Mara, N.; Fensin, S.; Gray, G.T. Quantifying heterogeneous deformation in grain boundary regions on shock loaded tantalum using spherical and sharp tip nanoindentation. Mater. Sci. Eng. 2018, 737, 373–382. [Google Scholar] [CrossRef]
- Leung, J.F.W.; Bedekar, V.; Voothaluru, R.; Neu, R.W. Mechanical Properties of White Etching Areas in Carburized Bearing Steel Using Spherical Nanoindentation. Metall. Mater. Trans. 2019, 50, 4949–4954. [Google Scholar] [CrossRef]
- Pathak, S.; Weaver, J.S.; Sun, C.; Wang, Y.; Kalidindi, S.R.; Mara, N.A. Spherical Nanoindentation Stress-Strain Analysis of Ion-Irradiated Tungsten; Minerals. Metals and Materials Series; Springer International Publishing: New York, NY, USA, 2019; pp. 617–635. [Google Scholar]
- Fernandez-Zelaia, P.; Joseph, V.R.; Kalidindi, S.R.; Melkote, S.N. Estimating mechanical properties from spherical indentation using Bayesian approaches. Mater. Des. 2018, 147, 92–105. [Google Scholar] [CrossRef]
- Weaver, J.S.; Sun, C.; Wang, Y.; Kalidindi, S.R.; Doerner, R.P.; Mara, N.A.; Pathak, S. Quantifying the mechanical effects of He, W and He + W ion irradiation on tungsten with spherical nanoindentation. J. Mater. Sci. 2018, 53, 5296–5316. [Google Scholar] [CrossRef]
- Iskakov, A.; Yabansu, Y.C.; Rajagopalan, S.; Kapustina, A.; Kalidindi, S.R. Application of spherical indentation and the materials knowledge system framework to establishing microstructure-yield strength linkages from carbon steel scoops excised from high-temperature exposed components. Acta Mater. 2018, 144, 758–767. [Google Scholar] [CrossRef]
- Pathak, S.; Kalidindi, S.R.; Weaver, J.S.; Wang, Y.; Doerner, R.P.; Mara, N.A. Probing nanoscale damage gradients in ion-irradiated metals using spherical nanoindentation. Sci. Rep. 2017, 7, 11918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khosravani, A.; Cecen, A.; Kalidindi, S.R. Development of high throughput assays for establishing process-structure-property linkages in multiphase polycrystalline metals: Application to dual-phase steels. Acta Mater. 2017, 123, 55–69. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Mochalin, V.N.; Neitzel, I.; Knoke, I.Y.; Han, J.; Klug, C.A.; Zhou, J.G.; Lelkes, P.I.; Gogotsi, Y. Fluorescent PLLA-nanodiamond composites for bone tissue engineering. Biomaterials 2011, 32, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Weaver, J.S.; Livescu, V.; Mara, N.A. A comparison of adiabatic shear bands in wrought and additively manufactured 316 L stainless steel using nanoindentation and electron backscatter diffraction. J. Mater. Sci. 2020, 55, 1738–1752. [Google Scholar] [CrossRef]
- Kim, H.N.; Mandal, S.; Basu, B.; Kalidindi, S.R. Probing Local Mechanical Properties in Polymer-Ceramic Hybrid Acetabular Sockets Using Spherical Indentation Stress-Strain Protocols. Integr. Mater. Manuf. Innov. 2019, 8, 257–272. [Google Scholar] [CrossRef]
- Pathak, S.; Kalidindi, S.R.; Klemenz, C.; Orlovskaya, N. Analyzing indentation stress–strain response of LaGaO3 single crystals using spherical indenters. J. Eur. Ceram. Soc. 2008, 28, 2213–2220. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Vachhani, S.J. Mechanical characterization of grain boundaries using nanoindentation. Curr. Opin. Solid State Mater. Sci. 2014, 18, 196–204. [Google Scholar] [CrossRef]
- Chang, C.; Verdi, D.; Garrido, M.A.; Ruiz-Hervias, J. Micro-scale mechanical characterization of Inconel cermet coatings deposited by laser cladding. Boletín Sociedad Española Cerámica Vidrio 2016, 55, 136–142. [Google Scholar] [CrossRef] [Green Version]
- Weaver, J.; Aydogan, E.; Mara, N.A.; Maloy, S.A. Nanoindentation of Electropolished FeCrAl Alloy Welds; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2017. [Google Scholar]
- Mohanty, D.P.; Wang, H.; Okuniewski, M.; Tomar, V. A nanomechanical Raman spectroscopy based assessment of stress distribution in irradiated and corroded SiC. J. Nucl. Mater. 2017, 497, 128–138. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, X.; Yang, Q.J.A.A. Extracting the isotropic uniaxial stress-strain relationship of hyperelastic soft materials based on new nonlinear indentation strain and stress measure. AIP Adv. 2018, 8, 115013. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Zelaia, P.; Melkote, S.N. Validation of Material Models for Machining Simulation Using Mechanical Properties of the Deformed Chip. Procedia CIRP 2017, 58, 535–538. [Google Scholar] [CrossRef]
- Weaver, J.; Nunez, U.C.; Krumwiede, D.; Saleh, T.A.; Hosemann, P.; Nelson, A.T.; Maloy, S.A.; Mara, N.A. Spherical Nanoindentation Stress-Strain Measurements of BOR-60 14YWT-NFA1 Irradiated Tubes; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2017. [Google Scholar]
- Rossi, A. Mechanical Response of Polymer Matrix Composites Using Indentation Stress-Strain Protocols. Level of Thesis, Georgia Institute of Technology, Atlanta, Georgia, 2018. [Google Scholar]
- Khosravani, A. High Throughput Prototyping and Multiscale Indentation Characterization of Metallic Alloys. Level of Thesis, Georgia Institute of Technology, Atlanta, Georgia, 2019. [Google Scholar]
- Vachhani, S.J.; Trujillo, C.; Mara, N.; Livescu, V.; Bronkhorst, C.; Gray, G.T.; Cerreta, E. Local Mechanical Property Evolution During High Strain-Rate Deformation of Tantalum. J. Dyn. Behav. Mater. 2016, 2, 511–520. [Google Scholar] [CrossRef] [Green Version]
- Weaver, J.S.; Khosravani, A.; Castillo, A.; Kalidindi, S.R. High Throughput Exploration of Process-Property Linkages in Al-6061 using Instrumented Spherical Microindentation and Microstructurally Graded Samples. Integr. Mater. Manuf. Innov. 2016, 5, 192–211. [Google Scholar] [CrossRef] [Green Version]
- Donohue, B.R.; Ambrus, A.; Kalidindi, S.R. Critical evaluation of the indentation data analyses methods for the extraction of isotropic uniaxial mechanical properties using finite element models. Acta Mater. 2012, 60, 3943–3952. [Google Scholar] [CrossRef]
- Patel, D.K.; Kalidindi, S.R. Correlation of spherical nanoindentation stress-strain curves to simple compression stress-strain curves for elastic-plastic isotropic materials using finite element models. Acta Mater. 2016, 112, 295–302. [Google Scholar] [CrossRef] [Green Version]
- Patel, D.K.; Al-Harbi, H.F.; Kalidindi, S.R. Extracting single-crystal elastic constants from polycrystalline samples using spherical nanoindentation and orientation measurements. Acta Mater. 2014, 79, 108–116. [Google Scholar] [CrossRef]
- Patel, D.K.; Kalidindi, S.R. Estimating the slip resistance from spherical nanoindentation and orientation measurements in polycrystalline samples of cubic metals. Int. J. Plast. 2017, 92, 19–30. [Google Scholar] [CrossRef] [Green Version]
- Ohmura, T.; Tsuzaki, K.; Matsuoka, S. Nanohardness measurement of high-purity Fe–C martensite. Scr. Mater. 2001, 45, 889–894. [Google Scholar] [CrossRef]
- Hutchinson, B.; Hagström, J.; Karlsson, O.; Lindell, D.; Tornberg, M.; Lindberg, F.; Thuvander, M. Microstructures and hardness of as-quenched martensites (0.1–0.5% C). Acta Mater. 2011, 59, 5845–5858. [Google Scholar] [CrossRef]
- Molina, R.C.; Pla, M.; Rossi, R.H.; Páramo, J.A.B. Analysis of the decrease of the apparent young’s modulus of advanced high strength steels and its effect in bending simulations. In Proceedings of the IDDRG 2009 International Conference, Golden, CO, USA, 1–3 June 2009; pp. 109–117. [Google Scholar]
- Chen, Z.; Gandhi, U.; Lee, J.; Wagoner, R.H. Variation and consistency of Young’s modulus in steel. J. Mater. Process. Technol. 2016, 227, 227–243. [Google Scholar] [CrossRef]
- Rana, R.; Liu, C.; Ray, R.K. Low-density low-carbon Fe–Al ferritic steels. Scr. Mater. 2013, 68, 354–359. [Google Scholar] [CrossRef]
- Furukawa, T.; Morikawa, H.; Endo, M.; Takechi, H.; Koyama, K.; Akisue, O.; Yamada, T. Process Factors for Cold-rolled Dual-phase Sheet Steels. Trans. Iron Steel Inst. Jpn. 1981, 21, 812–819. [Google Scholar] [CrossRef]
- Tomita, Y. Effect of morphology of second-phase martensite on tensile properties of Fe-0.1C dual phase steels. J. Mater. Sci. 1990, 25, 5179–5184. [Google Scholar]
- Byun, T.S.; Kim, I.S. Tensile properties and inhomogeneous deformation of ferrite-martensite dual-phase steels. J. Mater. Sci. 1993, 28, 2923–2932. [Google Scholar] [CrossRef]
- Chang, C. Correlation between the Microstructure of Dual Phase Steel and Industrial Tube Bending Performance. Master’s Thesis, University of Windsor, Windsor, ON, Canada, 2010. [Google Scholar]
- Sarwar, M.; Priestner, R. Influence of ferrite-martensite microstructural morphology on tensile properties of dual-phase steel. J. Mater. Sci. 1996, 31, 2091–2095. [Google Scholar] [CrossRef]
- Tavares, S.; Pedroza, P.; Teodosio, J.; Gurova, T.J.S.M. Mechanical properties of a quenched and tempered dual phase steel. Scr. Mater. 1999, 40, 887–892. [Google Scholar] [CrossRef]
- Bag, A.; Ray, K.; Dwarakadasa, E.J. Influence of martensite content and morphology on tensile and impact properties of high-martensite dual-phase steels. Metall. Mater. Trans. 1999, 30, 1193–1202. [Google Scholar] [CrossRef]
- Hayat, F.; Uzun, H. Effect of Heat Treatment on Microstructure, Mechanical Properties and Fracture Behaviour of Ship and Dual Phase Steels. J. Iron Steel Res. Int. 2011, 18, 65–72. [Google Scholar] [CrossRef]
- Kocatepe, K.; Cerah, M.; Erdogan, M. Effect of martensite volume fraction and its morphology on the tensile properties of ferritic ductile iron with dual matrix structures. J. Mater. Process. Technol. 2006, 178, 44–51. [Google Scholar] [CrossRef]
- Morsdorf, L.; Tasan, C.C.; Ponge, D.; Raabe, D. 3D structural and atomic-scale analysis of lath martensite: Effect of the transformation sequence. Acta Mater. 2015, 95, 366–377. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H.; Keehan, E.; Karlsson, L.; Andrén, H.O. Coalesced bainite. Trans. Indian Inst. Met. 2006, 59, 689–694. [Google Scholar]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.J.J. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bergstr, Y.; Granbom, Y.; Sterkenburg, D. A Dislocation-Based Theory for the Deformation Hardening Behavior of DP Steels: Impact of Martensite Content and Ferrite Grain Size. J. Metall. 2010. [Google Scholar] [CrossRef]
- Liedl, U.; Traint, S.; Werner, E.A. An unexpected feature of the stress–strain diagram of dual-phase steel. Comput. Mater. Sci. 2002, 25, 122–128. [Google Scholar] [CrossRef]
- Lorenz, D.; Zeckzer, A.; Hilpert, U.; Grau, P.; Johansen, H.; Leipner, H.S. Pop-in effect as homogeneous nucleation of dislocations during nanoindentation. Phys. Rev. 2003, 67, 172101. [Google Scholar] [CrossRef] [Green Version]
- Ahn, T.-H.; Oh, C.-S.; Lee, K.; George, E.P.; Han, H.N. Relationship between yield point phenomena and the nanoindentation pop-in behavior of steel. J. Mater. Res. 2012, 27, 39–44. [Google Scholar] [CrossRef]
- Pathak, S.; Riesterer, J.L.; Kalidindi, S.R.; Michler, J. Understanding pop-ins in spherical nanoindentation. Appl. Phys. Lett. 2014, 105, 161913. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.G.; Ngan, A.H.W. Indentation strain burst phenomenon induced by grain boundaries in niobium. J. Mater. Res. 2004, 19, 2478–2486. [Google Scholar] [CrossRef] [Green Version]
- Morris, J.R.; Bei, H.; Pharr, G.M.; George, E.P. Size effects and stochastic behavior of nanoindentation pop in. Phys. Rev. Lett. 2011, 106, 165502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phani, P.S.; Johanns, K.E.; George, E.P.; Pharr, G.M. A stochastic model for the size dependence of spherical indentation pop-in. J. Mater. Res. 2013, 28, 2728–2739. [Google Scholar] [CrossRef]
- Ohmura, T.; Hara, T.; Tsuzaki, K. Evaluation of temper softening behavior of Fe–C binary martensitic steels by nanoindentation. Scr. Mater. 2003, 49, 1157–1162. [Google Scholar] [CrossRef]
- Speich, G.R.; Leslie, W.C. Tempering of steel. Metall. Trans. 1972, 3, 1043–1054. [Google Scholar] [CrossRef]
- Caron, R.N.; Krauss, G. The tempering of Fe-C lath martensite. Metall. Trans. 1972, 3, 2381–2389. [Google Scholar] [CrossRef]
- Tkalcec, I.; Azcoıtia, C.; Crevoiserat, S.; Mari, D. Tempering effects on a martensitic high carbon steel. Mater. Sci. Eng. 2004, 387, 352–356. [Google Scholar] [CrossRef]
- Ohmura, T.; Tsuzaki, K.; Matsuoka, S. Evaluation of the matrix strength of Fe-0.4 wt% C tempered martensite using nanoindentation techniques. Philos. Mag. 2002, 82, 1903–1910. [Google Scholar]
- Waseda, O.; Veiga, R.G.A.; Morthomas, J.; Chantrenne, P.; Becquart, C.S.; Ribeiro, F.; Jelea, A.; Goldenstein, H.; Perez, M. Formation of carbon Cottrell atmospheres and their effect on the stress field around an edge dislocation. Scr. Mater. 2017, 129, 16–19. [Google Scholar] [CrossRef]
- Pereloma, E.V.; Miller, M.K.; Timokhina, I.B. On the decomposition of martensite during bake hardening of thermomechanically processed transformation-induced plasticity steels. Metall. Mater. Trans. 2008, 39, 3210–3216. [Google Scholar] [CrossRef] [Green Version]
- Waterschoot, T.; de Cooman, B.C.; De, A.K.; Vandeputte, S. Static strain aging phenomena in cold-rolled dual-phase steels. Metall. Mater. Trans. 2003, 34, 781–791. [Google Scholar] [CrossRef]
- Suresh, S.; Nieh, T.G.; Choi, B.W. Nano-indentation of copper thin films on silicon substrates. Scr. Mater. 1999, 41, 951–957. [Google Scholar] [CrossRef] [Green Version]
- Michalske, T.A.; Houston, J.E. Dislocation nucleation at nano-scale mechanical contacts. Acta Mater. 1998, 46, 391–396. [Google Scholar] [CrossRef]
- Pathak, S.; Stojakovic, D.; Doherty, R.; Kalidindi, S.R. Importance of surface preparation on the nano-indentation stress-strain curves measured in metals. J. Mater. Res. 2009, 24, 1142–1155. [Google Scholar] [CrossRef]





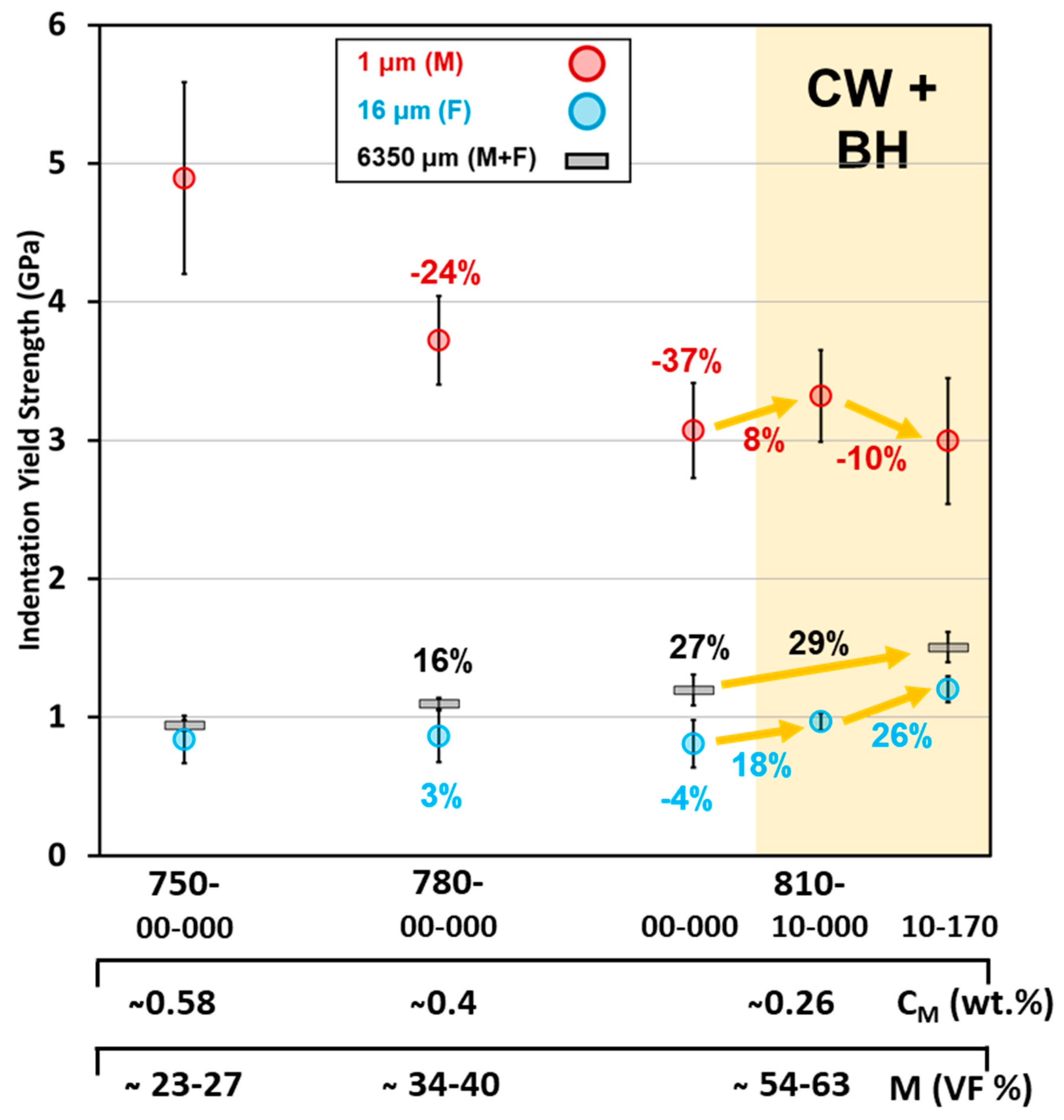
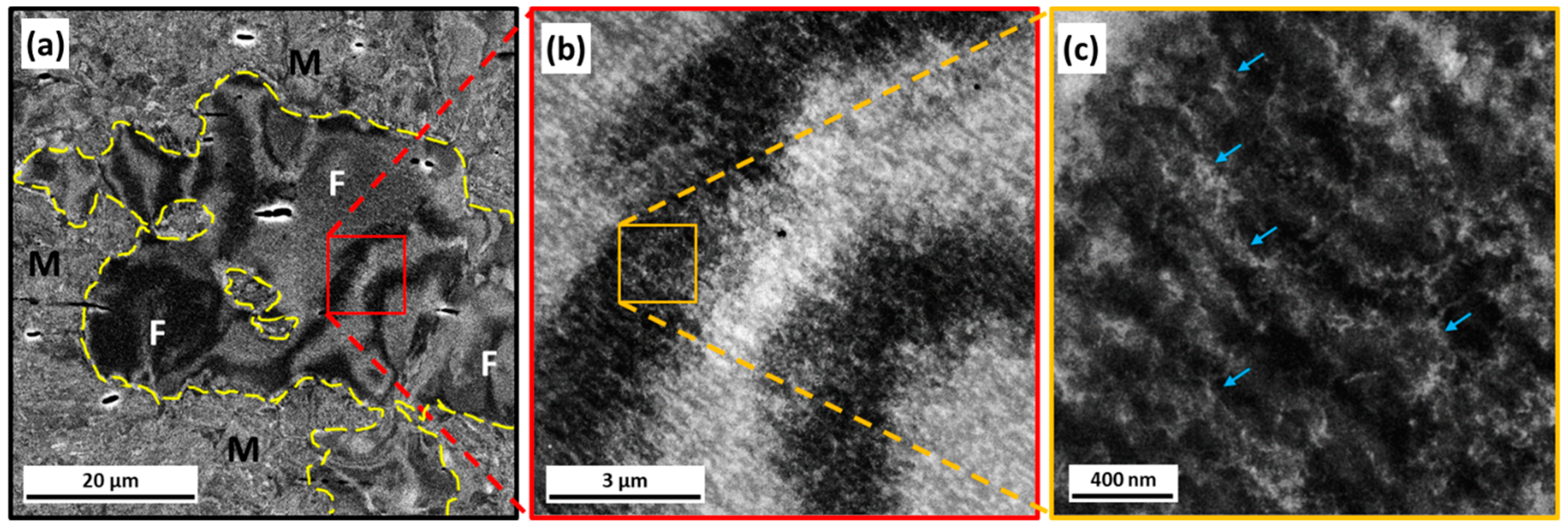

| Alloy Grade/Composition | Indenter Type | Max Depth (nm) | Max Load (mN) | Martensite Hardness (GPa) | Ferrite Hardness (GPa) | Reference |
|---|---|---|---|---|---|---|
| DP780 | Berkovich | - | 5 | 6.2 ± 0.11 | 3.7 ± 0.03 | 37 |
| DP1300 | Berkovich | - | 5 | 4.5-10 | 2-5 | 38 |
| 0.1C5Mn3Al | Berkovich | - | 5 | 4.7 ± 0.4 | 4.1 ± 0.3 | 39 |
| 0.1C5Mn3Al (60% TR) | Berkovich | - | 5 | 5.9 ± 0.7 | 5.0 ± 0.5 | |
| DP980 | Berkovich | - | 2.5 | 3-10 | 1.5–5.5 | 40 |
| DP980 (7% strain) | Berkovich | - | 2.5 | 3-13 | 2–7 | |
| (0.04, 0.07, 0.1) C1.2Mn0.15Si | spherical (R = 2.8, 5.7 μm) | - | 15 | - | 1.8–2, 1.3–1.6 | 41 |
| DP980 | Berkovich | 40 | - | 4.5–9 | 3–4.75 | 42 |
| API-X100 | Spherical (R = 0.5, 3 μm) | - | 15, 30 | - | 3.4–4.1, 1.9–2.4 | 43 |
| 0.16C1.5Mn1Si | cube-corner | - | 1 | 6.3–7.9 | 2.8 | 44 |
| 0.19C1.6Mn0.2Si | Berkovich | - | - | 3–10.8 | 2.8-6.8 | 45 |
| 0.18C0.75Mn0.4Si | Berkovich | - | 10 | 7.6 | 2.2 ± 0.2 | 46 |
| 0.38C0.67Mn0.2Si | Berkovich | - | 10 | 4.9–7.3 | - | 47 |
| DP980 | Berkovich | 50 | - | 6–11 | 4–5.5 | 48 |
| DP980 | Berkovich | - | 0.8 | 8.4 ± 0.9 | 4.1 ± 0.3 | 49 |
| 0.08C1.74Mn0.75Si | Berkovich | - | 0.05 | 4.5–5.5 | 3–3.5 | 50 |
| DP980 | Berkovich | - | 3 | 6.3–8.1 | 2.5–3.5 | 51 |
| DP590 | Berkovich | 50 | - | 3.5–4.1 | 1.5–1.8 | 52 |
| Sample Code | Martensite Volume Fraction (%) | Average Elastic Modulus (GPa) | Average Indentation Yield Strength (MPa) | Contact Area Diameter at Yield Point (µm) |
|---|---|---|---|---|
| 750-00-000 | 25.4 | 174.5 ± 25.3 | 899.5 ± 62.9 | 284.6 ± 14.0 |
| 750-05-170 | 27.5 | 193.4 ± 23.3 | 950.4 ± 29.7 | 333.4 ± 26.4 |
| 750-10-170 | 23.5 | 200.9 ± 22.3 | 1100.9 ± 130.3 | 352.4 ± 23.0 |
| 780-00-000 | 34.8 | 216.8 ± 23.3 | 1097.7 ± 41.6 | 331.4 ± 29.6 |
| 780-05-170 | 35.3 | 209.6 ± 15.4 | 1299.4 ± 68.7 | 356.2 ± 35.4 |
| 780-10-170 | 38.9 | 201.9 ± 16.7 | 1336.3 ± 69.5 | 362.6 ± 28.4 |
| 810-00-000 | 56.3 | 188.5 ± 14.7 | 1168.6 ± 186.8 | 306.6 ± 21.8 |
| 810-05-170 | 59.6 | 219.2 ± 14.5 | 1340.4 ± 130.9 | 338.6 ± 20.4 |
| 810-10-170 | 60.4 | 207.6 ± 9.7 | 1506.5 ± 132.3 | 361.0 ± 30.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khosravani, A.; Caliendo, C.M.; Kalidindi, S.R. New Insights into the Microstructural Changes During the Processing of Dual-Phase Steels from Multiresolution Spherical Indentation Stress–Strain Protocols. Metals 2020, 10, 18. https://doi.org/10.3390/met10010018
Khosravani A, Caliendo CM, Kalidindi SR. New Insights into the Microstructural Changes During the Processing of Dual-Phase Steels from Multiresolution Spherical Indentation Stress–Strain Protocols. Metals. 2020; 10(1):18. https://doi.org/10.3390/met10010018
Chicago/Turabian StyleKhosravani, Ali, Charles M. Caliendo, and Surya R. Kalidindi. 2020. "New Insights into the Microstructural Changes During the Processing of Dual-Phase Steels from Multiresolution Spherical Indentation Stress–Strain Protocols" Metals 10, no. 1: 18. https://doi.org/10.3390/met10010018
APA StyleKhosravani, A., Caliendo, C. M., & Kalidindi, S. R. (2020). New Insights into the Microstructural Changes During the Processing of Dual-Phase Steels from Multiresolution Spherical Indentation Stress–Strain Protocols. Metals, 10(1), 18. https://doi.org/10.3390/met10010018