Analysis and Control of Twist Defects of Aluminum Profiles with Large Z-Section in Roll Bending Process
Abstract
:1. Introduction
2. Roll-Bending Process for Z-Section Profiles
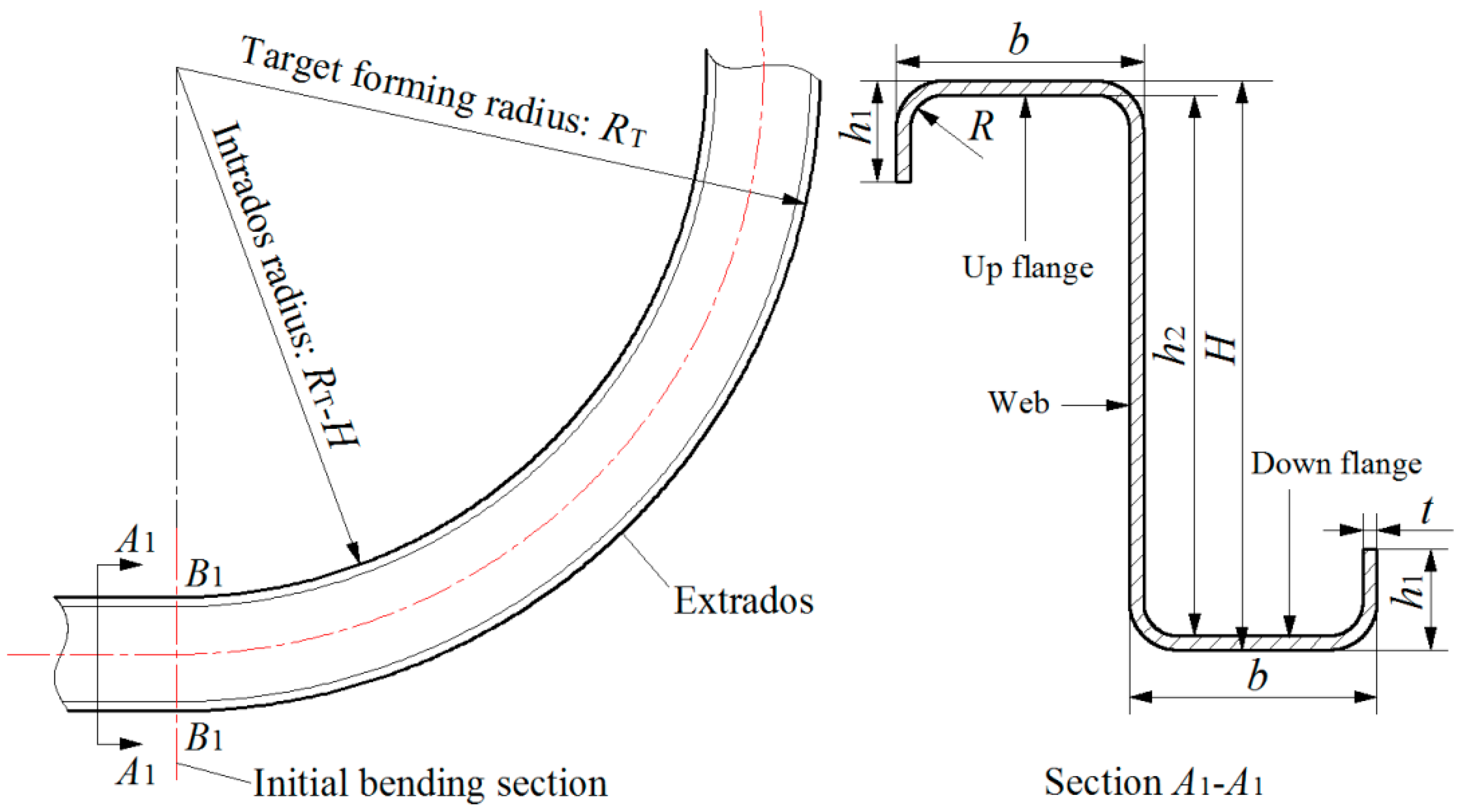
2.1. Geometric Parameters of Z-Section Profiles
2.2. Roll-Bending Process
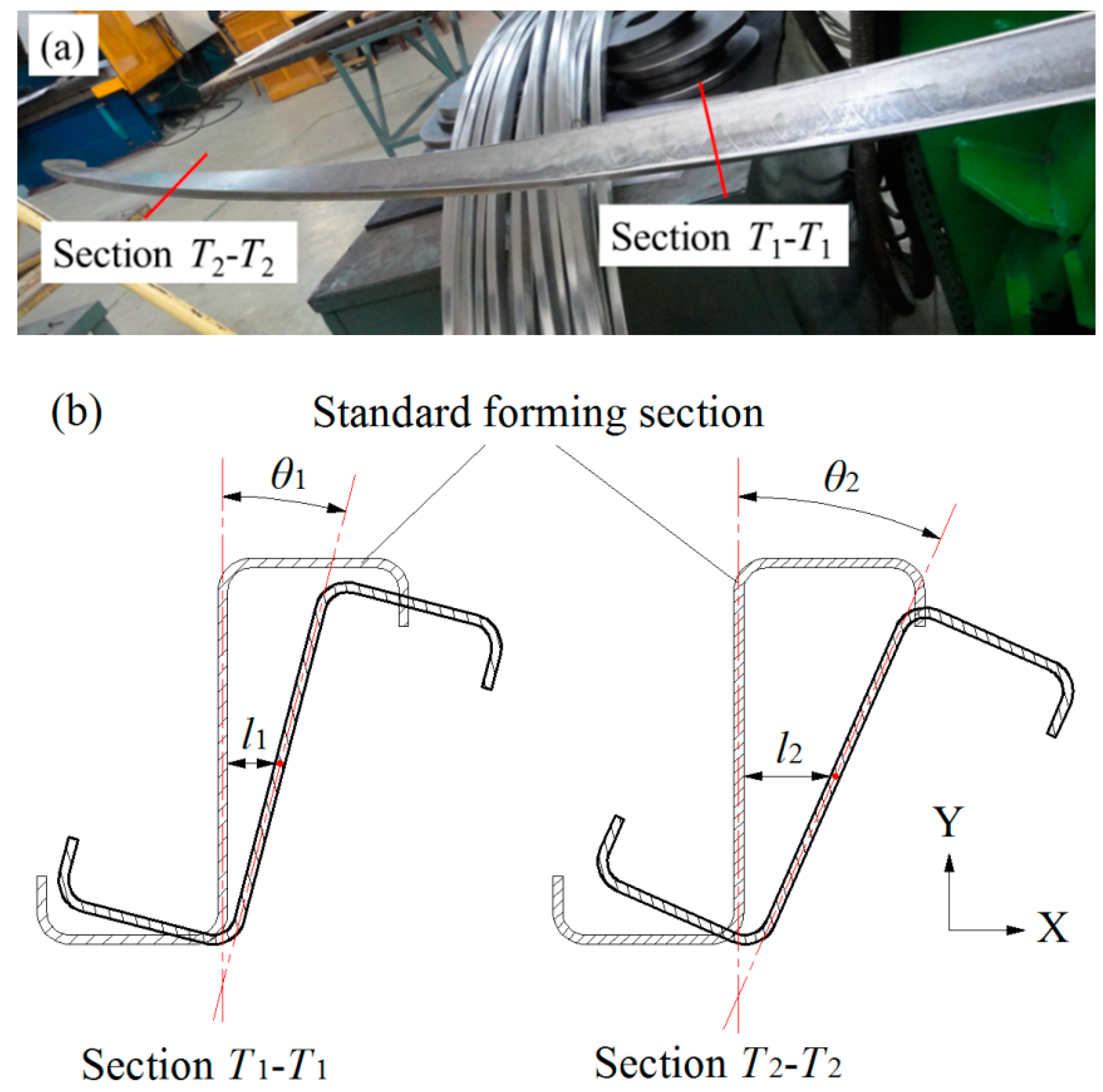
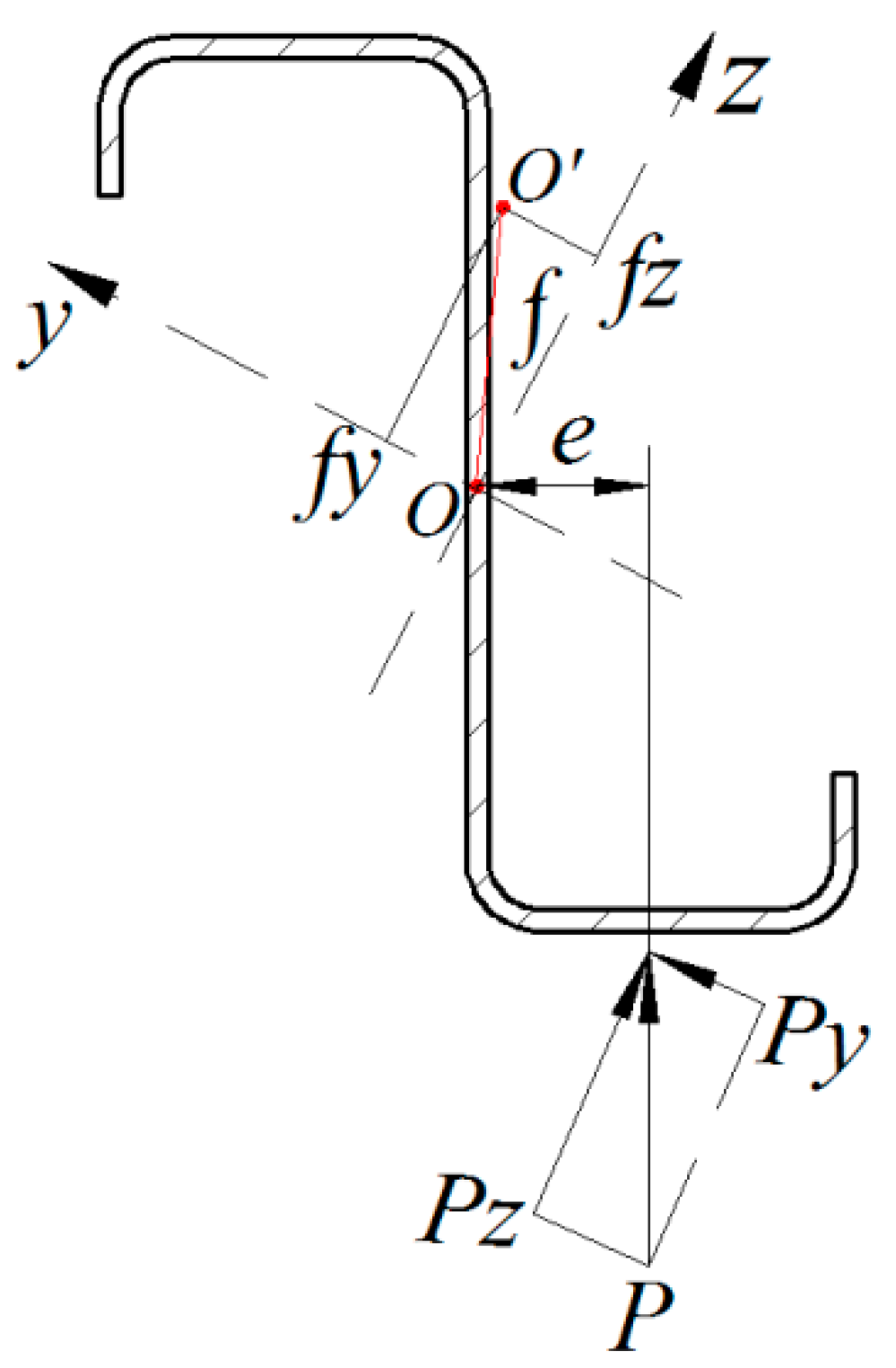
2.3. Analysis of Twist Defects
3. Finite Element Analysis of Twist Defects
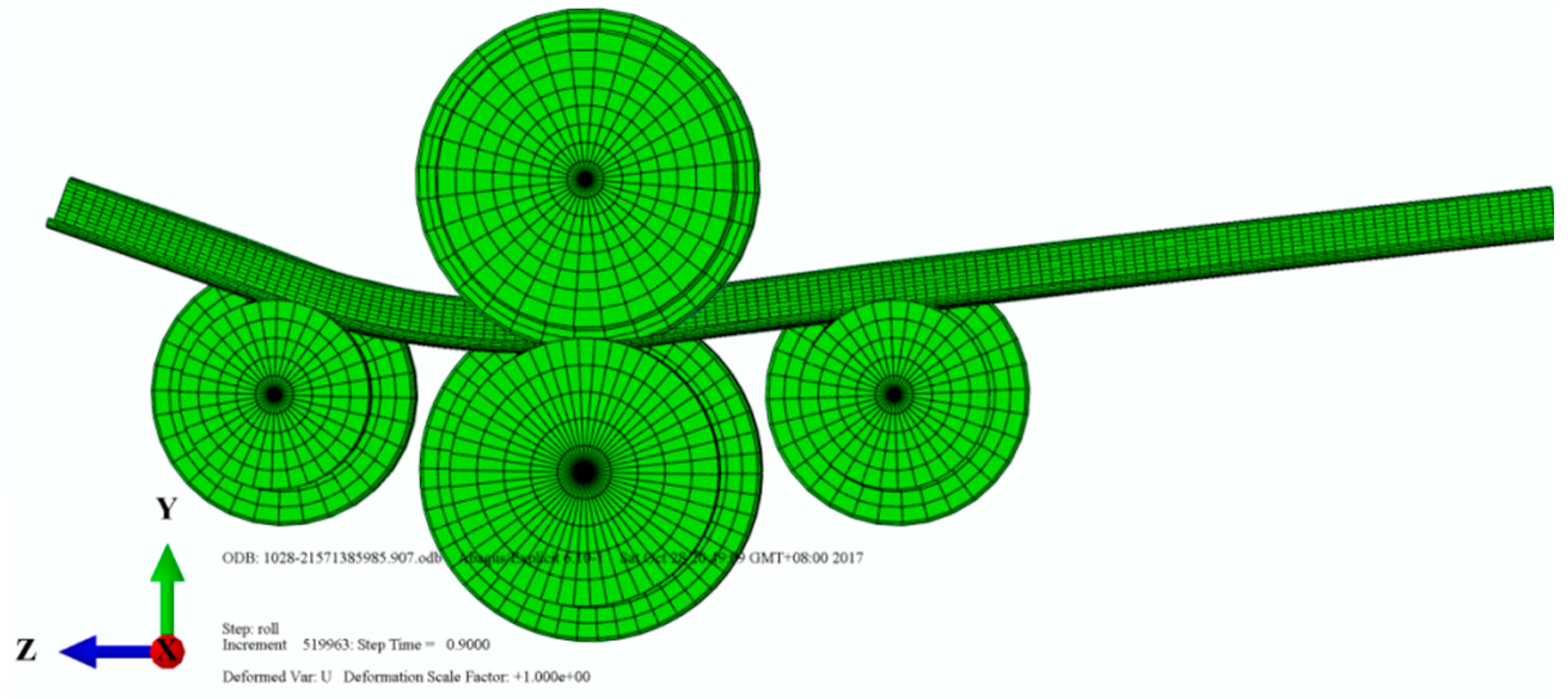
3.1. 3D-FEM of Roll-Bending Process
3.1.1. Procedure Type and Element
3.1.2. Interaction and Output
3.1.3. Boundary Conditions
3.2. Material and Properties for Simulation Input
3.3. Twist Defects Measurement
3.4. FE Analysis of Twist
3.4.1. Simulation Scheme
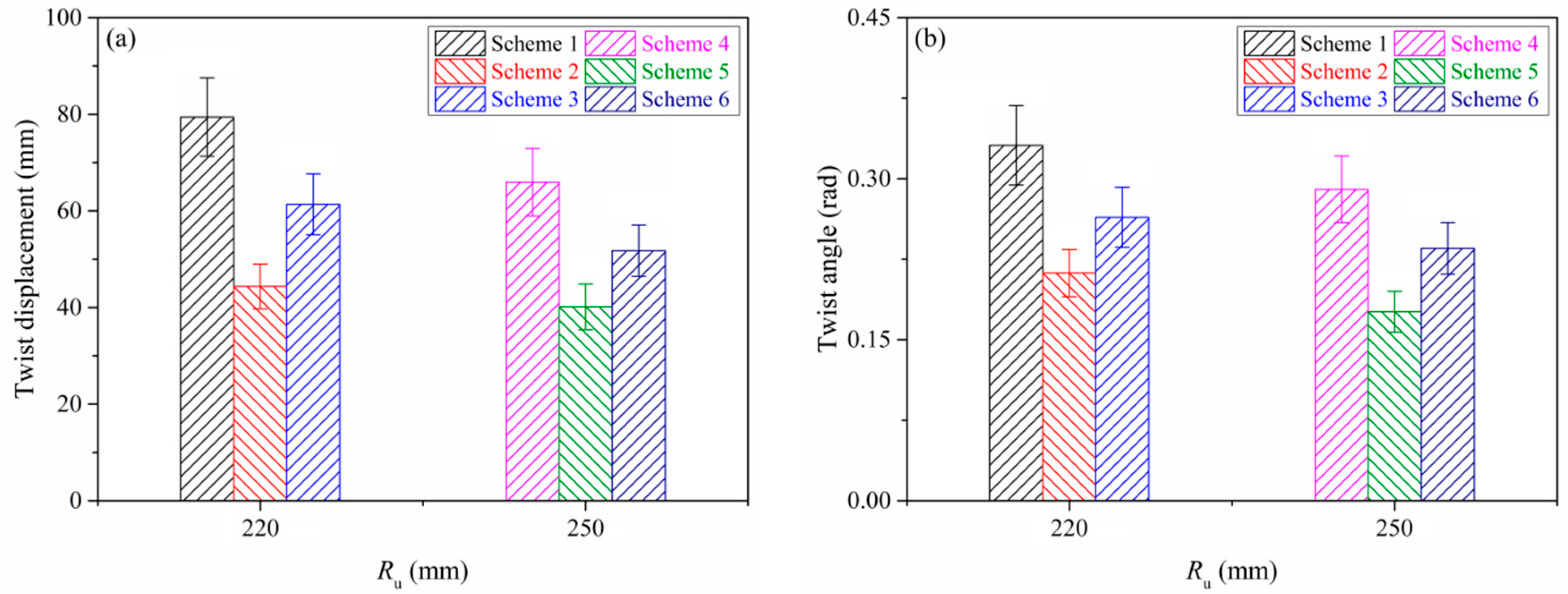
3.4.2. Effect of Loading Pattern of Side Rolls on Twist Defects
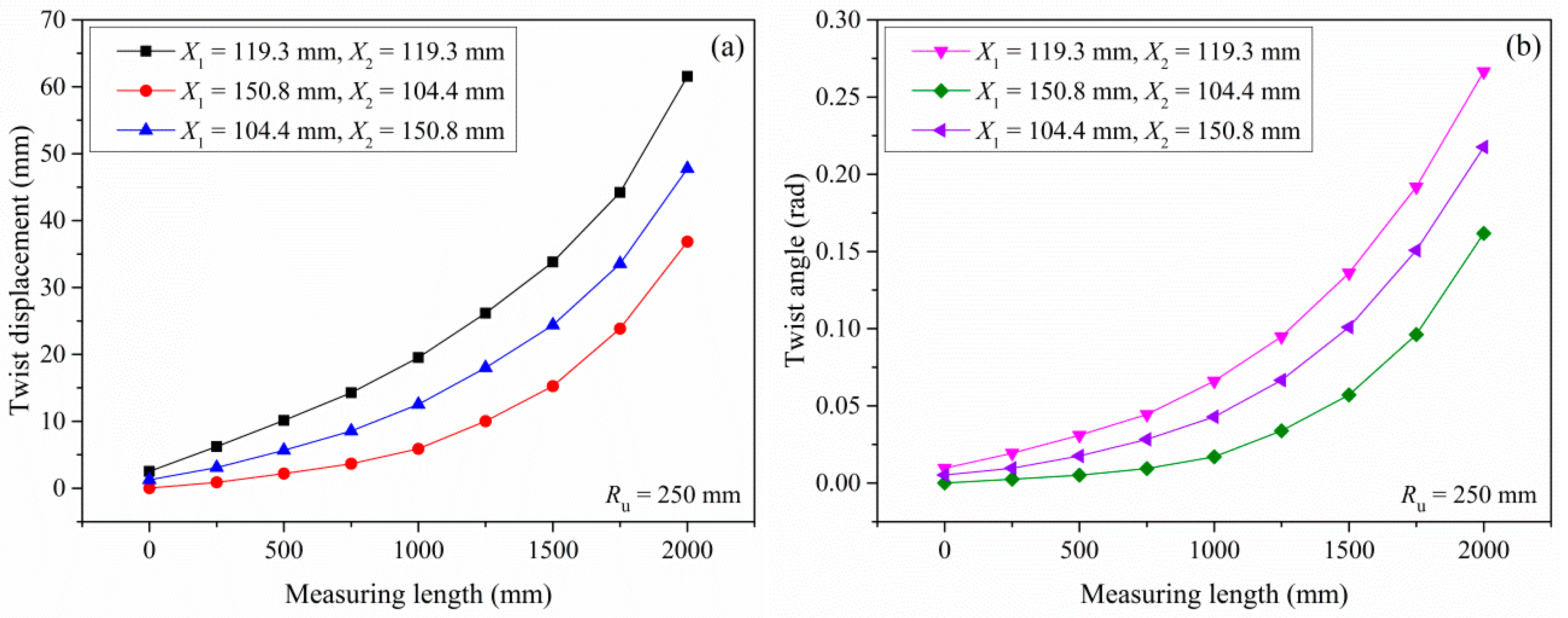
3.4.3. Effect of the Radius of Upper Roll on Twist Defects
4. Experimental Results and Discussion
4.1. Experimental Procedures
4.2. Validation of the Simulation Model
5. Conclusions
- (1)
- The roll bending process was simulated by ABAQUS and twist defects of Z-section profiles were analyzed under different loading patterns and the radius of upper roll. The maximum prediction error of the twist displacement and twist angle compared with the experimental results was within a reasonable range 10%.
- (2)
- The reason for the twist defects of the profile with asymmetrical section during the roll bending was explained, and the formula for the twist displacement and twist angle were deduced for Z-section profiles.
- (3)
- The asymmetrical loading pattern can be used to control twist defects. A significant inhibitory function on twist defects was obtained when the exit guide roll was adjusted higher than the entrance one.
- (4)
- The idea of using a larger radius of upper roll presented in this work was to increase the constraint region between the clamp rolls and profiles that could effectively inhibit twist defects.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lou, S.; Zhao, G.; Wang, R.; Wu, X. Modeling of aluminum alloy profile extrusion process using finite volume method. J. Mater. Process. Technol. 2008, 206, 481–490. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, G.; Chen, L. Analysis of longitudinal weld seam defects and investigation of solid-state bonding criteria in porthole die extrusion process of aluminum alloy profiles. J. Mater. Process. Technol. 2016, 237, 31–47. [Google Scholar] [CrossRef]
- Hua, M.; Baines, K.; Cole, I.M. Continuous four-roll plate bending: A production process for the manufacture of single seamed tubes of large and medium diameters. Int. J. Mach. Tools. Manuf. 1999, 39, 905–935. [Google Scholar] [CrossRef]
- Hua, M.; Baines, K.; Cole, I.M. Bending Mechanisms, Experimental Techniques and Preliminary Tests for the Continuous Four-Roll Plate Bending Process. J. Mater. Process. Technol. 1995, 48, 159–172. [Google Scholar] [CrossRef]
- Pham, C.H.; Thuillier, S.; Manach, P.Y. Twisting analysis of ultra-thin metallic sheets. J. Mater. Process. Technol. 2014, 214, 844–855. [Google Scholar] [CrossRef]
- Cha, W.; Kim, N. Study on twisting and bowing of roll formed products made of high strength steel. Int. J. Precis. Eng. Manuf. 2013, 14, 1527–1533. [Google Scholar] [CrossRef]
- Xue, X.; Liao, J.; Vincze, G.; Gracio, J. Twist Springback of Asymmetric Thin-walled Tube in Mandrel Rotary Draw Bending Process. Procedia Eng. 2014, 81, 2177–2183. [Google Scholar] [CrossRef] [Green Version]
- Dezelak, M.; Stepisnik, A.; Pahole, I. Evaluation of twist springback prediction after an AHSS forming process. Int. J. Simul. Model. 2014, 13, 171–182. [Google Scholar] [CrossRef]
- Xue, X.; Liao, J.; Vincze, G.; Gracio, J.J. Modelling of mandrel rotary draw bending for accurate twist springback prediction of an asymmetric thin-walled tube. J. Mater. Process. Technol. 2015, 216, 405–417. [Google Scholar] [CrossRef]
- Ona, H.; Jimma, T.; Fukaya, N. Experiments into the cold rollforming of straight asymmetrical channels. J. Mech. Work. Technol. 1983, 8, 2291–2723. [Google Scholar] [CrossRef]
- Takamura, M.; Sakata, M.; Fukui, A.; Hama, T.; Miyoshi, Y.; Sunaga, H.; Makinouchi, A.; Asakawa, M. Investigation of twist in curved hat channel products by elastic-plastic finite element analysis. Int. J. Mater. Form. 2010, 3, 131–134. [Google Scholar] [CrossRef]
- Chatti, S.; Hermes, M.; Tekkaya, A.E.; Kleiner, M. The new TSS bending process: 3D bending of profiles with arbitrary cross-sections. CIRP Ann. Manuf. Technol. 2010, 59, 315–318. [Google Scholar] [CrossRef] [Green Version]
- Gangwar, M.; Choubey, V.K.; Dwivedi, J.P.; Talukder, N.K.D. Springback analysis of thin tubes with arbitrary stress–strain curves. J. Mech. Eng. 2011, 8, 57–76. [Google Scholar]
- Liao, J.; Xue, X.; Lee, M.; Barlat, F.; Gracio, J. On twist springback prediction of asymmetric tube in rotary draw bending with different constitutive models. Int. J. Mech. Sci. 2014, 89, 311–322. [Google Scholar] [CrossRef]
- Xue, X.; Liao, J.; Vincze, G.; Pereira, A.B. Control strategy of twist springback for aluminium alloy hybrid thin-walled tube under mandrel-rotary draw bending. Int. J. Mater. Form. 2018, 11, 311–323. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, P.; Li, M.; Wang, L. Application and correction of L-shaped thin-wall aluminum in flexible-bending processing. Int. J. Adv. Manuf. Technol. 2017, 92, 981–988. [Google Scholar] [CrossRef]
- Yaser, T.; Hassan, M.N.; Roohollah, A.T.; Behrooz, S.B. A strategy to reduce the twist defect in roll-formed asymmetrical-channel sections. Thin. Wall. Struct. 2018, 130, 395–404. [Google Scholar]
- Marciniak, Z.; Duncan, J.L.; Hu, S.J. Mechanics of Sheet Metal. Forming; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Gandhi, A.H.; Shaikh, A.A.; Raval, H.K. Formulation of springback and machine setting parameters for multi-pass three-roller cone frustum bending with change of flexural modulus. Int. J. Mater. Form. 2009, 2, 45–57. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Anthony, M.P. Experimentl investigation of mechanical properties, formability and force measurement for AA7075-O aluminum alloy sheets formed by incremental forming. Int. J. Precis. Eng. Manuf. 2013, 14, 1891–1899. [Google Scholar] [CrossRef]
- Concli, F.; Gilioli, A. Numerical and experimental assessment of the mechanical properties of 3D printed 18-Ni300 steel trabecular structures produced by Selective Laser Melting—A lean design approach. Virt. Phys. Prototyp. 2019, 14, 267–276. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Y.; Wang, J.; Wang, S.; Wang, W.; Wu, J.; Xia, X. Springback analysis of Z & T-section 2196-T8511 and 2099-T83 Al–Li alloys extrusions in displacement controlled cold stretch bending. J. Mater. Process. Technol. 2015, 225, 295–309. [Google Scholar]
- Hua, M.; Sansome, D.H.; Baines, K. Mathematical modeling of the internal bending moment at the top roll contact in multi-pass four-roll thin-plate bending. J. Mater. Process. Technol. 1995, 52, 425–459. [Google Scholar] [CrossRef]









| Contact Type | Slip Type | Friction Type | Friction Coefficients |
|---|---|---|---|
| Point and face | Limited slip | Coulomb friction | 0.17 |
| Constraint | Specimen | Upper Roll | Lower Roll | Side Rolls |
|---|---|---|---|---|
| Displacement (mm) | X = 0 | XYZ = 0 | XZ = 0 | Z = 0 |
| Rotation (rad) | YZ = 0 | YZ = 0 | YZ = 0 | YZ = 0 |
| Element | Zn | Mg | Cu | Cr | Fe | Si | Mn | Ti | Al |
|---|---|---|---|---|---|---|---|---|---|
| wt. % | 5.70 | 2.50 | 1.70 | 0.19 | 0.12 | 0.08 | 0.01 | 0.04 | 89.66 |
| Material | Young’s Modulus | Yield Strength | Tensile Strength | Strength Coefficient | Hardening Index | Plastic Strain |
|---|---|---|---|---|---|---|
| 7475-O | 70289 (5296) | 88 (6.45) | 212 (4.08) | 345 (5.56) | 0.209 (0.087) | 0.00295 (0.0003) |
| Scheme | Feed Velocity | Clamping Force | Side Rolls Stroke (mm) | ||
|---|---|---|---|---|---|
| (bar) | |||||
| 1 | 220 | 200 | 1.0 | 134.1 | 134.1 |
| 2 | 171.5 | 107.2 | |||
| 3 | 107.2 | 171.5 | |||
| 4 | 250 | 200 | 1.0 | 119.3 | 119.3 |
| 5 | 150.8 | 104.4 | |||
| 6 | 104.4 | 150.8 | |||
| Test Number | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Twist displacement | Simulation (mm) | 73.45 | 40.73 | 56.49 | 61.56 | 36.85 | 47.75 |
| Experiment (mm) | 79.41 | 44.35 | 61.35 | 65.92 | 40.13 | 51.73 | |
| Error (%) | 8.11 | 8.89 | 8.60 | 7.08 | 8.90 | 8.34 | |
| Twist angle | Simulation (mm) | 0.304 | 0.195 | 0.247 | 0.267 | 0.162 | 0.218 |
| Experiment (mm) | 0.331 | 0.212 | 0.264 | 0.290 | 0.176 | 0.235 | |
| Error (%) | 8.88 | 8.72 | 6.88 | 8.49 | 8.64 | 7.69 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Xue, H.; Bayraktar, E.; Yang, Y.; Saud, S.; Chen, P. Analysis and Control of Twist Defects of Aluminum Profiles with Large Z-Section in Roll Bending Process. Metals 2020, 10, 31. https://doi.org/10.3390/met10010031
Wang A, Xue H, Bayraktar E, Yang Y, Saud S, Chen P. Analysis and Control of Twist Defects of Aluminum Profiles with Large Z-Section in Roll Bending Process. Metals. 2020; 10(1):31. https://doi.org/10.3390/met10010031
Chicago/Turabian StyleWang, Anheng, Hongqian Xue, Emin Bayraktar, Yanli Yang, Shah Saud, and Peng Chen. 2020. "Analysis and Control of Twist Defects of Aluminum Profiles with Large Z-Section in Roll Bending Process" Metals 10, no. 1: 31. https://doi.org/10.3390/met10010031
APA StyleWang, A., Xue, H., Bayraktar, E., Yang, Y., Saud, S., & Chen, P. (2020). Analysis and Control of Twist Defects of Aluminum Profiles with Large Z-Section in Roll Bending Process. Metals, 10(1), 31. https://doi.org/10.3390/met10010031






