Influence of the Miniaturisation Effect on the Effective Stiffness of Lattice Structures in Additive Manufacturing
Abstract
1. Introduction
2. Materials and Methods
3. Results
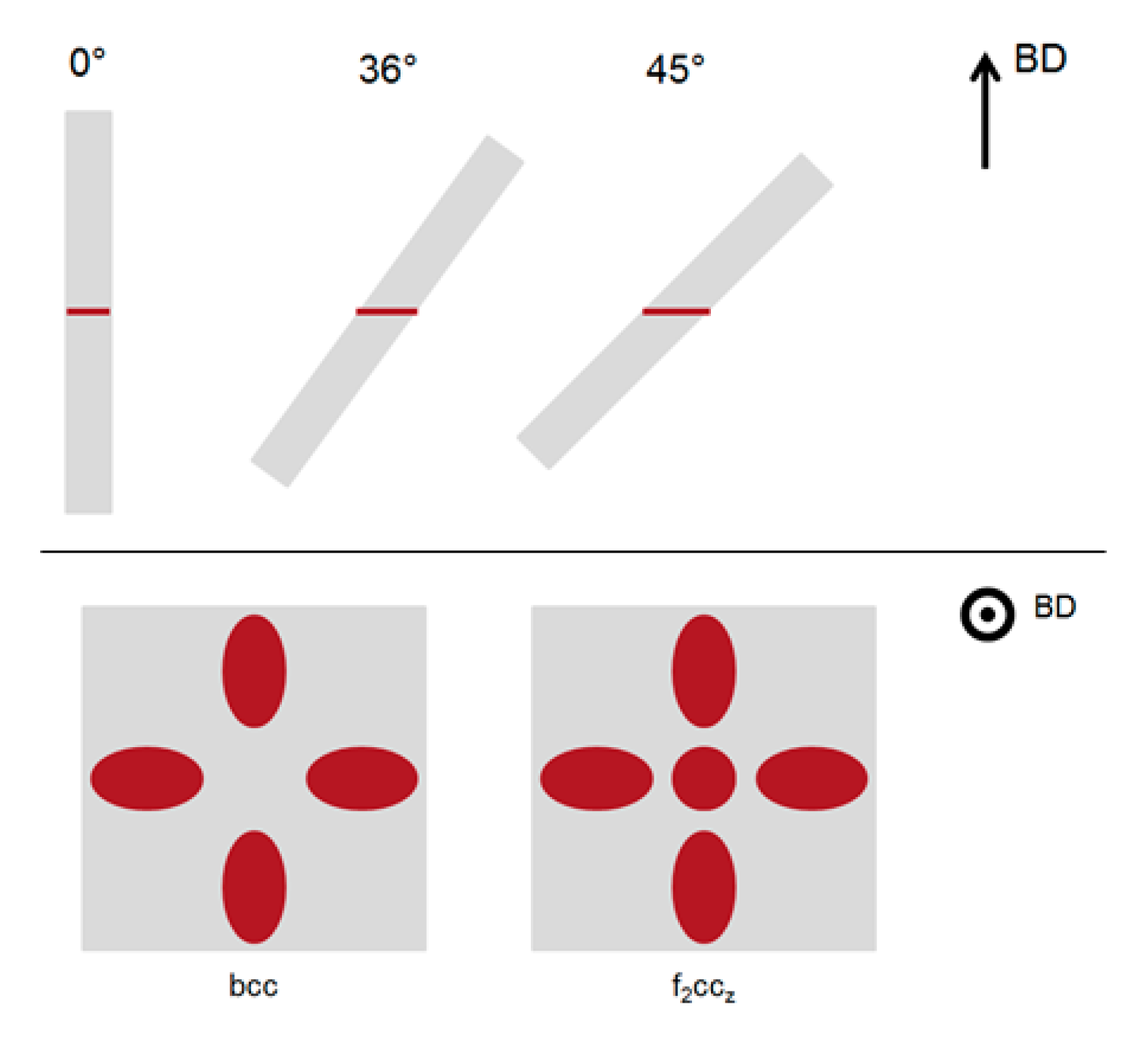
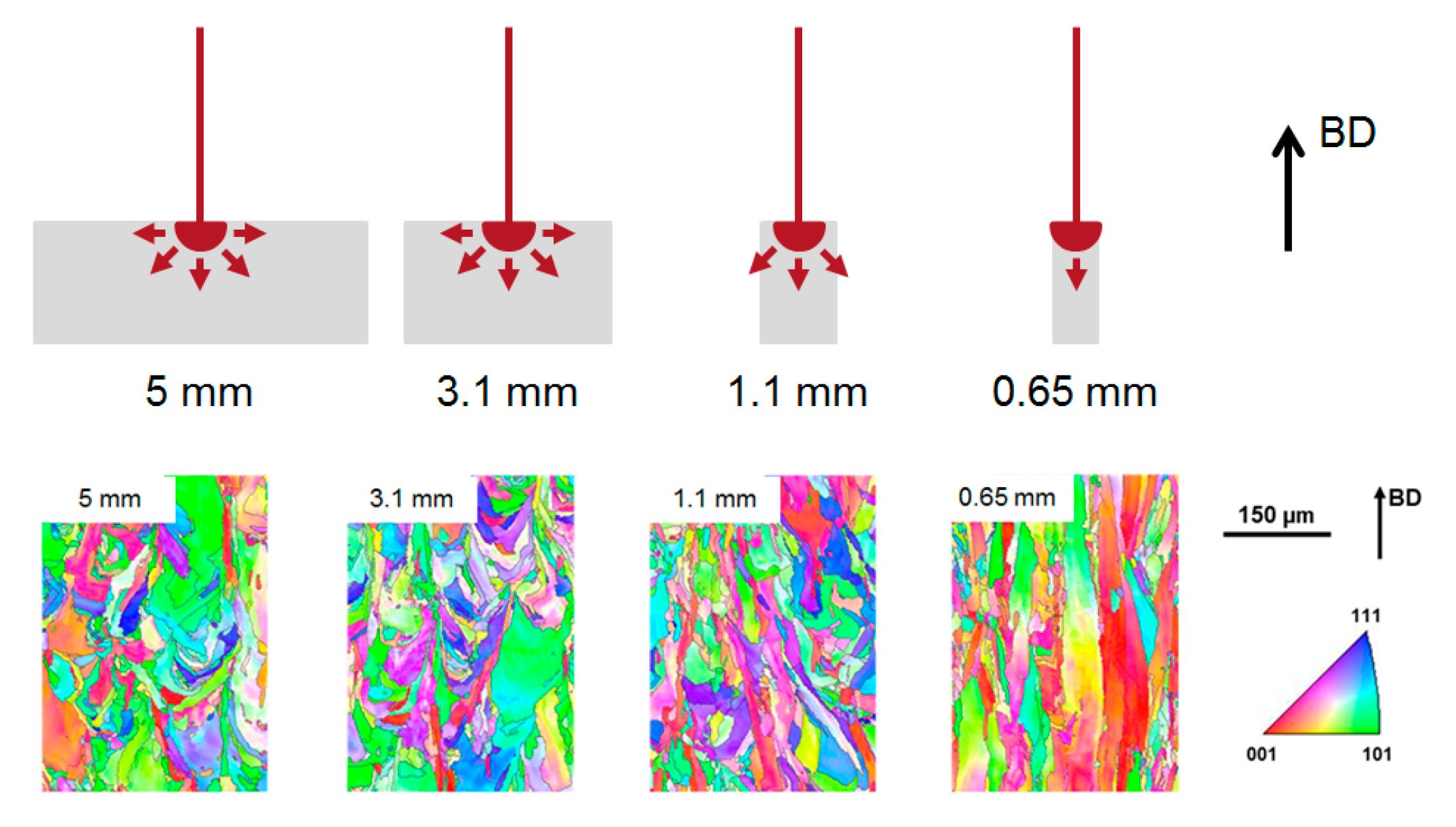
3.1. Microstructures
3.2. Lattice Structures
3.2.1. Local Deformation Behavior
3.2.2. Macroscopic Deformation Behavior
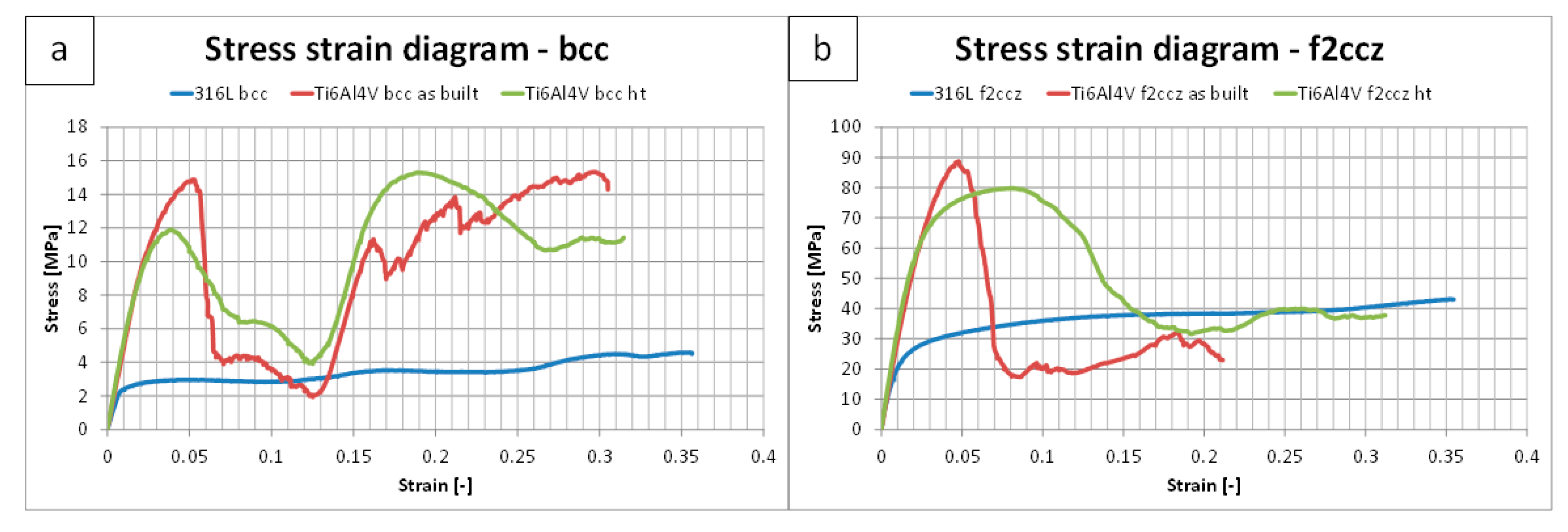
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Verein Deutscher Ingenieure. Konstruktionsempfehlungen für die Bauteilfertigung mit Laser-Sintern und Laser-Strahlschmelzen; VDI-Richtlinie 3405 Blatt 3; Verein Deutscher Ingenieure: Düsseldorf, Germany, 2014. [Google Scholar]
- Richard, H.A.; Schramm, B.; Zipsner, T. Additive Fertigung von Bauteilen und Strukturen; Springer Science and Business Media LLC: Berlin, Germany, 2017. [Google Scholar]
- Schmidt, T. Potentialbewertung Generativer Fertigungsverfahren für Leichtbauteile; Springer Science and Business Media LLC: Berlin, Germany, 2016. [Google Scholar]
- Yusuf, S.M.; Cutler, S.; Gao, N. Review: The Impact of Metal Additive Manufacturing on the Aerospace Industry. Metals 2019, 9, 1286. [Google Scholar] [CrossRef]
- Gebhardt, A.; Hötter, J.S. Additive Manufacturing 3D Printing for Prototyping and Manufacturing; Carl Hanser Verlag: München, Germany, 2016. [Google Scholar]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Ashby, M.F. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2005, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Vigliotti, A.; Deshpande, V.S.; Pasini, D. Non linear constitutive models for lattice materials. J. Mech. Phys. Solids 2014, 64, 44–60. [Google Scholar] [CrossRef]
- Bonatti, C.; Mohr, D. Large deformation response of additively-manufactured FCC metamaterials: From octet truss lattices towards continuous shell mesostructures. Int. J. Plast. 2017, 92, 122–147. [Google Scholar] [CrossRef]
- Messner, M.C. Optimal lattice-structured materials. J. Mech. Phys. Solids 2016, 96, 162–183. [Google Scholar] [CrossRef]
- Souza, J.; Großmann, A.; Mittelstedt, C. Micromechanical analysis of the effective properties of lattice structures in additive manufacturing. Addit. Manuf. 2018, 23, 53–69. [Google Scholar] [CrossRef]
- Van Bael, S.; Kerckhofs, G.; Moesen, M.; Pyka, G.; Schrooten, J.; Kruth, J. Micro-CT-based improvement of geometrical and mechanical controllability of selective laser melted Ti6Al4V porous structures. Mater. Sci. Eng. A 2011, 528, 7423–7431. [Google Scholar] [CrossRef]
- Dressler, A.D.; Jost, E.W.; Miers, J.C.; Moore, D.G.; Seepersad, C.C.; Boyce, B.L. Heterogeneities dominate mechanical performance of additively manufactured metal lattice struts. Addit. Manuf. 2019, 28, 692–703. [Google Scholar] [CrossRef]
- Qiu, C.; Yue, S.; Adkins, N.J.; Ward, M.; Hassanin, H.; Lee, P.D.; Withers, P.J.; Attallah, M.M. Influence of processing conditions on strut structure and compressive properties of cellular lattice structures fabricated by selective laser melting. Mater. Sci. Eng. A 2015, 628, 188–197. [Google Scholar] [CrossRef]
- Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and failure response of imperfect three-dimensional metallic lattices: The role of geometric defects induced by Selective Laser Melting. J. Mech. Phys. Solids 2017, 107, 160–184. [Google Scholar] [CrossRef]
- Sing, S.L.; Wiria, F.E.; Yeong, W.Y. Selective laser melting of lattice structures: A statistical approach to manufacturability and mechanical behavior. Robot. Comput. Manuf. 2018, 49, 170–180. [Google Scholar] [CrossRef]
- Tsopanos, S.; Mines, R.; McKown, S.; Shen, Y.; Cantwell, W.J.; Brooks, W.; Sutcliffe, C.J. The Influence of Processing Parameters on the Mechanical Properties of Selectively Laser Melted Stainless Steel Microlattice Structures. J. Manuf. Sci. Eng. 2010, 132, 041011. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Elambasseril, J.; McMillan, M.; Chirent, T.; Sun, Y.; Qian, M.; Easton, M.; Brandt, M. Selective laser melting (SLM) of AlSi12Mg lattice structures. Mater. Des. 2016, 98, 344–357. [Google Scholar] [CrossRef]
- Großmann, A.; Gosmann, J.; Mittelstedt, C. Lightweight lattice structures in selective laser melting: Design, fabrication and mechanical properties. Mater. Sci. Eng. A 2019, 766, 138356. [Google Scholar] [CrossRef]
- Suard, M.; Martin, G.; Lhuissier, P.; Dendievel, R.; Vignat, F.; Blandin, J.-J.; Villeneuve, F. Mechanical equivalent diameter of single struts for the stiffness prediction of lattice structures produced by Electron Beam Melting. Addit. Manuf. 2015, 8, 124–131. [Google Scholar] [CrossRef]
- Brenne, F.; Niendorf, T. Damage tolerant design by microstructural gradation—Influence of processing parameters and build orientation on crack growth within additively processed 316L. Mater. Sci. Eng. A 2019, 764, 138186. [Google Scholar] [CrossRef]
- Niendorf, T.; Leuders, S.; Riemer, A.; Richard, H.A.; Tröster, T.; Schwarze, D. Highly Anisotropic Steel Processed by Selective Laser Melting. Met. Mater. Trans. A 2013, 44, 794–796. [Google Scholar] [CrossRef]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; Van Humbeeck, J.; Kruth, J.-P. A study of the microstructural evolution during selective laser melting of Ti-6Al-4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Thijs, L.; Sistiaga, M.L.M.; Wauthle, R.; Xie, Q.; Kruth, J.-P.; Van Humbeeck, J. Strong morphological and crystallographic texture and resulting yield strength anisotropy in selective laser melted tantalum. Acta Mater. 2013, 61, 4657–4668. [Google Scholar] [CrossRef]
- Antonysamy, A.; Meyer, J.; Prangnell, P. Effect of build geometry on the β-grain structure and texture in additive manufacture of Ti6Al4V by selective electron beam melting. Mater. Charact. 2013, 84, 153–168. [Google Scholar] [CrossRef]
- Niendorf, T.; Brenne, F.; Schaper, M.; Riemer, A.; Leuders, S.; Reimche, W.; Schwarze, D.; Maier, H.J. Labelling additively manufactured parts by microstructural gradation–advanced copy-proof design. Rapid Prototyp. J. 2016, 22, 630–635. [Google Scholar] [CrossRef]
- Ishimoto, T.; Hagihara, K.; Hisamoto, K.; Sun, S.H.; Nakano, T. Crystallographic texture control of beta-type Ti-15Mo-5Zr-3Al alloy by selective laser melting for the development of novel implants with a biocompatible low Young’s modulus. Scrpitamat 2017, 132, 34–38. [Google Scholar] [CrossRef]
- Kurzynowski, T.; Gruber, K.; Stopyra, W.; Kuźnicka, B.; Chlebus, E. Correlation between process parameters, microstructure and properties of 316 L stainless steel processed by selective laser melting. Mater. Sci. Eng. A 2018, 718, 64–73. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, Y.; Zhang, Q.; Ge, J.; Ji, S.; Li, W.; Liang, J. Microstructural heterogeneity of AlSi10Mg alloy lattice structures fabricated by selective laser melting: Phenomena and mechanism. J. Alloys Compd. 2020, 833, 155071. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, Y.; Li, W.; Liang, J. Orientation dependency for microstructure, geometric accuracy and mechanical properties of selective lase melting AlSi10Mg lattices. J. Alloys Compd. 2019, 791, 490–500. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Wauthle, R.; Vrancken, B.; Beynaerts, B.; Jorissen, K.; Schrooten, J.; Kruth, J.-P.; Van Humbeeck, J. Effects of build orientation and heat treatment on the microstructure and mechanical properties of selective laser melted Ti6Al4V lattice structures. Addit. Manuf. 2015, 5, 77–84. [Google Scholar] [CrossRef]
- Delroisse, P.; Jacques, P.J.; Maire, E.; Rigo, O.; Simar, A. Effect of strut orientation on the microstructure heterogeneities in AlSi10Mg lattices processed by selective laser melting. Scr. Mater. 2017, 141, 32–35. [Google Scholar] [CrossRef]
- Huynh, L.; Rotella, J.; Sangid, M.D. Fatigue behavior of IN718 microtrusses produced by additive manufacturing. Mater. Des. 2016, 105, 278–389. [Google Scholar] [CrossRef]
- Brenne, F. Selektives Laserschmelzen Metallischer Materialien: Einfluss von Prozessparametern und Miniaturisierung auf Mikrostruktur und Mechanisches Verhalten Geometrisch Komplexer Strukturen; Kassel University: Kassel, Germany, 2018. [Google Scholar]
- Wang, X.; Muñiz-Lerma, J.A.; Sánchez-Mata, O.; Shandiz, M.A.; Brochu, M. Microstructure and mechanical properties of stainless steel 316L vertical struts manufactured by laser powder bed fusion process. Mater. Sci. Eng. A 2018, 736, 27–40. [Google Scholar] [CrossRef]
- Brenne, F.; Niendorf, T.; Maier, H. Additively manufactured cellular structures: Impact of microstructure and local strains on the monotonic and cyclic behavior under uniaxial and bending load. J. Mater. Process. Technol. 2013, 213, 1558–1564. [Google Scholar] [CrossRef]
- Niendorf, T.; Brenne, F.; Schaper, M. Lattice structures manufactured by SLM–On the effect of geometrical dimensions on microstructure evolution during processing. Metall. Mater. Trans. B 2014, 45, 1181–1185. [Google Scholar] [CrossRef]
- Brenne, F.; Niendorf, T. Load distribution and damage evolution in bending and stretch dominated Ti-6Al-4V cellular structures processed by selective laser melting. Int. J. Fatigue 2019, 121, 219–228. [Google Scholar] [CrossRef]
- Gorny, B.; Niendorf, T.; Lackmann, J.; Thoene, M.; Troester, T.; Maier, H. In situ characterization of the deformation and failure behavior of non-stochastic porous structures processed by selective laser melting. Mater. Sci. Eng. A 2011, 528, 7962–7967. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M.; Prager, W. Theory of Elastic Stability, Second Edition. J. Appl. Mech. 1962, 29, 220–221. [Google Scholar] [CrossRef]
- Röttger, A.; Boes, J.; Theisen, W.; Thiele, M.; Esen, C.; Edelmann, A.; Hellmann, R. Microstructure and mechanical properties of 316L austenitic stainless steel processed by different SLM devices. Int. J. Adv. Manuf. Technol. 2020, 108, 769–783. [Google Scholar] [CrossRef]
- Karolewska, K.; Ligaj, B.; Wirwicki, M.; Szala, G. Strength analysis of Ti6Al4V titanium alloy produced by the use of additive manufacturing method under static load conditions. J. Mater. Res. Technol. 2020, 9, 1365–1379. [Google Scholar] [CrossRef]
- Leuders, S.; Thöne, M.; Riemer, A.; Niendorf, T.; Troster, T.; Richard, H.; Maier, H. On the mechanical behaviour of titanium alloy TiAl6V4 manufactured by selective laser melting: Fatigue resistance and crack growth performance. Int. J. Fatigue 2013, 48, 300–307. [Google Scholar] [CrossRef]
- Mazur, M.; Leary, M.; Sun, S.; Vcelka, M.; Shidid, D.; Brandt, M. Deformation and failure behaviour of Ti-6Al-4V lattice structures manufactured by selective laser melting. Int. J. Adv. Manuf. Technol. 2016, 84, 1391–1411. [Google Scholar] [CrossRef]
- Niendorf, T.; Brenne, F.; Maier, H.J. Damage evolution in truss structures manufactured by selective laser melting–effect of loading conditions. In Proceedings of the CELLMAT 2012, Dresden, Germany, 7–9 November 2012. [Google Scholar]
- Boniotti, L.; Beretta, S.; Patriarca, L.; Rigoni, L.; Foletti, S. Experimental and numerical investigation on compressive fatigue strength of lattice structures of AlSi7Mg manufactured by SLM. Int. J. Fatigue 2019, 128, 105181. [Google Scholar] [CrossRef]
- Rehme, O. Cellular Design for Laser Freeform Fabrication, 1st ed.; Vol. v.4 of Schriftenreihe Lasertechnik; Cuvillier Verlag: Göttingen, Germany, 2010. [Google Scholar]
- Merkt, S.; Klocke, F. Qualifizierung von Generativ Gefertigten Gitterstrukturen für maßgeschneiderte Bauteilfunktionen; RWTH Aachen: Aachen, Germany, 2015. [Google Scholar]
- Said, J.M.; Ismail, M.H.; Abidin, N.A.Z.; Haris, N.A.; Roslan, A.N.M. Additive Manufacturing of 316L Stainless Steel. Int. J. Recent Technol. Eng. 2019, 8, 6825–6829. [Google Scholar] [CrossRef]
- Olakanmi, E. Selective laser sintering/melting (SLS/SLM) of pure Al, Al–Mg, and Al–Si powders: Effect of processing conditions and powder properties. J. Mater. Process. Technol. 2013, 213, 1387–1405. [Google Scholar] [CrossRef]
- Reu, P.L.; Sweatt, W.; Miller, T.; Fleming, D. Camera System Resolution and its Influence on Digital Image Correlation. Exp. Mech. 2014, 55, 9–25. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D. Fundamentals of Solidification; Trans Tech Publ. Ltd.: Weinheim, Germany, 1998. [Google Scholar] [CrossRef]
- Gäumann, M.; Henry, S.; Cléton, F.; Wagnière, J.-D.; Kurz, W. Epitaxial laser metal forming: Analysis of microstructure formation. Mater. Sci. Eng. A 1999, 271, 232–241. [Google Scholar] [CrossRef]
- Kotzem, D.; Arold, T.; Niendorf, T.; Walther, F. Damage Tolerance Evaluation of E-PBF-Manufactured Inconel 718 Strut Geometries by Advanced Characterization Techniques. Materials 2020, 13, 247. [Google Scholar] [CrossRef]
- Takata, N.; Kodaira, H.; Suzuki, A.; Kobashi, M. Size dependence of microstructure of AlSi10Mg alloy fabricated by selective laser melting. Mater. Charact. 2018, 143, 18–26. [Google Scholar] [CrossRef]








| 316L | Fe | Cr | Ni | Mo | C | Si | Mn | |
| Rest | 16.5–18.5 | 10–13 | 2–2.5 | <0.03 | <1 | <2 | ||
| Ti-6Al-4V | Ti | Al | V | Fe | O | C | N | H |
| Rest | 5.5–6.5 | 3.4–4.5 | <0.25 | <0.13 | <0.08 | <0.05 | <0.012 |
| Material/System | Laser Power (W) | Scan Speed (mm·s−1) | Hatch Distance (mm) | Layer Thickness (µm) |
|---|---|---|---|---|
| 316L | 175 | 750 | 0.12 | 30 |
| Ti-6Al-4V | 175 | 710 | 0.12 | 30 |
| Material/System | Laser Power (W) | Scan Speed (mm·s−1) | Hatch Distance (mm) | Layer Thickness (µm) |
|---|---|---|---|---|
| 316L | 175 | 750 | 0.12 | 30 |
| Ti-6Al-4V | 175 | 710 | 0.12 | 30 |
| Material | E (GPa) | ν (−) |
|---|---|---|
| 316L [42] | 210 | 0.30 |
| Ti6Al4V [43] | 110 | 0.31 |
| Material-System | RVE Size a (mm) | Strut Diameter t (mm) | Aspect Ratio AR (−) |
|---|---|---|---|
| 316L-bcc | 1.93 | 0.314 | 6.146 |
| 316L-f2ccz | 1.81 | 0.371 | 4.879 |
| Ti6Al4V-bcc | 2.06 | 0.424 | 4.858 |
| Ti6Al4V–f2ccz | 2.04 | 0.399 | 5.113 |
| Material-System | ||
|---|---|---|
| 316L-bcc | 367 | 2.38 |
| 316L-f2ccz | 8849 | 20.51 |
| Ti6Al4V-bcc | 463 | 4.75 |
| Ti6Al4V-f2ccz | 4150 | 18.36 |
| Material-System | (%) | ||
|---|---|---|---|
| 316L-bcc | 339 | 367 | −7.6 |
| 316L-f2ccz | 2824 | 8849 | −68.1 |
| Ti6Al4V-bcc | 542 | 463 | 17.1 |
| Ti6Al4V-bcc-HT | 504 | 8.9 | |
| Ti6Al4V-f2ccz | 3296 | 4150 | −20.6 |
| Ti6Al4V-f2ccz-HT | 3113 | −25.0 |
| Material-System | ||||
|---|---|---|---|---|
| 316L-bcc | 285 | 28.8 | 467 | −21.4 |
| 316L-f2ccz | 7724 | 14.6 | 10,093 | −12.3 |
| Ti6Al4V-bcc | 383 | 20.9 | 556 | −16.7 |
| Ti6Al4V-f2ccz | 3665 | 13.2 | 4683 | −11.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meyer, G.; Brenne, F.; Niendorf, T.; Mittelstedt, C. Influence of the Miniaturisation Effect on the Effective Stiffness of Lattice Structures in Additive Manufacturing. Metals 2020, 10, 1442. https://doi.org/10.3390/met10111442
Meyer G, Brenne F, Niendorf T, Mittelstedt C. Influence of the Miniaturisation Effect on the Effective Stiffness of Lattice Structures in Additive Manufacturing. Metals. 2020; 10(11):1442. https://doi.org/10.3390/met10111442
Chicago/Turabian StyleMeyer, Guillaume, Florian Brenne, Thomas Niendorf, and Christian Mittelstedt. 2020. "Influence of the Miniaturisation Effect on the Effective Stiffness of Lattice Structures in Additive Manufacturing" Metals 10, no. 11: 1442. https://doi.org/10.3390/met10111442
APA StyleMeyer, G., Brenne, F., Niendorf, T., & Mittelstedt, C. (2020). Influence of the Miniaturisation Effect on the Effective Stiffness of Lattice Structures in Additive Manufacturing. Metals, 10(11), 1442. https://doi.org/10.3390/met10111442







