Movable Die and Loading Path Design in Tube Hydroforming of Irregular Bellows
Abstract
:1. Introduction
2. Movable Die Design and Loading Path Definition
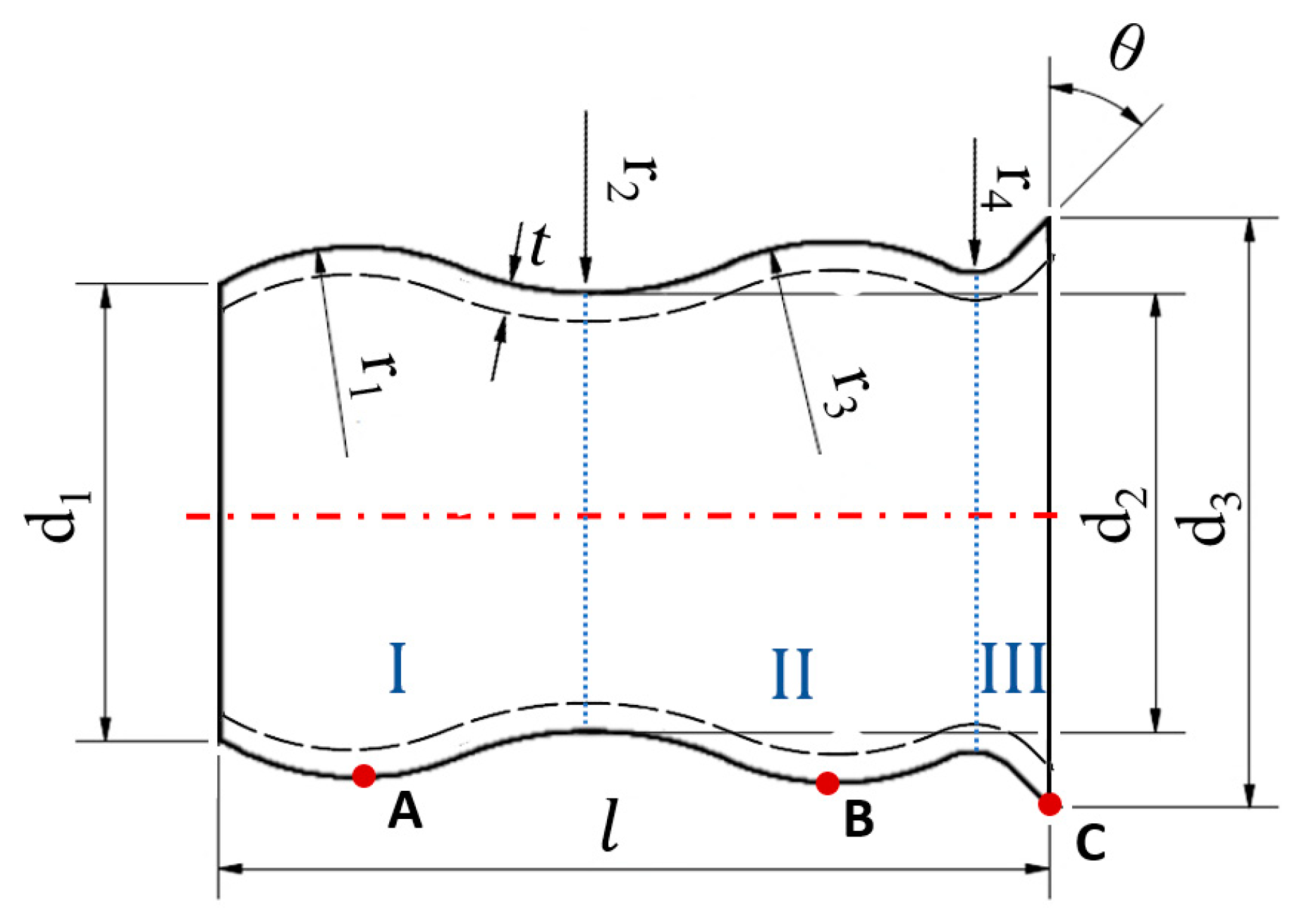
2.1. Shape and Geometry
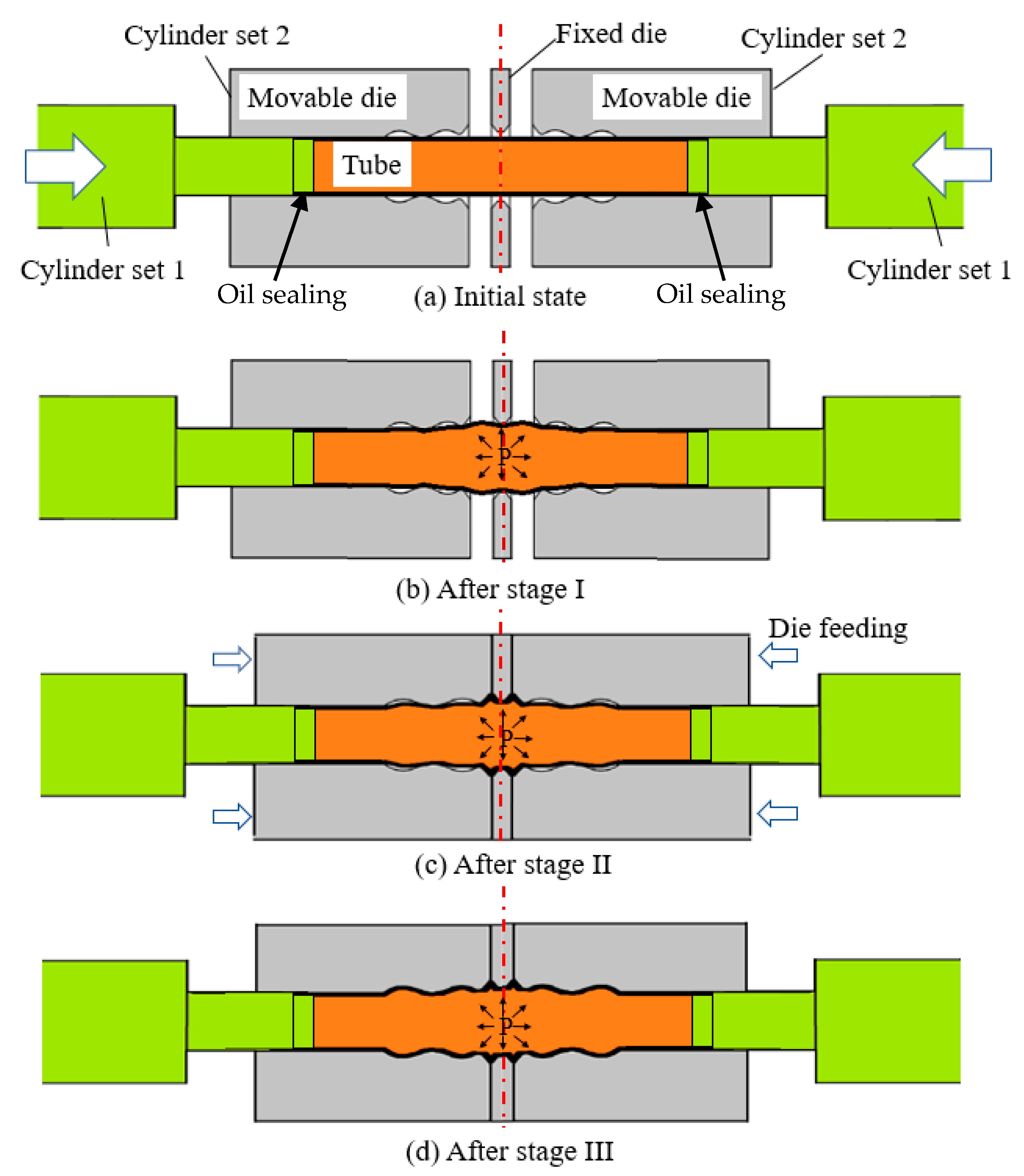
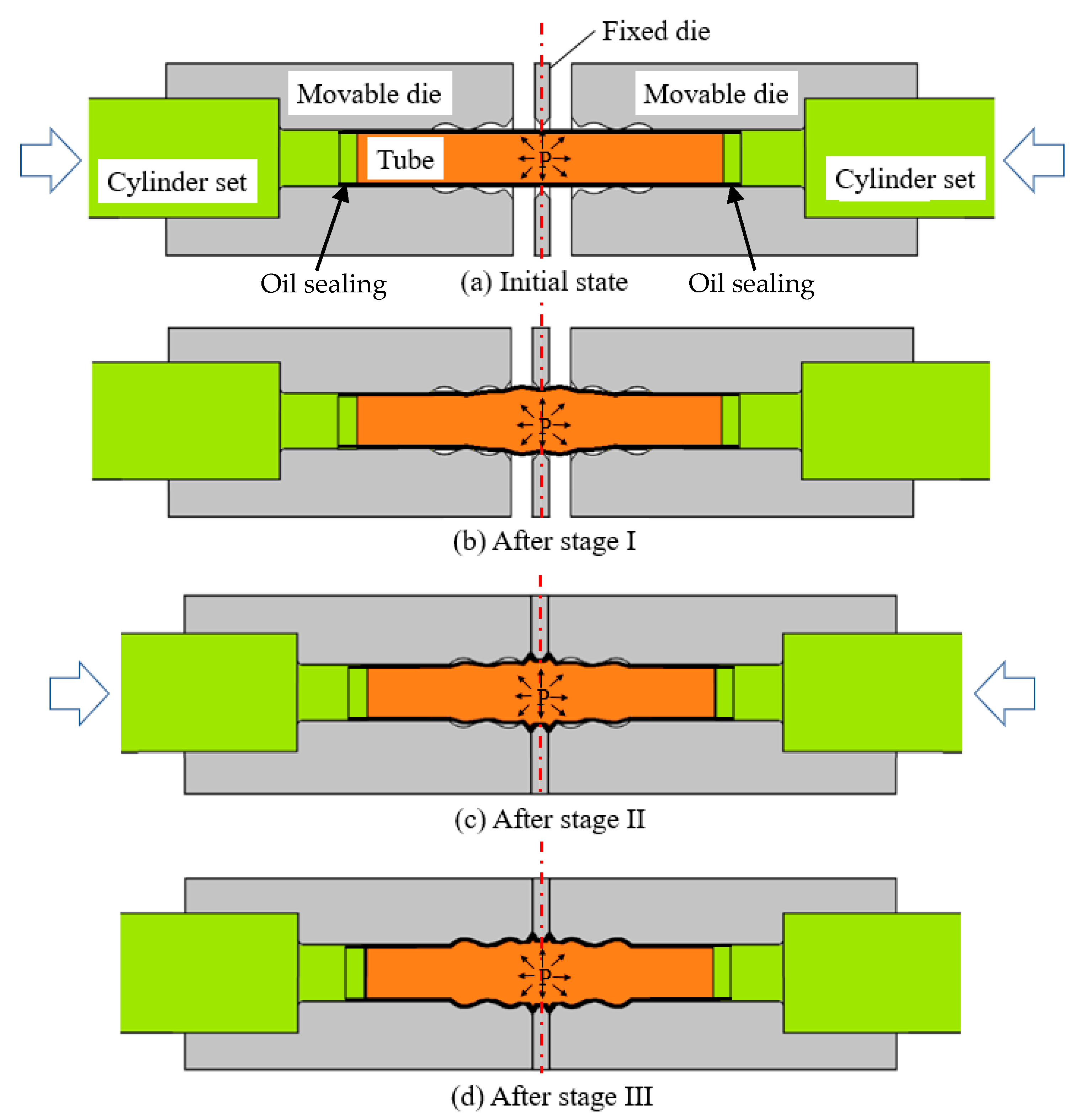
2.2. Movable Die Design
2.3. Movable Die Feeding Types
3. Finite Element Simulations
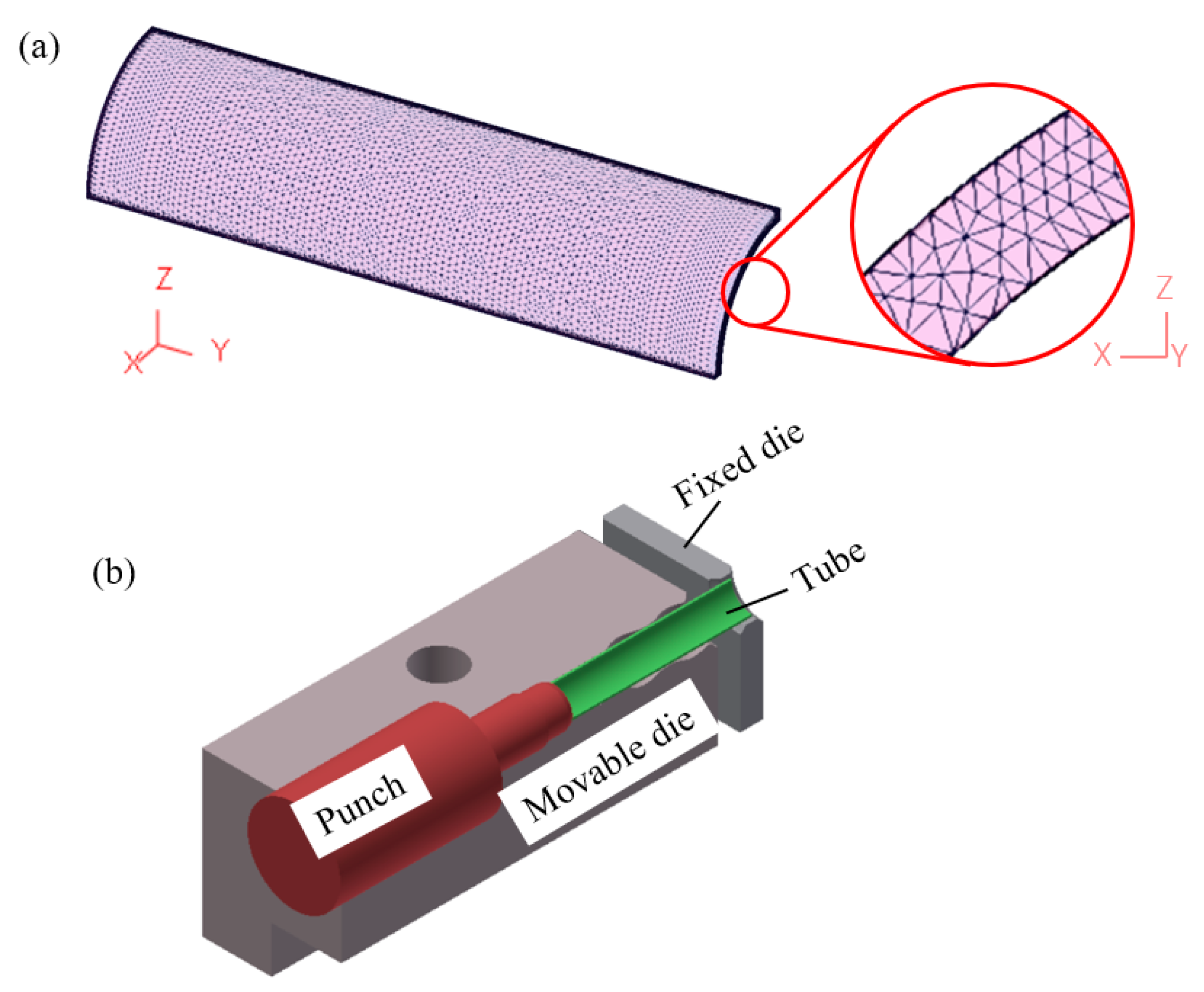
3.1. Finite Element Modeling
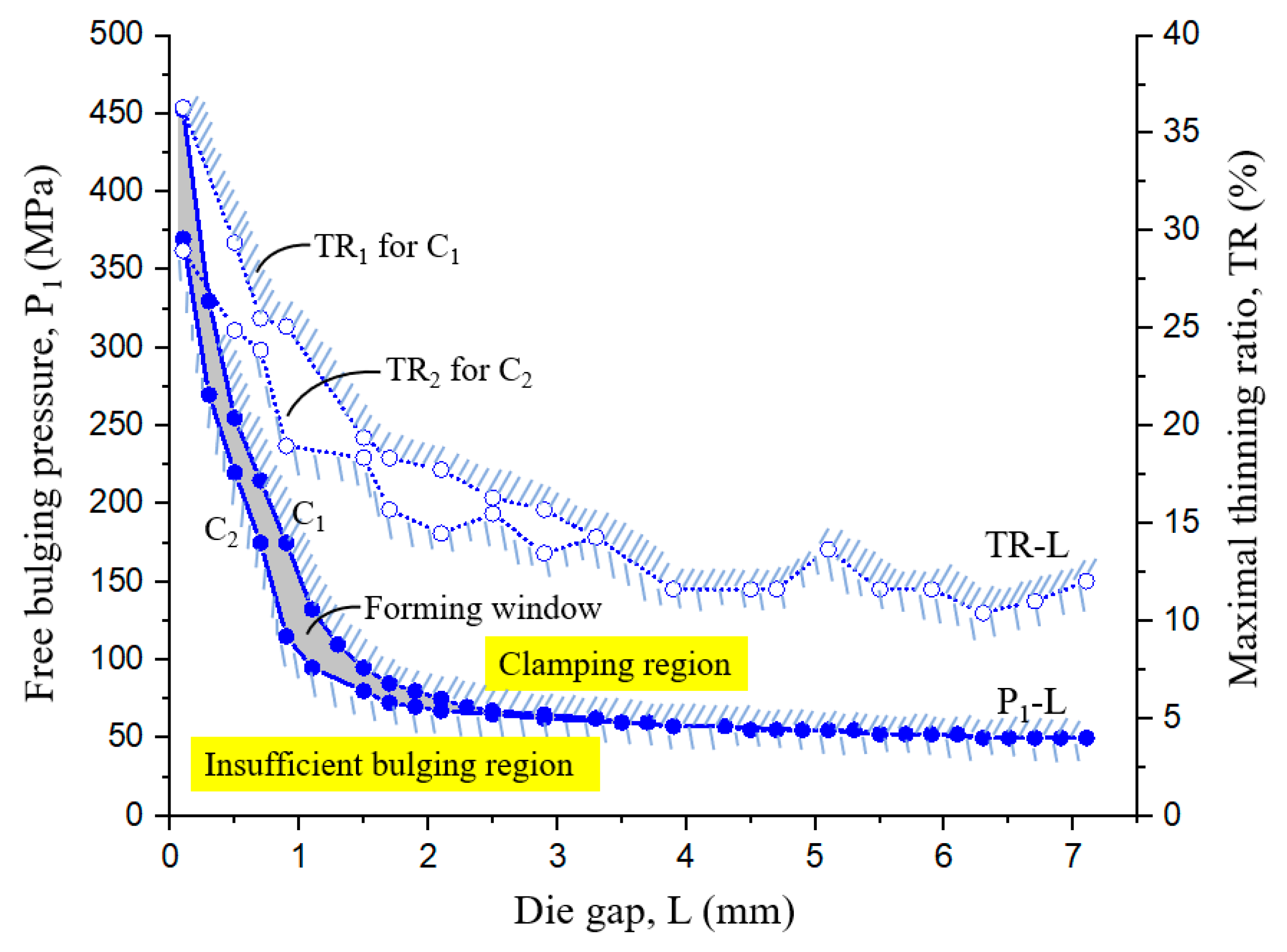
3.2. Forming Windows for Different Feeding Types
3.2.1. Forming Windows for Feeding Type 1
3.2.2. Forming Windows for Feeding Type 2
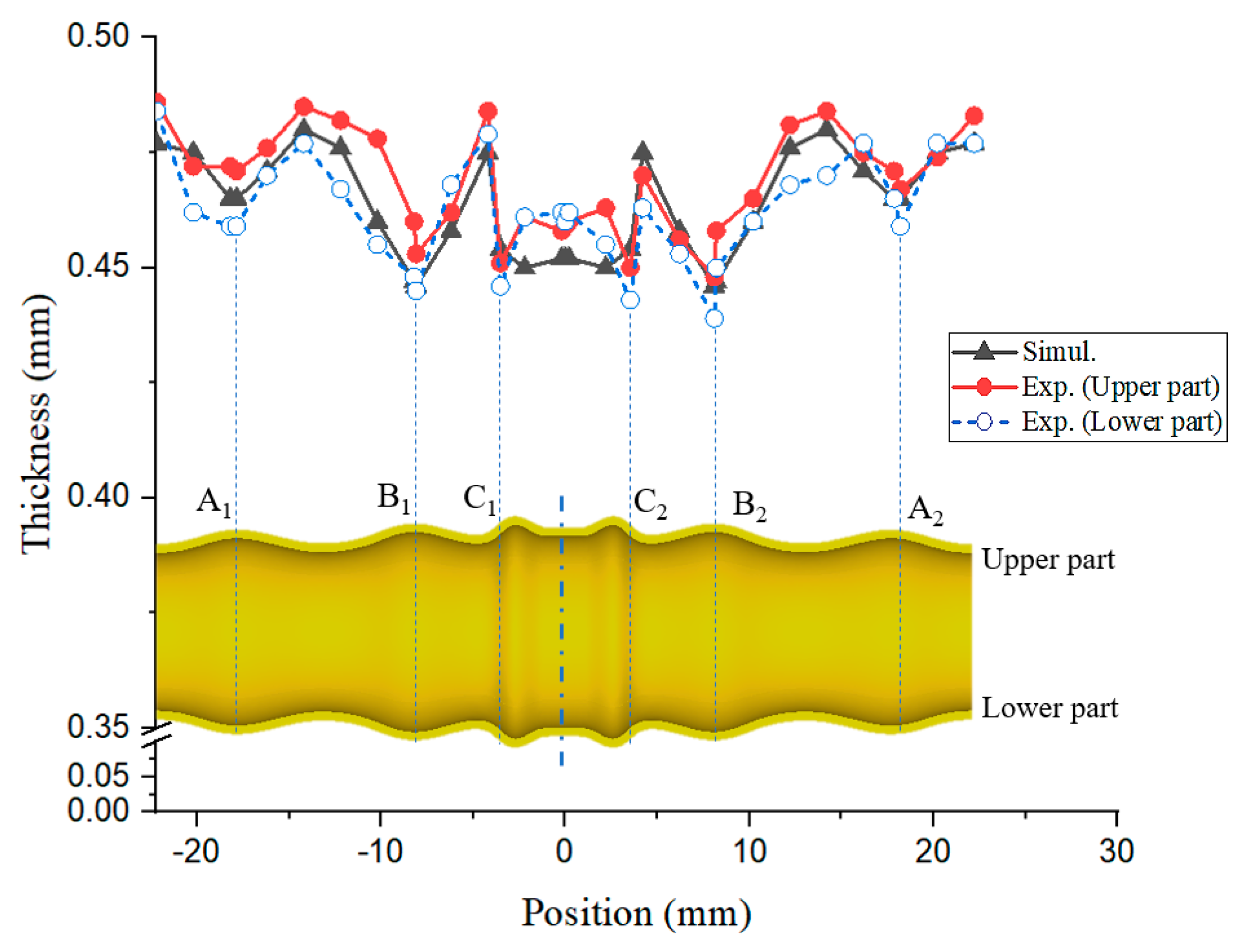
4. Tube Hydroforming Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahmetoglu, M.; Altan, T. Tube hydroforming: State-of-the-art and future trends. J. Mater. Process. Technol. 2000, 98, 25–33. [Google Scholar] [CrossRef]
- Kang, B.H.; Lee, H.Y.; Shon, S.M.; Moon, Y.H. Forming various shapes of tubular bellows using a single-step hydroforming process. J. Mater. Process. Technol. 2007, 194, 1–6. [Google Scholar] [CrossRef]
- Faraji, G.H.; Mosavi Mashhadi, M.; Norouzifard, V. Evaluation of effective parameters in metal bellows forming process. J. Mater. Process. Technol. 2009, 209, 3431–3437. [Google Scholar] [CrossRef]
- Lee, S.W. Study on the forming parameters of the metal bellows. J. Mater. Process. Technol. 2002, 130–131, 47–53. [Google Scholar] [CrossRef]
- Bakhshi-Jooybari, M.; Elyasi, M.; Gorji, A. Numerical and experimental investigation of the effect of the pressure path on forming metallic bellows. J. Eng. Manuf. 2009, 224, 95–101. [Google Scholar] [CrossRef]
- Ngaile, G.; Lowrie, J. Punch design for floating based micro-tube hydroforming die assembly. J. Mater. Process. Technol. 2018, 253, 168–177. [Google Scholar] [CrossRef]
- Shinde, R.A.; Patil, B.T.; Joshi, K.N. Optimization of Tube Hydroforming Process (without Axial feed) by using FEA Simulations. In Proceedings of the 3rd International Conference on Innovations in Automation and Mechatronics Engineering, Vallabh Vidhyanagar, India, 5–6 February 2016; pp. 398–405. [Google Scholar]
- Elyasi, M.; Bakhshi-Jooybari, M.; Gorji, A.; Hosseinipour, S.J.; Nourouzi, S. New die design for improvement of die corner filling in hydroforming of cylindrical stepped tubes. J. Eng. Manuf. 2009, 223, 821–827. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, C.D.; Zhao, S.D. Numerical simulation on hydroforming tube-like eccentric shaft part by using movable die. In Proceedings of the 5th International Conference on Tube Hydroforming, Hokkaido, Japan, 24–27 July 2011; pp. 149–152. [Google Scholar]
- Tomizawa, A.; Kubota, H.; Kurokawa, H.; Kojima, M. Development of tube hydroforming technology using axial movable dies. JSTP 2015, 56, 40–46. [Google Scholar] [CrossRef] [Green Version]
- Hwang, Y.M.; Chen, Y.C. Study of compound hydroforming of profiled tubes. Procedia Eng. 2017, 207, 2328–2333. [Google Scholar] [CrossRef]
- Hwang, Y.M.; Hsieh, S.Y.; Kuo, N.J. Study of large-expansion-ratio tube hydroforming with movable dies. Key Eng. Mater. 2016, 725, 616–622. [Google Scholar] [CrossRef]
- Yuan, S.J.; Wang, X.S.; Liu, G.; Wang, Z.R. Control and use of wrinkles in tube hydroforming. J. Mater. Process. Tchnol. 2007, 182, 6–11. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, S.H.; Cheng, M.; Song, H.W.; Zhang, X.S. Application of pulsating hydroforming in manufacture of engine. Procedia Eng. 2014, 81, 2205–2210. [Google Scholar] [CrossRef] [Green Version]
- Imaninejad, M.; Subhash, G.; Loukus, A. Loading path optimization of tube hydroforming process. Int. J. Mach. Tools Manuf. 2005, 45, 1504–1514. [Google Scholar] [CrossRef]
- Hama, T.; Ohkubo, T.; Kurisu, K.; Fujimoto, H.; Takuda, H. Formability of tube hydroforming under various loading paths. J. Mater. Process. Technol. 2006, 177, 676–679. [Google Scholar] [CrossRef]
- Liu, G.; Yuan, S.; Teng, B. Analysis of thinning at the transition corner in tube hydroforming. J. Mater. Process. Technol. 2006, 177, 688–691. [Google Scholar] [CrossRef]










| Material | SUS321 |
|---|---|
| Young’s modulus (GPa) | 178 |
| Yield stress (MPa) | 403 |
| Flow stress (MPa) | σ = 403 + 1270 ε0.66 |
| Poisson’s ratio | 0.33 |
| Tube outer diameter, do (mm) | 9.53 |
| Tube thickness, t0 (mm) | 0.49 |
| Punch velocity (mm/s) | 0.1 |
| Movable die velocity (mm/s) | 0.1 |
| Friction coefficient | 0.05 |
| Mesh number | 75,000 |
| Mesh layer number in thickness direction | 4 |
| Minimum mesh length (mm) | 0.09 |
| Variables | Values |
|---|---|
| d1 | 10.08 mm |
| d2 | 9.65 mm |
| d3 | 13.25 mm |
| r1 | 5.84 mm |
| r2 | 7.62 mm |
| r3 | 5.94 mm |
| r4 | 1.27 mm |
| 18.33 mm | |
| 45° |
| Experimental Results (mm) | Simulation (mm) | ||
|---|---|---|---|
| Average thickness | tA1 = 0.465 (Deviation = 0%) | tA2 = 0.468 (Deviation = 0.64%) | tA = 0.465 |
| tB1 = 0.449 (Deviation = 0.67%) | tB2 = 0.444 (Deviation = 0.45%) | tB = 0.446 | |
| tC1 = 0.449 (Deviation = 1.11%) | tC2 = 0.447 (Deviation = 1.57%) | tC = 0.454 | |
| Diameter | dA1 = 11.64 (Deviation = 4.47%) | dA2 = 11.64 (Deviation = 4.47%) | dA = 11.12 |
| dB1 = 11.84 (Deviation = 0.42%) | dB2 = 11.84 (Deviation = 0.42%) | dB = 11.79 | |
| dC1 = 13.40 (Deviation = 5.31%) | dC2 = 13.45 (Deviation = 5.28%) | dC = 12.74 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, Y.-M.; Tsai, Y.-J. Movable Die and Loading Path Design in Tube Hydroforming of Irregular Bellows. Metals 2020, 10, 1518. https://doi.org/10.3390/met10111518
Hwang Y-M, Tsai Y-J. Movable Die and Loading Path Design in Tube Hydroforming of Irregular Bellows. Metals. 2020; 10(11):1518. https://doi.org/10.3390/met10111518
Chicago/Turabian StyleHwang, Yeong-Maw, and Yau-Jiun Tsai. 2020. "Movable Die and Loading Path Design in Tube Hydroforming of Irregular Bellows" Metals 10, no. 11: 1518. https://doi.org/10.3390/met10111518





