An Analytical Model for Predicting the Stress Intensity Factor of Single-Hole-Edge Crack in Diffusion Bonding Laminates with Preset Unbonded Area
Abstract
:1. Introduction
2. Experiment
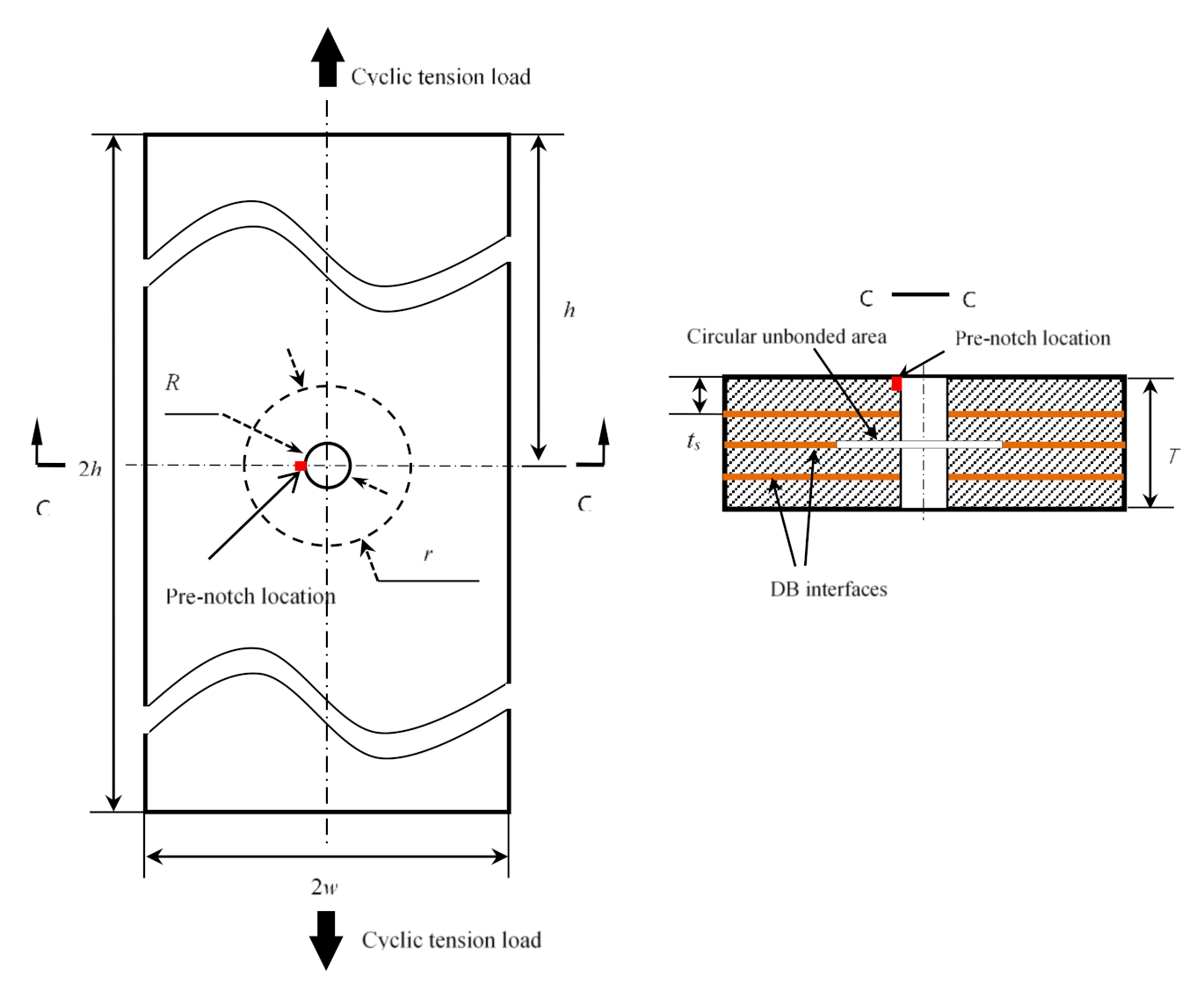
2.1. Specimen
- The Ti-6Al-4V titanium alloy sheets were chosen to make the specimen. In this paper, the sheet thickness is 2 mm. So, each sublaminate of the specimen has a thickness ts = 2 mm.
- The unbonded areas were located at diffusion bonding interface in the specimen. So, we arranged solder mask on the sheet follow the design of the specimen before diffusion bonding process for producing the unbonded areas at the interfaces.
- Four Ti-6Al-4V titanium alloy sheets were utilized to manufacture a titanium alloy laminate using diffusion bonding technology at 900 °C/1.5 MPa/1.5 h. The laminates had a thickness t = 8 mm.
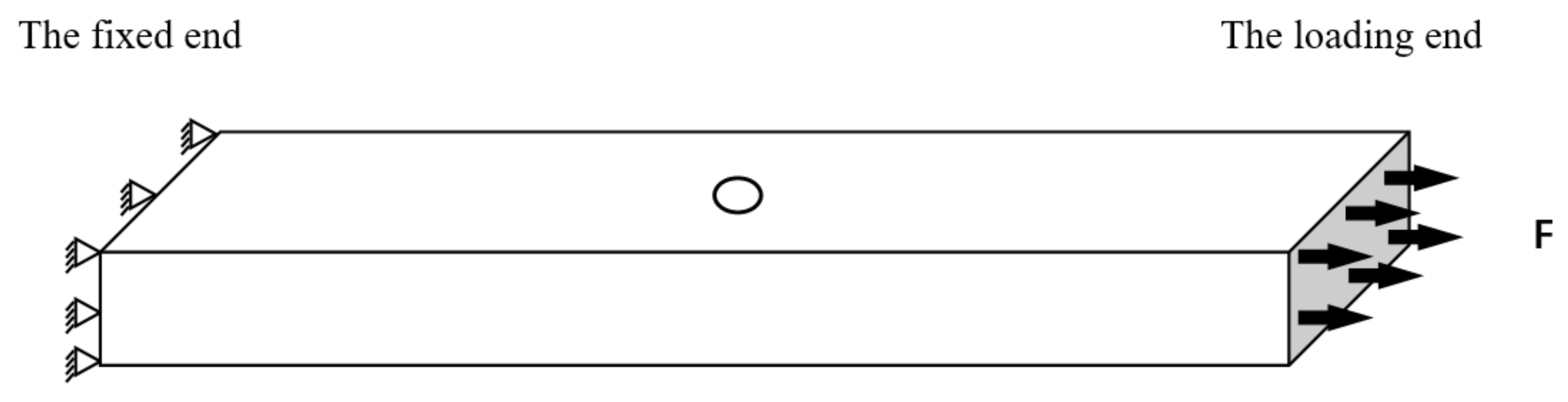
- The laminates were cut into specimens following the design. Moreover, a through thickness hole was drilled at its center for each specimen. The specimen was subjected to a tension–tension cyclic loading, which is a typical load for a bolt joint.
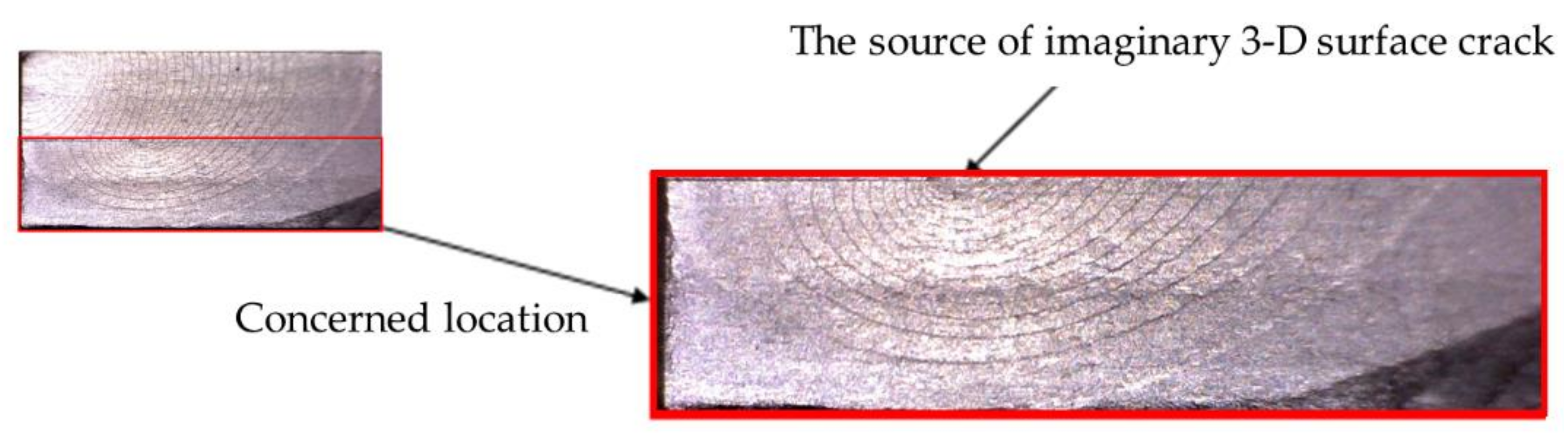
- This study focusses on the fatigue crack growth process, so we made the notch at the single hole edge using electrodischarge machining (EDM), shown in Figure 1.
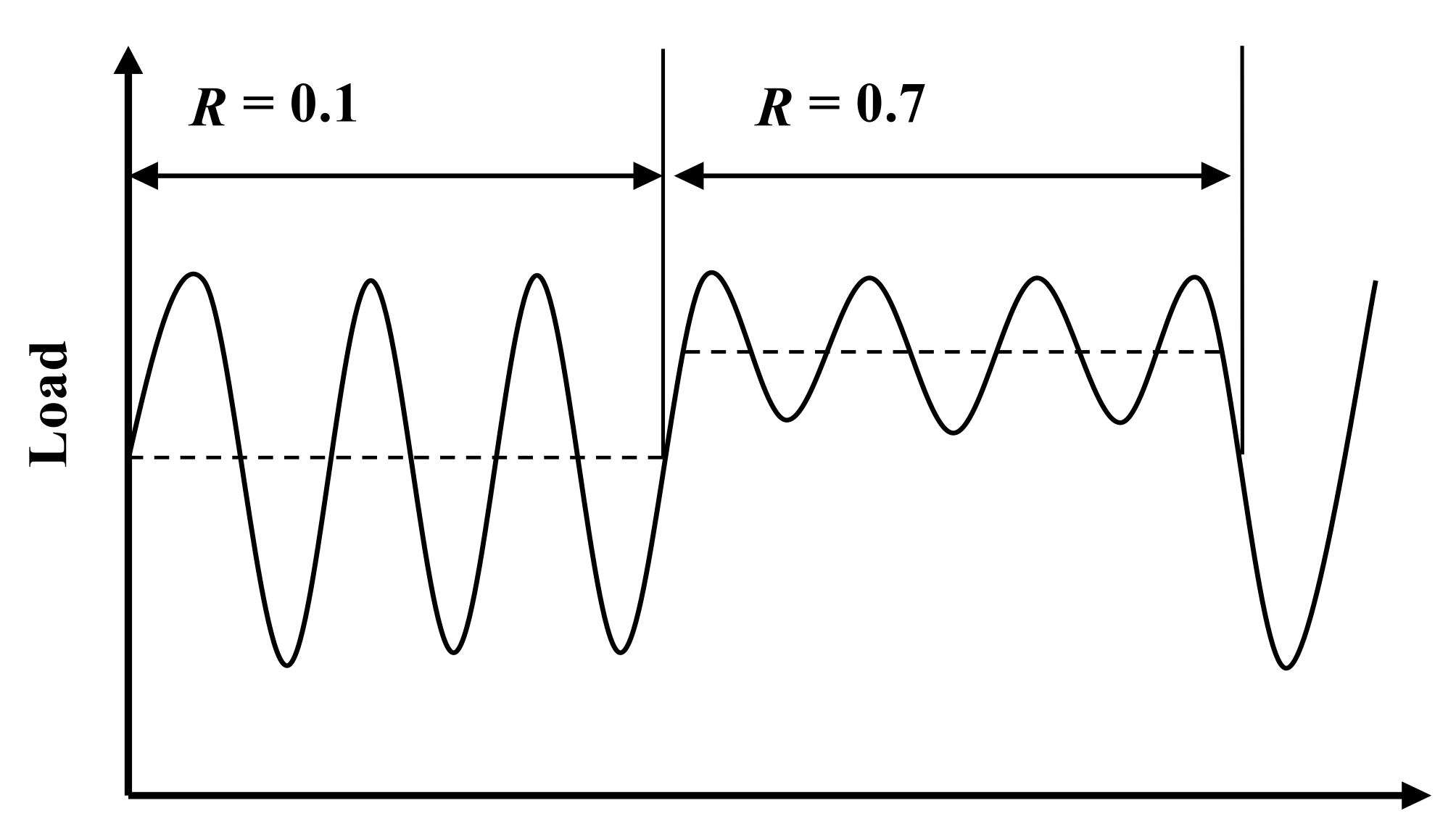
2.2. Test Conditions and Procedures
3. The Stress Intensity Factor (SIF) Formula
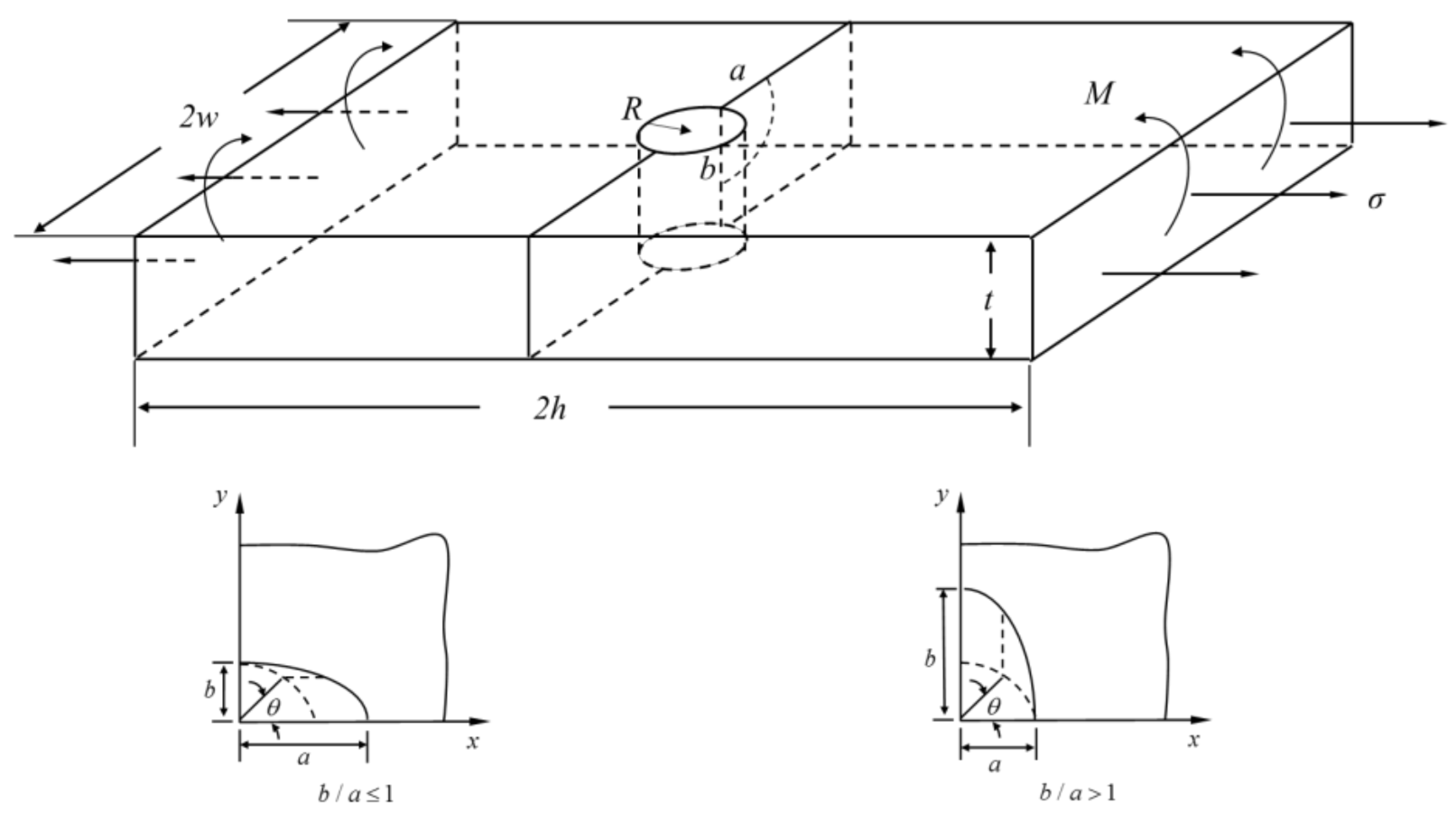
3.1. The Expression of
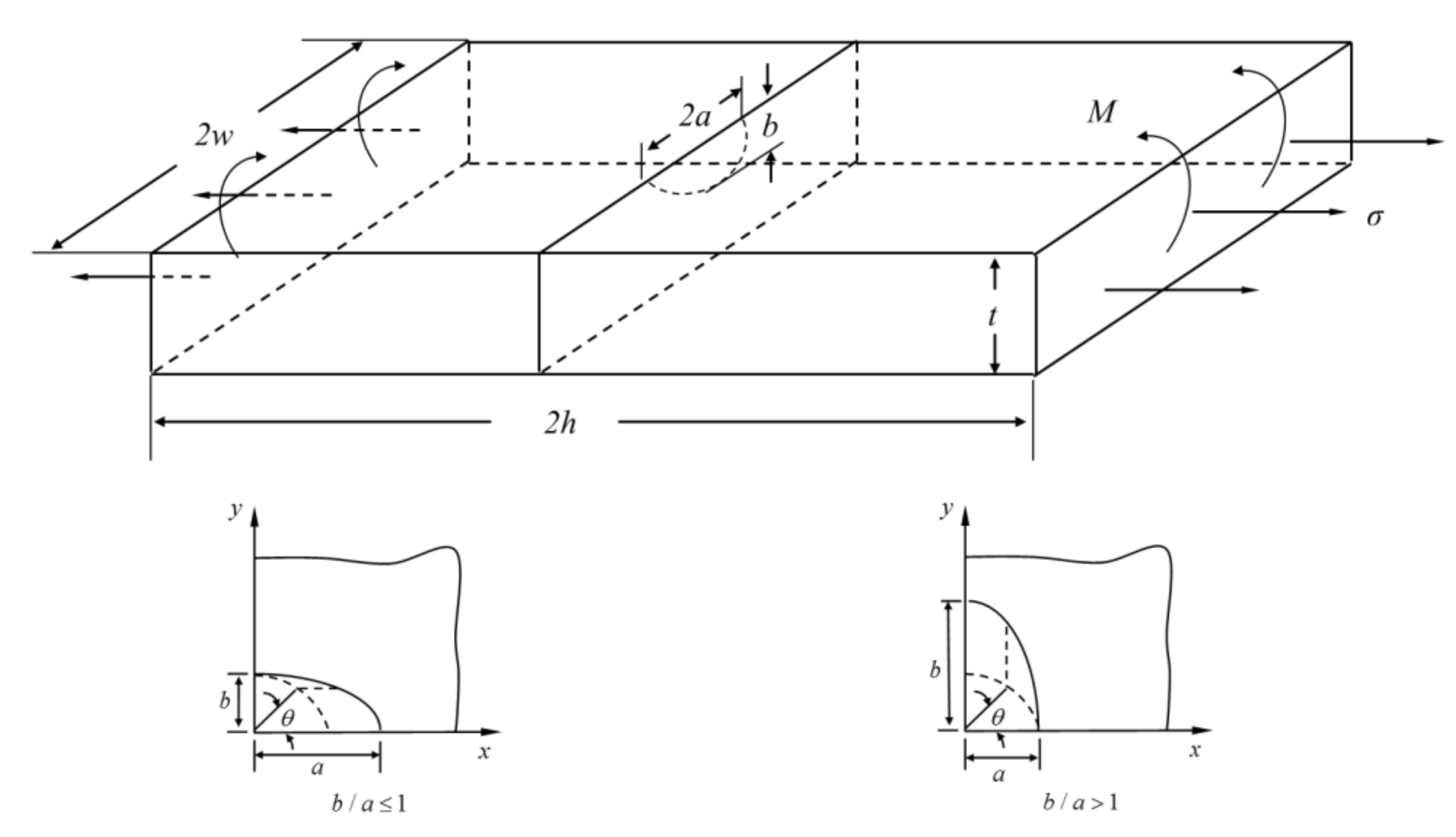
3.2. The Expression of
3.3. The Expression of
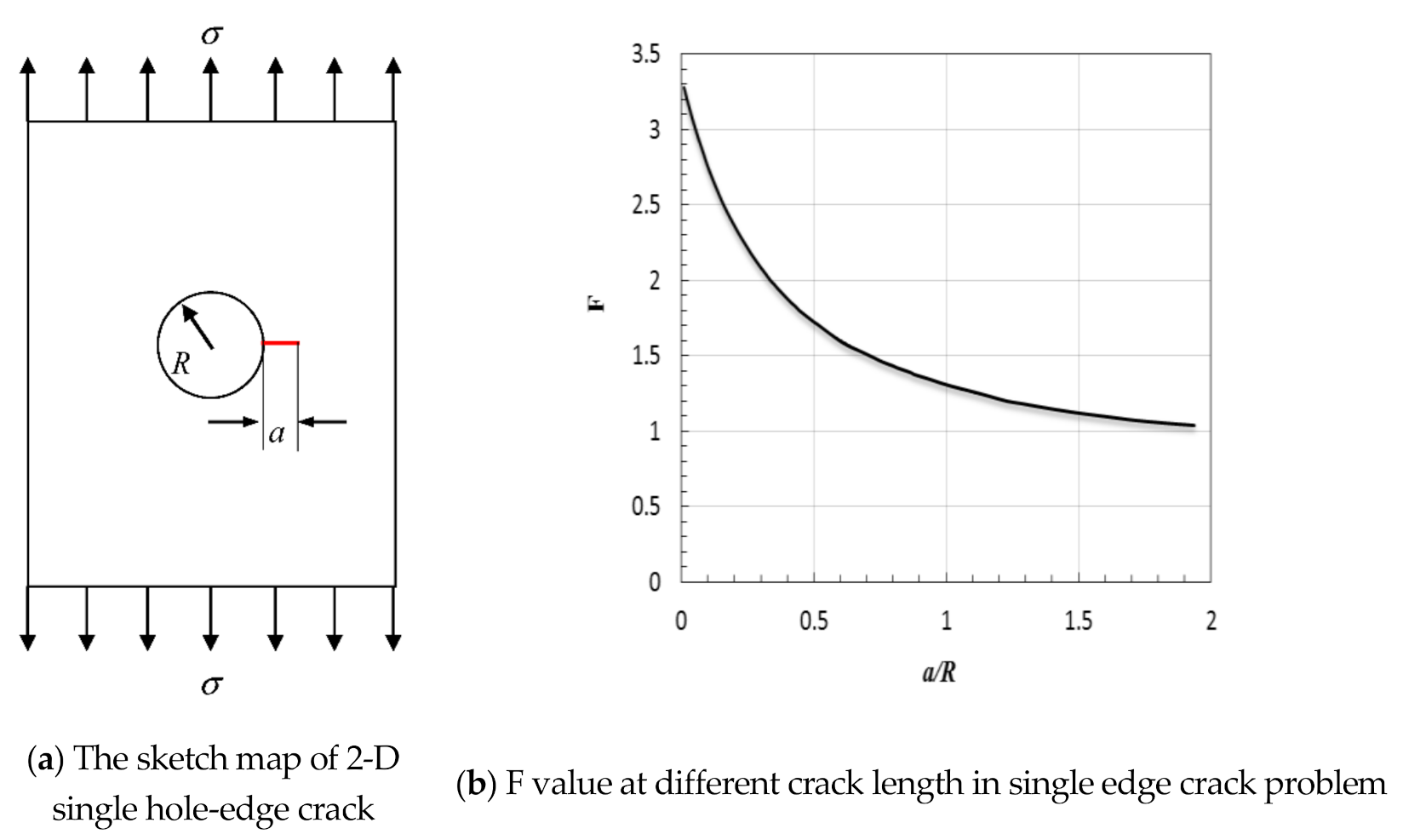
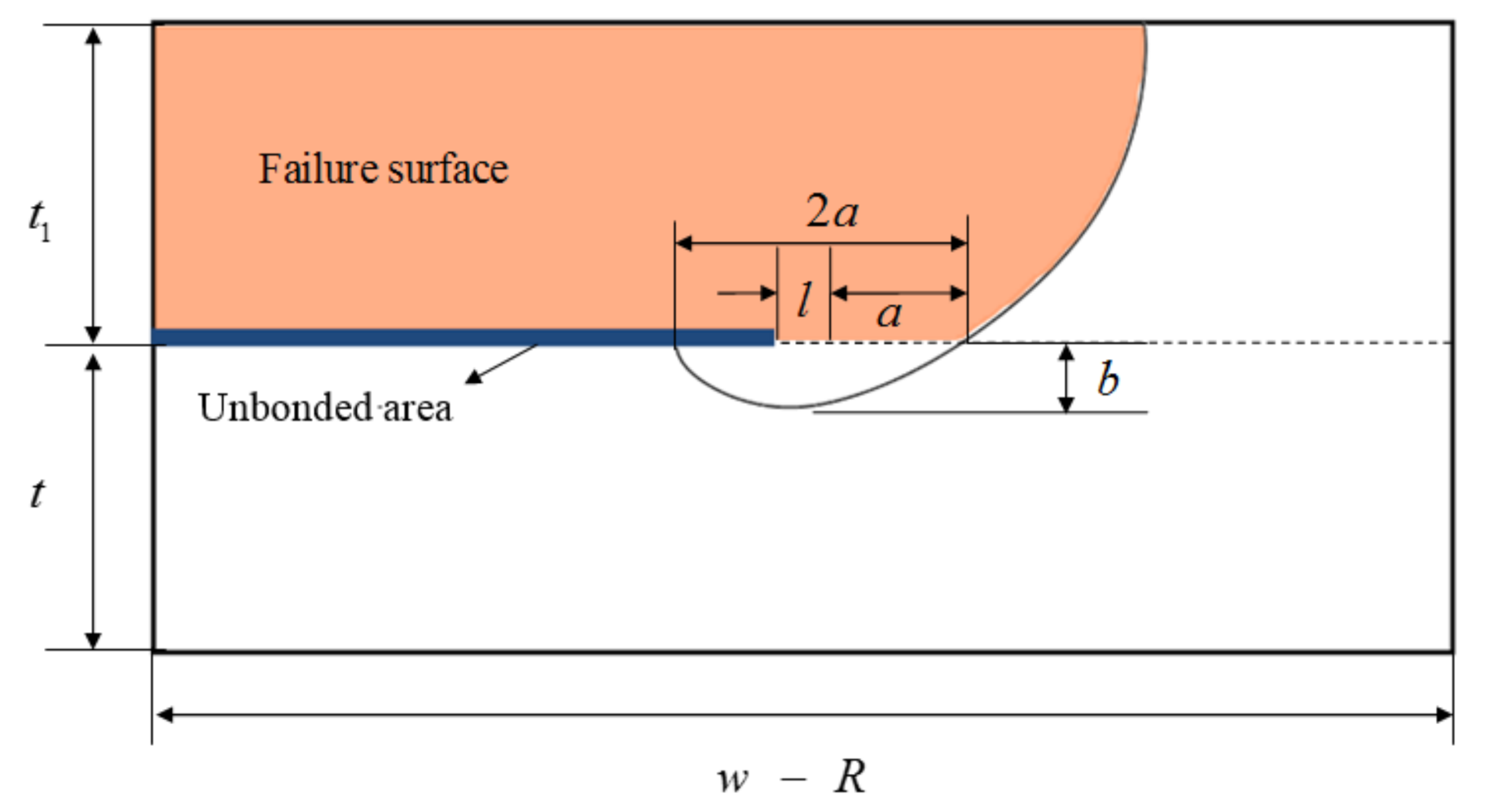
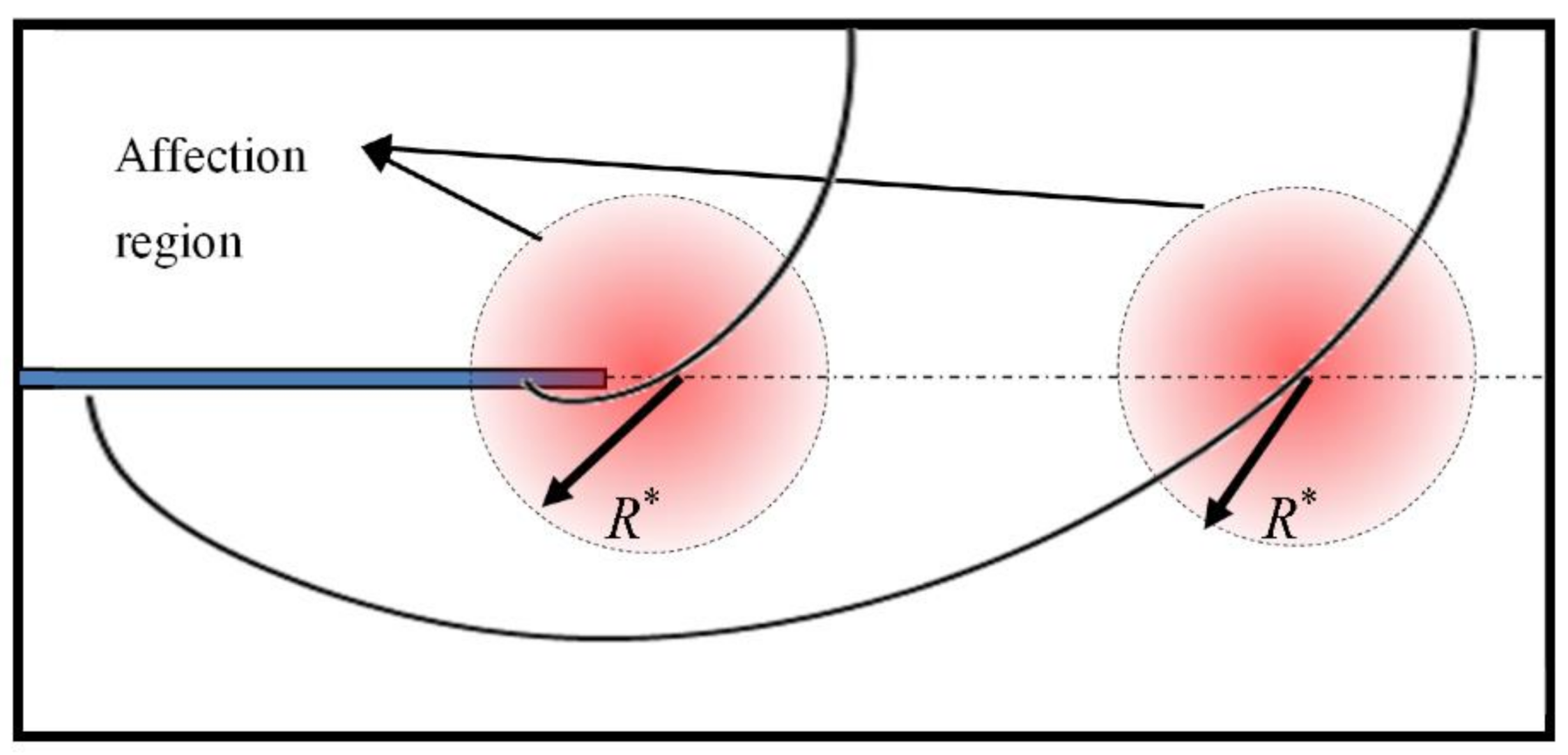
- The laminates in this paper have an open hole, and there is stress concentration near the hole. Formula (8) did not consider the hole, and that needs correction.
- When the crack grows to the third stage, there are already considerable fracture surfaces in the laminates. The tension stress needs correction.
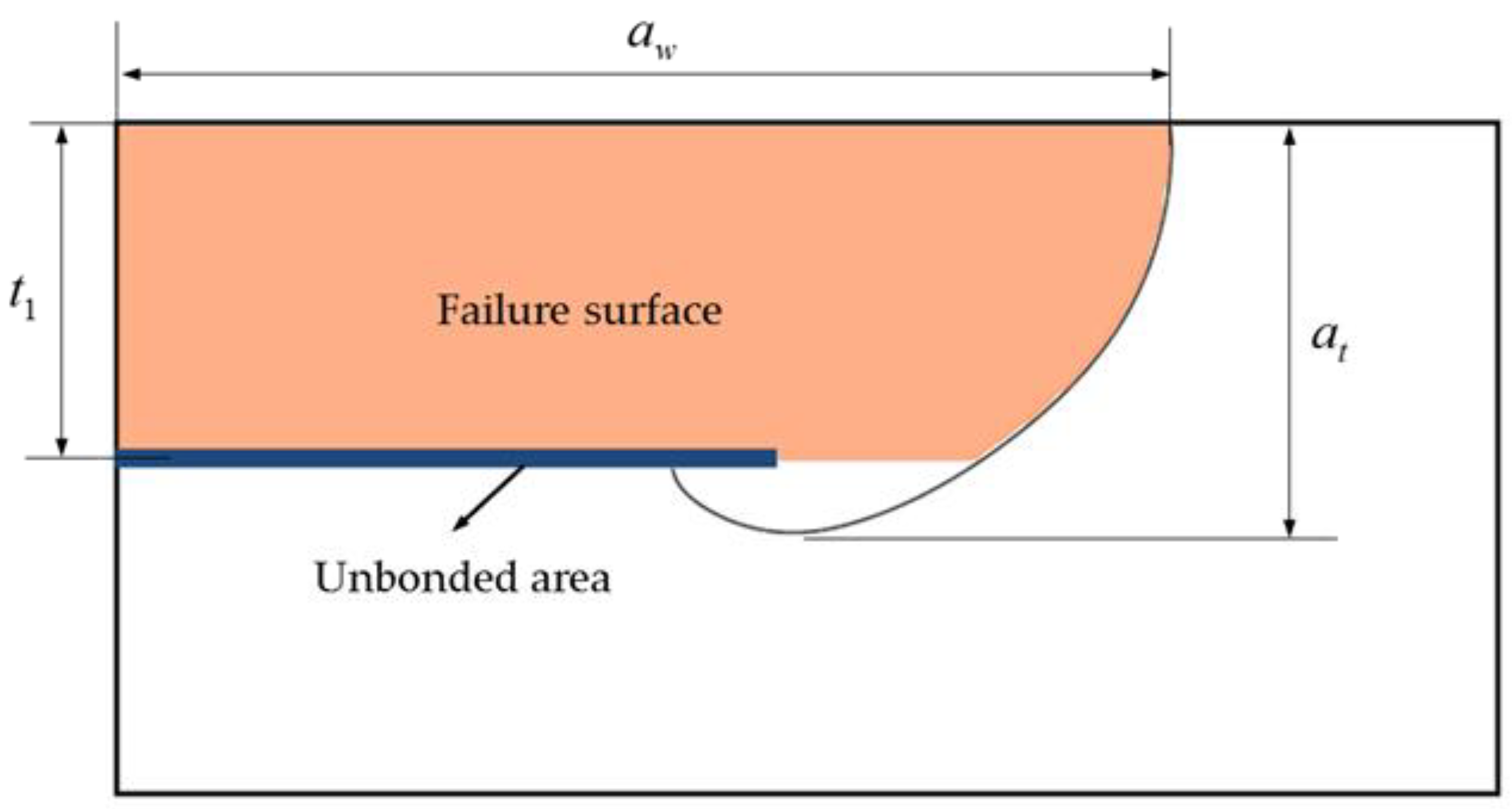
- Though the condition is tension loading in this paper, in the third stage, there is already some fracture surface. The fracture surface caused some eccentric bending moment to the left part. Formula (8) did not consider the additional eccentric bending moment, and that needs correction.
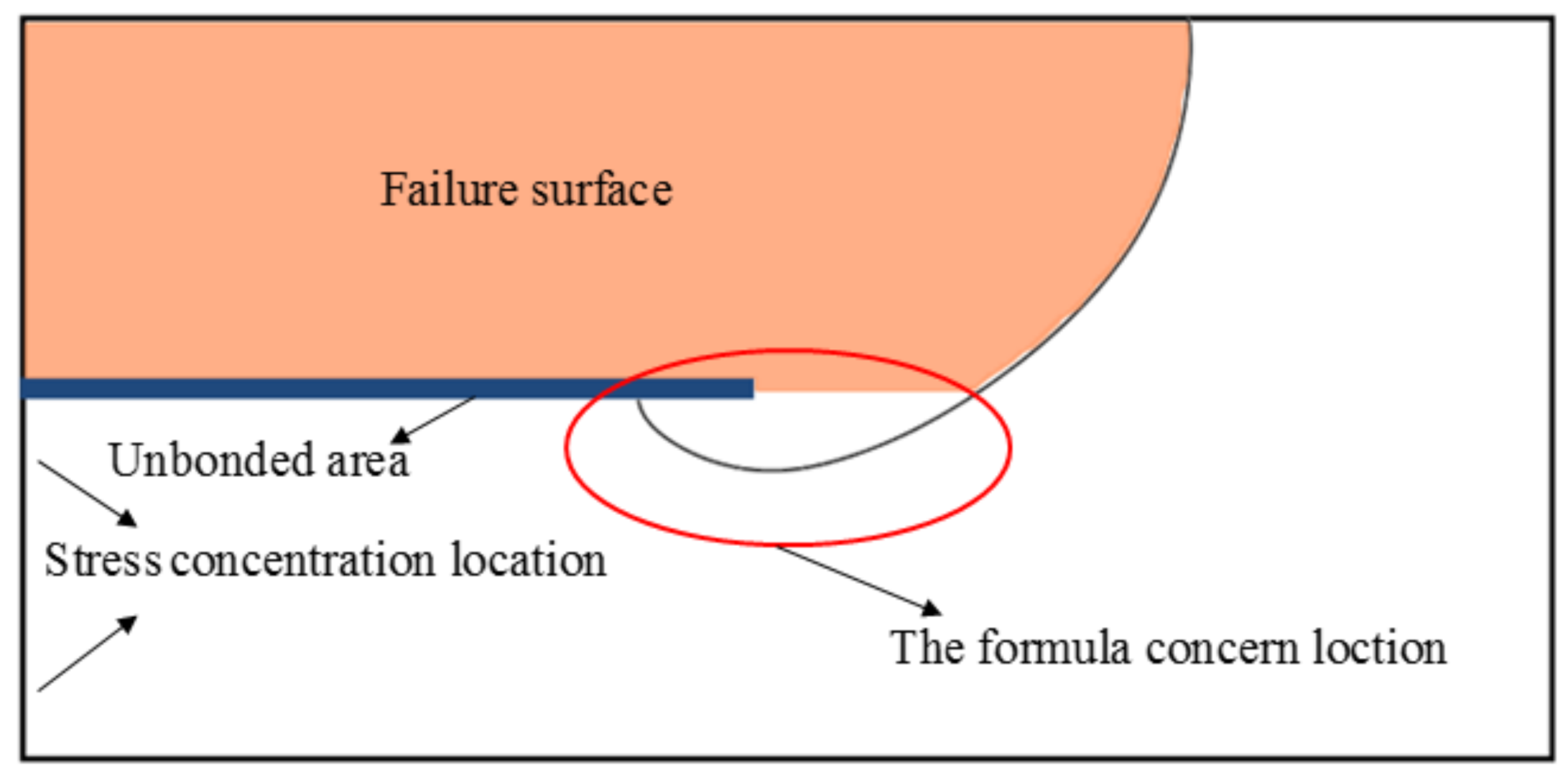
- In Formula (8), the surface of the plate is free surface. However, in DBTALPUA, the side with unbonded area is approximate to a free surface, while the other side of the crack is not a free surface, as shown in Figure 10, and that needs correction.
4. Validation of Formula
4.1. The Trace Line Modeling
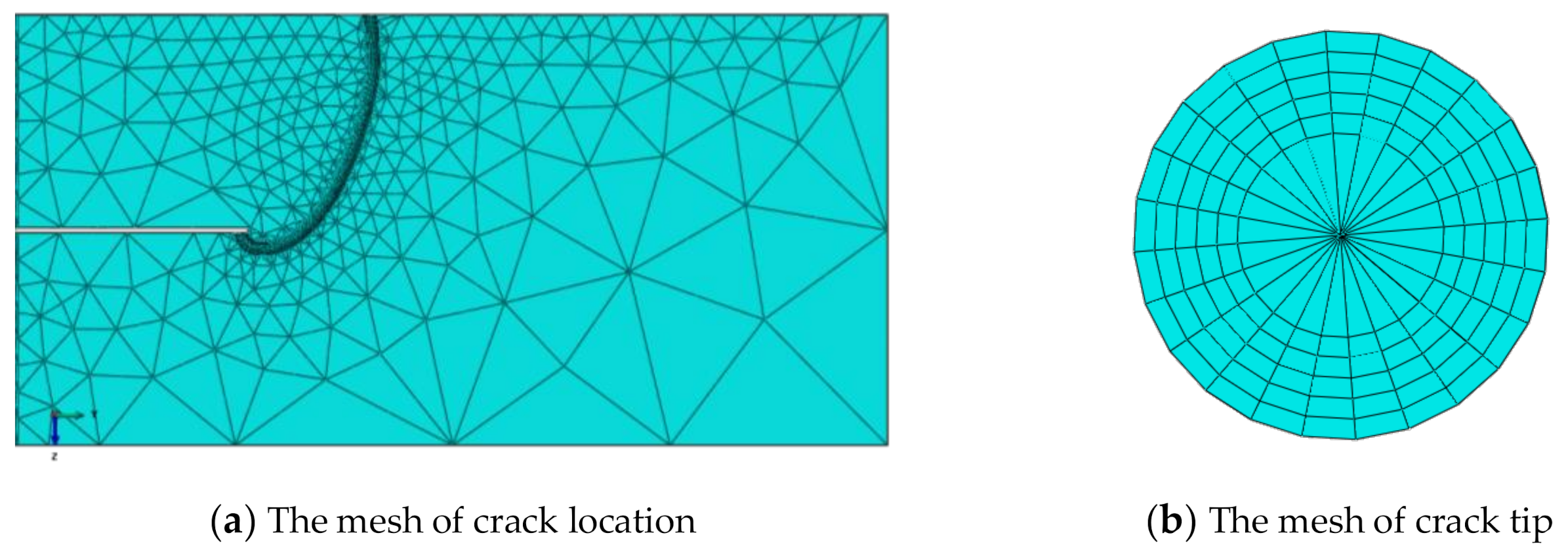
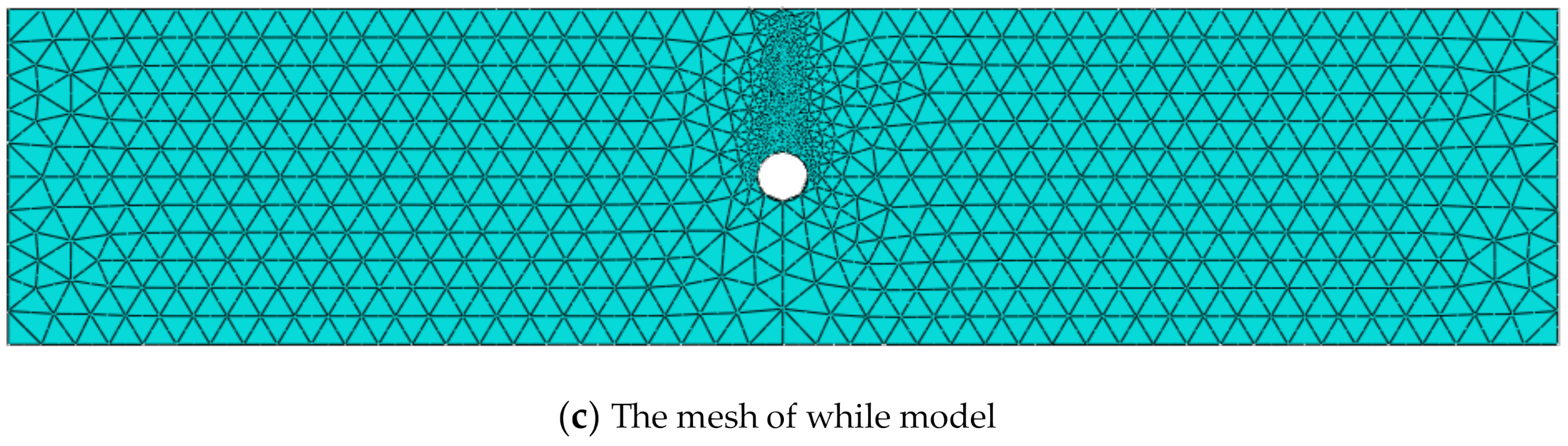
4.2. Finite Element Modeling
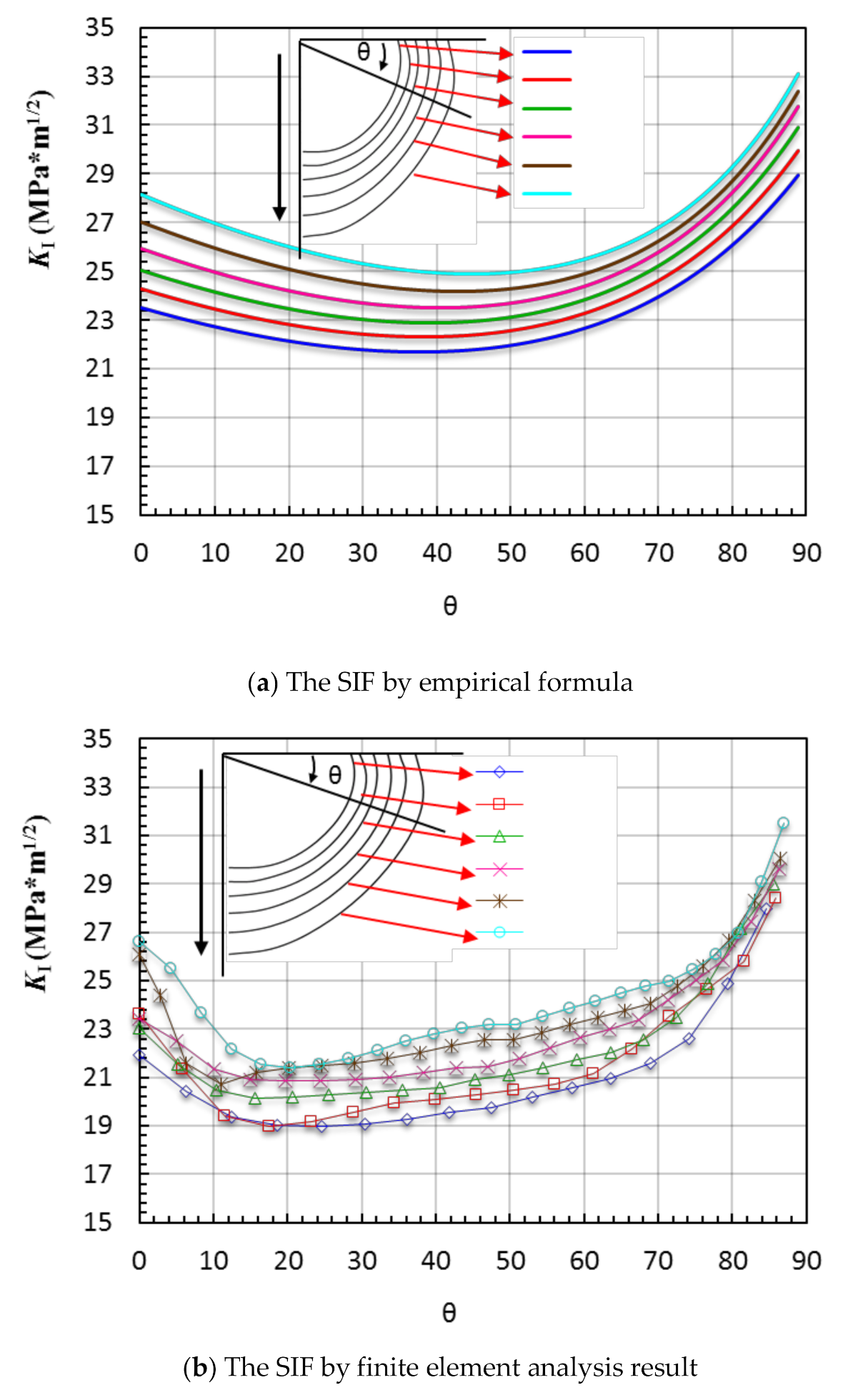
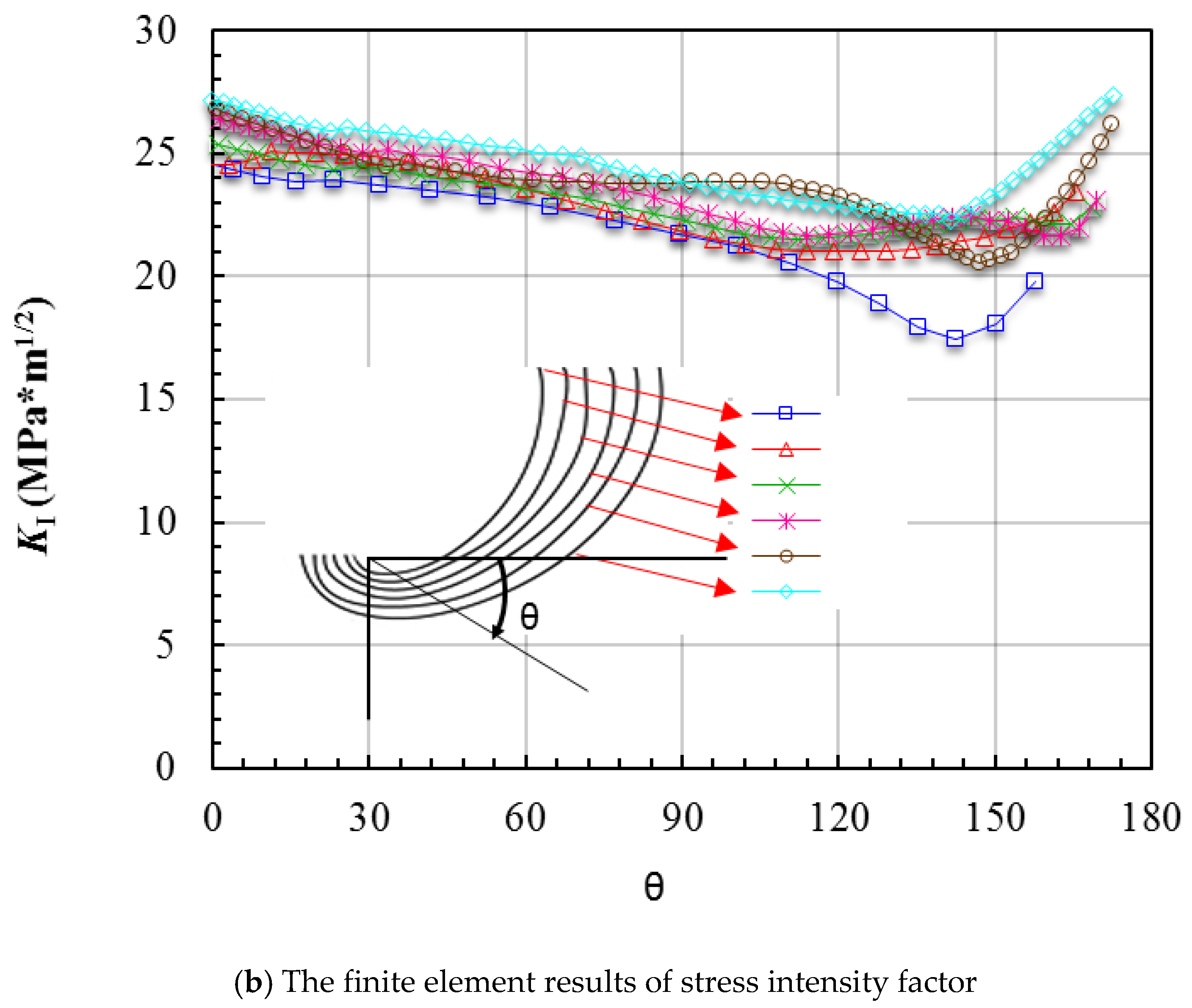
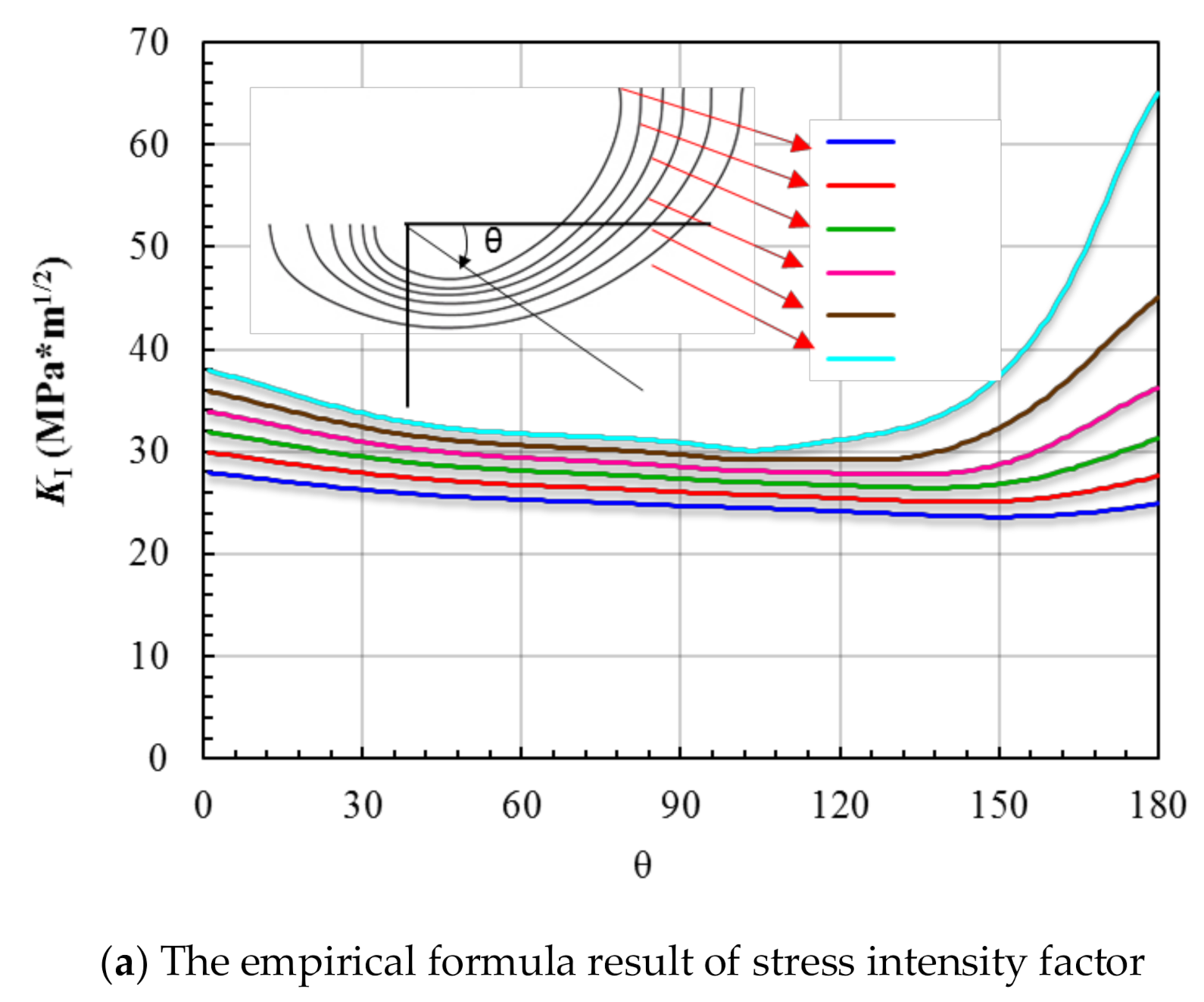
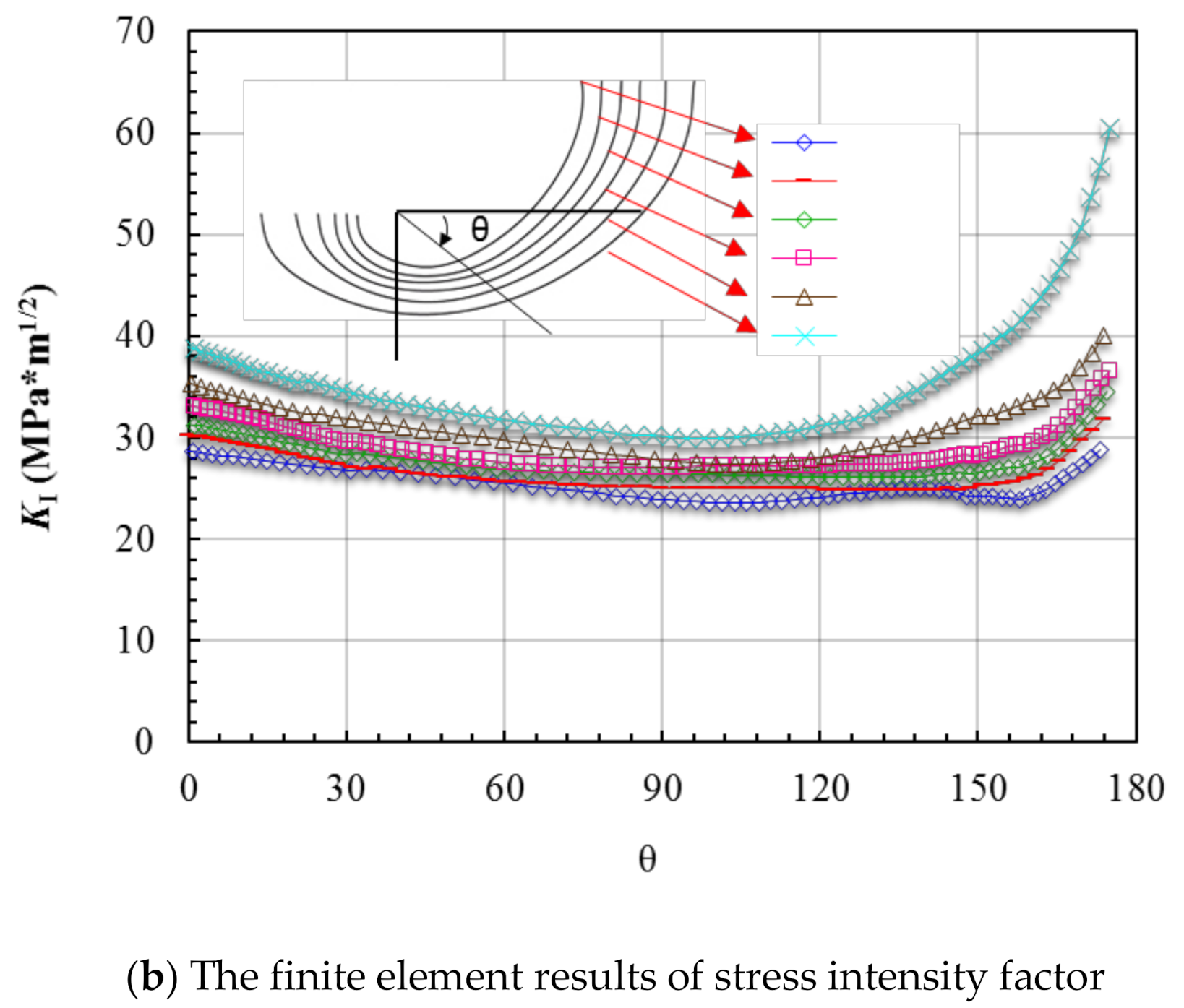
4.3. Validation and Errors Analysis
4.3.1. The Analysis of the First Stage during the Crack Growth Process
4.3.2. The Analysis of the Second Stage during the Crack Growth Process
4.3.3. The Analysis of the Third Stage during the Crack Growth Process
5. Conclusions
- The analytical formula for the first two stages has higher precision than that for the third stage.
- In the very beginning of the third stage, the analytical formula has comparatively low precision, and the precision increased as the fracture surface increased.
- When the curve of crack front is closed to a part of ellipse, the analytical formula gives fined precision. For the curve of crack front with curvature mutation, there is low precision at the curvature mutation location.
Author Contributions
Funding
Conflicts of Interest
References
- Williams, J.C. Titanium Alloys: Production, Behavior and Application; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Oguma, H.; Nakamura, T. Fatigue crack propagation properties of Ti–6Al–4V in vacuum environments. Int. J. Fatigue 2013, 50, 89–93. [Google Scholar] [CrossRef]
- Owolabi, G.; Okeyoyin, O.; Olasumboye, A.; Whitworth, H. A new approach to estimating the fatigue notch factor of Ti-6Al-4V components. Int. J. Fatigue 2016, 82, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Nalla, R.; Ritchie, R.; Boyce, B.; Campbell, J.; Peters, J. Influence of microstructure on high-cycle fatigue of Ti-6Al-4V: Bimodal vs. lamellar structures. Metall. Mater. Trans. A 2002, 33, 899–918. [Google Scholar] [CrossRef]
- Makabe, C.; Murdani, A.; Kuniyoshi, K.; Irei, Y.; Saimoto, A. Crack-growth arrest by redirecting crack growth by drilling stop holes and inserting pins into them. Eng. Fail. Anal. 2009, 16, 475–483. [Google Scholar] [CrossRef]
- Oguma, H.; Nakamura, T. The effect of microstructure on very high cycle fatigue properties in Ti–6Al–4V. Scr. Mater. 2010, 63, 32–36. [Google Scholar] [CrossRef] [Green Version]
- Campbell, J.; Ritchie, R. Mixed-mode, high-cycle fatigue-crack growth thresholds in Ti–6Al–4V: II. Quantification of crack-tip shielding. Eng. Fract. Mech. 2000, 67, 229–278. [Google Scholar] [CrossRef]
- Gunderson, A.; Gegel, H.; Lyon, S. Fatigue Behavior of Diffusion Bonded Ti-6A1-4V Having Very Small Defects. In Titanium Science and Technology; Springer: Berlin/Heidelberg, Germany, 1973; pp. 649–659. [Google Scholar]
- Kaibyshev, O.A.; Safiullin, R.V.; Lutfullin, R.; Valiakhmetov, O.R.; Galeyev, R.M.; Dutta, A.; Raghu, T.; Saha, G.G. Advanced superplastic forming and diffusion bonding of titanium alloy. Mater. Sci. Technol. 2006, 22, 343–351. [Google Scholar] [CrossRef]
- Derby, B.; Wallach, E. Theoretical model for diffusion bonding. Met. Sci. 1982, 16, 49–56. [Google Scholar] [CrossRef]
- Kazakov, N.F. Diffusion Bonding of Materials; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Dunford, D.V.; Wisbey, A. Diffusion Bonding of Advanced Aerospace Metallics; MRS Online Proceedings Library Archive: San Francisco, CA, USA, 1993. [Google Scholar]
- Wang, X.; Liu, W. Design and Application of Aircraft Titanium Alloy Structure; National Defense Industry Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- He, X.; Liu, W.; Sun, Y.; Wang, X. Fatigue crack growth characteristic for diffusion bonded laminates of titanium alloy with centered hole. Eng. Mech. 2015, 4, 244–249. (In Chinese) [Google Scholar]
- Liu, Y.; Zhang, Y.; Liu, S.; Xiao, S.; Sun, Y.; Wang, X. Effect of unbonded areas around hole on the fatigue crack growth life of diffusion bonded titanium alloy laminates. Eng. Fract. Mech. 2016, 1, 176–188. [Google Scholar] [CrossRef]
- He, X.; Dong, Y.; Li, Y.; Wang, X. Fatigue crack growth in diffusion-bonded Ti-6Al-4V laminate with unbonded zones. Int. J. Fatigue 2018, 106, 1–10. [Google Scholar] [CrossRef]
- Xiao, S.; Bi, J.; Sun, Y. XFEM-based analysis for crack growth characteristic of diffusion bonded laminate of titanium-alloy. Aeronaut Manuf. Technol. 2015, 17, 86–89. (In Chinese) [Google Scholar]
- Liu, Y.; Zhang, Y.; Liu, S.; Xiao, S.; Wang, X.; Sun, Y. XFEM-Based Analysis for Crack Growth Characteristics of Diffusion Bonded Laminates of Titanium Alloy with Localized Nonwelded Zone. Math. Prob. Eng. 2013, 10, 1256–1271. [Google Scholar] [CrossRef]
- Li, X.; Gai, P.; Zeng, Y.; Bi, J.; Shi, Y.; Liu, J. Manufacturing of titanium alloy laminated joint based on damage tolerance design. Aeronaut Manuf. Technol. 2015, 17, 66–68. (In Chinese) [Google Scholar]
- Gai, P.; Li, X.; Liu, J.; Han, X. Research on crack propagation characteristic for diffusion bonded laminates of titanium alloy. J. Plast. Eng. 2016, 5, 156–159. (In Chinese) [Google Scholar]
- Murakami, Y.; Keer, L.M. Stress intensity factors handbook, vol. 3. J. Appl. Mech. 1993, 60, 1063. [Google Scholar] [CrossRef] [Green Version]






| Element | Al | V | Fe | C | O | N | Ti |
|---|---|---|---|---|---|---|---|
| Content (%) | 5.5–6.75 | 3.5–4.5 | ≤0.5 | ≤0.1 | ≤0.2 | ≤0.05 | Bal. |
| Elastic Modulus | Ultimate Strength | Fracture Toughness | Poisson’s Ratio |
|---|---|---|---|
| ν | |||
| 110 | 913 | 78.3 | 0.34 |
| No. | b | a |
|---|---|---|
| 1 | 2.03 | 1.59 |
| 2 | 2.28 | 1.77 |
| 3 | 2.54 | 1.95 |
| 4 | 2.85 | 2.15 |
| 5 | 3.19 | 2.31 |
| 6 | 3.58 | 2.52 |
| No. | Formula 0° | Numerical 0° | Diff. (%) | Formula 90° | Numerical 90° | Diff. (%) |
|---|---|---|---|---|---|---|
| 1 | 23.51 | 21.90 | 7.39 | 28.94 | 30.09 | −3.81 |
| 2 | 24.27 | 23.60 | 2.88 | 29.95 | 30.98 | −3.30 |
| 3 | 25.04 | 23.03 | 8.75 | 30.91 | 28.99 | 6.62 |
| 4 | 25.95 | 23.43 | 10.76 | 31.78 | 29.63 | 7.26 |
| 5 | 27.03 | 26.08 | 3.66 | 32.36 | 30.05 | 7.69 |
| 6 | 28.14 | 26.62 | 5.74 | 33.11 | 31.48 | 5.17 |
| No. | Formula | Numerical (Average) | Diff. (%) |
|---|---|---|---|
| 1 | 29.17 | 29.29 | −0.42 |
| 2 | 29.40 | 29.28 | 0.42 |
| 3 | 29.67 | 29.39 | 0.98 |
| 4 | 30.02 | 29.43 | 2.01 |
| 5 | 30.45 | 29.59 | 2.90 |
| 6 | 30.79 | 29.52 | 4.30 |
| 7 | 31.11 | 29.86 | 4.16 |
| No. | Formula 180° | Numerical 180° | Diff. (%) | Formula (Average) | Numerical (Average) | Diff. (%) |
|---|---|---|---|---|---|---|
| 1 | 20.8 | 19.7 | 5.4 | 22.2 | 21.5 | 3.5 |
| 2 | 20.9 | 23.4 | −10.8 | 22.4 | 22.8 | −1.4 |
| 3 | 21.1 | 22.7 | −7.1 | 22.6 | 22.9 | −1.1 |
| 4 | 21.6 | 23.0 | −6.2 | 23.0 | 23.4 | −2.0 |
| 5 | 22.1 | 26.7 | −17.2 | 23.6 | 23.5 | 0.43 |
| 6 | 23.6 | 27.3 | −13.6 | 24.3 | 24.6 | −1.2 |
| No. | Formula 180° | Numerical 180° | Diff. (%) | Formula (Average) | Numerical (Average) | Diff. (%) |
|---|---|---|---|---|---|---|
| 7 | 24.9 | 28.7 | −13.2 | 25.0 | 25.3 | −1.4 |
| 8 | 27.6 | 31.8 | −13.1 | 26.6 | 26.5 | 0.090 |
| 9 | 31.3 | 34.4 | −9.1 | 28.2 | 27.8 | 1.5 |
| 10 | 36.2 | 36.6 | −0.95 | 29.9 | 29.1 | 2.7 |
| 11 | 45.0 | 40.0 | 12.4 | 32.2 | 31.2 | 3.0 |
| 12 | 65.0 | 60.4 | 7.5 | 35.6 | 35.9 | −1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, S. An Analytical Model for Predicting the Stress Intensity Factor of Single-Hole-Edge Crack in Diffusion Bonding Laminates with Preset Unbonded Area. Metals 2020, 10, 1526. https://doi.org/10.3390/met10111526
Liu Y, Liu S. An Analytical Model for Predicting the Stress Intensity Factor of Single-Hole-Edge Crack in Diffusion Bonding Laminates with Preset Unbonded Area. Metals. 2020; 10(11):1526. https://doi.org/10.3390/met10111526
Chicago/Turabian StyleLiu, Yang, and Shutian Liu. 2020. "An Analytical Model for Predicting the Stress Intensity Factor of Single-Hole-Edge Crack in Diffusion Bonding Laminates with Preset Unbonded Area" Metals 10, no. 11: 1526. https://doi.org/10.3390/met10111526
APA StyleLiu, Y., & Liu, S. (2020). An Analytical Model for Predicting the Stress Intensity Factor of Single-Hole-Edge Crack in Diffusion Bonding Laminates with Preset Unbonded Area. Metals, 10(11), 1526. https://doi.org/10.3390/met10111526




