Next Article in Journal
Renewable Hydrogen Production Processes for the Off-Gas Valorization in Integrated Steelworks through Hydrogen Intensified Methane and Methanol Syntheses
Previous Article in Journal
Geometric Optimization of Drills Used to Repair Holes in Magnesium Aeronautical Components
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 10
Issue 11
10.3390/met10111532
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Crystallization of FCC and BCC Liquid Metals Studied by Molecular Dynamics Simulation

by
Dmitri V. Louzguine-Luzgin
1,2,* and
Andrey I. Bazlov
3,4
1
WPI Advanced Institute for Materials Research, Tohoku University, Sendai 980-8577, Japan
2
Mathematics for Advanced Materials-OIL, National Institute of Advanced Industrial Science and Technology (AIST), Sendai 980-8577, Japan
3
Department of Physical Metallurgy of Non-Ferrous Metals, National University of Science and Technology “MISiS”, 119049 Moscow, Russia
4
Laboratory for Mechanics of Advanced Bulk Nanomaterials for Innovative Engineering Applications, St. Petersburg State University, 7/9 Universitetskaya nab., 199034 St. Petersburg, Russia
*
Author to whom correspondence should be addressed.
Metals 2020, 10(11), 1532; https://doi.org/10.3390/met10111532
Submission received: 6 October 2020 / Revised: 4 November 2020 / Accepted: 13 November 2020 / Published: 18 November 2020
(This article belongs to the Section Metal Casting, Forming and Heat Treatment)
Browse Figures
Versions Notes

Abstract

:
The atomic structure variations on cooling, vitrification and crystallization processes in liquid metals face centered cubic (FCC) Cu are simulated in the present work in comparison with body centered cubic (BCC) Fe. The process is done on continuous cooling and isothermal annealing using a classical molecular-dynamics computer simulation procedure with an embedded-atom method potential at constant pressure. The structural changes are monitored with direct structure observation in the simulation cells containing from about 100 k to 1 M atoms. The crystallization process is analyzed under isothermal conditions by monitoring density and energy variation as a function of time. A common-neighbor cluster analysis is performed. The results of thermodynamic calculations on estimating the energy barrier for crystal nucleation and a critical nucleus size are compared with those obtained from simulation. The differences in crystallization of an FCC and a BCC metal are discussed.

1. Introduction

Crystallization of metals and alloys from the melt (liquid state) takes place by nucleation and growth [1]. This process has occupied the minds of scientists for quite some time owing to still unresolved issues, especially related to high nucleation and growth rates of pure substances. Pure metals are known to exhibit a high crystal nucleation rate at a low enough temperature [1] and high growth rates in a wide temperature range [2]. Crystallization of different substances [3,4] including liquid metals [5] and alloys [6] has been studied by molecular-dynamics (MD) simulation with various potentials. Furthermore, MD simulation of glass transition of pure metals, such as Fe [7,8], Ni [9,10], Cu [11], Al [12] and other metals [13] has been performed. In a recent work possible heterogeneous nucleation of Fe was studied at 0.67Tm and 0.58Tm (Tm is the melting point which in pure metals is equal to the liquidus temperature Tl) [14]. However, one should mention that Tm of 2400 K given by the potential used is significantly overestimated compared to the experimental value. Recent embedded atom potentials provide a better correspondence to the experimental values. The crystallization behavior of other metals was also studied via MD simulation [15] and compared with the experimental data [16]. The energy barriers for crystallization of pure metals were also compared with those obtained from computer simulation [17]. In the present work the atomic structure variation, vitrification and crystallization processes in liquid metals (FCC Cu and BCC Fe) are simulated on continuous cooling and isothermal annealing using a classical MD computer simulation procedure with an embedded-atom method potential at constant pressure.

2. Computational Procedure

Molecular dynamics (MD) computer simulation using a software package for classical molecular dynamics (LAMMPS) [18] was used to model the crystallization process of Fe and Cu metals at periodic boundary conditions. The simulation was performed at 1 fs time step using the embedded atom potentials for Cu [19] and Fe [20] at nearly constant temperature and pressure. In order to let crystallization occur, the cubic cell size was typically chosen to be about 10 nm. A typical crystalline cell of the atoms containing 108,000 for FCC and 128,000 atoms for BCC structure was heated to of 2500 K to melt and then cooled down to a certain temperature. In some cases, larger sized cells were used as indicated. Melting is confirmed by the radial distribution function and stabilization of the density variation with time. Cooling was performed to different temperatures at about 5 × 1013 K/s. Temperature upon simulation was maintained at ±6 K (Figure 1) while pressure was kept around zero.
Neither Fe nor Cu evaporated in the molten state as should have happened at zero pressure, likely because there was not enough time for a gaseous phase to nucleate from inside the atomic cell (a gaseous phase has to overcome an energy barrier to be formed as well as a crystalline one) and absence of the surfaces owing to periodic boundary conditions. A thermostat was used to control the temperature [21,22] while pressure was maintained by a Barostat [23]. A software package “OVITO” [24] was used to visualize and analyze the simulation results. Adaptive Common Neighbor Analysis (CNA) [25] was used to analyze structural changes in Fe and Cu.

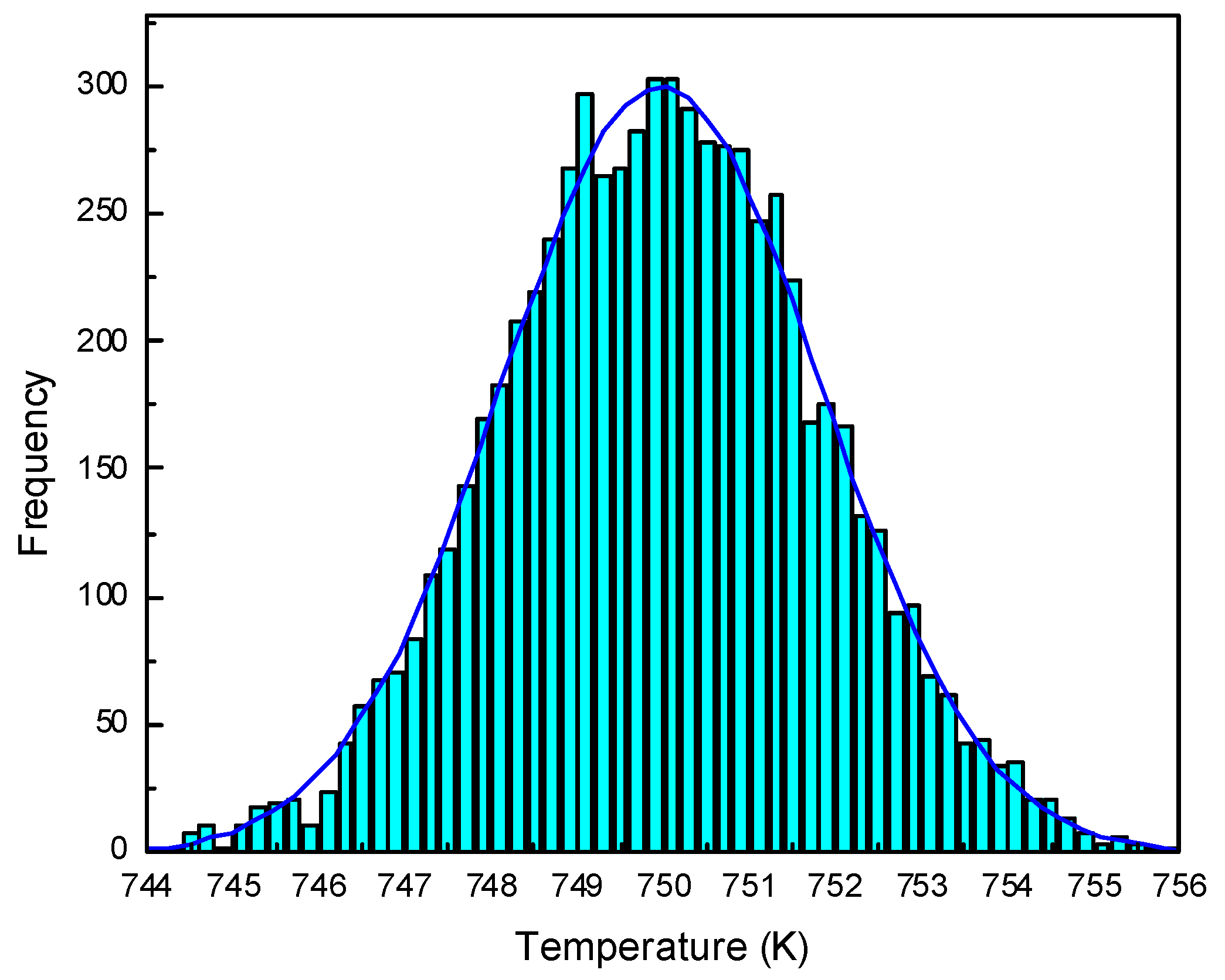
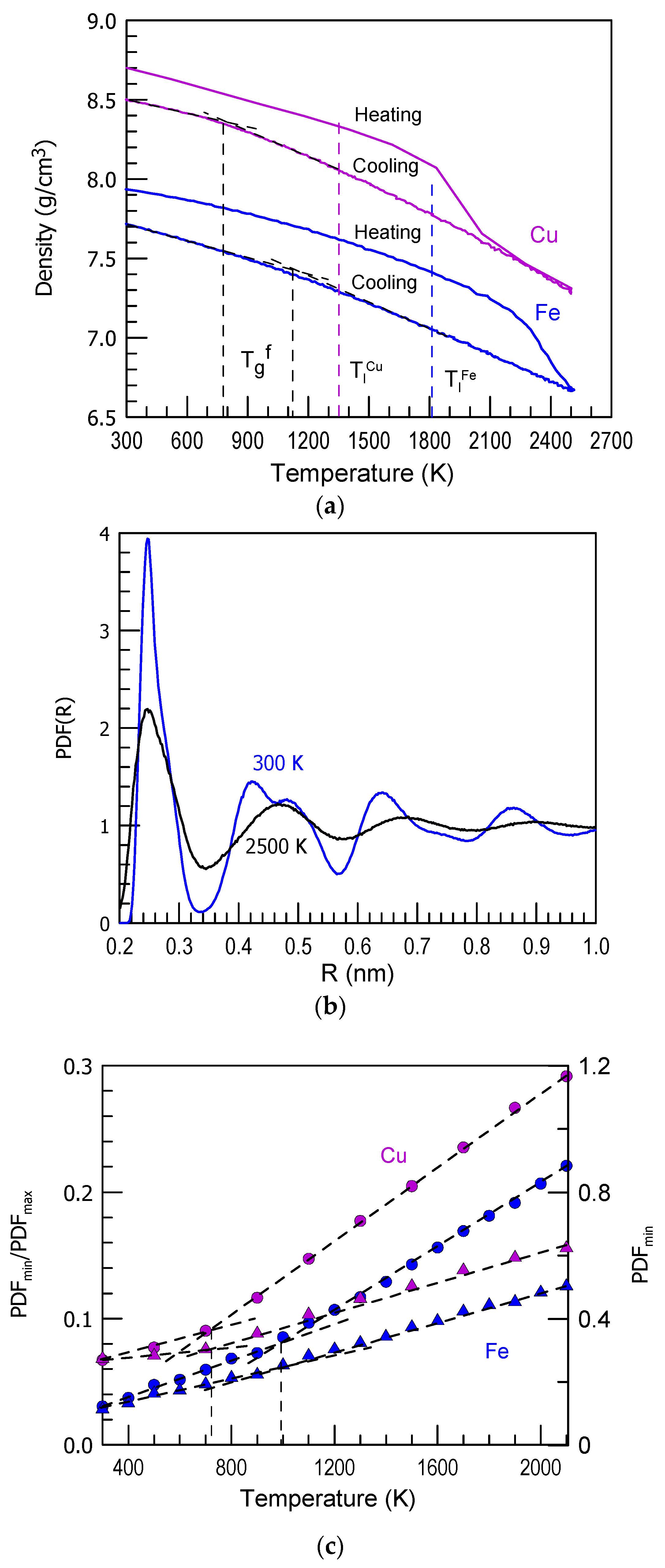
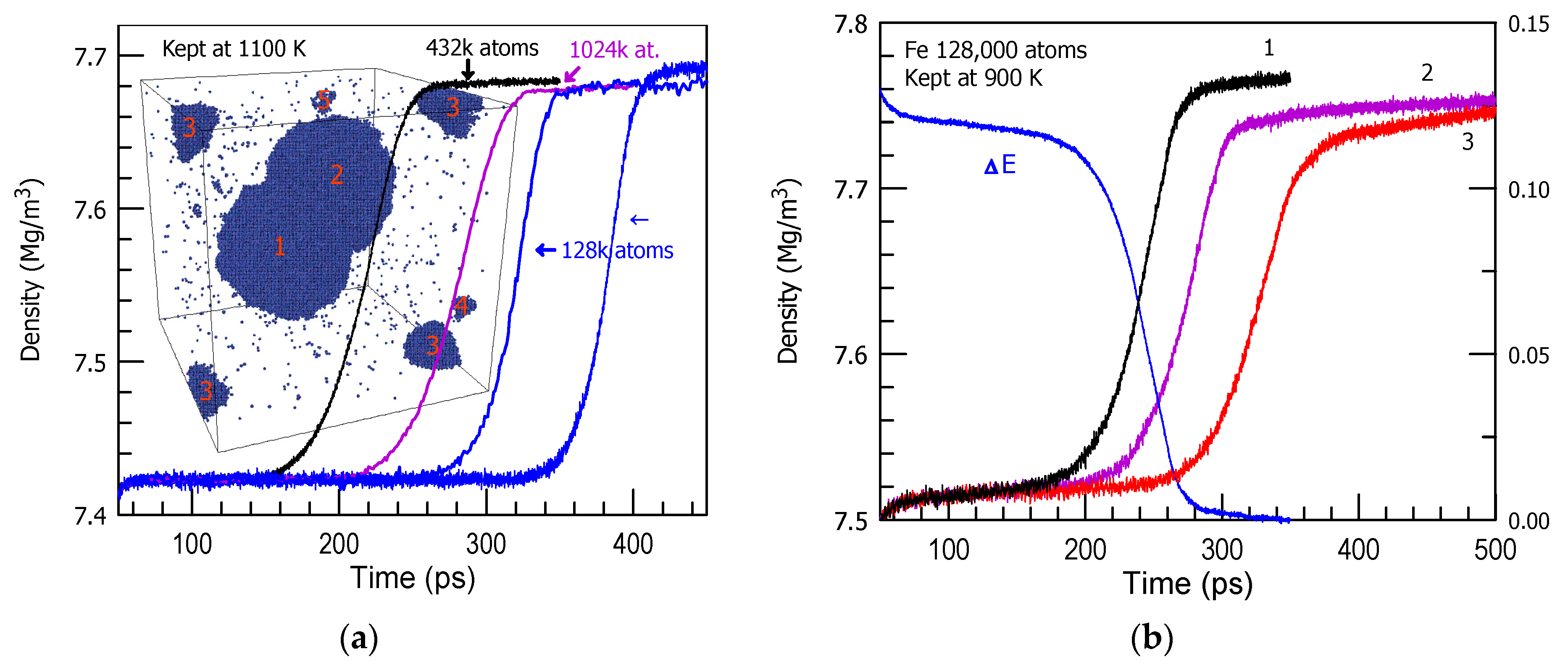
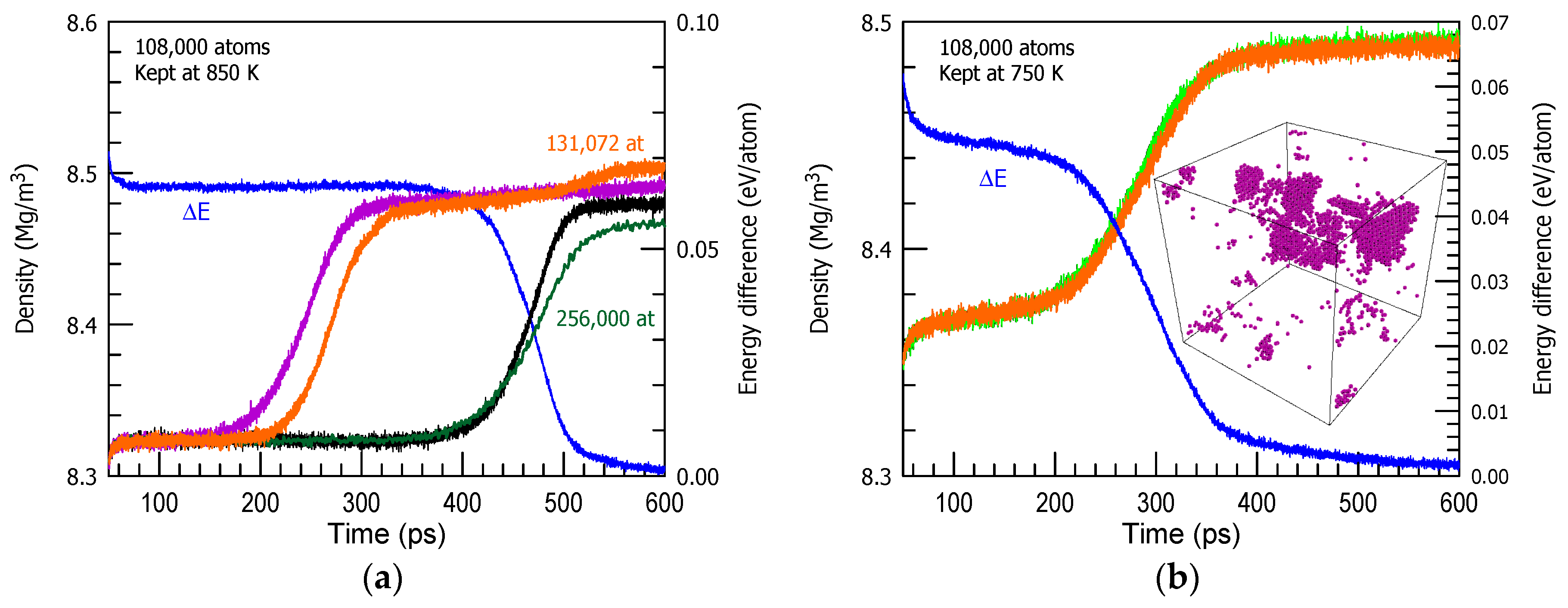
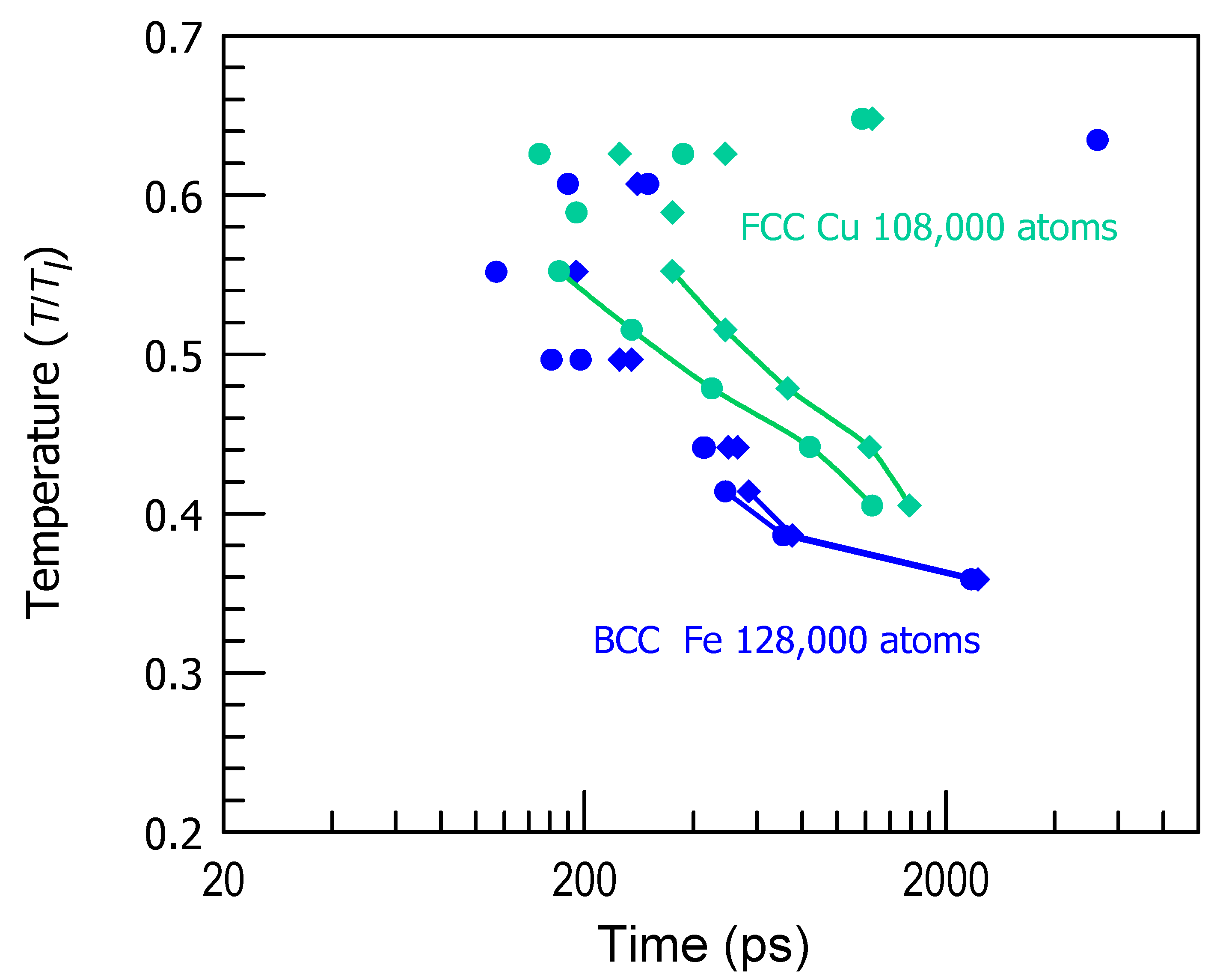
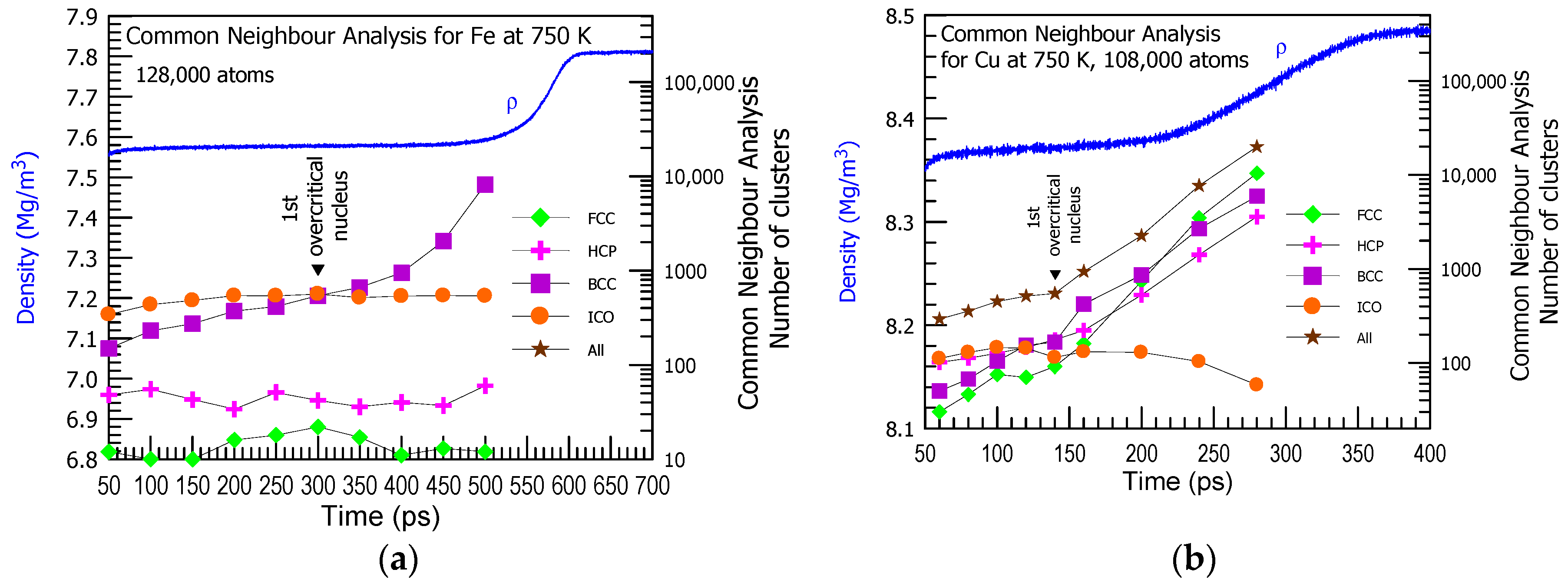
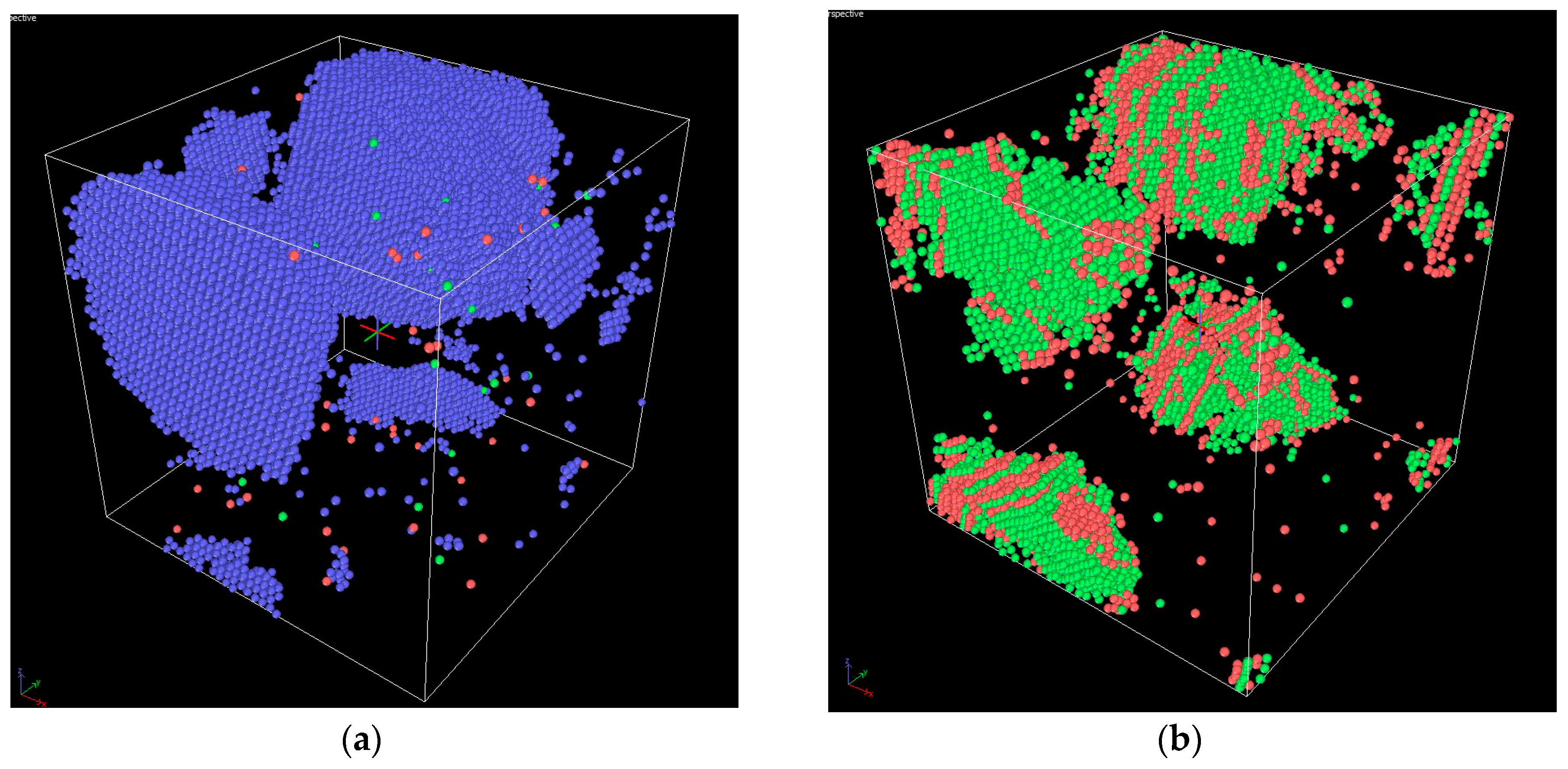
3. Results and Discussion

The density changes on heating and cooling as a function of temperature are illustrated in Figure 2a. Equilibrium liquid state was obtained at 2500 K in less than 1 ps. The holding time was also varied from 1 to 100 ps without visible changes in the liquid structure and density. Thus, the atomic cells have been kept for at least 10 ps at 2500 K prior to cooling.
Vitrification of both Fe and Cu liquids was attained at the cooling rate of about 5 × 1013 K/s (Figure 2). At the cooling rate of 5 × 1012 K/s and lower the studied metals start to crystallize directly on cooling. Similarly, high critical cooling rate values indicating high instability of the supercooled liquid were obtained in other works [13,26,27]. However, theoretical calculations [28] and the experimental results [29] suggest a lower critical cooling rate (of about 109 K/s) for glass-transition in pure metals, especially with BCC lattice. The difference could be connected with the type of potentials used.
The values of glass-transition temperature (Tg) defined by the change of the density as a function of temperature slope are about 1100 K for Fe and 800 K for Cu (Figure 2a). Of course, these values correspond to this very high cooling rate used when viscosity is still low. However, the value for Fe corresponds quite well to the isochoric conditions when the volume of the liquid becomes similar to that of the crystalline phase [30]. Two typical pair distribution functions (PDF) for Fe are shown in Figure 2b. The values of Tg derived from PDFmin [31] and ratios of PDFmin/PDFmax [32] are shown in Figure 2c. These values are about 100 K lower than those obtained from Figure 2a. As one can see for Fe, having a BCC lattice at room temperature has much lower PDFmin value compared to Cu which has an FCC lattice. It resembles the crystalline structure: there is a deeper gap between the coordination shells in BCC lattice. Splitting of the first and second pair distribution function (PDF(R)) maxima into two peaks is clearly observed in Figure 2b. It indicates short- and medium-range ordering of the liquid and glassy phases on cooling and that glassy Cu and Fe inherit the short-range order of the corresponding crystals.
Phase transformation kinetics for Fe and Cu are shown in Figure 3; Figure 4, respectively, by monitoring the density changes. Energy of the system changes in the way opposite to density. Please, note that the final product density is different from case to case owing to different fractions of the internal defects. Full system equilibration upon crystallization requires much longer time. While at 1100 K and above the density, volume and energy values are visibly stable within the incubation period (relaxation proceeds in 10 ps for liquid Fe at 1100 K) (Figure 3a), these values gradually change at a lower temperature owing to structural relaxation at low atomic mobility. The structure relaxation time becomes longer than the simulation time below 1100 K for Fe which corresponds quite well to the equivolume/isochoric glass-transition temperature determined before [30]. It also takes place at about 800 K for Cu when the density and energy of the system gradually change with time prior to crystallization. Both BCC and FCC crystals nucleate directly from the melt and no two-stage nucleation [33] is found.
As can be found for pure Fe in Figure 3, the incubation time (defined as an intersection of two tangents to the plot before and after the onset time) changes irregularly with the atomic cell size owing to stochastic character of nucleation. In a cell containing 432,000 atoms, two overcritical nuclei nucleated at about 120 ps. In a cell containing 1,024,000 atoms, the first nucleus was formed at 150 ps, the second at 170 ps, the third at 210 ps, the fourth at 230 ps and the fifth at 240 ps. If one assumes total nucleation time of 90 ps for four nuclei per a cell of 23 nm size, then the average homogeneous nucleation rate is 3.7 × 1033 m−3·s−1. It is a high value but quite close to that reported in an earlier work [8]. The growing nanocrystals have irregular but nearly spherical shape. In a cell containing 128,000 atoms, the first overcritical stably growing nucleus was formed at 280 ps and consumed the entire volume at about 410 ps. Thus, at these temperatures (1100 and 900 K which are 0.61 Tl and 0.50 Tl, respectively; when the liquidus temperature Tl = 1811 K) crystallization of Fe is hardly statistically predictable, and it is not so sensitive to the cell size if its length exceeds about 10 nm. BCC Cu at 750 K (which is 0.55 Tl) has even higher homogeneous nucleation rate of 8 × 1034 m−3s−1. At the homological temperature higher than 0.65 Tl crystallization of Cu and Fe is not detectable within 3 ns of maximum simulation time.
Owing to rather high nucleation rates, the isothermal crystallization curves can be statistically well reproduced below 0.55 Tl for Cu (Figure 4b) and below 0.4 Tl for Fe at the chosen atomic cells. An average incubation time is about 2 times longer than that on pure Ni studied earlier [34]. From this viewpoint Ni is a special liquid which is the least stable against crystallization among these metals. Furthermore, in spite of the fact that the nucleation barrier is quite high in pure Ni the nucleation rate is also high attributed to the high atom attachment kinetics [35].
From the isothermal crystallization plots, the beginning, also called an incubation time, and finish time of transformation can be calculated using two corresponding tangents to the plot before and after the inflection point. Note that actual transformation time is longer because the two tails of the S-curve are not taken into consideration when two tangents are applied. However, it becomes more difficult to detect the incubation period for each plot below 700 K owing to the long relaxation time manifested in constant variation of the baseline. Nevertheless, a time-temperature-transformation (TTT) diagram was constructed, and it is shown in Figure 5. The simulation results are well reproduced (owing to high nucleation rate) below 0.55 Tl for Cu and below 0.4 Tl for Fe. The nose of the TTT diagram is about 0.55 Tl for Fe and about 0.6 Tl for Cu.
According to adaptive common neighbor analysis (Figure 6), crystallization becomes detectable by volume and energy changes when the fraction of atoms in crystalline clusters attains about 2%. The increase in the numbers of atoms with the icosahedral-like configuration prior to the nucleation of crystalline phases found in earlier works [36,37] is not seen in the present study (see Figure 6). Although only BCC crystals form and grow in Fe FCC, BCC and hexagonal close packed (HCP) atomic arrangements are found in Cu owing to low stacking fault energy of this metal (well estimated experimentally) as seen in Figure 7.
Typical growth rates (crystal radius change as a function of time) are shown in Table 1. The growth rates are lower than those found earlier in simulations [15]. The growth rate of FCC Cu crystals is less temperature dependent than that of BCC Fe. Furthermore, one should note that some growing particles have much lower growth rate owing to interaction with other nuclei (even under-critical) [38]. At the same time the observed growth rate values for Fe are quite close to the experimental ones of 40 m/s [39]. The observed growth rate of the order of tens meters per second are lower than those obtained for flat interfaces.
A liquid/solid interfacial energy (σ) value of 0.37 J/m2 is obtained in the present work for Fe at 1100 K as an excess energy per surface area of a single particle of 1.8 nm radius. It is calculated taking into account the potential energy difference of 23.7 eV at 170 ps of the simulation time between its value for the entire atomic cell and a sum of that energy values for the atoms belonging to a crystalline particle of about 3.6 nm diameter formed at that stage (1657 atoms) and the potential energy of the other atoms in the cell belonging to liquid phase (128,000−1657 = 126,343 atoms). The potential energy for the liquid part of the atomic cell was obtained at the 50 ps stage when all atoms belonged to the supercooled liquid phase while that of a crystal was taken for fully crystalline state on heating the initial perfect crystal to 1100 K. The value of 0.33 J/m2 for the Cu crystal at 850 K is found in a similar way. These values are not too far from the experimental values of 0.28 and 0.18 J/m2 obtained for Fe and Cu, respectively [1]. Please note that although the calculated values are somewhat overestimated owing to the internal defects in the growing crystals, the value for Fe is still higher than that for Cu. The earlier simulation results indicated that the crystal–melt interfacial energy calculated from a planar interface needs to be adjusted to a smaller value in order to predict the correct nucleation rate at deep supercooling [40].
Calculation of the critical nucleus size (Rc) and work for the formation of critical nucleus (W*) was done according to classical nucleation theory:
Rc = 2σ/ΔGv
W* = 16πσ3/(3ΔGv2)
Using the Gibbs free energy difference (ΔGv). σ values of 0.277 J/m2 for Fe and 0.178 J/m2 for Cu were obtained from Ref. [1]. The temperature dependences of enthalpies of liquid and crystalline phases were used to estimate the enthalpy of melting at about 1809 K. The enthalpy difference of 0.164148 eV/at or 15.837 kJ/mol found for Fe is not far from the experimental value of 15.2 kJ/mol [1]. The value of 13 kJ/mol was used for Cu [1]. ΔGv can be estimated from the liquid crystallization enthalpy (ΔHc) and the liquidus temperatures Tl using the following equation [41]:
ΔGv = (ΔHc·ΔT/Tl)·(7T/(Tl + 6T))
According to thermodynamic calculations the critical nucleus radius in the studied temperature range is about 0.4–0.6 nm for Cu and for 0.5–0.6 nm Fe. Steadily growing particles found in this simulation were larger than 0.8 nm in size. At such small size the energy barrier W* to the thermal energy RT ratio is about 20 for Cu and about 30 for Fe. A higher energy barrier found for Fe is rather responsible for a lower number of nuclei found for Fe at the same homological temperature. It is interesting to note that even at such high energy barriers homogeneous nucleation takes place after hundreds of picoseconds.
The number of crystal nuclei formed within the typical cells of about 10 nm length in all metals ranges from 1 to 10, leading to the number density of precipitates of the order of 1024 m−3. The highest number density of nuclei is observed in Cu which leads to better reproducibility of the crystallization traces at different simulation runs. Such high number densities of precipitates are more or less typical for crystallization of pure metals at extremely low homological temperatures of about 0.55 Tl or lower, which are unattainable in the experiments on undercooling but quite common in various metallic glasses which nanocrystallize in a similar temperature range [42,43].

4. Conclusions

Liquid structure variation of cooling and glass transition indicated that glassy Cu and Fe inherit the short-range order of the corresponding crystals. Nevertheless, a nucleation and growth type (with an energy barrier) phase transformation is observed. The crystallization kinetics of FCC Cu and BCC Fe were analyzed in isothermal conditions by monitoring the density and energy variation as a function of time, and a TTT diagram was constructed. BCC Fe shows a lower number density of precipitates than FCC Cu. A higher energy barrier for nucleation found for Fe is rather responsible for a lower number of nuclei found for Fe at the same homological temperature. On the other hand, BCC Fe, in general, shows a shorter incubation period than FCC Cu and generally a higher growth rate though the nucleation rate of Cu crystals at a higher rate. The nose of the TTT diagram is about 0.55 Tl for Fe and about 0.6 Tl for Cu. Homogeneous nucleation of both metals becomes difficult to detect above about 0.65 Tl within a reasonable simulation time scale, while below ~0.6 Tl a high population density of crystalline precipitates is obtained. The growing nanocrystals have an irregular but nearly spherical shape. The observed growth rates of the order of tens meters per second are lower than those obtained for flat interfaces. Some of the crystalline particles displayed a lower growth rate than the others owing to the lattice defects within the growing crystals and existing order in the supercooled liquid. The crystal growth rate was scattered from crystal to crystal likely owing to the local order in surrounding environment and the lattice defects (mostly HCP staking faults) within the growing crystals in Cu. According to thermodynamic calculations the critical nucleus radius in the studied temperature range is about 0.4–0.6 nm for Cu and for 0.5–0.6 nm Fe. The energy barrier to the thermal energy ratio is about 20 for Cu and about 30 for Fe.

Author Contributions

Conceptualization, D.V.L.-L. and A.I.B.; methodology, D.V.L.-L.; software, D.V.L.-L.; validation, D.V.L.-L. and A.I.B.; formal analysis, D.V.L.-L. and A.I.B.; investigation, D.V.L.-L. and A.I.B.; resources, D.V.L.-L. and A.I.B.; data curation, D.V.L.-L. and A.I.B.; writing—original draft preparation, D.V.L.-L. and A.I.B.; writing—review and editing, D.V.L.-L. and A.I.B.; visualization, D.V.L.-L. and A.I.B.; supervision, D.V.L.-L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the World Premier International Research Center Initiative (WPI), MEXT, without a particular number, Program to Increase the Competitiveness of NUST “MISiS”, grant number K2-2020-006 and partly by RFBR, project number 19-33-60078.

Acknowledgments

The authors gratefully acknowledge the financial support received from the World Premier International Research Center Initiative (WPI), MEXT, Japan Science of the Russian Federation in the framework of the Program to Increase the Competitiveness of NUST “MISiS” (K2-2014-013 and K2-2020-006) and partly by RFBR, project number 19-33-60078.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kelton, K.F.; Greer, A.L. Nucleation in condensed matter applications in materials and biology. Pergamon Mater. Ser. 2010, 15, 1–743. [Google Scholar]
  2. Orava, J.; Greer, A.L. Fast and slow crystal growth kinetics in glass-forming melts. J. Chem. Phys. 2014, 140, 214504. [Google Scholar] [CrossRef]
  3. Buckle, E.R. Studies on the freezing of pure liquids. II. The kinetics of homogeneous nucleation in supercooled liquids. Proc. R. Soc. A 1961, 261, 189–196. [Google Scholar]
  4. Van Duijneveldt, J.S.; Frenkel, D. Computer simulation study of free energy barriers in crystal nucleation. J. Chem. Phys. 1992, 96, 4655. [Google Scholar] [CrossRef] [Green Version]
  5. E, J.C.; Wang, L.; Cai, Y.; Wu, H.A.; Luo, S.N. Crystallization in supercooled liquid Cu: Homogeneous nucleation and growth. J. Chem. Phys. 2015, 142, 064704. [Google Scholar] [CrossRef] [PubMed]
  6. Wang, Z.; Chen, C.L.; Ketov, S.V.; Akagi, K.; Tsarkov, A.A.; Ikuhara, Y.; Louzguine-Luzgin, D.V. Local chemical ordering within the incubation period as a trigger for nanocrystallization of a highly supercooled Ti-based liquid. Mater. Des. 2018, 156, 504–513. [Google Scholar] [CrossRef]
  7. Evteev, A.V.; Kosilov, A.T.; Levchenko, E.V. Atomic mechanisms of pure iron vitrification. J. Exp. Theor. Phys. 2004, 99, 522–529. [Google Scholar] [CrossRef]
  8. Okita, S.; Verestek, W.; Sakane, S.; Takaki, T.; Ohnoe, M.; Shibuta, Y. Molecular dynamics simulations investigating consecutive nucleation, solidification and grain growth in a twelve-million-atom Fe-system. J. Cryst. Growth 2017, 474, 140–145. [Google Scholar] [CrossRef]
  9. Jakse, N.; Pasturel, A. Ab initio molecular dynamics simulations of local structure of supercooled Ni. J. Chem. Phys. 2004, 120, 6124. [Google Scholar] [CrossRef]
  10. Louzguine-Luzgin, D.V.; Belosludov, R.; Saito, M.; Kawazoe, Y.; Inoue, A. Glass-transition behavior of Ni. Calculation, prediction and experiment. J. Appl. Phys. 2008, 104, 123529. [Google Scholar] [CrossRef]
  11. Fang, H.Z.; Hui, X.; Chen, G.L.; Liu, Z.K. Structural evolution of Cu during rapid quenching by ab initio molecular dynamics. Phys. Lett. A 2008, 372, 5831–5837. [Google Scholar] [CrossRef]
  12. Kirova, E.; Norman, G.E.; Pisarev, V. Simulation of the glass transition of a thin aluminum melt layer at ultrafast cooling under isobaric conditions. JETP Lett. 2019, 110, 359–363. [Google Scholar] [CrossRef]
  13. Han, J.J.; Wang, C.P.; Liu, X.J.; Wang, Y.; Liu, Z.-K.; Zhang, T.-Y.; Jiang, J.Z. Abnormal correlation between phase transformation and cooling rate for pure metals. Sci. Rep. 2016, 6, 22391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Shibuta, Y.; Sakane, S.; Miyoshi, E.; Okita, S.; Takaki, T.; Ohno, M. Heterogeneity in homogeneous nucleation from billion-atom molecular dynamics simulation of solidification of pure metal. Nat. Commun. 2017, 8, 10. [Google Scholar] [CrossRef] [PubMed]
  15. Ashkenazy, Y.; Averback, R.S. Kinetic stages in the crystallization of deeply undercooled body-centered-cubic and face-centered-cubic metals. Acta Mater. 2010, 58, 524–530. [Google Scholar] [CrossRef]
  16. Wilde, G.; Sebright, J.L.; Perepezko, J.H. Bulk liquid undercooling and nucleation in gold. Acta Mater. 2006, 54, 4759–4769. [Google Scholar] [CrossRef]
  17. Bokeloh, J.; Wilde, G.; Rozas, R.E.; Benjamin, R.; Horbach, J. Nucleation barriers for the liquid-to-crystal transition in simple metals: Experiment vs. Simulation. Eur. Phys. J. Spec. Top. 2014, 223, 511–526. [Google Scholar] [CrossRef]
  18. Plimpton, S.J. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1. [Google Scholar] [CrossRef] [Green Version]
  19. Mendelev, M.I.; Kramer, M.J.; Becker, C.A.; Asta, M. Analysis of semi-empirical interatomic potentials appropriate for simulation of crystalline and liquid Al and Cu. Philos. Mag. 2008, 88, 1723–1750. [Google Scholar] [CrossRef]
  20. Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. A 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
  21. Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef] [Green Version]
  22. Hoover, W.G. Canonical dynamics, Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1965. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
  24. Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool, Modelling Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar]
  25. Honeycutt, J.D.; Andersen, H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
  26. Zhong, L.; Wang, J.; Sheng, H.; Zhang, Z.; Mao, S.X. Formation of monatomic metallic glasses through ultrafast liquid quenching. Nature 2014, 512, 177–180. [Google Scholar] [CrossRef]
  27. Russo, J.; Tanaka, H. The microscopic pathway to crystallization in supercooled liquids. Sci. Rep. 2012, 2, 505. [Google Scholar] [CrossRef] [Green Version]
  28. Belousov, O.K. Estimation of the critical glass transition rate and the inorganic glass thickness. Russ. Metall. Met. 2009, 2009, 488–497. [Google Scholar] [CrossRef]
  29. Kim, Y.W.; Lin, H.M.; Kelly, T.F. Amorphous solidification of pure metals in submicron spheres. Acta Metall. 1989, 37, 247–255. [Google Scholar] [CrossRef]
  30. Louzguine-Luzgin, D.V.; Inoue, A. An extended criterion for estimation of glass-forming ability of metals. J. Mater. Res. 2007, 22, 1378–1383. [Google Scholar] [CrossRef]
  31. Ojovan, M.I.; Louzguine-Luzgin, D.V. Revealing structural changes at glass transition via radial distribution functions. J. Phys. Chem. B 2020, 124, 3186–3194. [Google Scholar] [CrossRef] [PubMed]
  32. Wendt, H.H.; Abraham, F.F. Empirical criterion for the glass transition region based on Monte Carlo simulations. Phys. Rev. Lett. 1978, 41, 1244–1246. [Google Scholar] [CrossRef]
  33. Sosso, G.S.; Chen, J.; Cox, S.J.; Fitzner, M.; Pedevilla, P.; Zen, A.; Michaelides, A. Nucleation in liquids: Open questions and future challenges in molecular dynamics simulations. Chem. Rev. 2016, 116, 7078–7116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Louzguine-Luzgin, D.V.; Miyama, M.; Nishio, K.; Tsarkov, A.A.; Greer, A.L. Vitrification and nanocrystallization of pure liquid Ni studied using molecular-dynamics simulation. J. Chem. Phys. 2019, 151, 124502. [Google Scholar] [CrossRef] [PubMed]
  35. Song, H.; Sun, Y.; Zhang, F.; Wang, C.Z.; Ho, K.M.; Mendelev, M.I. Nucleation of stoichiometric compounds from liquid: Role of the kinetic factor. Phys. Rev. Mater. 2018, 2, 023401. [Google Scholar] [CrossRef]
  36. Kurtuldu, G.; Sicco, A.; Rappaz, M. Icosahedral quasicrystal-enhanced nucleation of the fcc phase in liquid gold alloys. Acta. Mater. 2014, 70, 240–248. [Google Scholar] [CrossRef] [Green Version]
  37. Rappaz, M.; Kurtuldu, G. Quasicrystal-enhanced nucleation during the solidification of fcc metallic alloys: A tentative thermodynamic approach. J. Phase Equilib. Diffus. 2016, 37, 2–3. [Google Scholar] [CrossRef] [Green Version]
  38. Kirova, E.; Pisarev, V. System size effect on crystal nuclei morphology in supercooled metallic melt. J. Cryst. Growth 2019, 528, 125266. [Google Scholar] [CrossRef]
  39. Herlach, D.M. Containerless undercooling and solidification of pure metals. Annu. Rev. Mater. Sci. 1991, 21, 23–44. [Google Scholar] [CrossRef]
  40. Bai, X.-M.; Li, M. Comparing crystal–melt interfacial free energies through homogeneous nucleation rates. J. Phys. Condens. Matter 2008, 20, 375103. [Google Scholar] [CrossRef]
  41. Herlach, D.M. Non-equilibrium solidification of undercooled metallic melts. Mater. Sci. Eng. R 1994, 12, 177–272. [Google Scholar] [CrossRef]
  42. Louzguine-Luzgin, D.V.; Inoue, A. Observation of linear defects in Al particles below 7 nm in size. J. Mater. Res. 2006, 21, 1347. [Google Scholar] [CrossRef]
  43. Wang, Z.; Ketov, S.V.; Chen, C.L.; Shen, Y.; Ikuhara, Y.; Tsarkov, A.A.; Louzguine-Luzgin, D.V.; Perepezko, J.H. Nucleation and thermal stability of an icosahedral nanophase during the early crystallization stage in Zr-Co-Cu-Al metallic glasses. Acta Mater. 2017, 132, 298–306. [Google Scholar] [CrossRef]
Metals 10 01532 g001 550
Figure 1. Frequency distribution of temperature for Cu held at 750 K fitted with the Gaussian function with R2 > 0.99. The results were similar for all other cases.
Figure 1. Frequency distribution of temperature for Cu held at 750 K fitted with the Gaussian function with R2 > 0.99. The results were similar for all other cases.
Metals 10 01532 g001
Metals 10 01532 g002 550
Figure 2. Density changes on heating and cooling of Cu and Fe as a function temperature (a). Pair distribution functions (PDFs) of Fe in liquid (2500 K) and glassy (300 K) state (b). The values of pair distribution function first minimum PDFmin (●) and ratios of PDFmin/PDFmax (▲) (c) for Cu (violet) and Fe (blue).
Figure 2. Density changes on heating and cooling of Cu and Fe as a function temperature (a). Pair distribution functions (PDFs) of Fe in liquid (2500 K) and glassy (300 K) state (b). The values of pair distribution function first minimum PDFmin (●) and ratios of PDFmin/PDFmax (▲) (c) for Cu (violet) and Fe (blue).
Metals 10 01532 g002
Metals 10 01532 g003 550
Figure 3. Density change as a function of time for pure Fe at 1100 K (different atomic cell size used as indicated) (a) and 900 K (b) (three simulations, same cell size of 128,000 atoms). Inset in (a) shows an atomic cell of 1.024 million atoms at 250 ps containing 5 growing nuclei as marked. (b) also shows the total energy difference (ΔE) for graph 1 for comparison. Initial 50 ps are related to heating and cooling time.
Figure 3. Density change as a function of time for pure Fe at 1100 K (different atomic cell size used as indicated) (a) and 900 K (b) (three simulations, same cell size of 128,000 atoms). Inset in (a) shows an atomic cell of 1.024 million atoms at 250 ps containing 5 growing nuclei as marked. (b) also shows the total energy difference (ΔE) for graph 1 for comparison. Initial 50 ps are related to heating and cooling time.
Metals 10 01532 g003
Metals 10 01532 g004 550
Figure 4. Density change as a function of time for pure Cu at 850 K (a) and 750 K (b) for 108,000 atoms per cell. (b) also indicates the energy difference (ΔE) in blue for one plot. The insert indicates the atomic cell at 270 ps with atoms belonging to FCC clusters only. The initial 50 ps are related to heating, melting and cooling time.
Figure 4. Density change as a function of time for pure Cu at 850 K (a) and 750 K (b) for 108,000 atoms per cell. (b) also indicates the energy difference (ΔE) in blue for one plot. The insert indicates the atomic cell at 270 ps with atoms belonging to FCC clusters only. The initial 50 ps are related to heating, melting and cooling time.
Metals 10 01532 g004
Metals 10 01532 g005 550
Figure 5. Time-temperature-transformation (TTT) diagram for Fe (blue) and Cu (green). Circles indicate beginning of crystallization while diamonds show end of crystallization.
Figure 5. Time-temperature-transformation (TTT) diagram for Fe (blue) and Cu (green). Circles indicate beginning of crystallization while diamonds show end of crystallization.
Metals 10 01532 g005
Metals 10 01532 g006 550
Figure 6. Adaptive common neighbor cluster analysis for Fe (a) and Cu (b) cells at 750 K together with the density (ρ) curve (blue) as a function of time.
Figure 6. Adaptive common neighbor cluster analysis for Fe (a) and Cu (b) cells at 750 K together with the density (ρ) curve (blue) as a function of time.
Metals 10 01532 g006
Metals 10 01532 g007 550
Figure 7. Growing crystalline particles (a) of BCC Fe at 900 K (blue) and FCC Cu (green) at 850 K (b). HCP stacking faults are shown in red.
Figure 7. Growing crystalline particles (a) of BCC Fe at 900 K (blue) and FCC Cu (green) at 850 K (b). HCP stacking faults are shown in red.
Metals 10 01532 g007
Table
Table 1. Typical growth rates (UN) values at some temperatures for the studied metals estimated from an average single crystal radius measured in two mutually perpendicular directions.
Table 1. Typical growth rates (UN) values at some temperatures for the studied metals estimated from an average single crystal radius measured in two mutually perpendicular directions.
MetalT (K)UN (m/s)
Fe110048
90020
Cu85018
75016
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Louzguine-Luzgin, D.V.; Bazlov, A.I. Crystallization of FCC and BCC Liquid Metals Studied by Molecular Dynamics Simulation. Metals 2020, 10, 1532. https://doi.org/10.3390/met10111532

AMA Style

Louzguine-Luzgin DV, Bazlov AI. Crystallization of FCC and BCC Liquid Metals Studied by Molecular Dynamics Simulation. Metals. 2020; 10(11):1532. https://doi.org/10.3390/met10111532

Chicago/Turabian Style

Louzguine-Luzgin, Dmitri V., and Andrey I. Bazlov. 2020. "Crystallization of FCC and BCC Liquid Metals Studied by Molecular Dynamics Simulation" Metals 10, no. 11: 1532. https://doi.org/10.3390/met10111532

APA Style

Louzguine-Luzgin, D. V., & Bazlov, A. I. (2020). Crystallization of FCC and BCC Liquid Metals Studied by Molecular Dynamics Simulation. Metals, 10(11), 1532. https://doi.org/10.3390/met10111532

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop